Στοιχεῖα Εὐκλείδου θ΄

[Βιβλίον IX]

Αἱ Προτάσεις τῶν Στοιχείων θ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις κ΄. [20]

Οἱ πρῶτοι ἀριθμοὶ πλείους εἰσὶ παντὸς τοῦ προτεθέντος πλήθους πρώτων ἀριθμῶν.

Ἔστωσαν οἱ προτεθέντες πρῶτοι ἀριθμοὶ οἱ Α, Β, Γ· λέγω, ὅτι τῶν Α, Β, Γ πλείους εἰσὶ πρῶτοι ἀριθμοί.

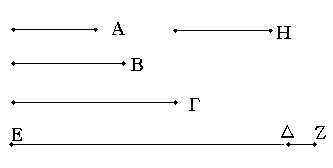
Εἰλήφθω γὰρ ὁ ὑπὸ τῶν Α, Β, Γ ἐλάχιστος μετρούμενος καὶ ἔστω ὁ ΔΕ, καὶ προσκείσθω τῷ ΔΕ μονὰς ἡ ΔΖ. ὁ δὴ ΕΖ ἤτοι πρῶτός ἐστιν ἢ οὔ. ἔστω πρότερον πρῶτος· εὑρημένοι ἄρα εἰσὶ πρῶτοι ἀριθμοὶ οἱ Α, Β, Γ, ΕΖ πλείους τῶν Α, Β, Γ.

Ἀλλὰ δὴ μὴ ἔστω ὁ ΕΖ πρῶτος· ὑπὸ πρώτου ἄρα τινὸς ἀριθμοῦ μετρεῖται. μετρείσθω ὑπὸ πρώτου τοῦ Η· λέγω, ὅτι ὁ Η οὐδενὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. εἰ γὰρ δυνατόν, ἔστω. οἱ δὲ Α, Β, Γ τὸν ΔΕ μετροῦσιν· καὶ ὁ Η ἄρα τὸν ΔΕ μετρήσει. μετρεῖ δὲ καὶ τὸν ΕΖ· καὶ λοιπὴν τὴν ΔΖ μονάδα μετρήσει ὁ Η ἀριθμὸς ὤν· ὅπερ ἄτοπον. οὐκ ἄρα ὁ Η ἑνὶ τῶν Α, Β, Γ ἐστιν ὁ αὐτός. καὶ ὑπόκειται πρῶτος. εὑρημένοι ἄρα εἰσὶ πρῶτοι ἀριθμοὶ πλείους τοῦ προτεθέντος πλήθους τῶν Α, Β, Γ οἱ Α, Β, Γ, Η· ὅπερ ἔδει δεῖξαι.

Μετάφραση Σχόλια Διασυνδέσεις

Θεώρημα κ΄ [20]

Οἱ πρῶτοι ἀριθμοὶ εἶναι περισσότεροι ἀπὸ κάθε δεδομένο σύνολο πρώτων ἀριθμῶν.

Ἔστωσαν οἱ δεδομένοι πρῶτοι ἀριθμοὶ Α, Β, Γ· λέγω, ὅτι ἐκτὸς ἀπ᾿ τοὺς Α, Β, Γ ὑπάρχουν καὶ ἄλλοι πρῶτοι ἀριθμοί.

Λαμβάνω τὸν ἀριθμὸ ΔΕ, τὸ ἐλάχιστο κοινό πολλαπλάσιο τῶν δεδομένων πρώτων ἀριθμῶν Α,Β,Γ (θεώρ_ζ΄36), καὶ προσθέτω σ᾿ αὐτὸν τὴ μονάδα ΔΖ. Ὁ νέος ἀριθμὸς ΕΖ εἴτε εἶναι πρῶτος εἴτε ὄχι. Ἔστω ὄτι εἶναι πρῶτος· τότε ἔχουμε πρώτους ἀριθμοὺς τοὺς Α, Β, Γ καὶ ΕΖ οἱ ὁποῖοι εἶναι περισσότεροι τῶν Α, Β, Γ.

Ἐάν ὁ ΕΖ δὲν εἶναι πρῶτος· τότε θὰ διαιρῆται ἀπὸ κάποιον πρῶτον ἀριθμὸ (θεώρ_ζ΄31). Ἔστω ἀπὸ τὸν Η· θὰ δείξουμε ὄτι ὁ Η εἶναι ἀδύνατον νὰ εἶναι ἕνας ἀπ᾿ τοὺς πρώτους Α, Β, Γ. Ἔστω ὄτι εἶναι ἕνας ἀπ' αὐτούς. Τότε ὁ ΔΕ ἀφοῦ εἶναι πολλαπλάσιος τῶν Α, Β, Γ · θὰ εἶναι καὶ πολλαπλάσιος τοῦ Η. Καὶ ὁ ΕΖ ὅμως εἶναι πολλαπλάσιος τοῦ Η· ἄρα καὶ ἡ διαφορά τους θὰ εἶναι πολλαπλάσια τοῦ Η, δηλαδὴ ἡ μονάδα· ὅπερ ἄτοπον. Ἄρα ὁ Η δὲν εἶναι ἕνας ἐκ τῶν Α, Β, Γ. καὶ εἶναι καὶ πρῶτος. Βρήκαμε ἐπομένως περισσότερους πρώτους ἀριθμοὺς ἀπὸ τοὺς δεδομένους Α, Β, Γ τοὺς Α, Β, Γ, Η· ὅπερ ἔδει δεῖξαι.

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων θ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου