Στοιχεῖα Εὐκλείδου α΄

[Βιβλίον I]

---

Αἱ Προτάσεις τῶν Στοιχείων α΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις ις΄. [16]

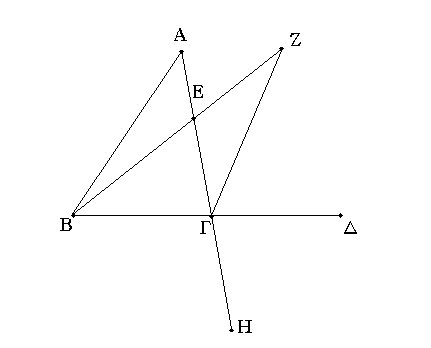
Παντὸς τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον γωνιῶν μείζων ἐστίν.

Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ προσεκβεβλήσθω αὐτοῦ μία πλευρὰ ἡ ΒΓ ἐπὶ τὸ Δ· λέγω, ὅτι ἡ ἐκτὸς γωνία ἡ ὑπὸ ΑΓΔ μείζων ἐστὶν ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον τῶν ὑπὸ ΓΒΑ, ΒΑΓ γωνιῶν.

• 

Τετμήσθω ἡ ΑΓ δίχα κατὰ τὸ Ε, καὶ ἐπιζευχθεῖσα ἡ ΒΕ ἐκβεβλήσθω ἐπ᾿ εὐθείας ἐπὶ τὸ Ζ, καὶ κείσθω τῇ ΒΕ ἴση ἡ ΕΖ, καὶ ἐπεζεύχθω ἡ ΖΓ, καὶ διήχθω ἡ ΑΓ ἐπὶ τὸ Η.

Ἐπεὶ οὖν ἴση ἐστὶν ἡ μὲν ΑΕ τῇ ΕΓ, ἡ δὲ ΒΕ τῇ ΕΖ, δύο δὴ αἱ ΑΕ, ΕΒ δυσὶ ταῖς ΓΕ, ΕΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΑΕΒ γωνίᾳ τῇ ὑπὸ ΖΕΓ ἴση ἐστίν· κατὰ κορυφὴν γάρ· βάσις ἄρα ἡ ΑΒ βάσει τῇ ΖΓ ἴση ἐστίν, καὶ τὸ ΑΒΕ τρίγωνον τῷ ΖΕΓ τριγώνῳ ἐστὶν ἴσον, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν· ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΑΕ τῇ ὑπὸ ΕΓΖ. μείζων δέ ἐστιν ἡ ὑπὸ ΕΓΔ τῆς ὑπὸ ΕΓΖ· μείζων ἄρα ἡ ὑπὸ ΑΓΔ τῆς ὑπὸ ΒΑΕ. ὁμοίως δὴ τῆς ΒΓ τετμημένης δίχα δειχθήσεται καὶ ἡ ὑπὸ ΒΓΗ, τουτέστιν ἡ ὑπὸ ΑΓΔ, μείζων καὶ τῆς ὑπὸ ΑΒΓ.

Παντὸς ἄρα τριγώνου μιᾶς τῶν πλευρῶν προσεκβληθείσης ἡ ἐκτὸς γωνία ἑκατέρας τῶν ἐντὸς καὶ ἀπεναντίον γωνιῶν μείζων ἐστίν· ὅπερ ἔδει δεῖξαι.

---

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου

---