Στοιχεῖα Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις η΄. [8]
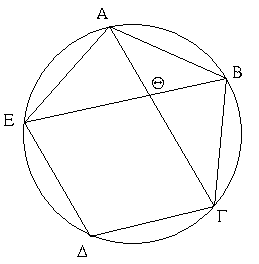
Ἐὰν πενταγώνου ἰσοπλεύρου καὶ ἰσογωνίου τὰς κατὰ τὸ ἑξῆς δύο γωνίας ὑποτείνωσιν εὐθεῖαι, ἄκρον καὶ μέσον λόγον τέμνουσιν ἀλλήλας, καὶ τὰ μείζονα αὐτῶν τμήματα ἴσα ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ.
Πενταγώνου γὰρ ἰσοπλεύρου καὶ ἰσογωνίου τοῦ ΑΒΓ ΔΕ δύο γωνίας τὰς κατὰ τὸ ἑξῆς τὰς πρὸς τοῖς Α, Β ὑποτεινέτωσαν εὐθεῖαι αἱ ΑΓ, ΒΕ τέμνουσαι ἀλλήλας κατὰ τὸ Θ σημεῖον· λέγω, ὅτι ἑκατέρα αὐτῶν ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ σημεῖον, καὶ τὰ μείζονα αὐτῶν τμήματα ἴσα ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ.
Περιγεγράφθω γὰρ περὶ τὸ ΑΒΓΔΕ πεντάγωνον κύκλος ὁ ΑΒΓΔΕ. καὶ ἐπεὶ δύο εὐθεῖαι αἱ ΕΑ, ΑΒ δυσὶ ταῖς ΑΒ, ΒΓ ἴσαι εἰσὶ καὶ γωνίας ἴσας περιέχουσιν, βάσις ἄρα ἡ ΒΕ βάσει τῇ ΑΓ ἴση ἐστίν, καὶ τὸ ΑΒΕ τρίγωνον τῷ ΑΒΓ τριγώνῳ ἴσον ἐστίν, καὶ αἱ λοιπαὶ γωνίαι ταῖς λοιπαῖς γωνίαις ἴσαι ἔσονται ἑκατέρα ἑκατέρᾳ, ὑφ᾿ ἃς αἱ ἴσαι πλευραὶ ὑποτείνουσιν. ἴση ἄρα ἐστὶν ἡ ὑπὸ ΒΑΓ γωνία τῇ ὑπὸ ΑΒΕ· διπλῆ ἄρα ἡ ὑπὸ ΑΘΕ τῆς ὑπὸ ΒΑΘ. ἔστι δὲ καὶ ἡ ὑπὸ ΕΑΓ τῆς ὑπὸ ΒΑΓ διπλῆ, ἐπειδήπερ καὶ περιφέρεια ἡ ΕΔΓ περιφερείας τῆς ΓΒ ἐστι διπλῆ· ἴση ἄρα ἡ ὑπὸ ΘΑΕ γωνία τῇ ὑπὸ ΑΘΕ· ὥστε καὶ ἡ ΘΕ εὐθεῖα τῇ ΕΑ, τουτέστι τῇ ΑΒ ἐστιν ἴση.
καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΑ εὐθεῖα τῇ ΑΕ, ἴση ἐστὶ καὶ γωνία ἡ ὑπὸ ΑΒΕ τῇ ὑπὸ ΑΕΒ. ἀλλὰ ἡ ὑπὸ ΑΒΕ τῇ ὑπὸ ΒΑΘ ἐδείχθη ἴση· καὶ ἡ ὑπὸ ΒΕΑ ἄρα τῇ ὑπὸ ΒΑΘ ἐστιν ἴση. καὶ κοινὴ τῶν δύο τριγώνων τοῦ τε ΑΒΕ καὶ τοῦ ΑΒΘ ἐστιν ἡ ὑπὸ ΑΒΕ· λοιπὴ ἄρα ἡ ὑπὸ ΒΑΕ γωνία λοιπῇ τῇ ὑπὸ ΑΘΒ ἐστιν ἴση· ἰσογώνιον ἄρα ἐστὶ τὸ ΑΒΕ τρίγωνον τῷ ΑΒΘ τριγώνῳ· ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΕΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΑΒ πρὸς τὴν ΒΘ. ἴση δὲ ἡ ΒΑ τῇ ΕΘ· ὡς ἄρα ἡ ΒΕ πρὸς τὴν ΕΘ, οὕτως ἡ ΕΘ πρὸς τὴν ΘΒ. μείζων δὲ ἡ ΒΕ τῆς ΕΘ· μείζων ἄρα καὶ ἡ ΕΘ τῆς ΘΒ. ἡ ΒΕ ἄρα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ, καὶ τὸ μεῖζον τμῆμα τὸ ΘΕ ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ ΑΓ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Θ, καὶ τὸ μεῖζον αὐτῆς τμῆμα ἡ ΓΘ ἴσον ἐστὶ τῇ τοῦ πενταγώνου πλευρᾷ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου