Στοιχεῖα Εὐκλείδου δ΄
[Βιβλίον IV]
Αἱ Προτάσεις τῶν Στοιχείων δ΄.
Προηγουμένη Πρότασις
Πρότασις ις΄. [16]
Εἰς τὸν δοθέντα κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
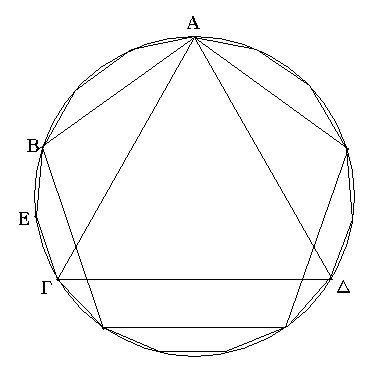
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓΔ· δεῖ δὴ εἰς τὸν ΑΒΓΔ κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον ἐγγράψαι.
Ἐγγεγράφθω εἰς τὸν ΑΒΓΔ κύκλον τριγώνου μὲν ἰσοπλεύρου τοῦ εἰς αὐτὸν ἐγγραφομένου πλευρὰ ἡ ΑΓ, πενταγώνου δὲ ἰσοπλεύρου ἡ ΑΒ· οἵων ἄρα ἐστὶν ὁ ΑΒΓΔ κύκλος ἴσων τμημάτων δεκαπέντε, τοιούτων ἡ μὲν ΑΒΓ περιφέρεια τρίτον οὖσα τοῦ κύκλου ἔσται πέντε, ἡ δὲ ΑΒ περιφέρεια πέμπτον οὖσα τοῦ κύκλου ἔσται τριῶν· λοιπὴ ἄρα ἡ ΒΓ τῶν ἴσων δύο. τετμήσθω ἡ ΒΓ δίχα κατὰ τὸ Ε· ἑκατέρα ἄρα τῶν ΒΕ, ΕΓ περιφερειῶν πεντεκαιδέκατόν ἐστι τοῦ ΑΒΓΔ κύκλου.
Ἐὰν ἄρα ἐπιζεύξαντες τὰς ΒΕ, ΕΓ ἴσας αὐταῖς κατὰ τὸ συνεχὲς εὐθείας ἐναρμόσωμεν εἰς τὸν ΑΒΓΔ[Ε] κύκλον, ἔσται εἰς αὐτὸν ἐγγεγραμμένον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον· ὅπερ ἔδει ποιῆσαι.
Ὁμοίως δὲ τοῖς ἐπὶ τοῦ πενταγώνου ἐὰν διὰ τῶν κατὰ τὸν κύκλον διαιρέσεων ἐφαπτομένας τοῦ κύκλου ἀγάγωμεν, περιγραφήσεται περὶ τὸν κύκλον πεντεκαιδεκάγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον. ἔτι δὲ διὰ τῶν ὁμοίων τοῖς ἐπὶ τοῦ πενταγώνου δείξεων καὶ εἰς τὸ δοθὲν πεντεκαιδεκάγωνον κύκλον ἐγγράψομέν τε καὶ περιγράψομεν· ὅπερ ἔδει ποιῆσαι.
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων δ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου