Στοιχεῖα Εὐκλείδου θ΄
[Βιβλίον IX]
Αἱ Προτάσεις τῶν Στοιχείων θ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ι΄. [10]
Ἐὰν ἀπὸ μονάδος ὁποσοιοῦν ἀριθμοὶ [ἑξῆς] ἀνάλογον ὦσιν, ὁ δὲ μετὰ τὴν μονάδα μὴ ᾖ τετράγωνος, οὐδ' ἄλλος οὐδεὶς τετράγωνος ἔσται χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος καὶ τῶν ἕνα διαλειπόντων πάντων. καὶ ἐὰν ὁ μετὰ τὴν μονάδα κύβος μὴ ᾖ, οὐδὲ ἄλλος οὐδεὶς κύβος ἔσται χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων πάντων.
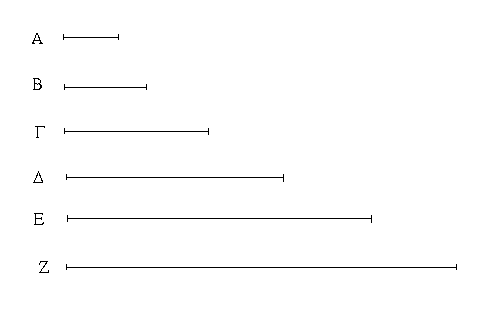
Ἔστωσαν ἀπὸ μονάδος ἑξῆς ἀνάλογον ὁσοιδηποτοῦν ἀριθμοὶ οἱ Α, Β, Γ, Δ, Ε, Ζ, ὁ δὲ μετὰ τὴν μονάδα ὁ Α μὴ ἔστω τετράγωνος· λέγω, ὅτι οὐδὲ ἄλλος οὐδεὶς τετράγωνος ἔσται χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος [καὶ τῶν ἕνα διαλειπόντων].
Εἰ γὰρ δυνατόν, ἔστω ὁ Γ τετράγωνος. ἔστι δὲ καὶ ὁ Β τετράγωνος· οἱ Β, Γ ἄρα πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν. καί ἐστιν ὡς ὁ Β πρὸς τὸν Γ, ὁ Α πρὸς τὸν Β· οἱ Α, Β ἄρα πρὸς ἀλλήλους λόγον ἔχουσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν· ὥστε οἱ Α, Β ὅμοιοι ἐπίπεδοί εἰσιν. καί ἐστι τετράγωνος ὁ Β· τετράγωνος ἄρα ἐστὶ καὶ ὁ Α· ὅπερ οὐχ ὑπέκειτο. οὐκ ἄρα ὁ Γ τετράγωνός ἐστιν. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλος οὐδεὶς τετράγωνός ἐστι χωρὶς τοῦ τρίτου ἀπὸ τῆς μονάδος καὶ τῶν ἕνα διαλειπόντων.
Ἀλλὰ δὴ μὴ ἔστω ὁ Α κύβος. λέγω, ὅτι οὐδ' ἄλλος οὐδεὶς κύβος ἔσται χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων.
Εἰ γὰρ δυνατόν, ἔστω ὁ Δ κύβος. ἔστι δὲ καὶ ὁ Γ κύβος· τέταρτος γάρ ἐστιν ἀπὸ τῆς μονάδος. καί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, ὁ Β πρὸς τὸν Γ· καὶ ὁ Β ἄρα πρὸς τὸν Γ λόγον ἔχει, ὃν κύβος πρὸς κύβον. καί ἐστιν ὁ Γ κύβος· καὶ ὁ Β ἄρα κύβος ἐστίν. καὶ ἐπεί ἐστιν ὡς ἡ μονὰς πρὸς τὸν Α, ὁ Α πρὸς τὸν Β, ἡ δὲ μονὰς τὸν Α μετρεῖ κατὰ τὰς ἐν αὐτῷ μονάδας, καὶ ὁ Α ἄρα τὸν Β μετρεῖ κατὰ τὰς ἐν αὑτῷ μονάδας· ὁ Α ἄρα ἑαυτὸν πολλαπλασιάσας κύβον τὸν Β πεποίηκεν. ἐὰν δὲ ἀριθμὸς ἑαυτὸν πολλαπλασιάσας κύβον ποιῇ, καὶ αὐτὸς κύβος ἔσται. κύβος ἄρα καὶ ὁ Α· ὅπερ οὐχ ὑπόκειται. οὐκ ἄρα ὁ Δ κύβος ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι οὐδ' ἄλλος οὐδεὶς κύβος ἐστὶ χωρὶς τοῦ τετάρτου ἀπὸ τῆς μονάδος καὶ τῶν δύο διαλειπόντων· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων θ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου