Στοιχεῖα Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ε΄. [5]
Ἐὰν εὐθεῖα γραμμὴ ἄκρον καὶ μέσον λόγον τμηθῇ, καὶ προστεθῇ αὐτῇ ἴση τῷ μείζονι τμήματι, ἡ ὅλη εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ἐξ ἀρχῆς εὐθεῖα.
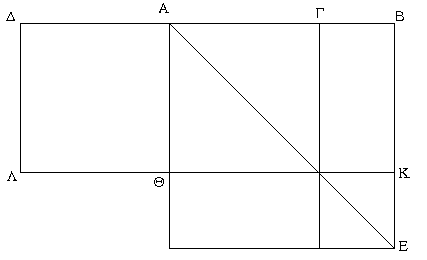
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τετμήσθω κατὰ τὸ Γ σημεῖον, καὶ ἔστω μεῖζον τμῆμα ἡ ΑΓ, καὶ τῇ ΑΓ ἴση [κείσθω] ἡ ΑΔ. λέγω, ὅτι ἡ ΔΒ εὐθεῖα ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Α, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ἐξ ἀρχῆς εὐθεῖα ἡ ΑΒ.
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΕ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ ἡ ΑΒ ἄκρον καὶ μέσον λόγον τέτμηται κατὰ τὸ Γ, τὸ ἄρα ὑπὸ ΑΒΓ ἴσον ἐστὶ τῷ ἀπὸ ΑΓ. καί ἐστι τὸ μὲν ὑπὸ ΑΒΓ τὸ ΓΕ, τὸ δὲ ἀπὸ τῆς ΑΓ τὸ ΓΘ· ἴσον ἄρα τὸ ΓΕ τῷ ΘΓ. ἀλλὰ τῷ μὲν ΓΕ ἴσον ἐστὶ τὸ ΘΕ, τῷ δὲ ΘΓ ἴσον τὸ ΔΘ· καὶ τὸ ΔΘ ἄρα ἴσον ἐστὶ τῷ ΘΕ [κοινὸν προσκείσθω τὸ ΘΒ]. ὅλον ἄρα τὸ ΔΚ ὅλῳ τῷ ΑΕ ἐστιν ἴσον. καί ἐστι τὸ μὲν ΔΚ τὸ ὑπὸ τῶν ΒΔ, ΔΑ· ἴση γὰρ ἡ ΑΔ τῇ ΔΛ· τὸ δὲ ΑΕ τὸ ἀπὸ τῆς ΑΒ· τὸ ἄρα ὑπὸ τῶν ΒΔΑ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ. ἔστιν ἄρα ὡς ἡ ΔΒ πρὸς τὴν ΒΑ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΔ. μείζων δὲ ἡ ΔΒ τῆς ΒΑ· μείζων ἄρα καὶ ἡ ΒΑ τῆς ΑΔ.
Ἡ ἄρα ΔΒ ἄκρον καὶ μέσον λόγον τέμηται κατὰ τὸ Α, καὶ τὸ μεῖζον τμῆμά ἐστιν ἡ ΑΒ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου