Στοιχεῖα Εὐκλείδου ια΄
[Βιβλίον XI]
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις κγ΄. [23]
Ἐκ τριῶν γωνιῶν ἐπιπέδων, ὧν αἱ δύο τῆς λοιπῆς μείζονές εἰσι πάντῃ μεταλαμβανόμεναι, στερεὰν γωνίαν συστήσασθαι· δεῖ δὴ τὰς τρεῖς τεσσάρων ὀρθῶν ἐλάσσονας εἶναι.
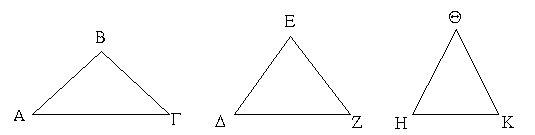
Ἔστωσαν αἱ δοθεῖσαι τρεῖς γωνίαι ἐπίπεδοι αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ, ὧν αἱ δύο τῆς λοιπῆς μείζονες ἔστωσαν πάντῃ μεταλαμβανόμεναι, ἔτι δὲ αἱ τρεῖς τεσσάρων ὀρθῶν ἐλάσσονες· δεῖ δὴ ἐκ τῶν ἴσων ταῖς ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ στερεὰν γωνίαν συστήσασθαι.
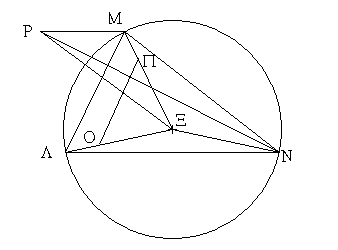
Ἀπειλήφθωσαν ἴσαι αἱ ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΔΖ, ΗΚ· δυνατὸν ἄρα ἐστὶν ἐκ τῶν ἴσων ταῖς ΑΓ, ΔΖ, ΗΚ τρίγωνον συστήσασθαι. συνεστάτω τὸ ΛΜΝ, ὥστε ἴσην εἶναι τὴν μὲν ΑΓ τῇ ΛΜ, τὴν δὲ ΔΖ τῇ ΜΝ, καὶ ἔτι τὴν ΗΚ τῇ ΝΛ, καὶ περιγεγράφθω περὶ τὸ ΛΜΝ τρίγωνον κύκλος ὁ ΛΜΝ καὶ εἰλήφθω αὐτοῦ τὸ κέντρον καὶ ἔστω τὸ Ξ, καὶ ἐπεζεύχθωσαν αἱ ΛΞ, ΜΞ, ΝΞ· λέγω, ὅτι ἡ ΑΒ μείζων ἐστὶ τῆς ΛΞ. εἰ γὰρ μή, ἤτοι ἴση ἐστὶν ἡ ΑΒ τῇ ΛΞ ἢ ἐλάττων. ἔστω πρότερον ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΛΞ, ἀλλὰ ἡ μὲν ΑΒ τῇ ΒΓ ἐστιν ἴση, ἡ δὲ ΞΛ τῇ ΞΜ, δύο δὴ αἱ ΑΒ, ΒΓ δύο ταῖς ΛΞ, ΞΜ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ βάσις ἡ ΑΓ βάσει τῇ ΛΜ ὑπόκειται ἴση· γωνία ἄρα ἡ ὑπὸ ΑΒΓ γωνίᾳ τῇ ὑπὸ ΛΞΜ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ μὲν ὑπὸ ΔΕΖ τῇ ὑπὸ ΜΞΝ ἐστιν ἴση, καὶ ἔτι ἡ ὑπὸ ΗΘΚ τῇ ὑπὸ ΝΞΛ· αἱ ἄρα τρεῖς αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ γωνίαι τρισὶ ταῖς ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ εἰσιν ἴσαι. ἀλλὰ αἱ τρεῖς αἱ ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ τέτταρσιν ὀρθαῖς εἰσιν ἴσαι· καὶ αἱ τρεῖς ἄρα αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τέτταρσιν ὀρθαῖς ἴσαι εἰσίν. ὑπόκεινται δὲ καὶ τεσσάρων ὀρθῶν ἐλάσσονες· ὅπερ ἄτοπον. οὐκ ἄρα ἡ ΑΒ τῇ ΛΞ ἴση ἐστίν.
λέγω δή, ὅτι οὐδὲ ἐλάττων ἐστὶν ἡ ΑΒ τῆς ΛΞ. εἰ γὰρ δυνατόν, ἔστω· καὶ κείσθω τῇ μὲν ΑΒ ἴση ἡ ΞΟ, τῇ δὲ ΒΓ ἴση ἡ ΞΠ, καὶ ἐπεζεύχθω ἡ ΟΠ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΒ τῇ ΒΓ, ἴση ἐστὶ καὶ ἡ ΞΟ τῇ ΞΠ· ὥστε καὶ λοιπὴ ἡ ΛΟ τῇ ΠΜ ἐστιν ἴση. παράλληλος ἄρα ἐστὶν ἡ ΛΜ τῇ ΟΠ, καὶ ἰσογώνιον τὸ ΛΜΞ τῷ ΟΠΞ· ἔστιν ἄρα ὡς ἡ ΞΛ πρὸς ΛΜ, οὕτως ἡ ΞΟ πρὸς ΟΠ· ἐναλλὰξ ὡς ἡ ΛΞ πρὸς ΞΟ, οὕτως ἡ ΛΜ πρὸς ΟΠ. μείζων δὲ ἡ ΛΞ τῆς ΞΟ· μείζων ἄρα καὶ ἡ ΛΜ τῆς ΟΠ. ἀλλὰ ἡ ΛΜ κεῖται τῇ ΑΓ ἴση· καὶ ἡ ΑΓ ἄρα τῆς ΟΠ μείζων ἐστίν. ἐπεὶ οὖν δύο αἱ ΑΒ, ΒΓ δυσὶ ταῖς ΟΞ, ΞΠ ἴσαι εἰσίν, καὶ βάσις ἡ ΑΓ βάσεως τῆς ΟΠ μείζων ἐστίν, γωνία ἄρα ἡ ὑπὸ ΑΒΓ γωνίας τῆς ὑπὸ ΟΞΠ μείζων ἐστίν. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἡ μὲν ὑπὸ ΔΕΖ τῆς ὑπὸ ΜΞΝ μείζων ἐστίν, ἡ δὲ ὑπὸ ΗΘΚ τῆς ὑπὸ ΝΞΛ. αἱ ἄρα τρεῖς γωνίαι αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τριῶν τῶν ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ μείζονές εἰσιν. ἀλλὰ αἱ ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ τεσσάρων ὀρθῶν ἐλάσσονες ὑπόκεινται· πολλῷ ἄρα αἱ ὑπὸ ΛΞΜ, ΜΞΝ, ΝΞΛ τεσσάρων ὀρθῶν ἐλάσσονές εἰσιν. ἀλλὰ καὶ ἴσαι· ὅπερ ἐστὶν ἄτοπον. οὐκ ἄρα ἡ ΑΒ ἐλάσσων ἐστὶ τῆς ΛΞ. ἐδείχθη δέ, ὅτι οὐδὲ ἴση· μείζων ἄρα ἡ ΑΒ τῆς ΛΞ. ἀνεστάτω δὴ ἀπὸ τοῦ Ξ σημείου τῷ τοῦ ΛΜΝ κύκλου ἐπιπέδῳ πρὸς ὀρθὰς ἡ ΞΡ, καὶ ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τετράγωνον τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον ἔστω τὸ ἀπὸ τῆς ΞΡ, καὶ ἐπεζεύχθωσαν αἱ ΡΛ, ΡΜ, ΡΝ. καὶ ἐπεὶ ἡ ΡΞ ὀρθή ἐστι πρὸς τὸ τοῦ ΛΜΝ κύκλου ἐπίπεδον, καὶ πρὸς ἑκάστην ἄρα τῶν ΛΞ, ΜΞ, ΝΞ ὀρθή ἐστιν ἡ ΡΞ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΛΞ τῇ ΞΜ, κοινὴ δὲ καὶ πρὸς ὀρθὰς ἡ ΞΡ, βάσις ἄρα ἡ ΡΛ βάσει τῇ ΡΜ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΡΝ ἑκατέρᾳ τῶν ΡΛ, ΡΜ ἐστιν ἴση· αἱ τρεῖς ἄρα αἱ ΡΛ, ΡΜ, ΡΝ ἴσαι ἀλλήλαις εἰσίν. καὶ ἐπεὶ ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον ὑπόκειται τὸ ἀπὸ τῆς ΞΡ, τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΛΞ, ΞΡ. τοῖς δὲ ἀπὸ τῶν ΛΞ, ΞΡ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΛΡ· ὀρθὴ γὰρ ἡ ὑπὸ ΛΞΡ· τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΡΛ· ἴση ἄρα ἡ ΑΒ τῇ ΡΛ. ἀλλὰ τῇ μὲν ΑΒ ἴση ἐστὶν ἑκάστη τῶν ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ, τῇ δὲ ΡΛ ἴση ἑκατέρα τῶν ΡΜ, ΡΝ· ἑκάστη ἄρα τῶν ΑΒ, ΒΓ, ΔΕ, ΕΖ, ΗΘ, ΘΚ ἑκάστῃ τῶν ΡΛ, ΡΜ, ΡΝ ἴση ἐστίν. καὶ ἐπεὶ δύο αἱ ΛΡ, ΡΜ δυσὶ ταῖς ΑΒ, ΒΓ ἴσαι εἰσίν, καὶ βάσις ἡ ΛΜ βάσει τῇ ΑΓ ὑπόκειται ἴση, γωνία ἄρα ἡ ὑπὸ ΛΡΜ γωνίᾳ τῇ ὑπὸ ΑΒΓ ἐστιν ἴση. διὰ τὰ αὐτὰ δὴ καὶ ἡ μὲν ὑπὸ ΜΡΝ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση, ἡ δὲ ὑπὸ ΛΡΝ τῇ ὑπὸ ΗΘΚ.
Ἐκ τριῶν ἄρα γωνιῶν ἐπιπέδων τῶν ὑπὸ ΛΡΜ, ΜΡΝ, ΛΡΝ, αἵ εἰσιν ἴσαι τρισὶ ταῖς δοθείσαις ταῖς ὑπὸ ΑΒΓ, ΔΕΖ, ΗΘΚ, στερεὰ γωνία συνέσταται ἡ πρὸς τῷ Ρ περιεχομένη ὑπὸ τῶν ΛΡΜ, ΜΡΝ, ΛΡΝ γωνιῶν· ὅπερ ἔδει ποιῆσαι.
Λῆμμα
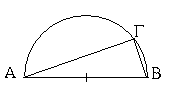
Ὃν δὲ τρόπον, ᾧ μεῖζόν ἐστι τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ, ἐκείνῳ ἴσον λαβεῖν ἔστι τὸ ἀπὸ τῆς ΞΡ, δείξομεν οὕτως. ἐκκείσθωσαν αἱ ΑΒ, ΛΞ εὐθεῖαι, καὶ ἔστω μείζων ἡ ΑΒ, καὶ γεγράφθω ἐπ᾿ αὐτῆς ἡμικύκλιον τὸ ΑΒΓ, καὶ εἰς τὸ ΑΒΓ ἡμικύκλιον ἐνηρμόσθω τῇ ΛΞ εὐθείᾳ μὴ μείζονι οὔσῃ τῆς ΑΒ διαμέτρου ἴση ἡ ΑΓ, καὶ ἐπεζεύχθω ἡ ΓΒ. ἐπεὶ οὖν ἐν ἡμικυκλίῳ τῷ ΑΓΒ γωνία ἐστὶν ἡ ὑπὸ ΑΓΒ, ὀρθὴ ἄρα ἐστὶν ἡ ὑπὸ ΑΓΒ.
τὸ ἄρα ἀπὸ τῆς ΑΒ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΓ, ΓΒ. ὥστε τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΑΓ μεῖζόν ἐστι τῷ ἀπὸ τῆς ΓΒ. ἴση δὲ ἡ ΑΓ τῇ ΛΞ. τὸ ἄρα ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ μεῖζόν ἐστι τῷ ἀπὸ τῆς ΓΒ. ἐὰν οὖν τῇ ΒΓ ἴσην τὴν ΞΡ ἀπολάβωμεν, ἔσται τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΛΞ μεῖζον τῷ ἀπὸ τῆς ΞΡ· ὅπερ προέκειτο ποιῆσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Περιεχόμενα Στοιχείων Εὐκλείδου