Στοιχεῖα Εὐκλείδου α΄
[Βιβλίον I]
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ιδ΄. [14]
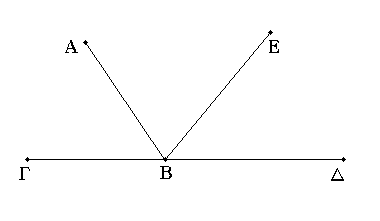
Ἐὰν πρός τινι εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ δύο εὐθεῖαι μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιῶσιν, ἐπ᾿ εὐθείας ἔσονται ἀλλήλαις αἱ εὐθεῖαι.
Πρὸς γάρ τινι εὐθείᾳ τῇ ΑΒ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Β δύο εὐθεῖαι αἱ ΒΓ, ΒΔ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας τὰς ὑπὸ ΑΒΓ, ΑΒΔ δύο ὀρθαῖς ἴσας ποιείτωσαν· λέγω, ὅτι ἐπ᾿ εὐθείας ἐστὶ τῇ ΓΒ ἡ ΒΔ.Εἰ γὰρ μή ἐστι τῇ ΒΓ ἐπ᾿ εὐθείας ἡ ΒΔ, ἔστω τῇ ΓΒ ἐπ᾿ εὐθείας ἡ ΒΕ.
Ἐπεὶ οὖν εὐθεῖα ἡ ΑΒ ἐπ᾿ εὐθεῖαν τὴν ΓΒΕ ἐφέστηκεν, αἱ ἄρα ὑπὸ ΑΒΓ, ΑΒΕ γωνίαι δύο ὀρθαῖς ἴσαι εἰσίν· εἰσὶ δὲ καὶ αἱ ὑπὸ ΑΒΓ, ΑΒΔ δύο ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΓΒΑ, ΑΒΕ ταῖς ὑπὸ ΓΒΑ, ΑΒΔ ἴσαι εἰσίν. κοινὴ ἀφῃρήσθω ἡ ὑπὸ ΓΒΑ· λοιπὴ ἄρα ἡ ὑπὸ ΑΒΕ λοιπῇ τῇ ὑπὸ ΑΒΔ ἐστιν ἴση, ἡ ἐλάσσων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἐπ᾿ εὐθείας ἐστὶν ἡ ΒΕ τῇ ΓΒ. ὁμοίως δὴ δείξομεν, ὅτι οὐδὲ ἄλλη τις πλὴν τῆς ΒΔ· ἐπ᾿ εὐθείας ἄρα ἐστὶν ἡ ΓΒ τῇ ΒΔ.
Ἐὰν ἄρα πρός τινι εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ δύο εὐθεῖαι μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιῶσιν, ἐπ᾿ εὐθείας ἔσονται ἀλλήλαις αἱ εὐθεῖαι· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου