Στοιχεῖα Εὐκλείδου β΄
[Βιβλίον II]
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις δ΄. [4]
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ.
Εὐθεῖα γὰρ γραμμὴ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ. λέγω, ὅτι τὸ ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ.
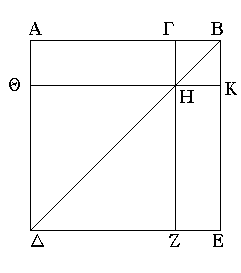
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΑΒ τετράγωνον τὸ ΑΔΕΒ, καὶ ἐπεζεύχθω ἡ ΒΔ, καὶ διὰ μὲν τοῦ Γ ὁποτέρᾳ τῶν ΑΔ, ΕΒ παράλληλος ἤχθω ἡ ΓΖ, διὰ δὲ τοῦ Η ὁποτέρᾳ τῶν ΑΒ, ΔΕ παράλληλος ἤχθω ἡ ΘΚ. καὶ ἐπεὶ παράλληλός ἐστιν ἡ ΓΖ τῇ ΑΔ, καὶ εἰς αὐτὰς ἐμπέπτωκεν ἡ ΒΔ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΓΗΒ ἴση ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΑΔΒ. ἀλλ' ἡ ὑπὸ ΑΔΒ τῇ ὑπὸ ΑΒΔ ἐστιν ἴση, ἐπεὶ καὶ πλευρὰ ἡ ΒΑ τῇ ΑΔ ἐστιν ἴση· καὶ ἡ ὑπὸ ΓΗΒ ἄρα γωνία τῇ ὑπὸ ΗΒΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΒΓ πλευρᾷ τῇ ΓΗ ἐστιν ἴση· ἀλλ' ἡ μὲν ΓΒ τῇ ΗΚ ἐστιν ἴση, ἡ δὲ ΓΗ τῇ ΚΒ· καὶ ἡ ΗΚ ἄρα τῇ ΚΒ ἐστιν ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΓΗΚΒ. λέγω δή, ὅτι καὶ ὀρθογώνιον. ἐπεὶ γὰρ παράλληλός ἐστιν ἡ ΓΗ τῇ ΒΚ [καὶ εἰς αὐτὰς ἐμπέπτωκεν εὐθεῖα ἡ ΓΒ], αἱ ἄρα ὑπὸ ΚΒΓ, ΗΓΒ γωνίαι δύο ὀρθαῖς εἰσιν ἴσαι. ὀρθὴ δὲ ἡ ὑπὸ ΚΒΓ· ὀρθὴ ἄρα καὶ ἡ ὑπὸ ΒΓΗ· ὥστε καὶ αἱ ἀπεναντίον αἱ ὑπὸ ΓΗΚ, ΗΚΒ ὀρθαί εἰσιν. ὀρθογώνιον ἄρα ἐστὶ τὸ ΓΗΚΒ· ἐδείχθη δὲ καὶ ἰσόπλευρον· τετράγωνον ἄρα ἐστίν· καί ἐστιν ἀπὸ τῆς ΓΒ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΘΖ τετράγωνόν ἐστιν· καί ἐστιν ἀπὸ τῆς ΘΗ, τουτέστιν [ἀπὸ] τῆς ΑΓ· τὰ ἄρα ΘΖ, ΚΓ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ εἰσιν. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΗ τῷ ΗΕ, καί ἐστι τὸ ΑΗ τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴση γὰρ ἡ ΗΓ τῇ ΓΒ· καὶ τὸ ΗΕ ἄρα ἴσον ἐστὶ τῷ ὑπὸ ΑΓ, ΓΒ· τὰ ἄρα ΑΗ, ΗΕ ἴσα ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ. ἔστι δὲ καὶ τὰ ΘΖ, ΓΚ τετράγωνα ἀπὸ τῶν ΑΓ, ΓΒ· τὰ ἄρα τέσσαρα τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ἴσα ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ. ἀλλὰ τὰ ΘΖ, ΓΚ, ΑΗ, ΗΕ ὅλον ἐστὶ τὸ ΑΔΕΒ, ὅ ἐστιν ἀπὸ τῆς ΑΒ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΑΒ τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν ΑΓ, ΓΒ τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ἀπὸ τῆς ὅλης τετράγωνον ἴσον ἐστὶ τοῖς τε ἀπὸ τῶν τμημάτων τετραγώνοις καὶ τῷ δὶς ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ· ὅπερ ἔδει δεῖξαι.
[Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐν τοῖς τετραγώνοις χωρίοις τὰ περὶ τὴν διάμετρον παραλληλόγραμμα τετράγωνά ἐστιν].Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Περιεχόμενα Στοιχείων Εὐκλείδου