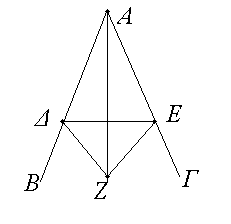Στοιχεῖα Εὐκλείδου α΄
[Βιβλίον I]
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις θ΄. [9]
Τὴν δοθεῖσαν γωνίαν εὐθύγραμμον δίχα τεμεῖν.
Ἔστω ἡ δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΒΑΓ. δεῖ δὴ αὐτὴν δίχα τεμεῖν.Εἰλήφθω ἐπὶ τῆς ΑΒ τυχὸν σημεῖον τὸ Δ, καὶ ἀφῃρήσθω ἀπὸ τῆς ΑΓ τῇ ΑΔ ἴση ἡ ΑΕ, καὶ ἐπεζεύχθω ἡ ΔΕ, καὶ συνεστάτω ἐπὶ τῆς ΔΕ τρίγωνον ἰσόπλευρον τὸ ΔΕΖ, καὶ ἐπεζεύχθω ἡ ΑΖ· λέγω, ὅτι ἡ ὑπὸ ΒΑΓ γωνία δίχα τέτμηται ὑπὸ τῆς ΑΖ εὐθείας. Ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΑΔ τῇ ΑΕ, κοινὴ δὲ ἡ ΑΖ, δύο δὴ αἱ ΔΑ, ΑΖ δυσὶ ταῖς ΕΑ, ΑΖ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ. καὶ βάσις ἡ ΔΖ βάσει τῇ ΕΖ ἴση ἐστίν· γωνία ἄρα ἡ ὑπὸ ΔΑΖ γωνίᾳ τῇ ὑπὸ ΕΑΖ ἴση ἐστίν. Ἡ ἄρα δοθεῖσα γωνία εὐθύγραμμος ἡ ὑπὸ ΒΑΓ δίχα τέτμηται ὑπὸ τῆς ΑΖ εὐθείας· ὅπερ ἔδει ποιῆσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων α΄.
Περιεχόμενα Στοιχείων Εὐκλείδου