Στοιχεῖα Εὐκλείδου β΄
[Βιβλίον II]
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις θ΄. [9]
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὰ ἀπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου.
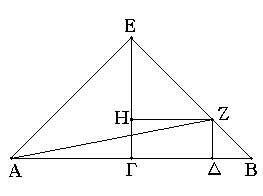
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω εἰς μὲν ἴσα κατὰ τὸ Γ, εἰς δὲ ἄνισα κατὰ τὸ Δ· λέγω, ὅτι τὰ ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
Ἤχθω γὰρ ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΕ, καὶ κείσθω ἴση ἑκατέρᾳ τῶν ΑΓ, ΓΒ, καὶ ἐπεζεύχθωσαν αἱ ΕΑ, ΕΒ, καὶ διὰ μὲν τοῦ Δ τῇ ΕΓ παράλληλος ἤχθω ἡ ΔΖ, διὰ δὲ τοῦ Ζ τῇ ΑΒ ἡ ΖΗ, καὶ ἐπεζεύχθω ἡ ΑΖ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΕ, ἴση ἐστὶ καὶ ἡ ὑπὸ ΕΑΓ γωνία τῇ ὑπὸ ΑΕΓ. καὶ ἐπεὶ ὀρθή ἐστιν ἡ πρὸς τῷ Γ, λοιπαὶ ἄρα αἱ ὑπὸ ΕΑΓ, ΑΕΓ μιᾷ ὀρθῇ ἴσαι εἰσίν· καί εἰσιν ἴσαι· ἡμίσεια ἄρα ὀρθῆς ἐστιν ἑκατέρα τῶν ὑπὸ ΓΕΑ, ΓΑΕ. διὰ τὰ αὐτὰ δὴ καὶ ἑκατέρα τῶν ὑπὸ ΓΕΒ, ΕΒΓ ἡμίσειά ἐστιν ὀρθῆς· ὅλη ἄρα ἡ ὑπὸ ΑΕΒ ὀρθή ἐστιν. καὶ ἐπεὶ ἡ ὑπὸ ΗΕΖ ἡμίσειά ἐστιν ὀρθῆς, ὀρθὴ δὲ ἡ ὑπὸ ΕΗΖ· ἴση γάρ ἐστι τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΕΓΒ· λοιπὴ ἄρα ἡ ὑπὸ ΕΖΗ ἡμίσειά ἐστιν ὀρθῆς· ἴση ἄρα [ἐστὶν] ἡ ὑπὸ ΗΕΖ γωνία τῇ ὑπὸ ΕΖΗ· ὥστε καὶ πλευρὰ ἡ ΕΗ τῇ ΗΖ ἐστιν ἴση. πάλιν ἐπεὶ ἡ πρὸς τῷ Β γωνία ἡμίσειά ἐστιν ὀρθῆς, ὀρθὴ δὲ ἡ ὑπὸ ΖΔΒ· ἴση γὰρ πάλιν ἐστὶ τῇ ἐντὸς καὶ ἀπεναντίον τῇ ὑπὸ ΕΓΒ· λοιπὴ ἄρα ἡ ὑπὸ ΒΖΔ ἡμίσειά ἐστιν ὀρθῆς· ἴση ἄρα ἡ πρὸς τῷ Β γωνία τῇ ὑπὸ ΔΖΒ· ὥστε καὶ πλευρὰ ἡ ΖΔ πλευρᾷ τῇ ΔΒ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΕ, ἴσον ἐστὶ καὶ τὸ ἀπὸ ΑΓ τῷ ἀπὸ ΓΕ· τὰ ἄρα ἀπὸ τῶν ΑΓ, ΓΕ τετράγωνα διπλάσιά ἐστι τοῦ ἀπὸ ΑΓ. τοῖς δὲ ἀπὸ τῶν ΑΓ, ΓΕ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΑ τετράγωνον· ὀρθὴ γὰρ ἡ ὑπὸ ΑΓΕ γωνία· τὸ ἄρα ἀπὸ τῆς ΕΑ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΑΓ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΕΗ τῇ ΗΖ, ἴσον καὶ τὸ ἀπὸ τῆς ΕΗ τῷ ἀπὸ τῆς ΗΖ· τὰ ἄρα ἀπὸ τῶν ΕΗ, ΗΖ τετράγωνα διπλάσιά ἐστι τοῦ ἀπὸ τῆς ΗΖ τετραγώνου. τοῖς δὲ ἀπὸ τῶν ΕΗ, ΗΖ τετραγώνοις ἴσον ἐστὶ τὸ ἀπὸ τῆς ΕΖ τετράγωνον· τὸ ἄρα ἀπὸ τῆς ΕΖ τετράγωνον διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΗΖ. ἴση δὲ ἡ ΗΖ τῇ ΓΔ· τὸ ἄρα ἀπὸ τῆς ΕΖ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΓΔ. ἔστι δὲ καὶ τὸ ἀπὸ τῆς ΕΑ διπλάσιον τοῦ ἀπὸ τῆς ΑΓ· τὰ ἄρα ἀπὸ τῶν ΑΕ, ΕΖ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων. τοῖς δὲ ἀπὸ τῶν ΑΕ, ΕΖ ἴσον ἐστὶ τὸ ἀπὸ τῆς ΑΖ τετράγωνον· ὀρθὴ γάρ ἐστιν ἡ ὑπὸ ΑΕΖ γωνία· τὸ ἄρα ἀπὸ τῆς ΑΖ τετράγωνον διπλάσιόν ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ. τῷ δὲ ἀπὸ τῆς ΑΖ ἴσα τὰ ἀπὸ τῶν ΑΔ, ΔΖ· ὀρθὴ γὰρ ἡ πρὸς τῷ Δ γωνία· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΖ διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων. ἴση δὲ ἡ ΔΖ τῇ ΔΒ· τὰ ἄρα ἀπὸ τῶν ΑΔ, ΔΒ τετράγωνα διπλάσιά ἐστι τῶν ἀπὸ τῶν ΑΓ, ΓΔ τετραγώνων.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὰ ἀπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων τετράγωνα διπλάσιά ἐστι τοῦ τε ἀπὸ τῆς ἡμισείας καὶ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Περιεχόμενα Στοιχείων Εὐκλείδου