Στοιχεῖα Εὐκλείδου η΄

[Βιβλίον VIII]

---

Αἱ Προτάσεις τῶν Στοιχείων η΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις

Πρότασις κδ΄. [24]

Ἐὰν δύο ἀριθμοὶ πρὸς ἀλλήλους λόγον ἔχωσιν, ὃν τετράγωνος ἀριθμὸς πρὸς τετράγωνον ἀριθμόν, ὁ δὲ πρῶτος τετράγωνος ᾖ, καὶ ὁ δεύτερος τετράγωνος ἔσται.

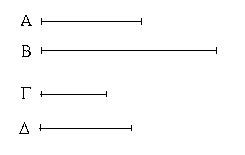
Δύο γὰρ ἀριθμοὶ οἱ Α, Β πρὸς ἀλλήλους λόγον ἐχέτωσαν, ὃν τετράγωνος ἀριθμὸς ὁ Γ πρὸς τετράγωνον ἀριθμὸν τὸν Δ, ὁ δὲ Α τετράγωνος ἔστω· λέγω, ὅτι καὶ ὁ Β τετράγωνός ἐστιν.

• 

Ἐπεὶ γὰρ οἱ Γ, Δ τετράγωνοί εἰσιν, οἱ Γ, Δ ἄρα ὅμοιοι ἐπίπεδοί εἰσιν. τῶν Γ, Δ ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. καί ἐστιν ὡς ὁ Γ πρὸς τὸν Δ, ὁ Α πρὸς τὸν Β· καὶ τῶν Α, Β ἄρα εἷς μέσος ἀνάλογον ἐμπίπτει ἀριθμός. καί ἐστιν ὁ Α τετράγωνος· καὶ ὁ Β ἄρα τετράγωνός ἐστιν· ὅπερ ἔδει δεῖξαι.

---

Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων η΄.
Περιεχόμενα Στοιχείων Εὐκλείδου

---