Στοιχεῖα Εὐκλείδου γ΄
[Βιβλίον III]
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις κζ΄. [27]
Ἐν τοῖς ἴσοις κύκλοις αἱ ἐπὶ ἴσων περιφερειῶν βεβηκυῖαι γωνίαι ἴσαι ἀλλήλαις εἰσίν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι.
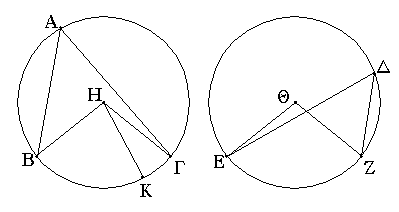
Ἐν γὰρ ἴσοις κύκλοις τοῖς ΑΒΓ, ΔΕΖ ἐπὶ ἴσων περιφερειῶν τῶν ΒΓ, ΕΖ πρὸς μὲν τοῖς Η, Θ κέντροις γωνίαι βεβηκέτωσαν αἱ ὑπὸ ΒΗΓ, ΕΘΖ, πρὸς δὲ ταῖς περιφερείαις αἱ ὑπὸ ΒΑΓ, ΕΔΖ· λέγω, ὅτι ἡ μὲν ὑπὸ ΒΗΓ γωνία τῇ ὑπὸ ΕΘΖ ἐστιν ἴση, ἡ δὲ ὑπὸ ΒΑΓ τῇ ὑπὸ ΕΔΖ ἐστιν ἴση.
Εἰ γὰρ ἄνισός ἐστιν ἡ ὑπὸ ΒΗΓ τῇ ὑπὸ ΕΘΖ, μία αὐτῶν μείζων ἐστίν. ἔστω μείζων ἡ ὑπὸ ΒΗΓ, καὶ συνεστάτω πρὸς τῇ ΒΗ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Η τῇ ὑπὸ ΕΘΖ γωνίᾳ ἴση ἡ ὑπὸ ΒΗΚ· αἱ δὲ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ὅταν πρὸς τοῖς κέντροις ὦσιν· ἴση ἄρα ἡ ΒΚ περιφέρεια τῇ ΕΖ περιφερείᾳ. ἀλλὰ ἡ ΕΖ τῇ ΒΓ ἐστιν ἴση· καὶ ἡ ΒΚ ἄρα τῇ ΒΓ ἐστιν ἴση ἡ ἐλάττων τῇ μείζονι· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα ἄνισός ἐστιν ἡ ὑπὸ ΒΗΓ γωνία τῇ ὑπὸ ΕΘΖ· ἴση ἄρα. καί ἐστι τῆς μὲν ὑπὸ ΒΗΓ ἡμίσεια ἡ πρὸς τῷ Α, τῆς δὲ ὑπὸ ΕΘΖ ἡμίσεια ἡ πρὸς τῷ Δ· ἴση ἄρα καὶ ἡ πρὸς τῷ Α γωνία τῇ πρὸς τῷ Δ.
Ἐν ἄρα τοῖς ἴσοις κύκλοις αἱ ἐπὶ ἴσων περιφερειῶν βεβηκυῖαι γωνίαι ἴσαι ἀλλήλαις εἰσίν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων γ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου