Στοιχεῖα Εὐκλείδου ιγ΄
[Βιβλίον XIII]
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ιδ΄. [14]
Ὀκτάεδρον συστήσασθαι καὶ σφαίρᾳ περιλαβεῖν, ᾗ καὶ τὰ πρότερα, καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασία ἐστὶ τῆς πλευρᾶς τοῦ ὀκταέδρου.
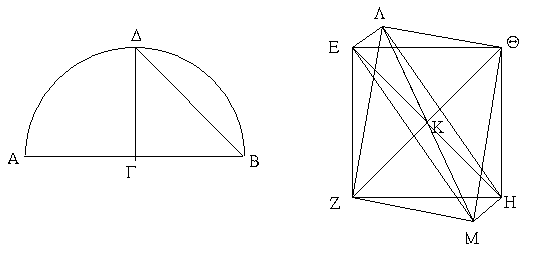
Ἐκκείσθω ἡ τῆς δοθείσης σφαίρας διάμετρος ἡ ΑΒ, καὶ τετμήσθω δίχα κατὰ τὸ Γ, καὶ γεγράφθω ἐπὶ τῆς ΑΒ ἡμικύκλιον τὸ ΑΔΒ, καὶ ἤχθω ἀπὸ τοῦ Γ τῇ ΑΒ πρὸς ὀρθὰς ἡ ΓΔ, καὶ ἐπεζεύχθω ἡ ΔΒ, καὶ ἐκκείσθω τετράγωνον τὸ ΕΖΗΘ ἴσην ἔχον ἑκάστην τῶν πλευρῶν τῇ ΔΒ, καὶ ἐπεζεύχθωσαν αἱ ΘΖ, ΕΗ, καὶ ἀνεστάτω ἀπὸ τοῦ Κ σημείου τῷ τοῦ ΕΖΗΘ τετραγώνου ἐπιπέδῳ πρὸς ὀρθὰς εὐθεῖα ἡ ΚΛ καὶ διήχθω ἐπὶ τὰ ἕτερα μέρη τοῦ ἐπιπέδου ὡς ἡ ΚΜ, καὶ ἀφῃρήσθω ἀφ' ἑκατέρας τῶν ΚΛ, ΚΜ μιᾷ τῶν ΕΚ, ΖΚ, ΗΚ, ΘΚ ἴση ἑκατέρα τῶν ΚΛ, ΚΜ, καὶ ἐπεζεύχθωσαν αἱ ΛΕ, ΛΖ, ΛΗ, ΛΘ, ΜΕ, ΜΖ, ΜΗ, ΜΘ. καὶ ἐπεὶ ἴση ἐστὶν ἡ ΚΕ τῇ ΚΘ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΕΚΘ γωνία, τὸ ἄρα ἀπὸ τῆς ΘΕ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΕΚ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΛΚ τῇ ΚΕ, καί ἐστιν ὀρθὴ ἡ ὑπὸ ΛΚΕ γωνία, τὸ ἄρα ἀπὸ τῆς ΕΛ διπλάσιόν ἐστι τοῦ ἀπὸ ΕΚ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΘΕ διπλάσιον τοῦ ἀπὸ τῆς ΕΚ· τὸ ἄρα ἀπὸ τῆς ΛΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΘ· ἴση ἄρα ἐστὶν ἡ ΛΕ τῇ ΕΘ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΛΘ τῇ ΘΕ ἐστιν ἴση· ἰσόπλευρον ἄρα ἐστὶ τὸ ΛΕΘ τρίγωνον. ὁμοίως δὴ δείξομεν, ὅτι καὶ ἕκαστον τῶν λοιπῶν τριγώνων, ὧν βάσεις μέν εἰσιν αἱ τοῦ ΕΖΗΘ τετραγώνου πλευραί, κορυφαὶ δὲ τὰ Λ, Μ σημεῖα, ἰσόπλευρόν ἐστιν· ὀκτάεδρον ἄρα συνέσταται ὑπὸ ὀκτὼ τριγώνων ἰσοπλεύρων περιεχόμενον.
Δεῖ δὴ αὐτὸ καὶ σφαίρᾳ περιλαβεῖν τῇ δοθείσῃ καὶ δεῖξαι, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασίων ἐστὶ τῆς τοῦ ὀκταέδρου πλευρᾶς.
Ἐπεὶ γὰρ αἱ τρεῖς αἱ ΛΚ, ΚΜ, ΚΕ ἴσαι ἀλλήλαις εἰσίν, τὸ ἄρα ἐπὶ τῆς ΛΜ γραφόμενον ἡμικύκλιον ἥξει καὶ διὰ τοῦ Ε. καὶ διὰ τὰ αὐτά, ἐὰν μενούσης τῆς ΛΜ περιενεχθὲν τὸ ἡμικύκλιον εἰς τὸ αὐτὸ ἀποκατασταθῇ, ὅθεν ἤρξατο φέρεσθαι, ἥξει καὶ διὰ τῶν Ζ, Η, Θ σημείων, καὶ ἔσται σφαίρᾳ περιειλημμένον τὸ ὀκτάεδρον. λέγω δή, ὅτι καὶ τῇ δοθείσῃ. ἐπεὶ γὰρ ἴση ἐστὶν ἡ ΛΚ τῇ ΚΜ, κοινὴ δὲ ἡ ΚΕ, καὶ γωνίας ὀρθὰς περιέχουσιν, βάσις ἄρα ἡ ΛΕ βάσει τῇ ΕΜ ἐστιν ἴση. καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΛΕΜ γωνία· ἐν ἡμικυκλίῳ γάρ· τὸ ἄρα ἀπὸ τῆς ΛΜ διπλάσιόν ἐστι τοῦ ἀπὸ τῆς ΛΕ. πάλιν, ἐπεὶ ἴση ἐστὶν ἡ ΑΓ τῇ ΓΒ, διπλασία ἐστὶν ἡ ΑΒ τῆς ΒΓ. ὡς δὲ ἡ ΑΒ πρὸς τὴν ΒΓ, οὕτως τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΔ· διπλάσιον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΑΒ τοῦ ἀπὸ τῆς ΒΔ. ἐδείχθη δὲ καὶ τὸ ἀπὸ τῆς ΛΜ διπλάσιον τοῦ ἀπὸ τῆς ΛΕ. καί ἐστιν ἴσον τὸ ἀπὸ τῆς ΔΒ τῷ ἀπὸ τῆς ΛΕ· ἴση γὰρ κεῖται ἡ ΕΘ τῇ ΔΒ. ἴσον ἄρα καὶ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΛΜ· ἴση ἄρα ἡ ΑΒ τῇ ΛΜ. καί ἐστιν ἡ ΑΒ ἡ τῆς δοθείσης σφαίρας διάμετρος· ἡ ΛΜ ἄρα ἴση ἐστὶ τῇ τῆς δοθείσης σφαίρας διαμέτρῳ.
Περιείληπται ἄρα τὸ ὀκτάεδρον τῇ δοθείσῃ σφαίρᾳ. καὶ συναποδέδεικται, ὅτι ἡ τῆς σφαίρας διάμετρος δυνάμει διπλασίων ἐστὶ τῆς τοῦ ὀκταέδρου πλευρᾶς· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιγ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου