Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις οβ΄ [72]
Δύο μέσων ἀσυμμέτρων ἀλλήλοις συντιθεμένων αἱ λοιπαὶ δύο ἄλογοι γίγνονται ἤτοι ἐκ δύο μέσων δευτέρα ἢ [ἡ] δύο μέσα δυναμένη.
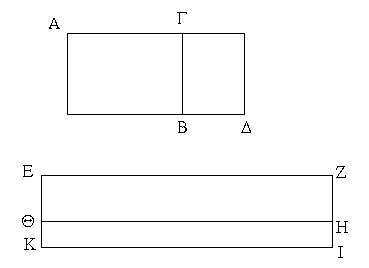
Συγκείσθω γὰρ δύο μέσα ἀσύμμετρα ἀλλήλοις τὰ ΑΒ, ΓΔ· λέγω, ὅτι ἡ τὸ ΑΔ χωρίον δυναμένη ἤτοι ἐκ δύο μέσων ἐστὶ δευτέρα ἢ δύο μέσα δυναμένη.
Τὸ γὰρ ΑΒ τοῦ ΓΔ ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. ἔστω, εἰ τύχοι, πρότερον μεῖζον τὸ ΑΒ τοῦ ΓΔ· καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τῷ μὲν ΑΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω τὸ ΕΗ πλάτος ποιοῦν τὴν ΕΘ, τῷ δὲ ΓΔ ἴσον τὸ ΘΙ πλάτος ποιοῦν τὴν ΘΚ. καὶ ἐπεὶ μέσον ἐστὶν ἑκάτερον τῶν ΑΒ, ΓΔ, μέσον ἄρα καὶ ἑκάτερον τῶν ΕΗ, ΘΙ. καὶ παρὰ ῥητὴν τὴν ΖΕ παράκειται πλάτος ποιοῦν τὰς ΕΘ, ΘΚ· ἑκατέρα ἄρα τῶν ΕΘ, ΘΚ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΑΒ τῷ ΓΔ, καί ἐστιν ἴσον τὸ μὲν ΑΒ τῷ ΕΗ, τὸ δὲ ΓΔ τῷ ΘΙ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΕΗ τῷ ΘΙ. ὡς δὲ τὸ ΕΗ πρὸς τὸ ΘΙ, οὕτως ἐστὶν ἡ ΕΘ πρὸς ΘΚ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΘ τῇ ΘΚ μήκει. αἱ ΕΘ, ΘΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἐκ δύο ἄρα ὀνομάτων ἐστὶν ἡ ΕΚ. ἤτοι δὲ ἡ ΕΘ τῆς ΘΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ ἢ τῷ ἀπὸ ἀσυμμέτρου. δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου ἑαυτῇ μήκει· καὶ οὐδετέρα τῶν ΕΘ, ΘΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ τῇ ΕΖ μήκει· ἡ ΕΚ ἄρα ἐκ δύο ὀνομάτων ἐστὶ τρίτη. ῥητὴ δὲ ἡ ΕΖ· ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων τρίτης, ἡ τὸ χωρίον δυναμένη ἐκ δύο μέσων ἐστὶ δευτέρα· ἡ ἄρα τὸ ΕΙ, τουτέστι τὸ ΑΔ, δυναμένη ἐκ δύο μέσων ἐστὶ δευτέρα. ἀλλὰ δὴ ἡ ΕΘ τῆς ΘΚ μεῖζον δυνάσθω τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ μήκει· καὶ ἀσύμμετρός ἐστιν ἑκατέρα τῶν ΕΘ, ΘΚ τῇ ΕΖ μήκει· ἡ ἄρα ΕΚ ἐκ δύο ὀνομάτων ἐστὶν ἕκτη. ἐὰν δὲ χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων ἕκτης, ἡ τὸ χωρίον δυναμένη ἡ δύο μέσα δυναμένη ἐστίν· ὥστε καὶ ἡ τὸ ΑΔ χωρίον δυναμένη ἡ δύο μέσα δυναμένη ἐστίν.
[Ὁμοίως δὴ δείξομεν, ὅτι κἂν ἔλαττον ᾖ τὸ ΑΒ τοῦ ΓΔ, ἡ τὸ ΑΔ χωρίον δυναμένη ἢ ἐκ δύο μέσων δευτέρα ἐστὶν ἤτοι δύο μέσα δυναμένη].
Δύο ἄρα μέσων ἀσυμμέτρων ἀλλήλοις συντιθεμένων αἱ λοιπαὶ δύο ἄλογοι γίγνονται ἤτοι ἐκ δύο μέσων δευτέρα ἢ δύο μέσα δυναμένη.
Ἡ ἐκ δύο ὀνομάτων καὶ αἱ μετ' αὐτὴν ἄλογοι οὔτε τῇ μέσῃ οὔτε ἀλλήλαις εἰσὶν αἱ αὐταί. τὸ μὲν γὰρ ἀπὸ μέσης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ῥητὴν καὶ ἀσύμμετρον τῇ παρ' ἣν παράκειται μήκει. τὸ δὲ ἀπὸ τῆς ἐκ δύο ὀνομάτων παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πρώτην. τὸ δὲ ἀπὸ τῆς ἐκ δύο μέσων πρώτης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων δευτέραν. τὸ δὲ ἀπὸ τῆς ἐκ δύο μέσων δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τρίτην. τὸ δὲ ἀπὸ τῆς μείζονος παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων τετάρτην. τὸ δὲ ἀπὸ τῆς ῥητὸν καὶ μέσον δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων πέμπτην. τὸ δὲ ἀπὸ τῆς δύο μέσα δυναμένης παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ τὴν ἐκ δύο ὀνομάτων ἕκτην. τὰ δ' εἰρημένα πλάτη διαφέρει τοῦ τε πρώτου καὶ ἀλλήλων, τοῦ μὲν πρώτου, ὅτι ῥητή ἐστιν, ἀλλήλων δέ, ὅτι τῇ τάξει οὐκ εἰσὶν αἱ αὐταί· ὥστε καὶ αὐταὶ αἱ ἄλογοι διαφέρουσιν ἀλλήλων.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου