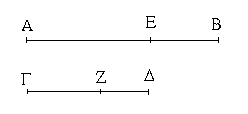Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ξη΄ [68]
Ἡ τῇ μείζονι σύμμετρος καὶ αὐτὴ μείζων ἐστίν.
Ἔστω μείζων ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἔστω ἡ ΓΔ· λέγω, ὅτι ἡ ΓΔ μείζων ἐστίν.
Διῃρήσθω ἡ ΑΒ κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα δυνάμει εἰσὶν ἀσύμμετροι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ῥητόν, τὸ δ' ὑπ' αὐτῶν μέσον· καὶ γεγονέτω τὰ αὐτὰ τοῖς πρότερον. καὶ ἐπεί ἐστιν ὡς ἡ ΑΒ πρὸς τὴν ΓΔ, οὕτως ἥ τε ΑΕ πρὸς τὴν ΓΖ καὶ ἡ ΕΒ πρὸς τὴν ΖΔ, καὶ ὡς ἄρα ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΒ πρὸς τὴν ΖΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ. σύμμετρος ἄρα καὶ ἑκατέρα τῶν ΑΕ, ΕΒ ἑκατέρᾳ τῶν ΓΖ, ΖΔ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΒ πρὸς τὴν ΖΔ, καὶ ἐναλλὰξ ὡς ἡ ΑΕ πρὸς ΕΒ, οὕτως ἡ ΓΖ πρὸς ΖΔ, καὶ συνθέντι ἄρα ἐστὶν ὡς ἡ ΑΒ πρὸς τὴν ΒΕ, οὕτως ἡ ΓΔ πρὸς τὴν ΔΖ· καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΕ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΔΖ. ὁμοίως δὴ δείξομεν, ὅτι καὶ ὡς τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΑΕ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΓΖ. καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΒ πρὸς τὰ ἀπὸ τῶν ΑΕ, ΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΔ πρὸς τὰ ἀπὸ τῶν ΓΖ, ΖΔ· καὶ ἐναλλὰξ ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΓΔ, οὕτως τὰ ἀπὸ τῶν ΑΕ, ΕΒ πρὸς τὰ ἀπὸ τῶν ΓΖ, ΖΔ. σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΒ τῷ ἀπὸ τῆς ΓΔ· σύμμετρα ἄρα καὶ τὰ ἀπὸ τῶν ΑΕ, ΕΒ τοῖς ἀπὸ τῶν ΓΖ, ΖΔ. καί ἐστι τὰ ἀπὸ τῶν ΑΕ, ΕΒ ἅμα ῥητόν, καὶ τὰ ἀπὸ τῶν ΓΖ, ΖΔ ἅμα ῥητόν ἐστιν. ὁμοίως δὲ καὶ τὸ δὶς ὑπὸ τῶν ΑΕ, ΕΒ σύμμετρόν ἐστι τῷ δὶς ὑπὸ τῶν ΓΖ, ΖΔ. καί ἐστι μέσον τὸ δὶς ὑπὸ τῶν ΑΕ, ΕΒ· μέσον ἄρα καὶ τὸ δὶς ὑπὸ τῶν ΓΖ, ΖΔ. αἱ ΓΖ, ΖΔ ἄρα δυνάμει ἀσύμμετροί εἰσι ποιοῦσαι τὸ μὲν συγκείμενον ἐκ τῶν ἀπ' αὐτῶν τετραγώνων ἅμα ῥητόν, τὸ δὲ δὶς ὑπ' αὐτῶν μέσον· ὅλη ἄρα ἡ ΓΔ ἄλογός ἐστιν ἡ καλουμένη μείζων.
Ἡ ἄρα τῇ μείζονι σύμμετρος μείζων ἐστίν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου