Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις νε΄ [55]
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ τῆς ἐκ δύο ὀνομάτων δευτέρας, ἡ τὸ χωρίον δυναμένη ἄλογός ἐστιν ἡ καλουμένη ἐκ δύο μέσων πρώτη.
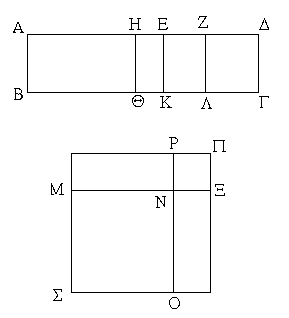
Περιεχέσθω γὰρ χωρίον τὸ ΑΒΓΔ ὑπὸ ῥητῆς τῆς ΑΒ καὶ τῆς ἐκ δύο ὀνομάτων δευτέρας τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΓ χωρίον δυναμένη ἐκ δύο μέσων πρώτη ἐστίν.
Ἐπεὶ γὰρ ἐκ δύο ὀνομάτων δευτέρα ἐστὶν ἡ ΑΔ, διῃρήσθω εἰς τὰ ὀνόματα κατὰ τὸ Ε, ὥστε τὸ μεῖζον ὄνομα εἶναι τὸ ΑΕ· αἱ ΑΕ, ΕΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ ἡ ΑΕ τῆς ΕΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ τὸ ἔλαττον ὄνομα ἡ ΕΔ σύμμετρόν ἐστι τῇ ΑΒ μήκει. τετμήσθω ἡ ΕΔ δίχα κατὰ τὸ Ζ, καὶ τῷ ἀπὸ τῆς ΕΖ ἴσον παρὰ τὴν ΑΕ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ τὸ ὑπὸ τῶν ΑΗΕ· σύμμετρος ἄρα ἡ ΑΗ τῇ ΗΕ μήκει.
καὶ διὰ τῶν Η, Ε, Ζ παράλληλοι ἤχθωσαν ταῖς ΑΒ, ΓΔ αἱ ΗΘ, ΕΚ, ΖΛ, καὶ τῷ μὲν ΑΘ παραλληλογράμμῳ ἴσον τετράγωνον συνεστάτω τὸ ΣΝ, τῷ δὲ ΗΚ ἴσον τετράγωνον τὸ ΝΠ, καὶ κείσθω ὥστε ἐπ᾿ εὐθείας εἶναι τὴν ΜΝ τῇ ΝΞ· ἐπ᾿ εὐθείας ἄρα [ἐστὶ] καὶ ἡ ΡΝ τῇ ΝΟ. καὶ συμπεπληρώσθω τὸ ΣΠ τετράγωνον· φανερὸν δὴ ἐκ τοῦ προδεδειγμένου, ὅτι τὸ ΜΡ μέσον ἀνάλογόν ἐστι τῶν ΣΝ, ΝΠ, καὶ ἴσον τῷ ΕΛ, καὶ ὅτι τὸ ΑΓ χωρίον δύναται ἡ ΜΞ. δεικτέον δή, ὅτι ἡ ΜΞ ἐκ δύο μέσων ἐστὶ πρώτη. ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΕ τῇ ΕΔ μήκει, σύμμετρος δὲ ἡ ΕΔ τῇ ΑΒ, ἀσύμμετρος ἄρα ἡ ΑΕ τῇ ΑΒ. καὶ ἐπεὶ σύμμετρός ἐστιν ἡ ΑΗ τῇ ΕΗ, σύμμετρός ἐστι καὶ ἡ ΑΕ ἑκατέρᾳ τῶν ΑΗ, ΗΕ. ἀλλὰ ἡ ΑΕ ἀσύμμετρος τῇ ΑΒ μήκει· καὶ αἱ ΑΗ, ΗΕ ἄρα ἀσύμμετροί εἰσι τῇ ΑΒ. αἱ ΒΑ, ΑΗ, ΗΕ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ὥστε μέσον ἐστὶν ἑκάτερον τῶν ΑΘ, ΗΚ. ὥστε καὶ ἑκάτερον τῶν ΣΝ, ΝΠ μέσον ἐστίν. καὶ αἱ ΜΝ, ΝΞ ἄρα μέσαι εἰσίν. καὶ ἐπεὶ σύμμετρος ἡ ΑΗ τῇ ΗΕ μήκει, σύμμετρόν ἐστι καὶ τὸ ΑΘ τῷ ΗΚ, τουτέστι τὸ ΣΝ τῷ ΝΠ, τουτέστι τὸ ἀπὸ τῆς ΜΝ τῷ ἀπὸ τῆς ΝΞ [ὥστε δυνάμει εἰσὶ σύμμετροι αἱ ΜΝ, ΝΞ]. καὶ ἐπεὶ ἀσύμμετρός ἐστιν ἡ ΑΕ τῇ ΕΔ μήκει, ἀλλ' ἡ μὲν ΑΕ σύμμετρός ἐστι τῇ ΑΗ, ἡ δὲ ΕΔ τῇ ΕΖ σύμμετρος, ἀσύμμετρος ἄρα ἡ ΑΗ τῇ ΕΖ· ὥστε καὶ τὸ ΑΘ τῷ ΕΛ ἀσύμμετρόν ἐστιν, τουτέστι τὸ ΣΝ τῷ ΜΡ, τουτέστιν ἡ ΟΝ τῇ ΝΡ, τουτέστιν ἡ ΜΝ τῇ ΝΞ ἀσύμμετρός ἐστι μήκει. ἐδείχθησαν δὲ αἱ ΜΝ, ΝΞ καὶ μέσαι οὖσαι καὶ δυνάμει σύμμετροι· αἱ ΜΝ, ΝΞ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. λέγω δή, ὅτι καὶ ῥητὸν περιέχουσιν. ἐπεὶ γὰρ ἡ ΔΕ ὑπόκειται ἑκατέρᾳ τῶν ΑΒ, ΕΖ σύμμετρος, σύμμετρος ἄρα καὶ ἡ ΕΖ τῇ ΕΚ. καὶ ῥητὴ ἑκατέρα αὐτῶν· ῥητὸν ἄρα τὸ ΕΛ, τουτέστι τὸ ΜΡ· τὸ δὲ ΜΡ ἐστι τὸ ὑπὸ τῶν ΜΝΞ. ἐὰν δὲ δύο μέσαι δυνάμει μόνον σύμμετροι συντεθῶσι ῥητὸν περιέχουσαι, ἡ ὅλη ἄλογός ἐστιν, καλεῖται δὲ ἐκ δύο μέσων πρώτη.
Ἡ ἄρα ΜΞ ἐκ δύο μέσων ἐστὶ πρώτη· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου