Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις κς΄. [26]
Μέσον μέσου οὐχ ὑπερέχει ῥητῷ.
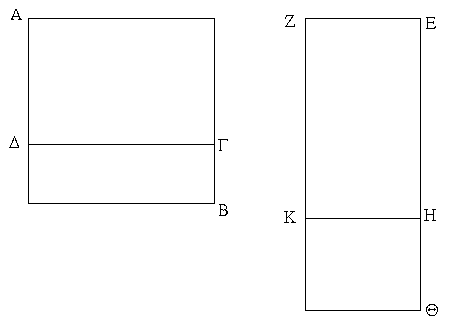
Εἰ γὰρ δυνατόν, μέσον τὸ ΑΒ μέσου τοῦ ΑΓ ὑπερεχέτω ῥητῷ τῷ ΔΒ, καὶ ἐκκείσθω ῥητὴ ἡ ΕΖ, καὶ τῷ ΑΒ ἴσον παρὰ τὴν ΕΖ παραβεβλήσθω παραλληλόγραμμον ὀρθογώνιον τὸ ΖΘ πλάτος ποιοῦν τὴν ΕΘ, τῷ δὲ ΑΓ ἴσον ἀφῃρήσθω τὸ ΖΗ· λοιπὸν ἄρα τὸ ΒΔ λοιπῷ τῷ ΚΘ ἐστιν ἴσον. ῥητὸν δέ ἐστι τὸ ΔΒ· ῥητὸν ἄρα ἐστὶ καὶ τὸ ΚΘ. ἐπεὶ οὖν μέσον ἐστὶν ἑκάτερον τῶν ΑΒ, ΑΓ, καί ἐστι τὸ μὲν ΑΒ τῷ ΖΘ ἴσον, τὸ δὲ ΑΓ τῷ ΖΗ, μέσον ἄρα καὶ ἑκάτερον τῶν ΖΘ, ΖΗ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἑκατέρα τῶν ΘΕ, ΕΗ καὶ ἀσύμμετρος τῇ ΕΖ μήκει. καὶ ἐπεὶ ῥητόν ἐστι τὸ ΔΒ καί ἐστιν ἴσον τῷ ΚΘ, ῥητὸν ἄρα ἐστὶ καὶ τὸ ΚΘ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται· ῥητὴ ἄρα ἐστὶν ἡ ΗΘ καὶ σύμμετρος τῇ ΕΖ μήκει. ἀλλὰ καὶ ἡ ΕΗ ῥητή ἐστι καὶ ἀσύμμετρος τῇ ΕΖ μήκει· ἀσύμμετρος ἄρα ἐστὶν ἡ ΕΗ τῇ ΗΘ μήκει. καί ἐστιν ὡς ἡ ΕΗ πρὸς τὴν ΗΘ, οὕτως τὸ ἀπὸ τῆς ΕΗ πρὸς τὸ ὑπὸ τῶν ΕΗ, ΗΘ· ἀσύμμετρον ἄρα ἐστὶ τὸ ἀπὸ τῆς ΕΗ τῷ ὑπὸ τῶν ΕΗ, ΗΘ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΕΗ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΕΗ, ΗΘ τετράγωνα· ῥητὰ γὰρ ἀμφότερα· τῷ δὲ ὑπὸ τῶν ΕΗ, ΗΘ σύμμετρόν ἐστι τὸ δὶς ὑπὸ τῶν ΕΗ, ΗΘ· διπλάσιον γάρ ἐστιν αὐτοῦ· ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΕΗ, ΗΘ τῷ δὶς ὑπὸ τῶν ΕΗ, ΗΘ· καὶ συναμφότερα ἄρα τά τε ἀπὸ τῶν ΕΗ, ΗΘ καὶ τὸ δὶς ὑπὸ τῶν ΕΗ, ΗΘ, ὅπερ ἐστὶ τὸ ἀπὸ τῆς ΕΘ, ἀσύμμετρόν ἐστι τοῖς ἀπὸ τῶν ΕΗ, ΗΘ. ῥητὰ δὲ τὰ ἀπὸ τῶν ΕΗ, ΗΘ· ἄλογον ἄρα τὸ ἀπὸ τῆς ΕΘ. ἄλογος ἄρα ἐστὶν ἡ ΕΘ. ἀλλὰ καὶ ῥητή· ὅπερ ἐστὶν ἀδύνατον.
Μέσον ἄρα μέσου οὐχ ὑπερέχει ῥητῷ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου