Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ρη΄ [108]
Ἀπὸ ῥητοῦ μέσου ἀφαιρουμένου ἡ τὸ λοιπὸν χωρίον δυναμένη μία δύο ἀλόγων γίνεται ἤτοι ἀποτομὴ ἢ ἐλάσσων.
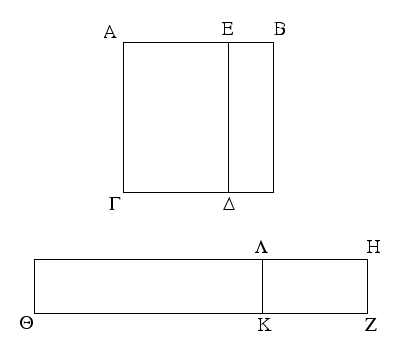
Ἀπὸ γὰρ ῥητοῦ τοῦ ΒΓ μέσον ἀφῃρήσθω τὸ ΒΔ· λέγω, ὅτι ἡ τὸ λοιπὸν δυναμένη τὸ ΕΓ μία δύο ἀλόγων γίνεται ἤτοι ἀποτομὴ ἢ ἐλάσσων.
Ἐκκείσθω γὰρ ῥητὴ ἡ ΖΗ, καὶ τῷ μὲν ΒΓ ἴσον παρὰ τὴν ΖΗ παραβεβλήσθω ὀρθογώνιον παραλληλόγραμμον τὸ ΗΘ, τῷ δὲ ΔΒ ἴσον ἀφῃρήσθω τὸ ΗΚ· λοιπὸν ἄρα τὸ ΕΓ ἴσον ἐστὶ τῷ ΛΘ. ἐπεὶ οὖν ῥητὸν μέν ἐστι τὸ ΒΓ, μέσον δὲ τὸ ΒΔ, ἴσον δὲ τὸ μὲν ΒΓ τῷ ΗΘ, τὸ δὲ ΒΔ τῷ ΗΚ, ῥητὸν μὲν ἄρα ἐστὶ τὸ ΗΘ, μέσον δὲ τὸ ΗΚ. καὶ παρὰ ῥητὴν τὴν ΖΗ παράκειται· ῥητὴ μὲν ἄρα ἡ ΖΘ καὶ σύμμετρος τῇ ΖΗ μήκει, ῥητὴ δὲ ἡ ΖΚ καὶ ἀσύμμετρος τῇ ΖΗ μήκει· ἀσύμμετρος ἄρα ἐστὶν ἡ ΖΘ τῇ ΖΚ μήκει. αἱ ΖΘ, ΖΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΘ, προσαρμόζουσα δὲ αὐτῇ ἡ ΚΖ. ἤτοι δὴ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἢ οὔ.
Δυνάσθω πρότερον τῷ ἀπὸ συμμέτρου. καί ἐστιν ὅλη ἡ ΘΖ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ· ἀποτομὴ ἄρα πρώτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς πρώτης περιεχόμενον ἡ δυναμένη ἀποτομή ἐστιν. ἡ ἄρα τὸ ΛΘ, τουτέστι τὸ ΕΓ, δυναμένη ἀποτομή ἐστιν.
Εἰ δὲ ἡ ΘΖ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ, καί ἐστιν ὅλη ἡ ΖΘ σύμμετρος τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ τετάρτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς τετάρτης περιεχόμενον ἡ δυναμένη ἐλάσσων ἐστίν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου