Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις Ϟγ΄ [93]
Ἐὰν χωρίον περιέχηται ὑπὸ ῥητῆς καὶ ἀποτομῆς τρίτης, ἡ τὸ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Χωρίον γὰρ τὸ ΑΒ περιεχέσθω ὑπὸ ῥητῆς τῆς ΑΓ καὶ ἀποτομῆς τρίτης τῆς ΑΔ· λέγω, ὅτι ἡ τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Ἔστω γὰρ τῇ ΑΔ προσαρμόζουσα ἡ ΔΗ· αἱ ΑΗ, ΗΔ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι, καὶ οὐδετέρα τῶν ΑΗ, ΗΔ σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΑΓ, ἡ δὲ ὅλη ἡ ΑΗ τῆς προσαρμοζούσης τῆς ΔΗ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. ἐπεὶ οὖν ἡ ΑΗ τῆς ΗΔ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, ἐὰν ἄρα τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΔΗ ἴσον παρὰ τὴν ΑΗ παραβληθῇ ἐλλεῖπον εἴδει τετραγώνῳ, εἰς σύμμετρα αὐτὴν διελεῖ. τετμήσθω οὖν ἡ ΔΗ δίχα κατὰ τὸ Ε, καὶ τῷ ἀπὸ τῆς ΕΗ ἴσον παρὰ τὴν ΑΗ παραβεβλήσθω ἐλλεῖπον εἴδει τετραγώνῳ, καὶ ἔστω τὸ ὑπὸ τῶν ΑΖ, ΖΗ. καὶ ἤχθωσαν διὰ τῶν Ε, Ζ, Η σημείων τῇ ΑΓ παράλληλοι αἱ ΕΘ, ΖΙ, ΗΚ· σύμμετροι ἄρα εἰσὶν αἱ ΑΖ, ΖΗ· σύμμετρον ἄρα καὶ τὸ ΑΙ τῷ ΖΚ. καὶ ἐπεὶ αἱ ΑΖ, ΖΗ σύμμετροί εἰσι μήκει, καὶ ἡ ΑΗ ἄρα ἑκατέρᾳ τῶν ΑΖ, ΖΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΑΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ὥστε καὶ αἱ ΑΖ, ΖΗ. ἑκάτερον ἄρα τῶν ΑΙ, ΖΚ μέσον ἐστίν. πάλιν, ἐπεὶ σύμμετρός ἐστιν ἡ ΔΕ τῇ ΕΗ μήκει, καὶ ἡ ΔΗ ἄρα ἑκατέρᾳ τῶν ΔΕ, ΕΗ σύμμετρός ἐστι μήκει. ῥητὴ δὲ ἡ ΗΔ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ῥητὴ ἄρα καὶ ἑκατέρα τῶν ΔΕ, ΕΗ καὶ ἀσύμμετρος τῇ ΑΓ μήκει· ἑκάτερον ἄρα τῶν ΔΘ, ΕΚ μέσον ἐστίν. καὶ ἐπεὶ αἱ ΑΗ, ΗΔ δυνάμει μόνον σύμμετροί εἰσιν, ἀσύμμετρος ἄρα ἐστὶ μήκει ἡ ΑΗ τῇ ΗΔ. ἀλλ' ἡ μὲν ΑΗ τῇ ΑΖ σύμμετρός ἐστι μήκει, ἡ δὲ ΔΗ τῇ ΕΗ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΑΖ τῇ ΕΗ μήκει. ὡς δὲ ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΕΚ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΑΙ τῷ ΕΚ.
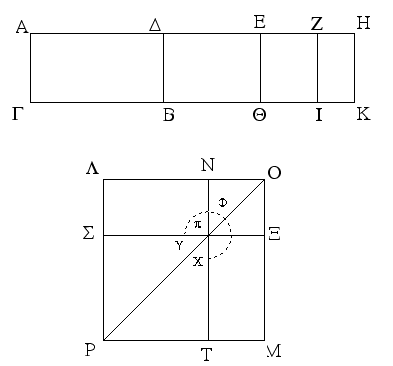
Συνεστάτω οὖν τῷ μὲν ΑΙ ἴσον τετράγωνον τὸ ΛΜ, τῷ δὲ ΖΚ ἴσον ἀφῃρήσθω τὸ ΝΞ περὶ τὴν αὐτὴν γωνίαν ὂν τῷ ΛΜ· περὶ τὴν αὐτὴν ἄρα διάμετρόν ἐστι τὰ ΛΜ, ΝΞ. ἔστω αὐτῶν διάμετρος ἡ ΟΡ, καὶ καταγεγράφθω τὸ σχῆμα. ἐπεὶ οὖν τὸ ὑπὸ τῶν ΑΖ, ΖΗ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΕΗ, ἔστιν ἄρα ὡς ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΗ. ἀλλ' ὡς μὲν ἡ ΑΖ πρὸς τὴν ΕΗ, οὕτως ἐστὶ τὸ ΑΙ πρὸς τὸ ΕΚ· ὡς δὲ ἡ ΕΗ πρὸς τὴν ΖΗ, οὕτως ἐστὶ τὸ ΕΚ πρὸς τὸ ΖΚ· καὶ ὡς ἄρα τὸ ΑΙ πρὸς τὸ ΕΚ, οὕτως τὸ ΕΚ πρὸς τὸ ΖΚ· τῶν ἄρα ΑΙ, ΖΚ μέσον ἀνάλογόν ἐστι τὸ ΕΚ. ἔστι δὲ καὶ τῶν ΛΜ, ΝΞ τετραγώνων μέσον ἀνάλογον τὸ ΜΝ· καί ἐστιν ἴσον τὸ μὲν ΑΙ τῷ ΛΜ, τὸ δὲ ΖΚ τῷ ΝΞ· καὶ τὸ ΕΚ ἄρα ἴσον ἐστὶ τῷ ΜΝ. ἀλλὰ τὸ μὲν ΜΝ ἴσον ἐστὶ τῷ ΛΞ, τὸ δὲ ΕΚ ἴσον [ἐστὶ] τῷ ΔΘ· καὶ ὅλον ἄρα τὸ ΔΚ ἴσον ἐστὶ τῷ ΥΦΧ γνώμονι καὶ τῷ ΝΞ. ἔστι δὲ καὶ τὸ ΑΚ ἴσον τοῖς ΛΜ, ΝΞ· λοιπὸν ἄρα τὸ ΑΒ ἴσον ἐστὶ τῷ ΣΤ, τουτέστι τῷ ἀπὸ τῆς ΛΝ τετραγώνῳ· ἡ ΛΝ ἄρα δύναται τὸ ΑΒ χωρίον.
Λέγω, ὅτι ἡ ΛΝ μέσης ἀποτομή ἐστι δευτέρα.
Ἐπεὶ γὰρ μέσα ἐδείχθη τὰ ΑΙ, ΖΚ καί ἐστιν ἴσα τοῖς ἀπὸ τῶν ΛΟ, ΟΝ, μέσον ἄρα καὶ ἑκάτερον τῶν ἀπὸ τῶν ΛΟ, ΟΝ· μέση ἄρα ἑκατέρα τῶν ΛΟ, ΟΝ. καὶ ἐπεὶ σύμμετρόν ἐστι τὸ ΑΙ τῷ ΖΚ, σύμμετρον ἄρα καὶ τὸ ἀπὸ τῆς ΛΟ τῷ ἀπὸ τῆς ΟΝ. πάλιν, ἐπεὶ ἀσύμμετρον ἐδείχθη τὸ ΑΙ τῷ ΕΚ, ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ΛΜ τῷ ΜΝ, τουτέστι τὸ ἀπὸ τῆς ΛΟ τῷ ὑπὸ τῶν ΛΟ, ΟΝ· ὥστε καὶ ἡ ΛΟ ἀσύμμετρός ἐστι τῇ ΟΝ· αἱ ΛΟ, ΟΝ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι.
Λέγω δή, ὅτι καὶ μέσον περιέχουσιν.
Ἐπεὶ γὰρ μέσον ἐδείχθη τὸ ΕΚ καί ἐστιν ἴσον τῷ ὑπὸ τῶν ΛΟ, ΟΝ, μέσον ἄρα ἐστὶ καὶ τὸ ὑπὸ τῶν ΛΟ, ΟΝ· ὥστε αἱ ΛΟ, ΟΝ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι. ἡ ΛΝ ἄρα μέσης ἀποτομή ἐστι δευτέρα· καὶ δύναται τὸ ΑΒ χωρίον.
Ἡ ἄρα τὸ ΑΒ χωρίον δυναμένη μέσης ἀποτομή ἐστι δευτέρα· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου