Στοιχεῖα Εὐκλείδου δ΄
[Βιβλίον IV]
Αἱ Προτάσεις τῶν Στοιχείων δ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις γ΄. [3]
Περὶ τὸν δοθέντα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον περιγράψαι.
Ἔστω ὁ δοθεὶς κύκλος ὁ ΑΒΓ, τὸ δὲ δοθὲν τρίγωνον τὸ ΔΕΖ· δεῖ δὴ περὶ τὸν ΑΒΓ κύκλον τῷ ΔΕΖ τριγώνῳ ἰσογώνιον τρίγωνον περιγράψαι.
Ἐκβεβλήσθω ἡ ΕΖ ἐφ' ἑκάτερα τὰ μέρη κατὰ τὰ Η, Θ σημεῖα, καὶ εἰλήφθω τοῦ ΑΒΓ κύκλου κέντρον τὸ Κ, καὶ διήχθω, ὡς ἔτυχεν, εὐθεῖα ἡ ΚΒ, καὶ συνεστάτω πρὸς τῇ ΚΒ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Κ τῇ μὲν ὑπὸ ΔΕΗ γωνίᾳ ἴση ἡ ὑπὸ ΒΚΑ, τῇ δὲ ὑπὸ ΔΖΘ ἴση ἡ ὑπὸ ΒΚΓ, καὶ διὰ τῶν Α, Β, Γ σημείων ἤχθωσαν ἐφαπτόμεναι τοῦ ΑΒΓ κύκλου αἱ ΛΑΜ, ΜΒΝ, ΝΓΛ.
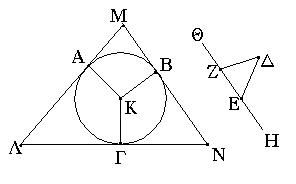
Καὶ ἐπεὶ ἐφάπτονται τοῦ ΑΒΓ κύκλου αἱ ΛΜ, ΜΝ, ΝΛ κατὰ τὰ Α, Β, Γ σημεῖα, ἀπὸ δὲ τοῦ Κ κέντρου ἐπὶ τὰ Α, Β, Γ σημεῖα ἐπεζευγμέναι εἰσὶν αἱ ΚΑ, ΚΒ, ΚΓ, ὀρθαὶ ἄρα εἰσὶν αἱ πρὸς τοῖς Α, Β, Γ σημείοις γωνίαι. καὶ ἐπεὶ τοῦ ΑΜΒΚ τετραπλεύρου αἱ τέσσαρες γωνίαι τέτρασιν ὀρθαῖς ἴσαι εἰσίν, ἐπειδήπερ καὶ εἰς δύο τρίγωνα διαιρεῖται τὸ ΑΜΒΚ, καί εἰσιν ὀρθαὶ αἱ ὑπὸ ΚΑΜ, ΚΒΜ γωνίαι, λοιπαὶ ἄρα αἱ ὑπὸ ΑΚΒ, ΑΜΒ δυσὶν ὀρθαῖς ἴσαι εἰσίν. εἰσὶ δὲ καὶ αἱ ὑπὸ ΔΕΗ, ΔΕΖ δυσὶν ὀρθαῖς ἴσαι· αἱ ἄρα ὑπὸ ΑΚΒ, ΑΜΒ ταῖς ὑπὸ ΔΕΗ, ΔΕΖ ἴσαι εἰσίν, ὧν ἡ ὑπὸ ΑΚΒ τῇ ὑπὸ ΔΕΗ ἐστιν ἴση· λοιπὴ ἄρα ἡ ὑπὸ ΑΜΒ λοιπῇ τῇ ὑπὸ ΔΕΖ ἐστιν ἴση. ὁμοίως δὴ δειχθήσεται, ὅτι καὶ ἡ ὑπὸ ΛΝΒ τῇ ὑπὸ ΔΖΕ ἐστιν ἴση· καὶ λοιπὴ ἄρα ἡ ὑπὸ ΜΛΝ [λοιπῇ] τῇ ὑπὸ ΕΔΖ ἐστιν ἴση. ἰσογώνιον ἄρα ἐστὶ τὸ ΛΜΝ τρίγωνον τῷ ΔΕΖ τριγώνῳ· καὶ περιγέγραπται περὶ τὸν ΑΒΓ κύκλον.
Περὶ τὸν δοθέντα ἄρα κύκλον τῷ δοθέντι τριγώνῳ ἰσογώνιον τρίγωνον περιγέγραπται· ὅπερ ἔδει ποιῆσαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων δ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου