Στοιχεῖα Εὐκλείδου ς΄
[Βιβλίον VI]
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις β΄. [2]
Ἐὰν τριγώνου παρὰ μίαν τῶν πλευρῶν ἀχθῇ τις εὐθεῖα, ἀνάλογον τεμεῖ τὰς τοῦ τριγώνου πλευράς· καὶ ἐὰν αἱ τοῦ τριγώνου πλευραὶ ἀνάλογον τμηθῶσιν, ἡ ἐπὶ τὰς τομὰς ἐπιζευγνυμένη εὐθεῖα παρὰ τὴν λοιπὴν ἔσται τοῦ τριγώνου πλευράν.
Τριγώνου γὰρ τοῦ ΑΒΓ παράλληλος μιᾷ τῶν πλευρῶν τῇ ΒΓ ἤχθω ἡ ΔΕ· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΕ, ΓΔ.
Ἴσον ἄρα ἐστὶ ΒΔΕ τρίγωνον τῷ ΓΔΕ τριγώνῳ· ἐπὶ γὰρ τῆς αὐτῆς βάσεώς ἐστι τῆς ΔΕ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΔΕ, ΒΓ· ἄλλο δέ τι τὸ ΑΔΕ τρίγωνον. τὰ δὲ ἴσα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον· ἔστιν ἄρα ὡς τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ [τρίγωνον], οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον. ἀλλ' ὡς μὲν τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ, οὕτως ἡ ΒΔ πρὸς τὴν ΔΑ· ὑπὸ γὰρ τὸ αὐτὸ ὕψος ὄντα τὴν ἀπὸ τοῦ Ε ἐπὶ τὴν ΑΒ κάθετον ἀγομένην πρὸς ἄλληλά εἰσιν ὡς αἱ βάσεις. διὰ τὰ αὐτὰ δὴ ὡς τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ· καὶ ὡς ἄρα ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ.
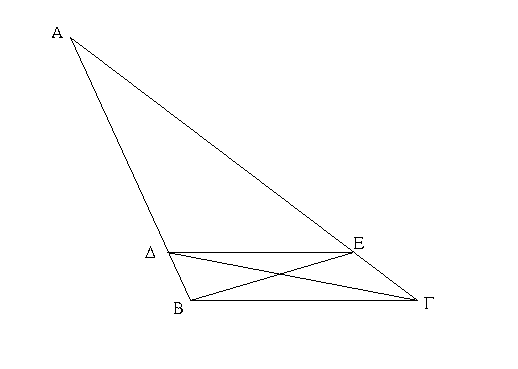
Ἀλλὰ δὴ αἱ τοῦ ΑΒΓ τριγώνου πλευραὶ αἱ ΑΒ, ΑΓ ἀνάλογον τετμήσθωσαν, ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ, καὶ ἐπεζεύχθω ἡ ΔΕ· λέγω, ὅτι παράλληλός ἐστιν ἡ ΔΕ τῇ ΒΓ.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως ἡ ΓΕ πρὸς τὴν ΕΑ, ἀλλ' ὡς μὲν ἡ ΒΔ πρὸς τὴν ΔΑ, οὕτως τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, ὡς δὲ ἡ ΓΕ πρὸς τὴν ΕΑ, οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, καὶ ὡς ἄρα τὸ ΒΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον, οὕτως τὸ ΓΔΕ τρίγωνον πρὸς τὸ ΑΔΕ τρίγωνον. ἑκάτερον ἄρα τῶν ΒΔΕ, ΓΔΕ τριγώνων πρὸς τὸ ΑΔΕ τὸν αὐτὸν ἔχει λόγον. ἴσον ἄρα ἐστὶ τὸ ΒΔΕ τρίγωνον τῷ ΓΔΕ τριγώνῳ· καί εἰσιν ἐπὶ τῆς αὐτῆς βάσεως τῆς ΔΕ. τὰ δὲ ἴσα τρίγωνα καὶ ἐπὶ τῆς αὐτῆς βάσεως ὄντα καὶ ἐν ταῖς αὐταῖς παραλλήλοις ἐστίν. παράλληλος ἄρα ἐστὶν ἡ ΔΕ τῇ ΒΓ.
Ἐὰν ἄρα τριγώνου παρὰ μίαν τῶν πλευρῶν ἀχθῇ τις εὐθεῖα, ἀνάλογον τεμεῖ τὰς τοῦ τριγώνου πλευράς· καὶ ἐὰν αἱ τοῦ τριγώνου πλευραὶ ἀνάλογον τμηθῶσιν, ἡ ἐπὶ τὰς τομὰς ἐπιζευγνυμένη εὐθεῖα παρὰ τὴν λοιπὴν ἔσται τοῦ τριγώνου πλευράν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Περιεχόμενα Στοιχείων Εὐκλείδου