Στοιχεῖα Εὐκλείδου β΄
[Βιβλίον II]
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις γ΄. [3]
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ προειρημένου τμήματος τετραγώνῳ.
Εὐθεῖα γὰρ ἡ ΑΒ τετμήσθω, ὡς ἔτυχεν, κατὰ τὸ Γ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΒΓ τετραγώνου.
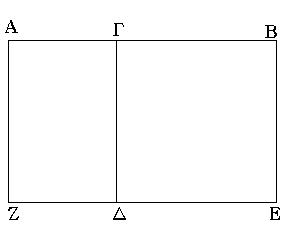
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΒ τετράγωνον τὸ ΓΔΕΒ, καὶ διήχθω ἡ ΕΔ ἐπὶ τὸ Ζ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΔ, ΒΕ παράλληλος ἤχθω ἡ ΑΖ. ἴσον δή ἐστι τὸ ΑΕ τοῖς ΑΔ, ΓΕ· καί ἐστι τὸ μὲν ΑΕ τὸ ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον· περιέχεται μὲν γὰρ ὑπὸ τῶν ΑΒ, ΒΕ, ἴση δὲ ἡ ΒΕ τῇ ΒΓ· τὸ δὲ ΑΔ τὸ ὑπὸ τῶν ΑΓ, ΓΒ· ἴση γὰρ ἡ ΔΓ τῇ ΓΒ· τὸ δὲ ΔΒ τὸ ἀπὸ τῆς ΓΒ τετράγωνον· τὸ ἄρα ὑπὸ τῶν ΑΒ, ΒΓ περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΓ, ΓΒ περιεχομένῳ ὀρθογωνίῳ μετὰ τοῦ ἀπὸ τῆς ΒΓ τετραγώνου.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ, ὡς ἔτυχεν, τὸ ὑπὸ τῆς ὅλης καὶ ἑνὸς τῶν τμημάτων περιεχόμενον ὀρθογώνιον ἴσον ἐστὶ τῷ τε ὑπὸ τῶν τμημάτων περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τοῦ προειρημένου τμήματος τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Περιεχόμενα Στοιχείων Εὐκλείδου