Στοιχεῖα Εὐκλείδου ιβ΄
[Βιβλίον XII]
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ζ΄. [7]
Πᾶν πρίσμα τρίγωνον ἔχον βάσιν διαιρεῖται εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους βάσεις ἐχούσας.
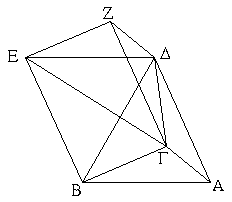
Ἔστω πρίσμα, οὗ βάσις μὲν τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ· λέγω, ὅτι τὸ ΑΒΓΔΕΖ πρίσμα διαιρεῖται εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους ἐχούσας βάσεις.
Ἐπεζεύχθωσαν γὰρ αἱ ΒΔ, ΕΓ, ΓΔ. ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΑΒΕΔ, διάμετρος δὲ αὐτοῦ ἐστιν ἡ ΒΔ, ἴσον ἄρα ἐστὶ τὸ ΑΒΔ τρίγωνον τῷ ΕΒΔ τριγώνῳ· καὶ ἡ πυραμὶς ἄρα, ἧς βάσις μὲν τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΔΕΒ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον. ἀλλὰ ἡ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΔΕΒ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἡ αὐτή ἐστι πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον· ὑπὸ γὰρ τῶν αὐτῶν ἐπιπέδων περιέχεται. καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον.
πάλιν, ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΖΓΒΕ, διάμετρος δέ ἐστιν αὐτοῦ ἡ ΓΕ, ἴσον ἐστὶ τὸ ΓΕΖ τρίγωνον τῷ ΓΒΕ τριγώνῳ. καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΒΓΕ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΕΓΖ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον. ἡ δὲ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΒΓΕ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐδείχθη πυραμίδι, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον· καὶ πυραμὶς ἄρα, ἧς βάσις μέν ἐστι τὸ ΓΕΖ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, ἴση ἐστὶ πυραμίδι, ἧς βάσις μὲν [ἐστι] τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον· διῄρηται ἄρα τὸ ΑΒΓΔΕΖ πρίσμα εἰς τρεῖς πυραμίδας ἴσας ἀλλήλαις τριγώνους ἐχούσας βάσεις.
Καὶ ἐπεὶ πυραμίς, ἧς βάσις μέν ἐστι τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, ἡ αὐτή ἐστι πυραμίδι, ἧς βάσις τὸ ΓΑΒ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον· ὑπὸ γὰρ τῶν αὐτῶν ἐπιπέδων περιέχονται· ἡ δὲ πυραμίς, ἧς βάσις τὸ ΑΒΔ τρίγωνον, κορυφὴ δὲ τὸ Γ σημεῖον, τρίτον ἐδείχθη τοῦ πρίσματος, οὗ βάσις τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ, καὶ ἡ πυραμὶς ἄρα, ἧς βάσις τὸ ΑΒΓ τρίγωνον, κορυφὴ δὲ τὸ Δ σημεῖον, τρίτον ἐστὶ τοῦ πρίσματος τοῦ ἔχοντος βάσιν τὴν αὐτὴν τὸ ΑΒΓ τρίγωνον, ἀπεναντίον δὲ τὸ ΔΕΖ.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι πᾶσα πυραμὶς τρίτον μέρος ἐστὶ τοῦ πρίσματος τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῇ καὶ ὕψος ἴσον [ἐπειδήπερ κἂν ἕτερόν τι σχῆμα εὐθύγραμμον ἔχῃ ἡ βάσις τοῦ πρίσματος, τοιοῦτο καὶ τὸ ἀπεναντίον, καὶ διαιρεῖται εἰς πρίσματα τρίγωνα ἔχοντα τὰς βάσεις καὶ τὰ ἀπεναντίον, καὶ ὡς ἡ ὅλη βάσις πρὸς ἕκαστον]· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ιβ΄.
Περιεχόμενα Στοιχείων Εὐκλείδου