Στοιχεῖα Εὐκλείδου ια΄
[Βιβλίον XI]
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις λα΄. [31]
Τὰ ἐπὶ ἴσων βάσεων ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν.
Ἔστω ἐπὶ ἴσων βάσεων τῶν ΑΒ, ΓΔ στερεὰ παραλληλεπίπεδα τὰ ΑΕ, ΓΖ ὑπὸ τὸ αὐτὸ ὕψος· λέγω, ὅτι ἴσον ἐστὶ τὸ ΑΕ στερεὸν τῷ ΓΖ στερεῷ.
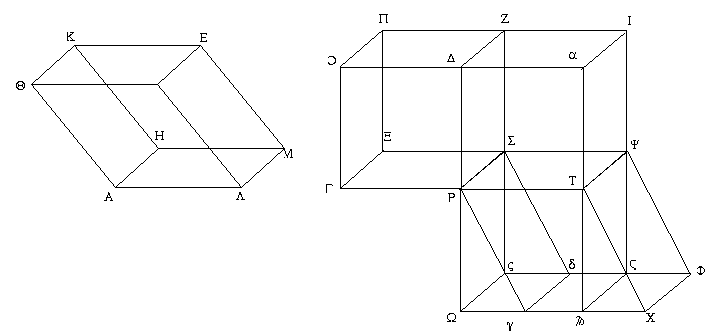
Ἔστωσαν δὴ πρότερον αἱ ἐφεστηκυῖαι αἱ ΘΚ, ΒΕ, ΑΗ, ΛΜ, ΟΠ, ΔΖ, ΓΞ, ΡΣ πρὸς ὀρθὰς ταῖς ΑΒ, ΓΔ βάσεσιν, καὶ ἐκβεβλήσθω ἐπ᾿ εὐθείας τῇ ΓΡ εὐθεῖα ἡ ΡΤ, καὶ συνεστάτω πρὸς τῇ ΡΤ εὐθείᾳ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Ρ τῇ ὑπὸ ΑΛΒ γωνίᾳ ἴση ἡ ὑπὸ ΤΡΥ, καὶ κείσθω τῇ μὲν ΑΛ ἴση ἡ ΡΤ, τῇ δὲ ΛΒ ἴση ἡ ΡΥ, καὶ συμπεπληρώσθω ἥ τε ΡΧ βάσις καὶ τὸ ΨΥ στερεόν. καὶ ἐπεὶ δύο αἱ ΤΡ, ΡΥ δυσὶ ταῖς ΑΛ, ΛΒ ἴσαι εἰσίν, καὶ γωνίας ἴσας περιέχουσιν, ἴσον ἄρα καὶ ὅμοιον τὸ ΡΧ παραλληλόγραμμον τῷ ΘΛ παραλληλογράμμῳ. καὶ ἐπεὶ πάλιν ἴση μὲν ἡ ΑΛ τῇ ΡΤ, ἡ δὲ ΛΜ τῇ ΡΣ, καὶ γωνίας ὀρθὰς περιέχουσιν, ἴσον ἄρα καὶ ὅμοιόν ἐστι τὸ ΡΨ παραλληλόγραμμον τῷ ΑΜ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ ΛΕ τῷ ΣΥ ἴσον τέ ἐστι καὶ ὅμοιον· τρία ἄρα παραλληλόγραμμα τοῦ ΑΕ στερεοῦ τρισὶ παραλληλογράμμοις τοῦ ΨΥ στερεοῦ ἴσα τέ ἐστι καὶ ὅμοια. ἀλλὰ τὰ μὲν τρία τρισὶ τοῖς ἀπεναντίον ἴσα τέ ἐστι καὶ ὅμοια, τὰ δὲ τρία τρισὶ τοῖς ἀπεναντίον· ὅλον ἄρα τὸ ΑΕ στερεὸν παραλληλεπίπεδον ὅλῳ τῷ ΨΥ στερεῷ παραλληλεπιπέδῳ ἴσον ἐστίν. διήχθωσαν αἱ ΔΡ, ΧΥ καὶ συμπιπτέτωσαν ἀλλήλαις κατὰ τὸ Ω, καὶ διὰ τοῦ Τ τῇ ΔΩ παράλληλος ἤχθω ἡ αΤϠ, καὶ ἐκβεβλήσθω ἡ ΟΔ κατὰ τὸ α, καὶ συμπεπληρώσθω τὰ ΩΨ, ΡΙ στερεά. ἴσον δή ἐστι τὸ ΨΩ στερεόν, οὗ βάσις μέν ἐστι τὸ ΡΨ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΩϚ, τῷ ΨΥ στερεῷ, οὗ βάσις μὲν τὸ ΡΨ παραλληλόγραμμον, ἀπεναντίον δὲ τὸ ΥΦ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΡΨ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι αἱ ΡΩ, ΡΥ, ΤϠ, ΤΧ, Σς, Σδ, ΨϚ, ΨΦ ἐπὶ τῶν αὐτῶν εἰσιν εὐθειῶν τῶν ΩΧ, ςΦ. ἀλλὰ τὸ ΨΥ στερεὸν τῷ ΑΕ ἐστιν ἴσον· καὶ τὸ ΨΩ ἄρα στερεὸν τῷ ΑΕ στερεῷ ἐστιν ἴσον. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΡΥΧΤ παραλληλόγραμμον τῷ ΩΤ παραλληλογράμμῳ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι τῆς ΡΤ καὶ ἐν ταῖς αὐταῖς παραλλήλοις ταῖς ΡΤ, ΩΧ· ἀλλὰ τὸ ΡΥΧΤ τῷ ΓΔ ἐστιν ἴσον, ἐπεὶ καὶ τῷ ΑΒ, καὶ τὸ ΩΤ ἄρα παραλληλόγραμμον τῷ ΓΔ ἐστιν ἴσον. ἄλλο δὲ τὸ ΔΤ· ἔστιν ἄρα ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ, οὕτως ἡ ΩΤ πρὸς τὴν ΔΤ. καὶ ἐπεὶ στερεὸν παραλληλεπίπεδον τὸ ΓΙ ἐπιπέδῳ τῷ ΡΖ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ βάσιν, οὕτως τὸ ΓΖ στερεὸν πρὸς τὸ ΡΙ στερεόν. διὰ τὰ αὐτὰ δή, ἐπεὶ στερεὸν παραλληλεπίπεδον τὸ ΩΙ ἐπιπέδῳ τῷ ΡΨ τέτμηται παραλλήλῳ ὄντι τοῖς ἀπεναντίον ἐπιπέδοις, ἔστιν ὡς ἡ ΩΤ βάσις πρὸς τὴν ΤΔ βάσιν, οὕτως τὸ ΩΨ στερεὸν πρὸς τὸ ΡΙ. ἀλλ' ὡς ἡ ΓΔ βάσις πρὸς τὴν ΔΤ, οὕτως ἡ ΩΤ πρὸς τὴν ΔΤ· καὶ ὡς ἄρα τὸ ΓΖ στερεὸν πρὸς τὸ ΡΙ στερεόν, οὕτως τὸ ΩΨ στερεὸν πρὸς τὸ ΡΙ. ἑκάτερον ἄρα τῶν ΓΖ, ΩΨ στερεῶν πρὸς τὸ ΡΙ τὸν αὐτὸν ἔχει λόγον· ἴσον ἄρα ἐστὶ τὸ ΓΖ στερεὸν τῷ ΩΨ στερεῷ. ἀλλὰ τὸ ΩΨ τῷ ΑΕ ἐδείχθη ἴσον· καὶ τὸ ΑΕ ἄρα τῷ ΓΖ ἐστιν ἴσον.
Μὴ ἔστωσαν δὴ αἱ ἐφεστηκυῖαι αἱ ΑΗ, ΘΚ, ΒΕ, ΛΜ, ΓΝ, ΟΠ, ΔΖ, ΡΣ πρὸς ὀρθὰς ταῖς ΑΒ, ΓΔ βάσεσιν· λέγω πάλιν, ὅτι ἴσον τὸ ΑΕ στερεὸν τῷ ΓΖ στερεῷ.
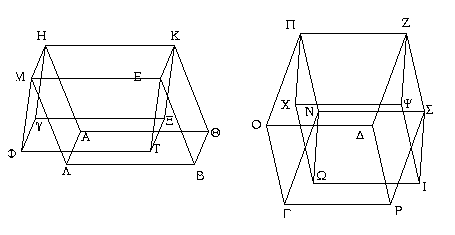
ἤχθωσαν γὰρ ἀπὸ τῶν Κ, Ε, Η, Μ, Π, Ζ, Ν, Σ σημείων ἐπὶ τὸ ὑποκείμενον ἐπίπεδον κάθετοι αἱ ΚΞ, ΕΤ, ΗΥ, ΜΦ, ΠΧ, ΖΨ, ΝΩ, ΣΙ, καὶ συμβαλλέτωσαν τῷ ἐπιπέδῳ κατὰ τὰ Ξ, Τ, Υ, Φ, Χ, Ψ, Ω, Ι σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΞΤ, ΞΥ, ΥΦ, ΤΦ, ΧΨ, ΧΩ, ΩΙ, ΙΨ. ἴσον δή ἐστι τὸ ΚΦ στερεὸν τῷ ΠΙ στερεῷ· ἐπί τε γὰρ ἴσων βάσεών εἰσι τῶν ΚΜ, ΠΣ καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι πρὸς ὀρθάς εἰσι ταῖς βάσεσιν. ἀλλὰ τὸ μὲν ΚΦ στερεὸν τῷ ΑΕ στερεῷ ἐστιν ἴσον, τὸ δὲ ΠΙ τῷ ΓΖ· ἐπί τε γὰρ τῆς αὐτῆς βάσεώς εἰσι καὶ ὑπὸ τὸ αὐτὸ ὕψος, ὧν αἱ ἐφεστῶσαι οὔκ εἰσιν ἐπὶ τῶν αὐτῶν εὐθειῶν. καὶ τὸ ΑΕ ἄρα στερεὸν τῷ ΓΖ στερεῷ ἐστιν ἴσον.
Τὰ ἄρα ἐπὶ ἴσων βάσεων ὄντα στερεὰ παραλληλεπίπεδα καὶ ὑπὸ τὸ αὐτὸ ὕψος ἴσα ἀλλήλοις ἐστίν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Περιεχόμενα Στοιχείων Εὐκλείδου