Στοιχεῖα Εὐκλείδου ς΄
[Βιβλίον VI]
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις γ΄. [3]
Ἐὰν τριγώνου ἡ γωνία δίχα τμηθῇ, ἡ δὲ τέμνουσα τὴν γωνίαν εὐθεῖα τέμνῃ καὶ τὴν βάσιν, τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἕξει λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς· καὶ ἐὰν τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἔχῃ λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς, ἡ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν τομὴν ἐπιζευγνυμένη εὐθεῖα δίχα τεμεῖ τὴν τοῦ τριγώνου γωνίαν.
Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ τετμήσθω ἡ ὑπὸ ΒΑΓ γωνία δίχα ὑπὸ τῆς ΑΔ εὐθείας· λέγω, ὅτι ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΓΔ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ.
Ἤχθω γὰρ διὰ τοῦ Γ τῇ ΔΑ παράλληλος ἡ ΓΕ καὶ διαχθεῖσα ἡ ΒΑ συμπιπτέτω αὐτῇ κατὰ τὸ Ε.
Καὶ ἐπεὶ εἰς παραλλήλους τὰς ΑΔ, ΕΓ εὐθεῖα ἐνέπεσεν ἡ ΑΓ, ἡ ἄρα ὑπὸ ΑΓΕ γωνία ἴση ἐστὶ τῇ ὑπὸ ΓΑΔ. ἀλλ' ἡ ὑπὸ ΓΑΔ τῇ ὑπὸ ΒΑΔ ὑπόκειται ἴση· καὶ ἡ ὑπὸ ΒΑΔ ἄρα τῇ ὑπὸ ΑΓΕ ἐστιν ἴση. πάλιν, ἐπεὶ εἰς παραλλήλους τὰς ΑΔ, ΕΓ εὐθεῖα ἐνέπεσεν ἡ ΒΑΕ, ἡ ἐκτὸς γωνία ἡ ὑπὸ ΒΑΔ ἴση ἐστὶ τῇ ἐντὸς τῇ ὑπὸ ΑΕΓ. ἐδείχθη δὲ καὶ ἡ ὑπὸ ΑΓΕ τῇ ὑπὸ ΒΑΔ ἴση· καὶ ἡ ὑπὸ ΑΓΕ ἄρα γωνία τῇ ὑπὸ ΑΕΓ ἐστιν ἴση· ὥστε καὶ πλευρὰ ἡ ΑΕ πλευρᾷ τῇ ΑΓ ἐστιν ἴση. καὶ ἐπεὶ τριγώνου τοῦ ΒΓΕ παρὰ μίαν τῶν πλευρῶν τὴν ΕΓ ἦκται ἡ ΑΔ, ἀνάλογον ἄρα ἐστὶν ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΕ. ἴση δὲ ἡ ΑΕ τῇ ΑΓ· ὡς ἄρα ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ.
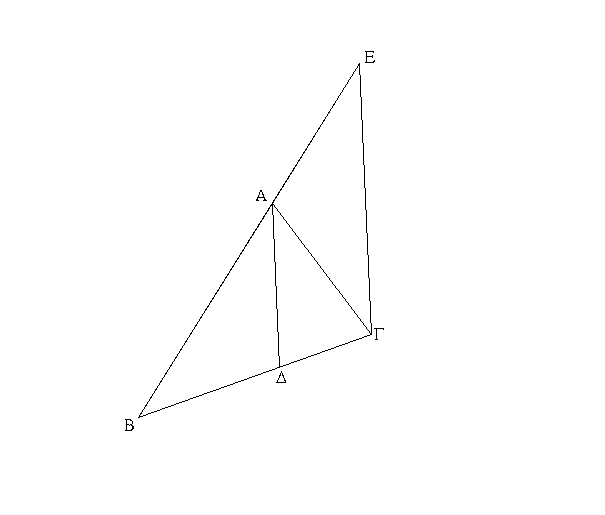
Ἀλλὰ δὴ ἔστω ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ, καὶ ἐπεζεύχθω ἡ ΑΔ· λέγω, ὅτι δίχα τέτμηται ἡ ὑπὸ ΒΑΓ γωνία ὑπὸ τῆς ΑΔ εὐθείας.
Τῶν γὰρ αὐτῶν κατασκευασθέντων, ἐπεί ἐστιν ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΓ, ἀλλὰ καὶ ὡς ἡ ΒΔ πρὸς τὴν ΔΓ, οὕτως ἐστὶν ἡ ΒΑ πρὸς τὴν ΑΕ· τριγώνου γὰρ τοῦ ΒΓΕ παρὰ μίαν τὴν ΕΓ ἦκται ἡ ΑΔ· καὶ ὡς ἄρα ἡ ΒΑ πρὸς τὴν ΑΓ, οὕτως ἡ ΒΑ πρὸς τὴν ΑΕ. ἴση ἄρα ἡ ΑΓ τῇ ΑΕ· ὥστε καὶ γωνία ἡ ὑπὸ ΑΕΓ τῇ ὑπὸ ΑΓΕ ἐστιν ἴση. ἀλλ' ἡ μὲν ὑπὸ ΑΕΓ τῇ ἐκτὸς τῇ ὑπὸ ΒΑΔ [ἐστιν] ἴση, ἡ δὲ ὑπὸ ΑΓΕ τῇ ἐναλλὰξ τῇ ὑπὸ ΓΑΔ ἐστιν ἴση· καὶ ἡ ὑπὸ ΒΑΔ ἄρα τῇ ὑπὸ ΓΑΔ ἐστιν ἴση. ἡ ἄρα ὑπὸ ΒΑΓ γωνία δίχα τέτμηται ὑπὸ τῆς ΑΔ εὐθείας.
Ἐὰν ἄρα τριγώνου ἡ γωνία δίχα τμηθῇ, ἡ δὲ τέμνουσα τὴν γωνίαν εὐθεῖα τέμνῃ καὶ τὴν βάσιν, τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἕξει λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς· καὶ ἐὰν τὰ τῆς βάσεως τμήματα τὸν αὐτὸν ἔχῃ λόγον ταῖς λοιπαῖς τοῦ τριγώνου πλευραῖς, ἡ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν τομὴν ἐπιζευγνυμένη εὐθεῖα δίχα τέμνει τὴν τοῦ τριγώνου γωνίαν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ς΄.
Περιεχόμενα Στοιχείων Εὐκλείδου