Στοιχεῖα Εὐκλείδου ια΄
[Βιβλίον XI]
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις λγ΄. [33]
Τὰ ὅμοια στερεὰ παραλληλεπίπεδα πρὸς ἄλληλα ἐν τριπλασίονι λόγῳ εἰσὶ τῶν ὁμολόγων πλευρῶν.
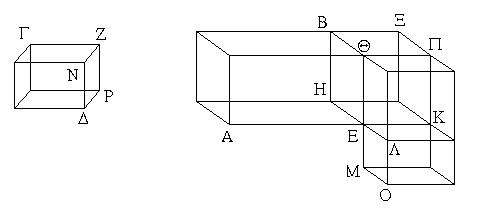
Ἔστω ὅμοια στερεὰ παραλληλεπίπεδα τὰ ΑΒ, ΓΔ, ὁμόλογος δὲ ἔστω ἡ ΑΕ τῇ ΓΖ· λέγω, ὅτι τὸ ΑΒ στερεὸν πρὸς τὸ ΓΔ στερεὸν τριπλασίονα λόγον ἔχει, ἤπερ ἡ ΑΕ πρὸς τὴν ΓΖ.
Ἐκβεβλήσθωσαν γὰρ ἐπ᾿ εὐθείας ταῖς ΑΕ, ΗΕ, ΘΕ αἱ ΕΚ, ΕΛ, ΕΜ, καὶ κείσθω τῇ μὲν ΓΖ ἴση ἡ ΕΚ, τῇ δὲ ΖΝ ἴση ἡ ΕΛ, καὶ ἔτι τῇ ΖΡ ἴση ἡ ΕΜ, καὶ συμπεπληρώσθω τὸ ΚΛ παραλληλόγραμμον καὶ τὸ ΚΟ στερεόν.
Καὶ ἐπεὶ δύο αἱ ΚΕ, ΕΛ δυσὶ ταῖς ΓΖ, ΖΝ ἴσαι εἰσίν, ἀλλὰ καὶ γωνία ἡ ὑπὸ ΚΕΛ γωνίᾳ τῇ ὑπὸ ΓΖΝ ἐστιν ἴση, ἐπειδήπερ καὶ ἡ ὑπὸ ΑΕΗ τῇ ὑπὸ ΓΖΝ ἐστιν ἴση διὰ τὴν ὁμοιότητα τῶν ΑΒ, ΓΔ στερεῶν, ἴσον ἄρα ἐστὶ [καὶ ὅμοιον] τὸ ΚΛ παραλληλόγραμμον τῷ ΓΝ παραλληλογράμμῳ. διὰ τὰ αὐτὰ δὴ καὶ τὸ μὲν ΚΜ παραλληλόγραμμον ἴσον ἐστὶ καὶ ὅμοιον τῷ ΓΡ [παραλληλογράμμῳ] καὶ ἔτι τὸ ΕΟ τῷ ΔΖ· τρία ἄρα παραλληλόγραμμα τοῦ ΚΟ στερεοῦ τρισὶ παραλληλογράμμοις τοῦ ΓΔ στερεοῦ ἴσα ἐστὶ καὶ ὅμοια. ἀλλὰ τὰ μὲν τρία τρισὶ τοῖς ἀπεναντίον ἴσα ἐστὶ καὶ ὅμοια, τὰ δὲ τρία τρισὶ τοῖς ἀπεναντίον ἴσα ἐστὶ καὶ ὅμοια· ὅλον ἄρα τὸ ΚΟ στερεὸν ὅλῳ τῷ ΓΔ στερεῷ ἴσον ἐστὶ καὶ ὅμοιον. συμπεπληρώσθω τὸ ΗΚ παραλληλόγραμμον, καὶ ἀπὸ βάσεων μὲν τῶν ΗΚ, ΚΛ παραλληλογράμμων, ὕψους δὲ τοῦ αὐτοῦ τῷ ΑΒ στερεὰ συμπεπληρώσθω τὰ ΕΞ, ΛΠ. καὶ ἐπεὶ διὰ τὴν ὁμοιότητα τῶν ΑΒ, ΓΔ στερεῶν ἐστιν ὡς ἡ ΑΕ πρὸς τὴν ΓΖ, οὕτως ἡ ΕΗ πρὸς τὴν ΖΝ, καὶ ἡ ΕΘ πρὸς τὴν ΖΡ, ἴση δὲ ἡ μέν ΓΖ τῇ ΕΚ, ἡ δὲ ΖΝ τῇ ΕΛ, ἡ δὲ ΖΡ τῇ ΕΜ, ἔστιν ἄρα ὡς ἡ ΑΕ πρὸς τὴν ΕΚ, οὕτως ἡ ΗΕ πρὸς τὴν ΕΛ καὶ ἡ ΘΕ πρὸς τὴν ΕΜ.
ἀλλ' ὡς μὲν ἡ ΑΕ πρὸς τὴν ΕΚ, οὕτως τὸ ΑΗ [παραλληλόγραμμον] πρὸς τὸ ΗΚ παραλληλόγραμμον, ὡς δὲ ἡ ΗΕ πρὸς τὴν ΕΛ, οὕτως τὸ ΗΚ πρὸς τὸ ΚΛ, ὡς δὲ ἡ ΘΕ πρὸς ΕΜ, οὕτως τὸ ΠΕ πρὸς τὸ ΚΜ· καὶ ὡς ἄρα τὸ ΑΗ παραλληλόγραμμον πρὸς τὸ ΗΚ, οὕτως τὸ ΗΚ πρὸς τὸ ΚΛ καὶ τὸ ΠΕ πρὸς τὸ ΚΜ. ἀλλ' ὡς μὲν τὸ ΑΗ πρὸς τὸ ΗΚ, οὕτως τὸ ΑΒ στερεὸν πρὸς τὸ ΕΞ στερεόν, ὡς δὲ τὸ ΗΚ πρὸς τὸ ΚΛ, οὕτως τὸ ΞΕ στερεὸν πρὸς τὸ ΠΛ στερεόν, ὡς δὲ τὸ ΠΕ πρὸς τὸ ΚΜ, οὕτως τὸ ΠΛ στερεὸν πρὸς τὸ ΚΟ στερεόν· καὶ ὡς ἄρα τὸ ΑΒ στερεὸν πρὸς τὸ ΕΞ, οὕτως τὸ ΕΞ πρὸς τὸ ΠΛ καὶ τὸ ΠΛ πρὸς τὸ ΚΟ. ἐὰν δὲ τέσσαρα μεγέθη κατὰ τὸ συνεχὲς ἀνάλογον ᾖ, τὸ πρῶτον πρὸς τὸ τέταρτον τριπλασίονα λόγον ἔχει ἤπερ πρὸς τὸ δεύτερον· τὸ ΑΒ ἄρα στερεὸν πρὸς τὸ ΚΟ τριπλασίονα λόγον ἔχει ἤπερ τὸ ΑΒ πρὸς τὸ ΕΞ. ἀλλ' ὡς τὸ ΑΒ πρὸς τὸ ΕΞ, οὕτως τὸ ΑΗ παραλληλόγραμμον πρὸς τὸ ΗΚ καὶ ἡ ΑΕ εὐθεῖα πρὸς τὴν ΕΚ· ὥστε καὶ τὸ ΑΒ στερεὸν πρὸς τὸ ΚΟ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΑΕ πρὸς τὴν ΕΚ. ἴσον δὲ τὸ [μὲν] ΚΟ στερεὸν τῷ ΓΔ στερεῷ, ἡ δὲ ΕΚ εὐθεῖα τῇ ΓΖ· καὶ τὸ ΑΒ ἄρα στερεὸν πρὸς τὸ ΓΔ στερεὸν τριπλασίονα λόγον ἔχει ἤπερ ἡ ὁμόλογος αὐτοῦ πλευρὰ ἡ ΑΕ πρὸς τὴν ὁμόλογον πλευρὰν τὴν ΓΖ.
Τὰ ἄρα ὅμοια στερεὰ παραλληλεπίπεδα ἐν τριπλασίονι λόγῳ ἐστὶ τῶν ὁμολόγων πλευρῶν· ὅπερ ἔδει δεῖξαι.
Πόρισμα
Ἐκ δὴ τούτου φανερόν, ὅτι ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, ἔσται ὡς ἡ πρώτη πρὸς τὴν τετάρτην, οὕτω τὸ ἀπὸ τῆς πρώτης στερεὸν παραλληλεπίπεδον πρὸς τὸ ἀπὸ τῆς δευτέρας τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον, ἐπείπερ καὶ ἡ πρώτη πρὸς τὴν τετάρτην τριπλασίονα λόγον ἔχει ἤπερ πρὸς τὴν δευτέραν.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ια΄.
Περιεχόμενα Στοιχείων Εὐκλείδου