Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἰ Προτάσεις τῶν Στοιχείων ι΄.
Παράρτημα 27
Ἀσύμμετρος ἡ διάμετρος τῇ πλευρᾷ μήκει.
Προκείσθω ἡμῖν δεῖξαι, ὅτι ἐπὶ τῶν τετραγώνων σχημάτων ἀσύμμετρός ἐστιν ἡ διάμετρος τῇ πλευρᾷ μήκει.
Ἔστω τετράγωνον τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ· λέγω, ὅτι ἡ ΓΑ ἀσύμμετρός ἐστι τῇ ΑΒ μήκει.
Εἰ γὰρ δυνατόν, ἔστω σύμμετρος· λέγω, ὅτι συμβήσεται τὸν αὐτὸν ἀριθμὸν ἄρτιον εἶναι καὶ περισσόν. φανερὸν μὲν οὖν, ὅτι τὸ ἀπὸ τῆς ΑΓ διπλάσιον τοῦ ἀπὸ τῆς ΑΒ. καὶ ἐπὶ σύμμετρός ἐστιν ἡ ΓΑ τῇ ΑΒ, ἡ ΓΑ ἄρα πρὸς τὴν ΑΒ λόγον ἔχει, ὃν ἀριθμὸς πρὸς ἀριθμόν. ἐχέτω, ὃν ὁ ΕΖ πρὸς Η, καὶ ἔστωσαν οἱ ΕΖ, Η ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς· οὐκ ἄρα μονὰς ἐστὶν ὁ ΕΖ. εἰ γὰρ ἔσται μονὰς ὁ ΕΖ, ἔχει δὲ λόγον πρὸς τὸν Η, ὃν ἔχει ἡ ΑΓ πρὸς τὴν ΑΒ, καὶ μείζων ἡ ΑΓ τῆς ΑΒ, μείζων ἄρα καὶ ἡ ΕΖ τοῦ Η ἀριθμοῦ· ὅπερ ἄτοπον· οὐκ ἄρα μονάς ἐστιν ὁ ΕΖ· ἀριθμὸς ἄρα. καὶ ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς τὴν ΑΒ, οὕτως ὁ ΕΖ πρὸς τὸν Η, καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΓΑ πρὸς τὸ ἀπὸ τῆς ΑΒ, οὕτως ὁ ἀπὸ τοῦ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η.
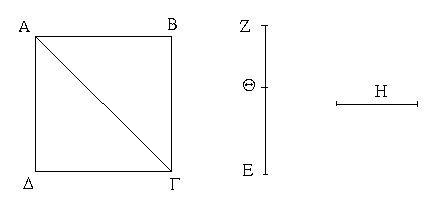
διπλάσιον δὲ τὸ ἀπὸ τῆς ΓΑ τοῦ ἀπὸ τῆς ΑΒ· διπλάσιον ἄρα καὶ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η· ἄρτιος ἄρα ἐστὶν ὁ ἀπὸ τοῦ ΕΖ· ὥστε καὶ αὐτὸς ἄρτιός ἐστιν. εἰ γὰρ ἦν περισσός, καὶ ὁ ἀπ᾿ αὐτοῦ τετράγωνος περισσὸς ἦν, ἐπειδήπερ, ἐὰν περισσοὶ ἀριθμοὶ ὁποσοιοῦν συντεθῶσιν, τὸ δὲ πλῆθος αὐτῶν περισσὸν ᾖ, ὁ ὅλος περισσὸς ἐστιν. ὁ ΕΖ ἄρα ἄρτιός ἐστιν. τετμήσθω δίχα κατὰ τὸ Θ. καὶ ἐπεὶ οἱ ΕΖ, Η ἀλάχιστοί είσι τῶν τὸν αὐτὸν λόγον ἐχόντων [αὐτοῖς], πρῶτοι πρὸς ἀλλήλους εἰσίν. καὶ ὁ ΕΖ ἄρτιος· περισσὸς ἄρα ἐστὶν ὁ Η. εἰ γὰρ ἦν ἄρτιος, τοὺς ΕΖ, Η δυὰς ἐμέτρει· πᾶς γὰρ ἄρτιος ἔχει μέρος ἥμισυ· πρώτους ὄντας πρὸς ἀλλήλους. ὅπερ ἐστὶν ἀδὺνατον· οὐκ ἄρα ἄρτιός ἐστιν ὁ Η· περισσὸς ἄρα, καὶ ἐπὶ διπλάσιος ὁ ΕΖ τοῦ ΕΘ, τετραπλάσιος ἄρα ὁ ἀπὸ ΕΖ τοῦ ἀπὸ ΕΘ. διπλάσιος δὲ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η. διπλάσιος ἄρα ὁ ἀπὸ τοῦ Η τοῦ ἀπὸ ΕΘ· ἄρτιος ἄρα ἐστὶν ὁ ἀπὸ τοῦ Η. ἄρτιος ἄρα διὰ τὰ εἰρημένα ὁ Η· ἀλλὰ καὶ περισσός. ὅσπερ ἐστὶν ἀδύνατον. οὐκ ἄρα σύμμετρός ἐστιν ἡ ΓΑ τῇ ΑΒ μήκει· ὅπερ ἔδει δεῖξαι.
Ἄλλως
[Δεικτέον καὶ ἑτέρως, ὅτι ἀσύμμετρός ἐστιν ἡ τοῦ τετραγώνου διάμετρος τῇ πλευρᾷ].
Ἔστω ἀντὶ μὲν τῆς διαμέτρου ἡ Α, ἀντὶ δὲ τῆς πλευρᾶς ἡ Β. λέγω, ὅτι ἀσύμμετρός ἐστιν ἡ Α τῇ Β μήκει. εἰ γὰρ δυνατόν, ἔστω [σύμμετρος· καὶ γεγονέτω] πάλιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ ΕΖ ἀριθμὸς πρὸς τὸν Η, καὶ ἔστωσαν ἐλάχιστοι τῶν τὸν αὐτὸν λόγον ἐχόντων αὐτοῖς οἱ ΕΖ, Η· οἱ ΕΖ, Η ἄρα πρῶτοι πρὸς ἀλλήλους εἰσίν. λέγω πρῶτον, ὅτι ὁ Η οὐκ ἔστι μονάς. εἰ γὰρ δυνατόν, ἔστω μονάς. καὶ ἐπεί ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ὁ ΕΖ πρὸς τὸν Η, καὶ ὡς ἄρα τὸ ἀπὸ τῆς Α, πρὸς τὸ ἀπὸ τῆς Β, οὕτως ὁ ἀπὸ τοῦ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η. διπλάσιον δὲ τὸ ἀπὸ τῆς Α τοῦ ἀπὸ τῆς Β· διπλάσιος ἄρα καὶ ὁ ἀπὸ τοῦ ΕΖ τοῦ ἀπὸ τοῦ Η. καὶ ἐστι μονὰς ὁ Η· δυὰς ἄρα ὁ ἀπὸ ΕΖ τετράγωνος· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα μονάς ἐστιν ὁ Η· ἀριθμὸς ἄρα. καὶ ἐπεί ἐστιν ὡς τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β, οὕτως ὁ ἀπὸ ΕΖ πρὸς τὸν ἀπὸ τοῦ Η, καὶ ἀνάπαλιν ὡς τὸ ἀπὸ τῆς Β πρὸς τὸ ἀπὸ τῆς Α, οὕτως ὁ ἀπὸ τοῦ Η πρὸς τὸν ἀπὸ τοῦ ΕΖ, μετρεῖ δὲ τὸ ἀπὸ τῆς Β τὸ ἀπὸ τῆς Α, μετρεῖ ἄρα καὶ ὁ ἀπὸ τοῦ Η τετράγωνος τὸν ἀπὸ τοῦ ΕΖ· ὥστε καὶ ἡ πλευρὰ αὐτὴ ὁ Η τὸν ΕΖ μετρεῖ. μετρεῖ δὲ καὶ ἑαυτὸν ὁ Η· ὁ Η ἄρα τοὺς ΕΖ, Η μετρεῖ πρώτους ὄντας πρὸς ἀλλήλους· ὅπερ ἐστὶν ἀδύνατον. οὐκ ἄρα σύμμετρός ἐστιν ἡ Α τῇ Β μήκει. ἀσύμμετρος ἄρα ἐστίν· ὅπερ ἔδει δεῖξαι.
Παράρτημα 28
Σχόλιον
Ἐπίπεδα, ἀσύμμετρα ἀλλήλοις.
Εὑρημένων δὴ τῶν μήκει ἀσυμμέτρων εὐθειῶν, ὡς τῶν Α, Β, εὑρίσκεται καὶ ἄλλα πλεῖστα μεγέθη ἐκ δύο διαστάσεων, λέγω δὴ ἐπίπεδα, ἀσύμμετρα ἀλλήλοις. ἐὰν γὰρ τῶν Α, Β εὐθειῶν μέσην ἀνάλογον λάβωμεν τὴν Γ, ἔσται ὡς ἡ Α πρὸς τὴν Β, οὕτως τὸ ἀπὸ τῆς Α ἐπίπεδον πρὸς τὸ ἀπὸ τῆς Γ τὸ ὅμοιον καὶ ὁμοίως ἀναγραφόμενον, εἴτε τετράγωνα εἴη τὰ ἀναγραφόμενα εἴτε ἕτερα εὐθύγραμμα ὅμοια, εἴτε κύκλοι περὶ διαμέτρους τὰς Α, Γ, ἐπείπερ οἱ κύκλοι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα. εὕρηνται ἄρα καὶ ἐπίπεδα χωρία ἀσύμμετρα ἀλλήλοις· ὅπερ ἔδει δεῖξαι.
Δεδειγμένων δὴ καὶ τῶν ἐκ δύο διαστάσεων διαφόρων ἀσυμμέτρων χωρίων δείξομεν τοῖς ἀπὸ τῆς τῶν στερεῶν θεωρίας, ὡς ἔστι καὶ στερεὰ σύμμετρά τε καὶ ἀσύμμετρα ἀλλήλοις. ἐὰν γὰρ ἐπὶ τῶν Α, Β τετραγώνων ἢ τῶν ἴσων αὐτοῖς εὐθυγράμμων ἀναστήσωμεν ἰσοϋψῆ στερεὰ παραλληλεπίπεδα ἢ πυραμίδας, ἢ πρίσματα, ἔσται τὰ ἀνασταθέντα πρὸς ἄλληλα ὡς αἱ βάσεις. καὶ εἰ μὲν σύμμετροί εἰσιν αἱ βάσεις, σύμμετρα ἔσται καὶ τὰ στερεά, εἰ δὲ ἀσύμμετροι, ἀσύμμετρα. ὅπερ ἔδει δεῖξαι.
Ἀλλὰ μὴν καὶ δύο κύκλων ὄντων τῶν Α, Β, ἐὰν ἀπ᾿ αὐτῶν ἰσοϋψεῖς κώνους ἢ κυλίνδρους ἀναγράψωμεν, ἔσονται πρὸς ἀλλήλους ὡς αἱ βάσεις, τουτέστιν ὡς οἱ Α, Β κύκλοι. καὶ εἰ μὲν σύμμετροί εἰσιν οἱ κύκλοι, σύμμετροι ἔσονται καὶ οἱ τε κῶνοι πρὸς ἀλλήλους καὶ οἱ κύλινδροι, εἰ δὲ ἀσύμμετροί εἰσιν οἱ κύκλοι, ἀσύμμετροι ἔσονται καὶ οἱ κῶνοι καὶ οἱ κύλινδροι. καὶ φανερὸν ἡμῖν γέγονεν, ὅτι οὐ μόνον ἐπὶ γραμμῶν καὶ ἐπιφανειῶν ἐστι συμμετρία τε καὶ ἀσυμμετρία, ἀλλα καὶ ἐπὶ τῶν στερεῶν σχημάτων.
Αἰ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου