Στοιχεῖα Εὐκλείδου β΄
[Βιβλίον II]
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ε΄. [5]
Ἐὰν εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ.
Εὐθεῖα γάρ τις ἡ ΑΒ τετμήσθω εἰς μὲν ἴσα κατὰ τὸ Γ, εἰς δὲ ἄνισα κατὰ τὸ Δ· λέγω, ὅτι τὸ ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ.
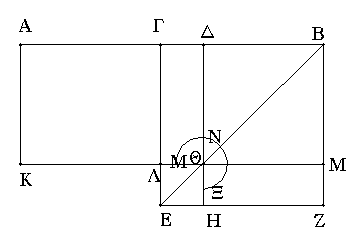
Ἀναγεγράφθω γὰρ ἀπὸ τῆς ΓΒ τετράγωνον τὸ ΓΕΖΒ, καὶ ἐπεζεύχθω ἡ ΒΕ, καὶ διὰ μὲν τοῦ Δ ὁποτέρᾳ τῶν ΓΕ, ΒΖ παράλληλος ἤχθω ἡ ΔΗ, διὰ δὲ τοῦ Θ ὁποτέρᾳ τῶν ΑΒ, ΕΖ παράλληλος πάλιν ἤχθω ἡ ΚΜ, καὶ πάλιν διὰ τοῦ Α ὁποτέρᾳ τῶν ΓΛ, ΒΜ παράλληλος ἤχθω ἡ ΑΚ. καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΓΘ παραπλήρωμα τῷ ΘΖ παραπληρώματι, κοινὸν προσκείσθω τὸ ΔΜ· ὅλον ἄρα τὸ ΓΜ ὅλῳ τῷ ΔΖ ἴσον ἐστίν. ἀλλὰ τὸ ΓΜ τῷ ΑΛ ἴσον ἐστίν, ἐπεὶ καὶ ἡ ΑΓ τῇ ΓΒ ἐστιν ἴση· καὶ τὸ ΑΛ ἄρα τῷ ΔΖ ἴσον ἐστίν. κοινὸν προσκείσθω τὸ ΓΘ· ὅλον ἄρα τὸ ΑΘ τῷ ΜΝΞ γνώμονι ἴσον ἐστίν. ἀλλὰ τὸ ΑΘ τὸ ὑπὸ τῶν ΑΔ, ΔΒ ἐστιν· ἴση γὰρ ἡ ΔΘ τῇ ΔΒ· καὶ ὁ ΜΝΞ ἄρα γνώμων ἴσος ἐστὶ τῷ ὑπὸ ΑΔ, ΔΒ. κοινὸν προσκείσθω τὸ ΛΗ, ὅ ἐστιν ἴσον τῷ ἀπὸ τῆς ΓΔ· ὁ ἄρα ΜΝΞ γνώμων καὶ τὸ ΛΗ ἴσα ἐστὶ τῷ ὑπὸ τῶν ΑΔ, ΔΒ περιεχομένῳ ὀρθογωνίῳ καὶ τῷ ἀπὸ τῆς ΓΔ τετραγώνῳ. ἀλλὰ ὁ ΜΝΞ γνώμων καὶ τὸ ΛΗ ὅλον ἐστὶ τὸ ΓΕΖΒ τετράγωνον, ὅ ἐστιν ἀπὸ τῆς ΓΒ· τὸ ἄρα ὑπὸ τῶν ΑΔ, ΔΒ περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς ΓΔ τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ΓΒ τετραγώνῳ.
Ἐὰν ἄρα εὐθεῖα γραμμὴ τμηθῇ εἰς ἴσα καὶ ἄνισα, τὸ ὑπὸ τῶν ἀνίσων τῆς ὅλης τμημάτων περιεχόμενον ὀρθογώνιον μετὰ τοῦ ἀπὸ τῆς μεταξὺ τῶν τομῶν τετραγώνου ἴσον ἐστὶ τῷ ἀπὸ τῆς ἡμισείας τετραγώνῳ· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων β΄.
Περιεχόμενα Στοιχείων Εὐκλείδου