Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις Ϟθ΄ [99]
Τὸ ἀπὸ μέσης ἀποτομῆς δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τρίτην.
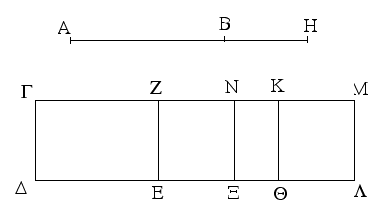
Ἔστω μέσης ἀποτομὴ δευτέρα ἡ ΑΒ, ῥητὴ δὲ ἡ ΓΔ, καὶ τῷ ἀπὸ τῆς ΑΒ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΕ πλάτος ποιοῦν τὴν ΓΖ· λέγω, ὅτι ἡ ΓΖ ἀποτομή ἐστι τρίτη.
Ἔστω γὰρ τῇ ΑΒ προσαρμόζουσα ἡ ΒΗ· αἱ ἄρα ΑΗ, ΗΒ μέσαι εἰσὶ δυνάμει μόνον σύμμετροι μέσον περιέχουσαι. καὶ τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον παρὰ τὴν ΓΔ παραβεβλήσθω τὸ ΓΘ πλάτος ποιοῦν τὴν ΓΚ, τῷ δὲ ἀπὸ τῆς ΒΗ ἴσον παρὰ τὴν ΚΘ παραβεβλήσθω τὸ ΚΛ πλάτος ποιοῦν τὴν ΚΜ· ὅλον ἄρα τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ [καί ἐστι μέσα τὰ ἀπὸ τῶν ΑΗ, ΗΒ]· μέσον ἄρα καὶ τὸ ΓΛ. καὶ παρὰ ῥητὴν τὴν ΓΔ παραβέβληται πλάτος ποιοῦν τὴν ΓΜ· ῥητὴ ἄρα ἐστὶν ἡ ΓΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ ὅλον τὸ ΓΛ ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΑΗ, ΗΒ, ὧν τὸ ΓΕ ἴσον ἐστὶ τῷ ἀπὸ τῆς ΑΒ, λοιπὸν ἄρα τὸ ΛΖ ἴσον ἐστὶ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. τετμήσθω οὖν ἡ ΖΜ δίχα κατὰ τὸ Ν σημεῖον, καὶ τῇ ΓΔ παράλληλος ἤχθω ἡ ΝΞ· ἑκάτερον ἄρα τῶν ΖΞ, ΝΛ ἴσον ἐστὶ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. μέσον δὲ τὸ ὑπὸ τῶν ΑΗ, ΗΒ· μέσον ἄρα ἐστὶ καὶ τὸ ΖΛ. καὶ παρὰ ῥητὴν τὴν ΕΖ παράκειται πλάτος ποιοῦν τὴν ΖΜ· ῥητὴ ἄρα καὶ ἡ ΖΜ καὶ ἀσύμμετρος τῇ ΓΔ μήκει. καὶ ἐπεὶ αἱ ΑΗ, ΗΒ δυνάμει μόνον εἰσὶ σύμμετροι, ἀσύμμετρος ἄρα [ἐστὶ] μήκει ἡ ΑΗ τῇ ΗΒ· ἀσύμμετρον ἄρα ἐστὶ καὶ τὸ ἀπὸ τῆς ΑΗ τῷ ὑπὸ τῶν ΑΗ, ΗΒ. ἀλλὰ τῷ μὲν ἀπὸ τῆς ΑΗ σύμμετρά ἐστι τὰ ἀπὸ τῶν ΑΗ, ΗΒ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ τὸ δὶς ὑπὸ τῶν ΑΗ, ΗΒ· ἀσύμμετρα ἄρα ἐστὶ τὰ ἀπὸ τῶν ΑΗ, ΗΒ τῷ δὶς ὑπὸ τῶν ΑΗ, ΗΒ. ἀλλὰ τοῖς μὲν ἀπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τὸ ΓΛ, τῷ δὲ δὶς ὑπὸ τῶν ΑΗ, ΗΒ ἴσον ἐστὶ τὸ ΖΛ· ἀσύμμετρον ἄρα ἐστὶ τὸ ΓΛ τῷ ΖΛ. ὡς δὲ τὸ ΓΛ πρὸς τὸ ΖΛ, οὕτως ἐστὶν ἡ ΓΜ πρὸς τὴν ΖΜ· ἀσύμμετρος ἄρα ἐστὶν ἡ ΓΜ τῇ ΖΜ μήκει. καί εἰσιν ἀμφότεραι ῥηταί· αἱ ἄρα ΓΜ, ΜΖ ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΓΖ.
Λέγω δή, ὅτι καὶ τρίτη.
Ἐπεὶ γὰρ σύμμετρόν ἐστι τὸ ἀπὸ τῆς ΑΗ τῷ ἀπὸ τῆς ΗΒ, σύμμετρον ἄρα καὶ τὸ ΓΘ τῷ ΚΛ· ὥστε καὶ ἡ ΓΚ τῇ ΚΜ. καὶ ἐπεὶ τῶν ἀπὸ τῶν ΑΗ, ΗΒ μέσον ἀνάλογόν ἐστι τὸ ὑπὸ τῶν ΑΗ, ΗΒ, καί ἐστι τῷ μὲν ἀπὸ τῆς ΑΗ ἴσον τὸ ΓΘ, τῷ δὲ ἀπὸ τῆς ΗΒ ἴσον τὸ ΚΛ, τῷ δὲ ὑπὸ τῶν ΑΗ, ΗΒ ἴσον τὸ ΝΛ, καὶ τῶν ΓΘ, ΚΛ ἄρα μέσον ἀνάλογόν ἐστι τὸ ΝΛ· ἔστιν ἄρα ὡς τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως τὸ ΝΛ πρὸς τὸ ΚΛ. ἀλλ' ὡς μὲν τὸ ΓΘ πρὸς τὸ ΝΛ, οὕτως ἐστὶν ἡ ΓΚ πρὸς τὴν ΝΜ, ὡς δὲ τὸ ΝΛ πρὸς τὸ ΚΛ, οὕτως ἐστὶν ἡ ΝΜ πρὸς τὴν ΚΜ· ὡς ἄρα ἡ ΓΚ πρὸς τὴν ΜΝ, οὕτως ἐστὶν ἡ ΜΝ πρὸς τὴν ΚΜ· τὸ ἄρα ὑπὸ τῶν ΓΚ, ΚΜ ἴσον ἐστὶ τῷ [ἀπὸ τῆς ΜΝ, τουτέστι τῷ] τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ. ἐπεὶ οὖν δύο εὐθεῖαι ἄνισοί εἰσιν αἱ ΓΜ, ΜΖ, καὶ τῷ τετάρτῳ μέρει τοῦ ἀπὸ τῆς ΖΜ ἴσον παρὰ τὴν ΓΜ παραβέβληται ἐλλεῖπον εἴδει τετραγώνῳ καὶ εἰς σύμμετρα αὐτὴν διαιρεῖ, ἡ ΓΜ ἄρα τῆς ΜΖ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ. καὶ οὐδετέρα τῶν ΓΜ, ΜΖ σύμμετρός ἐστι μήκει τῇ ἐκκειμένῃ ῥητῇ τῇ ΓΔ· ἡ ἄρα ΓΖ ἀποτομή ἐστι τρίτη.
Τὸ ἄρα ἀπὸ μέσης ἀποτομῆς δευτέρας παρὰ ῥητὴν παραβαλλόμενον πλάτος ποιεῖ ἀποτομὴν τρίτην· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου