Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ξζ΄ [67]
Ἡ τῇ ἐκ δύο μέσων μήκει σύμμετρος καὶ αὐτὴ ἐκ δύο μέσων ἐστὶ καὶ τῇ τάξει ἡ αὐτή.
Ἔστω ἐκ δύο μέσων ἡ ΑΒ, καὶ τῇ ΑΒ σύμμετρος ἔστω μήκει ἡ ΓΔ· λέγω, ὅτι ἡ ΓΔ ἐκ δύο μέσων ἐστὶ καὶ τῇ τάξει ἡ αὐτὴ τῇ ΑΒ.
Ἐπεὶ γὰρ ἐκ δύο μέσων ἐστὶν ἡ ΑΒ, διῃρήσθω εἰς τὰς μέσας κατὰ τὸ Ε· αἱ ΑΕ, ΕΒ ἄρα μέσαι εἰσὶ δυνάμει μόνον σύμμετροι. καὶ γεγονέτω ὡς ἡ ΑΒ πρὸς ΓΔ, ἡ ΑΕ πρὸς ΓΖ· καὶ λοιπὴ ἄρα ἡ ΕΒ πρὸς λοιπὴν τὴν ΖΔ ἐστιν, ὡς ἡ ΑΒ πρὸς ΓΔ. σύμμετρος δὲ ἡ ΑΒ τῇ ΓΔ μήκει· σύμμετρος ἄρα καὶ ἑκατέρα τῶν ΑΕ, ΕΒ ἑκατέρᾳ τῶν ΓΖ, ΖΔ. μέσαι δὲ αἱ ΑΕ, ΕΒ· μέσαι ἄρα καὶ αἱ ΓΖ, ΖΔ. καὶ ἐπεί ἐστιν ὡς ἡ ΑΕ πρὸς ΕΒ, ἡ ΓΖ πρὸς ΖΔ, αἱ δὲ ΑΕ, ΕΒ δυνάμει μόνον σύμμετροί εἰσιν, καὶ αἱ ΓΖ, ΖΔ [ἄρα] δυνάμει μόνον σύμμετροί εἰσιν. ἐδείχθησαν δὲ καὶ μέσαι· ἡ ΓΔ ἄρα ἐκ δύο μέσων ἐστίν.
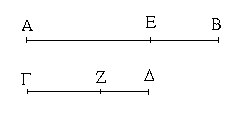
Λέγω δή, ὅτι καὶ τῇ τάξει ἡ αὐτή ἐστι τῇ ΑΒ.
Ἐπεὶ γάρ ἐστιν ὡς ἡ ΑΕ πρὸς ΕΒ, ἡ ΓΖ πρὸς ΖΔ, καὶ ὡς ἄρα τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ὑπὸ τῶν ΑΕΒ, οὕτως τὸ ἀπὸ τῆς ΓΖ πρὸς τὸ ὑπὸ τῶν ΓΖΔ· ἐναλλὰξ ὡς τὸ ἀπὸ τῆς ΑΕ πρὸς τὸ ἀπὸ τῆς ΓΖ, οὕτως τὸ ὑπὸ τῶν ΑΕΒ πρὸς τὸ ὑπὸ τῶν ΓΖΔ. σύμμετρον δὲ τὸ ἀπὸ τῆς ΑΕ τῷ ἀπὸ τῆς ΓΖ· σύμμετρον ἄρα καὶ τὸ ὑπὸ τῶν ΑΕΒ τῷ ὑπὸ τῶν ΓΖΔ. εἴτε οὖν ῥητόν ἐστι τὸ ὑπὸ τῶν ΑΕΒ, καὶ τὸ ὑπὸ τῶν ΓΖΔ ῥητόν ἐστιν [καὶ διὰ τοῦτό ἐστιν ἐκ δύο μέσων πρώτη]. εἴτε μέσον, μέσον, καί ἐστιν ἑκατέρα δευτέρα
.Καὶ διὰ τοῦτο ἔσται ἡ ΓΔ τῇ ΑΒ τῇ τάξει ἡ αὐτή· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου