Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ιδ΄. [14]
Ἐὰν τέσσαρες εὐθεῖαι ἀνάλογον ὦσιν, δύνηται δὲ ἡ πρώτη τῆς δευτέρας μεῖζον τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει], καὶ ἡ τρίτη τῆς τετάρτης μεῖζον δυνήσεται τῷ ἀπὸ συμμέτρου ἑαυτῇ [μήκει]. καὶ ἐὰν ἡ πρώτη τῆς δευτέρας μεῖζον δύνηται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει], καὶ ἡ τρίτη τῆς τετάρτης μεῖζον δυνήσεται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει].
Ἔστωσαν τέσσαρες εὐθεῖαι ἀνάλογον αἱ Α, Β, Γ, Δ, ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ, καὶ ἡ Α μὲν τῆς Β μεῖζον δυνάσθω τῷ ἀπὸ τῆς Ε, ἡ δὲ Γ τῆς Δ μεῖζον δυνάσθω τῷ ἀπὸ τῆς Ζ· λέγω, ὅτι, εἴτε σύμμετρός ἐστιν ἡ Α τῇ Ε, σύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ, εἴτε ἀσύμμετρός ἐστιν ἡ Α τῇ Ε, ἀσύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ.
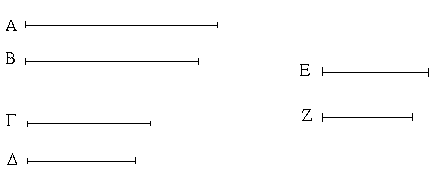
Ἐπεὶ γάρ ἐστιν ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ, ἔστιν ἄρα καὶ ὡς τὸ ἀπὸ τῆς Α πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὸ ἀπὸ τῆς Γ πρὸς τὸ ἀπὸ τῆς Δ. ἀλλὰ τῷ μὲν ἀπὸ τῆς Α ἴσα ἐστὶ τὰ ἀπὸ τῶν Ε, Β, τῷ δὲ ἀπὸ τῆς Γ ἴσα ἐστὶ τὰ ἀπὸ τῶν Δ, Ζ. ἔστιν ἄρα ὡς τὰ ἀπὸ τῶν Ε, Β πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὰ ἀπὸ τῶν Δ, Ζ πρὸς τὸ ἀπὸ τῆς Δ· διελόντι ἄρα ἐστὶν ὡς τὸ ἀπὸ τῆς Ε πρὸς τὸ ἀπὸ τῆς Β, οὕτως τὸ ἀπὸ τῆς Ζ πρὸς τὸ ἀπὸ τῆς Δ· ἔστιν ἄρα καὶ ὡς ἡ Ε πρὸς τὴν Β, οὕτως ἡ Ζ πρὸς τὴν Δ· ἀνάπαλιν ἄρα ἐστὶν ὡς ἡ Β πρὸς τὴν Ε, οὕτως ἡ Δ πρὸς τὴν Ζ. ἔστι δὲ καὶ ὡς ἡ Α πρὸς τὴν Β, οὕτως ἡ Γ πρὸς τὴν Δ· δι' ἴσου ἄρα ἐστὶν ὡς ἡ Α πρὸς τὴν Ε, οὕτως ἡ Γ πρὸς τὴν Ζ. εἴτε οὖν σύμμετρός ἐστιν ἡ Α τῇ Ε, σύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ, εἴτε ἀσύμμετρός ἐστιν ἡ Α τῇ Ε, ἀσύμμετρός ἐστι καὶ ἡ Γ τῇ Ζ.
Ἐὰν ἄρα, καὶ τὰ ἑξῆς.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου