Στοιχεῖα Εὐκλείδου ι΄
[Βιβλίον X]
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Προηγουμένη Πρότασις
Ἑπομένη Πρότασις
Πρότασις ρι΄ [110]
Ἀπὸ μέσου μέσου ἀφαιρουμένου ἀσυμμέτρου τῷ ὅλῳ αἱ λοιπαὶ δύο ἄλογοι γίνονται ἤτοι μέσης ἀποτομὴ δευτέρα ἢ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα.
Ἀφῃρήσθω γὰρ ὡς ἐπὶ τῶν προκειμένων καταγραφῶν ἀπὸ μέσου τοῦ ΒΓ μέσον τὸ ΒΔ ἀσύμμετρον τῷ ὅλῳ· λέγω, ὅτι ἡ τὸ ΕΓ δυναμένη μία ἐστὶ δύο ἀλόγων ἤτοι μέσης ἀποτομὴ δευτέρα ἢ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα.
Ἐπεὶ γὰρ μέσον ἐστὶν ἑκάτερον τῶν ΒΓ, ΒΔ, καὶ ἀσύμμετρον τὸ ΒΓ τῷ ΒΔ, ἔσται ἀκολούθως ῥητὴ ἑκατέρα τῶν ΖΘ, ΖΚ καὶ ἀσύμμετρος τῇ ΖΗ μήκει. καὶ ἐπεὶ ἀσύμμετρόν ἐστι τὸ ΒΓ τῷ ΒΔ, τουτέστι τὸ ΗΘ τῷ ΗΚ, ἀσύμμετρος καὶ ἡ ΘΖ τῇ ΖΚ· αἱ ΖΘ, ΖΚ ἄρα ῥηταί εἰσι δυνάμει μόνον σύμμετροι· ἀποτομὴ ἄρα ἐστὶν ἡ ΚΘ [προσαρμόζουσα δὲ ἡ ΖΚ. ἤτοι δὴ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἢ τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ].
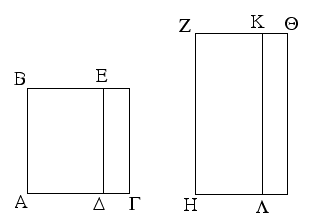
Εἰ μὲν δὴ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ συμμέτρου ἑαυτῇ, καὶ οὐθετέρα τῶν ΖΘ, ΖΚ σύμμετρός ἐστι τῇ ἐκκειμένῃ ῥητῇ μήκει τῇ ΖΗ, ἀποτομὴ τρίτη ἐστὶν ἡ ΚΘ. ῥητὴ δὲ ἡ ΚΛ, τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς τρίτης περιεχόμενον ὀρθογώνιον ἄλογόν ἐστιν, καὶ ἡ δυναμένη αὐτὸ ἄλογός ἐστιν, καλεῖται δὲ μέσης ἀποτομὴ δευτέρα· ὥστε ἡ τὸ ΛΘ, τουτέστι τὸ ΕΓ, δυναμένη μέσης ἀποτομή ἐστι δευτέρα.
Εἰ δὲ ἡ ΖΘ τῆς ΖΚ μεῖζον δύναται τῷ ἀπὸ ἀσυμμέτρου ἑαυτῇ [μήκει], καὶ οὐθετέρα τῶν ΘΖ, ΖΚ σύμμετρός ἐστι τῇ ΖΗ μήκει, ἀποτομὴ ἕκτη ἐστὶν ἡ ΚΘ. τὸ δ' ὑπὸ ῥητῆς καὶ ἀποτομῆς ἕκτης ἡ δυναμένη ἐστὶ μετὰ μέσου μέσον τὸ ὅλον ποιοῦσα. ἡ τὸ ΛΘ ἄρα, τουτέστι τὸ ΕΓ, δυναμένη μετὰ μέσου μέσον τὸ ὅλον ποιοῦσά ἐστιν· ὅπερ ἔδει δεῖξαι.
Ἑπομένη Πρότασις
Προηγουμένη Πρότασις
Αἱ Προτάσεις τῶν Στοιχείων ι΄.
Περιεχόμενα Στοιχείων Εὐκλείδου