Ἀσύμμετρα Μεγέθη
Ὁρισμός
«Σύμμετρα μεγέθη λέγεται τὰ τῷ αὐτῷ μέτρῳ μετρούμενα, ἀσύμμετρα δέ, ὧν μηδὲν ἐνδέχεται κοινὸν μέτρον γενέσθαι». Στοιχεῖα Εὐκλείδου ι΄
Βιβλίον X
Ὅροι δ΄ 4. α΄
Δηλαδὴ Σύμμετρα μεγέθη ὀνομάζονται αὐτὰ τὰ ὁποῖα μετριοῦνται μὲ τὸ αὐτὸ μέτρο, ἀσύμμετρα δὲ, αὐτὰ γιὰ τὰ ὁποῖα ἐνδεχομένως κανένα μέτρο δὲν μπορεῖ νὰ γίνει κοινό.
Ὁ ὁρισμὸς καὶ ὅλοι οἱ σχετικοὶ ὅροι καὶ προτάσεις (θεωρήματα) ποὺ ἀναφέρονται στὰ Ἀσύμμετρα καὶ σύμμετρα μεγέθη εἶναι ἐδῶ
Ἀπόδειξις ὑπάρξεως ἀσύμμετρων μεγεθῶν
μὲ σημερινοὺς ὄρους καὶ γραφή. (Ἡ πρωταρχικὴ απόδειξις εἶναι ἐδῶ)
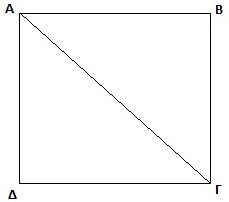
Ἔστω τὸ τετράγωνο ΑΒΓΔ ⇔ (ΑΓ)2 =2 (ΑΒ)2 (1).
Ἔστω ὅτι τὰ ΑΓ καὶ ΑΒ εἶναι σύμμετρα τότε: ΑΓ/ΑΒ=ΕΖ/Η (2),
ὅπου τὰ ΕΖ καὶ Η ἒστω οἱ ἀντίστοιχοι ἀκέραιοι τῶν μετρουμένων μὲ τὸ κοινὸ μέτρο ΑΓ καὶ ΑΒ,
τὸ ΕΖ/Η ἄν δὲν εἶναι ἀνάγωγο τὸ κάνουμε, ΕΖ/Η =Ἀνάγωγον (3).
(1) & (2) ⇔ (ΕΖ)2=2 Η2 ⇔ (ΕΖ)2 = Ἄρτιος ⇔ ΕΖ = Ἄρτιος (4).
(3) & (4) ⇔ Η = Περιττός.
(4) ⇔ ΕΖ= 2 (ΚΛ) ⇔ (ΕΖ)2 =4 (ΚΛ)2 ⇔ 2 Η2 = 4 (ΚΛ)2 ⇔ Η2 = 2 (ΚΛ)2 ⇔
⇔ Η2 = Ἄρτιος ⇔ Η = Ἄρτιος.
Ὅπερ Ἄτοπον
Ὁ Ἀριστοτέλης γνώριζε πολὺ καλὰ τὴν ἀπόδειξη αὐτοῦ τοῦ θεωρήματος καὶ τὴν ἀναφέρει συνοπτικῶς καὶ παρεμπιπτόντως στὰ «Ἀναλυτικά Πρότερα» στὸ κεφάλαιο ὅπου ἀποδεικνύει τὴν «ἀποδεικτικὴ ἰσχύ» ποὺ ἔχει ἡ μέθοδος τῆς «εἰς ἄτοπον ἀπαγωγῆς». (Ἐδῶ νὰ διευκρινίσουμε ὅτι ἡ «διαγώνιος» προκειμένου γιὰ ἐγγράψιμα σχήματα ἀναφέρεται καὶ ὡς «διάμετρος», γιὰ νὰ τονιστεῖ ἀκριβῶς αὐτό.)
«ἀσύμμετρος ἡ διάμετρος διὰ τὸ γίνεσθαι τὰ περιττὰ ἴσα τοῖς ἀρτίοις συμμέτρου τεθείσης»
Ἀριστοτέλης Ἀναλ. Προτ. 41α 26
Τὸ θεώρημα εἶναι πολύ παλαιό, ἀναφέρεται καὶ στὰ Στοιχεῖα Εὐκλείδου, ἀλλὰ εἶναι Πυθαγόρειας προέλευσης.
Ἡ ἀξία του εἶναι ὑψίστη, καθότι ἀποδεικνύει κάτι, τὸ ὁποῖο ὁ κοινός νοῦς δὲν μπορεῖ κἂν νὰ τὸ φανταστεῖ, οὔτε ἐκ τῶν ὑστέρων!
Δηλαδή, ὅτι γιὰ δύο μήκη (καὶ μάλιστα εὐθύγραμμα καὶ μάλιστα μὲ γνωστὴ σχέση μεταξύ τους), δὲν ὑπάρχει κοινὸ μέτρο, ἄρα δὲν μποροῦν νὰ μετρηθοῦν!
Πόσο μᾶλλον γιὰ ἄλλα ἄσχετα μεταξὺ τους μεγέθη!
Τὸ τελικὸ «ἀδιανόητο» συμπέρασμα εἶναι ὅτι τίποτε δὲν μετριέται!!