Loading...
Ἡ Μέτρηση
Τὸ «ἀδύνατον» τῆς ἀκριβοῦς μέτρησης
Ἐνδεικτικὰ ἀναφέρω μερικὰ παραδείγματα.
- Ἡ ἀρχὴ καὶ τὸ τέλος ἑνὸς χρονικοῦ διαστήματος δὲν προσδιορίζονται ἐπακριβῶς.
- Ἡ ἀκρίβεια καὶ ἡ ἀξιοπιστία τῶν ὀργάνων ποὺ χρησιμοποιοῦμε κάθε φορά εἶναι περιορισμένη.
- Συχνὰ τὸ μῆκος μιᾶς ράβδου εἶναι ἀδύνατον νὰ προσδιορισθεῖ ἐπακριβῶς, (αὐτὸ γενικῶς ἰσχύει γιὰ τὰ ὅρια ὁποιουδήποτε φυσικοῦ μεγέθους).
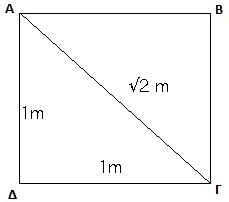
- Εἶναι γνωστὸ ἀπὸ τὴν ἀρχαιότητα ὅτι ἡ διαγώνιος τοῦ τετραγώνου δὲν ἐκφράζεται ὡς κλάσμα τῆς μορφῆς (α/β), ὅπου α καὶ β ἀκέραιοι ἀριθμοί. Αὐτὸ σημαίνει ὅτι ἂν ἡ πλευρὰ ΑΔ εἶναι 1m, τὸ μῆκος ΑΓ (ρίζα 2 m) δὲν δίδεται ἀπὸ δεκαδικὸ ἀριθμὸ μὲ πεπερασμένο ἀριθμὸ ψηφίων. Μπορεῖ ὅμως νὰ ἐκφραστεῖ μὲ ὅση ἀκρίβεια χρειαζόμαστε (μὲ ἐπαρκῆ ἀριθμὸ ψηφίων).
- Μορφὲς γραφῆς τῆς Μέτρησης
- Μέθοδοι ἐκτίμησης καὶ ὑπολογισμοῦ τῆς ἀβεβαιότητας (σφάλματος) τῆς Μέτρησης
- Ἡ διάδοση τοῦ σφάλματος καὶ οἱ τρεῖς μέθοδοι ὑπολογισμοῦ του
- Γενικὲς ἀρχὲς γιὰ ἀξιόπιστες Μετρήσεις
- Συστήματα Μονάδων, Προθέματα.
- Ἡ Ἀναγκαιότητα τῆς Μέτρησης
- Τὸ π στὶς μετρήσεις
- Ἀνέκδοτα μετρήσεων
- Μονάδες μέτρησης φυσικῶν μεγεθῶν
- Φυσικὲς σταθερές