Στην παρούσα σελίδα παρατίθενται τα χαρακτηριστικά των οργάνων που χρησιμοποιούνται για τις μετρήσεις τεχνικών μεγεθών όπως είναι η θερμοκρασία, η πίεση, η παροχή, η ηλεκτρική τάση, η ένταση του ηλεκτρικού ρεύματος και πολλά άλλα.

Eισαγωγή

Κάθε Μηχανικός ή Τεχνικός που θέλει να μετρήσει ένα τεχνικό μέγεθος όπως π.χ. θερμοκρασία, πίεση, μήκος, βάρος κλπ, γνωρίζει ότι η τιμή που θα πάρει έχει κάποιο σφάλμα το μέγεθος του οποίου εξαρτάται από πολλές παραμέτρους κάποιες από τις οποίες αφορούν τα τεχνικά χαρακτηριστικά του οργάνου που χρησιμοποιεί για τη μέτρηση. Στο κείμενο αυτό παρατίθεται η ερμηνεία των χαρακτηριστικών των οργάνων μέτρησης όταν το σήμα είναι στατικό ή δυναμικό.

Στατικά – Δυναμικά χαρακτηριστικά

Τα χαρακτηριστικά των οργάνων μέτρησης που αφορούν την ακρίβεια της μέτρησης χωρίζονται σε δύο κατηγορίες ανάλογα με το αν το μετρούμενο μέγεθος είναι ή δεν είναι χρονικά μεταβαλλόμενο:

– Στατικά χαρακτηριστικά όπου το μετρούμενο μέγεθος παραμένει σταθερό

– Δυναμικά χαρακτηριστικά όπου το μετρούμενο μέγεθος μεταβάλλεται με το χρόνο

Στατικά χαρακτηριστικά

Τα στατικά χαρακτηριστικά των οργάνων μέτρησης είναι τα εξής:

Ορθότητα – Accuracy

Είναι η απόκλιση της τιμής που δίνει το όργανο μέτρησης από την “αληθινή” ή πραγματική τιμή του μετρούμενου μεγέθους η οποία δεν είναι σχεδόν ποτέ γνωστή και ορίζεται μέσω κάποιου πρότυπου. Η τιμή της ορίζεται σαν ποσοστό πλήρους κλίμακας (Full Scale Deflection – FSD). Ουσιαστικά αποτελεί μέτρο του μέγιστου εύρους των σφαλμάτων στις ενδείξεις ενός οργάνου. Ορίζεται ως το μισό του διαστήματος που περιέχει την ένδειξη του οργάνου και μέσα στο οποίο αναμένεται να περιέχεται η ορθή τιμή του μετρούμενου μεγέθους. Για να είναι το σφάλμα όσο το δυνατόν μικρότερο θα πρέπει η κλίμακα του οργάνου να είναι όσο το δυνατόν πλησιέστερα στο εύρος του μετρούμενου μεγέθους.

Παράδειγμα: Έστω ότι μετράται η πίεση αερίου η μέγιστη τιμής της οποίας είναι 1 bar με δύο μανόμετρα κλίμακας 0~1 bar και 0~10 bar τα οποία έχουν σφάλμα 1 % FSD. Αυτό σημαίνει ότι το μέγιστο σφάλμα του πρώτου οργάνου είναι 1*1/100=0.01 bar και είναι το 1 % της μετρούμενης πίεσης ενώ του δεύτερου οργάνου είναι 10*1/100=0.1 bar και αντιστοιχεί στο 10 % της μετρούμενης πίεσης.

Συναφείς όροι που συναντώνται είναι:

ορθότητα ανάγνωσης (reading accuracy). Αντιστοιχεί στην απόκλιση της ένδειξης του οργάνου από την “αληθινή” τιμή.

Παράδειγμα: η απόκλιση στην ένδειξη ενός μανόμετρου είναι ±2.18 bar για τιμή πίεσης 12.5 bar. Η ορθότητα ένδειξης είναι (2.18/12.5)*100=17.44%.

απόλυτη ορθότητα (absolute accuracy). Είναι η απόκλιση ενός οργάνου από την αληθή τιμή εκφρασμένη σαν ποσότητα και όχι σαν ποσοστό.

Παράδειγμα: Η απόλυτη ορθότητα ενός βολτόμετρου είναι ±3 V στην κλίμακα των 100 V. Αυτό σημαίνει ότι η απόκλιση είναι ±3 V σε όλες τις ενδείξεις δηλαδή 10±3 V, 25±3 V, 80±3 V κ.ο.κ

Πιστότητα – Precision

Ο όρος πιστότητα περιγράφει την ιδιότητα του οργάνου να παραμένει ανεπηρέαστο από τυχαία σφάλματα. Αν ληφθεί μεγάλος αριθμός μετρήσεων του ίδιου μεγέθους με όργανο μεγάλης πιστότητας, η διασπορά των τιμών θα είναι πολύ μικρή. Ο όρος πιστότητα (precision) δεν πρέπει να συγχέεται με τον όρο ορθότητα (accuracy). Ένα όργανο μεγάλης πιστότητας δεν σημαίνει απαραίτητα ότι είναι υψηλής ορθότητας. Συνήθως η χαμηλή ορθότητα ενός οργάνου υψηλής πιστότητας προκύπτει συνήθως σαν αποτέλεσμα εισαγωγής συστηματικού σφάλματος το οποίο δύναται να εξαλειφθεί με τη διακρίβωση. Στην Εικ. 1 αποτυπώνονται παραστατικά οι έννοιες της ορθότητας και της πιστότητας.

Εικ. 1 Παραστατική απεικόνιση των εννοιών της ορθότητας και της πιστότητας

Επαναληψιμότητα – Repeatability

Με τον όρο επαναληψιμότητα αποδίδεται η έννοια της απόκλισης μεταξύ των τιμών σε επαναλαμβανόμενες μετρήσεις του ίδιου μεγέθους μέσα σε σύντομο χρονικό διάστημα όπου παραμένουν ίδια οι συνθήκες μέτρησης, το όργανο, ο χειριστής, η τοποθεσία και οι περιβαλλοντικές συνθήκες καθώς και ο τρόπος χειρισμού του οργάνου.

Αναπαραγωγιμότητα – Reproducibility

Με την αναπαρωγιμότητα αποδίδεται -όπως και στην επαναληψιμότητα- η έννοια της απόκλισης των τιμών μεταξύ τους σε επαναλαμβανόμενες μετρήσεις του ίδιου μεγέθους όταν διαφέρουν η μέθοδος μέτρησης, ο χειριστής, το όργανο, η τοποθεσία, οι συνθήκες και ο χρόνος.

Και τα δύο προηγούμενα χαρακτηριστικά περιγράφουν τη διασπορά των τιμών ενός σταθερού μεγέθους. Όταν οι συνθήκες μέτρησης παραμένουν σταθερές χρησιμοποιείται ο όρος επαναληψιμότητα ενώ όταν μεταβάλλονται, ο όρος αναπαραγωγιμότητα.

Οι έννοιες επαναληψιμότητα και αναπαραγωγιμότητα είναι εναλλακτικές του όρου της πιστότητας.

Εύρος (range – span)

Το εύρος ενός οργάνου είναι το αλγεβρικό άθροισμα της ελάχιστης και μέγιστης τιμής του μεγέθους που μπορεί να μετρήσει.

Παράδειγμα: το εύρος ενός θερμομέτρου με τιμές κλίμακας – 40 έως 100 °C είναι 100 –(– 40) = 140 °C

Διακριτότητα – Resolution

Είναι η μικρότερη μεταβολή του μετρούμενου μεγέθους η οποία προκαλεί μεταβολή της ένδειξης του οργάνου.

Παράδειγμα: προσθέτοντας με αργό ρυθμό βάρος σε ένα ζυγό, η ένδειξη μεταβάλλεται από 5.4 σε 5.5 kg. Η διακριτότητα του ζυγού είναι 0.1 kg.

Γραμμικότητα – Linearity

Η γραμμικότητα είναι ο βαθμός της γραμμικής συνάρτησης των τιμών του μεγέθους με τις μετρήσεις.

Ευαισθησία – Sensitivity

Η ευαισθησία K ορίζεται ως ο λόγος της μεταβολής της ένδειξης του οργάνου προς τη μεταβολή του μετρούμενου μεγέθους. Είναι γνωστή και ως συνάρτηση μεταφοράς. Όταν το όργανο συμπεριφέρεται γραμμικά, η ευαισθησία του είναι σταθερή σε όλο το εύρος.

Παράδειγμα: Για μεταβολή πίεσης 100 Pa, η έξοδος ενός μορφομετατροπέα πίεσης είναι 320 mV. Η ευαισθησία προκύπτει ως 3.2 mV/Pa.

Ένα όργανο υψηλής ευαισθησίας προτιμάται καθώς παρέχει “δυνατό σήμα” όμως αυτό μπορεί να αποβεί σε βάρος της γραμμικότητας, του εύρους και της ορθότητας.

Υστέρηση – Hysteresis

Είναι η απόκλιση στη μέτρηση συγκεκριμένης τιμής ενός μεγέθους όταν η κατεύθυνση προς την τιμή είναι αυξανόμενη ή μειούμενη.

Παράδειγμα: Με ζυγό εύρους 20.0 kg μετράται το βάρος αντικειμένου 10.0 kg. Τοποθετείται στο ζυγό δεύτερο αντικείμενο ιδίου βάρους το οποίο στη συνέχεια αφαιρείται. Η νέα ένδειξη είναι 9.9 kg.

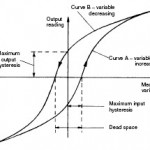
Η υστέρηση οφείλεται σε παραμένουσες τάσεις στα στοιχεία του οργάνου. Στην παρακάτω εικόνα φαίνεται παραστατικά η έννοια της υστέρησης.

Εικ. 2 Χαρακτηριστική οργάνου με υστέρηση [4]

Νεκρή ζώνη – Dead band

Είναι το πεδίο τιμών εισόδου για τις οποίες δεν υφίσταται αλλαγή στην ένδειξη. Κάθε όργανο το οποίο παρουσιάζει υστέρηση έχει και νεκρή ζώνη όπως φαίνεται και στην Εικ. 2. Επίσης υπάρχουν όργανα τα οποία αν και δεν παρουσιάζουν υστέρηση, έχουν νεκρή ζώνη όπως είναι χαρακτηριστικά τα όργανα τα οποία φέρουν μηχανισμούς με γρανάζια.

Offset

Είναι η ένδειξη του οργάνου για μηδενική είσοδο. Ταυτίζεται με την ολίσθηση μηδενός. Συνήθως είναι μι =α σταθερή ποσότητα σε όλη την κλίμακα του οργάνου.

Ολίσθηση – Drift

Η διακρίβωση και τα τεχνικά χαρακτηριστικά κάθε οργάνου ισχύουν σε καθορισμένες περιβαλλοντικές συνθήκες τις τιμές των οποίων παρέχει ο κατασκευαστής όπως το εύρος θερμοκρασιών, πίεση, επιτάχυνση κλπ. Οι αλλαγές των συνθηκών επηρεάζουν τα στατικά χαρακτηριστικά των οργάνων. Οι επιδράσεις αυτές παρέχονται με την ολίσθηση του μηδενός (zero drift) και με την ολίσθηση ευαισθησίας (sensitivity drift).

Ολίσθηση μηδενός – Zero drift

Συναντάται και ως bias. Είναι η ένδειξη του οργάνου με μηδενική είσοδο στις καθορισμένες συνθήκες περιβάλλοντος. Είναι ένα σταθερό σφάλμα το οποίο υφίσταται σε όλη την κλίμακα ενδείξεων του οργάνου. Τυπική περίπτωση οργάνων με ολίσθηση μηδενός είναι οι μηχανικοί ζυγοί. Αντίστοιχη ολίσθηση παρουσιάζουν και άλλα όργανα όπως τα βολτόμετρα τα οποία επηρεάζονται από τη μεταβολή της θερμοκρασίας και συνήθως η ολίσθηση μετράται σε V/°C και ονομάζεται συντελεστής ολίσθησης μηδενός (zero drift coefficient). Για κάποιο όργανο ενδέχεται να παρέχονται περισσότεροι του ενός συντελεστές και κάθε ένας να σχετίζεται με μία περιβαλλοντική παράμετρο π.χ. θερμοκρασία, πίεση κλπ.

Ολίσθηση ευαισθησίας – Sensitivity drift.

Είναι η μεταβολή της ευαισθησίας ενός οργάνου με τη μεταβολή των συνθηκών περιβάλλοντος. Στην Εικ. 3 φαίνονται οι διάφορες περιπτώσεις ολίσθησης.

Παράδειγμα: Η δυναμοκυψέλη ενός ζυγού διακριβώνεται στους 20°C και έχει τα ακόλουθα χαρακτηριστικά:

Βάρος (kg)	0	2	4	6
Τάση (mV)	0	40	80	120

Η διακρίβωση ελέγχεται στους 30 °C με τα ακόλουθα χαρακτηριστικά:

Βάρος (kg)	0	2	4	6
Τάση (mV)	5	54	99	142

Από τα παραπάνω προκύπτει ότι στους 20°C η χαρακτηριστική φορτίου-τάσης είναι ευθεία και η ευαισθησία της κυψέλης είναι 20 mV/kg. Στους 30°C η χαρακτηριστική είναι και πάλι ευθεία και η ευαισθησία είναι 22 mV/kg.

Ολίσθηση μηδενός: 5 mV

Ολίσθηση ευαισθησίας = 22-20 = 2 mV/kg

Ολίσθηση μηδενός / °C = 5/10 = 0.5 mV/°C

Ολίσθηση ευαισθησίας / °C = 2/10 = 0.2 mV/(kg*°C)

Κατώφλι – Theshold

Είναι η ελάχιστη μεταβολή του μεγέθους από μηδενική τιμή η οποία είναι ανιχνεύσιμη από το όργανο.

Παράδειγμα: Αν ένα ταχύμετρο αυτοκινήτου έχει κατώφλι 15 km/h τότε το αυτοκίνητο θα πρέπει να υπερβεί τα 15 km/h πριν το ταχύμετρο παρέχει ενδείξεις ταχύτητας.

Εικ. 3. Ολίσθηση μηδενός, ευαισθησίας και συνδυασμός τους

Δυναμικά χαρακτηριστικά

Τα δυναμικά χαρακτηριστικά των οργάνων μέτρησης αφορούν την απόκριση του οργάνου όταν το σήμα είναι χρονικά μεταβαλλόμενο. Τα δυναμικά χαρακτηριστικά περιγράφουν τη συμπεριφορά του οργάνου ανάμεσα στα χρονικά σημεία της αλλαγής της τιμής του φυσικού μεγέθους και της σταθεροποίησης της ένδειξης του οργάνου. Όπως και με τα στατικά χαρακτηριστικά, οι τιμές των δυναμικών χαρακτηριστικών ισχύουν όταν το όργανο χρησιμοποιείται σε καθορισμένες περιβαλλοντικές συνθήκες.

Σε κάθε γραμμικό^[1], χρονικά αμετάβλητο^[2] σύστημα ισχύει η ακόλουθη σχέση ανάμεσα στην είσοδο και την απόκριση:

$\dpi{100} $$\eqalign{ & {a_n}{{{d^n}V} \over {d{t^n}}} + {a_{n - 1}}{{{d^{n - 1}}V} \over {d{t^{n - 1}}}} + ... + {a_1}{{dV} \over {dt}} + {a_0}V = \cr & {b_m}{{{d^m}S} \over {d{t^m}}} + {b_{m - 1}}{{{d^{m - 1}}S} \over {d{t^{m - 1}}}} + {b_1}{{dS} \over {dt}} + {b_0}S \cr} $$$ (1)

όπου

V: η τιμή του μετρούμενου μεγέθους (input)

S: η ένδειξη του οργάνου (output)

a₀…a_n, b₀,…b_n: σταθερές

Θεωρώντας βηματική μεταβολή (συνάρτηση βαθμίδας) του φυσικού μεγέθους, η (1) γίνεται:

$\dpi{100} $${a_n}{{{d^n}V} \over {d{t^n}}} + {a_n}{{{d^{n - 1}}V} \over {d{t^{n - 1}}}} + ... + {a_1}{{dV} \over {dt}} + {a_0}V = {b_0}S$$$ (2)

Η συνάρτηση βαθμίδας περιγράφεται από τη σχέση S=A(t), όπου

A(t)=0, t<0

A(t)=A, t>0

Η (2) δύναται να απλοποιηθεί περαιτέρω θεωρώντας διάφορες περιπτώσεις οι οποίες αφορούν σχεδόν όλα τα μετρητικά συστήματα.

[1] Γραμμικό λέγεται το σύστημα το οποί $% MathType!MTEF!2!1!+- % feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa % aaleaacaaIWaaabeaakiaadAfacqGH9aqpcaWGIbWaaSbaaSqaaiaa % icdaaeqaaOGaam4uaaaa!3C39! \[{a_0}V = {b_0}S\]$ $% MathType!MTEF!2!1!+- % feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqipu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBa % aaleaacaaIWaaabeaakiaadAfacqGH9aqpcaWGIbWaaSbaaSqaaiaa % icdaaeqaaOGaam4uaaaa!3C39! \[{a_0}V = {b_0}S\]$ ο αν στις εισόδους x₁(t) και x₂(t) έχει αποκρίσεις y₁(t) και y₂(t) αντίστοιχα, τότε στην είσοδο ax₁(t)+bx₂(t) έχει απόκριση ay₁(t)+by₂(t) όπου a,b πραγματικές σταθερές.

[2] Χρονικά αμετάβλητο λέγεται το σύστημα η απόκριση του οποίου δεν εξαρτάται από το χρονικό σημείο επιβολής της εισόδου.

Κατηγορίες οργάνων

Τα όργανα χωρίζονται γενικότερα σε τρεις κατηγορίες ανάλογα με τη μορφή της απόκρισής τους σε δυναμικά σήματα: τα όργανα μηδενικής, πρώτης και δεύτερης τάξης

Όργανo μηδενικής τάξης

Ένα όργανο λέγεται μηδενικής τάξης (zero order instrument) όταν η απόκρισή του είναι απόλυτα άμεση με τη μεταβολή του φυσικού μεγέθους. Η εξίσωση που περιγράφει τη συμπεριφορά ενός τέτοιου οργάνου είναι:

${a_0}V = {b_0}S$ ή $\dpi{100} $$V = {b_0}S/{a_0} = KS \equiv KA$$$

όπου K είναι η ευαισθησία του οργάνου όπως αυτή ορίζεται στα στατικά χαρακτηριστικά.

Παράδειγμα τέτοιου οργάνου είναι το ποτενσιόμετρο όπου η μεταβολή της γωνίας μετατρέπεται άμεσα σε μεταβολή τάσης.

Όργανο πρώτης τάξης

Όταν το μετρούμενο μέγεθος μεταβληθεί βηματικά και η ένδειξη του οργάνου χρειάζεται κάποιο χρόνο για να σταθεροποιηθεί, τότε το όργανο λέγεται πρώτης τάξης και και η απόκρισή του περιγράφεται από την εξίσωση:

$\dpi{100} $${a_1}{{dV} \over {dt}} + {a_0}V = {b_0}S \equiv {b_0}A$$$ (3)

Η αναλυτική λύση της για βηματική είσοδο και αυθαίρετες αρχικές συνθήκες είναι

$\dpi{100} $$V(t) = {V_o}{e^{ - t/\tau }} + KA(1 - {e^{ - t/\tau }})$$$ (4)

όπου:

V_o :αρχική ένδειξη του οργάνου

V :τιμή μετρούμενου μεγέθους

τ :σταθερά χρόνου.

Αν η αρχική ένδειξη V_o του οργάνου είναι ίση με μηδέν, η (4) γίνεται

$\dpi{100} $$V(t) = KA(1 - {e^{ - t/\tau }}) = {V_{\max }}(1 - {e^{ - t/\tau }})$$$ (5)

Η σταθερά χρόνου είναι ένας δείκτης της αδράνειας του οργάνου. Αντικαθιστώντας τον χρόνο t με πολλαπλάσια της σταθεράς χρόνου –nτ– προκύπτει ότι

$\dpi{100} $$V/{V_{\max }} = 1 - {1 \over {{e^n}}}$$$

από όπου για διάφορες τιμές του n προκύπτει

n=1, V/V_max=0.6321

n=2, V/V_max=0.8647

n=3, V/V_max=0.9502

n=4, V/V_max=0.9817

n=5, V/V_max=0.9933

Από τα παραπάνω βγαίνει το συμπέρασμα ότι σε 5 σταθερές χρόνου η ένδειξη του οργάνου ισούται με το 99.33% της τελικής τιμής και πρακτικά έχει σταθεροποιηθεί. Η μορφή της απόκρισης ενός οργάνου για βηματική μεταβολή του φυσικού μεγέθους φαίνεται στην Εικ. 4. Αν η λήψη της ένδειξης γίνει πριν τη σταθεροποίησή της προκύπτει σφάλμα ΔV το μέγεθος του οποίου εξαρτάται από το χρόνο.

Εικ. 4. Απόκριση οργάνου πρώτης τάξης

Τα όργανα πρώτης τάξης προδιαγράφονται με διάφορες παραμέτρους από τους κατασκευαστές. Χαρακτηριστικές παράμετροι είναι η συχνότητα απόκρισης και η ταχύτητα απόκρισης.

Συχνότητα απόκρισης – frequency response

Είναι τυπική παράμετρος η οποία καθορίζει την ταχύτητα αντίδρασης του οργάνου σε μεταβολή του μετρούμενου μεγέθους. Η συχνότητα απόκρισης εκφράζεται σε Hz ή r/s και καθορίζει τη σχετική μείωση του σήματος εξόδου σε κάποια συχνότητα. Συνηθίζεται να προδιαγράφεται η συχνότητα για την οποία η μείωση είναι -3 dB και αντιστοιχεί σε μείωση της ένδειξης ~30 %.

Ταχύτητα απόκρισης – speed response

Αντιστοιχεί στο χρόνο που μεσολαβεί μέχρι το όργανο να αντιληφθεί το σήμα εισόδου και συνήθως προδιαγράφεται στο 90 % της τελικής ένδειξης του οργάνου σε βηματική είσοδο. Η συχνότητα απόκρισης συνδέεται άμεσα με την ταχύτητα η οποία δίνεται σε μονάδες του σήματος εισόδου ανα μονάδα χρόνου.

Παράδειγμα οργάνου πρώτης τάξεως είναι το υδραργυρικό θερμόμετρο του οποίου η ένδειξη μεταβάλλεται σταδιακά όταν βρεθεί σε περιβάλλον διαφορετικής θερμοκρασίας.

Όργανο δεύτερης τάξης

Η χαρακτηριστική του οργάνου δεύτερης τάξης περιγράφεται από την εξίσωση

$\dpi{100} $${a_2}{{{d^2}V} \over {d{t^2}}} + {a_1}{{dV} \over {dt}} + {a_0}V = {b_0}S$$$ (6)

Αναδιατάσσοντας την προκύπτει

$\dpi{100} $${{{d^2}V} \over {d{t^2}}} + {{{a_1}} \over {{a_2}}}{{dV} \over {dt}} + {{{a_0}} \over {{a_2}}}V = {{{b_0}} \over {{a_2}}}S$$$ (7)

Η (7) λύνεται εισάγοντας 2 χαρακτηριστικές παραμέτρους, τη φυσική συχνότητα ω_n και το λόγο απόσβεσης ζ όπου

$\dpi{100} ${\omega _n} = \sqrt {{{{a_0}} \over {{a_2}}}} $$ $\dpi{100} $\zeta = {1 \over 2}{{{a_1}} \over {\sqrt {{a_0}{a_2}} }}$$

και ισχύει τ=1/ζω . Η φυσική συχνότητα και ο λόγος απόσβεσης παρέχονται από τον κατασκευαστή. Αντικαθιστώντας, η (7) γίνεται

$\dpi{100} $${{{d^2}V} \over {d{t^2}}} + 2\zeta {\omega _n}{{dV} \over {dt}}\omega _n^2V = {\rm K}S\omega _n^2 \equiv KA\omega _n^2$$$ (8)

Η αναλυτική λύση της (8) για βηματική είσοδο είναι

$\dpi{100} $$V(t) = KA\left[ {1 - {{{\omega _n}{e^{ - t/\tau }}} \over {{\omega _d}}}\sin ({\omega _d}t + \varphi )} \right]$$$

όπου

$\dpi{100} $$\varphi \equiv {\tan ^{ - 1}}({\omega _d}\tau )$$$

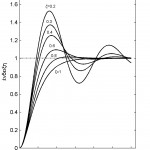
Εικ. 5: Καμπύλες απόκρισης οργάνου δεύτερης τάξης για διάφορες τιμές του λόγου απόσβεσης ζ.

Η παράμετρος $\inline \dpi{100} ${\omega _d} = {\omega _n}\sqrt {1 - {\zeta ^2}} $$ λέγεται φυσική συχνότητα με απόσβεση.

Το αντίστροφο της σταθεράς χρόνου 1/τ λέγεται συντελεστής απόσβεσης.

Γενικότερα επιλέγεται όργανο η φυσική συχνότητα του οποίου υπερβαίνει κατά 60 % τουλάχιστον τη συχνότητα του μετρούμενου μεγέθους.

Συχνότητα αποκοπής

Είναι η ελάχιστη ή μέγιστη συχνότητα του μετρούμενου μεγέθους που δύναται να αντιληφθεί το όργανο.

Αβεβαιότητα

Έστω ότι μετράται ένα μέγεθος y το οποίο είναι συνδυασμός άλλων μεγεθών x₁, x₂, …x_n όπου η μέτρηση κάθε επιμέρους μεγέθους υπόκειται σε αβεβαιότητα u(xi), i=1…n.

H συνδυασμένη αβεβαιότητα u(y) της μέτρησης του y δίνεται από τη σχέση

$u^2(y) = {\left( {{{\partial y} \over {\partial {x_1}}}} \right)^2}{u^2}({x_1}) + {\left( {{{\partial y} \over {\partial {x_2}}}} \right)^2}{u^2}({x_2}) + ... + {\left( {{{\partial y} \over {\partial {x_n}}}} \right)^2}{u^2}({x_n}) = \sum\limits_{i = 1}^n {{{\left( {{{\partial y} \over {\partial {x_i}}}} \right)}^2}{u^2}({x_i})}$

Παράδειγμα:

Η ταχύτητα v του κύματος σε μια τεντωμένη χορδή δίνεται από τη σχέση

$v = \sqrt {{T \over m}}$

όπου Τ είναι η τάση της χορδής και m είναι η κατανομή της μάζας ανά μονάδα μήκους της χορδής. Κατά τις μετρήσεις βρέθηκε ότι:

Τ = 20 Ν , u(T) = 0.6 N, m = .0064 kg/m, u(m) = .0008 kg/m.

Να υπολογιστεί η τυπική αβεβαιότητα στον υπολογισμό της ταχύτητας.

Απάντηση:

Από τη σχέση διάδοσης της αβεβαιότητας προκύπτει ${u^2}(v) = {\left( {{\partial \over {\partial T}}\sqrt {{T \over m}} } \right)^2}{u^2}(T) + {\left( {{\partial \over {\partial m}}\sqrt {{T \over m}} } \right)^2}{u^2}(m) = {\left( {{1 \over {2\sqrt {T \cdot m} }}} \right)^2}{u^2}(T) + {\left( { - {1 \over 2}\sqrt T \cdot {m^{ - {3 \over 2}}}} \right)^2}{u^2}(m)$

από όπου με αντικατάσταση προκύπτει u(v) = 1.3 m/s

Βιβλιογραφία

[1] Μανώλης Μαθιουλάκης, Μέτρηση, Ποιότητα Μέτρησης και Αβεβαιότητα, Ελληνική Ένωση Εργαστηρίων, Αθήνα 2004, ISBN 960-88226-0-2.

[2] Σ. Σιμόπουλος, Μετρήσεις Τεχνικών Μεγεθών, ΕΜΠ, Αθήνα 1989.

[3] William C. Dunn, Fundamentals of Industrial Instrumentation and Process Control, McGraw-Hill, 2005, ISBN 0-07-145735-6.

[4] Alan S. Morris, Measurement and Instrumentation Principles, Butterworth-Heinemann, 2001, ISBN 0-7506- 5081-8.

[5] DiStefano J. et al, Feedback and Control Systems, 2^nd ed., Schaum’s outline series, 1990, ISBN 0-07-017047-9.

[6] Ν. Κρικέλης, Εισαγωγή στον Αυτόματο Έλεγχο – Θεωρία και Εφαρμογές, Συμμετρία, 1990.

[7] Wikipedia.org

Απρίλιος 2013

Για οποιαδήποτε παρατήρηση, διόρθωση, συμπλήρωση κλπ, επικοινωνήστε με το συγγραφέα:

Γεώργιος Ζαννής, Δρ Μηχανολόγος Μηχανικός

Εργαστήριο Ετερογενών Μειγμάτων & Συστημάτων Καύσης

Τομέας Θερμότητας

Σχολή Μηχανολόγων Μηχανικών

Εθνικό Μετσόβιο Πολυτεχνείο

Χαρακτηριστικά οργάνων μέτρησης τεχνικών μεγεθών