Το μοντέλο μας αποτελείται από ένα τετραγωνικό πλέγμα
LxL.
Το κάθε σημείο (site) του
πλέγματος μπορεί να είναι κατειλημμένο(ή
τιμή 1) με πιθανότητα p και μη κατειλημμένο
(ή τιμή 0) με πιθανότητα 1-p. Η πιθανότητα p ένα site να είναι
κατειλημμένο είναι ανεξάρτητη από αυτή των γειτόνων
του.
Ορίζουμε σαν συσσωμάτωμα (cluster)
το σύνολο των κατειλημμένων θέσεων που βρίσκονται σε απόσταση
πρώτων γειτόνων μεταξύ τους.
Η περιγραφή του προγράμματος έχει ως εξής:
- Σε κάθε σημείο του πλέγματος αντιστοιχούμε ένα τυχαίο
αριθμό
- Εάν ο τυχαίος αριθμός είναι μικρότερος ή ίσος με την
πιθανότητα κατάληψης τότε το σημείο θεωρείται κατηλειμένο
και παίρνει την τιμή 1, διαφορετικά έχει την τιμή 0.
Για να το πετύχουμε αυτό στην mathematica αρκεί
να γράψουμε την εντολή:
Percolation[p_, L_] := Table[Floor[1
+ p - Random[]], {L}, {L}];
όπου ορίζουμε την συνάρτηση Percolation με
ορίσματα την πιθανότητα κατάληψης p και την διάσταση του πλέγματος
L. H Random[] δημιουργεί ένα τυχαίο αριθμό. Η Table[expr,{L},{L}]
φτιάχνει πίνακα LxL. H Floor[x] δίνει τον μεγαλύτερο ακέραιο
που είναι μικρότερος ή ίσος με x, άρα 0 για Random[]>p
και 1 για Random[]<=p.
Γράφοντας τώρα την εντολή
SeedRandom[];
r = Percolation[0.2, 10]
{{0, 0, 0, 1, 1, 1, 0, 1, 0, 0}, {0, 0, 0, 0,
0, 0, 0, 0, 0, 0}, {0, 0, 0, 1,
1, 0, 0, 1, 1, 0}, {1, 1, 0, 0, 1, 0, 0, 0, 0, 0}, {0, 0,
1, 0, 0, 0, 0,
0, 0, 0}, {0, 0, 0, 0, 0, 0, 0, 1, 0, 1}, {0, 0, 0, 1, 0,
0, 0, 0, 1,
0}, {0, 0, 0, 1, 0, 0, 1, 0, 1, 0}, {0, 0, 1, 0, 1, 0, 0,
0, 1, 1}, {0, 0,
1, 0, 0, 0, 0, 0, 0, 1}}
έχουμε τον πίνακα r που αντιστοιχεί σε πλέγμα
10x10 με p=0.2. Για να τον δούμε σε καλύτερη μορφή γράφουμε
TableForm[r]
Επίσης μπορούμε να οπτικοποιήσουμε τα 0 και
1 με την εντολή
Show[Graphics[ RasterArray[ Reverse[r]
/.{1 -> RGBColor[0, 0, 0], 0 -> RGBColor[1, 1, 1]}]],
AspectRatio -> 1]
οπότε παίρνουμε σαν αποτέλεσμα πλέγματα με μαύρα
και άσπρα sites της μορφής, όπου τα μαύρα τετράγωνα αντιστοιχούν
σε κατειλημμένα site (1) ενώ τα λευκά σε μη κατειλημμένα (0)
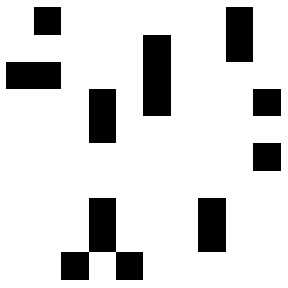
Μπορείτε
να κατεβάσετε το πρόγραμμα σε μορφή Mathematica Notepad κάνοντας
click εδώ!!!!
Θα εκτελέσουμε το παραπάνω πρόγραμμα για
διάφορες τιμές του p και του L αναζητώντας άπειρο
συσσωμάτωμα, δηλαδή συσσωμάτωμα που εκτείνεται από
την μία έως την άλλη άκρη του πλέγματος. Η δημιουργεία άπειρου
συσσωματώματος γίνεται όπως θα δούμε μετά από μία κρίσιμη
πιθανότητα κατάληψης pc. Έχουμε δηλαδή
μία γεωμετρική μετάπτωση φάσης. Η συγκέντρωση
των κατειλημμένων θέσεων στο πρόβλημα της διήθησης παίζει
τον ίδιο ρόλο με τη θερμοκρασία στις θερμικές μεταπτώσεις
φάσης.
Κάποια από τα αποτελέσματα φαίνονται παρακάτω.

Παρατηρούμε ότι για p=0.5=pc και μετά,
έχουμε άπειρο συσσωμάτωμα.

Διπλασιάζοντας το L τώρα για p=0.6=pc
έχουμε άπειρο συσσωμάτωμα. Παρατηρήθηκε όμως ότι για L=20
είχαμε άπειρο συσσωμάτωμα και για p=0.5 σε διαφορετικά 'runs'
του προγράμματος.

Πρατηρούμε ότι η κρίσιμη πιθανότητα εξαρτάται
από το πεπερασμένο μέγεθος του πλέγματος μας, και έτσι μας
είναι δύσκολο να ορίσουμε με ακρίβεια το pc
.
Βιβλιογραφία
Για οποιαδήποτε παρατήρηση παρακαλώ επικοινωνήστε μαζί μου.
Θεοδώνης Ιωάννης
email :ytheod@mail.ntua.gr
homepage:
http://users.ntua.gr/ytheod
Αθήνα 13/2/2003
|