Θεωρητική Μελέτη
Το κίνητρο για
το μοντέλο Ising είναι η επεξήγηση της συμπεριφοράς της μαγνήτισης
σαν συνάρτηση της θερμοκρασίας σε διάφορα υλικά (π.χ. Σίδηρος).
Ποιοτικά η ύπαρξη
μακροσκοπικού μαγνητικού πεδίου σε κάποιο κομμάτι ύλης (π.χ.
σιδήρου) εξαρτάται από την σχετική σημαντικότητα δύο φυσικών
διεργασιών, της διεργασίας ελαχιστοποίησης της ενέργειας και
της αύξησης της εντροπίας του συστήματος. Ένα από τα πιο σημαντικά
επιτευγματά της φυσικής του 19ου αιώνα ήταν η ανακάλυψη της
κατάληλης συνάρτησης πιθανότητας που χαρακτηρίζει τη σχετική
σημαντικότητα των πιθανών μικροκαταστάσεων ενός συστήματος.
Ας υποθέσουμε
ότι S μία μικροκατάσταση ενός συστήματος που βρίσκεται σε
σταθερή θερμοκρασία T.Τότε η πιθανότητα P(S) το σύστημα να
βρεθεί στην μικροκατάσταση S δίνεται από την συνάρτηση πιθανότητας
Boltzmann
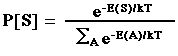
Εξίσωση 1
όπου E(S) η ενέργεια της μικροκατάστασης S, Τ η θερμοκρασία
στην οποία βρίσκεται το σύστημα, k η σταθερά Boltzmann και
η άβροιση στον παρονομαστή γίνεται σε όλες τις δυνατές μικροκαταστάσεις
εξασφαλίζοντας ότι το άθροισμα σε όλα τα P(S) είναι μονάδα.
Η σημασία της θερμοκρασίας γίνεται φαίνεται καλύτερα εάν
θεωρήσουμε δύο μικροκαταστάσεις έστω A και B με E(A)<E(B).
Η σχετική πιθανότητα τότε δίνεται από τον τύπο
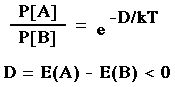
Εξίσωση 2
Σε
υψηλές θερμοκρασίες (για kT πολύ μεγαλύτερο του |D|) το εκθετικό
γίνεται μονάδα, δηλαδή οι δύο καταστάσεις έχουν την ίδια πιθανότητα
να συμβούν και έτσι 'κερδίζει' η τυχαιότητα. Αντιθέτως για
χαμηλές θερμοκρασίες (για |D| πολύ μεγαλύτερο του kT) πιο
πιθανή να συμβεί είναι η κατάσταση με την μικρότερη ενέργεια.
Από
την στιγμή που έχουμε την συνάρτηση πιθανότητας μπορούμε να
υπολογίσουμε αναμενόμενες τιμές για τα μεγέθη που μας ενδιαφέρουν
και στην προκειμένη περίπτωση είναι η Μαγνήτιση M και η ενέργεια
E του συστήματος μας. Χρειαζόμαστε λοιπόν μια έκφραση για
να υπολογίζουμε τόσο τα Μ,Ε.
Το μοντέλο Ising απλοποιεί τις αλληλεπιδράσεις των ατόμων
του στερεού μας σε αλληλεπιδράσεις των spin τους. Επιπλέον
θεωρεί ότι τα άτομα βρίσκονται πακτωμένα σε πλεγαμτικά σημεία
και ότι το spin μπορεί να πάρουν δύο τιμές +1 ή -1. Επίσης
μία ακόμα απλούστευση είναι ότι θεωρεί αλληλεπιδράσεις μόνο
μεταξύ πρώτων γειτόνων.
Έτσι
έχουμε μία έκφραση για την ενέργεια μιάς μικροκατάστασης
του συστήματος της μορφής
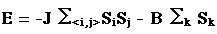
Εξίσωση 3
όπου
- Sj είναι η τιμή του σπιν στο πλεγματικό
σημείο j με S(j)=+1 για όταν το σπιν είναι προσανατολισμένο
'επάνω' και Sj=-1 για όταν το σπιν
είναι προσανατολισμένο 'κάτω',
- ο συμβολισμός <i,j> σημαίνει ότι η άθροιση
γίνεται σε όλους τους πρώτους γείτονες,
- η σταθερά J
έχει μονάδες ενέργειας και λέγεται σταθερά σύζευξης (μπορεί
να μην είναι η ίδια για όλα τα πλεγματικά σημεια αλλά για
χάρη απλότητας θεωρείται ίδια εδώ)
- Η σταθερά Β
(πάλι μονάδες ενέργειας) υποδηλώνει την ύπαρξη εξωτερικού
μαγνητικού πεδίου.
Στο μοντέλο αυτό
η μαγνήτιση Μ(S) μιας μικροκατάστασης του συστήματος
δίνεται από τον αριθμό των σπιν που δείχνουν επάνω
μείον τον αριθμό των σπιν που δείχνουν κάτω.
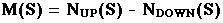
Εξίσωση 4
Φαίνεται
πολύ απλό πλέον να υπολογίσουμε τόσο την αναμενόμενη τιμή
της μαγνήτισης όσο και την αναμενόμενη τιμή της Ενέργειας
του συστηματός μας. Έστω για την αναμενόμενη τιμή της μαγνήτισης
αρκεί ο τύπος
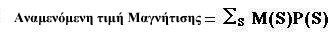
Εξίσωση 5
Φαίνεται πολύ απλό αρκεί να κάνουμε μία άθροιση
αλλά δυστηχώς δεν είναι. Δεν πρέπει να ξεχνάμε ότι η άθροιση
γίνεται σε όλες τις δυνατές μικροκαταστάσεις που στην περίπτωση
του μοντέλου Ising είναι οι όλοι οι διαφορετικοί δυνατοί τρόποι
προσανατολισμού των σπιν των πλεγματικών σημείων. Ο αριθμός
των τρόπων είναι δυστυχώς 2^Ν όπου Ν ο αριθμός των πλεγματικών
σημείων. Έτσι ο υπολογισμός γίνεται αδύνατος αφού για ένα
μικρό πλέγμα π.χ. 16x16 (256 συνολικά σημεία) υπάρχουν 10^77
διαφορετικές μικροκαταστάσεις στο άθροισμα. Έστω ότι ένας
πολύ γρήγορος υπολογιστής κάνει 10^10 υπολοισμούς το δευτερόλεπτο
τότε ο συνολικός υπολογισμός χρειάζεται 10^67 δευτερόλεπτα,
που είναι ένα πολύ μεγάλο χρονικό διάστημα εάν σκεφτούμε ότι
η ηλικία του σύμπαντος είναι 10^20 δευτερόλεπτα (sic).
Η επακριβής απαρίθμηση λοιπόν είναι αδύνατη.
Ένας άλλος τρόπος λοιπόν χρειάζεται για να βρούμε τις αναμενόμενες
τιμές των μεγεθών που μας ενδιαφέρουν. Θα μπορούσαμε να στήσουμε
ένα πείραμα για το σύστημα που μας ενδιαφέρει και να μετρήσουμε
το μέγεθος που θέλουμε έστω την μαγνήτιση Μ, θεωρώντας ότι
δεν επηρεάζουμε το σύστημα με την μετρησή μας αυτή. Σε ένα
σωστό πείραμα δεν κάνουμε μόνο μία μέτρηση αλλά πολλές έστω
L, και σαν αποτέλεσμα παίρνουμε το μέσο όρο αυτών.
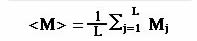
Εξίσωση 6
Σύμφωνα με το θεώρημα των μεγάλων αριθμών (Markov)
ο μέσος όρος των μετρήσεων μας είναι μια πολύ καλή εκτίμηση
της αναμενόμενης τιμής που προβλέπει η θεωρία μας (με σφάλμα
1/sqrt(L)).
Εξίσωση 7
Ένας
τρόπος να 'μιμιθούμε' την φύση είναι η μέθοδος Monte Carlo
(τυχαίων αριθμών) σε συνδιασμό με τον αλγόριθμο Metropolis.
Η μπορούμε να μιμιθούμε τη φύση εάν
- Αντικαταστήσουμε
την πλήρη άρθοιση της εξίσωσης 5 με μία άθροιση πάνω σε
ένα αντιπροσωπευτικό δείγμα μικροκαταστάσεων.
- Επιλέξουμε
το αντιπροσωπευτικό δείγμα προσεκτικά σύμφωνα με την συνάρτηση
πιθανότητας της εξίσωσης 1
Η συχνότητα εμφάνισης στο αντιπροσωπευτικό δείγμα δηλαδή,
κάποιας μικροκατάστασης πρέπει να είναι αντίστοιχη της πιθανότητας
που δίνεται από την εξίσωση 1
Ο αλγόριθμος (Metropolis) που το πετυχαίνει αυτό περιγράφεται
ως εξής
- Οι καταστάσεις των σπιν του πλέγματος (+1 ή -1) καταχωρούνται
σε ένα μεγάλο πίνακα. Στην αρχή του υπολογισμού δίνουμε
στις καταστάσεις των σπιν μία αρχική τιμή (π.χ. όλα τα σπίν
προσανατολισμένα επάνω ή τυχαίος προσανατολισμός των σπιν)
- Ένα sweep (πέρασμα) ορίζεται το να περάσουμε (επεξεργασία)
από όλα τα σπίν του πλέγματος μία φορά. Σε κάθε πλεγματικό
σημείο ο αλγόριθμος πρέπει να απαντήσει στην ερώτηση
Πρέπει το σπιν στη θέση αυτή να αλλάξει?
Η απόφαση αυτή καθορίζεται χρησιμοποιώντας την
συνάρτηση πιθανότητας Boltzmann της εξίσωσης 1 και το μοντέλο
Ising (εξίσωση 3) για τον υπολογισμό της ενέργειας του συστήματος.
Εκτελούμε τα εξής βήματα
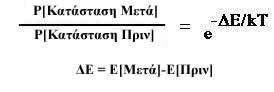Εξίσωση 8
- Μια μέτρηση του μεγέθους που μας ενδιαφέρει (με την ένοια
της εξίσωσης 6 ) παίρνεται μόνο αφού έχουμε κάνει ένα αριθμό
από sweeps (ας πούμε 100). 'Ετσι εξασφαλίζουμε οι μετρήσεις
μας να είναι ανεξάρτητες.
Μετά από μερικά sweeps, ώστε να ξεθωριάσει η αρχική μας επιλογή
των σπιν του πλέγματος, η παραπάνω διαδικασία δημιουργεί διαμορφώσεις
των σπιν του πλέγματος που ακολουθούν την πραγματική συνάρτηση
πιθανότητας. Έτσι οι φυσικές ποσότητες (π.χ. Μαγνήτιση) μπορούν
να υπολογιστούν με τον μέσο όρο μετρήσεων στο προσομοιωμένο
συστημά και για δίαφορες θερμοκρασίες.
Για το απλό πλέγμα των δύο διαστάσεων ηεξάρτηση της μαγνήτισης
από την θερμοκρασία έχει λυθεί αναλυτικά, χρησιμοποιώντας
το μοντέλο Ising, το 1954 από τον Onsager και η λύση φαίνεται
στην παρακάτω εξίσωση
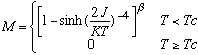
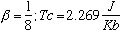
Εξίσωση 9
όπου K=Kb η σταθερά Boltzmann και Τc η κρίσιμη
θερμοκρασία ή θερμοκρασία Curie κάτω από την οποία η μαγνήτιση
χάνεται. Για τις τρεις διαστάσεις το πρόβλημα δεν έχει λυθεί
αναλυτικά.
Βιβλιογραφία
|
