Research

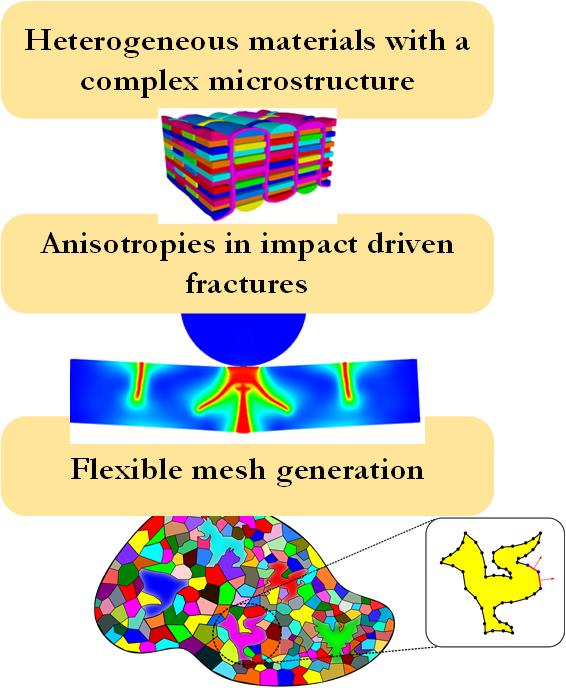
We develop novel, high-fidelity, robust, and rapid methods to simulate coupled physics across length scales. Our interest here is on the simulation of complex and largely coupled physics with applications across the spectrum of engineered materials. To this end, we develop novel methodologies and provide in-house source code implementations for multi-scale multi-physics simulations using a variety of discretization stragies. We further investigate, both experimentally and numerically, the merits and bottlenecks of composite materials with applications varying from the aerospace to the construction industry. Indicative projects involve:

Topology optimisation of additively manufactured composites Within the context of the EU funded AI2AM project, we develop numerical methods and digital tools to facilitate the design of optimum additively manufactured topologies. To this end, we leverage the flexibility of scaled boundary and virtual element methods for the discritization of tesselated domains and coupled them with phase field methods to accurate simulate fractures in anisotropic domains. All this, embedded within a topology optimisation framework.

Damage modelling of aerospace grade composites We focus on developing novel damage modelling methods for thin-ply composites, specifically for spread-tow unidirectional and spread-tow woven-fabric reinforced variants. To this end, we deploy phase field methods to account for the diverse anisotropic composite failure modes, e.g. fibre cracking, fibre pullouts, fibre bridging, plastic shear deformation of the matrix and its cracking under tensile and in-plane shear. This research endeavour received EU funding under the SAFE-FLY project.

Vibro-acoustics of foam type materials We have developed a novel computational theory incorporating Virtual Element Methods and Heterogeneous Multiscale Methods explicitly with a purpose to efficiently and accurately resolve elastostatic and poromechanical behaviour (consolidation and vibroacoustics) over complex and highly heterogeneous material domains. The overarching aim was to establish an accurate yet rapid framework for the vibro-acoustic analysis of composite systems with a poro-elastic core. This research endeavour received EU funding under the NO2NOISE project.

Polygonal element technologies provide a flexibile route for resolving complex shaped mesoscale heterogeneous morphologies that in principle necessitate fine resolutions, thus rendering the problem expensive. To this end we have developed VEM and SBFEM solvers to treat poro-mechanis problems also within a heterogeous multi-scale setting.

Structural strengthening with composite materials We focus on leveraging the merits of advanced composite materials to strengthen existing structures. Our work has both an experimental and a numerical flavour looking into the effectivness of textile reinforced mortars for the structural upgrading of masonry and reinforced concrete sub-assemblies. To this end, we have performed extensive experimental campaigns to investigate bond, strength, and progressive damage aspects.

Multiscale modelling is a rigorous mathematical approach for the scaling of complex numerical problems. Multiscale methods and corresponding homogenization techniques are frequently implemented for the analysis of materials whose micro-structure significantly affects their overall macroscopic behaviour. Applications vary from examining the high speed dynamics of granular materials to highly sophisticated cellular and honeycomb materials. The ultimate objective of this project is to establish a robust and efficient method for the analysis of computationally intensive problems including the nonlinear parameter identification and optimization of novel materials.

Material Point Methods provide the computational canvas for resolving large displacement and large strain kinematics within an Eulerian-Lagrangian setting. To this end, we have been developing MPM variants to treat impact driven fracture and are currently actively working on further treating some of the primary bottlenecks of the method, i.e., stress oscillations and computational costs.

Phase transformation of metallic materials is (e.g. dual phase steels and shape memory alloys) an intriguing process by which the material’s microstructure is altered under mechanical and/ or thermal stimuli. Shape memory alloys for example can undergo large deformations and yet return into their prior undeformed configuration when subject to external thermo-mechanical stimuli. Due to these unique properties such materials are currently being implemented in the aerospace, automotive and defence industry. To further optimize and generalize their implementation, accurate representations of the actual material behaviour are required. To accomplish that, a consistent finite strain generalised plasticity model is established in this project aiming to provide a generic framework for the modelling of materials undergoing phase transformations.