ΑΡΧΙΜΗΔΗΣ 287-212 π.Χ.

ΠΕΡΙΕΧΟΜΕΝΑ
ΑΠΑΝΤΑ ΣΕ ΜΙΑ ΙΣΤΟΣΕΛΙΔΑ

• ΠΕΡΙ ΣΦΑΙΡΑΣ ΚΑΙ ΚΥΛΙΝΔΡΟΥ Α΄
• ΠΕΡΙ ΣΦΑΙΡΑΣ ΚΑΙ ΚΥΛΙΝΔΡΟΥ Β΄
• ΚΥΚΛΟΥ ΜΕΤΡΗΣΙΣ
• ΠΕΡΙ ΚΩΝΟΕΙΔΕΩΝ ΚΑΙ ΣΦΑΙΡΟΕΙΔΕΩΝ
• ΠΕΡΙ ΕΛΙΚΩΝ
• ΜΗΧΑΝΙΚΑ Α΄ ΠΕΡΙ ΕΠΙΠΕΔΩΝ ΙΣΟΡΡΟΠΙΩΝ Α΄
• ΜΗΧΑΝΙΚΑ Β΄ ΠΕΡΙ ΕΠΙΠΕΔΩΝ ΙΣΟΡΡΟΠΙΩΝ Β΄
• ΨΑΜΜΙΤΗΣ
• ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΟΡΘΟΓΩΝΙΟΥ ΚΩΝΟΥ ΤΟΜΗΣ ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΠΑΡΑΒΟΛΗΣ
• ΠΕΡΙ ΟΧΟΥΜΕΝΩΝ Α΄
• ΠΕΡΙ ΟΧΟΥΜΕΝΩΝ Β΄
• ΣΤΟΜΑΧΙΟΝ
• ΠΕΡΙ ΜΗΧΑΝΙΚΩΝ ΘΕΩΡΗΜΑΤΩΝ
  ΠΡΟΣ ΕΡΑΤΟΣΘΕΝΗ ΕΦΟΔΟΣ (=ΜΕΘΟΔΟΣ)
• ΠΡΟΒΛΗΜΑ ΒΟΕΙΚΟΝ

• ΟΙ ΑΝΑΦΟΡΕΣ ΣΤΟΝ ΑΡΧΙΜΗΔΗ
• ΑΝΤΙ ΠΡΟΛΟΓΟΥ

---

ΣΥΓΓΡΑΜΑΤΑ ΜΗ ΑΠΟΚΑΛΥΦΘΕΝΤΑ ΜΕΧΡΙ ΣΗΜΕΡΑ

• ΑΡΙΘΜΗΤΙΚΑ
• ΒΑΡΟΥΛΚΟΣ, ΥΔΡΟΣΚΟΠΙΑΙ, ΠΝΕΥΜΑΤΙΚΗ
• ΕΠΙΣΙΔΙΑ ΒΙΒΛΙΑ
• ΠΕΡΙ ΤΡΙΓΩΝΩΝ
• ΠΕΡΙ ΤΕΤΡΑΠΛΕΥΡΟΥ
• ΠΕΡΙ ζΕΥΓΩΝ
• ΠΕΡΙ 13 ΗΜΙΚΑΝΟΝΙΚΩΝ ΠΟΛΥΕΔΡΩΝ
• ΙΣΟΠΕΡΙΜΕΤΡΙΚΑ
• ΙΣΟΡΡΟΠΙΑΙ
• ΚΑΥΣΙΣ ΔΙΑ ΚΑΤΟΠΤΡΩΝ
• ΠΕΡΙ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ
• ΠΕΡΙ ΒΑΡΥΤΗΤΟΣ ΚΑΙ ΕΛΑΦΡΟΤΗΤΟΣ
• ΠΕΡΙ ΔΡΟΜΟΜΕΤΡΩΝ
• ΠΕΡΙ ΚΕΝΤΡΟΥ ΒΑΡΟΥΣ Η ΚΕΝΤΡΟΒΑΡΙΚΑ
• ΚΑΤΟΠΤΡΙΚΑ
• ΠΕΡΙ ΠΑΡΑΛΛΗΛΩΝ ΓΡΑΜΜΩΝ
• ΠΕΡΙ ΚΟΙΛΩΝ ΚΑΙ ΠΑΡΑΒΟΛΙΚΩΝ ΚΑΤΟΠΤΡΩΝ
• ΠΡΟΟΠΤΙΚΗ
• ΣΤΟΙΧΕΙΑ ΜΗΧΑΝΙΚΩΝ
• ΠΛΙΝΘΙΔΕΣ ΚΑΙ ΚΥΛΙΝΔΡΟΙ
• ΣΤΟΙΧΕΙΑ ΕΠΙ ΤΩΝ ΣΤΗΡΙΞΕΩΝ
• ΠΕΡΙ ΣΦΑΙΡΟΠΟΙΙΑΣ

---

ΠΕΡΙ ΣΦΑΙΡΑΣ ΚΑΙ ΚΥΛΙΝΔΡΟΥ Α΄

Ἀρχιμήδης Δοσιθέῳ χαίρειν

[8]Πρότερον μὲν ἀπέσταλκά σοι τῶν ὑφ᾿ ἡμῶν τεθεωρημένων γράψας μετὰ ἀποδείξεως, ὅτι πᾶν τμῆμα τὸ περιεχόμενον ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομῆς ἐπίτριτόν ἐστι τριγώνου τοῦ βάσιν τὴν αὐτὴν ἔχοντος τῷ τμήματι καὶ ὕψος ἴσον· ὕστερον δὲ ἡμῖν ὑποπεσόντων θεωρημάτων ἀξίων λόγου πεπραγματεύμεθα περὶ τὰς ἀποδείξεις αὐτῶν. Ἔστιν δὲ τάδε· πρῶτον μέν, ὅτι πάσης σφαίρας ἡ ἐπιφάνεια τετραπλασία ἐστὶν τοῦ μεγίστου κύκλου τῶν ἐν αὐτῇ· ἔπειτα δέ, ὅτι παντὸς τμήματος σφαίρας τῇ ἐπιφανείᾳ ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ εὐθείᾳ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἀγομένῃ ἐπὶ τὴν περιφέρειαν τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος· πρὸς δὲ τούτοις, ὅτι πάσης σφαίρας ὁ κύλινδρος ὁ βάσιν μὲν ἔχων ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας αὐτός τε ἡμιόλιός ἐστιν τῆς σφαίρας, καὶ ἡ ἐπιφάνεια αὐτοῦ τῆς ἐπιφανείας τῆς σφαίρας. Ταῦτα δὲ τὰ συμπτώματα τῇ φύσει προυπῆρχεν περὶ τὰ εἰρημένα σχήματα, ἠγνοεῖτο δὲ ὑπὸ τῶν πρὸ ἡμῶν περὶ γεωμετρίαν ἀνεστραμμένων οὐδενὸς αὐτῶν ἐπινενοηκότος ὅτι τούτων τῶν σχημάτων ἐστὶν συμμετρία· [9] διόπερ οὐκ ἂν ὀκνήσαιμι ἀντιπαραβαλεῖν αὐτὰ πρός τε τὰ τοῖς ἄλλοις γεωμέτραις τεθεωρημένα καὶ πρὸς τὰ δόξαντα πολὺ ὑπερέχειν τῶν ὑπὸ Εὐδόξου περὶ τὰ στερεὰ θεωρηθέντων, ὅτι πᾶσα πυραμὶς τρίτον ἐστὶ μέρος πρίσματος τοῦ βάσιν ἔχοντος τὴν αὐτὴν τῇ πυραμίδι καὶ ὕψος ἴσον, καὶ ὅτι πᾶς κῶνος τρίτον μέρος ἐστὶν τοῦ κυλίνδρου τοῦ βάσιν ἔχοντος τὴν αὐτὴν τῷ κώνῳ καὶ ὕψος ἴσον· καὶ γὰρ τούτων προυπαρχόντων φυσικῶς περὶ ταῦτα τὰ σχήματα, πολλῶν πρὸ Εὐδόξου γεγενημένων ἀξίων λόγου γεωμετρῶν συνέβαινεν ὑπὸ πάντων ἀγνοεῖσθαι μηδ᾿ ὑφ᾿ ἑνὸς κατανοηθῆναι. Ἐξέσται δὲ περὶ τούτων ἐπισκέψασθαι τοῖς δυνησομένοις. Ὤφειλε μὲν οὖν Κόνωνος ἔτι ζῶντος ἐκδίδοσθαι ταῦτα· τῆνον γὰρ ὑπολαμβάνομέν που μάλιστα ἂν δύνασθαι κατανοῆσαι ταῦτα καὶ τὴν ἁρμόζουσαν ὑπὲρ αὐτῶν ἀπόφασιν ποιήσασθαι· δοκιμάζοντες δὲ καλῶς ἔχειν μεταδιδόναι τοῖς οἰκείοις τῶν μαθημάτων ἀποστέλλομέν σοι τὰς ἀποδείξεις ἀναγράψαντες, ὑπὲρ ὧν ἐξέσται τοῖς περὶ τὰ μαθήματα ἀναστρεφομένοις ἐπισκέψασθαι. Ἐρρωμένως.

   Γράφονται πρῶτον τά τε ἀξιώματα καὶ τὰ λαμβανόμενα εἰς τὰς ἀποδείξεις αὐτῶν.

ΑΞΙΩΜΑΤΑ

   α΄. Εἰσί τινες ἐν ἐπιπέδῳ καμπύλαι γραμμαὶ πεπερασμέναι, αἳ τῶν τὰ πέρατα ἐπιζευγνυουσῶν αὐτῶν εὐθειῶν ἤτοι ὅλαι ἐπὶ τὰ αὐτά εἰσιν ἢ οὐδὲν ἔχουσιν ἐπὶ τὰ ἕτερα.

   β΄. Ἐπὶ τὰ αὐτὰ δὴ κοίλην καλῶ τὴν τοιαύτην γραμμήν, ἐν ᾗ ἐὰν δύο σημείων λαμβανομένων ὁποιωνοῦν αἱ μεταξὺ [10] τῶν σημείων εὐθεῖαι ἤτοι πᾶσαι ἐπὶ τὰ αὐτὰ πίπτουσιν τῆς γραμμῆς, ἢ τινὲς μὲν ἐπὶ τὰ αὐτά, τινὲς δὲ κατ᾿ αὐτῆς, ἐπὶ τὰ ἕτερα δὲ μηδεμία.

   γ΄. Ὁμοίως δὲ καὶ ἐπιφάνειαί τινές εἰσιν πεπερασμέναι, αὐταὶ μὲν οὐκ ἐν ἐπιπέδῳ, τὰ δὲ πέρατα ἔχουσαι ἐν ἐπιπέδῳ, αἳ τοῦ ἐπιπέδου, ἐν ᾧ τὰ πέρατα ἔχουσιν, ἤτοι ὅλαι ἐπὶ τὰ αὐτὰ ἔσονται ἢ οὐδὲν ἔχουσιν ἐπὶ τὰ ἕτερα.

   δ΄. Ἐπὶ τὰ αὐτὰ δὴ κοίλας καλῶ τὰς τοιαύτας ἐπιφανείας, ἐν αἷς ἂν δύο σημείων λαμβανομένων αἱ μεταξὺ τῶν σημείων εὐθεῖαι ἤτοι πᾶσαι ἐπὶ τὰ αὐτὰ πίπτουσιν τῆς ἐπιφανείας, ἢ τινὲς μὲν ἐπὶ τὰ αὐτά, τινὲς δὲ κατ᾿ αὐτῆς, ἐπὶ τὰ ἕτερα δὲ μηδεμία.

   ε΄. Τομέα δὲ στερεὸν καλῶ, ἐπειδὰν σφαῖραν κῶνος τέμνῃ κορυφὴν ἔχων πρὸς τῷ κέντρῳ τῆς σφαίρας, τὸ ἐμπεριεχόμενον σχῆμα ὑπό τε τῆς ἐπιφανείας τοῦ κώνου καὶ τῆς ἐπιφανείας τῆς σφαίρας ἐντὸς τοῦ κώνου.

   Ϛ΄. Ῥόμβον δὲ καλῶ στερεόν, ἐπειδὰν δύο κῶνοι τὴν αὐτὴν βάσιν ἔχοντες τὰς κορυφὰς ἔχωσιν ἐφ᾿ ἑκάτερα τοῦ ἐπιπέδου τῆς βάσεως, ὅπως οἱ ἄξονες αὐτῶν ἐπ᾿ εὐθείας ὦσι κείμενοι, τὸ ἐξ ἀμφοῖν τοῖν κώνοιν συγκείμενον στερεὸν σχῆμα.

ΛΑΜΒΑΝΟΜΕΝΑ

   Λαμβάνω δὲ ταῦτα·

   α΄. Τῶν τὰ αὐτὰ πέρατα ἐχουσῶν γραμμῶν ἐλαχίστην εἶναι τὴν εὐθεῖαν.

   β΄. Τῶν δὲ ἄλλων γραμμῶν, ἐὰν ἐν ἐπιπέδῳ οὖσαι τὰ αὐτὰ πέρατα ἔχωσιν, ἀνίσους εἶναι τὰς τοιαύτας, [11] ἐπειδὰν ὦσιν ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαι, καὶ ἤτοι ὅλη περιλαμβάνηται ἡ ἑτέρα αὐτῶν ὑπὸ τῆς ἑτέρας καὶ τῆς εὐθείας τῆς τὰ αὐτὰ πέρατα ἐχούσης αὐτῇ, ἢ τινὰ μὲν περιλαμβάνηται, τινὰ δὲ κοινὰ ἔχῃ, καὶ ἐλάσσονα εἶναι τὴν περιλαμβανομένην.

   γ΄. Ὁμοίως δὲ καὶ τῶν ἐπιφανειῶν τῶν τὰ αὐτὰ πέρατα ἐχουσῶν, ἐὰν ἐν ἐπιπέδῳ τὰ πέρατα ἔχωσιν, ἐλάσσονα εἶναι τὴν ἐπίπεδον.

   δ΄. Τῶν δὲ ἄλλων ἐπιφανειῶν καὶ τὰ αὐτὰ πέρατα ἐχουσῶν, ἐὰν ἐν ἐπιπέδῳ τὰ πέρατα ᾖ, ἀνίσους εἶναι τὰς τοιαύτας, ἐπειδὰν ὦσιν ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαι, καὶ ἤτοι ὅλη περιλαμβάνηται ὑπὸ τῆς ἑτέρας ἡ ἑτέρα ἐπιφάνεια καὶ τῆς ἐπιπέδου τῆς τὰ αὐτὰ πέρατα ἐχούσης αὐτῇ, ἢ τινὰ μὲν περιλαμβάνηται, τινὰ δὲ κοινὰ ἔχῃ, καὶ ἐλάσσονα εἶναι τὴν περιλαμβανομένην.

   ε΄. Ἔτι δὲ τῶν ἀνίσων γραμμῶν καὶ τῶν ἀνίσων ἐπιφανειῶν καὶ τῶν ἀνίσων στερεῶν τὸ μεῖζον τοῦ ἐλάσσονος ὑπερέχειν τοιούτῳ, ὃ συντιθέμενον αὐτὸ ἑαυτῷ δυνατόν ἐστιν ὑπερέχειν παντὸς τοῦ προτεθέντος τῶν πρὸς ἄλληλα λεγομένων.

   Τούτων δὲ ὑποκειμένων, ἐὰν εἰς κύκλον πολύγωνον ἐγγραφῇ, φανερὸν ὅτι ἡ περίμετρος τοῦ ἐγγραφέντος πολυγώνου ἐλάσσων ἐστὶν τῆς τοῦ κύκλου περιφερείας· ἑκάστη γὰρ τῶν τοῦ πολυγώνου πλευρῶν ἐλάσσων ἐστὶ τῆς τοῦ κύκλου περιφερείας τῆς ὑπὸ τῆς αὐτῆς ἀποτεμνομένης.

[12]    α΄.

   Ἐὰν περὶ κύκλον πολύγωνον περιγραφῇ, ἡ τοῦ περιγραφέντος πολυγώνου περίμετρος μείζων ἐστὶν τῆς περιμέτρου τοῦ κύκλου.

   Περὶ γὰρ κύκλον πολύγωνον περιγεγράφθω τὸ ὑποκείμενον. Λέγω ὅτι ἡ περίμετρος τοῦ πολυγώνου μείζων ἐστὶν τῆς περιμέτρου τοῦ κύκλου.

   Ἐπεὶ γὰρ συναμφότερος ἡ ΒΑΛ μείζων ἐστὶ τῆς ΒΛ περιφερείας διὰ τὸ τὰ αὐτὰ πέρατα ἔχουσαν περιλαμβάνειν τὴν περιφέρειαν, ὁμοίως δὲ καὶ συναμφότερος μὲν ἡ ΔΓ, ΓΒ τῆς ΔΒ, συναμφότερος δὲ ἡ ΛΚ, ΚΘ τῆς ΛΘ, συναμφότερος δὲ ἡ ΖΗΘ τῆς ΖΘ, ἔτι δὲ συναμφότερος ἡ ΔΕ, ΕΖ τῆς ΔΖ, ὅλη ἄρα ἡ περίμετρος τοῦ πολυγώνου μείζων ἐστὶ τῆς περιφερείας τοῦ κύκλου.

   β΄.

   Δύο μεγεθῶν ἀνίσων δοθέντων δυνατόν ἐστιν εὑρεῖν δύο εὐθείας ἀνίσους, ὥστε τὴν μείζονα εὐθεῖαν πρὸς τὴν [13] ἐλάσσονα λόγον ἔχειν ἐλάσσονα ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον.

   Ἔστω δύο μεγέθη ἄνισα τὰ ΑΒ, Δ, καὶ ἔστω μεῖζον τὸ ΑΒ. Λέγω ὅτι δυνατόν ἐστι δύο εὐθείας ἀνίσους εὑρεῖν τὸ εἰρημένον ἐπίταγμα ποιούσας.

   Κείσθω διὰ τὸ β΄ τοῦ α΄ τῶν Εὐκλείδου τῷ Δ ἴσον τὸ ΒΓ, καὶ κείσθω τις εὐθεῖα γραμμὴ ἡ ΖΗ· τὸ δὴ ΓΑ ἑαυτῷ ἐπισυντιθέμενον ὑπερέξει τοῦ Δ. Πεπολλαπλασιάσθω οὖν, καὶ ἔστω τὸ ΑΘ, καὶ ὁσαπλάσιόν ἐστι τὸ ΑΘ τοῦ ΑΓ, τοσαυταπλάσιος ἔστω ἡ ΖΗ τῆς ΗΕ· ἔστιν ἄρα, ὡς τὸ ΘΑ πρὸς ΑΓ, οὕτως ἡ ΖΗ πρὸς ΗΕ· καὶ ἀνάπαλίν ἐστιν, ὡς ἡ ΕΗ πρὸς ΗΖ, οὕτως τὸ ΑΓ πρὸς ΑΘ. Καὶ ἐπεὶ μεῖζόν ἐστιν τὸ ΑΘ τοῦ Δ, τουτέστι τοῦ ΓΒ, τὸ ἄρα ΓΑ πρὸς τὸ ΑΘ λόγον ἐλάσσονα ἔχει ἤπερ τὸ ΓΑ πρὸς ΓΒ. Ἀλλ᾿ ὡς τὸ ΓΑ πρὸς ΑΘ, οὕτως ἡ ΕΗ πρὸς ΗΖ· ἡ ΕΗ ἄρα πρὸς ΗΖ ἐλάσσονα λόγον ἔχει ἤπερ τὸ ΓΑ πρὸς ΓΒ· καὶ συνθέντι ἡ ΕΖ [ἄρα] πρὸς ΖΗ ἐλάσσονα λόγον ἔχει ἤπερ τὸ ΑΒ πρὸς ΒΓ [διὰ λῆμμα]. Ἴσον δὲ τὸ ΒΓ τῷ Δ· ἡ ΕΖ ἄρα πρὸς ΖΗ ἐλάσσονα λόγον ἔχει ἤπερ τὸ ΑΒ πρὸς τὸ Δ.

   Εὑρημέναι εἰσὶν ἄρα δύο εὐθεῖαι ἄνισοι ποιοῦσαι τὸ [14] εἰρημένον ἐπίταγμα [τουτέστιν τὴν μείζονα πρὸς τὴν ἐλάσσονα λόγον ἔχειν ἐλάσσονα ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον].

   γ΄.

   Δύο μεγεθῶν ἀνίσων δοθέντων καὶ κύκλου δυνατόν ἐστιν εἰς τὸν κύκλον πολύγωνον ἐγγράψαι καὶ ἄλλο περιγράψαι, ὅπως ἡ τοῦ περιγραφομένου πολυγώνου πλευρὰ πρὸς τὴν τοῦ ἐγγραφομένου πολυγώνου πλευρὰν ἐλάσσονα λόγον ἔχῃ ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλαττον.

   Ἔστω τὰ δοθέντα δύο μεγέθη τὰ Α, Β, ὁ δὲ δοθεὶς κύκλος ὁ ὑποκείμενος. Λέγω οὖν ὅτι δυνατόν ἐστι ποιεῖν τὸ ἐπίταγμα.

   Εὑρήσθωσαν γὰρ δύο εὐθεῖαι αἱ Θ, ΚΛ, ὧν μείζων ἔστω ἡ Θ, ὥστε τὴν Θ πρὸς τὴν ΚΛ ἐλάσσονα λόγον [15] ἔχειν ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλαττον, καὶ ἤχθω ἀπὸ τοῦ Λ τῇ ΛΚ πρὸς ὀρθὰς ἡ ΛΜ, καὶ ἀπὸ τοῦ Κ τῇ Θ ἴση κατήχθω ἡ ΚΜ [δυνατὸν γὰρ τοῦτο], καὶ ἤχθωσαν τοῦ κύκλου δύο διάμετροι πρὸς ὀρθὰς ἀλλήλαις αἱ ΓΕ, ΔΖ. Τέμνοντες οὖν τὴν ὑπὸ τῶν ΔΗΓ γωνίαν δίχα καὶ τὴν ἡμίσειαν αὐτῆς δίχα καὶ αἰεὶ τοῦτο ποιοῦντες λείψομέν τινα γωνίαν ἐλάσσονα ἢ διπλασίαν τῆς ὑπὸ ΛΚΜ. Λελείφθω καὶ ἔστω ἡ ὑπὸ ΝΗΓ, καὶ ἐπεζεύχθω ἡ ΝΓ· ἡ ἄρα ΝΓ πολυγώνου ἐστὶ πλευρὰ ἰσοπλεύρου [ἐπείπερ ἡ ὑπὸ ΝΗΓ γωνία μετρεῖ τὴν ὑπὸ ΔΗΓ ὀρθὴν οὖσαν, καὶ ἡ ΝΓ ἄρα περιφέρεια μετρεῖ τὴν ΓΔ τέταρτον οὖσαν κύκλου· ὥστε καὶ τὸν κύκλον μετρεῖ. Πολυγώνου ἄρα ἐστὶ πλευρὰ ἰσοπλεύρου· φανερὸν γάρ ἐστι τοῦτο]. Καὶ τετμήσθω ἡ ὑπὸ ΓΗΝ γωνία δίχα τῇ ΗΞ εὐθείᾳ, καὶ ἀπὸ τοῦ Ξ ἐφαπτέσθω τοῦ κύκλου ἡ ΟΞΠ, καὶ ἐκβεβλήσθωσαν αἱ ΗΝΠ, ΗΓΟ· ὥστε καὶ ἡ ΠΟ πολυγώνου ἐστὶ πλευρὰ τοῦ περιγραφομένου περὶ τὸν κύκλον καὶ ἰσοπλεύρου [φανερὸν ὅτι καὶ ὁμοίου τῷ ἐγγραφομένῳ, οὗ πλευρὰ ἡ ΝΓ]. Ἐπεὶ δὲ ἐλάσσων ἐστὶν ἢ διπλασία ἡ ὑπὸ ΝΗΓ τῆς ὑπὸ ΛΚΜ, διπλασία δὲ τῆς ὑπὸ ΤΗΓ, ἐλάσσων ἄρα ἡ ὑπὸ ΤΗΓ τῆς ὑπὸ ΛΚΜ. Καί εἰσιν ὀρθαὶ αἱ πρὸς τοῖς Λ, Τ· ἡ ἄρα ΜΚ πρὸς ΛΚ μείζονα λόγον ἔχει ἤπερ ἡ ΓΗ πρὸς ΗΤ. Ἴση δὲ ἡ ΓΗ τῇ ΗΞ· ὥστε ἡ ΗΞ πρὸς ΗΤ ἐλάσσονα λόγον ἔχει, τουτέστιν ἡ ΠΟ πρὸς ΝΓ, ἤπερ ἡ ΜΚ πρὸς ΚΛ· ἔτι δὲ ἡ ΜΚ πρὸς ΚΛ ἐλάσσονα λόγον ἔχει ἤπερ τὸ Α πρὸς τὸ Β. Καί ἐστιν ἡ μὲν ΠΟ πλευρὰ τοῦ [16] περιγραφομένου πολυγώνου, ἡ δὲ ΓΝ τοῦ ἐγγραφομένου· ὅπερ προέκειτο εὑρεῖν.

   δ΄.

   Πάλιν δύο μεγεθῶν ἀνίσων ὄντων καὶ τομέως δυνατόν ἐστι περὶ τὸν τομεὰ πολύγωνον περιγράψαι καὶ ἄλλο ἐγγράψαι, ὥστε τὴν τοῦ περιγεγραμμένου πλευρὰν πρὸς τὴν τοῦ ἐγγεγραμμένου πλευρὰν ἐλάσσονα λόγον ἔχειν ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον.

   Ἔστω γὰρ πάλιν δύο μεγέθη ἄνισα τὰ Ε, Ζ, ὧν μεῖζον ἔστω τὸ Ε, κύκλος δέ τις ὁ ΑΒΓ κέντρον ἔχων τὸ Δ, καὶ πρὸς τῷ Δ τομεὺς συνεστάτω ὁ ΑΔΒ· δεῖ δὴ περιγράψαι καὶ ἐγγράψαι πολύγωνον περὶ τὸν ΑΒΔ τομέα ἴσας ἔχον τὰς πλευρὰς χωρὶς τῶν ΒΔΑ, ὅπως γένηται τὸ ἐπίταγμα.

   Εὑρήσθωσαν γὰρ δύο εὐθεῖαι αἱ Η, ΘΚ ἄνισοι καὶ μείζων ἡ Η, ὥστε τὴν Η πρὸς τὴν ΘΚ ἐλάσσονα λόγον ἔχειν ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον [δυνατὸν γὰρ τοῦτο], καὶ ἀπὸ τοῦ Θ ὁμοίως ἀχθείσης πρὸς ὀρθὰς τῇ ΚΘ προσβεβλήσθω τῇ Η ἴση ἡ ΚΛ [δυνατὸν γάρ, ἐπεὶ [17] μείζων ἐστὶν ἡ Η τῆς ΘΚ]. Τεμνομένης δὴ τῆς ὑπὸ τῶν ΑΔΒ γωνίας δίχα καὶ τῆς ἡμισείας δίχα καὶ ἀεὶ τούτου γινομένου λειφθήσεταί τις γωνία ἐλάσσων οὖσα ἢ διπλασία τῆς ὑπὸ ΛΚΘ. Λελείφθω οὖν ἡ ὑπὸ ΑΔΜ· ἡ ΑΜ οὖν γίνεται πολυγώνου πλευρὰ ἐγγραφομένου εἰς τὸν κύκλον. Καὶ ἐὰν τέμωμεν τὴν ὑπὸ ΑΔΜ γωνίαν δίχα τῇ ΔΝ καὶ ἀπὸ τοῦ Ν ἀγάγωμεν ἐφαπτομένην τοῦ κύκλου τὴν ΝΞΟ, αὕτη πλευρὰ ἔσται τοῦ πολυγώνου τοῦ περιγραφομένου περὶ τὸν αὐτὸν κύκλον ὁμοίου τῷ εἰρημένῳ· καὶ ὁμοίως τοῖς προειρημένοις ἡ ΞΟ πρὸς τὴν ΑΜ ἐλάσσονα λόγον ἔχει ἤπερ τὸ Ε μέγεθος πρὸς τὸ Ζ.

   ε΄.

   Κύκλου δοθέντος καὶ δύο μεγεθῶν ἀνίσων περιγράψαι περὶ τὸν κύκλον πολύγωνον καὶ ἄλλο ἐγγράψαι ὥστε τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχειν ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον.

   Ἐκκείσθω κύκλος ὁ Α καὶ δύο μεγέθη ἄνισα τὰ Ε, Ζ, καὶ μεῖζον τὸ Ε· δεῖ οὖν πολύγωνον ἐγγράψαι εἰς τὸν κύκλον καὶ ἄλλο περιγράψαι, ἵνα γένηται τὸ ἐπιταχθέν.

[18]    Λαμβάνω γὰρ δύο εὐθείας ἀνίσους τὰς Γ, Δ, ὧν μείζων ἔστω ἡ Γ, ὥστε τὴν Γ πρὸς τὴν Δ ἐλάσσονα λόγον ἔχειν ἢ τὴν Ε πρὸς τὴν Ζ· καὶ τῶν Γ, Δ μέσης ἀνάλογον ληφθείσης τῆς Η μείζων ἄρα καὶ ἡ Γ τῆς Η. Περιγεγράφθω δὴ περὶ κύκλον πολύγωνον καὶ ἄλλο ἐγγεγράφθω, ὥστε τὴν τοῦ περιγραφέντος πολυγώνου πλευρὰν πρὸς τὴν τοῦ ἐγγραφέντος ἐλάσσονα λόγον ἔχειν ἢ τὴν Γ πρὸς τὴν Η [καθὼς ἐμάθομεν]· διὰ τοῦτο δὴ καὶ ὁ διπλάσιος λόγος τοῦ διπλασίου ἐλάσσων ἐστί. Καὶ τοῦ μὲν τῆς πλευρᾶς πρὸς τὴν πλευρὰν διπλάσιός ἐστι ὁ τοῦ πολυγώνου πρὸς τὸ πολύγωνον [ὅμοια γάρ], τῆς δὲ Γ πρὸς τὴν Η ὁ τῆς Γ πρὸς τὴν Δ· καὶ τὸ περιγραφὲν ἄρα πολύγωνον πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχει ἤπερ ἡ Γ πρὸς τὴν Δ· πολλῷ ἄρα τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχει ἤπερ τὸ Ε πρὸς τὸ Ζ.

   Ϛ΄.

   Ὁμοίως δὴ δείξομεν ὅτι δύο μεγεθῶν ἀνίσων δοθέντων καὶ τομέως δυνατόν ἐστιν περὶ τὸν τομέα πολύγωνον περιγράψαι καὶ ἄλλο ἐγγράψαι ὅμοιον αὐτῷ, ἵνα τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχῃ ἢ τὸ μεῖζον μέγεθος πρὸς τὸ ἔλασσον.

   Φανερὸν δὲ καὶ τοῦτο ὅτι, ἐὰν δοθῇ κύκλος ἢ τομεὺς καὶ χωρίον τι, δυνατόν ἐστιν ἐγγράφοντα εἰς τὸν κύκλον [19] ἢ τὸν τομέα πολύγωνα ἰσόπλευρα καὶ ἔτι ἀεὶ εἰς τὰ περιλειπόμενα τμήματα λείπειν τινὰ τμήματα τοῦ κύκλου ἢ τομέως, ἅπερ ἔσται ἐλάσσονα τοῦ προκειμένου χωρίου· ταῦτα γὰρ ἐν τῇ Στοιχειώσει παραδέδοται.

   Δεικτέον δὲ ὅτι καὶ κύκλου δοθέντος ἢ τομέως καὶ χωρίου δυνατόν ἐστι περιγράψαι πολύγωνον περὶ τὸν κύκλον ἢ τὸν τομέα, ὥστε τὰ περιλειπόμενα τῆς περιγραφῆς τμήματα ἐλάσσονα εἶναι τοῦ δοθέντος χωρίου· ἔσται γὰρ ἐπὶ κύκλου δείξαντα μεταγαγεῖν τὸν ὅμοιον λόγον καὶ ἐπὶ τοῦ τομέως.

   Δεδόσθω κύκλος ὁ Α καὶ χωρίον τι τὸ Β. Δυνατὸν δὴ περιγράψαι περὶ τὸν κύκλον πολύγωνον, ὥστε τὰ ἀπολειφθέντα τμήματα μεταξὺ τοῦ κύκλου καὶ τοῦ πολυγώνου ἐλάσσονα εἶναι τοῦ Β χωρίου· καὶ γὰρ ὄντων δύο μεγεθῶν ἀνίσων, μείζονος μὲν συναμφοτέρου τοῦ τε χωρίου καὶ τοῦ κύκλου, ἐλάσσονος δὲ τοῦ κύκλου, περιγεγράφθω περὶ τὸν κύκλον πολύγωνον καὶ ἄλλο ἐγγεγράφθω, ὥστε τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχειν [20] ἢ τὸ εἰρημένον μεῖζον μέγεθος πρὸς τὸ ἔλασσον. Τοῦτο δὴ τὸ περιγραφόμενον πολύγωνόν ἐστιν, οὗ τὰ περιλείμματα ἔσται ἐλάσσονα τοῦ προτεθέντος χωρίου τοῦ Β.

   Εἰ γὰρ τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχει ἢ τὸ συναμφότερον ὅ τε κύκλος καὶ τὸ Β χωρίον πρὸς αὐτὸν τὸν κύκλον, τοῦ δὲ ἐγγραφομένου μείζων ὁ κύκλος, πολλῷ μᾶλλον τὸ περιγραφὲν πρὸς τὸν κύκλον ἐλάσσονα λόγον ἔχει ἢ τὸ συναμφότερον ὅ τε κύκλος καὶ τὸ Β χωρίον πρὸς αὐτὸν τὸν κύκλον· καὶ διελόντι ἄρα τὰ ἀπολείμματα τοῦ περιγεγραμμένου πολυγώνου πρὸς τὸν κύκλον ἐλάσσονα λόγον ἔχει ἤπερ τὸ Β χωρίον πρὸς τὸν κύκλον· ἐλάσσονα ἄρα τὰ ἀπολείμματα τοῦ περιγεγραμμένου πολυγώνου τοῦ Β χωρίου. Ἢ οὕτως· ἐπεὶ τὸ περιγραφὲν πρὸς τὸν κύκλον ἐλάσσονα λόγον ἔχει ἢ τὸ συναμφότερον ὅ τε κύκλος καὶ τὸ Β χωρίον πρὸς τὸν κύκλον, διὰ τοῦτο δὴ ἔλασσον ἔσται τὸ περιγραφὲν συναμφοτέρου· ὥστε καὶ ὅλα τὰ περιλείμματα ἐλάσσονα ἔσται τοῦ χωρίου τοῦ Β.

   Ὁμοίως δὲ καὶ ἐπὶ τοῦ τομέως.

   ζ΄.

   Ἐὰν ἐν ἰσοσκελεῖ κώνῳ πυραμὶς ἐγγραφῇ ἰσόπλευρον ἔχουσα βάσιν, ἡ ἐπιφάνεια αὐτῆς χωρὶς τῆς βάσεως ἴση ἐστι τριγώνῳ βάσιν μὲν ἔχοντι ἴσην τῇ περιμέτρῳ τῆς βάσεως, ὕψος δὲ τὴν ἀπὸ τῆς κορυφῆς ἐπὶ μίαν πλευρὰν τῆς βάσεως κάθετον ἀγομένην.

   Ἔστω κῶνος ἰσοσκελής, οὗ βάσις ὁ ΑΒΓ κύκλος, καὶ εἰς αὐτὸν ἐγγεγράφθω πυραμὶς ἰσόπλευρον ἔχουσα βάσιν τὸ ΑΒΓ· λέγω ὅτι ἡ ἐπιφάνεια αὐτῆς χωρὶς τῆς βάσεως ἴση ἐστὶ τῷ εἰρημένῳ τριγώνῳ.

[21]    Ἐπεὶ γὰρ ἰσοσκελὴς ὁ κῶνος, καὶ ἰσόπλευρος ἡ βάσις τῆς πυραμίδος, τὰ ὕψη τῶν περιεχόντων τριγώνων τὴν πυραμίδα ἴσα ἐστὶν ἀλλήλοις. Καὶ βάσιν μὲν ἔχει τὰ τρίγωνα τὰς ΑΒ, ΒΓ, ΓΑ, ὕψος δὲ τὸ εἰρημένον· ὥστε τὰ τρίγωνα ἴσα ἐστὶ τριγώνῳ βάσιν μὲν ἔχοντι τὴν ἴσην ταῖς ΑΒ, ΒΓ, ΓΑ, ὕψος δὲ τὴν εἰρημένην εὐθεῖαν [τουτέστιν ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τοῦ ΑΒΓ τριγώνου].

[Σαφέστερον ἄλλως ἡ δεῖξις.

   Ἔστω κῶνος ἰσοσκελής, οὗ βάσις μὲν ὁ ΑΒΓ κύκλος, κορυφὴ δὲ τὸ Δ σημεῖον, καὶ ἐγγεγράφθω εἰς τὸν κῶνον πυραμὶς βάσιν [μὲν] ἔχουσα ἰσόπλευρον τρίγωνον τὸ ΑΒΓ, καὶ ἐπεζεύχθωσαν αἱ ΔΑ, ΔΓ, ΔΒ· λέγω ὅτι τὰ ΑΔΒ, ΑΔΓ, ΒΔΓ τρίγωνα ἴσα ἐστὶ τριγώνῳ, οὗ ἡ μὲν βάσις ἴση ἐστὶ τῇ περιμέτρῳ τοῦ ΑΒΓ τριγώνου, ἡ δὲ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν βάσιν κάθετος ἴση τῇ καθέτῳ τῇ ἀπὸ τοῦ Δ ἐπὶ τὴν ΒΓ ἀγομένῃ.

   Ἤχθωσαν γὰρ κάθετοι αἱ ΔΚ, ΔΛ, ΔΜ· αὗται ἄρα ἴσαι ἀλλήλαις εἰσίν. Καὶ κείσθω τρίγωνον τὸ ΕΖΗ ἔχον τὴν μὲν ΕΖ βάσιν τῇ περιμέτρῳ τοῦ ΑΒΓ τριγώνου ἴσην, τὴν δὲ [22] ΗΘ κάθετον τῇ ΔΛ ἴσην. Ἐπεὶ οὖν τὸ ὑπὸ τῶν ΒΓ, ΔΛ διπλάσιόν ἐστι τοῦ ΔΒΓ τριγώνου, ἔστιν δὲ καὶ τὸ μὲν ὑπὸ τῶν ΑΒ, ΔΚ διπλάσιον τοῦ ΑΒΔ τριγώνου, τὸ δὲ ὑπὸ ΑΓ, ΔΜ διπλάσιον τοῦ ΑΔΓ τριγώνου, τὸ ἄρα ὑπὸ τῆς περιμέτρου τοῦ ΑΒΓ τριγώνου, τουτέστι τῆς ΕΖ, καὶ τῆς ΔΛ, τουτέστι τῆς ΗΘ, διπλάσιόν ἐστι τῶν ΑΔΒ, ΒΔΓ, ΑΔΓ τριγώνων. Ἔστι δὲ καὶ τὸ ὑπὸ ΕΖ, ΗΘ διπλάσιον τοῦ ΕΖΗ τριγώνου· ἴσον ἄρα τὸ ΕΖΗ τρίγωνον τοῖς ΑΔΒ, ΒΔΓ, ΑΔΓ τριγώνοις].

   η΄.

   Ἐὰν περὶ κῶνον ἰσοσκελῆ πυραμὶς περιγραφῇ, ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως ἴση ἐστὶν [23] τριγώνῳ βάσιν μὲν ἔχοντι τὴν ἴσην τῇ περιμέτρῳ τῆς βάσεως, ὕψος δὲ τὴν πλευρὰν τοῦ κώνου.

   Ἔστω κῶνος, οὗ βάσις ὁ ΑΒΓ κύκλος, καὶ πυραμὶς περιγεγράφθω, ὥστε τὴν βάσιν αὐτῆς, τουτέστι τὸ ΔΕΖ πολύγωνον, περιγεγραμμένον περὶ τὸν ΑΒΓ κύκλον εἶναι· λέγω ὅτι ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως ἴση ἐστὶ τῷ εἰρημένῳ τριγώνῳ.

   Ἐπεὶ γὰρ [ὁ ἄξων τοῦ κώνου ὀρθός ἐστι πρὸς τὴν βάσιν, τουτέστι πρὸς τὸν ΑΒΓ κύκλον, καὶ] αἱ ἀπὸ τοῦ κέντρου τοῦ κύκλου ἐπὶ τὰς ἁφὰς ἐπιζευγνύμεναι εὐθεῖαι κάθετοί εἰσιν ἐπὶ τὰς ἐφαπτομένας, ἔσονται ἄρα καὶ αἱ ἀπὸ τῆς κορυφῆς τοῦ κώνου ἐπὶ τὰς ἁφὰς ἐπιζευγνύμεναι κάθετοι ἐπὶ τὰς ΔΕ, ΖΕ, ΖΔ. Αἱ ΗΑ, ΗΒ, ΗΓ ἄρα αἱ εἰρη μέναι [24] κάθετοι ἴσαι εἰσὶν ἀλλήλαις· πλευραὶ γάρ εἰσιν τοῦ κώνου. Κείσθω δὴ τὸ τρίγωνον τὸ ΘΚΛ ἴσην ἔχον τὴν μὲν ΘΚ τῇ περιμέτρῳ τοῦ ΔΕΖ τριγώνου, τὴν δὲ ΛΜ κάθετον ἴσην τῇ ΗΑ. Ἐπεὶ οὖν τὸ μὲν ὑπὸ ΔΕ, ΑΗ διπλάσιόν ἐστι τοῦ ΕΔΗ τριγώνου, τὸ δὲ ὑπὸ ΔΖ, ΗΒ διπλάσιόν ἐστι τοῦ ΔΖΗ τριγώνου, τὸ δὲ ὑπὸ ΕΖ, ΓΗ διπλάσιόν ἐστιν τοῦ ΕΗΖ τριγώνου, ἔστιν ἄρα τὸ ὑπὸ τῆς ΘΚ καὶ τῆς ΑΗ, τουτέστι τῆς ΜΛ, διπλάσιον τῶν ΕΔΗ, ΖΔΗ, ΕΗΖ τριγώνων. Ἔστιν δὲ καὶ τὸ ὑπὸ τῶν ΘΚ, ΛΜ διπλάσιον τοῦ ΛΚΘ τριγώνου· διὰ τοῦτο δὴ ἴση ἐστὶν ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως τριγώνῳ βάσιν μὲν ἔχοντι ἴσην τῇ περιμέτρῳ τοῦ ΔΕΖ, ὕψος δὲ τὴν πλευρὰν τοῦ κώνου.

   θ΄.

   Ἐὰν κώνου τινὸς ἰσοπλεύρου εἰς τὸν κύκλον, ὅς ἐστι βάσις τοῦ κώνου, εὐθεῖα γραμμὴ ἐμπέσῃ, ἀπὸ δὲ τῶν περάτων αὐτῆς εὐθεῖαι γραμμαὶ ἀχθῶσιν ἐπὶ τὴν κορυφὴν τοῦ κώνου, τὸ περιληφθὲν τρίγωνον ὑπό τε τῆς ἐμπεσούσης καὶ τῶν ἐπιζευχθεισῶν ἐπὶ τὴν κορυφὴν ἔλασσον ἔσται τῆς ἐπιφανείας τοῦ κώνου τῆς μεταξὺ τῶν ἐπὶ τὴν κορυφὴν ἐπιζευχθεισῶν.

   Ἔστω κώνου ἰσοσκελοῦς βάσις ὁ ΑΒΓ κύκλος, κορυφὴ δὲ τὸ Δ, καὶ διήχθω τις εἰς αὐτὸν εὐθεῖα ἡ ΑΓ, καὶ ἀπὸ τῆς κορυφῆς ἐπὶ τὰ Α, Γ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΓ· λέγω ὅτι τὸ ΑΔΓ τρίγωνον ἔλασσόν ἐστιν τῆς ἐπιφανείας τῆς κωνικῆς τῆς μεταξὺ τῶν ΑΔΓ.

[25]    Τετμήσθω ἡ ΑΒΓ περιφέρεια δίχα κατὰ τὸ Β, καὶ ἐπεζεύχθωσαν αἱ ΑΒ, ΓΒ, ΔΒ· ἔσται δὴ τὰ ΑΒΔ, ΒΓΔ τρίγωνα μείζονα τοῦ ΑΔΓ τριγώνου. Ὧι δὴ ὑπερέχει τὰ εἰρημένα τρίγωνα τοῦ ΑΔΓ τριγώνου, ἔστω τὸ Θ. Τὸ δὴ Θ ἤτοι τῶν ΑΒ, ΒΓ τμημάτων ἔλασσόν ἐστι ἢ οὔ.

   Ἔστω μὴ ἔλασσον πρότερον. Ἐπεὶ οὖν δύο εἰσὶν ἐπιφάνειαι ἥ τε κωνικὴ ἡ μεταξὺ τῶν ΑΔΒ μετὰ τοῦ ΑΕΒ τμήματος καὶ ἡ τοῦ ΑΔΒ τριγώνου τὸ αὐτὸ πέρας ἔχουσαι τὴν περίμετρον τοῦ τριγώνου τοῦ ΑΔΒ, μείζων ἔσται ἡ περιλαμβάνουσα τῆς περιλαμβανομένης· μείζων ἄρα ἐστὶν ἡ κωνικὴ ἐπιφάνεια ἡ μεταξὺ τῶν ΑΔΒ μετὰ τοῦ ΑΕΒ τμήματος τοῦ ΑΒΔ τριγώνου. Ὁμοίως δὲ καὶ ἡ μεταξὺ τῶν ΒΔΓ μετὰ τοῦ ΓΖΒ τμήματος μείζων ἐστὶν τοῦ ΒΔΓ τριγώνου· ὅλη ἄρα ἡ κωνικὴ ἐπιφάνεια μετὰ τοῦ Θ χωρίου μείζων ἐστὶ τῶν εἰρημένων τριγώνων. Τὰ δὲ εἰρημένα τρίγωνα ἴσα ἐστὶν τῷ τε ΑΔΓ τριγώνῳ καὶ τῷ Θ χωρίῳ. Κοινὸν ἀφῃρήσθω τὸ Θ χωρίον· λοιπὴ ἄρα ἡ [26] κωνικὴ ἐπιφάνεια ἡ μεταξὺ τῶν ΑΔΓ μείζων ἐστὶν τοῦ ΑΔΓ τριγώνου.

   Ἔστω δὴ τὸ Θ ἔλασσον τῶν ΑΒ, ΒΓ τμημάτων. Τέμνοντες δὴ τὰς ΑΒ, ΒΓ περιφερείας δίχα καὶ τὰς ἡμισείας αὐτῶν δίχα λείψομεν τμήματα ἐλάσσονα ὄντα τοῦ Θ χωρίου. Λελείφθω τὰ ἐπὶ τῶν ΑΕ, ΕΒ, ΒΖ, ΖΓ εὐθειῶν, καὶ ἐπεζεύχθωσαν αἱ ΔΕ, ΔΖ. Πάλιν τοίνυν κατὰ τὰ αὐτὰ ἡ μὲν ἐπιφάνεια τοῦ κώνου ἡ μεταξὺ τῶν ΑΔΕ μετὰ τοῦ ἐπὶ τῆς ΑΕ τμήματος μείζων ἐστὶν τοῦ ΑΔΕ τριγώνου, ἡ δὲ μεταξὺ τῶν ΕΔΒ μετὰ τοῦ ἐπὶ τῆς ΕΒ τμήματος μείζων ἐστὶν τοῦ ΕΔΒ τριγώνου· ἡ ἄρα ἐπιφάνεια ἡ μεταξὺ τῶν ΑΔΒ μετὰ τῶν ἐπὶ τῶν ΑΕ, ΕΒ τμημάτων μείζων ἐστὶν τῶν ΑΔΕ, ΕΒΔ τριγώνων. Ἐπεὶ δὲ τὰ ΑΕΔ, ΔΕΒ τρίγωνα μείζονά ἐστιν τοῦ ΑΒΔ τριγώνου, καθὼς δέδεικται, πολλῷ ἄρα ἡ ἐπιφάνεια τοῦ κώνου ἡ μεταξὺ τῶν ΑΔΒ μετὰ τῶν ἐπὶ τῶν ΑΕ, ΕΒ τμημάτων μείζων ἐστὶ τοῦ ΑΔΒ τριγώνου. Διὰ τὰ αὐτὰ δὴ καὶ ἡ ἐπιφάνεια ἡ μεταξὺ τῶν ΒΔΓ μετὰ τῶν ἐπὶ τῶν ΒΖ, ΖΓ τμημάτων μείζων ἐστὶν τοῦ ΒΔΓ τριγώνου· ὅλη ἄρα ἡ ἐπιφάνεια ἡ μεταξὺ τῶν ΑΔΓ μετὰ τῶν εἰρημένων τμημάτων μείζων ἐστὶ τῶν ΑΒΔ, ΔΒΓ τριγώνων. Ταῦτα δέ ἐστιν ἴσα τῷ ΑΔΓ τριγώνῳ καὶ τῷ Θ χωρίῳ· ὧν τὰ εἰρημένα τμήματα ἐλάσσονα τοῦ Θ χωρίου· λοιπὴ ἄρα ἡ ἐπιφάνεια ἡ μεταξὺ τῶν ΑΔΓ μείζων ἐστὶν τοῦ ΑΔΓ τριγώνου.

   ι΄.

   Ἐὰν ἐπιψαύουσαι ἀχθῶσιν τοῦ κύκλου, ὅς ἐστι βάσις τοῦ κώνου, ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι τῷ κύκλῳ καὶ [27] συμπίπτουσαι ἀλλήλαις, ἀπὸ δὲ τῶν ἁφῶν καὶ τῆς συμπτώσεως ἐπὶ τὴν κορυφὴν τοῦ κώνου εὐθεῖαι ἀχθῶσιν, τὰ περιεχόμενα τρίγωνα ὑπὸ τῶν ἐπιψαυουσῶν καὶ τῶν ἐπὶ τὴν κορυφὴν τοῦ κώνου ἐπιζευχθεισῶν εὐθειῶν μείζονά ἐστιν τῆς τοῦ κώνου ἐπιφανείας τῆς ἀπολαμβανομένης ὑπ᾿ αὐτῶν.

   Ἔστω κῶνος οὗ βάσις μὲν ὁ ΑΒΓ κύκλος, κορυφὴ δὲ τὸ Ε σημεῖον, καὶ τοῦ ΑΒΓ κύκλου ἐφαπτόμεναι ἤχθωσαν ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι αἱ ΑΔ, ΓΔ, καὶ ἀπὸ τοῦ Ε σημείου, ὅ ἐστιν κορυφὴ τοῦ κώνου, ἐπὶ τὰ Α, Δ, Γ ἐπεζεύχθωσαν αἱ ΕΑ, ΕΔ, ΕΓ· λέγω ὅτι τὰ ΑΔΕ, ΔΕΓ τρίγωνα μείζονά ἐστι τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕ, ΓΕ εὐθειῶν καὶ τῆς ΑΒΓ περιφερείας.

   Ἤχθω γὰρ ἡ ΗΒΖ ἐφαπτομένη τοῦ κύκλου καὶ παράλληλος οὖσα τῇ ΑΓ δίχα τμηθείσης τῆς ΑΒΓ περιφερείας κατὰ τὸ Β, καὶ ἀπὸ τῶν Η, Ζ ἐπὶ τὸ Ε ἐπεζεύχθωσαν αἱ ΗΕ, ΖΕ. Καὶ ἐπεὶ μείζους εἰσὶν αἱ ΗΔ, ΔΖ τῆς ΗΖ, κοιναὶ προσκείσθωσαν αἱ ΗΑ, ΖΓ· ὅλαι ἄρα αἱ ΑΔ, ΔΓ μείζους εἰσὶν τῶν ΑΗ, ΗΖ, ΖΓ. Καὶ ἐπεὶ αἱ ΑΕ, ΕΒ, ΕΓ πλευραί εἰσιν τοῦ κώνου, ἴσαι εἰσὶν διὰ τὸ ἰσοσκελῆ εἶναι τὸν κῶνον· ὁμοίως δὲ καὶ κάθετοί εἰσιν [ὡς ἐδείχθη ἐν τῷ λήμματι, τὰ δὲ ὑπὸ τῶν καθέτων καὶ τῶν βάσεων διπλασίονά ἐστιν τῶν τριγώνων]· μείζονα ἄρα ἐστὶ τὰ ΑΕΔ, ΔΕΓ τρίγωνα τῶν ΑΗΕ, ΗΕΖ, ΖΕΓ τριγώνων [εἰσὶν γὰρ αἱ μὲν ΑΗ, ΗΖ, ΖΓ ἐλάσσους τῶν ΓΔ, ΔΑ, τὰ δὲ ὕψη αὐτῶν ἴσα] [φανερὸν γὰρ ὅτι ἡ ἀπὸ τῆς κορυφῆς τοῦ ὀρθοῦ κώνου ἐπὶ τὴν ἐφαπὴν τῆς βάσεως ἐπιζευγνυμένη κάθετός ἐστιν ἐπὶ τὴν ἐφαπτομένην]. Ὧι δὴ μείζονά ἐστιν τὰ ΑΕΔ, ΔΓΕ τρίγωνα τῶν ΑΕΗ, ΗΕΖ, ΖΕΓ τριγώνων, ἔστω τὸ Θ [28] χωρίον. Τὸ δὴ Θ χωρίον ἤτοι ἔλαττόν ἐστιν τῶν ΑΗΒΚ, ΒΖΓΛ ἀποτμημάτων ἢ οὐκ ἔλαττον.

   Ἔστω πρότερον μὴ ἔλαττον. Ἐπεὶ οὖν εἰσιν ἐπιφάνειαι σύνθετοι, ἥ τε τῆς πυραμίδος τῆς ἐπὶ βάσεως τοῦ ΗΑΓΖ τραπεζίου κορυφὴν ἔχουσα τὸ Ε καὶ ἡ κωνικὴ ἐπιφάνεια ἡ μεταξὺ τῶν ΑΕΓ μετὰ τοῦ ΑΒΓ τμήματος, καὶ πέρας ἔχουσι τὴν αὐτὴν περίμετρον τοῦ ΑΕΓ τριγώνου, δῆλον ὡς ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τοῦ ΑΕΓ τριγώνου μείζων ἐστὶν τῆς κωνικῆς ἐπιφανείας μετὰ τοῦ τμήματος τοῦ ΑΒΓ. Κοινὸν ἀφῃρήσθω τὸ ΑΒΓ τμῆμα· λοιπὰ ἄρα τὰ τρίγωνα τὰ ΑΗΕ, ΗΕΖ, ΖΕΓ μετὰ τῶν ΑΗΒΚ, ΒΖΓΛ [29] περιλειμμάτων μείζονά ἐστιν τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕ, ΕΓ. Τῶν δὲ ΑΗΒΚ, ΒΖΓΛ περιλειμμάτων οὐκ ἔλασσόν ἐστιν τὸ Θ χωρίον· πολλῷ ἄρα τὰ ΑΗΕ, ΗΕΖ, ΖΕΓ τρίγωνα μετὰ τοῦ Θ μείζονα ἔσται τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕΓ. Ἀλλὰ τὰ ΑΗΕ, ΗΕΖ, ΖΕΓ τρίγωνα μετὰ τοῦ Θ ἐστὶν τὰ ΑΕΔ, ΔΕΓ τρίγωνα· τὰ ἄρα ΑΕΔ, ΔΕΓ τρίγωνα μείζονα ἔσται τῆς εἰρημένης κωνικῆς ἐπιφανείας.

   Ἔστω δὴ τὸ Θ ἔλασσον τῶν περιλειμμάτων. Ἀεὶ δὴ περιγράφοντες πολύγωνα περὶ τὰ τμήματα ὁμοίως δίχα τεμνομένων τῶν περιλειπομένων περιφερειῶν καὶ ἀγομένων ἐφαπτομένων λείψομέν τινα ἀπολείμματα, ἃ ἔσται ἐλάσσονα τοῦ Θ χωρίου. Λελείφθω καὶ ἔστω τὰ ΑΜΚ, ΚΝΒ, ΒΞΛ, ΛΟΓ ἐλάσσονα ὄντα τοῦ Θ χωρίου, καὶ ἐπεζεύχθω ἐπὶ τὸ Ε. Πάλιν δὴ φανερὸν ὅτι τὰ ΑΗΕ, ΗΕΖ, ΖΕΓ τρίγωνα τῶν ΑΕΜ, ΜΕΝ, ΝΕΞ, ΞΕΟ, ΟΕΓ τριγώνων ἔσται μείζονα [αἵ τε γὰρ βάσεις τῶν βάσεών εἰσι μείζους καὶ τὸ ὕψος ἴσον]. Ἔτι δὲ πάλιν ὁμοίως μείζονα ἔχει ἐπιφάνειαν ἡ πυραμὶς ἡ βάσιν μὲν ἔχουσα τὸ ΑΜΝΞΟΓ πολύγωνον, κορυφὴν δὲ τὸ Ε, χωρὶς τοῦ ΑΕΓ τριγώνου, τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕΓ μετὰ τοῦ ΑΒΓ τμήματος. Κοινὸν ἀφῃρήσθω τὸ ΑΒΓ τμῆμα· λοιπὰ ἄρα τὰ ΑΕΜ, ΜΕΝ, ΝΕΞ, ΞΕΟ, ΟΕΓ τρίγωνα μετὰ τῶν ΑΜΚ, ΚΝΒ, ΒΞΛ, ΛΟΓ περιλειμμάτων μείζονα ἔσται τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕΓ. Ἀλλὰ τῶν μὲν εἰρημένων περιλειμμάτων μεῖζόν ἐστιν τὸ Θ χωρίον, τῶν δὲ ΑΕΜ, ΜΕΝ, ΝΕΞ, ΞΕΟ, ΟΕΓ τριγώνων μείζονα ἐδείχθη τὰ ΑΕΗ, [30] ΗΕΖ, ΖΕΓ τρίγωνα· πολλῷ ἄρα τὰ ΑΕΗ, ΗΕΖ, ΖΕΓ τρίγωνα μετὰ τοῦ Θ χωρίου, τουτέστι τὰ ΑΔΕ, ΔΕΓ τρίγωνα, μείζονά ἐστιν τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν ΑΕΓ εὐθειῶν.

   ια΄.

   Ἐὰν ἐν ἐπιφανείᾳ ὀρθοῦ κυλίνδρου δύο εὐθεῖαι ὦσιν, ἡ ἐπιφάνεια τοῦ κυλίνδρου ἡ μεταξὺ τῶν εὐθειῶν μείζων ἐστὶν τοῦ παραλληλογράμμου τοῦ περιεχομένου ὑπό τε τῶν ἐν τῇ ἐπιφανείᾳ τοῦ κυλίνδρου εὐθειῶν καὶ τῶν ἐπιζευγνυουσῶν τὰ πέρατα αὐτῶν.

   Ἔστω κύλινδρος ὀρθός, οὗ βάσις μὲν ὁ ΑΒ κύκλος, ἀπεναντίον δὲ ὁ ΓΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΒΔ· λέγω ὅτι ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν μείζων ἐστὶν τοῦ ΑΓΒΔ παραλληλογράμμου.

   Τετμήσθω γὰρ ἑκατέρα τῶν ΑΒ, ΓΔ δίχα κατὰ τὰ Ε, Ζ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΑΕ, ΕΒ, ΓΖ, ΖΔ. Καὶ ἐπεὶ [31] αἱ ΑΕ, ΕΒ τῆς ΑΒ [διαμέτρου] μείζους εἰσίν, καί ἐστιν ἰσοϋψῆ τὰ παραλληλόγραμμα τὰ ἐπ᾿ αὐτῶν, μείζονα οὖν ἐστιν τὰ παραλληλόγραμμα, ὧν [αἱ] βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, τοῦ ΑΒΔΓ παραλληλογράμμου. Τίνι ἄρα μείζονά ἐστιν; Ἔστω τῷ Η χωρίῳ. Τὸ δὴ Η χωρίον ἤτοι ἔλασσον τῶν ΑΕ, ΕΒ, ΓΖ, ΖΔ ἐπιπέδων ἐστὶ τμημάτων ἢ οὐκ ἔλασσον.

   Ἔστω πρότερον μὴ ἔλασσον. Καὶ ἐπεὶ ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΕΒ, ΓΖΔ [τρίγωνα] πέρας ἔχει τὸ τοῦ ΑΓΒΔ παραλληλογράμμου ἐπίπεδον, ἀλλὰ καὶ ἡ συγκειμένη ἐπιφάνεια ἐκ τῶν παραλληλογράμμων, ὧν βάσεις μὲν ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, καὶ τὰ ΑΕΒ, ΓΖΔ [ἐπίπεδα] πέρας ἔχει τὸ τοῦ ΑΔΒΓ παραλληλογράμμου ἐπίπεδον, καὶ ἡ ἑτέρα τὴν ἑτέραν περιλαμβάνει, καὶ ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαί εἰσιν, μείζων οὖν ἐστιν ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΕΒ, ΓΖΔ ἐπίπεδα τμήματα τῆς συγκειμένης ἐπιφανείας ἐκ τῶν παραλληλογράμμων, ὧν [αἱ] βάσεις μὲν αἱ ΑΕ, ΕΒ, [32] ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, καὶ τῶν ΑΕΒ, ΓΖΔ τριγώνων. Κοινὰ ἀφῃρήσθω τὰ ΑΕΒ, ΓΖΔ τρίγωνα· λοιπὴ οὖν ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΕ, ΕΒ, ΓΖ, ΖΔ ἐπίπεδα τμήματα μείζονά ἐστι τῆς συγκειμένης ἐπιφανείας ἐκ τῶν παραλληλογράμμων, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ. Τὰ δὲ παραλληλόγραμμα, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, ἴσα ἐστὶν τῷ ΑΓΒΔ παραλληλογράμμῳ καὶ τῷ Η χωρίῳ· λοιπὴ ἄρα ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν μείζων ἐστὶ τοῦ ΑΓΒΔ παραλληλογράμμου.

   Ἀλλὰ δὴ ἔστω ἔλασσον τὸ Η χωρίον τῶν ΑΕ, ΕΒ, ΓΖ, ΖΔ ἐπιπέδων τμημάτων. Καὶ τετμήσθω ἑκάστη τῶν ΑΕ, ΕΒ, ΓΖ, ΖΔ περιφερειῶν δίχα κατὰ τὰ Θ, Κ, Λ, Μ σημεῖα, καὶ ἐπεζεύχθωσαν αἱ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ [τῶν δὲ ΑΕ, ΕΒ, ΓΖ, ΖΔ ἄρα ἐπιπέδων τμημάτων ἀφαιρεῖται οὐκ ἔλασσον ἢ τὸ ἥμισυ τὰ ΑΘΕ, ΕΚΒ, ΓΛΖ, ΖΜΔ τρίγωνα]. Τούτου οὖν ἑξῆς γινομένου καταλειφθήσεταί τινα τμήματα, ἃ ἔσται ἐλάσσονα τοῦ Η χωρίου. Καταλελείφθω καὶ ἔστω τὰ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ. Ὁμοίως δὴ δείξομεν ὅτι τὰ παραλληλόγραμμα, ὧν βάσεις μὲν αἱ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, μείζονα ἔσται τῶν παραλληλογράμμων, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ. Καὶ ἐπεὶ ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΕΒ, ΓΖΔ ἐπίπεδα τμήματα πέρας ἔχει τὸ τοῦ ΑΓΒΔ παραλληλογράμμου ἐπίπεδον, ἀλλὰ καὶ ἡ συγκειμένη ἐπιφάνεια ἐκ τῶν παραλληλογράμμων, ὧν [33] βάσεις μὲν αἱ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, καὶ τῶν ΑΘΕΚΒ, ΓΛΖΜΔ εὐθυγράμμων, κοινὰ ἀφῃρήσθω τὰ ΑΘΕΚΒ, ΓΛΖΜΔ εὐθύγραμμα· λοιπὴ ἄρα ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ ἐπίπεδα τμήματα μείζονά ἐστιν τῆς συγκειμένης ἐπιφανείας ἐκ τῶν παραλληλογράμμων, ὧν βάσεις μὲν αἱ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ. Τὰ δὲ παραλληλόγραμμα, ὧν βάσεις μὲν αἱ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, μείζονά ἐστιν τῶν παραλληλογράμμων, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ· καὶ ἡ ἀποτεμνομένη ἄρα κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ ἐπίπεδα τμήματα μείζονά ἐστιν τῶν παραλληλογράμμων, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ. Τὰ δὲ παραλληλόγραμμα, ὧν βάσεις μὲν αἱ ΑΕ, ΕΒ, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, ἴσα ἐστὶν τῷ ΑΓΔΒ παραλληλογράμμῳ καὶ τῷ Η χωρίῳ· καὶ ἡ ἀποτεμνομένη ἄρα κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν καὶ τὰ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ ἐπίπεδα τμήματα μείζονά ἐστιν τοῦ ΑΓΒΔ παραλληλογράμμου καὶ τοῦ Η χωρίου. Ἀφαιρεθέντα δὲ τὰ ΑΘ, ΘΕ, ΕΚ, ΚΒ, ΓΛ, ΛΖ, ΖΜ, ΜΔ τμήματα τοῦ Η χωρίου ἐλάσσονα λοιπὴ ἄρα ἡ ἀποτεμνομένη κυλινδρικὴ ἐπιφάνεια ὑπὸ τῶν ΑΓ, ΒΔ εὐθειῶν μείζων ἐστὶν τοῦ ΑΓΒΔ παραλληλογράμμου.

   ιβ΄.

   Ἐὰν ἐν ἐπιφανείᾳ κυλίνδρου τινὸς ὀρθοῦ δύο εὐθεῖαι ὦσιν, ἀπὸ δὲ τῶν περάτων τῶν εὐθειῶν ἀχθῶσίν τινες [34] ἐπιψαύουσαι τῶν κύκλων, οἵ εἰσιν βάσεις τοῦ κυλίνδρου, ἐν τῷ ἐπιπέδῳ αὐτῶν οὖσαι καὶ συμπέσωσιν, τὰ παραλληλόγραμμα τὰ περιεχόμενα ὑπό τε τῶν ἐπιψαυουσῶν καὶ τῶν πλευρῶν τοῦ κυλίνδρου μείζονα ἔσται τῆς ἐπιφανείας τοῦ κυλίνδρου τῆς μεταξὺ τῶν εὐθειῶν τῶν ἐν τῇ ἐπιφανείᾳ τοῦ κυλίνδρου.

   Ἔστω κυλίνδρου τινὸς ὀρθοῦ βάσις ὁ ΑΒΓ κύκλος, καὶ ἔστωσαν ἐν τῇ ἐπιφανείᾳ αὐτοῦ δύο εὐθεῖαι, ὧν πέρατα τὰ Α, Γ, ἀπὸ δὲ τῶν Α, Γ ἤχθωσαν ἐπιψαύουσαι τοῦ κύκλου ἐν τῷ αὐτῷ ἐπιπέδῳ οὖσαι καὶ συμπιπτέτωσαν κατὰ τὸ Η, νοείσθωσαν δὲ καὶ ἐν τῇ ἑτέρᾳ βάσει τοῦ κυλίνδρου ἀπὸ τῶν περάτων τῶν ἐν τῇ ἐπιφανείᾳ εὐθεῖαι ἠγμέναι ἐπιψαύουσαι τοῦ κύκλου· δεικτέον ὅτι τὰ παραλληλόγραμμα τὰ περιεχόμενα ὑπὸ τῶν ἐπιψαυουσῶν καὶ τῶν πλευρῶν τοῦ κυλίνδρου μείζονά ἐστι τῆς κατὰ τὴν ΑΒΓ περιφέρειαν ἐπιφανείας τοῦ κυλίνδρου.

   Ἤχθω γὰρ ἡ ΕΖ ἐπιψαύουσα, καὶ ἀπὸ τῶν Ε, Ζ σημείων ἤχθωσάν τινες εὐθεῖαι παρὰ τὸν ἄξονα τοῦ κυλίνδρου [35] ἕως [τῆς ἐπιφανείας] τῆς ἑτέρας βάσεως· τὰ δὴ παραλληλόγραμμα τὰ περιεχόμενα ὑπὸ τῶν ΑΗ, ΗΓ καὶ τῶν πλευρῶν τοῦ κυλίνδρου μείζονά ἐστιν τῶν παραλληλογράμμων τῶν περιεχομένων ὑπό τε τῶν ΑΕ, ΕΖ, ΖΓ καὶ τῆς πλευρᾶς τοῦ κυλίνδρου [ἐπεὶ γὰρ αἱ ΕΗ, ΗΖ τῆς ΕΖ μείζους εἰσίν, κοιναὶ προσκείσθωσαν αἱ ΑΕ, ΖΓ]. Ὧι δὴ μείζονά ἐστιν, ἔστω τὸ Κ χωρίον. Τοῦ δὴ Κ χωρίου τὸ ἥμισυ ἤτοι μεῖζόν ἐστι τῶν σχημάτων τῶν περιεχομένων ὑπὸ τῶν ΑΕ, ΕΖ, ΖΓ εὐθειῶν καὶ τῶν ΑΔ, ΔΒ, ΒΘ, ΘΓ περιφερειῶν ἢ οὔ. Ἔστω πρότερον μεῖζον. Τῆς δὴ ἐπιφανείας τῆς συγκειμένης ἔκ τε τῶν παραλληλογράμμων τῶν κατὰ τὰς ΑΕ, ΕΖ, ΖΓ καὶ τοῦ ΑΕΖΓ τραπεζίου καὶ τοῦ κατεναντίον αὐτοῦ ἐν τῇ ἑτέρα βάσει τοῦ κυλίνδρου πέρας ἐστὶν ἡ περίμετρος τοῦ παραλληλογράμμου τοῦ κατὰ τὴν ΑΓ. Ἔστιν δὲ καὶ τῆς ἐπιφανείας τῆς συγκειμένης ἐκ τῆς ἐπιφανείας τοῦ κυλίνδρου τῆς κατὰ τὴν ΑΒΓ περιφέρειαν καὶ τῶν τμημάτων τοῦ τε ΑΒΓ καὶ τοῦ ἀπεναντίον αὐτοῦ πέρας ἡ αὐτὴ περίμετρος· αἱ οὖν εἰρημέναι ἐπιφάνειαι τὸ αὐτὸ πέρας ἔχουσαι τυγχάνουσιν, ὅπερ ἐστὶν ἐν ἐπιπέδῳ, καί εἰσιν ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαι, καί τινα μὲν περιλαμβάνει ἡ ἑτέρα αὐτῶν, τινὰ δὲ κοινὰ ἔχουσιν· ἐλάσσων ἄρα ἐστὶν ἡ περιλαμβανομένη. Ἀφαιρεθέντων οὖν κοινῶν τοῦ τε ΑΒΓ τμήματος καὶ τοῦ ἀπεναντίον αὐτοῦ ἐλάσσων ἐστὶν ἡ ἐπιφάνεια τοῦ κυλίνδρου ἡ κατὰ τὴν ΑΒΓ περιφέρειαν τῆς συγκειμένης ἐπιφανείας ἔκ τε τῶν παραλληλογράμμων τῶν κατὰ τὰς ΑΕ, ΕΖ, ΖΓ καὶ τῶν σχημάτων τῶν ΑΕΒ, ΒΖΓ καὶ τῶν ἀπεναντίον αὐτῶν. Αἱ δὲ τῶν εἰρημένων παραλληλογράμμων ἐπιφάνειαι μετὰ τῶν εἰρημένων [36] σχημάτων ἐλάττους εἰσὶν τῆς ἐπιφανείας τῆς συγκειμένης ἔκ τε τῶν παραλληλογράμμων τῶν κατὰ τὰς ΑΗ, ΗΓ [μετὰ γὰρ τοῦ Κ μείζονος ὄντος τῶν σχημάτων ἴσαι ἦσαν αὐτοῖς]· δῆλον οὖν ὅτι τὰ παραλληλόγραμμα τὰ περιεχόμενα ὑπὸ τῶν ΑΗ, ΓΗ καὶ τῶν πλευρῶν τοῦ κυλίνδρου μείζονά ἐστι τῆς ἐπιφανείας τοῦ κυλίνδρου τῆς κατὰ τὴν ΑΒΓ περιφέρειαν.

   Εἰ δὲ μή ἐστιν μεῖζον τὸ ἥμισυ τοῦ Κ χωρίου τῶν εἰρημένων σχημάτων, ἀχθήσονται εὐθεῖαι ἐπιψαύουσαι τοῦ τμήματος, ὥστε γενέσθαι τὰ περιλειπόμενα σχήματα ἐλάσσονα τοῦ ἡμίσους τοῦ Κ, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς ἔμπροσθεν δειχθήσεται.

‹ΠΟΡΙΣΜΑ.›

   Τούτων δὴ δεδειγμένων φανερὸν [ἐπὶ μὲν τῶν προειρημένων] ὅτι, ἐὰν εἰς κῶνον ἰσοσκελῆ πυραμὶς ἐγγραφῇ, ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως ἐλάσσων ἐστὶ τῆς κωνικῆς ἐπιφανείας [ἕκαστον γὰρ τῶν περιεχόντων τὴν πυραμίδα τριγώνων ἔλασσόν ἐστιν τῆς κωνικῆς ἐπιφανείας τῆς μεταξὺ τῶν τοῦ τριγώνου πλευρῶν· ὥστε καὶ ὅλη ‹ἡ› ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως ἐλάσσων ἐστὶ τῆς ἐπιφανείας τοῦ κώνου χωρὶς τῆς βάσεως], καὶ ὅτι, ἐὰν περὶ κῶνον ἰσοσκελῆ πυραμὶς περιγραφῇ, ἡ ἐπιφάνεια τῆς πυραμίδος χωρὶς τῆς βάσεως μείζων ἐστὶν τῆς ἐπιφανείας τοῦ κώνου χωρὶς τῆς βάσεως [κατὰ τὸ συνεχὲς ἐκείνῳ].

‹ΠΟΡΙΣΜΑ.›

[37]   Φανερὸν δὲ ἐκ τῶν ἀποδεδειγμένων ὅτι τε, ἐὰν εἰς κύλινδρον ὀρθὸν πρίσμα ἐγγραφῇ, ἡ ἐπιφάνεια τοῦ πρίσματος ἡ ἐκ τῶν παραλληλογράμμων συγκειμένη ἐλάσσων ἐστὶ τῆς ἐπιφανείας τοῦ κυλίνδρου χωρὶς τῆς βάσεως [ἔλασσον γὰρ ἕκαστον παραλληλόγραμμον τοῦ πρίσματός ἐστι τῆς καθ᾿ αὑτὸ τοῦ κυλίνδρου ἐπιφανείας], καὶ ὅτι, ἐὰν περὶ κύλινδρον ὀρθὸν πρίσμα περιγραφῇ, ἡ ἐπιφάνεια τοῦ πρίσματος ἡ ἐκ τῶν παραλληλογράμμων συγκειμένη μείζων ἐστὶ τῆς ἐπιφανείας τοῦ κυλίνδρου χωρὶς τῆς βάσεως.

   ιγ΄.

   Παντὸς κυλίνδρου ὀρθοῦ ἡ ἐπιφάνεια χωρὶς τῆς βάσεως ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου μέσον λόγον ἔχει τῆς πλευρᾶς τοῦ κυλίνδρου καὶ τῆς διαμέτρου τῆς βάσεως τοῦ κυλίνδρου.

   Ἔστω κυλίνδρου τινὸς ὀρθοῦ βάσις ὁ Α κύκλος, καὶ ἔστω τῇ μὲν διαμέτρῳ τοῦ Α κύκλου ἴση ἡ ΓΔ, τῇ δὲ πλευρᾷ τοῦ κυλίνδρου ἡ ΕΖ, ἐχέτω δὲ μέσον λόγον τῶν ΔΓ, ΕΖ ἡ Η, καὶ κείσθω κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ Η, ὁ Β· δεικτέον ὅτι ὁ Β κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ κυλίνδρου χωρὶς τῆς βάσεως.

[38]    Εἰ γὰρ μή ἐστιν ἴσος, ἤτοι μείζων ἐστὶ ἢ ἐλάσσων. Ἔστω πρότερον, εἰ δυνατόν, ἐλάσσων. Δύο δὴ μεγεθῶν ὄντων ἀνίσων τῆς τε ἐπιφανείας τοῦ κυλίνδρου καὶ τοῦ Β κύκλου δυνατόν ἐστιν εἰς τὸν Β κύκλον ἰσόπλευρον πολύγωνον ἐγγράψαι καὶ ἄλλο περιγράψαι, ὥστε τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ἡ ἐπιφάνεια τοῦ κυλίνδρου πρὸς τὸν Β κύκλον. Νοείσθω δὴ περιγεγραμμένον καὶ ἐγγεγραμμένον, καὶ περὶ τὸν Α κύκλον περιγεγράφθω εὐθύγραμμον ὅμοιον τῷ περὶ τὸν Β περιγεγραμμένῳ, καὶ ἀναγεγράφθω ἀπὸ τοῦ εὐθυγράμμου πρίσμα· ἔσται δὴ περὶ τὸν κύλινδρον περιγεγραμμένον. Ἔστω δὲ καὶ τῇ περιμέτρῳ τοῦ εὐθυγράμμου τοῦ περὶ τὸν Α κύκλον ἴση ἡ ΚΔ καὶ τῇ ΚΔ ἴση ἡ ΔΖ, τῆς δὲ ΓΔ ἡμίσεια ἔστω ἡ ΓΤ· ἔσται δὴ τὸ ΚΔΤ τρίγωνον ἴσον τῷ περιγεγραμμένῳ εὐθυγράμμῳ περὶ τὸν Α κύκλον [ἐπειδὴ βάσιν μὲν ἔχει τῇ περιμέτρῳ ἴσην, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τοῦ Α κύκλου], τὸ δὲ ΕΛ παραλληλόγραμμον τῇ ἐπιφανείᾳ τοῦ πρίσματος τοῦ περὶ τὸν κύλινδρον περιγεγραμμένου [ἐπειδὴ περιέχεται [39] ὑπὸ τῆς πλευρᾶς τοῦ κυλίνδρου καὶ τῆς ἴσης τῇ περιμέτρῳ τῆς βάσεως τοῦ πρίσματος]. Κείσθω δὴ τῇ ΕΖ ἴση ἡ ΕΡ· ἴσον ἄρα ἐστὶν τὸ ΖΡΛ τρίγωνον τῷ ΕΛ παραλληλογράμμῳ, ὥστε καὶ τῇ ἐπιφανείᾳ τοῦ πρίσματος. Καὶ ἐπεὶ ὅμοιά ἐστιν τὰ εὐθύγραμμα τὰ περὶ τοὺς Α, Β κύκλους περιγεγραμμένα, τὸν αὐτὸν ἕξει λόγον [τὰ εὐθύγραμμα], ὅνπερ αἱ ἐκ τῶν κέντρων δυνάμει· ἕξει ἄρα τὸ ΚΤΔ τρίγωνον πρὸς τὸ περὶ τὸν Β κύκλον εὐθύγραμμον λόγον, ὃν ἡ ΤΔ πρὸς Η δυνάμει [αἱ γὰρ ΤΔ, Η ἴσαι εἰσὶν ταῖς ἐκ τῶν κέντρων]. Ἀλλ᾿ ὃν ἔχει λόγον ἡ ΤΔ πρὸς Η δυνάμει, τοῦτον ἔχει τὸν λόγον ἡ ΤΔ πρὸς ΡΖ μήκει [ἡ γὰρ Η τῶν ΤΔ, ΡΖ μέση ἐστὶ ἀνάλογον διὰ τὸ καὶ τῶν ΓΔ, ΕΖ· πῶς δὲ τοῦτο; ἐπεὶ γὰρ ἴση ἐστὶν ἡ μὲν ΔΤ τῇ ΤΓ, ἡ δὲ ΡΕ τῇ ΕΖ, διπλασία ἄρα ἐστὶν ἡ ΓΔ τῆς ΤΔ, καὶ ἡ ΡΖ τῆς ΡΕ· ἔστιν ἄρα ὡς ἡ ΔΓ πρὸς ΔΤ, οὕτως ἡ ΡΖ πρὸς ΖΕ. Τὸ ἄρα ὑπὸ τῶν ΓΔ, ΕΖ ἴσον ἐστὶν τῷ ὑπὸ τῶν ΤΔ, ΡΖ. Τῷ δὲ ὑπὸ τῶν ΓΔ, ΕΖ ἴσον ἐστὶν τὸ ἀπὸ Η· καὶ τῷ ὑπὸ τῶν ΤΔ, ΡΖ ἄρα ἴσον ἐστὶ τὸ ἀπὸ τῆς Η· ἔστιν ἄρα ὡς ἡ ΤΔ πρὸς Η, οὕτως ἡ Η πρὸς ΡΖ. Ἔστιν ἄρα ὡς ἡ ΤΔ πρὸς ΡΖ, τὸ ἀπὸ τῆς ΤΔ πρὸς τὸ ἀπὸ τῆς Η· ἐὰν γὰρ τρεῖς εὐθεῖαι ἀνάλογον ὦσιν, ἔστιν ὡς ἡ πρώτη πρὸς τὴν τρίτην, τὸ ἀπὸ τῆς πρώτης εἶδος πρὸς τὸ ἀπὸ τῆς δευτέρας εἶδος τὸ ὅμοιον καὶ ὁμοίως ἀναγεγραμμένον]· ὃν δὲ λόγον ἔχει ἡ ΤΔ πρὸς ΡΖ μήκει, τοῦτον ἔχει τὸ ΚΤΔ τρίγωνον πρὸς τὸ ΡΛΖ [ἐπειδήπερ ἴσαι εἰσὶν αἱ ΚΔ, ΛΖ]· τὸν αὐτὸν ἄρα λόγον ἔχει τὸ ΚΤΔ τρίγωνον πρὸς τὸ εὐθύγραμμον τὸ περὶ τὸν Β κύκλον περιγεγραμμένον, ὅνπερ τὸ ΤΚΔ τρίγωνον πρὸς τὸ ΡΖΛ τρίγωνον. Ἴσον ἄρα ἐστὶν τὸ ΖΛΡ τρίγωνον τῷ περὶ τὸν Β κύκλον [40] περιγεγραμμένῳ εὐθυγράμμῳ· ὥστε καὶ ἡ ἐπιφάνεια τοῦ πρίσματος τοῦ περὶ τὸν Α κύλινδρον περιγεγραμμένου τῷ εὐθυγράμμῳ τῷ περὶ τὸν Β κύκλον ἴση ἐστίν. Καὶ ἐπεὶ ἐλάσσονα λόγον ἔχει τὸ εὐθύγραμμον τὸ περὶ τὸν Β κύκλον πρὸς τὸ ἐγγεγραμμένον ἐν τῷ κύκλῳ τοῦ ὃν ἔχει ἡ ἐπιφάνεια τοῦ Α κυλίνδρου πρὸς τὸν Β κύκλον, ἐλάσσονα λόγον ἕξει καὶ ἡ ἐπιφάνεια τοῦ πρίσματος τοῦ περὶ τὸν κύλινδρον περιγεγραμμένου πρὸς τὸ εὐθύγραμμον τὸ ἐν τῷ κύκλῳ τῷ Β ἐγγεγραμμένον ἤπερ ἡ ἐπιφάνεια τοῦ κυλίνδρου πρὸς τὸν Β κύκλον· καὶ ἐναλλάξ· ὅπερ ἀδύνατον [ἡ μὲν γὰρ ἐπιφάνεια τοῦ πρίσματος τοῦ περιγεγραμμένου περὶ τὸν κύλινδρον μείζων οὖσα δέδεικται τῆς ἐπιφανείας τοῦ κυλίνδρου, τὸ δὲ ἐγγεγραμμένον εὐθύγραμμον ἐν τῷ Β κύκλῳ ἔλασσόν ἐστιν τοῦ Β κύκλου]. Οὐκ ἄρα ἐστὶν ὁ Β κύκλος ἐλάσσων τῆς ἐπιφανείας τοῦ κυλίνδρου.

   Ἔστω δή, εἰ δυνατόν, μείζων. Πάλιν δὴ νοείσθω εἰς τὸν Β κύκλον εὐθύγραμμον ἐγγεγραμμένον καὶ ἄλλο περιγεγραμμένον, ὥστε τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχειν ἢ τὸν Β κύκλον πρὸς τὴν ἐπιφάνειαν τοῦ κυλίνδρου, καὶ ἐγγεγράφθω εἰς τὸν Α κύκλον πολύγωνον ὅμοιον τῷ εἰς τὸν Β κύκλον ἐγγεγραμμένῳ, καὶ πρίσμα ἀναγεγράφθω ἀπὸ τοῦ ἐν τῷ κύκλῳ ἐγγεγραμμένου πολυγώνου· καὶ πάλιν ἡ ΚΔ ἴση ἔστω τῇ περιμέτρῳ τοῦ εὐθυγράμμου τοῦ ἐν τῷ Α κύκλῳ ἐγγεγραμμένου, καὶ ἡ ΖΛ ἴση αὐτῇ ἔστω. Ἔσται δὴ τὸ μὲν ΚΤΔ τρίγωνον μεῖζον τοῦ εὐθυγράμμου τοῦ ἐν τῷ Α κύκλῳ ἐγγεγραμμένου [διότι βάσιν μὲν ἔχει τὴν [41] περίμετρον αὐτοῦ, ὕψος δὲ μεῖζον τῆς ἀπὸ τοῦ κέντρου {πλευρᾶς} ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου ἀγομένης καθέτου], τὸ δὲ ΕΛ παραλληλόγραμμον ἴσον τῇ ἐπιφανείᾳ τοῦ πρίσματος τῇ ἐκ τῶν παραλληλογράμμων συγκειμένῃ [διότι περιέχεται ὑπὸ τῆς πλευρᾶς τοῦ κυλίνδρου καὶ τῆς ἴσης τῇ περιμέτρῳ τοῦ εὐθυγράμμου, ὅ ἐστιν βάσις τοῦ πρίσματος]· ὥστε καὶ τὸ ΡΛΖ τρίγωνον ἴσον ἐστὶ τῇ ἐπιφανείᾳ τοῦ πρίσματος. Καὶ ἐπεὶ ὅμοιά ἐστι τὰ εὐθύγραμμα τὰ ἐν τοῖς Α, Β κύκλοις ἐγγεγραμμένα, τὸν αὐτὸν ἔχει λόγον πρὸς ἄλληλα ὃν αἱ ἐκ τῶν κέντρων αὐτῶν δυνάμει. Ἔχει δὲ καὶ τὰ ΚΤΔ, ΖΡΔ τρίγωνα πρὸς ἄλληλα λόγον, ὃν αἱ ἐκ τῶν κέντρων τῶν κύκλων δυνάμει· τὸν αὐτὸν ἄρα λόγον ἔχει τὸ εὐθύγραμμον τὸ ἐν τῷ Α κύκλῳ ἐγγεγραμμένον πρὸς τὸ εὐθύγραμμον τὸ ἐν τῷ Β ἐγγεγραμμένον καὶ τὸ ΚΤΔ τρίγωνον πρὸς τὸ ΛΖΡ τρίγωνον. Ἔλασσον δέ ἐστι τὸ εὐθύγραμμον τὸ ἐν τῷ Α κύκλῳ ἐγγεγραμμένον τοῦ ΚΤΔ τριγώνου· ἔλασσον ἄρα καὶ τὸ εὐθύγραμμον τὸ ἐν τῷ Β κύκλῳ ἐγγεγραμμένον τοῦ ΖΡΛ τριγώνου· ὥστε καὶ τῆς ἐπιφανείας τοῦ πρίσματος τοῦ ἐν τῷ κυλίνδρῳ ἐγγεγραμμένου· ὅπερ ἀδύνατον [ἐπεὶ γὰρ ἐλάσσονα λόγον ἔχει τὸ περιγεγραμμένον εὐθύγραμμον περὶ τὸν Β κύκλον πρὸς τὸ ἐγγεγραμμένον ἢ ὁ Β κύκλος πρὸς τὴν ἐπιφάνειαν τοῦ κυλίνδρου, καὶ ἐναλλάξ, μεῖζον δέ ἐστι τὸ περιγεγραμμένον περὶ τὸν Β κύκλον τοῦ Β κύκλου, μεῖζον ἄρα ἐστὶν τὸ ἐγγεγραμμένον ἐν τῷ Β κύκλῳ τῆς ἐπιφανείας τοῦ κυλίνδρου· ὥστε καὶ τῆς ἐπιφανείας τοῦ πρίσματος]. Οὐκ ἄρα μείζων ἐστὶν ὁ Β κύκλος τῆς ἐπιφανείας τοῦ κυλίνδρου. Ἐδείχθη δὲ ὅτι οὐδὲ ἐλάσσων· ἴσος ἄρα ἐστίν.

[42]    ιδ΄.

   Παντὸς κώνου ἰσοσκελοῦς χωρὶς τῆς βάσεως ἡ ἐπιφάνεια ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου μέσον λόγον ἔχει τῆς πλευρᾶς τοῦ κώνου καὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου, ὅς ἐστιν βάσις τοῦ κώνου.

   Ἔστω κῶνος ἰσοσκελής, οὗ βάσις ὁ Α κύκλος, ἡ δὲ ἐκ τοῦ κέντρου ἔστω ἡ Γ, τῇ δὲ πλευρᾷ τοῦ κώνου ἔστω ἴση ἡ Δ, τῶν δὲ Γ, Δ μέση ἀνάλογον ἡ Ε, ὁ δὲ Β κύκλος ἐχέτω τὴν ἐκ τοῦ κέντρου τῇ Ε ἴσην· λέγω ὅτι ὁ Β κύκλος ἐστὶν ἴσος τῇ ἐπιφανείᾳ τοῦ κώνου χωρὶς τῆς βάσεως.

   Εἰ γὰρ μή ἐστιν ἴσος, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω πρότερον ἐλάσσων. Ἔστι δὴ δύο μεγέθη ἄνισα ἥ τε ἐπιφάνεια τοῦ κώνου καὶ ὁ Β κύκλος, καὶ μείζων ἡ ἐπιφάνεια τοῦ κώνου· δυνατὸν ἄρα εἰς τὸν Β κύκλον πολύγωνον ἰσόπλευρον ἐγγράψαι καὶ ἄλλο περιγράψαι ὅμοιον τῷ ἐγγεγραμμένῳ, ὥστε τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ἡ ἐπιφάνεια τοῦ κώνου πρὸς τὸν Β κύκλον. Νοείσθω δὴ καὶ περὶ τὸν Α κύκλον πολύγωνον περιγεγραμμένον ὅμοιον τῷ περὶ τὸν Β κύκλον περιγεγραμμένῳ, καὶ ἀπὸ τοῦ περὶ τὸν Α κύκλον περιγεγραμμένου πολυγώνου [43] πυραμὶς ἀνεστάτω ἀναγεγραμμένη τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ. Ἐπεὶ οὖν ὅμοιά ἐστιν τὰ πολύγωνα τὰ περὶ τοὺς Α, Β κύκλους περιγεγραμμένα, τὸν αὐτὸν ἔχει λόγον πρὸς ἄλληλα, ὃν αἱ ἐκ τοῦ κέντρου δυνάμει πρὸς ἀλλήλας, τουτέστιν ὃν ἔχει ἡ Γ πρὸς Ε δυνάμει, τουτέστιν ἡ Γ πρὸς Δ μήκει. Ὃν δὲ λόγον ἔχει ἡ Γ πρὸς Δ μήκει, τοῦτον ἔχει τὸ περιγεγραμμένον πολύγωνον περὶ τὸν Α κύκλον πρὸς τὴν ἐπιφάνειαν τῆς πυραμίδος τῆς περιγεγραμμένης περὶ τὸν κῶνον [ἡ μὲν γὰρ Γ ἴση ἐστὶ τῇ ἀπὸ τοῦ κέντρου καθέτῳ ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου, ἡ δὲ Δ τῇ πλευρᾷ τοῦ κώνου· κοινὸν δὲ ὕψος ἡ περίμετρος τοῦ πολυγώνου πρὸς τὰ ἡμίση τῶν ἐπιφανειῶν]· τὸν αὐτὸν ἄρα λόγον ἔχει τὸ εὐθύγραμμον τὸ περὶ τὸν Α κύκλον πρὸς τὸ εὐθύγραμμον τὸ περὶ τὸν Β κύκλον καὶ αὐτὸ τὸ εὐθύγραμμον πρὸς τὴν ἐπιφάνειαν τῆς πυραμίδος τῆς περιγεγραμμένης περὶ τὸν κῶνον· ὥστε ἴση ἐστὶν ἡ ἐπιφάνεια τῆς πυραμίδος τῷ εὐθυγράμμῳ τῷ περὶ τὸν Β κύκλον περιγεγραμμένῳ. Ἐπεὶ οὖν ἐλάσσονα λόγον ἔχει τὸ εὐθύγραμμον τὸ περὶ τὸν Β κύκλον περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἤπερ ἡ ἐπιφάνεια τοῦ κώνου πρὸς τὸν Β κύκλον, ἐλάσσονα λόγον ἕξει ἡ ἐπιφάνεια τῆς πυραμίδος τῆς περὶ τὸν κῶνον περιγεγραμμένης πρὸς τὸ εὐθύγραμμον τὸ ἐν τῷ Β κύκλῳ ἐγγεγραμμένον ἤπερ ἡ ἐπιφάνεια τοῦ κώνου πρὸς τὸν Β κύκλον· ὅπερ ἀδύνατον [ἡ μὲν γὰρ ἐπιφάνεια τῆς πυραμίδος μείζων οὖσα δέδεικται τῆς ἐπιφανείας τοῦ κώνου, τὸ δὲ ἐγγεγραμμένον εὐθύγραμμον ἐν τῷ Β κύκλῳ ἔλασσον ἔσται τοῦ Β κύκλου]. Οὐκ ἄρα ὁ Β κύκλος ἐλάσσων ἔσται τῆς ἐπιφανείας τοῦ κώνου.

   Λέγω δὴ ὅτι οὐδὲ μείζων. Εἰ γὰρ δυνατόν ἐστιν, ἔστω [44] μείζων. Πάλιν δὴ νοείσθω εἰς τὸν Β κύκλον πολύγωνον ἐγγεγραμμένον καὶ ἄλλο περιγεγραμμένον, ὥστε τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ὁ Β κύκλος πρὸς τὴν ἐπιφάνειαν τοῦ κώνου, καὶ εἰς τὸν Α κύκλον νοείσθω ἐγγεγραμμένον πολύγωνον ὅμοιον τῷ εἰς τὸν Β κύκλον ἐγγεγραμμένῳ, καὶ ἀναγεγράφθω ἀπ᾿ αὐτοῦ πυραμὶς τὴν αὐτὴν κορυφὴν ἔχουσα τῷ κώνῳ. Ἐπεὶ οὖν ὅμοιά ἐστι τὰ ἐν τοῖς Α, Β κύκλοις ἐγγεγραμμένα, τὸν αὐτὸν ἕξει λόγον πρὸς ἄλληλα, ὃν αἱ ἐκ τῶν κέντρων δυνάμει πρὸς ἀλλήλας· τὸν αὐτὸν ἄρα λόγον ἔχει τὸ πολύγωνον πρὸς τὸ πολύγωνον καὶ ἡ Γ πρὸς τὴν Δ μήκει. Ἡ δὲ Γ πρὸς τὴν Δ μείζονα λόγον ἔχει ἢ τὸ πολύγωνον τὸ ἐν τῷ Α κύκλῳ ἐγγεγραμμένον πρὸς τὴν ἐπιφάνειαν τῆς πυραμίδος τῆς ἐγγεγραμμένης εἰς τὸν κῶνον [ἡ γὰρ ἐκ τοῦ κέντρου τοῦ Α κύκλου πρὸς τὴν πλευρὰν τοῦ κώνου μείζονα λόγον ἔχει ἤπερ ἡ ἀπὸ τοῦ κέντρου ἀγομένη κάθετος ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου πρὸς τὴν ἐπὶ τὴν πλευρὰν τοῦ πολυγώνου κάθετον ἀγομένην ἀπὸ τῆς κορυφῆς τοῦ κώνου]· μείζονα ἄρα λόγον ἔχει τὸ πολύγωνον τὸ ἐν τῷ Α κύκλῳ ἐγγεγραμμένον πρὸς τὸ πολύγωνον τὸ ἐν τῷ Β ἐγγεγραμμένον ἢ αὐτὸ τὸ πολύγωνον πρὸς τὴν ἐπιφάνειαν τῆς πυραμίδος· μείζων ἄρα ἐστὶν ἡ ἐπιφάνεια τῆς πυραμίδος τοῦ ἐν τῷ Β πολυγώνου ἐγγεγραμμένου. Ἐλάσσονα δὲ λόγον ἔχει τὸ πολύγωνον τὸ περὶ τὸν Β κύκλον περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἢ ὁ Β κύκλος πρὸς τὴν ἐπιφάνειαν τοῦ κώνου· πολλῷ ἄρα τὸ πολύγωνον τὸ περὶ τὸν Β κύκλον περιγεγραμμένον πρὸς τὴν ἐπιφάνειαν τῆς πυραμίδος τῆς ἐν τῷ κώνῳ ἐγγεγραμμένης ἐλάσσονα λόγον ἔχει ἢ ὁ Β κύκλος πρὸς τὴν ἐπιφάνειαν τοῦ κώνου· ὅπερ [45] ἀδύνατον [τὸ μὲν γὰρ περιγεγραμμένον πολύγωνον μεῖζόν ἐστιν τοῦ Β κύκλου, ἡ δὲ ἐπιφάνεια τῆς πυραμίδος τῆς ἐν τῷ κώνῳ ἐλάσσων ἐστὶ τῆς ἐπιφανείας τοῦ κώνου]. Οὐκ ἄρα οὐδὲ μείζων ἐστὶν ὁ κύκλος τῆς ἐπιφανείας τοῦ κώνου. Ἐδείχθη δὲ ὅτι οὐδὲ ἐλάσσων· ἴσος ἄρα.

   ιε΄.

   Παντὸς κώνου ἰσοσκελοῦς ἡ ἐπιφάνεια πρὸς τὴν βάσιν τὸν αὐτὸν ἔχει λόγον, ὃν ἡ πλευρὰ τοῦ κώνου πρὸς τὴν ἐκ τοῦ κέντρου τῆς βάσεως τοῦ κώνου.

   Ἔστω κῶνος ἰσοσκελής, οὗ βάσις ὁ Α κύκλος, ἔστω δὲ τῇ μὲν ἐκ τοῦ κέντρου τοῦ Α ἴση ἡ Β, τῇ δὲ πλευρᾷ τοῦ κώνου ἡ Γ· δεικτέον ὅτι τὸν αὐτὸν ἔχει λόγον ἡ ἐπιφάνεια τοῦ κώνου πρὸς τὸν Α κύκλον καὶ ἡ Γ πρὸς τὴν Β.

   Εἰλήφθω γὰρ τῶν Β, Γ μέση ἀνάλογον ἡ Ε, καὶ ἐκκείσθω κύκλος ὁ Δ ἴσην ἔχων τὴν ἐκ τοῦ κέντρου τῇ Ε· ὁ Δ ἄρα κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ κώνου [τοῦτο γὰρ ἐδείχθη ἐν τῷ πρὸ τούτου]. Ἐδείχθη δὲ ὁ Δ κύκλος πρὸς τὸν Α κύκλον λόγον ἔχων τὸν αὐτὸν τῷ τῆς Γ πρὸς Β μήκει [ἑκάτερος γὰρ ὁ αὐτός ἐστι τῷ τῆς Ε πρὸς Β δυνάμει διὰ τὸ τοὺς κύκλους πρὸς ἀλλήλους εἶναι ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα πρὸς ἄλληλα, ὁμοίως δὲ καὶ τὰ ἀπὸ τῶν ἐκ τῶν κέντρων τῶν κύκλων· εἰ γὰρ [46] αἱ διάμετροι, καὶ τὰ ἡμίση, τουτέστιν αἱ ἐκ τῶν κέντρων· ταῖς δὲ ἐκ τῶν κέντρων ἴσαι εἰσὶν αἱ Β, Ε]. Δῆλον οὖν ὅτι ἡ ἐπιφάνεια τοῦ κώνου πρὸς τὸν Α κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν ἡ Γ πρὸς Β μήκει.

   ιϚ΄.

   Ἐὰν κῶνος ἰσοσκελὴς ἐπιπέδῳ τμηθῇ παραλλήλῳ τῇ βάσει, τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων ἐπιφανείᾳ ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου μέσον λόγον ἔχει τῆς τε πλευρᾶς τοῦ κώνου τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων καὶ τῆς ἴσης ἀμφοτέραις ταῖς ἐκ τῶν κέντρων τῶν κύκλων τῶν ἐν τοῖς παραλλήλοις ἐπιπέδοις.

   Ἔστω κῶνος, οὗ τὸ διὰ τοῦ ἄξονος τρίγωνον ἴσον τῷ ΑΒΓ, καὶ τετμήσθω παραλλήλῳ ἐπιπέδῳ τῇ βάσει, καὶ ποιείτω τομὴν ΔΕ, ἄξων δὲ τοῦ κώνου ἔστω ὁ ΒΗ, κύκλος δέ τις ἐκκείσθω, οὗ ἡ ἐκ τοῦ κέντρου μέση ἀνάλογόν ἐστι τῆς τε ΑΔ καὶ συναμφοτέρου τῆς ΔΖ, ΗΑ, ἔστω δὲ κύκλος ὁ Θ· λέγω ὅτι ὁ Θ κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν ΔΕ, ΑΓ.

[47]    Ἐκκείσθωσαν γὰρ κύκλοι οἱ Λ, Κ, καὶ τοῦ μὲν Κ κύκλου ἡ ἐκ τοῦ κέντρου δυνάσθω τὸ ὑπὸ ΒΔΖ, τοῦ δὲ Λ ἡ ἐκ τοῦ κέντρου δυνάσθω τὸ ὑπὸ ΒΑΗ· ὁ μὲν ἄρα Λ κύκλος ἴσος ἐστὶν τῇ ἐπιφανείᾳ τοῦ ΑΒΓ κώνου, ὁ δὲ Κ κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΔΕΒ. Καὶ ἐπεὶ τὸ ὑπὸ τῶν ΒΑ, ΑΗ ἴσον ἐστὶ τῷ τε ὑπὸ τῶν ΒΔ, ΔΖ καὶ τῷ ὑπὸ τῆς ΑΔ καὶ συναμφοτέρου τῆς ΔΖ, ΑΗ διὰ τὸ παράλληλον εἶναι τὴν ΔΖ τῇ ΑΗ, ἀλλὰ τὸ μὲν ὑπὸ ΑΒ, ΑΗ δύναται ἡ ἐκ τοῦ κέντρου τοῦ Λ κύκλου, τὸ δὲ ὑπὸ ΒΔ, ΔΖ δύναται ἡ ἐκ τοῦ κέντρου τοῦ Κ κύκλου, τὸ δὲ ὑπὸ τῆς ΔΑ καὶ συναμφοτέρου τῆς ΔΖ, ΑΗ δύναται ἡ ἐκ τοῦ κέντρου τοῦ Θ, τὸ ἄρα ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Λ κύκλου ἴσον ἐστὶ τοῖς ἀπὸ τῶν ἐκ τῶν κέντρων τῶν Κ, Θ κύκλων· ὥστε καὶ ὁ Λ κύκλος ἴσος ἐστὶ τοῖς Κ, Θ κύκλοις. Ἀλλ᾿ ὁ μὲν Λ ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΒΑΓ κώνου, ὁ δὲ Κ τῇ ἐπιφανείᾳ τοῦ ΔΒΕ κώνου· λοιπὴ ἄρα ἡ ἐπιφάνεια τοῦ κώνου ἡ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν ΔΕ, ΑΓ ἴση ἐστὶ τῷ Θ κύκλῳ.

   [Ἔστω παραλληλόγραμμον τὸ ΒΑΗ, καὶ διάμετρος αὐτοῦ ἔστω ἡ ΒΗ. Τετμήσθω ἡ ΒΑ πλευρά, ὡς ἔτυχεν, κατὰ τὸ Δ, καὶ διὰ τοῦ Δ ἤχθω παράλληλος τῇ ΑΗ ἡ ΔΘ, διὰ δὲ τοῦ Ζ τῇ ΒΑ ἡ ΚΛ· λέγω ὅτι τὸ ὑπὸ ΒΑΗ ἴσον ἐστὶ τῷ τε ὑπὸ ΒΔΖ καὶ τῷ ὑπὸ ΔΑ καὶ συναμφοτέρου τῆς ΔΖ, ΑΗ.

[48]    Ἐπεὶ γὰρ τὸ μὲν ὑπὸ ΒΑΗ ὅλον ἐστὶ τὸ ΒΗ, τὸ δὲ ὑπὸ ΒΔΖ τὸ ΒΖ, τὸ δὲ ὑπὸ ΔΑ καὶ συναμφοτέρου τῆς ΔΖ, ΑΗ ὁ ΜΝΞ γνώμων· τὸ μὲν γὰρ ὑπὸ ΔΑΗ ἴσον ἐστὶν τῷ ΚΗ διὰ τὸ ἴσον εἶναι τὸ ΚΘ παραπλήρωμα τῷ ΔΛ παραπληρώματι, τὸ δὲ ὑπὸ ΔΑ, ΔΖ τῷ ΔΛ· ὅλον ἄρα τὸ ΒΗ, ὅπερ ἐστὶν τὸ ὑπὸ ΒΑΗ, ἴσον ἐστὶ τῷ τε ὑπὸ ΒΔΖ καὶ τῷ ΜΝΞ γνώμονι, ὅς ἐστιν ἴσος τῷ ὑπὸ ΔΑ καὶ συναμφοτέρου τῆς ΑΗ, ΔΖ].

ΛΗΜΜΑΤΑ.

   α΄. Οἱ κῶνοι οἱ ἴσον ὕψος ἔχοντες τὸν αὐτὸν ἔχουσι λόγον ταῖς βάσεσιν· καὶ οἱ ἴσας ἔχοντες βάσεις τὸν αὐτὸν ἔχουσι λόγον τοῖς ὕψεσιν.

   β΄. Ἐὰν κύλινδρος ἐπιπέδῳ τμηθῇ παρὰ τὴν βάσιν, ἔστιν, ὡς ὁ κύλινδρος πρὸς τὸν κύλινδρον, ὁ ἄξων πρὸς τὸν ἄξονα.

   γ΄. Τοῖς δὲ κυλίνδροις ἐν τῷ αὐτῷ λόγῳ εἰσὶν οἱ κῶνοι οἱ ἔχοντες τὰς αὐτὰς βάσεις τοῖς κυλίνδροις.

   δ΄. Καὶ τῶν ἴσων κώνων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· καὶ ὧν ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν, ἴσοι εἰσίν.

   ε΄. Καὶ οἱ κῶνοι, ὧν αἱ διάμετροι τῶν βάσεων τὸν αὐτὸν λόγον ἔχουσιν τοῖς ἄξοσιν [τουτέστιν τοῖς ὕψεσι], πρὸς ἀλλήλους ἐν τριπλασίονι λόγῳ εἰσὶν τῶν ἐν ταῖς βάσεσι διαμέτρων.

   Ταῦτα δὲ πάντα ὑπὸ τῶν πρότερον ἀπεδείχθη.

[49]    ιζ΄.

   Ἐὰν ὦσιν δύο κῶνοι ἰσοσκελεῖς, ἡ δὲ τοῦ ἑτέρου κώνου ἐπιφάνεια ἴση ᾖ τῇ τοῦ ἑτέρου βάσει, ἡ δὲ ἀπὸ τοῦ κέντρου τῆς βάσεως ἐπὶ τὴν πλευρὰν τοῦ κώνου κάθετος ἀγομένη τῷ ὕψει ἴση ᾖ, ἴσοι ἔσονται οἱ κῶνοι.

   Ἔστωσαν δύο κῶνοι ἰσοσκελεῖς οἱ ΑΒΓ, ΔΕΖ, καὶ τοῦ ΑΒΓ ἡ μὲν βάσις ἴση ἔστω τῇ ἐπιφανείᾳ τοῦ ΔΕΖ, τὸ δὲ ὕψος τὸ ΑΗ ἴσον ἔστω τῇ ἀπὸ τοῦ κέντρου τῆς βάσεως τοῦ Θ ἐπὶ μίαν πλευρὰν τοῦ κώνου, οἷον ἐπὶ τὴν ΔΕ, καθέτῳ ἠγμένῃ τῇ ΚΘ· λέγω ὅτι ἴσοι εἰσὶν οἱ κῶνοι.

   Ἐπεὶ γὰρ ἴση ἐστὶν ἡ βάσις τοῦ ΑΒΓ τῇ ἐπιφανείᾳ τοῦ ΔΕΖ [τὰ δὲ ἴσα πρὸς τὸ αὐτὸ τὸν αὐτὸν ἔχει λόγον], ὡς ἄρα ἡ τοῦ ΒΑΓ βάσις πρὸς τὴν τοῦ ΔΕΖ βάσιν, οὕτως ἡ ἐπιφάνεια τοῦ ΔΕΖ πρὸς τὴν βάσιν τοῦ ΔΕΖ. Ἀλλ᾿ ὡς ἡ ἐπιφάνεια πρὸς τὴν ἰδίαν βάσιν, οὕτως ἡ ΔΘ πρὸς τὴν ΘΚ [ἐδείχθη γὰρ τοῦτο, ὅτι παντὸς κώνου ἰσοσκελοῦς ἡ ἐπιφάνεια πρὸς τὴν βάσιν τὸν αὐτὸν λόγον ἔχει, ὃν [50] ἡ πλευρὰ τοῦ κώνου πρὸς τὴν ἐκ τοῦ κέντρου τῆς βάσεως, ἡ ΔΕ τουτέστι πρὸς ΕΘ. Ὡς δὲ ἡ ΕΔ πρὸς ΘΔ, οὕτως ἡ ΕΘ πρὸς ΘΚ· ἰσογώνια γάρ ἐστι τὰ τρίγωνα]. Ἴση δέ ἐστιν ἡ ΘΚ τῇ ΑΗ· ὡς ἄρα ἡ βάσις τοῦ ΒΑΓ πρὸς τὴν βάσιν τοῦ ΔΕΖ, οὕτως τὸ ὕψος τοῦ ΔΕΖ πρὸς τὸ ὕψος τοῦ ΑΒΓ. Τῶν ΑΒΓ, ΔΕΖ ἄρα ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· ἴσος ἄρα ἐστὶν ὁ ΒΑΓ τῷ ΔΕΖ κώνῳ.

   ιη΄.

   Παντὶ ῥόμβῳ ἐξ ἰσοσκελῶν κώνων συγκειμένῳ ἴσος ἐστὶ κῶνος ὁ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ ἑτέρου κώνου τῶν περιεχόντων τὸν ῥόμβον, ὕψος δὲ ἴσον τῇ ἀπὸ τῆς κορυφῆς τοῦ ἑτέρου κώνου καθέτῳ ἀγομένῃ ἐπὶ μίαν πλευρὰν τοῦ ἑτέρου κώνου.

   Ἔστω ῥόμβος ἐξ ἰσοσκελῶν κώνων συγκείμενος ὁ ΑΒΓΔ, οὗ βάσις ὁ περὶ διάμετρον τὴν ΒΓ κύκλος, ὕψος δὲ τὸ ΑΔ, ἐκκείσθω δέ τις ἕτερος ὁ ΗΘΚ τὴν μὲν βάσιν ἔχων τῇ ἐπιφανείᾳ τοῦ ΑΒΓ κώνου ἴσην, τὸ δὲ ὕψος ἴσον τῇ ἀπὸ τοῦ Δ σημείου καθέτῳ ἐπὶ τὴν ΑΒ ἢ τὴν ἐπ᾿ εὐθείας αὐτῇ ἠγμένῃ, ἔστω δὲ ἡ ΔΖ, τὸ δὲ ὕψος τοῦ ΘΗΚ κώνου ἔστω τὸ ΘΛ· ἴσον δή ἐστιν τὸ ΘΛ τῇ ΔΖ· λέγω ὅτι ἴσος ἐστὶν ὁ κῶνος τῷ ῥόμβῳ.

[51]    Ἐκκείσθω γὰρ ἕτερος κῶνος ὁ ΜΝΞ τὴν μὲν βάσιν ἔχων ἴσην τῇ βάσει τοῦ ΑΒΓ κώνου, τὸ δὲ ὕψος ἴσον τῇ ΑΔ, καὶ ἔστω τὸ ὕψος αὐτοῦ τὸ ΝΟ. Ἐπεὶ οὖν ἡ ΝΟ τῇ ΑΔ ἴση ἐστίν, ἔστιν ἄρα, ὡς ἡ ΝΟ πρὸς ΔΕ, οὕτως ἡ ΑΔ πρὸς ΔΕ. Ἀλλ᾿ ὡς μὲν ἡ ΑΔ πρὸς ΔΕ, οὕτως ὁ ΑΒΓΔ ῥόμβος πρὸς τὸν ΒΓΔ κῶνον, ὡς δὲ ἡ ΝΟ πρὸς τὴν ΔΕ, οὕτως ὁ ΜΝΞ κῶνος πρὸς τὸν ΒΓΔ κῶνον [διὰ τὸ τὰς βάσεις αὐτῶν εἶναι ἴσας]· ὡς ἄρα ὁ ΜΝΞ κῶνος πρὸς τὸν ΒΓΔ κῶνον, οὕτως ὁ ΑΒΓΔ ῥόμβος πρὸς τὸν ΒΓΔ κῶνον· ἴσος ἄρα ἐστὶν ὁ ΜΝΞ τῷ ΑΒΓΔ ῥόμβῳ. Καὶ ἐπεὶ ἡ ἐπιφάνεια τοῦ ΑΒΓ ἴση ἐστὶ τῇ βάσει τοῦ ΗΘΚ, ὡς ἄρα ἡ ἐπιφάνεια τοῦ ΑΒΓ πρὸς τὴν ἰδίαν βάσιν, οὕτως ἡ βάσις τοῦ ΗΘΚ πρὸς τὴν βάσιν τοῦ ΜΝΞ [ἡ γὰρ βάσις τοῦ ΑΒΓ ἴση ἐστὶ τῇ βάσει τοῦ ΜΝΞ]. Ὡς δὲ ἡ ἐπιφάνεια τοῦ ΑΒΓ πρὸς τὴν ἰδίαν βάσιν, οὕτως ἡ ΑΒ πρὸς τὴν ΒΕ, τουτέστιν ἡ ΑΔ πρὸς ΔΖ [ὅμοια γὰρ τὰ τρίγωνα]· ὡς ἄρα ἡ βάσις τοῦ ΗΘΚ πρὸς τὴν βάσιν τοῦ ΜΝΞ, οὕτως ἡ ΑΔ πρὸς ΔΖ. Ἴση δὲ ἡ μὲν ΑΔ τῇ ΝΟ [ὑπέκειτο γάρ], ἡ δὲ ΔΖ [52] τῇ ΘΛ· ὡς ἄρα ἡ βάσις τοῦ ΗΘΚ πρὸς τὴν βάσιν τοῦ ΜΝΞ, οὕτως τὸ ΝΟ ὕψος πρὸς τὸ ΘΛ. Τῶν ΗΘΚ, ΜΝΞ ἄρα κώνων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν· ἴσοι ἄρα εἰσὶν οἱ κῶνοι. Ἐδείχθη δὲ ὁ ΜΝΞ ἴσος τῷ ΑΒΓΔ ῥόμβῳ· καὶ ὁ ΗΘΚ ἄρα κῶνος ἴσος ἐστὶ τῷ ΑΒΓΔ ῥόμβῳ.

   ιθ΄.

   Ἐὰν κῶνος ἰσοσκελὴς ἐπιπέδῳ τμηθῇ παραλλήλῳ τῇ βάσει, ἀπὸ δὲ τοῦ γενομένου κύκλου κῶνος ἀναγραφῇ κορυφὴν ἔχων τὸ κέντρον τῆς βάσεως, ὁ δὲ γενόμενος ῥόμβος ἀφαιρεθῇ ἀπὸ τοῦ ὅλου κώνου, τῷ περιλείμματι ἴσος ἔσται κῶνος ὁ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ κέντρου τῆς βάσεως ἐπὶ μίαν πλευρὰν τοῦ κώνου καθέτῳ ἠγμένῃ.

[53]    Ἔστω κῶνος ἰσοσκελὴς ὁ ΑΒΓ καὶ τετμήσθω ἐπιπέδῳ παραλλήλῳ τῇ βάσει, καὶ ποιείτω τομὴν τὴν ΔΕ, κέντρον δὲ τῆς βάσεως ἔστω τὸ Ζ, καὶ ἀπὸ τοῦ περὶ διάμετρον τὴν ΔΕ κύκλου κῶνος ἀναγεγράφθω κορυφὴν ἔχων τὸ Ζ· ἔσται δὴ ῥόμβος ὁ ΒΔΖΕ ἐξ ἰσοσκελῶν κώνων συγκείμενος. Ἐκκείσθω δή τις κῶνος ὁ ΚΘΛ, οὗ ἡ μὲν βάσις ἔστω ἴση τῇ ἐπιφανείᾳ τῇ μεταξὺ τῶν ΔΕ, ΑΓ, τὸ δὲ ὕψος, ἀχθείσης ἀπὸ τοῦ Ζ σημείου καθέτου ἐπὶ τὴν ΑΒ τῆς ΖΗ, ἔστω ἴσον τῇ ΖΗ· λέγω ὅτι, ἐὰν ἀπὸ τοῦ ΑΒΓ κώνου νοηθῇ ἀφῃρημένος ὁ ΒΔΖΕ ῥόμβος, τῷ περιλείμματι ἴσος ἔσται ὁ ΘΚΛ κῶνος.

   Ἐκκείσθωσαν γὰρ δύο κῶνοι οἱ ΜΝΞ, ΟΠΡ, ὥστε τὴν μὲν τοῦ ΜΝΞ βάσιν ἴσην εἶναι τοῦ ΑΒΓ κώνου τῇ ἐπιφανείᾳ, τὸ δὲ ὕψος ἴσον τῇ ΖΗ [διὰ δὴ τοῦτο ἴσος ἐστὶν ὁ ΜΝΞ κῶνος τῷ ΑΒΓ κώνῳ· ἐὰν γὰρ ὦσι δύο κῶνοι ἰσοσκελεῖς, ἡ δὲ τοῦ ἑτέρου κώνου ἐπιφάνεια ἴση ᾖ τῇ τοῦ ἑτέρου βάσει, ἔτι δὲ ἡ ἀπὸ τοῦ κέντρου τῆς βάσεως ἐπὶ τὴν πλευρὰν τοῦ κώνου ἀγομένη κάθετος τῷ ὕψει ἴση, ἴσοι ἔσονται οἱ κῶνοι], τὴν δὲ τοῦ ΟΠΡ κώνου βάσιν ἴσην εἶναι τῇ ἐπιφανείᾳ τοῦ ΔΒΕ κώνου, ὕψος δὲ τῇ ΖΗ [διὰ δὴ τοῦτο καὶ ἴσος ἐστὶν ὁ ΟΠΡ κῶνος τῷ ΒΔΖΕ ῥόμβῳ· τοῦτο γὰρ προαπεδείχθη]. Ἐπεὶ δὲ ἡ τοῦ ΑΒΓ κώνου ἐπιφάνεια σύγκειται ἔκ τε τῆς τοῦ ΔΒΕ ἐπιφανείας καὶ τῆς μεταξὺ τῶν ΔΕ, ΑΓ, ἀλλ᾿ ἡ μὲν τοῦ ΑΒΓ κώνου ἐπιφάνεια ἴση ἐστὶ τῇ βάσει τοῦ ΜΝΞ κώνου, ἡ δὲ τοῦ ΔΒΕ ἐπιφάνεια ἴση ἐστὶν τῇ βάσει τοῦ ΟΠΡ, ἡ δὲ μεταξὺ τῶν ΔΕ, ΑΓ ἴση ἐστὶ τῇ βάσει τοῦ ΘΚΛ, ἡ ἄρα τοῦ ΜΝΞ βάσις ἴση ἐστὶ ταῖς βάσεσιν τῶν ΘΚΛ, ΟΠΡ. Καί εἰσιν οἱ κῶνοι ὑπὸ τὸ αὐτὸ ὕψος· ἴσος ἄρα ἐστὶν καὶ ὁ ΜΝΞ κῶνος τοῖς ΘΚΛ, ΟΠΡ κώνοις. Ἀλλ᾿ ὁ μὲν ΜΝΞ κῶνος ἴσος ἐστὶ [54] τῷ ΑΒΓ κώνῳ, ὁ δὲ ΠΟΡ τῷ ΒΔΕΖ ῥόμβῳ· λοιπὸς ἄρα ὁ ΘΚΛ κῶνος τῷ περιλείμματι ἴσος ἐστίν.

   κ΄.

   Ἐὰν ῥόμβου ἐξ ἰσοσκελῶν κώνων συγκειμένου ὁ ἕτερος κῶνος ἐπιπέδῳ τμηθῇ παραλλήλῳ τῇ βάσει, ἀπὸ δὲ τοῦ γενομένου κύκλου κῶνος ἀναγραφῇ κορυφὴν ἔχων τὴν αὐτὴν τῷ ἑτέρῳ κώνῳ, ἀπὸ δὲ τοῦ ὅλου ῥόμβου ὁ γενόμενος ῥόμβος ἀφαιρεθῇ, τῷ περιλείμματι ἴσος ἔσται ὁ κῶνος ὁ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων, ὕψος δὲ ἴσον τῇ ἀπὸ τῆς κορυφῆς τοῦ ἑτέρου κώνου ἐπὶ τὴν πλευρὰν τοῦ ἑτέρου κώνου καθέτῳ ἠγμένῃ.

   Ἔστω ῥόμβος ἐξ ἰσοσκελῶν κώνων συγκείμενος ὁ ΑΒΓΔ, καὶ τμηθήτω ὁ ἕτερος κῶνος ἐπιπέδῳ παραλλήλῳ τῇ βάσει, καὶ ποιείτω τομὴν τὴν ΕΖ, ἀπὸ δὲ τοῦ περὶ διάμετρον τὴν ΕΖ κύκλου κῶνος ἀναγεγράφθω τὴν κορυφὴν ἔχων τὸ Δ σημεῖον· ἔσται δὴ γεγονὼς ῥόμβος ὁ ΕΒΔΖ. Καὶ νοείσθω ἀφῃρημένος ἀπὸ τοῦ ὅλου ῥόμβου, ἐκκείσθω δέ τις κῶνος ὁ ΘΚΛ τὴν μὲν βάσιν ἴσην ἔχων τῇ ἐπιφανείᾳ τῇ μεταξὺ τῶν ΑΓ, ΕΖ, τὸ δὲ ὕψος ἴσον τῇ ἀπὸ τοῦ Δ σημείου καθέτῳ ἀγομένῃ ἐπὶ τὴν ΒΑ ἢ τὴν ἐπ᾿ εὐθείας αὐτῇ· λέγω ὅτι ὁ ΘΚΛ κῶνος ἴσος ἐστὶ τῷ εἰρημένῳ περιλείμματι.

[55]    Ἐκκείσθωσαν γὰρ δύο κῶνοι οἱ ΜΝΞ, ΟΠΡ, καὶ ἡ μὲν βάσις τοῦ ΜΝΞ κώνου ἴση ἔστω τῇ ἐπιφανείᾳ τοῦ ΑΒΓ, τὸ δὲ ὕψος ἴσον τῇ ΔΗ [διὰ δὴ τὰ προδειχθέντα ἴσος ἐστὶν ὁ ΜΝΞ κῶνος τῷ ΑΒΓΔ ῥόμβῳ], τοῦ δὲ ΟΠΡ κώνου ἡ μὲν βάσις ἴση ἔστω τῇ ἐπιφανείᾳ τοῦ ΕΒΖ κώνου, τὸ δὲ ὕψος ἴσον τῇ ΔΗ [ὁμοίως δὴ ἴσος ἐστὶν ὁ ΟΠΡ κῶνος τῷ ΕΒΔΖ ῥόμβῳ]. Ἐπεὶ δὲ ὁμοίως ἡ ἐπιφάνεια τοῦ ΑΒΓ κώνου σύγκειται ἔκ τε τῆς τοῦ ΕΒΖ καὶ τῆς μεταξὺ τῶν ΕΖ, ΑΓ, ἀλλὰ ἡ μὲν τοῦ ΑΒΓ κώνου ἐπιφάνεια ἴση ἐστὶ τῇ βάσει τοῦ ΜΝΞ, ἡ δὲ τοῦ ΕΒΖ κώνου ἐπιφάνεια ἴση ἐστὶ τῇ βάσει τοῦ ΟΡΠ κώνου, ἡ δὲ μεταξὺ τῶν ΕΖ, ΑΓ ἴση ἐστὶ τῇ βάσει τοῦ ΘΚΛ, ἡ ἄρα βάσις τοῦ ΜΝΞ ἴση ἐστὶ ταῖς βάσεσιν τῶν ΟΠΡ, ΘΚΛ. Καί εἰσιν οἱ κῶνοι ὑπὸ τὸ αὐτὸ ὕψος· καὶ ὁ ΜΝΞ ἄρα κῶνος ἴσος ἐστὶ τοῖς ΘΚΛ, ΟΠΡ κώνοις. Ἀλλ᾿ ὁ μὲν ΜΝΞ κῶνος ἴσος ἐστὶ τῷ ΑΒΓΔ ῥόμβῳ, ὁ δὲ ΟΠΡ κῶνος τῷ ΕΒΔΖ ῥόμβῳ· λοιπὸς ἄρα ὁ κῶνος ὁ ΘΚΛ ἴσος ἐστὶ τῷ περιλείμματι τῷ λοιπῷ.

[56]    κα΄.

   Ἐὰν εἰς κύκλον πολύγωνον ἐγγραφῇ ἀρτιόπλευρόν τε καὶ ἰσόπλευρον, καὶ διαχθῶσιν εὐθεῖαι ἐπιζευγνύουσα τὰς πλευρὰς τοῦ πολυγώνου, ὥστε αὐτὰς παραλλήλους εἶναι μιᾷ ὁποιᾳοῦν τῶν ὑπὸ δύο πλευρὰς τοῦ πολυγώνου ὑποτεινουσῶν, αἱ ἐπιζευγνύουσαι πᾶσαι πρὸς τὴν τοῦ κύκλου διάμετρον τοῦτον ἔχουσι τὸν λόγον, ὃν ἔχει ἡ ὑποτείνουσα τὰς μιᾷ ἐλάσσονας τῶν ἡμίσεων πρὸς τὴν πλευρὰν τοῦ πολυγώνου.

   Ἔστω κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ πολύγωνον ἐγγεγράφθω τὸ ΑΕΖΒΗΘΓΜΝΔΛΚ, καὶ ἐπεζεύχθωσαν αἱ ΕΚ ΖΛ, ΒΔ, ΗΝ, ΘΜ· δῆλον δὴ ὅτι παράλληλοί εἰσιν τῇ ὑπὸ δύο πλευρὰς τοῦ πολυγώνου ὑποτεινούσῃ· λέγω οὖν ὅτι αἱ εἰρημέναι πᾶσαι πρὸς τὴν τοῦ κύκλου διάμετρον τὴν ΑΓ τὸν αὐτὸν λόγον ἔχουσι τῷ τῆς ΓΕ πρὸς ΕΑ.

   Ἐπεζεύχθωσαν γὰρ αἱ ΖΚ, ΛΒ, ΗΔ, ΘΝ· παράλληλος ἄρα ἡ μὲν ΖΚ τῇ ΕΑ, ἡ δὲ ΒΛ τῇ ΖΚ, καὶ ἔτι ἡ μὲν ΔΗ τῇ ΒΛ, ἡ δὲ ΘΝ τῇ ΔΗ, καὶ ἡ ΓΜ τῇ ΘΝ [καὶ ἐπεὶ δύο παράλληλοί εἰσιν αἱ ΕΑ, ΚΖ, καὶ δύο διηγμέναι εἰσὶν αἱ ΕΚ, [57] ΑΟ], ἔστιν ἄρα, ὡς ἡ ΕΞ πρὸς ΞΑ, ἡ ΚΞ πρὸς ΞΟ. Ὡς δ᾿ ἡ ΚΞ πρὸς ΞΟ, ἡ ΖΠ πρὸς ΠΟ, ὡς δὲ ἡ ΖΠ πρὸς ΠΟ, ἡ ΛΠ πρὸς ΠΡ, ὡς δὲ ἡ ΛΠ πρὸς ΠΡ, οὕτως ἡ ΒΣ πρὸς ΣΡ, καὶ ἔτι ὡς ἡ μὲν ΒΣ πρὸς ΣΡ, ἡ ΔΣ πρὸς ΣΤ, ὡς δὲ ἡ ΔΣ πρὸς ΣΤ, ἡ ΗΥ πρὸς ΥΤ, καὶ ἔτι ὡς ἡ μὲν ΗΥ πρὸς ΥΤ, ἡ ΝΥ πρὸς ΥΦ, ὡς δὲ ἡ ΝΥ πρὸς ΥΦ, ἡ ΘΧ πρὸς ΧΦ, καὶ ἔτι ὡς μὲν ἡ ΘΧ πρὸς ΧΦ, ἡ ΜΧ πρὸς ΧΓ [καὶ πάντα ἄρα πρὸς πάντα ἐστὶν ὡς εἷς τῶν λόγων πρὸς ἕνα]· ὡς ἄρα ἡ ΕΞ πρὸς ΞΑ, οὕτως αἱ ΕΚ, ΖΛ, ΒΔ, ΗΝ, ΘΜ πρὸς τὴν ΑΓ διάμετρον. Ὡς δὲ ἡ ΕΞ πρὸς ΞΑ, οὕτως ἡ ΓΕ πρὸς ΕΑ· ἔσται ἄρα καὶ ὡς ἡ ΓΕ πρὸς ΕΑ, οὕτω πᾶσαι αἱ ΕΚ, ΖΛ, ΒΔ, ΗΝ, ΘΜ πρὸς τὴν ΑΓ διάμετρον.

   κβ΄.

   Ἐὰν εἰς τμῆμα κύκλου πολύγωνον ἐγγραφῇ τὰς πλευρὰς ἔχον χωρὶς τῆς βάσεως ἴσας καὶ ἀρτίους, ἀχθῶσιν δὲ εὐθεῖαι παρὰ τὴν βάσιν τοῦ τμήματος αἱ τὰς πλευρὰς ἐπιζευγνύουσαι τοῦ πολυγώνου, αἱ ἀχθεῖσαι πᾶσαι καὶ ἡ ἡμίσεια τῆς βάσεως πρὸς τὸ ὕψος τοῦ τμήματος τὸν αὐτὸν λόγον ἔχουσιν, ὃν ἡ ἀπὸ τῆς διαμέτρου τοῦ κύκλου ἐπὶ τὴν πλευρὰν τοῦ πολυγώνου ἐπιζευγνυμένη πρὸς τὴν τοῦ πολυγώνου πλευράν.

   Εἰς γὰρ κύκλον τὸν ΑΒΓΔ διήχθω τις εὐθεῖα ἡ ΑΓ, καὶ ἐπὶ τῆς ΑΓ πολύγωνον ἐγγεγράφθω εἰς τὸ ΑΒΓ τμῆμα ἀρτιόπλευρόν τε καὶ ἴσας ἔχον τὰς πλευρὰς χωρὶς τῆς βάσεως τῆς ΑΓ, καὶ ἐπεζεύχθωσαν αἱ ΖΗ, ΕΘ, αἵ εἰσιν παράλληλοι τῇ βάσει τοῦ τμήματος· λέγω ὅτι ἐστὶν ὡς αἱ ΖΗ, ΕΘ, ΑΞ πρὸς ΒΞ, οὕτως ἡ ΔΖ πρὸς ΖΒ.

[58]    Πάλιν γὰρ ὁμοίως ἐπεζεύχθωσαν αἱ ΗΕ, ΑΘ· παράλληλοι ἄρα εἰσὶν τῇ ΒΖ· διὰ δὴ ταὐτά ἐστιν, ὡς ἡ ΚΖ πρὸς ΚΒ, ἥ τε ΗΚ πρὸς ΚΛ καὶ ἡ ΕΜ πρὸς ΜΛ καὶ ἡ ΜΘ πρὸς ΜΝ καὶ ἡ ΞΑ πρὸς ΞΝ [καὶ ὡς ἄρα πάντα πρὸς πάντα, εἷς τῶν λόγων πρὸς ἕνα]· ὡς ἄρα αἱ ΖΗ, ΕΘ, ΑΞ πρὸς ΒΞ, οὕτως ἡ ΖΚ πρὸς ΚΒ. Ὡς δὲ ἡ ΖΚ πρὸς ΚΒ, οὕτως ἡ ΔΖ πρὸς ΖΒ· ὡς ἄρα ἡ ΔΖ πρὸς ΖΒ, οὕτως αἱ ΖΗ, ΕΘ, ΑΞ πρὸς ΞΒ.

   κγ΄.

   Ἔστω ἐν σφαίρᾳ μέγιστος κύκλος ὁ ΑΒΓΔ, καὶ ἐγγεγράφθω εἰς αὐτὸν πολύγωνον ἰσόπλευρον, τὸ δὲ πλῆθος τῶν πλευρῶν αὐτοῦ μετρείσθω ὑπὸ τετράδος, αἱ δὲ ΑΓ, ΔΒ διάμετροι ἔστωσαν. Ἐὰν δὴ μενούσης τῆς ΑΓ διαμέτρου περιενεχθῇ ὁ ΑΒΓΔ κύκλος ἔχων τὸ πολύγωνον, δῆλον ὅτι ἡ μὲν περιφέρεια αὐτοῦ κατὰ τῆς ἐπιφανείας τῆς σφαίρας ἐνεχθήσεται, αἱ δὲ τοῦ πολυγώνου γωνίαι χωρὶς τῶν πρὸς τοῖς Α, Γ σημείοις κατὰ κύκλων περιφερειῶν ἐνεχθήσονται ἐν τῇ ἐπιφανείᾳ τῆς σφαίρας γεγραμμένων ὀρθῶν [59] πρὸς τὸν ΑΒΓΔ κύκλον· διάμετροι δὲ αὐτῶν ἔσονται αἱ ἐπιζευγνύουσαι τὰς γωνίας τοῦ πολυγώνου παρὰ τὴν ΒΔ οὖσαι. Αἱ δὲ τοῦ πολυγώνου πλευραὶ κατά τινων κώνων ἐνεχθήσονται, αἱ μὲν ΑΖ, ΑΝ κατ᾿ ἐπιφανείας κώνου, οὗ βάσις μὲν ὁ κύκλος ὁ περὶ διάμετρον τὴν ΖΝ, κορυφὴ δὲ τὸ Α σημεῖον, αἱ δὲ ΖΗ, ΜΝ κατά τινος κωνικῆς ἐπιφανείας οἰσθήσονται, ἧς βάσις μὲν ὁ κύκλος ὁ περὶ διάμετρον τὴν ΜΗ, κορυφὴ δὲ τὸ σημεῖον, καθ᾿ ὃ συμβάλλουσιν ἐκβαλλόμεναι αἱ ΖΗ, ΜΝ ἀλλήλαις τε καὶ τῇ ΑΓ, αἱ δὲ ΒΗ, ΜΔ πλευραὶ κατὰ κωνικῆς ἐπιφανείας οἰσθήσονται, ἧς βάσις μέν ἐστιν ὁ κύκλος ὁ περὶ διάμετρον τὴν ΒΔ ὀρθὸς πρὸς τὸν ΑΒΓΔ κύκλον, κορυφὴ δὲ τὸ σημεῖον, καθ᾿ ὃ συμβάλλουσιν ἐκβαλλόμεναι αἱ ΒΗ, ΔΜ ἀλλήλαις τε καὶ τῇ ΓΑ· ὁμοίως δὲ καὶ αἱ ἐν τῷ ἑτέρῳ ἡμικυκλίῳ πλευραὶ κατὰ κωνικῶν ἐπιφανειῶν οἰσθήσονται πάλιν ὁμοίων ταύταις. Ἔσται δή τι σχῆμα ἐγγεγραμμένον ἐν τῇ σφαίρᾳ ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενον τῶν προειρημένων, οὗ ἡ ἐπιφάνεια ἐλάσσων ἔσται τῆς ἐπιφανείας τῆς σφαίρας.

[60]    Διαιρεθείσης γὰρ τῆς σφαίρας ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὴν ΒΔ ὀρθοῦ πρὸς τὸν ΑΒΓΔ κύκλον ἡ ἐπιφάνεια τοῦ ἑτέρου ἡμισφαιρίου καὶ ἡ ἐπιφάνεια τοῦ σχήματος τοῦ ἐν αὐτῷ ἐγγεγραμμένου τὰ αὐτὰ πέρατα ἔχουσιν ἐν ἑνὶ ἐπιπέδῳ· ἀμφοτέρων γὰρ τῶν ἐπιφανειῶν πέρας ἐστὶν τοῦ κύκλου ἡ ἐπιφάνεια τοῦ περὶ διάμετρον τὴν ΒΔ ὀρθοῦ πρὸς τὸν ΑΒΓΔ κύκλον· καί εἰσιν ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαι, καὶ περιλαμβάνεται αὐτῶν ἡ ἑτέρα ὑπὸ τῆς ἑτέρας ἐπιφανείας καὶ τῆς ἐπιπέδου τῆς τὰ αὐτὰ πέρατα ἐχούσης αὐτῇ. Ὁμοίως δὲ καὶ τοῦ ἐν τῷ ἑτέρῳ ἡμισφαιρίῳ σχήματος ἡ ἐπιφάνεια ἐλάσσων ἐστὶν τῆς τοῦ ἡμισφαιρίου ἐπιφανείας· καὶ ὅλη οὖν ἡ ἐπιφάνεια τοῦ σχήματος τοῦ ἐν τῇ σφαίρᾳ ἐλάσσων ἐστὶν τῆς ἐπιφανείας τῆς σφαίρας.

   κδ΄.    Ἡ τοῦ ἐγγραφομένου σχήματος εἰς τὴν σφαῖραν ἐπιφάνεια ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ περιεχόμενον ὑπό τε τῆς πλευρᾶς τοῦ σχήματος καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς πλευρὰς τοῦ πολυγώνου παραλλήλοις οὔσαις τῇ ὑπὸ δύο πλευρὰς τοῦ πολυγώνου ὑποτεινούσῃ εὐθείᾳ.

   Ἔστω ἐν σφαίρᾳ μέγιστος κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ πολύγωνον ἐγγεγράφθω ἰσόπλευρον, οὗ αἱ πλευραὶ ὑπὸ τετράδος μετροῦνται, καὶ ἀπὸ τοῦ πολυγώνου τοῦ ἐγγεγραμμένου νοείσθω τι εἰς τὴν σφαῖραν ἐγγραφὲν σχῆμα, καὶ ἐπεζεύχθωσαν αἱ ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ παράλληλοι οὖσαι τῇ ὑπὸ δύο πλευρὰς ὑποτεινούσῃ εὐθείᾳ, κύκλος δέ τις ἐκκείσθω ὁ Ξ, οὗ ἡ ἐκ τοῦ κέντρου δυνάσθω [61] τὸ περιεχόμενον ὑπό τε τῆς ΑΕ καὶ τῆς ἴσης ταῖς ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ· λέγω ὅτι ὁ κύκλος οὗτος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ εἰς τὴν σφαῖραν ἐγγραφομένου σχήματος.

   Ἐκκείσθωσαν γὰρ κύκλοι οἱ Ο, Π, Ρ, Σ, Τ, Υ, καὶ τοῦ μὲν Ο ἡ ἐκ τοῦ κέντρου δυνάσθω τὸ περιεχόμενον ὑπό τε τῆς ΕΑ καὶ τῆς ἡμισείας τῆς ΕΖ, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Π δυνάσθω τὸ περιεχόμενον ὑπό τε τῆς ΕΑ καὶ τῆς ἡμισείας τῶν ΕΖ, ΗΘ, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Ρ δυνάσθω τὸ περιεχόμενον ὑπὸ τῆς ΕΑ καὶ τῆς ἡμισείας τῶν ΗΘ, ΓΔ, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Σ δυνάσθω τὸ περιεχόμενον ὑπό τε τῆς ΕΑ καὶ τῆς ἡμισείας τῶν ΓΔ, ΚΛ, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Τ δυνάσθω τὸ περιεχόμενον ὑπό τε τῆς ΑΕ καὶ τῆς ἡμισείας τῶν ΚΛ, ΜΝ, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Υ δυνάσθω τὸ περιεχόμενον ὑπό τε τῆς ΑΕ καὶ τῆς ἡμισείας τῆς ΜΝ. Διὰ δὴ ταῦτα ὁ μὲν Ο κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΑΕΖ κώνου, ὁ δὲ Π τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν ΕΖ, ΗΘ, ὁ δὲ Ρ τῇ μεταξὺ τῶν ΗΘ, ΓΔ, ὁ δὲ Σ τῇ μεταξὺ τῶν ΔΓ, ΚΛ, καὶ ἔτι ὁ μὲν Τ ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν ΚΛ, ΜΝ, ὁ δὲ Υ τῇ τοῦ ΜΒΝ κώνου ἐπιφανείᾳ ἴσος ἐστίν· οἱ πάντες ἄρα κύκλοι ἴσοι εἰσὶν τῇ τοῦ ἐγγεγραμμένου σχήματος ἐπιφανείᾳ. Καὶ φανερὸν ὅτι αἱ ἐκ τῶν κέντρων τῶν Ο, Π, Ρ, Σ, Τ [62] κύκλων δύνανται τὸ περιεχόμενον ὑπό τε τῆς ΑΕ καὶ δὶς τῶν ἡμίσεων τῆς ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ, αἳ ὅλαι εἰσὶν αἱ ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ· αἱ ἄρα ἐκ τῶν κέντρων τῶν Ο, Π, Ρ, Σ, Τ, Υ κύκλων δύνανται τὸ περιεχόμενον ὑπό τε τῆς ΑΕ καὶ πασῶν τῶν ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ. Ἀλλὰ καὶ ἡ ἐκ τοῦ κέντρου τοῦ Ξ κύκλου δύναται τὸ ὑπὸ τῆς ΑΕ καὶ τῆς συγκειμένης ἐκ πασῶν τῶν ΕΖ, ΗΘ, ΓΔ, ΚΛ, ΜΝ· ἡ ἄρα ἐκ τοῦ κέντρου τοῦ Ξ κύκλου δύναται τὰ ἀπὸ τῶν ἐκ τῶν κέντρων τῶν Ο, Π, Ρ, Σ, Τ, Υ κύκλων· καὶ ὁ κύκλος ἄρα ὁ Ξ ἴσος ἐστὶ τοῖς Ο, Π, Ρ, Σ, Τ, Υ κύκλοις. Οἱ δὲ Ο, Π, Ρ, Σ, Τ, Υ κύκλοι ἀπεδείχθησαν ἴσοι τῇ εἰρημένῃ τοῦ σχήματος ἐπιφανείᾳ· καὶ ὁ Ξ ἄρα κύκλος ἴσος ἔσται τῇ ἐπιφανείᾳ τοῦ σχήματος.

   κε΄.

   Τοῦ ἐγγεγραμμένου σχήματος εἰς τὴν σφαῖραν ἡ ἐπιφάνεια ἡ περιεχομένη ὑπὸ τῶν κωνικῶν ἐπιφανειῶν ἐλάσσων ἐστὶν ἢ τετραπλασία τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ.

   Ἔστω ἐν σφαίρᾳ μέγιστος κύκλος ὁ ΑΒΓΔ, καὶ ἐν αὐτῷ ἐγγεγράφθω πολύγωνον [ἀρτιόγωνον] ἰσόπλευρον, οὗ αἱ πλευραὶ ὑπὸ τετράδος μετροῦνται, καὶ ἀπ᾿ αὐτοῦ νοείσθω ἐπιφάνεια ἡ ὑπὸ τῶν κωνικῶν ἐπιφανειῶν περιεχομένη· λέγω ὅτι ἡ ἐπιφάνεια τοῦ ἐγγραφέντος ἐλάσσων ἐστὶν ἢ τετραπλασία τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ.

[63]    Ἐπεζεύχθωσαν γὰρ αἱ ὑπὸ δύο πλευρὰς ὑποτείνουσαι τοῦ πολυγώνου αἱ ΕΙ, ΘΜ καὶ ταύταις παράλληλοι αἱ ΖΚ, ΔΒ, ΗΛ, ἐκκείσθω δέ τις κύκλος ὁ Ρ, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ τῆς ΕΑ καὶ τῆς ἴσης πάσαις ταῖς ΕΙ, ΖΚ, ΒΔ, ΗΛ, ΘΜ· διὰ δὴ τὸ προδειχθὲν ἴσος ἐστὶν ὁ κύκλος τῇ τοῦ εἰρημένου σχήματος ἐπιφανείᾳ. Καὶ ἐπεὶ ἐδείχθη ὅτι ἐστίν, ὡς ἡ ἴση πάσαις ταῖς ΕΙ, ΖΚ, ΒΔ, ΗΛ, ΘΜ πρὸς τὴν διάμετρον τοῦ κύκλου τὴν ΑΓ, οὕτως ἡ ΓΕ πρὸς ΕΑ, τὸ ἄρα ὑπὸ τῆς ἴσης πάσαις ταῖς εἰρημέναις καὶ τῆς ΕΑ, τουτέστιν τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Ρ κύκλου, ἴσον ἐστὶν τῷ ὑπὸ τῶν ΑΓ, ΓΕ. Ἀλλὰ καὶ τὸ ὑπὸ ΑΓ, ΓΕ ἔλασσόν ἐστι τοῦ ἀπὸ τῆς ΑΓ· ἔλασσον ἄρα ἐστὶν τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Ρ τοῦ ἀπὸ τῆς ΑΓ [ἐλάσσων ἄρα ἐστὶν ἡ ἐκ τοῦ κέντρου τοῦ Ρ τῆς ΑΓ· ὥστε ἡ διάμετρος τοῦ Ρ κύκλου ἐλάσσων ἐστὶν ἢ διπλασία τῆς διαμέτρου τοῦ ΑΒΓΔ κύκλου, καὶ δύο ἄρα τοῦ ΑΒΓΔ κύκλου διάμετροι μείζους εἰσὶ τῆς διαμέτρου τοῦ Ρ κύκλου, καὶ τὸ τετράκις ἀπὸ τῆς διαμέτρου τοῦ ΑΒΓΔ κύκλου, τουτέστι τῆς ΑΓ, μεῖζόν ἐστι τοῦ ἀπὸ τῆς τοῦ Ρ κύκλου διαμέτρου. Ὡς δὲ τὸ τετράκις ἀπὸ τῆς ΑΓ πρὸς τὸ ἀπὸ τῆς τοῦ Ρ κύκλου διαμέτρου, οὕτως [64] τέσσαρες κύκλοι οἱ ΑΒΓΔ πρὸς τὸν Ρ κύκλον· τέσσαρες ἄρα κύκλοι οἱ ΑΒΓΔ μείζους εἰσὶν τοῦ Ρ κύκλου]· ὁ ἄρα κύκλος ὁ Ρ ἐλάσσων ἐστὶν ἢ τετραπλάσιος τοῦ μεγίστου κύκλου. Ὁ δὲ Ρ κύκλος ἴσος ἐδείχθη τῇ εἰρημένῃ ἐπιφανείᾳ τοῦ σχήματος· ἡ ἄρα ἐπιφάνεια τοῦ σχήματος ἐλάσσων ἐστὶν ἢ τετραπλασία τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ.

   κϚ΄.

   Τῷ ἐγγραφομένῳ ἐν τῇ σφαίρᾳ σχήματι τῷ περιεχομένῳ ὑπὸ τῶν ἐπιφανειῶν τῶν κωνικῶν ἴσος ἐστὶν κῶνος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν ἴσον τῇ ἐπιφανείᾳ τοῦ σχήματος τοῦ ἐγγραφέντος ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ.

[65]    Ἔστω ἡ σφαῖρα καὶ ὁ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΓΔ καὶ τὰ ἄλλα τὰ αὐτὰ τῷ πρότερον, ἔστω δὲ κῶνος ὀρθὸς ὁ Ρ βάσιν μὲν ἔχων τὴν ἐπιφάνειαν τοῦ σχήματος τοῦ ἐγγεγραμμένου ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ· δεικτέον ὅτι ὁ κῶνος ὁ Ρ ἴσος ἐστὶν τῷ ἐγγεγραμμένῳ ἐν τῇ σφαίρᾳ σχήματι.

   Ἀπὸ γὰρ τῶν κύκλων, ὧν εἰσι διάμετροι αἱ ΖΝ, ΗΜ, ΘΛ, ΙΚ, κῶνοι ἀναγεγράφθωσαν κορυφὴν ἔχοντες τὸ τῆς σφαίρας κέντρον· ἔσται δὴ ῥόμβος στερεὸς ἔκ τε τοῦ κώνου, οὗ βάσις μέν ἐστιν ὁ κύκλος ὁ περὶ τὴν ΖΝ, κορυφὴ δὲ τὸ Α σημεῖον, καὶ τοῦ κώνου, οὗ βάσις ὁ αὐτὸς κύκλος, κορυφὴ δὲ τὸ Χ σημεῖον· ἴσος ἐστὶ τῷ κώνῳ τῷ βάσιν μὲν ἔχοντι τὴν ἐπιφάνειαν τοῦ ΝΑΖ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ Χ καθέτῳ ἠγμένῃ. Πάλιν δὲ καὶ τὸ περιλελειμμένον τοῦ ῥόμβου τὸ περιεχόμενον ὑπό τε τῆς ἐπιφανείας τοῦ κώνου τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΖΝ, ΗΜ καὶ τῶν ἐπιφανειῶν τῶν κώνων τοῦ τε ΖΝΧ καὶ τοῦ ΗΜΧ ἴσον ἐστὶ τῷ κώνῳ τῷ βάσιν μὲν ἔχοντι ἴσην τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΜΗ, ΖΝ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ Χ ἐπὶ τὴν ΖΗ καθέτῳ ἠγμένῃ· δέδεικται γὰρ ταῦτα. Ἔτι δὲ καὶ τὸ περιλειπόμενον τοῦ κώνου τὸ περιεχόμενον ὑπό τε τῆς ἐπιφανείας τοῦ κώνου τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΗΜ, ΒΔ καὶ τῆς ἐπιφανείας τοῦ ΜΗΧ κώνου καὶ τοῦ κύκλου τοῦ περὶ διάμετρον τὴν ΒΔ ἴσον τῷ κώνῳ τῷ βάσιν μὲν ἔχοντι τὴν ἴσην τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν ἐπιπέδων τῶν κατὰ τὰς ΗΜ, [66] ΒΔ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ Χ ἐπὶ τὴν ΒΗ καθέτῳ ἠγμένῃ. Ὁμοίως δὲ καὶ ἐν τῷ ἑτέρῳ ἡμισφαιρίῳ ὅ τε ῥόμβος ὁ ΧΚΓΙ καὶ τὰ περιλείμματα τῶν κώνων ἴσα ἔσται τοσούτοις καὶ τηλικούτοις κώνοις, ὅσοι καὶ πρότερον ἐρρήθησαν· δῆλον οὖν ὅτι καὶ ὅλον τὸ σχῆμα τὸ ἐγγεγραμμένον ἐν τῇ σφαίρᾳ ἴσον ἐστὶν πᾶσιν τοῖς εἰρημένοις κώνοις. Οἱ δὲ κῶνοι ἴσοι εἰσὶν τῷ Ρ κώνῳ, ἐπειδὴ ὁ Ρ κῶνος ὕψος μὲν ἔχει ἑκάστῳ ἴσον τῶν εἰρημένων κώνων, βάσιν δὲ ἴσην πάσαις ταῖς βάσεσιν αὐτῶν· δῆλον οὖν ὅτι τὸ ἐν τῇ σφαίρᾳ ἐγγεγραμμένον ἴσον ἐστὶν τῷ ἐκκειμένῳ κώνῳ.

   κζ΄.

   Τὸ ἐγγεγραμμένον σχῆμα ἐν τῇ σφαίρᾳ τὸ περιεχόμενον ὑπὸ τῶν ἐπιφανειῶν τῶν κωνικῶν ἔλασσόν ἐστιν ἢ τετραπλάσιον τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας.

   Ἔστω γὰρ γινόμενος κῶνος ἴσος τῷ σχήματι τῷ ἐγγεγραμμένῳ ἐν τῷ σφαίρᾳ τὴν βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ ἐγγεγραμμένου σχήματος, τὸ δὲ ὕψος ἴσον τῇ ἀπὸ τοῦ κέντρου τοῦ κύκλου καθέτῳ ἀγομένῃ ἐπὶ μίαν πλευρὰν τοῦ ἐγγραφέντος πολυγώνου ὁ Ρ, ὁ δὲ κῶνος ὁ Ξ ἔστω βάσιν ἔχων ἴσην τῷ ΑΒΓΔ κύκλῳ, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τοῦ ΑΒΓΔ κύκλου.

   Ἐπεὶ οὖν ὁ Ρ κῶνος βάσιν ἔχει ἴσην τῇ ἐπιφανείᾳ τοῦ ἐγγεγραμμένου σχήματος ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ Χ καθέτῳ ἀγομένῃ ἐπὶ τὴν ΑΖ, ἐδείχθη δὲ ἡ ἐπιφάνεια τοῦ ἐγγεγραμμένου σχήματος ἐλάσσων ἢ [67] τετραπλασία τοῦ ἐν τῇ σφαίρᾳ μεγίστου κύκλου, ἔσται ἄρα ἡ τοῦ Ρ κώνου βάσις ἐλάσσων ἢ τετραπλασία τῆς βάσεως τοῦ Ξ κώνου. Ἔστιν δὲ καὶ τὸ ὕψος τοῦ Ρ ἔλασσον τοῦ ὕψους τοῦ Ξ κώνου· ἐπεὶ οὖν ὁ Ρ κῶνος τὴν μὲν βάσιν ἔχει ἐλάσσονα ἢ τετραπλασίαν τῆς τοῦ Ξ βάσεως, τὸ δὲ ὕψος ἔλασσον τοῦ ὕψους, δῆλον ὡς καὶ αὐτὸς ὁ Ρ κῶνος ἐλάσσων ἐστὶν ἢ τετραπλάσιος τοῦ Ξ κώνου. Ἀλλὰ καὶ ὁ Ρ κῶνος ἴσος ἐστὶ τῷ ἐγγεγραμμένῳ σχήματι· τὸ ἄρα ἐγγεγραμμένον σχῆμα ἔλασσόν ἐστιν ἢ τετραπλάσιον τοῦ Ξ κώνου.

   κη΄.

   Ἔστω ἐν σφαίρᾳ μέγιστος κύκλος ὁ ΑΒΓΔ, περὶ δὲ τὸν ΑΒΓΔ κύκλον περιγεγράφθω πολύγωνον ἰσόπλευρόν τε καὶ ἰσογώνιον, τὸ δὲ πλῆθος τῶν πλευρῶν αὐτοῦ μετρείσθω ὑπὸ τετράδος, τὸ δὲ περὶ τὸν κύκλον περιγεγραμμένον πολύγωνον κύκλος περιγεγραμμένος περιλαμβανέτω περὶ [68] τὸ αὐτὸ κέντρον γενόμενος τῷ ΑΒΓΔ. Μενούσης δὴ τῆς ΕΗ περιενεχθήτω τὸ ΕΖΗΘ ἐπίπεδον, ἐν ᾧ τό τε πολύγωνον καὶ ὁ κύκλος· δῆλον οὖν ὅτι ἡ μὲν περιφέρεια τοῦ ΑΒΓΔ κύκλου κατὰ τῆς ἐπιφανείας τῆς σφαίρας οἰσθήσεται, ἡ δὲ περιφέρεια τοῦ ΕΖΗΘ κατ᾿ ἄλλης ἐπιφανείας σφαίρας τὸ αὐτὸ κέντρον ἐχούσης τῇ ἐλάσσονι οἰσθήσεται, αἱ δὲ ἁφαί, καθ᾿ ἃς ἐπιψαύουσιν αἱ πλευραί, γράφουσιν κύκλους ὀρθοὺς πρὸς τὸν ΑΒΓΔ κύκλον ἐν τῇ ἐλάσσονι σφαίρᾳ, αἱ δὲ γωνίαι τοῦ πολυγώνου χωρὶς τῶν πρὸς τοῖς Ε, Η σημείοις κατὰ κύκλων περιφερειῶν οἰσθήσονται ἐν τῇ ἐπιφανείᾳ τῆς μείζονος σφαίρας γεγραμμένων ὀρθῶν πρὸς τὸν ΕΖΗΘ κύκλον, αἱ δὲ πλευραὶ τοῦ πολυγώνου κατὰ κωνικῶν ἐπιφανειῶν οἰσθήσονται, καθάπερ ἐπὶ τῶν πρὸ τούτου· ἔσται οὖν τὸ σχῆμα τὸ περιεχόμενον ὑπὸ τῶν ἐπιφανειῶν τῶν κωνικῶν περὶ μὲν τὴν ἐλάσσονα σφαῖραν περιγεγραμμένον, ἐν δὲ τῇ μείζονι ἐγγεγραμμένον. Ὅτι δὲ ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος μείζων ἐστὶ τῆς ἐπιφανείας τῆς σφαίρας οὕτως δειχθήσεται· ἔστω γὰρ ἡ ΚΔ διάμετρος κύκλου τινὸς τῶν ἐν τῇ ἐλάσσονι [69] σφαίρᾳ τῶν Κ, Δ σημείων ὄντων, καθ᾿ ἃ ἅπτονται τοῦ ΑΒΓΔ κύκλου αἱ πλευραὶ τοῦ περιγεγραμμένου πολυγώνου. Διῃρημένης δὴ τῆς σφαίρας ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὴν ΚΔ ὀρθοῦ πρὸς τὸν ΑΒΓΔ κύκλον καὶ ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος περὶ τὴν σφαῖραν διαιρεθήσεται ὑπὸ τοῦ ἐπιπέδου. Καὶ φανερὸν ὅτι τὰ αὐτὰ πέρατα ἔχουσιν ἐν ἐπιπέδῳ· ἀμφοτέρων γὰρ τῶν ἐπιπέδων πέρας ἐστὶν ἡ τοῦ κύκλου περιφέρεια τοῦ περὶ διάμετρον τὴν ΚΔ ὀρθοῦ πρὸς τὸν ΑΒΓΔ κύκλον· καί εἰσιν ἀμφότεραι ἐπὶ τὰ αὐτὰ κοῖλαι, καὶ περιλαμβάνεται ἡ ἑτέρα αὐτῶν ὑπὸ τῆς ἑτέρας ἐπιφανείας καὶ τῆς ἐπιπέδου τῆς τὰ αὐτὰ πέρατα ἐχούσης· ἐλάσσων οὖν ἐστιν ἡ περιλαμβανομένη τοῦ τμήματος τῆς σφαίρας ἐπιφάνεια τῆς ἐπιφανείας τοῦ σχήματος τοῦ περιγεγραμμένου περὶ αὐτήν. Ὁμοίως δὲ καὶ ἡ τοῦ λοιποῦ τμήματος τῆς σφαίρας ἐπιφάνεια ἐλάσσων ἐστὶν τῆς ἐπιφανείας τοῦ σχήματος τοῦ περιγεγραμμένου περὶ αὐτήν· δῆλον οὖν ὅτι καὶ ὅλη ἡ ἐπιφάνεια τῆς σφαίρας ἐλάσσων ἐστὶ τῆς ἐπιφανείας τοῦ σχήματος τοῦ περιγεγραμμένου περὶ αὐτήν.

   κθ΄.

   Τῇ ἐπιφανείᾳ τοῦ περιγεγραμμένου σχήματος περὶ τὴν σφαῖραν ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε μιᾶς πλευρᾶς τοῦ πολυγώνου καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς γωνίας τοῦ πολυγώνου οὔσαις παρά τινα τῶν ὑπὸ δύο πλευρὰς τοῦ πολυγώνου ὑποτεινουσῶν.

   Τὸ γὰρ περιγεγραμμένον περὶ τὴν ἐλάσσονα σφαῖραν ἐγγέγραπται εἰς τὴν μείζονα σφαῖραν· τοῦ δὲ ἐγγεγραμμένου ἐν τῇ σφαίρᾳ περιεχομένου ὑπὸ τῶν ἐπιφανειῶν [70] τῶν κωνικῶν δέδεικται ὅτι τῇ ἐπιφανείᾳ ἴσος ἐστὶν ὁ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ περιεχόμενον ὑπό τε μιᾶς πλευρᾶς τοῦ πολυγώνου καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς γωνίας τοῦ πολυγώνου οὔσαις παρά τινα τῶν ὑπὸ δύο πλευρὰς ὑποτεινουσῶν· δῆλον οὖν ἐστι τὸ προειρημένον.

   λ΄.

   Τοῦ σχήματος τοῦ περιγεγραμμένου περὶ τὴν σφαῖραν ἡ ἐπιφάνεια μείζων ἐστὶν ἢ τετραπλασία τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ.

   Ἔστω γὰρ ἥ τε σφαῖρα καὶ ὁ κύκλος καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον προκειμένοις, καὶ ὁ Λ κύκλος ἴσος τῇ ἐπιφανείᾳ ἔστω τοῦ προκειμένου περιγεγραμμένου περὶ τὴν ἐλάσσονα σφαῖραν.

   Ἐπεὶ οὖν ἐν τῷ ΕΖΗΘ κύκλῳ πολύγωνον ἰσόπλευρον [71] ἐγγέγραπται καὶ ἀρτιογώνιον, αἱ ἐπιζευγνύουσαι τὰς τοῦ πολυγώνου πλευρὰς παράλληλοι οὖσαι τῇ ΖΘ πρὸς τὴν ΖΘ τὸν αὐτὸν λόγον ἔχουσιν, ὃν ἡ ΘΚ πρὸς ΚΖ· ἴσον ἄρα ἐστὶν τὸ περιεχόμενον σχῆμα ὑπό τε μιᾶς πλευρᾶς τοῦ πολυγώνου καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς γωνίας τοῦ πολυγώνου τῷ περιεχομένῳ ὑπὸ τῶν ΖΘΚ· ὥστε ἡ ἐκ τοῦ κέντρου τοῦ Λ κύκλου ἴσον δύναται τῷ ὑπὸ ΖΘΚ· μείζων ἄρα ἐστὶν ἡ ἐκ τοῦ κέντρου τοῦ Λ κύκλου τῆς ΘΚ. Ἡ δὲ ΘΚ ἴση ἐστὶ τῇ διαμέτρῳ τοῦ ΑΒΓΔ κύκλου [διπλασία γάρ ἐστιν τῆς ΧΣ οὔσης ἐκ τοῦ κέντρου τοῦ ΑΒΓΔ κύκλου]· δῆλον οὖν ὅτι μείζων ἐστὶν ἢ τετραπλάσιος ὁ Λ κύκλος, τουτέστιν ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος περὶ τὴν ἐλάσσονα σφαῖραν, τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ.

   λα΄.

   Τῷ περιγεγραμμένῳ σχήματι περὶ τὴν ἐλάσσονα σφαῖραν ἴσος ἐστὶ κῶνος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν ἴσον τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας.

   Τὸ γὰρ περιγεγραμμένον σχῆμα περὶ τὴν ἐλάσσονα σφαῖραν ἐγγέγραπται ἐν τῇ μείζονι σφαίρᾳ· τῷ δὲ ἐγγεγραμμένῳ σχήματι περιεχομένῳ ὑπὸ τῶν κωνικῶν ἐπιφανειῶν δέδεικται ἴσος κῶνος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν ἴσον τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ ἴσον τῇ ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ· αὕτη δέ ἐστιν ἴση τῇ ἐκ τοῦ κέντρου τῆς ἐλάσσονος σφαίρας· δῆλον οὖν ἐστι τὸ προτεθέν.

[72]

ΠΟΡΙΣΜΑ.

   Ἐκ τούτου δὲ φανερὸν ὅτι τὸ σχῆμα τὸ περιγραφόμενον περὶ τὴν ἐλάσσονα σφαῖραν μεῖζόν ἐστιν ἢ τετραπλάσιον κώνου τοῦ βάσιν μὲν ἔχοντος τὸν μέγιστον κύκλον τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς σφαίρας. Ἐπειδὴ γὰρ ἴσος ἐστὶ τῷ σχήματι κῶνος ὁ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ αὐτοῦ, ὕψος δὲ ἴσον [τῇ ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ, τουτέστιν] τῇ ἐκ τοῦ κέντρου τῆς ἐλάσσονος σφαίρας, ἔστι δὲ ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος περὶ τὴν σφαῖραν μείζων ἢ τετραπλασία τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ, μεῖζον ἄρα ἢ τετραπλάσιον ἔσται τὸ σχῆμα τὸ περιγεγραμμένον περὶ τὴν σφαῖραν τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος τὸν μέγιστον κύκλον, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς σφαίρας, ἐπειδὴ καὶ ὁ κῶνος ὁ ἴσος αὐτῷ μείζων ἢ τετραπλάσιος γίνεται τοῦ εἰρημένου κώνου [βάσιν τε γὰρ μείζονα ἢ τετραπλασίαν ἔχει καὶ ὕψος ἴσον].

   λβ΄.

   Ἐὰν ᾖ ἐν σφαίρᾳ σχῆμα ἐγγεγραμμένον καὶ ἄλλο περιγεγραμμένον ὑπὸ ὁμοίων πολυγώνων τὸν αὐτὸν τρόπον τοῖς πρότερον κατεσκευασμένα, ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος πρὸς τὴν τοῦ ἐγγεγραμμένου ἐπιφάνειαν διπλασίονα λόγον ἔχει ἤπερ ἡ πλευρὰ τοῦ περιγεγραμμένου πολυγώνου περὶ τὸν μέγιστον κύκλον πρὸς τὴν πλευρὰν τοῦ ἐγγεγραμμένου πολυγώνου ἐν τῷ αὐτῷ κύκλῳ, αὐτὸ δὲ τὸ σχῆμα [τὸ περιγεγραμμένον] [73] πρὸς τὸ σχῆμα τριπλασίονα λόγον ἔχει τοῦ αὐτοῦ λόγου.

   Ἔστω ἐν σφαίρᾳ κύκλος ὁ ΑΒΓΔ, καὶ ἐγγεγράφθω εἰς αὐτὸν πολύγωνον ἰσόπλευρον, τὸ δὲ πλῆθος τῶν πλευρῶν αὐτοῦ μετρείσθω ὑπὸ τετράδος, καὶ ἄλλο περιγεγράφθω περὶ τὸν κύκλον ὅμοιον τῷ ἐγγεγραμμένῳ, ἔτι δὲ αἱ τοῦ περιγεγραμμένου πολυγώνου πλευραὶ ἐπιψαυέτωσαν τοῦ κύκλου κατὰ μέσα τῶν περιφερειῶν τῶν ἀποτεμνομένων ὑπὸ τῶν τοῦ ἐγγεγραμμένου πολυγώνου πλευρῶν, αἱ δὲ ΕΗ, ΖΘ διάμετροι πρὸς ὀρθὰς ἔστωσαν ἀλλήλαις τοῦ κύκλου τοῦ περιλαμβάνοντος τὸ περιγεγραμμένον πολύγωνον καὶ ὁμοίως κείμεναι ταῖς ΑΓ, ΒΔ διαμέτροις, καὶ νοείσθωσαν ἐπιζευγνύμεναι ἐπὶ τὰς ἀπεναντίον γωνίας τοῦ πολυγώνου, αἳ γίγνονται ἀλλήλαις τε καὶ τῇ ΖΒΔΘ παράλληλοι. Μενούσης δὴ τῆς ΕΗ διαμέτρου καὶ περιενεχθεισῶν τῶν περιμέτρων τῶν πολυγώνων περὶ τὴν τοῦ κύκλου περιφέρειαν τὸ μὲν ἐγγεγραμμένον σχῆμα ἔσται ἐν τῇ σφαίρᾳ, τὸ δὲ περιγεγραμμένον· δεικτέον οὖν ὅτι ἡ μὲν ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου διπλασίονα λόγον ἔχει ἤπερ ἡ ΕΛ πρὸς ΑΚ, τὸ δὲ σχῆμα τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον τριπλασίονα λόγον ἔχει τοῦ αὐτοῦ λόγου.

   Ἔστω γὰρ ὁ μὲν Μ κύκλος ἴσος τῇ ἐπιφανείᾳ τοῦ περιγεγραμμένου περὶ τὴν σφαῖραν, ὁ δὲ Ν ἴσος τῇ ἐπιφανείᾳ τοῦ ἐγγεγραμμένου· δύναται ἄρα τοῦ μὲν Μ ἡ ἐκ τοῦ κέντρου τὸ περιεχόμενον ὑπὸ τῆς ΕΛ καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς γωνίας τοῦ πολυγώνου τοῦ περιγεγραμμένου, ἡ δὲ ἐκ τοῦ κέντρου τοῦ Ν τὸ ὑπὸ [74] τῆς ΑΚ καὶ τῆς ἴσης πάσαις ταῖς ἐπιζευγνυούσαις τὰς γωνίας. Καὶ ἐπεὶ ὅμοιά ἐστιν τὰ πολύγωνα, ὅμοια ἂν εἴη καὶ τὰ περιεχόμενα χωρία ὑπὸ τῶν εἰρημένων γραμμῶν [τουτέστι τῶν ἐπὶ τὰς γωνίας καὶ τῶν πλευρῶν τῶν πολυγώνων, ὥστε τὸν αὐτὸν λόγον ἔχειν πρὸς ἄλληλα, ὃν ἔχουσιν αἱ τῶν πολυγώνων πλευραὶ δυνάμει. Ἀλλὰ καὶ ὃν ἔχει λόγον τὰ περιεχόμενα ὑπὸ τῶν εἰρημένων γραμμῶν, τοῦτον ἔχουσιν αἱ ἐκ τῶν κέντρων τῶν Μ, Ν κύκλων πρὸς ἀλλήλας δυνάμει· ὥστε καὶ αἱ τῶν Μ, Ν διάμετροι τὸν [75] αὐτὸν ἔχουσι λόγον ταῖς τῶν πολυγώνων πλευραῖς. Οἱ δὲ κύκλοι πρὸς ἀλλήλους διπλασίονα λόγον ἔχουσιν τῶν διαμέτρων, οἵτινες ἴσοι εἰσὶν ταῖς ἐπιφανείαις τοῦ περιγεγραμμένου καὶ τοῦ ἐγγεγραμμένου]· δῆλον οὖν ὅτι ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος περὶ τὴν σφαῖραν πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου σχήματος εἰς τὴν σφαῖραν διπλασίονα λόγον ἔχει ἤπερ ἡ ΕΛ πρὸς ΑΚ.

   Εἰλήφθωσαν δὴ δύο κῶνοι οἱ Ο, Ξ, καὶ ἔστω ὁ μὲν Ξ κῶνος βάσιν ἔχων τὸν Ξ κύκλον ἴσον τῷ Μ, ὁ δὲ Ο βάσιν ἔχων τὸν Ο κύκλον ἴσον τῷ Ν, ὕψος δὲ ὁ μὲν Ξ κῶνος τὴν ἐκ τοῦ κέντρου τῆς σφαίρας, ὁ δὲ Ο τὴν ἀπὸ τοῦ κέντρου ἐπὶ τὴν ΑΚ κάθετον ἠγμένην· ἴσος ἄρα ὁ μὲν Ξ κῶνος τῷ σχήματι τῷ περιγεγραμμένῳ περὶ τὴν σφαῖραν, ὁ δὲ Ο τῷ ἐγγεγραμμένῳ [δέδεικται οὖν ταῦτα]. Καὶ ἐπεὶ ὅμοιά ἐστι τὰ πολύγωνα, τὸν αὐτὸν ἔχει λόγον ἡ ΕΛ πρὸς τὴν ΑΚ, ὃν ἡ ἐκ τοῦ κέντρου τῆς σφαίρας πρὸς τὴν ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ τὴν ΑΚ κάθετον ἀγομένην· τὸν αὐτὸν ἄρα λόγον ἔχει τὸ ὕψος τοῦ Ξ κώνου πρὸς τὸ ὕψος τοῦ Ο κώνου, ὃν ἡ ΕΛ πρὸς ΑΚ. Ἔχει δὲ καὶ ἡ διάμετρος τοῦ Μ κύκλου πρὸς τὴν διάμετρον τοῦ Ν κύκλου λόγον, ὃν ἔχει ἡ ΕΛ πρὸς ΑΚ· τῶν ἄρα Ξ, Ο κώνων αἱ διάμετροι τῶν βάσεων τοῖς ὕψεσι τὸν αὐτὸν ἔχουσι λόγον [ὅμοιοι ἄρα εἰσίν], καὶ διὰ τοῦτο τριπλασίονα λόγον ἕξει ὁ Ξ κῶνος πρὸς τὸν Ο κῶνον ἤπερ ἡ διάμετρος τοῦ Μ κύκλου πρὸς τὴν διάμετρον τοῦ Ν κύκλου. Δῆλον οὖν ὅτι καὶ τὸ σχῆμα τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον τριπλασίονα λόγον ἕξει ἤπερ ἡ ΕΛ πρὸς ΑΚ.

[76]    λγ΄.

   Πάσης σφαίρας ἡ ἐπιφάνεια τετραπλασία ἐστὶ τοῦ μεγίστου κύκλου τῶν ἐν αὐτῇ.

   Ἔστω γὰρ σφαῖρά τις καὶ ἔστω τετραπλάσιος τοῦ μεγίστου κύκλου ὁ Α· λέγω ὅτι ὁ Α ἴσος ἐστὶ τῇ ἐπιφανεία τῆς σφαίρας.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω πρότερον μείζων ἡ ἐπιφάνεια τῆς σφαίρας τοῦ κύκλου. Ἔστι δὴ δύο μεγέθη ἄνισα ἥ τε ἐπιφάνεια τῆς σφαίρας καὶ ὁ Α κύκλος· δυνατὸν ἄρα ἐστὶ λαβεῖν δύο εὐθείας ἀνίσους, ὥστε τὴν μείζονα πρὸς τὴν ἐλάσσονα λόγον ἔχειν ἐλάσσονα τοῦ ὃν ἔχει ἡ ἐπιφάνεια τῆς σφαίρας πρὸς τὸν κύκλον. Εἰλήφθωσαν αἱ Β, Γ, καὶ τῶν Β, Γ μέση ἀνάλογον ἔστω ἡ Δ, νοείσθω δὲ καὶ ἡ σφαῖρα ἐπιπέδῳ τετμημένη διὰ τοῦ κέντρου κατὰ τὸν ΕΖΗΘ κύκλον, νοείσθω δὲ καὶ εἰς τὸν κύκλον ἐγγεγραμμένον καὶ περιγεγραμμένον πολύγωνον, ὥστε ὅμοιον εἶναι τὸ περιγεγραμμένον τῷ ἐγγεγραμμένῳ πολυγώνῳ καὶ τὴν τοῦ περιγεγραμμένου πλευρὰν ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ἡ Β πρὸς Δ [καὶ ὁ διπλάσιος ἄρα λόγος τοῦ διπλασίου λόγου ἐστὶν ἐλάσσων. Καὶ τοῦ μὲν τῆς Β πρὸς Δ διπλάσιός ἐστιν ὁ τῆς Β πρὸς τὴν Γ, τῆς δὲ πλευρᾶς τοῦ περιγεγραμμένου πολυγώνου πρὸς τὴν πλευρὰν τοῦ ἐγγεγραμμένου διπλάσιος ὁ τῆς ἐπιφανείας τοῦ περιγεγραμμένου στερεοῦ πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου]· ἡ ἐπιφάνεια ἄρα τοῦ περιγεγραμμένου σχήματος περὶ τὴν σφαῖραν πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου σχήματος ἐλάσσονα λόγον ἔχει ἤπερ ἡ ἐπιφάνεια τῆς σφαίρας πρὸς τὸν Α κύκλον· ὅπερ ἄτοπον· ἡ μὲν γὰρ ἐπιφάνεια τοῦ περιγεγραμμένου τῆς ἐπιφανείας τῆς [77] σφαίρας μείζων ἐστίν, ἡ δὲ ἐπιφάνεια τοῦ ἐγγεγραμμένου σχήματος τοῦ Α κύκλου ἐλάσσων ἐστί [δέδεικται γὰρ ἡ ἐπιφάνεια τοῦ ἐγγεγραμμένου ἐλάσσων τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ ἢ τετραπλασία, τοῦ δὲ μεγίστου κύκλου τετραπλάσιός ἐστιν ὁ Α κύκλος]. Οὐκ ἄρα ἡ ἐπιφάνεια τῆς σφαίρας μείζων ἐστὶ τοῦ Α κύκλου.

   Λέγω δὴ ὅτι οὐδὲ ἐλάσσων. Εἰ γὰρ δυνατόν, ἔστω· καὶ ὁμοίως εὑρήσθωσαν αἱ Β, Γ εὐθεῖαι ὥστε τὴν Β πρὸς Γ ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ὁ Α κύκλος πρὸς τὴν ἐπιφάνειαν τῆς σφαίρας, καὶ τῶν Β, Γ μέση ἀνάλογον ἡ Δ, καὶ ἐγγεγράφθω καὶ περιγεγράφθω πάλιν, ὥστε τὴν τοῦ περιγεγραμμένου ἐλάσσονα λόγον ἔχειν τοῦ τῆς Β πρὸς Δ [καὶ τὰ διπλάσια ἄρα]· ἡ ἐπιφάνεια ἄρα τοῦ περιγεγραμμένου πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου ἐλάσσονα λόγον ἔχει ἤπερ [ἡ Β πρὸς Γ. Ἡ δὲ Β πρὸς Γ ἐλάσσονα λόγον ἔχει ἤπερ] ὁ Α κύκλος πρὸς τὴν ἐπιφάνειαν τῆς σφαίρας· ὅπερ ἄτοπον· ἡ μὲν γὰρ τοῦ περιγεγραμμένου [78] ἐπιφάνεια μείζων ἐστὶ τοῦ Α κύκλου, ἡ δὲ τοῦ ἐγγεγραμμένου ἐλάσσων τῆς ἐπιφανείας τῆς σφαίρας.

   Οὐκ ἄρα οὐδὲ ἐλάσσων ἡ ἐπιφάνεια τῆς σφαίρας τοῦ Α κύκλου. Ἐδείχθη δὲ ὅτι οὐδὲ μείζων· ἡ ἄρα ἐπιφάνεια τῆς σφαίρας ἴση ἐστὶ τῷ Α κύκλῳ, τουτέστι τῷ τετραπλασίῳ τοῦ μεγίστου κύκλου.

   λδ΄.

   Πᾶσα σφαῖρα τετραπλασία ἐστὶ κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ μεγίστω κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς σφαίρας.

   Ἔστω γὰρ σφαῖρά τις καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΓΔ. Εἰ οὖν μή ἐστιν ἡ σφαῖρα τετραπλασία τοῦ εἰρημένου κώνου, ἔστω, εἰ δυνατόν, μείζων ἢ τετραπλασία· ἔστω δὲ ὁ Ξ κῶνος βάσιν μὲν ἔχων τετραπλασίαν τοῦ ΑΒΓΔ κύκλου, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας· μείζων οὖν ἐστιν ἡ σφαῖρα τοῦ Ξ κώνου. Ἔσται δὴ δύο μεγέθη ἄνισα ἥ τε σφαῖρα καὶ ὁ κῶνος· δυνατὸν οὖν δύο εὐθείας λαβεῖν ἀνίσους, ὥστε ἔχειν τὴν μείζονα πρὸς τὴν ἐλάσσονα ἐλάσσονα λόγον τοῦ ὃν ἔχει ἡ σφαῖρα πρὸς τὸν Ξ κῶνον. Ἔστωσαν οὖν αἱ Κ, Η, αἱ δὲ Ι, Θ εἰλημμέναι, ὥστε τῷ ἴσῳ ἀλλήλων ὑπερέχειν τὴν Κ τῆς Ι καὶ τὴν Ι τῆς Θ καὶ τὴν Θ τῆς Η, νοείσθω δὲ καὶ εἰς τὸν ΑΒΓΔ κύκλον ἐγγεγραμμένον πολύγωνον, οὗ τὸ πλῆθος τῶν πλευρῶν μετρείσθω ὑπὸ τετράδος, καὶ ἄλλο περιγεγραμμένον ὅμοιον τῷ ἐγγεγραμμένῳ, καθάπερ ἐπὶ τῶν πρότερον, ἡ δὲ τοῦ περιγεγραμμένου πολυγώνου πλευρὰ πρὸς τὴν τοῦ ἐγγεγραμμένου ἐλάσσονα λόγον ἐχέτω τοῦ ὃν ἔχει ἡ Κ πρὸς Ι, καὶ ἔστωσαν αἱ ΑΓ, ΒΔ διάμετροι πρὸς ὀρθὰς ἀλλήλαις. Εἰ οὖν μενούσης τῆς ΑΓ διαμέτρου

[79] περιενεχθείη τὸ ἐπίπεδον, ἐν ᾧ τὰ πολύγωνα, ἔσται σχήματα τὸ μὲν ἐγγεγραμμένον ἐν τῇ σφαίρᾳ, τὸ δὲ περιγεγραμμένον, καὶ ἕξει τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον τριπλασίονα λόγον ἤπερ ἡ πλευρὰ τοῦ περιγεγραμμένου πρὸς τὴν τοῦ ἐγγεγραμμένου εἰς τὸν ΑΒΓΔ κύκλον. Ἡ δὲ πλευρὰ πρὸς τὴν πλευρὰν ἐλάσσονα λόγον ἔχει ἤπερ ἡ Κ πρὸς τὴν Ι· ὥστε τὸ σχῆμα τὸ περιγεγραμμένον ἐλάσσονα λόγον ἔχει ἢ τριπλασίονα τοῦ Κ πρὸς Ι. Ἔχει δὲ καὶ ἡ Κ πρὸς Η μείζονα λόγον ἢ τριπλάσιον τοῦ ὃν ἔχει ἡ Κ πρὸς Ι [τοῦτο γὰρ φανερὸν διὰ λημμάτων]· πολλῷ ἄρα τὸ περιγραφὲν πρὸς τὸ ἐγγραφὲν ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἡ Κ πρὸς Η. Ἡ δὲ Κ πρὸς Η ἐλάσσονα λόγον ἔχει ἤπερ ἡ σφαῖρα πρὸς τὸν Ξ κῶνον· καὶ ἐναλλάξ· [80] ὅπερ ἀδύνατον· τὸ γὰρ σχῆμα τὸ περιγεγραμμένον μεῖζόν ἐστι τῆς σφαίρας, τὸ δὲ ἐγγεγραμμένον ἔλασσον τοῦ Ξ κώνου [διότι ὁ μὲν Ξ κῶνος τετραπλάσιός ἐστι τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ ΑΒΓΔ κύκλῳ, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας, τὸ δὲ ἐγγεγραμμένον σχῆμα ἔλασσον τοῦ εἰρημένου κώνου ἢ τετραπλάσιον]. Οὐκ ἄρα μείζων ἢ τετραπλασία ἡ σφαῖρα τοῦ εἰρημένου.

   Ἔστω, εἰ δυνατόν, ἐλάσσων ἢ τετραπλασία· ὥστε ἐλάσσων ἐστὶν ἡ σφαῖρα τοῦ Ξ κώνου. Εἰλήφθωσαν δὴ αἱ Κ, Η εὐθεῖαι, ὥστε τὴν Κ μείζονα εἶναι τῆς Η καὶ ἐλάσσονα λόγον ἔχειν πρὸς αὐτὴν τοῦ ὃν ἔχει ὁ Ξ κῶνος πρὸς τὴν σφαῖραν, καὶ αἱ Θ, Ι ἐκκείσθωσαν, καθὼς πρότερον, καὶ εἰς τὸν ΑΒΓΔ κύκλον νοείσθω πολύγωνον ἐγγεγραμμένον καὶ ἄλλο περιγεγραμμένον, ὥστε τὴν πλευρὰν τοῦ περιγεγραμμένου πρὸς τὴν πλευρὰν τοῦ ἐγγεγραμμένου ἐλάσσονα λόγον ἔχειν ἤπερ ἡ Κ πρὸς Ι, καὶ τὰ ἄλλα κατεσκευασμένα τὸν αὐτὸν τρόπον τοῖς πρότερον· ἕξει ἄρα καὶ τὸ περιγεγραμμένον στερεὸν σχῆμα πρὸς τὸ ἐγγεγραμμένον τριπλασίονα λόγον ἤπερ ἡ πλευρὰ τοῦ περιγεγραμμένου περὶ τὸν ΑΒΓΔ κύκλον πρὸς τὴν τοῦ ἐγγεγραμμένου. Ἡ δὲ πλευρὰ πρὸς τὴν πλευρὰν ἐλάσσονα λόγον ἔχει ἤπερ ἡ Κ πρὸς Ι· ἕξει οὖν τὸ σχῆμα τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἢ τριπλάσιον τοῦ ὃν ἔχει ἡ Κ πρὸς τὴν Ι. Ἡ δὲ Κ πρὸς τὴν Η μείζονα λόγον ἔχει ἢ τριπλάσιον τοῦ ὃν ἔχει ἡ Κ πρὸς τὴν Ι· ὥστε ἐλάσσονα λόγον ἔχει τὸ σχῆμα τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἢ ἡ Κ πρὸς τὴν Η. Ἡ δὲ Κ πρὸς τὴν Η ἐλάσσονα λόγον ἔχει ἢ ὁ Ξ κῶνος [81] πρὸς τὴν σφαῖραν· ὅπερ ἀδύνατον· τὸ μὲν γὰρ ἐγγεγραμμένον ἔλασσόν ἐστι τῆς σφαίρας, τὸ δὲ περιγεγραμμένον μεῖζον τοῦ Ξ κώνου. Οὐκ ἄρα οὐδὲ ἐλάσσων ἐστὶν ἢ τετραπλασία ἡ σφαῖρα τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ ΑΒΓΔ κύκλῳ, ὕψος δὲ τὴν ἴσην τῇ ἐκ τοῦ κέντρου τῆς σφαίρας. Ἐδείχθη δὲ, ὅτι οὐδὲ μείζων· τετραπλασία ἄρα.

[ΠΟΡΙΣΜΑ.]

   Προδεδειγμένων δὲ τούτων φανερὸν ὅτι πᾶς κύλινδρος βάσιν μὲν ἔχων τὸν μέγιστον κύκλον τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας, ἡμιόλιός ἐστι τῆς σφαίρας καὶ ἡ ἐπιφάνεια αὐτοῦ μετὰ τῶν βάσεων ἡμιολία τῆς ἐπιφανείας τῆς σφαίρας.

   Ὁ μὲν γὰρ κύλινδρος ὁ προειρημένος ἑξαπλάσιός ἐστι τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος τὴν αὐτήν, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου, ἡ δὲ σφαῖρα δέδεικται τοῦ αὐτοῦ κώνου τετραπλασία οὖσα· δῆλον οὖν ὅτι ὁ κύλινδρος ἡμιόλιός ἐστι τῆς σφαίρας. Πάλιν, ἐπεὶ ἡ ἐπιφάνεια τοῦ κυλίνδρου χωρὶς τῶν βάσεων ἴση δέδεικται κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου μέση ἀνάλογόν ἐστι τῆς τοῦ κυλίνδρου πλευρᾶς καὶ τῆς διαμέτρου τῆς βάσεως, τοῦ δὲ εἰρημένου κυλίνδρου τοῦ περὶ τὴν σφαῖραν ἡ πλευρὰ ἴση ἐστὶ τῇ διαμέτρῳ τῆς βάσεως [δῆλον ὅτι ἡ μέση αὐτῶν ἀνάλογον ἴση γίνεται τῇ διαμέτρῳ τῆς βάσεως], ὁ δὲ κύκλος ὁ τὴν ἐκ τοῦ κέντρου ἔχων ἴσην τῇ διαμέτρῳ τῆς βάσεως τετραπλάσιός ἐστι τῆς βάσεως, τουτέστι τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ, ἔσται ἄρα καὶ ἡ ἐπιφάνεια τοῦ κυλίνδρου χωρὶς τῶν βάσεων τετραπλασία τοῦ μεγίστου κύκλου· ὅλη ἄρα μετὰ τῶν βάσεων ἡ ἐπιφάνεια τοῦ κυλίνδρου ἑξαπλασία [82] ἔσται τοῦ μεγίστου κύκλου. Ἔστιν δὲ καὶ ἡ τῆς σφαίρας ἐπιφάνεια τετραπλασία τοῦ μεγίστου κύκλου. Ὅλη ἄρα ἡ ἐπιφάνεια τοῦ κυλίνδρου ἡμιολία ἐστὶ τῆς ἐπιφανείας τῆς σφαίρας.

   λε΄.

   Ἡ ἐπιφάνεια τοῦ ἐγγεγραμμένου σχήματος εἰς τὸ τμῆμα τῆς σφαίρας ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε μιᾶς πλευρᾶς τοῦ ἐγγεγραμμένου πολυγώνου ἐν τῷ τμήματι τοῦ μεγίστου κύκλου καὶ τῆς ἴσης πάσαις ταῖς παραλλήλοις τῇ βάσει τοῦ τμήματος σὺν τῇ ἡμισείᾳ τῆς τοῦ τμήματος βάσεως.

   Ἔστω σφαῖρα καὶ ἐν αὐτῇ τμῆμα, οὗ βάσις ὁ περὶ τὴν ΑΗ κύκλος [ἐγγεγράφθω σχῆμα εἰς αὐτό, οἷον εἴρηται, περιεχόμενον ὑπὸ κωνικῶν ἐπιφανειῶν], καὶ μέγιστος κύκλος ὁ ΑΗΘ καὶ ἀρτιόπλευρον πολύγωνον τὸ ΑΓΕΘΖΔΗ χωρὶς τῆς ΑΗ πλευρᾶς, καὶ εἰλήφθω κύκλος ὁ Λ, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε τῆς ΑΓ πλευρᾶς καὶ ὑπὸ πασῶν τῶν ΕΖ, ΓΔ καὶ ἔτι τῆς ἡμισείας τῆς βάσεως, τουτέστι τῆς ΑΚ· δεικτέον ὅτι ὁ κύκλος ἴσος ἐστὶ τῇ τοῦ σχήματος ἐπιφανείᾳ.

[83]    Εἰλήφθω γὰρ κύκλος ὁ Μ, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ περιεχόμενον ὑπό τε τῆς ΕΘ πλευρᾶς καὶ τῆς ἡμισείας τῆς ΕΖ· γίνεται δὴ ὁ Μ κύκλος ἴσος τῇ ἐπιφανείᾳ τοῦ κώνου, οὗ βάσις μὲν ὁ περὶ τὴν ΕΖ κύκλος, κορυφὴ δὲ τὸ Θ σημεῖον. Εἰλήφθω δὲ καὶ ἄλλος ὁ Ν, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε τῆς ΕΓ καὶ τῆς ἡμισείας συναμφοτέρου τῆς ΕΖ, ΓΔ· ἔσται οὖν οὗτος ἴσος τῇ ἐπιφανείᾳ τοῦ κώνου τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΕΖ, ΓΔ. Καὶ ἄλλος ὁμοίως ὁ Ξ εἰλήφθω κύκλος, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ περιεχόμενον ὑπό τε τῆς ΑΓ καὶ τῆς ἡμισείας συναμφοτέρων τῶν ΓΔ, ΑΗ· καὶ αὐτὸς οὖν ἴσος ἐστὶ τῇ κωνικῇ ἐπιφανείᾳ τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΑΗ, ΓΔ. Πάντες οὖν οἱ κύκλοι ἴσοι ἔσονται τῇ ὅλῃ τοῦ σχήματος ἐπιφανείᾳ, καὶ αἱ ἐκ τῶν κέντρων αὐτῶν ἴσον δυνήσονται τῷ περιεχομένῳ ὑπὸ μιᾶς πλευρᾶς τῆς ΑΓ καὶ τῆς ἴσης ταῖς ΕΖ, ΓΔ καὶ τῇ ἡμισείᾳ τῆς βάσεως τῇ ΑΚ. Ἐδύνατο δὲ καὶ ἡ ἐκ τοῦ κέντρου τοῦ Λ κύκλου ἴσον τῷ αὐτῷ χωρίῳ· ὁ ἄρα Λ κύκλος ἴσος ἔσται τοῖς Μ, Ν, Ξ κύκλοις· ὥστε καὶ τῇ ἐπιφανείᾳ τοῦ ἐγγεγραμμένου σχήματος.

   λϚ΄.

   Τετμήσθω σφαῖρα μὴ διὰ τοῦ κέντρου ἐπιπέδῳ, καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΕΖ τέμνων πρὸς ὀρθὰς τὸ ἐπίπεδον τὸ τέμνον, καὶ ἐγγεγράφθω εἰς τὸ ΑΒΓ τμῆμα πολύγωνον ἰσόπλευρόν τε καὶ ἀρτιόγωνον χωρὶς τῆς βάσεως τῆς ΑΒ. Ὁμοίως δὴ τοῖς πρότερον, ἐὰν μενούσης τῆς ΓΖ περιενεχθῇ τὸ σχῆμα, αἱ μὲν Δ, Ε, Α, Β γωνίαι κατὰ κύκλων οἰσθήσονται, ὧν διάμετροι αἱ ΔΕ, ΑΒ, αἱ δὲ

[84] πλευραὶ τοῦ τμήματος κατὰ κωνικῆς ἐπιφανείας, καὶ ἔσται τὸ γενηθὲν σχῆμα στερεὸν ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενον βάσιν μὲν ἔχον κύκλον, οὗ διάμετρος ἡ ΑΒ, κορυφὴν δὲ τὸ Γ. Ὁμοίως δὴ τοῖς πρότερον τὴν ἐπιφάνειαν ἐλάσσονα ἕξει τῆς τοῦ τμήματος ἐπιφανείας τοῦ περιλαμβάνοντος· τὸ γὰρ αὐτὸ πέρας αὐτῶν ἐστιν ἐν ἐπιπέδῳ τοῦ τε τμήματος καὶ τοῦ σχήματος ἡ περιφέρεια τοῦ κύκλου, οὗ διάμετρος ἡ ΑΒ, καὶ ἐπὶ τὰ αὐτὰ κοῖλαι ἀμφότεραί εἰσιν αἱ ἐπιφάνειαι, καὶ περιλαμβάνεται ἡ ἑτέρα ὑπὸ τῆς ἑτέρας.

   λζ΄.

   Ἡ ἐπιφάνεια τοῦ ἐγγεγραμμένου σχήματος ἐν τῷ τμήματι τῆς σφαίρας ἐλάσσων ἐστὶ τοῦ κύκλου, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος.

   Ἔστω σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΕΖ, καὶ ἔστω τμῆμα ἐν τῇ σφαίρᾳ, οὗ βάσις ὁ περὶ διάμετρον τὴν ΑΒ [καὶ ἐγγεγράφθω εἰς αὐτὸ τὸ εἰρημένον σχῆμα, καὶ ἐν τῷ τμήματι τοῦ κύκλου πολύγωνον], καὶ τὰ λοιπὰ τὰ αὐτὰ [85] διαμέτρου μὲν τῆς σφαίρας οὔσης τῆς ΘΛ, ἐπεζευγμένων δὲ τῶν ΛΕ, ΘΑ, καὶ ἔστω κύκλος ὁ Μ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἔστω τῇ ΑΘ· δεικτέον ὅτι ὁ Μ κύκλος μείζων ἐστὶ τῆς τοῦ σχήματος ἐπιφανείας.

   Ἡ γὰρ ἐπιφάνεια τοῦ σχήματος δέδεικται ἴση οὖσα κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε τῆς ΕΘ καὶ τῶν ΕΖ, ΓΔ, ΚΑ· τὸ δὲ ὑπὸ τῆς ΕΘ καὶ τῶν ΕΖ, ΓΔ, ΚΑ δέδεικται ἴσον τῷ ὑπὸ τῶν ΕΛ, ΚΘ περιεχομένῳ· τὸ δὲ ὑπὸ τῶν ΕΛ, ΚΘ ἔλασσόν ἐστι τοῦ ἀπὸ τῆς ΑΘ [καὶ γὰρ τοῦ ΛΘ, ΚΘ]· φανερὸν οὖν ὅτι ἡ ἐκ τοῦ κέντρου τοῦ κύκλου, ὅς ἐστιν ἴσος τῇ ἐπιφανείᾳ τοῦ σχήματος, ἐλάσσων ἐστὶ τῆς ἐκ τοῦ κέντρου τοῦ Μ· δῆλον ἄρα ὅτι ὁ Μ κύκλος μείζων ἐστὶ τῆς ἐπιφανείας τοῦ σχήματος.

   λη΄.

   Τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ τμήματι ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενον σὺν τῷ κώνῳ τῷ βάσιν μὲν τὴν αὐτὴν ἔχοντι τῷ σχήματι, κορυφὴν δὲ τὸ κέντρον τῆς [86] σφαίρας, ἴσον ἐστὶ τῷ κώνῳ τῷ βάσιν ἔχοντι ἴσην τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ τῇ ἀπὸ τοῦ κέντρου τῆς σφαίρας ἐπὶ μίαν πλευρὰν τῶν τοῦ πολυγώνου καθέτῳ ἠγμένῃ.

   Ἔστω γὰρ σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος καὶ τμῆμα ἔλασσον ἡμικυκλίου τὸ ΑΒΓ καὶ κέντρον τὸ Ε, καὶ ἐγγεγράφθω εἰς τὸ ΑΒΓ τμῆμα πολύγωνον ἀρτιόπλευρον χωρὶς τῆς ΑΓ ὁμοίως τοῖς πρότερον, καὶ μενούσης τῆς ΒΛ περιενεχθεῖσα ἡ σφαῖρα ποιείτω σχῆμά τι ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενον, καὶ ἀπὸ τοῦ κύκλου τοῦ περὶ διάμετρον τὴν ΑΓ κῶνος ἀναγεγράφθω κορυφὴν ἔχων τὸ κέντρον, καὶ εἰλήφθω κῶνος ὁ Κ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ τῇ ἀπὸ τοῦ Ε κέντρου ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ· δεικτέον ὅτι ὁ Κ κῶνος ἴσος ἐστὶ τῷ περιεχομένῳ σχήματι σὺν τῷ κώνῳ τῷ ΑΕΓ.

   Ἀναγεγράφθωσαν δὴ καὶ κῶνοι ἀπὸ τῶν κύκλων τῶν περὶ διαμέτρους τὰς ΘΗ, ΔΖ κορυφὴν ἔχοντες τὸ Ε σημεῖον· οὐκοῦν ὁ μὲν ΗΒΘΕ ῥόμβος στερεὸς ἴσος ἐστὶ κώνῳ, οὗ ἡ μὲν βάσις ἴση ἐστὶ τῇ ἐπιφανείᾳ τοῦ [87] ΗΒΘ κώνου, τὸ ὕψος δὲ τῇ ἀπὸ τοῦ Ε ἐπὶ τὴν ΗΒ ἀγομένῃ καθέτῳ, τὸ δὲ περίλειμμα τὸ περιεχόμενον ὑπὸ τῆς ἐπιφανείας τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΗΘ, ΖΔ καὶ τῶν κωνικῶν τῶν ΖΕΔ, ΗΕΘ ἴσον ἐστὶ κώνῳ, οὗ ἡ βάσις μέν ἐστιν ἴση τῇ ἐπιφανείᾳ τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΗΘ, ΖΔ, ὕψος δὲ τῇ ἀπὸ τοῦ Ε ἐπὶ τὴν ΖΗ καθέτῳ ἠγμένῃ. Πάλιν τὸ περίλειμμα τὸ περιεχόμενον ὑπό τε τῆς ἐπιφανείας τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΖΔ, ΑΓ καὶ τῶν κωνικῶν τῶν ΑΕΓ, ΖΕΔ ἴσον ἐστὶ κώνῳ, οὗ ἡ μὲν βάσις ἴση ἐστὶ τῇ ἐπιφανείᾳ τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων τῶν κατὰ τὰς ΖΔ, ΑΓ, ὕψος δὲ τῇ ἀπὸ τοῦ Ε ἐπὶ τὴν ΖΑ καθέτῳ ἠγμένῃ· οἱ οὖν εἰρημένοι κῶνοι ἴσοι ἔσονται τῷ σχήματι μετὰ τοῦ ΑΕΓ κώνου. Καὶ ὕψος μὲν ἴσον ἔχουσιν τῇ ἀπὸ τοῦ Ε ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ, τὰς δὲ βάσεις ἴσας τῇ ἐπιφανείᾳ του ΑΖΗΒΘΔΓ σχήματος· ἔχει δὲ καὶ ὁ Κ κῶνος τὸ αὐτὸ ὕψος καὶ βάσιν ἴσην τῇ ἐπιφανείᾳ τοῦ σχήματος· ἴσος ἄρα ἐστὶν ὁ κῶνος τοῖς εἰρημένοις κώνοις. Οἱ δὲ εἰρημένοι κῶνοι ἐδείχθησαν ἴσοι τῷ σχήματι καὶ τῷ ΑΕΓ κώνῳ· καὶ ὁ Κ ἄρα κῶνος ἴσος ἐστὶ τῷ τε σχήματι καὶ τῷ ΑΕΓ κώνῳ.

ΠΟΡΙΣΜΑ.

   Ἐκ δὴ τούτου φανερὸν ὅτι ὁ κῶνος ὁ βάσιν μὲν ἔχων τὸν κύκλον, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς [88] ἐστι βάσις τοῦ τμήματος, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας, μείζων ἐστὶ τοῦ ἐγγεγραμμένου σχήματος σὺν τῷ κώνῳ· ὁ γὰρ προειρημένος κῶνος μείζων ἐστὶ τοῦ κώνου τοῦ ἴσου τῷ σχήματι σὺν τῷ κώνῳ τῷ βάσιν μὲν ἔχοντι τὴν βάσιν τοῦ τμήματος, τὴν δὲ κορυφὴν πρὸς τῷ κέντρῳ, τουτέστι τοῦ τὴν βάσιν μὲν ἔχοντος ἴσην τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ τῇ ἀπὸ τοῦ κέντρου ἐπὶ μίαν πλευρὰν τοῦ πολυγώνου καθέτῳ ἠγμένῃ· ἥ τε γὰρ βάσις τῆς βάσεως μείζων ἐστὶ [δέδεικται γὰρ τοῦτο] καὶ τὸ ὕψος τοῦ ὕψους.

   λθ΄.

   Ἔστω σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΓ, καὶ τετμήσθω ἔλασσον ἡμικυκλίου, ὃ ἀποτέμνει ἡ ΑΒ, καὶ κέντρον τὸ Δ, καὶ ἀπὸ τοῦ κέντρου τοῦ Δ ἐπὶ τὰ Α, Β ἐπεζεύχθωσαν αἱ ΑΔ, ΔΒ, καὶ περὶ τὸν γεννηθέντα τομέα περιγεγράφθω πολύγωνον καὶ περὶ αὐτὸ κύκλος· ἕξει δὴ τὸ αὐτὸ κέντρον τῷ ΑΒΓ κύκλῳ. Ἐὰν δὴ μενούσης τῆς ΕΚ περιενεχθὲν τὸ πολύγωνον εἰς τὸ αὐτὸ πάλιν ἀποκατασταθῇ, ὁ περιγεγραμμένος κύκλος κατὰ ἐπιφανείας οἰσθήσεται σφαίρας, καὶ αἱ γωνίαι τοῦ πολυγώνου κύκλους γράψουσιν, ὧν αἱ διάμετροι ἐπιζευγνύουσιν τὰς γωνίας τοῦ πολυγώνου οὖσαι παράλληλοι τῇ ΑΒ, τὰ δὲ σημεῖα, καθ᾿ ἃ ἅπτονται τοῦ ἐλάσσονος κύκλου αἱ τοῦ πολυγώνου πλευραί, κύκλους γράφουσιν ἐν τῇ ἐλάσσονι σφαίρᾳ, ὧν διάμετροι ἔσονται αἱ ἐπιζευγνύουσαι τὰς ἁφὰς παράλληλοι οὖσαι τῇ ΑΒ, αἱ δὲ πλευραὶ κατὰ κωνικῶν ἐπιφανειῶν οἰσθήσονται, καὶ ἔσται τὸ περιγραφὲν σχῆμα ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενον, οὗ βάσις ὁ περὶ τὴν ΖΗ κύκλος· [89] ἡ δὴ τοῦ εἰρημένου σχήματος ἐπιφάνεια μείζων ἐστὶ τῆς τοῦ ἐλάσσονος τμήματος ἐπιφανείας, οὗ βάσις ὁ περὶ τὴν ΑΒ κύκλος.

   Ἤχθωσαν γὰρ ἐφαπτόμεναι αἱ ΑΜ, ΒΝ· κατὰ κωνικῆς ἄρα ἐπιφανείας οἰσθήσονται, καὶ τὸ σχῆμα τὸ γενηθὲν ὑπὸ τοῦ πολυγώνου τοῦ ΑΜΘΕΛΝΒ μείζονα ἕξει τὴν ἐπιφάνειαν τοῦ τμήματος τῆς σφαίρας, οὗ βάσις ὁ περὶ διάμετρον τὴν ΑΒ κύκλος [πέρας γὰρ ἐν ἑνὶ ἐπιπέδῳ τὸ αὐτὸ ἔχουσιν τὸν περὶ διάμετρον τὴν ΑΒ κύκλον, καὶ περιλαμβάνεται τὸ τμῆμα ὑπὸ τοῦ σχήματος]. Ἀλλ᾿ ἡ γεγενημένη ὑπὸ τῶν ΖΜ, ΗΝ ἐπιφάνεια κώνου μείζων ἐστὶ τῆς γεγενημένης ὑπὸ τῶν ΜΑ, ΝΒ· ἡ μὲν γὰρ ΖΜ τῆς ΜΑ μείζων ἐστὶ [ὑπὸ γὰρ ὀρθὴν ὑποτείνει], ἡ δὲ ΝΗ τῆς ΝΒ, ὅταν δὲ τοῦτο ᾖ, μείζων γίνεται ἡ ἐπιφάνεια τῆς ἐπιφανείας [ταῦτα γὰρ δέδεικται ἐν τοῖς λήμμασιν]. Δῆλον οὖν ὅτι καὶ τοῦ περιγεγραμμένου σχήματος ἡ ἐπιφάνεια μείζων ἐστὶ τῆς τοῦ τμήματος ἐπιφανείας τῆς ἐλάσσονος σφαίρας.

ΠΟΡΙΣΜΑ.

[90]   Καὶ φανερὸν ὅτι ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος τοῦ περὶ τὸν τομέα ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ περιεχόμενον ὑπό τε μιᾶς πλευρᾶς τοῦ πολυγώνου καὶ τῶν ἐπιζευγνυουσῶν πασῶν τὰς γωνίας τοῦ πολυγώνου καὶ ἔτι τῆς ἡμισείας τῆς βάσεως τοῦ εἰρημένου πολυγώνου [τὸ γὰρ ὑπὸ τοῦ πολυγώνου γεγραμμένον σχῆμα ἐγγεγραμμένον ἐστὶν εἰς τὸ τμῆμα τῆς μείζονος σφαίρας, τοῦτο δὲ δῆλον διὰ τὸ προγεγραμμένον].

   μ΄.

   Τοῦ περιγεγραμμένου σχήματος τῷ τομεῖ ἡ ἐπιφάνεια μείζων ἐστὶ κύκλου, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἠγμένῃ ἐπὶ τὴν περιφέρειαν τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος.

[91]    Ἔστω γὰρ σφαῖρα καὶ μέγιστος κύκλος ἐπ᾿ αὐτῆς ὁ ΑΒΓΔ καὶ κέντρον τὸ Ε, καὶ περὶ τὸν τομέα περιγεγράφθω τὸ ΛΚΖ πολύγωνον, καὶ περὶ αὐτὸ κύκλος περιγεγράφθω, καὶ γεγενήσθω σχῆμα, καθάπερ πρότερον, καὶ ἔστω κύκλος ὁ Ν, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε μιᾶς πλευρᾶς τοῦ πολυγώνου καὶ πασῶν τῶν ἐπιζευγνυουσῶν σὺν τῇ ἡμισείᾳ τῆς ΚΛ. Ἀλλὰ τὸ εἰρημένον χωρίον ἴσον ἐστὶ τῷ ὑπὸ τῆς ΜΘ καὶ ΖΗ [ὃ δή ἐστιν ὕψος τοῦ τμήματος τῆς μείζονος σφαίρας· τοῦτο γὰρ προδέδεικται]. Τοῦ ἄρα Ν κύκλου ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ ὑπὸ ΜΘ, ΗΖ περιεχομένῳ. Ἀλλ᾿ ἡ μὲν ΗΖ μείζων ἐστὶ τῆς ΔΞ [ὅ ἐστιν ὕψος τοῦ ἐλάσσονος τμήματος· ἐὰν γὰρ ἐπιζεύξωμεν τὴν ΚΖ, ἔσται παράλληλος τῇ ΔΑ. Ἔστιν δὲ καὶ ἡ ΑΒ τῇ ΚΛ παράλληλος, καὶ κοινὴ ἡ ΖΕ· ὅμοιον ἄρα τὸ ΖΚΗ τρίγωνον τῷ ΔΑΞ τριγώνῳ. Καί ἐστιν μείζων ἡ ΖΚ τῆς ΑΔ· μείζων ἄρα καὶ ἡ ΖΗ τῆς ΔΞ], ἴση δὲ ἡ ΜΘ τῇ διαμέτρῳ τῇ ΓΔ [ἐὰν γὰρ ἐπιζευχθῇ ἡ ΕΟ, ἐπεὶ ἴση ἐστὶν ἡ μὲν ΜΟ τῇ ΟΖ, ἡ δ ΘΕ τῇ ΕΖ, παράλληλος ἄρα ἐστὶν ἡ ΕΟ τῇ ΜΘ· διπλασία ἄρα ἐστὶν ἡ ΜΘ τῇ ΕΟ. Ἀλλὰ καὶ ἡ ΓΔ διπλασία ἐστὶν τῆς ΕΟ· ἴση ἄρα ἐστὶν ἡ ΜΘ τῇ ΓΔ], τὸ δὲ ὑπὸ τῶν ΓΔ, ΔΞ ἴσον τῷ ἀπὸ τῆς ΑΔ· ἡ ἄρα τοῦ σχήματος τοῦ ΚΖΛ ἐπιφάνεια μείζων ἐστὶ τοῦ κύκλου, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος, τοῦ περὶ διάμετρον τὴν ΑΒ· ὁ γὰρ Ν κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ περιγεγραμμένου περὶ τὸν τομέα σχήματος.

[92]

ΠΟΡΙΣΜΑ α΄.

   Γίνεται δὴ καὶ τὸ περιγεγραμμένον σχῆμα περὶ τὸν τομέα σὺν τῷ κώνῳ, οὗ βάσις ὁ περὶ διάμετρον τὴν ΚΛ κύκλος, κορυφὴ δὲ τὸ κέντρον, ἴσον κώνῳ, οὗ ἡ μὲν βάσις ἴση ἐστὶ τῇ ἐπιφανείᾳ τοῦ σχήματος, ὕψος δὲ τῇ ἀπὸ τοῦ κέντρου ἐπὶ τὴν πλευρὰν καθέτῳ ἠγμένῃ [ἣ δὴ ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου τῆς σφαίρας· τὸ γὰρ περιγεγραμμένον σχῆμα τῷ τομεῖ ἐγγεγραμμένον ἐστὶν εἰς τὸ τμῆμα τῆς μείζονος σφαίρας, ἧς κέντρον ἐστὶ τὸ αὐτό· δῆλον οὖν τὸ λεγόμενόν ἐστιν ἐκ τοῦ προγεγραμμένου].

ΠΟΡΙΣΜΑ β΄.

   Ἐκ τούτου δὲ φανερὸν ὅτι τὸ περιγεγραμμένον σχῆμα σὺν τῷ κώνῳ μεῖζόν ἐστι κώνου τοῦ βάσιν μὲν ἔχοντος τὸν κύκλον, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος τῆς ἐλάσσονος σφαίρας ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος, ὕψος δὲ τῇ ἐκ τοῦ κέντρου· ὁ γὰρ ἴσος κῶνος τῷ σχήματι σὺν τῷ κώνῳ τὴν μὲν βάσιν μείζονα ἕξει τοῦ εἰρημένου κύκλου, τὸ δὲ ὕψος ἴσον τῇ ἐκ τοῦ κέντρου τῆς ἐλάσσονος σφαίρας.

   μα΄.

   Ἔστω πάλιν σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος καὶ τμῆμα ἔλασσον ἡμικυκλίου τὸ ΑΒΓ καὶ κέντρον τὸ Δ, καὶ εἰς τὸν ΑΒΓ τομέα ἐγγεγράφθω πολύγωνον ἀρτιόγωνον, καὶ τούτῳ ὅμοιον περιγεγράφθω, καὶ παράλληλοι ἔστωσαν αἱ πλευραὶ ταῖς πλευραῖς, καὶ κύκλος περιγεγράφθω περὶ [93] τὸ περιγεγραμμένον πολύγωνον, καὶ ὁμοίως τοῖς πρότερον μενούσης τῆς ΗΒ περιενεχθέντες οἱ κύκλοι ποιείτωσαν σχήματα ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενα· δεικτέον ὅτι ἡ τοῦ περιγεγραμμένου σχήματος ἐπιφάνεια πρὸς τὴν τοῦ ἐγγεγραμμένου σχήματος ἐπιφάνειαν διπλασίονα λόγον ἔχει ἢ ἡ πλευρὰ ἡ τοῦ περιγεγραμμένου πολυγώνου πρὸς τὴν πλευρὰν τοῦ ἐγγεγραμμένου πολυγώνου, τὸ δὲ σχῆμα σὺν τῷ κώνῳ τριπλασίονα λόγον ἔχει τοῦ αὐτοῦ.

   Ἔστω γὰρ ὁ Μ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ ὑπό τε μιᾶς πλευρᾶς τοῦ περιγεγραμμένου πολυγώνου καὶ πασῶν τῶν ἐπιζευγνυουσῶν τὰς γωνίας καὶ ἔτι τῆς ἡμισείας τῆς ΕΖ· ἔσται δὴ ὁ Μ κύκλος ἴσος τῇ ἐπιφανείᾳ [94] τοῦ περιγεγραμμένου σχήματος. Εἰλήφθω δὴ καὶ ὁ Ν κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴσον δύναται τῷ περιεχομένῳ ὑπό τε μιᾶς πλευρᾶς τοῦ ἐγγεγραμμένου πολυγώνου καὶ πασῶν τῶν ἐπιζευγνυουσῶν τὰς γωνίας σὺν τῇ ἡμισείᾳ τῆς ΑΓ· ἔσται δὴ καὶ οὗτος ἴσος τῇ ἐπιφανείᾳ τοῦ ἐγγεγραμμένου σχήματος. Ἀλλὰ τὰ εἰρημένα χωρία ἐστὶ πρὸς ἄλληλα ὡς τὸ ἀπὸ τῆς ΕΚ πλευρᾶς πρὸς τὸ ἀπὸ τῆς ΑΛ πλευρᾶς [καὶ ὡς ἄρα τὸ πολύγωνον πρὸς τὸ πολύγωνον, ὁ Μ κύκλος πρὸς τὸν Ν κύκλον]· φανερὸν οὖν ὅτι καὶ ἡ ἐπιφάνεια τοῦ περιγεγραμμένου σχήματος πρὸς τὴν ἐπιφάνειαν τοῦ ἐγγεγραμμένου σχήματος διπλασίονα λόγον ἔχει ἤπερ ἡ ΕΚ πρὸς ΑΛ [τὸν δὲ αὐτόν, ὃν καὶ τὸ πολύγωνον].

   Ἔστω πάλιν κῶνος ὁ Ξ βάσιν μὲν ἔχων τῷ Μ ἴσην, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς ἐλάσσονος σφαίρας· ἴσος δὴ οὗτός ἐστιν ὁ κῶνος τῷ περιγεγραμμένῳ σχήματι σὺν τῷ κώνῳ, οὗ βάσις ὁ περὶ τὴν ΕΖ κύκλος, κορυφὴ δὲ τὸ Δ. Καὶ ἔστω ἄλλος κῶνος ὁ Ο βάσιν μὲν ἴσην ἔχων τῷ Ν, ὕψος δὲ τὴν ἀπὸ τοῦ Δ ἐπὶ τὴν ΑΛ κάθετον ἠγμένην· ἔσται δὴ καὶ οὗτος ἴσος τῷ ἐγγεγραμμένῳ σχήματι σὺν τῷ κώνῳ, οὗ βάσις ὁ περὶ διάμετρον τὴν ΑΓ κύκλος, κορυφὴ δὲ τὸ Δ κέντρον· ταῦτα γὰρ πάντα προγέγραπται. Καὶ [ἐπεί] ἐστιν ὡς ἡ ΕΚ πρὸς τὴν ἐκ τοῦ κέντρου τῆς ἐλάσσονος σφαίρας οὕτως ἡ ΑΛ πρὸς τὴν ἀπὸ τοῦ κέντρου [τοῦ Δ] ἐπὶ τὴν ΑΛ κάθετον ἠγμένην, ἐδείχθη δὲ ὡς ἡ ΕΚ πρὸς τὴν ΑΛ οὕτως ἡ ἐκ τοῦ κέντρου τοῦ Μ κύκλου πρὸς τὴν ἐκ τοῦ κέντρου τοῦ Ν κύκλου [καὶ ἡ διάμετρος πρὸς τὴν διάμετρον]· ἔσται ἄρα ὡς ἡ διάμετρος τοῦ κύκλου, ὅς ἐστι βάσις τοῦ Ξ, πρὸς τὴν διάμετρον τοῦ κύκλου, ὅς ἐστι βάσις τοῦ Ο, οὕτως τὸ ὕψος τοῦ Ξ κώνου πρὸς τὸ ὕψος τοῦ [95] Ο κώνου [ὅμοιοι ἄρα εἰσὶν οἱ κῶνοι]. Ὁ Ξ ἄρα κῶνος πρὸς τὸν Ο κῶνον τριπλασίονα λόγον ἔχει ἤπερ ἡ διάμετρος πρὸς τὴν διάμετρον· φανερὸν οὖν ὅτι καὶ τὸ σχῆμα τὸ περιγεγραμμένον σὺν τῷ κώνῳ πρὸς τὸ ἐγγεγραμμένον σὺν τῷ κώνῳ τριπλασίονα λόγον ἔχει ἤπερ ἡ ΕΚ πρὸς ΑΛ.

   μβ΄.

   Παντὸς τμήματος σφαίρας ἐλάσσονος ἡμισφαιρίου ἡ ἐπιφάνεια ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος τῆς σφαίρας.

   Ἔστω σφαῖρα καὶ μέγιστος ἐν αὐτῇ κύκλος ὁ ΑΒΓ καὶ τμῆμα ἐν αὐτῇ ἔλασσον ἡμισφαιρίου, οὗ βάσις ὁ περὶ τὴν ΑΓ κύκλος πρὸς ὀρθὰς ὢν τῷ ΑΒΓ κύκλῳ, καὶ εἰλήφθω κύκλος ὁ Ζ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΑΒ· δεῖ δὴ δεῖξαι ὅτι ἡ ἐπιφάνεια τοῦ ΑΒΓ τμήματος ἴση ἐστὶ τῷ Ζ κύκλῳ.

[96]    Εἰ γὰρ μή, ἔστω μείζων ἡ ἐπιφάνεια τοῦ Ζ κύκλου, καὶ εἰλήφθω τὸ Δ κέντρον, καὶ ἀπὸ τοῦ Δ ἐπὶ τὰ Α, Γ ἐπιζευχθεῖσαι ἐκβεβλήσθωσαν· καὶ δύο μεγεθῶν ἀνίσων ὄντων, τῆς τε ἐπιφανείας τοῦ τμήματος καὶ τοῦ Ζ κύκλου, ἐγγεγράφθω εἰς τὸν ΑΒΓ τομέα πολύγωνον ἰσόπλευρον καὶ ἀρτιογώνιον, καὶ ἄλλο τούτῳ ὅμοιον περιγεγράφθω, ὥστε τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχειν ἤπερ ἡ ἐπιφάνεια τοῦ τμήματος τῆς σφαίρας πρὸς τὸν Ζ κύκλον, περιενεχθέντος δὲ τοῦ κύκλου, ὡς καὶ πρότερον, ἔσται δύο σχήματα ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενα, ὧν τὸ μὲν περιγεγραμμένον, τὸ δὲ ἐγγεγραμμένον, καὶ ἡ τοῦ περιγεγραμμένου σχήματος ἐπιφάνεια πρὸς τὴν τοῦ ἐγγεγραμμένου ἔσται ὡς τὸ περιγεγραμμένον πολύγωνον πρὸς τὸ ἐγγεγραμμένον· ἑκάτερος γὰρ τῶν λόγων διπλάσιός ἐστι τοῦ ὃν ἔχει ἡ τοῦ περιγεγραμμένου πολυγώνου πλευρὰ πρὸς τὴν τοῦ ἐγγεγραμμένου πλευράν. Ἀλλὰ τὸ περιγεγραμμένον πολύγωνον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχει ἤπερ ἡ τοῦ εἰρημένου τμήματος ἐπιφάνεια πρὸς τὸν Ζ κύκλον, μείζων δέ ἐστιν ἡ τοῦ περιγεγραμμένου σχήματος ἐπιφάνεια τῆς ἐπιφανείας τοῦ τμήματος· καὶ ἡ τοῦ ἐγγεγραμμένου σχήματος ἐπιφάνεια ἄρα μείζων ἐστὶ τοῦ Ζ κύκλου· ὅπερ ἀδύνατον· δέδεικται γὰρ ἡ εἰρημένη τοῦ σχήματος ἐπιφάνεια ἐλάσσων οὖσα τοῦ τηλικούτου κύκλου.

   Ἔστω πάλιν ὁ κύκλος μείζων τῆς ἐπιφανείας, καὶ περιγεγράφθω καὶ ἐγγεγράφθω ὅμοια πολύγωνα, καὶ τὸ περιγεγραμμένον πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἐχέτω τοῦ ὃν ἔχει ὁ κύκλος πρὸς τὴν ἐπιφάνειαν τοῦ τμήματος. Οὐκ ἄρα μείζων ἡ ἐπιφάνεια τοῦ Ζ κύκλου. Ἐδείχθη δὲ ὡς οὐδὲ ἐλάσσων· ἴση ἄρα.

[97]    μγ΄.

   Καὶ ἐὰν μεῖζον ἡμισφαιρίου ᾖ τμῆμα, ὁμοίως αὐτοῦ ἡ ἐπιφάνεια ἴση ἐστὶ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἔσται τῇ ἀπὸ τῆς κορυφῆς ἐπὶ τὴν περιφέρειαν ἠγμένῃ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος.

   Ἔστω γὰρ σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος, καὶ νοείσθω τετμημένη ἐπιπέδῳ ὀρθῷ τῷ κατὰ τὴν ΑΔ, καὶ τὸ ΑΒΔ ἔλασσον ἔστω ἡμισφαιρίου, καὶ διάμετρος ἡ ΒΓ πρὸς ὀρθὰς τῇ ΑΔ, καὶ ἀπὸ τῶν Β, Γ ἐπὶ τὸ Α ἐπεζεύχθωσαν αἱ ΒΑ, ΑΓ, καὶ ἔστω ὁ μὲν Ε κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΑΒ, ὁ δὲ Ζ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΑΓ, ὁ δὲ Η κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΒΓ· καὶ ὁ Η ἄρα κύκλος ἴσος ἐστὶ τοῖς δυσὶ κύκλοις τοῖς Ε, Ζ. Ὁ δὲ Η κύκλος ἴσος ἐστὶν ὅλῃ τῇ ἐπιφανείᾳ τῆς σφαίρας [ἐπειδήπερ ἑκατέρα τετραπλασία ἐστὶ τοῦ περὶ διάμετρον τὴν ΒΓ κύκλου], ὁ δὲ Ε κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΑΒΔ τμήματος [δέδεικται γὰρ τοῦτο ἐπὶ τοῦ ἐλάσσονος ἡμισφαιρίου]· λοιπὸς ἄρα ὁ Ζ κύκλος ἴσος ἐστὶ τῇ τοῦ ΑΓΔ τμήματος ἐπιφανείᾳ, ὃ δή ἐστι μεῖζον ἡμισφαιρίου.

[98]    μδ΄.

   Παντὶ τομεῖ σφαίρας ἴσος ἐστὶ κῶνος ὁ βάσιν μὲν ἔχων ἴσην τῇ ἐπιφανείᾳ τοῦ τμήματος τῆς σφαίρας τοῦ κατὰ τὸν τομέα, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας.

   Ἔστω σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΔ καὶ κέντρον τὸ Γ καὶ κῶνος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν ἴσον τῇ κατὰ τὴν ΑΒΔ περιφέρειαν ἐπιφανείᾳ, ὕψος δὲ ἴσον τῇ ΒΓ· δεικτέον ὅτι ὁ τομεὺς ὁ ΑΒΓΔ ἴσος ἐστὶ τῷ εἰρημένῳ κώνῳ. [99] Εἰ γὰρ μή, ἔστω μείζων ὁ τομεὺς τοῦ κώνου, καὶ κείσθω ὁ Θ κῶνος, οἷος εἴρηται· δύο δὴ μεγεθῶν ἀνίσων ὄντων, τοῦ τομέως καὶ τοῦ Θ κώνου, εὑρήσθωσαν δύο γραμμαὶ αἱ Δ, Ε, μείζων δὲ ἡ Δ τῆς Ε, καὶ ἐλάσσονα λόγον ἐχέτω ἡ Δ πρὸς Ε ἤπερ ὁ τομεὺς πρὸς τὸν κῶνον, καὶ εἰλήφθωσαν δύο γραμμαὶ αἱ Ζ, Η, ὅπως τῷ ἴσῳ ὑπερέχῃ ἡ Δ τῆς Ζ καὶ ἡ Ζ τῆς Η καὶ ἡ Η τῆς Ε, καὶ περὶ τὸν ἐπίπεδον τομέα τοῦ κύκλου περιγεγράφθω πολύγωνον ἰσόπλευρον καὶ ἀρτιογώνιον, καὶ τούτῳ ὅμοιον ἐγγεγράφθω, ὅπως ἡ τοῦ περιγεγραμμένου πλευρὰ ἐλάσσονα λόγον ἔχῃ πρὸς τὴν τοῦ ἐγγεγραμμένου τοῦ ὃν ἔχει ἡ Δ πρὸς Ζ, καὶ ὁμοίως τοῖς πρότερον περιενεχθέντος τοῦ κύκλου γεγενήσθω δύο σχήματα ὑπὸ κωνικῶν ἐπιφανειῶν περιεχόμενα· τὸ ἄρα περιγεγραμμένον σὺν τῷ κώνῳ τῷ κορυφὴν ἔχοντι τὸ Γ σημεῖον πρὸς τὸ ἐγγεγραμμένον σὺν τῷ κώνῳ τριπλασίονα λόγον ἔχει τοῦ ὃν ἔχει ἡ πλευρὰ τοῦ περιγεγραμμένου πολυγώνου πρὸς τὴν πλευρὰν τοῦ ἐγγεγραμμένου. Ἀλλὰ ἡ τοῦ περιγεγραμμένου ἐλάσσονα λόγον ἔχει ἤπερ ἡ Δ πρὸς Ζ· ἐλάσσονα λόγον ἄρα ἕξει ἢ τριπλάσιον τὸ εἰρημένον στερεὸν σχῆμα τοῦ τῆς Δ πρὸς Ζ. Ἡ δὲ Δ πρὸς Ε μείζονα λόγον ἔχει ἢ τριπλάσιον τοῦ τῆς Δ πρὸς Ζ· τὸ ἄρα περιγεγραμμένον σχῆμα στερεὸν τῷ τομεῖ πρὸς τὸ ἐγγεγραμμένον σχῆμα ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἡ Δ πρὸς Ε. Ἡ δὲ Δ πρὸς Ε ἐλάσσονα λόγον ἔχει ἢ ὁ στερεὸς τομεὺς πρὸς τὸν Θ κῶνον· μείζονα ἄρα λόγον ἔχει ὁ στερεὸς τομεὺς πρὸς τὸν Θ κῶνον ἢ τὸ περιγεγραμμένον τῷ τομεῖ σχῆμα πρὸς τὸ ἐγγεγραμμένον. Καὶ ἐναλλάξ· μεῖζον δέ ἐστι τὸ περιγεγραμμένον στερεὸν σχῆμα τοῦ τμήματος· καὶ τὸ ἐγγεγραμμένον ἄρα σχῆμα ἐν τῷ τομεῖ [100] μεῖζόν ἐστι τοῦ Θ κώνου· ὅπερ ἀδύνατον· δέδεικται γὰρ ἐν τοῖς ἄνω ἔλασσον ὂν τοῦ τηλικούτου κώνου [τουτέστι τοῦ ἔχοντος βάσιν μὲν κύκλον, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν ἐπιζευγνυμένῃ εὐθείᾳ τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς σφαίρας· οὗτος δέ ἐστιν ὁ εἰρημένος κῶνος ὁ Θ· βάσιν τε γὰρ ἔχει κύκλον ἴσον τῇ ἐπιφανείᾳ τοῦ τμήματος, τουτέστι τῷ εἰρημένῳ κύκλῳ, καὶ ὕψος ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας]· οὐκ ἄρα ὁ στερεὸς τομεὺς μείζων ἐστὶ τοῦ Θ κώνου.

   Ἔστω δὴ πάλιν ὁ Θ κῶνος τοῦ στερεοῦ τομέως μείζων. Πάλιν δὴ ὁμοίως ἡ Δ πρὸς τὴν Ε μείζων αὐτῆς οὖσα ἐλάσσονα λόγον ἐχέτω τοῦ ὃν ἔχει ὁ κῶνος πρὸς τὸν τομέα, καὶ ὁμοίως εἰλήφθωσαν αἱ Ζ, Η, ὥστε εἶναι τὰς διαφορὰς τὰς αὐτάς, καὶ τοῦ περιγεγραμμένου περὶ τὸν ἐπίπεδον τομέα πολυγώνου ἀρτιογώνου ἡ πλευρὰ πρὸς τὴν τοῦ ἐγγεγραμμένου ἐλάσσονα λόγον ἐχέτω τοῦ ὃν ἔχει ἡ Δ πρὸς Ζ [καὶ γεγενήσθω τὰ περὶ τὸν στερεὸν τομέα στερεὰ σχήματα]· ὁμοίως οὖν δείξομεν ὅτι τὸ περιγεγραμμένον περὶ τὸν τομέα στερεὸν σχῆμα πρὸς τὸ ἐγγεγραμμένον ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἡ Δ πρὸς Ε καὶ τοῦ ὃν ἔχει ὁ Θ κῶνος πρὸς τὸν τομέα [ὥστε καὶ ὁ τομεὺς πρὸς τὸν κῶνον ἐλάσσονα λόγον ἔχει ἤπερ τὸ ἐγγεγραμμένον στερεὸν ἐν τῷ τμήματι πρὸς τὸ περιγεγραμμένον]. Μείζων δέ ἐστιν ὁ τομεὺς τοῦ ἐγγεγραμμένου εἰς αὐτὸν σχήματος· μείζων ἄρα ὁ Θ κῶνος τοῦ περιγεγραμμένου σχήματος· ὅπερ ἀδύνατον [δέδεικται γὰρ τοῦτο ὅτι ὁ τηλικοῦτος κῶνος ἐλάσσων ἐστὶ τοῦ περιγεγραμμένου σχήματος περὶ τὸν τομέα]· ἴσος ἄρα ὁ τομεὺς τῷ Θ κώνῳ.

---

ΠΕΡΙ ΣΦΑΙΡΑΣ ΚΑΙ ΚΥΛΙΝΔΡΟΥ Β΄

Ἀρχιμήδης Δοσιθέῳ χαίρειν.

[101]   Πρότερον μὲν ἐπέστειλάς μοι γράψαι τῶν προβλημάτων τὰς ἀποδείξεις, ὧν αὐτὸς τὰς προτάσεις ἀπέστειλα Κόνωνι· συμβαίνει δὲ αὐτῶν τὰ πλεῖστα γράφεσθαι διὰ τῶν θεωρημάτων, ὧν πρότερον ἀπέστειλά σοι τὰς ἀποδείξεις, ὅτι τε πάσης σφαίρας ἡ ἐπιφάνεια τετραπλασία ἐστὶ τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ, καὶ δὴ ὅτι παντὸς τμήματος σφαίρας τῇ ἐπιφανείᾳ ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ εὐθείᾳ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος ἐπὶ τὴν περιφέρειαν τῆς βάσεως ἀγομένῃ, καὶ διότι πάσης σφαίρας ὁ κύλινδρος ὁ βάσιν μὲν ἔχων τὸν μέγιστον κύκλον τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας, αὐτός τε ἡμιόλιός ἐστι τῷ μεγέθει τῆς σφαίρας καὶ ἡ ἐπιφάνεια αὐτοῦ ἡμιολία τῆς ἐπιφανείας τῆς σφαίρας, καὶ διότι πᾶς τομεὺς στερεὸς ἴσος ἐστὶ κώνῳ τῷ βάσιν μὲν ἔχοντι τὸν κύκλον τὸν ἴσον τῇ ἐπιφανείᾳ τοῦ τμήματος τῆς σφαίρας τοῦ ἐν τῷ τομεῖ, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας. Ὅσα μὲν οὖν τῶν θεωρημάτων καὶ προβλημάτων γράφεται διὰ τούτων τῶν θεωρημάτων, ἐν τῷδε τῷ βιβλίῳ γράψας ἀπέσταλκά σοι, ὅσα δὲ δι᾿ ἄλλης εὑρίσκονται θεωρίας, τά τε περὶ ἑλίκων καὶ τὰ περὶ τῶν κωνοειδῶν, πειράσομαι διὰ τάχους ἀποστεῖλαι.

[102]    Τὸ δὲ πρῶτον ἦν τῶν προβλημάτων τόδε· Σφαίρας δοθείσης ἐπίπεδον χωρίον εὑρεῖν ἴσον τῇ ἐπιφανείᾳ τῆς σφαίρας. Ἔστιν δὲ τοῦτο φανερὸν δεδειγμένον ἐκ τῶν προειρημένων θεωρημάτων· τὸ γὰρ τετραπλάσιον τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ ἐπίπεδόν τε χωρίον ἐστὶ καὶ ἴσον τῇ ἐπιφανείᾳ τῆς σφαίρας.

   α΄.

   Τὸ δεύτερον ἦν· Κώνου δοθέντος ἢ κυλίνδρου σφαῖραν εὑρεῖν τῷ κώνῳ ἢ τῷ κυλίνδρῳ ἴσην.

   Ἔστω διδόμενος κῶνος ἢ κύλινδρος ὁ Α καὶ τῷ Α ἴση ἡ Β σφαῖρα, καὶ κείσθω τοῦ Α κώνου ἢ κυλίνδρου ἡμιόλιος κύλινδρος ὁ ΓΖΔ, τῆς δὲ Β σφαίρας ἡμιόλιος κύλινδρος, οὗ βάσις ὁ περὶ διάμετρον τὴν ΗΘ κύκλος, ἄξων δὲ ὁ ΚΛ ἴσος τῇ διαμέτρῳ τῆς Β σφαίρας· ἴσος ἄρα ἐστὶν ὁ Ε [103] κύλινρδος τῷ Κ κυλίνδρῳ [τῶν δὲ ἴσων κυλίνδρων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν]· ὡς ἄρα ὁ Ε κύκλος πρὸς τὸν Κ κύκλον, τουτέστιν ὡς τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ τῆς ΗΘ, οὕτως ἡ ΚΛ πρὸς ΕΖ. Ἴση δὲ ἡ ΚΛ τῇ ΗΘ [ὁ γὰρ ἡμιόλιος κύλινδρος τῆς σφαίρας ἴσον ἔχει τὸν ἄξονα τῇ διαμέτρῳ τῆς σφαίρας, καὶ ὁ Κ κύκλος μέγιστός ἐστι τῶν ἐν τῇ σφαίρᾳ]· ὡς ἄρα τὸ ἀπὸ ΓΔ πρὸς τὸ ἀπὸ ΗΘ, οὕτως ἡ ΗΘ πρὸς τὴν ΕΖ. Ἔστω τῷ ἀπὸ ΗΘ ἴσον τὸ ὑπὸ ΓΔ, ΜΝ· ὡς ἄρα ἡ ΓΔ πρὸς ΜΝ, οὕτως τὸ ἀπὸ ΓΔ πρὸς τὸ ἀπὸ ΗΘ, τουτέστιν ἡ ΗΘ πρὸς ΕΖ, καὶ ἐναλλάξ, ὡς ἡ ΓΔ πρὸς τὴν ΗΘ, οὕτως ἡ ΗΘ πρὸς τὴν ΜΝ καὶ ἡ ΜΝ πρὸς τὴν ΕΖ. Καί ἐστιν δοθεῖσα ἑκατέρα τῶν ΓΔ, ΕΖ· δύο ἄρα δοθεισῶν εὐθειῶν τῶν ΓΔ, ΕΖ δύο μέσαι ἀνάλογόν εἰσιν αἱ ΗΘ, ΜΝ· δοθεῖσα ἄρα ἑκατέρα τῶν ΗΘ, ΜΝ.

   Συντεθήσεται δὴ τὸ πρόβλημα οὕτως· ἔστω δὴ ὁ δοθεὶς κῶνος ἢ κύλινδρος ὁ Α· δεῖ δὴ τῷ Α κώνῳ ἢ κυλίνδρῳ ἴσην σφαῖραν εὑρεῖν.

   Ἔστω τοῦ Α κώνου ἢ κυλίνδρου ἡμιόλιος κύλινδρος, οὗ βάσις ὁ περὶ διάμετρον τὴν ΓΔ κύκλος, ἄξων δὲ ὁ ΕΖ, καὶ εἰλήφθω τῶν ΓΔ, ΕΖ δύο μέσαι ἀνάλογον αἱ ΗΘ, ΜΝ, ὥστε εἶναι ὡς τὴν ΓΔ πρὸς τὴν ΗΘ, τὴν ΗΘ πρὸς τὴν ΜΝ καὶ τὴν ΜΝ πρὸς τὴν ΕΖ, καὶ νοείσθω κύλινδρος, οὗ βάσις ὁ περὶ διάμετρον τὴν ΗΘ κύκλος, ἄξων δὲ ὁ ΚΛ ἴσος τῇ ΗΘ διαμέτρῳ· λέγω δὴ ὅτι ἴσος ἐστὶν ὁ Ε κύλινδρος τῷ Κ κυλίνδρῳ.

   Καὶ ἐπεί ἐστιν, ὡς ἡ ΓΔ πρὸς ΗΘ, ἡ ΜΝ πρὸς ΕΖ, καὶ ἐναλλάξ, καὶ ἴση ἡ ΗΘ τῇ ΚΛ [ὡς ἄρα ἡ ΓΔ πρὸς ΜΝ, τουτέστιν ὡς τὸ ἀπὸ τῆς ΓΔ πρὸς τὸ ἀπὸ ΗΘ, οὕτως ὁ Ε κύκλος πρὸς τὸν Κ κύκλον], ὡς ἄρα ὁ Ε κύκλος πρὸς τὸν Κ κύκλον, οὕτως ἡ ΚΔ πρὸς τὴν ΕΖ [τῶν ἄρα Ε, Κ κυλίνδρων [104] ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν]· ἴσος ἄρα ὁ Ε κύλινδρος τῷ Κ κυλίνδρῳ. Ὁ δὲ Κ κύλινδρος τῆς σφαίρας, ἧς διάμετρος ἡ ΗΘ, ἡμιόλιός ἐστιν· καὶ ἡ σφαῖρα ἄρα, ἧς ἡ διάμετρος ἴση ἐστὶ τῇ ΗΘ, τουτέστιν ἡ Β, ἴση ἐστὶ τῷ Α κώνῳ ἢ κυλίνδρῳ.

   β΄.

   Παντὶ τμήματι τῆς σφαίρας ἴσος ἐστὶ κῶνος ὁ βάσιν μὲν ἔχων τὴν αὐτὴν τῷ τμήματι, ὕψος δὲ εὐθεῖαν, ἥτις πρὸς τὸ ὕψος τοῦ τμήματος τὸν αὐτὸν λόγον ἔχει, ὃν συναμφότερος ἥ τε ἐκ τοῦ κέντρου τῆς σφαίρας καὶ τὸ ὕψος τοῦ λοιποῦ τμήματος πρὸς τὸ ὕψος τοῦ λοιποῦ τμήματος.

   Ἔστω σφαῖρα, ἐν ᾗ μέγιστος κύκλος, οὗ διάμετρος ἡ ΑΓ, καὶ τετμήσθω ἐπιπέδῳ ἡ σφαῖρα τῷ διὰ τῆς ΒΖ πρὸς ὀρθὰς τῇ ΑΓ, καὶ ἔστω κέντρον τὸ Θ, καὶ πεποιήσθω, ὡς συναμφότερος ἡ ΘΑ, ΑΕ πρὸς τὴν ΑΕ, οὕτως ἡ ΔΕ πρὸς ΓΕ, καὶ πάλιν πεποιήσθω, ὡς συναμφότερος ἡ ΘΓ, ΓΕ πρὸς ΓΕ, οὕτως ἡ ΚΕ πρὸς ΕΑ, καὶ ἀναγεγράφθωσαν κῶνοι ἀπὸ τοῦ κύκλου τοῦ περὶ διάμετρον τὴν ΒΖ κορυφὰς ἔχοντες τὰ Κ, Δ σημεῖα· λέγω ὅτι ἴσος ἐστὶν ὁ μὲν ΒΔΖ κῶνος τῷ κατὰ τὸ Γ τμήματι τῆς σφαίρας, ὁ δὲ ΒΚΖ τῷ κατὰ τὸ Α σημεῖον.

[105]    Ἐπεζεύχθωσαν γὰρ αἱ ΒΘ, ΘΖ, καὶ νοείσθω κῶνος βάσιν μὲν ἔχων τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, κορυφὴν δὲ τὸ Θ σημεῖον, καὶ ἔστω κῶνος ὁ Μ βάσιν ἔχων κύκλον ἴσον τῇ ἐπιφανείᾳ τοῦ ΒΓΖ τμήματος τῆς σφαίρας, τουτέστιν οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΒΓ, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας· ἔσται δὴ ὁ Μ κῶνος ἴσος τῷ ΒΓΘΖ στερεῷ τομεῖ· τοῦτο γὰρ δέδεικται ἐν τῷ πρώτῳ βιβλίῳ. Ἐπεὶ δέ ἐστιν, ὡς ἡ ΔΕ πρὸς ΕΓ, οὕτως συναμφότερος ἡ ΘΑ, ΑΕ πρὸς ΑΕ, διελόντι ἔσται, ὡς ἡ ΓΔ πρὸς ΓΕ, οὕτως ἡ ΘΑ πρὸς ΑΕ, τουτέστιν ἡ ΓΘ πρὸς ΑΕ, καὶ ἐναλλάξ, ὡς ἡ ΔΓ πρὸς ΓΘ ἐστίν, οὕτως ἡ ΓΕ πρὸς ΕΑ, καὶ συνθέντι, ὡς ἡ ΘΔ πρὸς ΘΓ, ἡ ΓΑ πρὸς ΑΕ, τουτέστι τὸ ἀπὸ ΓΒ πρὸς τὸ ἀπὸ ΒΕ· ὡς ἄρα ἡ ΔΘ πρὸς ΓΘ, τὸ ἀπὸ ΓΒ πρὸς τὸ ἀπὸ ΒΕ. Ἴση δέ ἐστιν ἡ ΓΒ τῇ ἐκ τοῦ κέντρου τοῦ Μ κύκλου, ἡ δὲ ΒΕ ἐκ τοῦ κέντρου ἐστὶ τοῦ περὶ διάμετρον τὴν ΒΖ κύκλου· ὡς ἄρα ἡ ΔΘ πρὸς ΘΓ, ὁ Μ κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον. Καί ἐστιν ἴση ἡ ΘΓ τῷ ἄξονι του Μ κώνου· καὶ ὡς ἄρα ἡ ΔΘ πρὸς τὸν ἄξονα τοῦ Μ κώνου, οὕτως ὁ Μ κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον· ἴσος ἄρα ὁ κῶνος ὁ βάσιν μὲν ἔχων τὸν Μ κύκλον, ὕψος δὲ τὴν ἐκ [106] τοῦ κέντρου τῆς σφαίρας, τῷ ΒΔΖΘ στερεῷ ῥόμβῳ [τοῦτο γὰρ ἐν τοῖς λήμμασι τοῦ πρώτου βιβλίου δέδεικται. Ἢ οὕτως· Ἐπεί ἐστιν, ὡς ἡ ΔΘ πρὸς τὸ ὕψος τοῦ Μ κώνου, οὕτως ὁ Μ κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, ἴσος ἄρα ἐστὶν ὁ Μ κῶνος τῷ κώνῳ, οὗ βάσις μὲν ὁ περὶ διάμετρον τὴν ΒΖ κύκλος, ὕψος δὲ ἡ ΔΘ· ἀντιπεπόνθασι γὰρ αὐτῶν αἱ βάσεις τοῖς ὕψεσιν. Ἀλλ᾿ ὁ κῶνος ὁ βάσιν μὲν ἔχων τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, ὕψος δὲ τὴν ΔΘ, ἴσος ἐστὶ τῷ ΒΔΖΘ στερεῷ ῥόμβῳ]. Ἀλλ᾿ ὁ Μ κῶνος ἴσος ἐστὶ τῷ ΒΓΖΘ στερεῷ τομεῖ· καὶ ὁ ΒΓΖΘ στερεὸς τομεὺς ἄρα ἴσος ἐστὶ τῷ ΒΔΖΘ στερεῷ ῥόμβῳ. Κοινοῦ ἀφαιρεθέντος τοῦ κώνου, οὗ βάσις μέν ἐστιν ὁ περὶ διάμετρον τὴν ΒΖ κύκλος, ὕψος δὲ ἡ ΕΘ, λοιπὸς ἄρα ὁ ΒΔΖ κῶνος ἴσος ἐστὶ τῷ ΒΖΓ τμήματι τῆς σφαίρας. Ὁμοίως δὲ δειχθήσεται καὶ ὁ ΒΚΖ κῶνος ἴσος τῷ ΒΑΖ τμήματι τῆς σφαίρας. Ἐπεὶ γάρ ἐστιν, ὡς συναμφότερος ἡ ΘΓΕ πρὸς ΓΕ, οὕτως ἡ ΚΕ πρὸς ΕΑ, διελόντι ἄρα, ὡς ἡ ΚΑ πρὸς ΑΕ, οὕτως ἡ ΘΓ πρὸς ΓΕ. Ἴση δὲ ἡ ΘΓ τῇ ΘΑ· καὶ ἐναλλὰξ ἄρα ἐστίν, ὡς ἡ ΚΑ πρὸς ΑΘ, οὕτως ἡ ΑΕ πρὸς ΕΓ· ὥστε καὶ συνθέντι, ὡς ἡ ΚΘ πρὸς ΘΑ, ἡ ΑΓ πρὸς ΓΕ, τουτέστι τὸ ἀπὸ ΒΑ πρὸς τὸ ἀπὸ ΒΕ. Κείσθω δὴ πάλιν κύκλος ὁ Ν ἴσην ἔχων τὴν ἐκ τοῦ κέντρου τῇ ΑΒ· ἴσος ἄρα ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΒΑΖ τμήματος. Καὶ νοείσθω [ὁ] κῶνος ὁ Ν ἴσον ἔχων τὸ ὕψος τῇ ἐκ τοῦ κέντρου τῆς σφαίρας· ἴσος ἄρα ἐστὶ τῷ ΒΘΖΑ στερεῷ τομεῖ· τοῦτο γὰρ ἐν τῷ πρώτῳ δέδεικται. Καὶ ἐπεὶ ἐδείχθη, ὡς ἡ ΚΘ πρὸς ΘΑ, οὕτως τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΒΕ, τουτέστι τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Ν κύκλου πρὸς [107] τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ περὶ διάμετρον τὴν ΒΖ κύκλου, τουτέστιν ὁ Ν κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, ἴση δὲ ἡ ΑΘ τῷ ὕψει τοῦ Ν κώνου, ὡς ἄρα ἡ ΚΘ πρὸς τὸ ὕψος τοῦ Ν κώνου, οὕτως ὁ Ν κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον· ἴσος ἄρα ἐστὶν ὁ Ν κῶνος, τουτέστιν ὁ ΒΘΖΑ τομεύς, τῷ ΒΘΖΚ σχήματι. Κοινὸς προσκείσθω ὁ κῶνος, οὗ βάσις μὲν ὁ περὶ τὴν ΒΖ κύκλος, ὕψος δὲ ἡ ΕΘ· ὅλον ἄρα τὸ ΑΒΖ τμῆμα τῆς σφαίρας ἴσον ἐστὶν τῷ ΒΖΚ κώνῳ· ὅπερ ἔδει δεῖξαι.

ΠΟΡΙΣΜΑ.

   Καὶ φανερὸν ὅτι γίγνεται καθόλου τμῆμα σφαίρας πρὸς κῶνον τὸν βάσιν μὲν ἔχοντα τὴν αὐτὴν τῷ τμήματι καὶ ὕψος ἴσον, ὡς συναμφότερος ἥ τε ἐκ τοῦ κέντρου τῆς σφαίρας καὶ ἡ κάθετος τοῦ λοιποῦ τμήματος πρὸς τὴν κάθετον τοῦ λοιποῦ τμήματος· ὡς γὰρ ἡ ΔΕ πρὸς ΕΓ, οὕτως ὁ ΔΖΒ κῶνος, τουτέστι τὸ ΒΓΖ τμῆμα, πρὸς τὸν ΒΓΖ κῶνον.

[108]    Τῶν αὐτῶν ὑποκειμένων, ὅτι καὶ ὁ ΚΒΖ κῶνος ἴσος ἐστὶ τῷ ΒΑΖ τμήματι τῆς σφαίρας. Ἔστω γὰρ ὁ Ν κῶνος βάσιν μὲν ἔχων [τὴν] ἴσην τῇ ἐπιφανείᾳ τῆς σφαίρας, ὕψος δὲ τὴν ἐκ τοῦ κέντρου τῆς σφαίρας· ἴσος ἄρα ἐστὶν ὁ κῶνος τῇ σφαίρᾳ [ἡ γὰρ σφαῖρα δέδεικται τετραπλασία τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος τὸν μέγιστον κύκλον καὶ ὕψος τὴν ἐκ τοῦ κέντρου. Ἀλλὰ μὴν καὶ ὁ Ν κῶνος τοῦ αὐτοῦ ἐστι τετραπλάσιος, ἐπεὶ καὶ ἡ βάσις τῆς βάσεως καὶ ἡ ἐπιφάνεια τῆς σφαίρας τοῦ μεγίστου κύκλου τῶν ἐν αὐτῇ]. Καὶ ἐπεί ἐστιν, ὡς συναμφότερος ἡ ΘΑ, ΑΕ πρὸς ΑΕ, ἡ ΔΕ πρὸς ΕΓ, διελόντι καὶ ἐναλλάξ, ὡς ἡ ΘΓ πρὸς ΓΔ, ἡ ΑΕ πρὸς ΕΓ. Πάλιν, ἐπεί ἐστιν, ὡς ἡ ΚΕ πρὸς ΕΑ, συναμφότερος ἡ ΘΓΕ πρὸς ΓΕ, διελόντι καὶ ἐναλλάξ, ὡς ἡ ΚΑ πρὸς ΓΘ, τουτέστι πρὸς ΘΑ, οὕτως ἡ ΑΕ πρὸς ΕΓ, τουτέστιν ἡ ΘΓ πρὸς ΓΔ. Καὶ συνθέντι· ἴση δὲ ἡ ΑΘ τῇ ΘΓ· ὡς ἄρα ἡ ΚΘ πρὸς ΘΓ, ἡ ΘΔ πρὸς ΔΓ, καὶ ὅλη ἡ ΚΔ πρὸς ΔΘ ἐστίν, ὡς ἡ ΔΘ πρὸς ΔΓ, τουτέστιν ὡς ἡ ΚΘ πρὸς ΘΑ· ἴσον ἄρα τὸ ὑπὸ ΔΚ, ΘΑ τῷ ὑπὸ τῶν ΔΘΚ. Πάλιν, ἐπεί ἐστιν, ὡς ἡ ΚΘ πρὸς ΘΓ, ἡ ΘΔ πρὸς ΓΔ, ἐναλλάξ· ὡς δὲ ἡ ΘΓ πρὸς ΓΔ, ἐδείχθη ἡ ΑΕ πρὸς ΕΓ· ὡς ἄρα ἡ ΚΘ πρὸς ΘΔ, ἡ ΑΕ πρὸς ΕΓ· καὶ ὡς ἄρα τὸ ἀπὸ ΚΔ πρὸς τὸ ὑπὸ ΚΘΔ, τὸ ἀπὸ ΑΓ πρὸς τὸ ὑπὸ τῶν ΑΕΓ. Τὸ δὲ ὑπὸ τῶν ΚΘΔ ἴσον ἐδείχθη τῷ ὑπὸ ΚΔ, ΑΘ· ὡς ἄρα τὸ ἀπὸ ΚΔ πρὸς τὸ ὑπὸ τῶν ΚΔ, ΑΘ, τουτέστιν ἡ ΚΔ πρὸς ΑΘ, τὸ ἀπὸ ΑΓ πρὸς τὸ ὑπὸ ΑΕΓ, τουτέστι πρὸς τὸ ἀπὸ ΕΒ. Καί ἐστιν ἴση ἡ ΑΓ τῇ ἐκ τοῦ κέντρου τοῦ Ν κύκλου· ὡς ἄρα τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Ν κύκλου πρὸς τὸ ἀπὸ ΒΕ, τουτέστιν ὁ Ν κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, οὕτως ἡ [109] ΚΔ πρὸς ΑΘ, τουτέστιν ἡ ΚΔ πρὸς τὸ ὕψος τοῦ Ν κώνου· ἴσος ἄρα ἐστὶν ὁ Ν κῶνος, τουτέστιν ἡ σφαῖρα, τῷ ΒΔΖΚ στερεῷ ῥόμβῳ [ἢ οὕτως· ἔστιν ἄρα, ὡς ὁ Ν κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΒΖ κύκλον, οὕτως ἡ ΔΚ πρὸς τὸ ὕψος τοῦ Ν κώνου· ἴσος ἄρα ἐστὶν ὁ Ν κῶνος τῷ κώνῳ, οὗ βάσις μέν ἐστιν ὁ περὶ διάμετρον τὴν ΒΖ κύκλος, ὕψος δὲ ἡ ΔΚ· ἀντιπεπόνθασιν γὰρ αὐτῶν αἱ βάσεις τοῖς ὕψεσιν. Ἀλλ᾿ οὗτος ὁ κῶνος ἴσος ἐστὶ τῷ ΒΔΖΚ στερεῷ ῥόμβῳ· καὶ ὁ Ν ἄρα κῶνος, τουτέστιν ἡ σφαῖρα, ἴση ἐστὶ τῷ ΒΖΚΔ στερεῷ ῥόμβῳ]. Ὧν ὁ ΒΔΖ κῶνος ἴσος ἐδείχθη τῷ ΒΓΖ τμήματι τῆς σφαίρας· λοιπὸς ἄρα ὁ ΒΚΖ κῶνος ἴσος ἐστὶ τῷ ΒΑΖ τμήματι τῆς σφαίρας.

   γ΄.

   Τρίτον ἦν πρόβλημα τόδε· Τὴν δοθεῖσαν σφαῖραν ἐπιπέδῳ τεμεῖν, ὅπως αἱ τῶν τμημάτων ἐπιφάνειαι πρὸς ἀλλήλας λόγον ἔχωσιν τὸν αὐτὸν τῷ δοθέντι.

   Γεγονέτω, καὶ ἔστω τῆς σφαίρας μέγιστος κύκλος ὁ ΑΔΒΕ, διάμετρος δὲ αὐτοῦ ἡ ΑΒ, καὶ ἐκβεβλήσθω πρὸς τὴν ΑΒ ἐπίπεδον ὀρθόν, καὶ ποιείτω τὸ ἐπίπεδον ἐν τῷ ΑΔΒΕ κύκλῳ τομὴν τὴν ΔΕ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΒΔ.

   Ἐπεὶ οὖν λόγος ἐστὶ τῆς ἐπιφανείας τοῦ ΔΑΕ τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ΔΒΕ τμήματος, ἀλλὰ τῇ ἐπιφανείᾳ τοῦ ΔΑΕ τμήματος ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΑΔ, τῇ δὲ ἐπιφανείᾳ τοῦ ΔΒΕ τμήματος ἴσος ἐστὶ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΔΒ, ὡς δὲ οἱ εἰρημένοι κύκλοι πρὸς ἀλλήλους, οὕτως τὸ ἀπὸ ΑΔ πρὸς τὸ ἀπὸ ΔΒ, τουτέστιν ἡ ΑΓ πρὸς ΓΒ, λόγος ἄρα τῆς ΑΓ πρὸς ΓΒ δοθείς· ὥστε δοθέν ἐστι τὸ Γ σημεῖον. [110] Καί ἐστι τῇ ΑΒ πρὸς ὀρθὰς ἡ ΔΕ· θέσει ἄρα καὶ τὸ διὰ τῆς ΔΕ ἐπίπεδον.

   Συντεθήσεται δὴ οὕτως· ἔστω σφαῖρα, ἧς μέγιστος κύκλος ὁ ΑΒΔΕ καὶ διάμετρος ἡ ΑΒ, ὁ δὲ δοθεὶς λόγος ὁ τῆς Ζ πρὸς Η, καὶ τετμήσθω ἡ ΑΒ κατὰ τὸ Γ, ὥστε εἶναι, ὡς τὴν ΑΓ πρὸς ΒΓ, οὕτως τὴν Ζ πρὸς Η, καὶ διὰ τοῦ Γ ἐπιπέδῳ τετμήσθω ἡ σφαῖρα πρὸς ὀρθὰς τῇ ΑΒ εὐθείᾳ, καὶ ἔστω κοινὴ τομὴ ἡ ΔΕ, καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΔΒ, καὶ ἐκκείσθωσαν δύο κύκλοι οἱ Θ, Κ, ὁ μὲν Θ ἴσην ἔχων τὴν ἐκ τοῦ κέντρου τῇ ΑΔ, ὁ δὲ Κ τὴν ἐκ τοῦ κέντρου ἴσην ἔχων τῇ ΔΒ· ἔστιν ἄρα ὁ μὲν Θ κύκλος ἴσος τῇ ἐπιφανείᾳ τοῦ ΔΑΕ τμήματος, ὁ δὲ Κ τοῦ ΔΒΕ τμήματος· τοῦτο γὰρ προδέδεικται ἐν τῷ πρώτῳ βιβλίῳ. Καὶ ἐπεὶ ὀρθή ἐστιν ἡ ὑπὸ ΑΔΒ καὶ κάθετος ἡ ΓΔ, ἔστιν, ὡς ἡ ΑΓ πρὸς ΓΒ, τουτέστιν ἡ Ζ πρὸς Η, τὸ ἀπὸ ΑΔ πρὸς τὸ ἀπὸ ΔΒ, τουτέστι τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Θ κύκλου πρὸς τὸ ἀπὸ τῆς ἐκ τοῦ κέντρου τοῦ Κ κύκλου, τουτέστιν ὁ Θ κύκλος πρὸς τὸν Κ κύκλον, τουτέστιν ἡ ἐπιφάνεια τοῦ ΔΑΕ τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ΔΒΕ τμήματος τῆς σφαίρας.

[111]    δ΄.

   Τὴν δοθεῖσαν σφαῖραν τεμεῖν, ὥστε τὰ τμήματα τῆς σφαίρας πρὸς ἄλληλα λόγον ἔχειν τὸν αὐτὸν τῷ δοθέντι.

   Ἔστω ἡ δοθεῖσα σφαῖρα ἡ ΑΒΓΔ· δεῖ δὴ αὐτὴν τεμεῖν ἐπιπέδῳ, ὥστε τὰ τμήματα τῆς σφαίρας πρὸς ἄλληλα λόγον ἔχειν τὸν δοθέντα.

   Τετμήσθω διὰ τῆς ΑΓ ἐπιπέδῳ· λόγος ἄρα τοῦ ΑΔΓ τμήματος τῆς σφαίρας πρὸς τὸ ΑΒΓ τμῆμα τῆς σφαίρας δοθείς. Τετμήσθω δὲ ἡ σφαῖρα διὰ τοῦ κέντρου, καὶ ἔστω ἡ τομὴ μέγιστος κύκλος ὁ ΑΒΓΔ, κέντρον δὲ τὸ Κ καὶ διάμετρος ἡ ΔΒ, καὶ πεποιήσθω, ὡς μὲν συναμφότερος ἡ ΚΔΧ πρὸς ΔΧ, οὕτως ἡ ΡΧ πρὸς ΧΒ, ὡς δὲ συναμφότερος ἡ ΚΒΧ πρὸς ΒΧ, οὕτως ἡ ΛΧ πρὸς ΧΔ, καὶ ἐπεζεύχθωσαν αἱ ΑΛ, ΛΓ, ΑΡ, ΡΓ· ἴσος ἄρα ἐστὶν ὁ ΑΛΓ κῶνος τῷ ΑΔΓ τμήματι τῆς σφαίρας, ὁ δὲ ΑΡΓ τῷ ΑΒΓ· λόγος ἄρα καὶ τοῦ ΑΛΓ κώνου πρὸς τὸν ΑΡΓ κῶνον δοθείς.

   Ὡς δὲ ὁ κῶνος πρὸς τὸν κῶνον, οὕτως ἡ ΛΧ πρὸς ΧΡ [ἐπείπερ τὴν αὐτὴν βάσιν ἔχουσιν τὸν περὶ διάμετρον τὴν ΑΓ κύκλον]· λόγος ἄρα καὶ τῆς ΛΧ πρὸς ΧΡ δοθείς. Καὶ διὰ ταὐτὰ τοῖς πρότερον διὰ τῆς κατασκευῆς, ὡς ἡ ΛΔ πρὸς ΚΔ, ἡ ΚΒ πρὸς ΒΡ καὶ ἡ ΔΧ πρὸς ΧΒ. Καὶ ἐπεί [112] ἐστιν, ὡς ἡ ΡΒ πρὸς ΒΚ, ἡ ΚΔ πρὸς ΛΔ, συνθέντι, ὡς ἡ ΡΚ πρὸς ΚΒ, τουτέστι πρὸς ΚΔ, οὕτως ἡ ΚΛ πρὸς ΛΔ· καὶ ὅλη ἄρα ἡ ΡΛ πρὸς ὅλην τὴν ΚΛ ἐστίν, ὡς ἡ ΚΛ πρὸς ΛΔ. Ἴσον ἄρα τὸ ὑπὸ τῶν ΡΛΔ τῷ ἀπὸ ΛΚ. Ὡς ἄρα ἡ ΡΛ πρὸς ΛΔ, τὸ ἀπὸ ΚΛ πρὸς τὸ ἀπὸ ΛΔ. Καὶ ἐπεί ἐστιν, ὡς ἡ ΛΔ πρὸς ΔΚ, οὕτως ἡ ΔΧ πρὸς ΧΒ, ἔσται ἀνάπαλιν καὶ συνθέντι, ὡς ἡ ΚΛ πρὸς ΛΔ, οὕτως ἡ ΒΔ πρὸς ΔΧ [καὶ ὡς ἄρα τὸ ἀπὸ ΚΛ πρὸς τὸ ἀπὸ ΛΔ, οὕτως τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ. Πάλιν, ἐπεί ἐστιν, ὡς ἡ ΛΧ πρὸς ΔΧ, συναμφότερος ἡ ΚΒ, ΒΧ πρὸς ΒΧ, διελόντι, ὡς ἡ ΛΔ πρὸς ΔΧ, οὕτως ἡ ΚΒ πρὸς ΒΧ]. Καὶ κείσθω τῇ ΚΒ ἴση ἡ ΒΖ· ὅτι γὰρ ἐκτὸς τοῦ Ρ πεσεῖται δῆλον [καὶ ἔσται, ὡς ἡ ΛΔ πρὸς ΔΧ, οὕτως ἡ ΖΒ πρὸς ΒΧ· ὥστε καί, ὡς ἡ ΔΛ πρὸς ΛΧ, ἡ ΒΖ πρὸς ΖΧ]. Ἐπεὶ δὲ λόγος ἐστὶ τῆς ΔΛ πρὸς ΛΧ δοθείς, καὶ τῆς ΡΛ ἄρα πρὸς ΛΧ λόγος ἐστὶ δοθείς. Ἐπεὶ οὖν ὁ τῆς ΡΛ πρὸς ΛΧ λόγος συνῆπται ἔκ τε τοῦ ὃν ἔχει ἡ ΡΛ πρὸς ΛΔ, καὶ ἡ ΔΛ πρὸς ΛΧ, ἀλλ᾿ ὡς μὲν ἡ ΡΛ πρὸς ΛΔ, τὸ ἀπὸ ΔΒ πρὸς τὸ ἀπὸ ΔΧ, ὡς δὲ ἡ ΔΛ πρὸς ΛΧ, οὕτως ἡ ΒΖ πρὸς ΖΧ, ὁ ἄρα τῆς ΡΛ πρὸς ΛΧ λόγος συνῆπται ἔκ τε τοῦ ὃν ἔχει τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ, καὶ ἡ ΒΖ πρὸς ΖΧ. Πεποιήσθω δέ, ὡς ἡ ΡΛ πρὸς ΛΧ, ἡ ΒΖ πρὸς ΖΘ· λόγος δὲ τῆς ΡΛ πρὸς ΛΧ δοθείς· λόγος ἄρα καὶ τῆς ΖΒ πρὸς ΖΘ δοθείς. Δοθεῖσα δὲ ἡ ΒΖ· ἴση γάρ ἐστι τῇ ἐκ τοῦ κέντρου· δοθεῖσα ἄρα καὶ ἡ ΖΘ. Καὶ ὁ τῆς ΒΖ ἄρα λόγος πρὸς ΖΘ συνῆπται ἔκ τε τοῦ ὃν ἔχει τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ, καὶ ἡ ΒΖ πρὸς ΖΧ. Ἀλλ᾿ ὁ ΒΖ πρὸς ΖΘ λόγος συνῆπται ἔκ τε τοῦ τῆς ΒΖ πρὸς ΖΧ καὶ τοῦ τῆς ΖΧ πρὸς ΖΘ [κοινὸς ἀφῃρήσθω ὁ τῆς ΒΖ πρὸς ΖΧ]· λοιπὸν ἄρα ἐστίν, ὡς τὸ ἀπὸ ΒΔ, [113] τουτέστι δοθέν, πρὸς τὸ ἀπὸ ΔΧ, οὕτως ἡ ΧΖ πρὸς ΖΘ, τουτέστι πρὸς δοθέν. Καί ἐστιν δοθεῖσα ἡ ΖΔ εὐθεῖα· εὐθεῖαν ἄρα δοθεῖσαν τὴν ΔΖ τεμεῖν δεῖ κατὰ τὸ Χ καὶ ποιεῖν, ὡς τὴν ΧΖ πρὸς δοθεῖσαν [τὴν ΖΘ], οὕτως τὸ δοθὲν [τὸ ἀπὸ ΒΔ] πρὸς τὸ ἀπὸ ΔΧ. Τοῦτο οὕτως ἁπλῶς μὲν λεγόμενον ἔχει διορισμόν, προστιθεμένων δὲ τῶν προβλημάτων τῶν ἐνθάδε ὑπαρχόντων [τουτέστι τοῦ τε διπλασίαν εἶναι τὴν ΔΒ τῆς ΒΖ καὶ τοῦ μείζονα τῆς ΖΘ τὴν ΖΒ, ὡς κατὰ τὴν ἀνάλυσιν] οὐκ ἔχει διορισμόν· καὶ ἔσται τὸ πρόβλημα τοιοῦτον· δύο δοθεισῶν εὐθειῶν τῶν ΒΔ, ΒΖ καὶ διπλασίας οὔσης τῆς ΒΔ τῆς ΒΖ καὶ σημείου ἐπὶ τῆς ΒΖ τοῦ Θ τεμεῖν τὴν ΔΒ κατὰ τὸ Χ καὶ ποιεῖν, ὡς τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ, τὴν ΧΖ πρὸς ΖΘ· ἑκάτερα δὲ ταῦτα ἐπὶ τέλει ἀναλυθήσεταί τε καὶ συντεθήσεται.

   Συντεθήσεται δὴ τὸ πρόβλημα οὕτως· ἔστω ὁ δοθεὶς λόγος ὁ τῆς Π πρὸς Σ μείζονος πρὸς ἐλάσσονα, καὶ δεδόσθω τις σφαῖρα καὶ τετμήσθω ἐπιπέδῳ διὰ τοῦ κέντρου, καὶ ἔστω τομὴ ὁ ΑΒΓΔ κύκλος, καὶ διάμετρος ἔστω ἡ ΒΔ, κέντρον δὲ τὸ Κ, καὶ τῇ ΚΒ ἴση κείσθω ἡ ΒΖ, καὶ τετμήσθω ἡ ΒΖ κατὰ τὸ Θ, ὥστε εἶναι, ὡς τὴν ΘΖ πρὸς ΘΒ, τὴν Π πρὸς Σ, καὶ ἔτι τετμήσθω ἡ ΒΔ κατὰ τὸ Χ, ὥστε εἶναι, ὡς τὴν ΧΖ πρὸς ΘΖ, τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ, καὶ διὰ τοῦ Χ ἐπίπεδον ἐκβεβλήσθω ὀρθὸν πρὸς τὴν ΒΔ· λέγω ὅτι τὸ ἐπίπεδον τοῦτο τεμεῖ τὴν σφαῖραν, ὥστε εἶναι, ὡς τὸ μεῖζον τμῆμα πρὸς τὸ ἔλασσον, τὴν Π πρὸς Σ.

   Πεποιήσθω γάρ, ὡς μὲν συναμφότερος ἡ ΚΒΧ πρὸς ΒΧ, οὕτως ἡ ΛΧ πρὸς ΔΧ, ὡς δὲ συναμφότερος ἡ ΚΔΧ πρὸς ΧΔ, ἡ ΡΧ πρὸς ΧΒ, καὶ ἐπεζεύχθωσαν αἱ ΑΛ, ΛΓ, ΑΡ, ΡΓ· [114] ἔσται δὴ διὰ τὴν κατασκευήν, ὡς ἐδείξαμεν ἐν τῇ ἀναλύσει, ἴσον τὸ ὑπὸ ΡΛΔ τῷ ἀπὸ ΛΚ, καὶ ὡς ἡ ΚΛ πρὸς ΛΔ, ἡ ΒΔ πρὸς ΔΧ· ὥστε καί, ὡς τὸ ἀπὸ ΚΛ πρὸς τὸ ἀπὸ ΛΔ, τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ. Καὶ ἐπεὶ τὸ ὑπὸ τῶν ΡΛΔ τῷ ἀπὸ ΛΚ ἐστὶν ἴσον [ἔστιν, ὡς ἡ ΡΛ πρὸς ΛΔ, τὸ ἀπὸ ΛΚ πρὸς τὸ ἀπὸ ΛΔ], ἔσται ἄρα καί, ὡς ἡ ΡΛ πρὸς ΛΔ, τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΔΧ, τουτέστιν ἡ ΧΖ πρὸς ΖΘ. Καὶ ἐπεί ἐστιν, ὡς συναμφότερος ἡ ΚΒΧ πρὸς ΒΧ, οὕτως ἡ ΛΧ πρὸς ΧΔ, ἴση δέ ἐστιν ἡ ΚΒ τῇ ΒΖ, ἔσται ἄρα καί, ὡς ἡ ΖΧ πρὸς ΧΒ, οὕτως ἡ ΛΧ πρὸς ΧΔ. Ἀναστρέψαντι, ὡς ἡ ΧΖ πρὸς ΖΒ, οὕτως ἡ ΧΛ πρὸς ΛΔ· ὥστε καί, ὡς ἡ ΛΔ πρὸς ΛΧ, οὕτως ἡ ΒΖ πρὸς ΖΧ. Καὶ ἐπεί ἐστιν, ὡς ἡ ΡΛ πρὸς ΛΔ, οὕτως ἡ ΧΖ πρὸς ΖΘ, ὡς δὲ ἡ ΔΛ πρὸς ΛΧ, οὕτως ἡ ΒΖ πρὸς ΖΧ, καὶ δι᾿ ἴσου ἐν τῇ τεταραγμένῃ ἀναλογίᾳ, ὡς ἡ ΡΛ πρὸς ΛΧ, οὕτως ἡ ΒΖ πρὸς ΖΘ· καὶ ὡς ἄρα ἡ ΛΧ πρὸς ΧΡ, οὕτως ἡ ΖΘ πρὸς ΘΒ. Ὡς δὲ ἡ ΖΘ πρὸς ΘΒ, οὕτως ἡ Π πρὸς Σ· καὶ ὡς ἄρα ἡ ΛΧ πρὸς ΧΡ, τουτέστιν ὁ ΑΓΛ κῶνος πρὸς τὸν ΑΡΓ κῶνον, τουτέστι τὸ ΑΔΓ τμῆμα τῆς σφαίρας πρὸς τὸ ΑΒΓ τμῆμα τῆς σφαίρας, οὕτως ἡ Π πρὸς Σ.

[115]    ε΄.

   Τῷ δοθέντι τμήματι σφαίρας ὅμοιον καὶ ἄλλῳ τῷ δοθέντι ἴσον αὐτὸ συστήσασθαι.

   Ἔστω τὰ δύο δοθέντα τμήματα σφαίρας τὰ ΑΒΓ, ΕΖΗ, καὶ ἔστω τοῦ μὲν ΑΒΓ τμήματος βάσις ὁ περὶ διάμετρον τὴν ΑΒ κύκλος, κορυφὴ δὲ τὸ Γ σημεῖον, τοῦ δὲ ΕΖΗ βάσις ὁ περὶ διάμετρον τὴν ΕΖ, κορυφὴ δὲ τὸ Η σημεῖον· δεῖ δὴ εὑρεῖν τμῆμα σφαίρας, ὃ ἔσται τῷ μὲν ΑΒΓ τμήματι ἴσον, τῷ δὲ ΕΖΗ ὅμοιον.

   Εὑρήσθω καὶ ἔστω τὸ ΘΚΛ, καὶ ἔστω αὐτοῦ βάσις μὲν ὁ περὶ διάμετρον τὴν ΘΚ κύκλος, κορυφὴ δὲ τὸ Λ σημεῖον· ἔστωσαν δὴ καὶ κύκλοι ἐν ταῖς σφαίραις οἱ ΑΝΒΓ, ΘΞΚΛ, ΕΟΖΗ, διάμετροι δὲ αὐτῶν πρὸς ὀρθὰς ταῖς βάσεσιν τῶν τμημάτων αἱ ΓΝ, ΛΞ, ΗΟ, καὶ ἔστω κέντρα τὰ Π, Ρ, Σ, καὶ πεποιήσθω, ὡς μὲν συναμφότερος ἡ ΠΝ, ΝΤ πρὸς τὴν [116] ΝΤ, οὕτως ἡ ΧΤ πρὸς ΤΓ, ὡς δὲ συναμφότερος ἡ ΡΞ, ΞΥ πρὸς ΞΥ, οὕτως ἡ ΨΥ πρὸς ΥΛ, ὡς δὲ συναμφότερος ἡ ΣΟ, ΟΦ πρὸς ΟΦ, οὕτως ἡ ΩΦ πρὸς ΦΗ, καὶ νοείσθωσαν κῶνοι, ὧν βάσεις μέν εἰσιν οἱ περὶ διαμέτρους τὰς ΑΒ, ΘΚ, ΕΖ κύκλοι, κορυφαὶ δὲ τὰ Χ, Ψ, Ω σημεῖαι· ἔσται δὴ ἴσος ὁ μὲν ΑΒΧ κῶνος τῷ ΑΒΓ τμήματι τῆς σφαίρας, ὁ δὲ ΨΘΚ τῷ ΘΚΛ, ὁ δὲ ΕΩΖ τῷ ΕΗΖ· τοῦτο γὰρ δέδεικται. Καὶ ἐπεὶ ἴσον ἐστὶ τὸ ΑΒΓ τμῆμα τῆς σφαίρας τῷ ΘΚΛ τμήματι, ἴσος ἄρα καὶ ὁ ΑΧΒ κῶνος τῷ ΨΘΚ κώνῳ [τῶν δὲ ἴσων κώνων ἀντιπεπόνθασιν αἱ βάσεις τοῖς ὕψεσιν]· ἔστιν ἄρα, ὡς ὁ κύκλος ὁ περὶ διάμετρον τὴν ΑΒ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΘΚ, οὕτως ἡ ΨΥ πρὸς ΧΤ. Ὡς δὲ ὁ κύκλος πρὸς τὸν κύκλον, τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ· ὡς ἄρα τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ, οὕτως ἡ ΨΥ πρὸς ΧΤ. Καὶ ἐπεὶ ὅμοιόν ἐστι τὸ ΕΖΗ τμῆμα τῷ ΘΚΛ τμήματι, ὅμοιος ἄρα ἐστὶ καὶ ὁ ΕΖΩ κῶνος τῷ ΨΘΚ κώνῳ [τοῦτο γὰρ δειχθήσεται]· ἔστιν ἄρα, ὡς ἡ ΩΦ πρὸς τὴν ΕΖ, οὕτως ἡ ΨΥ πρὸς ΘΚ. Λόγος δὲ τῆς ΩΦ πρὸς τὴν ΕΖ δοθείς· λόγος ἄρα καὶ τῆς ΨΥ πρὸς τὴν ΘΚ δοθείς. Ὁ αὐτὸς ἔστω ὁ τῆς ΧΤ πρὸς Δ· καί ἐστι δοθεῖσα ἡ ΧΤ· δοθεῖσα ἄρα καὶ ἡ Δ. Καὶ ἐπεί ἐστιν, ὡς ἡ ΨΥ πρὸς ΧΤ, τουτέστι τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ, οὕτως ἡ ΘΚ πρὸς Δ, κείσθω τῷ ἀπὸ ΘΚ ἴσον τὸ ὑπὸ ΑΒ, Ϛ· ἔσται ἄρα καί, ὡς τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ, οὕτως ἡ ΑΒ πρὸς τὴν Ϛ. Ἐδείχθη δὲ καί, ὡς τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ, οὕτως ἡ ΘΚ πρὸς Δ, καὶ ἐναλλάξ, ὡς ἡ ΑΒ πρὸς ΘΚ, οὕτως ἡ Ϛ πρὸς Δ. Ὡς δὲ ἡ ΑΒ πρὸς ΘΚ, οὕτως ἡ [117] ΘΚ πρὸς Ϛ [διὰ τὸ ἴσον εἶναι τὸ ἀπὸ ΘΚ τῷ ὑπὸ τῶν ΑΒ, Ϛ]· ὡς ἄρα ἡ ΑΒ πρὸς ΘΚ, οὕτως ἡ ΘΚ πρὸς Ϛ καὶ ἡ Ϛ πρὸς Δ. Δύο ἄρα δοθεισῶν τῶν ΑΒ, Δ δύο μέσαι κατὰ τὸ συνεχὲς ἀνάλογόν εἰσιν αἱ ΘΚ, Ϛ.

   Συντεθήσεται δὴ τὸ πρόβλημα οὕτως· ἔστω, ᾧ μὲν δεῖ ἴσον τμῆμα συστήσθαι, τὸ ΑΒΓ, ᾧ δὲ ὅμοιον, τὸ ΕΖΗ, καὶ ἔστωσαν μέγιστοι κύκλοι τῶν σφαιρῶν οἱ ΑΒΓΝ, ΕΗΖΟ, διάμετροι δὲ αὐτῶν αἱ ΓΝ, ΗΟ καὶ κέντρα τὰ Π, Σ, καὶ πεποιήσθω, ὡς μὲν συναμφότερος ἡ ΠΝ, ΝΤ πρὸς ΝΤ, οὕτως ἡ ΧΤ πρὸς ΤΓ, ὡς δὲ συναμφότερος ἡ ΣΟΦ πρὸς ΟΦ, ἡ ΩΦ πρὸς ΦΗ· ἴσος ἄρα ἐστὶν ὁ μὲν ΧΑΒ κῶνος τῷ ΑΒΓ τμήματι τῆς σφαίρας, ὁ δὲ ΖΩΕ τῷ ΕΗΖ. Πεποιήσθω, ὡς ἡ ΩΦ πρὸς ΕΖ, οὕτως ἡ ΧΤ πρὸς Δ, καὶ δύο δοθεισῶν εὐθειῶν τῶν ΑΒ, Δ δύο μέσαι ἀνάλογον εἰλήφθωσαν αἱ ΘΚ, Ϛ, ὥστε εἶναι, ὡς τὴν ΑΒ πρὸς ΘΚ, οὕτως τὴν ΚΘ πρὸς Ϛ καὶ τὴν Ϛ πρὸς Δ, καὶ ἐπὶ τῆς ΘΚ κύκλου τμῆμα ἐπεστάσθω τὸ ΘΚΛ ὅμοιον τῷ ΕΖΗ κύκλου τμήματι, καὶ ἀναπεπληρώσθω ὁ κύκλος, καὶ ἔστω αὐτοῦ διάμετρος ἡ ΛΞ, καὶ νοείσθω σφαῖρα, ἧς μέγιστος κύκλος ἐστὶν ὁ ΛΘΞΚ, κέντρον δὲ τὸ Ρ, καὶ διὰ τῆς ΘΚ ἐπίπεδον ὀρθὸν ἐκβεβλήσθω πρὸς τὴν ΛΞ· ἔσται δὴ τὸ τμῆμα τῆς σφαίρας τὸ ἐπὶ τὰ αὐτὰ τῷ Λ ὅμοιον τῷ ΕΗΖ τμήματι τῆς σφαίρας, ἐπειδὴ καὶ τῶν κύκλων τὰ τμήματα ἦν ὅμοια. Λέγω δὲ ὅτι καὶ ἴσον ἐστὶ τῷ ΑΒΓ τμήματι τῆς σφαίρας. Πεποιήσθω, ὡς συναμφότερος ἡ ΡΞ, ΞΥ πρὸς τὴν ΞΥ, οὕτως ἡ ΨΥ πρὸς ΥΛ· ἴσος ἄρα ὁ ΨΘΚ κῶνος τῷ ΘΚΛ τμήματι τῆς σφαίρας. Καὶ ἐπειδὴ ὅμοιός ἐστιν ὁ ΨΘΚ κῶνος τῷ ΖΩΕ κώνῳ, ἔστιν ἄρα, ὡς ἡ ΦΩ πρὸς ΕΖ, τουτέστιν ἡ ΧΤ πρὸς Δ, οὕτως ἡ ΨΥ πρὸς ΘΚ· καὶ ἐναλλὰξ καὶ ἀνάπαλιν· ὡς ἄρα ἡ ΨΥ πρὸς ΧΤ, [118] ἡ ΘΚ πρὸς Δ. Καὶ ἐπειδὴ ἀνάλογόν εἰσιν αἱ ΑΒ, ΚΘ, Ϛ, Δ, ἔστιν, ὡς τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΘΚ, ἡ ΘΚ πρὸς Δ. Ὡς δὲ ἡ ΘΚ πρὸς Δ, ἡ ΨΥ πρὸς ΧΤ· καὶ ὡς ἄρα τὸ ἀπὸ ΑΒ πρὸς τὸ ἀπὸ ΚΘ, τουτέστιν ὁ περὶ διάμετρον τὴν ΑΒ κύκλος πρὸς τὸν περὶ διάμετρον τὴν ΘΚ κύκλον, οὕτως ἡ ΨΥ πρὸς τὴν ΧΤ· ἴσος ἄρα ἐστὶν ὁ ΧΑΒ κῶνος τῷ ΨΘΚ κώνῳ· ὥστε καὶ τὸ ΑΒΓ τμῆμα τῆς σφαίρας ἴσον ἐστὶ τῷ ΘΚΛ τμήματι τῆς σφαίρας. Τῷ δοθέντι ἄρα τμήματι τῷ ΑΓΒ ἴσον καὶ ἄλλῳ δοθέντι ὅμοιον τῷ ΕΖΗ τὸ αὐτὸ συνέσταται τὸ ΘΚΛ.

   Ϛ΄.

   Δύο δοθέντων σφαίρας τμημάτων εἴτε τῆς αὐτῆς εἴτε μὴ εὑρεῖν τμῆμα σφαίρας, ὃ ἔσται ἑνὶ μὲν τῶν δοθέντων ὅμοιον, τὴν δὲ ἐπιφάνειαν ἕξει ἴσην τῇ τοῦ ἑτέρου τμήματος ἐπιφανείᾳ.

   Ἔστω τὰ δοθέντα τμήματα σφαιρικὰ κατὰ τὰς ΑΒΓ, ΔΕΖ περιφερείας, καὶ ἔστω, ᾧ μὲν δεῖ ὅμοιον εὑρεῖν, τὸ κατὰ τὴν ΑΒΓ περιφέρειαν, οὗ δὲ τὴν ἐπιφάνειαν ἴσην ἔχειν τῇ ἐπιφανείᾳ, τὸ κατὰ τὴν ΔΕΖ.

[119]    Καὶ γεγενήσθω, καὶ ἔστω τὸ ΚΛΜ τμῆμα τῆς σφαίρας τῷ μὲν ΑΒΓ τμήματι ὅμοιον, τὴν δὲ ἐπιφάνειαν ἴσην ἐχέτω τῇ τοῦ ΔΕΖ τμήματος ἐπιφανείᾳ, καὶ νοείσθω τὰ κέντρα τῶν σφαιρῶν, καὶ δι᾿ αὐτῶν ἐπίπεδα ἐκβεβλήσθω ὀρθὰ πρὸς τὰς τῶν τμημάτων βάσεις, καὶ ἐν μὲν ταῖς σφαίραις τομαὶ ἔστωσαν οἱ ΚΛΜΝ, ΒΑΓΘ, ΕΖΗΔ μέγιστοι κύκλοι, ἐν δὲ ταῖς βάσεσι τῶν τμημάτων αἱ ΚΜ, ΑΓ, ΔΖ εὐθεῖαι, διάμετροι δὲ τῶν σφαιρῶν πρὸς ὀρθὰς οὖσαι ταῖς ΚΜ, ΑΓ, ΔΖ ἔστωσαν αἱ ΛΝ, ΒΘ, ΕΗ, καὶ ἐπεζεύχθωσαν αἱ ΛΜ, ΒΓ, ΕΖ. Καὶ ἐπεὶ ἴση ἐστὶν ἡ τοῦ ΚΛΜ τμήματος τῆς σφαίρας ἐπιφάνεια τῇ τοῦ ΔΕΖ τμήματος ἐπιφανείᾳ, ἴσος ἄρα ἐστὶν καὶ ὁ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΛΜ, τῷ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΕΖ [αἱ γὰρ ἐπιφάνειαι τῶν εἰρημένων τμημάτων ἴσαι ἐδείχθησαν κύκλοις, ὧν αἱ ἐκ τῶν κέντρων ἴσαι εἰσὶν ταῖς ἀπὸ τῶν κορυφῶν τῶν τμημάτων ἐπὶ τὰς βάσεις ἐπιζευγνυούσαις]· ὥστε καὶ ἡ ΜΑ τῇ ΕΖ ἴση ἐστίν. Ἐπεὶ δὲ ὅμοιόν ἐστι τὸ ΚΛΜ τῷ ΑΒΓ τμήματι, ἔστιν, ὡς ἡ ΛΡ πρὸς ΡΝ, ἡ ΒΠ πρὸς ΠΘ· καὶ ἀνάπαλιν καὶ συνθέντι, ὡς ἡ ΝΛ πρὸς ΛΡ, οὕτως ἡ ΘΒ πρὸς ΒΠ. Ἀλλὰ καί, ὡς ἡ ΡΛ πρὸς ΛΜ, οὕτως ἡ ΒΠ πρὸς ΓΒ [ὅμοια γὰρ τὰ τρίγωνα]· ὡς ἄρα ἡ ΝΛ πρὸς ΛΜ, τουτέστι πρὸς ΕΖ, οὕτως ἡ ΘΒ πρὸς ΒΓ. Καὶ ἐναλλάξ· λόγος δὲ τῆς ΕΖ πρὸς ΒΓ δοθείς· δοθεῖσα γὰρ ἑκατέρα· λόγος ἄρα καὶ τῆς ΛΝ πρὸς ΒΘ δοθείς. Καί ἐστι δοθεῖσα ἡ ΒΘ· δοθεῖσα ἄρα καὶ ἡ ΛΝ· ὥστε ἄρα καὶ ἡ σφαῖρα δοθεῖσά ἐστιν.

   Συντεθήσεται δὴ οὕτως· ἔστω τὰ δοθέντα δύο τμήματα σφαίρας τὰ ΑΒΓ, ΔΕΖ, τὸ μὲν ΑΒΓ, ᾧ δεῖ ὅμοιον, τὸ δὲ [120] ΔΕΖ, οὗ τὴν ἐπιφάνειαν ἴσην ἔχειν τῇ ἐπιφανείᾳ, καὶ τὰ αὐτὰ κατεσκευάσθω τοῖς ἐπὶ τῆς ἀναλύσεως, καὶ πεποιήσθω, ὡς [μὲν] ἡ ΒΓ πρὸς ΕΖ, οὕτως ἡ ΒΘ πρὸς ΛΝ, καὶ περὶ διάμετρον τὴν ΛΝ κύκλος γεγράφθω, καὶ νοείσθω σφαῖρα, ἧς μέγιστος ἔστω κύκλος ὁ ΛΚΝΜ, καὶ τετμήσθω ἡ ΝΛ κατὰ τὸ Ρ, ὥστε εἶναι, ὡς τὴν ΘΠ πρὸς ΠΒ, τὴν ΝΡ πρὸς ΡΛ, καὶ διὰ τοῦ Ρ ἐπιπέδῳ τετμήσθω ἡ ἐπιφάνεια ὀρθῷ πρὸς τὴν ΛΝ, καὶ ἐπεζεύχθω ἡ ΛΜ· ὅμοια ἄρα ἐστὶν τὰ ἐπὶ τῶν ΚΜ, ΑΓ εὐθειῶν τῶν κύκλων τμήματα· ὥστε καὶ τὰ τμήματα τῶν σφαιρῶν ἐστιν ὅμοια. Καὶ ἐπεί ἐστιν, ὡς ἡ ΘΒ πρὸς ΒΠ, οὕτως ἡ ΝΛ πρὸς ΛΡ· καὶ γὰρ τὰ κατὰ διαίρεσιν· ἀλλὰ καί, ὡς ἡ ΠΒ πρὸς ΒΓ, οὕτως ἡ ΡΛ πρὸς ΛΜ, καὶ ὡς ἄρα ἡ ΘΒ πρὸς ΝΛ, ἡ ΒΓ πρὸς ΛΜ. Ἦν δὲ καί, ὣς ἡ ΘΒ πρὸς ΛΝ, ἡ ΒΓ πρὸς ΕΖ· ἴση ἄρα ἐστὶν ἡ ΕΖ τῇ ΛΜ· ὥστε καὶ ὁ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἐστὶν ἡ ΕΖ, ἴσος ἐστὶ τῷ κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΛΜ. Καὶ ὁ μὲν τὴν ἐκ τοῦ κέντρου ἔχων τὴν ΕΖ κύκλος ἴσος ἐστὶ τῇ ἐπιφανείᾳ τοῦ ΔΕΖ τμήματος, ὁ δὲ κύκλος, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ΛΜ, ἴσος ἐστὶ ἐπιφανείᾳ τῇ τοῦ ΚΛΜ τμήματος· τοῦτο γὰρ ἐν τῷ πρώτῳ δέδεικται· ἴση ἄρα καὶ ἡ ἐπιφάνεια τοῦ ΚΛΜ τμήματος τῇ ἐπιφανείᾳ τοῦ ΔΕΖ τμήματος τῆς σφαίρας. Καί ἐστιν ὅμοιον τὸ ΚΛΜ τῷ ΑΒΓ.

   ζ΄.

   Ἀπὸ τῆς δοθείσης σφαίρας τμῆμα τεμεῖν ἐπιπέδῳ, ὥστε τὸ τμῆμα πρὸς τὸν κῶνον τὸν βάσιν ἔχοντα τὴν αὐτὴν τῷ τμήματι καὶ ὕψος ἴσον τὸν δοθέντα λόγον ἔχειν.

[121]    Ἔστω ἡ δοθεῖσα σφαῖρα, ἧς μέγιστος κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτῆς ἡ ΒΔ· δεῖ δὴ τὴν σφαῖραν ἐπιπέδῳ τεμεῖν τῷ διὰ τῆς ΑΓ, ὅπως τὸ ΑΒΓ τμῆμα τῆς σφαίρας πρὸς τὸν ΑΒΓ κῶνον λόγον ἔχῃ τὸν αὐτὸν τῷ δοθέντι.

   Γεγονέτω, καὶ ἔστω κέντρον τῆς σφαίρας τὸ Ε, καὶ ὡς συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ, οὕτως ἡ ΗΖ πρὸς ΖΒ· ἴσος ἄρα ἐστὶν ὁ ΑΓΗ κῶνος τῷ ΑΒΓ τμήματι. Λόγος ἄρα καὶ τοῦ ΑΗΓ κώνου πρὸς τὸν ΑΒΓ κῶνον δοθείς· λόγος ἄρα τῆς ΗΖ πρὸς ΖΒ δοθείς. Ὡς δὲ ἡ ΗΖ πρὸς ΖΒ, συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ· λόγος ἄρα συναμφοτέρου τῆς ΕΔΖ πρὸς ΔΖ δοθείς [ὥστε καὶ τῆς ΕΔ πρὸς ΔΖ· δοθεῖσα ἄρα καὶ ἡ ΔΖ]· ὥστε καὶ ἡ ΑΓ. Καὶ ἐπεὶ συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ μείζονα λόγον ἔχει ἤπερ συναμφότερος ἡ ΕΔΒ πρὸς ΔΒ, καί ἐστιν συναμφότερος μὲν ἡ ΕΔΒ τρὶς ἡ ΕΔ, ἡ δὲ ΒΔ δὶς ἡ ΕΔ, συναμφότερος ἄρα ἡ ΕΔΖ πρὸς ΔΖ μείζονα λόγον ἔχει τοῦ ὃν ἔχει τρία πρὸς δύο. Καί ἐστιν ὁ συναμφοτέρου τῆς ΕΔΖ πρὸς ΖΔ λόγος ὁ αὐτὸς τῷ δοθέντι· δεῖ ἄρα τὸν διδόμενον λόγον εἰς τὴν σύνθεσιν μείζονα εἶναι τοῦ ὃν ἔχει τρία πρὸς δύο.

   Συντεθήσεται δὴ τὸ πρόβλημα οὕτως· ἔστω ἡ δοθεῖσα σφαῖρα, ἧς μέγιστος κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ ἡ ΒΔ,

[122] κέντρον δὲ τὸ Ε, ὁ δὲ δοθεὶς λόγος ὁ τῆς ΘΚ πρὸς ΚΛ μείζων τοῦ ὃν ἔχει τρία πρὸς δύο. Ἔστι δέ, ὡς τρία πρὸς δύο, συναμφότερος ἡ ΕΔΒ πρὸς ΔΒ· καὶ ἡ ΘΚ ἄρα πρὸς ΚΛ μείζονα λόγον ἔχει τοῦ ὃν ἔχει συναμφότερος ἡ ΕΔΒ πρὸς ΔΒ· διελόντι ἄρα ἡ ΘΛ πρὸς ΛΚ μείζονα λόγον ἔχει ἤπερ ἡ ΕΔ πρὸς ΔΒ. Καὶ πεποιήσθω, ὡς ἡ ΘΛ πρὸς ΛΚ, οὕτως ἡ ΕΔ πρὸς ΔΖ, καὶ διὰ τοῦ Ζ τῇ ΒΔ πρὸς ὀρθὰς ἤχθω ἡ ΑΖΓ, καὶ διὰ τῆς ΓΑ ἤχθω ἐπίπεδον ὀρθὸν πρὸς τὴν ΒΔ· λέγω ὅτι τὸ [ἀπὸ] ΑΒΓ τμῆμα τῆς σφαίρας πρὸς τὸν ΑΒΓ κῶνον λόγον ἔχει τὸν αὐτὸν τῷ ΘΚ πρὸς ΚΛ.

   Πεποιήσθω γάρ, ὡς συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ, οὕτως ἡ ΗΖ πρὸς ΖΒ· ἴσος ἄρα ἐστὶν ὁ ΓΑΗ κῶνος τῷ ΑΒΓ τμήματι τῆς σφαίρας. Καὶ ἐπεί ἐστιν, ὡς ἡ ΘΚ πρὸς ΚΛ, οὕτως συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ, τουτέστιν ἡ ΗΖ πρὸς ΖΒ, τουτέστιν ὁ ΑΗΓ κῶνος πρὸς τὸν ΑΒΓ κῶνον, ἴσος δὲ ὁ ΑΗΓ κῶνος τῷ ΑΒΓ τμήματι τῆς σφαίρας, ὡς ἄρα τὸ ΑΒΓ τμῆμα πρὸς τὸν ΑΒΓ κῶνον, οὕτως ἡ ΘΚ πρὸς ΚΛ.

[123]    η΄.

   Ἐὰν σφαῖρα ἐπιπέδῳ τμηθῇ μὴ διὰ τοῦ κέντρου, τὸ μεῖζον τμῆμα πρὸς τὸ ἔλασσον ἐλάσσονα μὲν λόγον ἔχει ἢ διπλάσιον τοῦ ὃν ἔχει ἡ τοῦ μείζονος τμήματος ἐπιφάνεια πρὸς τὴν τοῦ ἐλάσσονος ἐπιφάνειαν, μείζονα δὲ ἢ ἡμιόλιον.

   Ἔστω σφαῖρα καὶ ἐν αὐτῇ μέγιστος κύκλος ὁ ΑΒΓΔ καὶ διάμετρος ἡ ΒΔ, καὶ τετμήσθω ἐπιπέδῳ διὰ τῆς ΑΓ ὀρθῷ πρὸς τὸν ΑΒΓΔ κύκλον, καὶ ἔστω μεῖζον τμῆμα τῆς σφαίρας τὸ ΑΒΓ· λέγω ὅτι τὸ ΑΒΓ τμῆμα πρὸς τὸ ΑΔΓ ἐλάσσονα μὲν ἢ διπλασίονα λόγον ἔχει ἤπερ ἡ ἐπιφάνεια τοῦ μείζονος τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ἐλάσσονος τμήματος, μείζονα δὲ ἢ ἡμιόλιον.

   Ἐπεζεύχθωσαν γὰρ αἱ ΒΑΔ, καὶ ἔστω κέντρον τὸ Ε, καὶ πεποιήσθω, ὡς μὲν συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ, ἡ ΘΖ πρὸς ΖΒ, ὡς δὲ συναμφότερος ἡ ΕΒΖ πρὸς ΒΖ, οὕτως ἡ ΗΖ πρὸς ΖΔ, καὶ νοείσθωσαν κῶνοι βάσιν ἔχοντες τὸν περὶ διάμετρον τὴν ΑΓ κύκλον, κορυφὰς δὲ τὰ Θ, Η σημεῖα· ἔσται δὴ ἴσος ὁ μὲν ΑΘΓ κῶνος τῷ ΑΒΓ τμήματι τῆς σφαίρας, ὁ δὲ ΑΓΗ τῷ ΑΔΓ, καί ἐστιν, ὡς τὸ ἀπὸ ΒΑ πρὸς τὸ ἀπὸ ΑΔ, οὕτως ἡ ἐπιφάνεια τοῦ ΑΒΓ τμήματος πρὸς [124] τὴν ἐπιφάνειαν τοῦ ΑΔΓ τμήματος· τοῦτο γὰρ προγέγραπται [δεικτέον ὅτι τὸ μεῖζον τμῆμα τῆς σφαίρας πρὸς τὸ ἔλασσον ἐλάσσονα λόγον ἔχει ἢ διπλάσιον ἤπερ ἡ ἐπιφάνεια τοῦ μείζονος τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ἐλάσσονος τμήματος]. Λέγω ὅτι καὶ ὁ ΑΘΓ κῶνος πρὸς τὸν ΑΗΓ, τουτέστιν ἡ ΖΘ πρὸς ΖΗ, ἐλάσσονα λόγον ἔχει ἢ διπλάσιον τοῦ ὃν ἔχει τὸ ἀπὸ ΒΑ πρὸς τὸ ἀπὸ ΑΔ, τουτέστιν ἡ ΒΖ πρὸς ΖΔ. Καὶ ἐπεί ἐστιν, ὡς [μὲν] συναμφότερος ἡ ΕΔΖ πρὸς ΔΖ, οὕτως ἡ ΘΖ πρὸς ΖΒ [ὡς δὲ συναμφότερος ἡ ΕΒΖ πρὸς ΒΖ, οὕτως ἡ ΖΗ πρὸς ΖΔ], ἔσται καί, ὡς ἡ ΒΖ πρὸς ΖΔ, ἡ ΘΒ πρὸς ΒΕ· ἴση γὰρ ἡ ΒΕ τῇ ΔΕ [τοῦτο γὰρ ἐν τοῖς ἐπάνω συναποδέδεικται]. Πάλιν, ἐπεί ἐστιν, ὡς συναμφότερος ἡ ΕΒΖ πρὸς ΒΖ, ἡ ΗΖ πρὸς ΖΔ, ἔστω τῇ ΒΕ ἴση ἡ ΒΚ· δῆλον γὰρ ὅτι μείζων ἐστὶν ἡ ΘΒ τῆς ΒΕ, ἐπεὶ καὶ ΒΖ τῆς ΖΔ· καὶ ἔσται, ὡς ἡ ΚΖ πρὸς ΖΒ, ἡ ΗΖ πρὸς ΖΔ. Ὡς δὲ ἡ ΖΒ πρὸς ΖΔ, ἐδείχθη ἡ ΘΒ πρὸς ΒΕ, ἴση δὲ ἡ ΒΕ τῇ ΚΒ· ὡς ἄρα ἡ ΘΒ πρὸς ΒΚ, οὕτως ἡ ΚΖ πρὸς ΖΗ. Καὶ ἐπεὶ ἡ ΘΖ πρὸς ΖΚ ἐλάσσονα λόγον ἔχει ἤπερ ἡ ΘΒ πρὸς ΒΚ, ὡς δὲ ἡ ΘΒ πρὸς ΒΚ, ἐδείχθη ἡ ΚΖ πρὸς ΖΗ, ἡ ΘΖ ἄρα πρὸς ΖΚ ἐλάσσονα λόγον ἔχει ἤπερ ἡ ΚΖ πρὸς ΖΗ· ἔλασσον ἄρα τὸ ὑπὸ τῶν ΘΖΗ τοῦ ἀπὸ ΖΚ. Τὸ ἄρα ὑπὸ τῶν ΘΖΗ πρὸς τὸ ἀπὸ ΖΗ [τουτέστιν ἡ ΖΘ πρὸς ΖΗ] ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει τὸ ἀπὸ τῆς ΚΖ πρὸς τὸ ἀπὸ ΖΗ [τὸ δὲ ἀπὸ ΚΖ πρὸς τὸ ἀπὸ ΖΗ διπλασίονα λόγον ἔχει ἤπερ ἡ ΚΖ πρὸς ΖΗ]· ἡ ἄρα ΘΖ πρὸς ΖΗ ἐλάσσονα λόγον ἔχει ἢ διπλασίονα τοῦ ὃν ἔχει ἡ ΚΖ πρὸς ΖΗ [ἡ ΚΖ πρὸς ΖΗ ἐλάσσονα λόγον ἔχει ἢ διπλασίονα τοῦ ὃν ἔχει ἡ ΒΖ πρὸς ΖΔ]· τοῦτο δὲ ἐζητοῦμεν. Καὶ ἐπεὶ ἴση ἐστὶν ἡ ΒΕ τῇ ΕΔ, ἔλασσον ἄρα τὸ ὑπὸ τῶν ΒΖΔ τοῦ ὑπὸ [125] τῶν ΒΕΔ· ἡ ΖΒ ἄρα πρὸς ΒΕ ἐλάσσονα λόγον ἔχει ἤπερ ἡ ΕΔ πρὸς ΔΖ, τουτέστιν ἡ ΘΒ πρὸς ΒΖ· ἔλασσον ἄρα τὸ ἀπὸ ΖΒ τοῦ ὑπὸ τῶν ΘΒΕ, τουτέστι τοῦ ὑπὸ τῶν ΘΒΚ. Ἔστω ἴσον τὸ ἀπὸ ΒΝ τῷ ὑπὸ ΘΒΚ· ἔστιν ἄρα, ὡς ἡ ΘΒ πρὸς ΒΚ, τὸ ἀπὸ ΘΝ πρὸς τὸ ἀπὸ ΝΚ. Τὸ δὲ ἀπὸ ΘΖ πρὸς τὸ ἀπὸ ΖΚ μείζονα λόγον ἔχει ἢ τὸ ἀπὸ ΘΝ πρὸς τὸ ἀπὸ ΝΚ [καὶ τὸ ἀπὸ ΘΖ ἄρα πρὸς τὸ ἀπὸ ΖΚ μείζονα λόγον ἔχει ἤπερ ἡ ΘΒ πρὸς ΒΚ, τουτέστιν ἡ ΘΒ πρὸς ΒΕ, τουτέστιν ἡ ΚΖ πρὸς ΖΗ]· ἡ ἄρα ΘΖ πρὸς ΖΗ μείζονα λόγον ἔχει ἢ ἡμιόλιον τοῦ τῆς ΚΖ πρὸς ΖΗ [τοῦτο γὰρ ἐπὶ τέλει]. Καί ἐστιν, ὡς μὲν ἡ ΘΖ πρὸς ΖΗ, ὁ ΑΘΓ κῶνος πρὸς τὸν ΑΗΓ κῶνον, τουτέστι τὸ ΑΒΓ τμῆμα πρὸς τὸ ΑΔΓ τμῆμα, ὡς δὲ ἡ ΚΖ πρὸς ΖΗ, ἡ ΒΖ πρὸς ΖΔ, τουτέστι τὸ ἀπὸ ΒΑ πρὸς τὸ ἀπὸ ΑΔ, τουτέστιν ἡ ἐπιφάνεια τοῦ ΑΒΓ τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ΑΔΓ τμήματος· ὥστε τὸ μεῖζον τμῆμα πρὸς τὸ ἔλασσον ἐλάσσονα μὲν ἢ διπλασίονα λόγον ἔχει τοῦ ὃν ἔχει ἡ ἐπιφάνεια τοῦ μείζονος τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ἐλάσσονος τμήματος, μείζονα δὲ ἢ ἡμιόλιον.

ΑΛΛΩΣ.

   Ἔστω σφαῖρα, ἐν ᾗ μέγιστος κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ ἡ ΑΓ, κέντρον δὲ τὸ Ε, καὶ τετμήσθω ἐπιπέδῳ ὀρθῷ διὰ τῆς ΒΔ πρὸς τὴν ΑΓ· λέγω ὅτι τὸ μεῖζον τμῆμα τὸ ΔΑΒ πρὸς τὸ ἔλασσον τὸ ΒΓΔ ἐλάσσονα ἢ διπλάσιον λόγον ἔχει τοῦ ὃν ἔχει ἡ ἐπιφάνεια τοῦ ΑΒΔ τμήματος πρὸς τὴν ἐπιφάνειαν τοῦ ΒΓΔ τμήματος, μείζονα δὲ ἢ ἡμιόλιον.

   Ἐπεζεύχθωσαν γὰρ αἱ ΑΒ, ΒΓ· ὁ δὲ τῆς ἐπιφανείας πρὸς τὴν ἐπιφάνειαν λόγος ὁ τοῦ κύκλου ἐστίν, οὗ ἡ ἐκ τοῦ κέντρου ἡ ΑΒ, πρὸς τὸν κύκλον, οὗ ἡ ἐκ τοῦ κέντρου [126] ἡ ΒΓ, τουτέστιν ὁ τῆς ΑΘ πρὸς τὴν ΘΓ. Κείσθω τῇ ἐκ τοῦ κέντρου τοῦ κύκλου ἴση ἑκατέρα τῶν ΑΖ, ΓΗ. Ὁ δὴ τοῦ ΒΑΔ τμήματος πρὸς τὸ ΒΓΔ λόγος συνῆπται ἐκ τοῦ ὃν ἔχει τὸ ΒΑΔ τμῆμα πρὸς τὸν κῶνον, οὗ [ἡ] βάσις μέν ἐστιν ὁ περὶ διάμετρον τὴν ΒΔ κύκλος, κορυφὴ δὲ τὸ Α σημεῖον, καὶ ὁ αὐτὸς κῶνος πρὸς τὸν κῶνον τὸν βάσιν μὲν ἔχοντα τὴν αὐτήν, κορυφὴν δὲ τὸ Γ σημεῖον, καὶ ὁ εἰρημένος κῶνος πρὸς τὸ ΒΓΔ τμῆμα. Ἀλλ᾿ ὁ μὲν τοῦ ΒΑΔ τμήματος λόγος πρὸς τὸν ΒΑΔ κῶνον ὁ τῆς ΗΘ ἐστὶ πρὸς ΘΓ, ὁ δὲ τοῦ κώνου πρὸς τὸν κῶνον ὁ τῆς ΑΘ πρὸς ΘΓ, ὁ δὲ τοῦ ΒΓΔ κώνου πρὸς τὸ τμῆμα τὸ ΒΓΔ ὁ τῆς ΑΘ ἐστὶ πρὸς ΘΖ· ὁ δὲ συνημμένος ἐκ τοῦ τῆς ΗΘ πρὸς ΘΓ καὶ τῆς ΑΘ πρὸς ΘΓ ὁ τοῦ ὑπὸ τῶν ΗΘΑ ἐστὶ πρὸς τὸ ἀπὸ ΘΓ, ὁ δὲ τοῦ ὑπὸ ΗΘ, ΘΑ πρὸς τὸ ἀπὸ ΘΓ μετὰ τοῦ τῆς ΑΘ πρὸς ΘΖ ὁ τοῦ ὑπὸ τῶν ΗΘ, ΘΑ ἐστὶν ἐπὶ τὴν ΘΑ πρὸς τὸ ἀπὸ ΘΓ ἐπὶ τὴν ΘΖ, ὁ δὲ τοῦ ὑπὸ τῶν ΗΘΑ ἐπὶ τὴν ΘΑ ὁ τοῦ ἀπὸ τῆς ΘΑ ἐστὶ ἐπὶ τὴν ΘΗ· ὅτι ἄρα τὸ ἀπὸ ΘΑ ἐπὶ τὴν ΘΗ πρὸς τὸ ἀπὸ ΓΘ ἐπὶ τὴν ΘΖ ἐλάσσονα λόγον ἔχει τοῦ τῆς ΑΘ πρὸς ΘΓ διπλασίου [τοῦ δὲ τῆς ΑΘ πρὸς ΘΓ διπλασίων [127] ἐστὶν ὁ τοῦ ἀπὸ ΑΘ πρὸς τὸ ἀπὸ ΘΓ]. Τὸ ἄρα ἀπὸ ΑΘ ἐπὶ τὴν ΗΘ πρὸς τὸ ἀπὸ ΘΓ ἐπὶ τὴν ΘΖ ἐλάσσονα λόγον ἔχει ἤπερ τὸ ἀπὸ ΑΘ ἐπὶ τὴν ΗΘ πρὸς τὸ ἀπὸ ΓΘ ἐπὶ τὴν ΘΗ. Ὅτι ἄρα μεῖζόν ἐστι τὸ ἀπὸ ΓΘ ἐπὶ τὴν ΖΘ τοῦ ἀπὸ ΓΘ ἐπὶ τὴν ΘΗ. Ὅτι ἄρα μείζων ἐστὶν ἡ ΘΖ τῆς ΘΗ.

   Φημὶ δὴ ὅτι καὶ τὸ μεῖζον τμῆμα πρὸς τὸ ἔλασσον μείζονα λόγον ἔχει ἢ ἡμιόλιον τοῦ τῆς ἐπιφανείας λόγου. Ἀλλ᾿ ὁ μὲν τῶν τμημάτων ἐδείχθη ὁ αὐτὸς τῷ ὃν ἔχει τὸ ἀπὸ ΑΘ ἐπὶ τὴν ΘΗ πρὸς τὸ ἀπὸ ΘΓ ἐπὶ τὴν ΘΖ, τοῦ δὲ τῆς ἐπιφανείας λόγου ἡμιόλιός ἐστιν ὁ τοῦ ἀπὸ ΑΒ κύβου πρὸς τὸν ἀπὸ ΒΓ κύβον· φημὶ δὴ ὅτι τὸ ἀπὸ ΑΘ ἐπὶ τὴν ΘΗ πρὸς τὸ ἀπὸ ΓΘ ἐπὶ τὴν ΘΖ μείζονα λόγον ἔχει ἤπερ [ὁ ἀπὸ τῆς ΑΒ κύβος πρὸς τὸν ἀπὸ τῆς ΒΓ κύβον, τουτέστιν] ὁ ἀπὸ τῆς ΑΘ κύβος πρὸς τὸν ἀπὸ ΘΒ κύβον, τουτέστιν ὁ τοῦ ἀπὸ ΑΘ πρὸς τὸ ἀπὸ ΒΘ καὶ ὁ τῆς ΑΘ πρὸς ΘΒ. Ὁ δὲ τοῦ ἀπὸ ΑΘ πρὸς τὸ ἀπὸ ΘΒ προσλαβὼν τὸν τῆς ΑΘ πρὸς ΘΒ ὁ τοῦ ἀπὸ ΑΘ ἐστὶν πρὸς τὸ ὑπὸ τῶν ΓΘΒ· ὁ δὲ τοῦ ἀπὸ ΑΘ πρὸς τὸ ὑπὸ τῶν ΒΘΓ ὁ τοῦ ἀπὸ ΑΘ ἐστὶν ἐπὶ τὴν ΘΗ πρὸς τὸ ὑπὸ τῶν ΒΘΓ ἐπὶ τὴν ΘΗ· φημὶ δὴ ὅτι [ἄρα] τὸ ἀπὸ ΑΘ ἐπὶ τὴν ΘΗ πρὸς τὸ ἀπὸ ΓΘ ἐπὶ τὴν ΘΖ μείζονα λόγον ἔχει ἤπερ [τὸ ἀπὸ ΑΘ πρὸς τὸ ὑπὸ ΒΘΓ, τουτέστι] τὸ ἀπὸ ΑΘ ἐπὶ τὴν ΘΗ πρὸς τὸ ὑπὸ ΒΘΓ ἐπὶ τὴν ΘΗ. Δεικτέον οὖν ὅτι τὸ ἀπὸ ΘΓ ἐπὶ τὴν ΘΖ ἔλασσόν ἐστι τοῦ ὑπὸ τῶν ΒΘΓ ἐπὶ τὴν ΗΘ· ὃ ταὐτόν ἐστι τῷ δεῖξαι ὅτι τὸ ἀπὸ ΓΘ πρὸς τὸ ὑπὸ ΒΘΓ ἐλάσσονα λόγον ἔχει ἤπερ ἡ ΗΘ πρὸς ΘΖ [δεῖ ἄρα δεῖξαι ὅτι ἡ ΗΘ πρὸς ΘΖ μείζονα λόγον ἔχει ἤπερ ἡ ΓΘ πρὸς ΘΒ].

[128]    Ἤχθω ἀπὸ τοῦ Ε τῇ ΕΓ πρὸς ὀρθὰς ἡ ΕΚ καὶ ἀπὸ τοῦ Β κάθετος ἐπ᾿ αὐτὴν ἡ ΒΛ· ἐπίλοιπον ἡμῖν δεῖξαι δεῖ ὅτι ἡ ΗΘ πρὸς ΘΖ μείζονα λόγον ἔχει ἤπερ ἡ ΓΘ πρὸς ΘΒ. Ἴση δέ ἐστιν ἡ ΘΖ συναμφοτέρῳ τῇ ΑΘ, ΚΕ· δεῖξαι ἄρα δεῖ ὅτι ἡ ΗΘ πρὸς συναμφότερον τὴν ΘΑ, ΚΕ μείζονα λόγον ἔχει ἤπερ ἡ ΓΘ πρὸς ΘΒ· καὶ ἀφαιρεθείσης ἄρα ἀπὸ τῆς ΘΗ τῆς ΓΘ, ἀπὸ δὲ τῆς ΚΕ τῆς ΕΛ ἴσης τῇ ΒΘ, δεήσει δειχθῆναι ὅτι λοιπὴ ἡ ΓΗ πρὸς λοιπὴν συναμφότερον τὴν ΑΘ, ΚΛ μείζονα λόγον ἔχει ἤπερ ἡ ΓΘ πρὸς ΘΒ, τουτέστιν ἡ ΘΒ πρὸς ΘΑ, τουτέστιν ἡ ΛΕ πρὸς ΘΑ, καὶ ἐναλλάξ, ὅτι ἡ ΚΕ πρὸς ΕΛ μείζονα λόγον ἔχει ἤπερ συναμφότερος ἡ ΚΛ, ΘΑ πρὸς ΘΑ, καὶ διελόντι ἡ ΚΛ πρὸς ΛΕ μείζονα λόγον ἔχει ἤπερ ἡ ΚΛ πρὸς ΘΑ. Ὅτι ἐλάσσων ἐστὶν ἡ ΛΕ τῆς ΘΑ.

   θ΄.

   Τῶν τῇ ἴσῃ ἐπιφανείᾳ περιεχομένων σφαιρικῶν τμημάτων μεῖζόν ἐστι τὸ ἡμισφαίριον.

   Ἔστω ἐν σφαίρᾳ μέγιστος κύκλος ὁ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἡ ΑΓ, καὶ ἄλλη σφαῖρα, ἧς μέγιστος κύκλος ὁ ΕΖΗΘ, διάμετρος δὲ αὐτοῦ ἡ ΕΗ, καὶ τετμήσθω ἐπιπέδῳ ἡ μὲν ἑτέρα σφαῖρα διὰ τοῦ κέντρου, ἡ δὲ ἑτέρα μὴ διὰ τοῦ κέντρου, ἔστω δὲ τὰ μὲν τέμνοντα ἐπίπεδα ὀρθὰ πρὸς τὰς ΑΓ, ΕΗ διαμέτρους, καὶ τετμήσθωσαν κατὰ τὰς ΔΒ, ΖΘ γραμμάς· ἔστιν δὴ τὸ μὲν κατὰ τὴν ΖΕΘ περιφέρειαν τμῆμα τῆς σφαίρας ἡμισφαίριον [τῶν δὲ κατὰ τὴν ΒΑΔ περιφέρειαν τομῶν ἐν μὲν τῷ ἑτέρῳ σχήματι, πρὸς ὃ τὸ Ϡ σημεῖον, μεῖζον ἡμισφαιρίου, ἐν δὲ τῷ ἑτέρῳ ἔλασσον [129] ἡμισφαιρίου], ἴσαι δὲ ἔστωσαν αἱ τῶν εἰρημένων τμημάτων ἐπιφάνειαι· λέγω οὖν ὅτι μεῖζόν ἐστι τὸ κατὰ τὴν ΖΕΘ περιφέρειαν ἡμισφαίριον τοῦ κατὰ τὴν ΒΑΔ περιφέρειαν τμήματος.

   Ἐπεὶ γὰρ ἴσαι εἰσὶν αἱ ἐπιφάνειαι τῶν εἰρημένων τμημάτων, φανερὸν ὅτι ἴση ἐστὶν ἡ ΒΑ τῇ ΕΖ εὐθείᾳ [δέδεικται γὰρ ἑκάστου τμήματος ἡ ἐπιφάνεια ἴση οὖσα κύκλῳ, οὗ ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἀπὸ τῆς κορυφῆς τοῦ τμήματος εὐθείᾳ ἀγομένῃ ἐπὶ τὴν περιφέρειαν τοῦ κύκλου, ὅς ἐστι βάσις τοῦ τμήματος. Καὶ ἐπεὶ μείζων ἐστὶν ἡμίσεως κύκλου ἡ ΒΑΔ περιφέρεια ἐν τῷ ἑτέρῳ τμήματι, πρὸς ὃ τὸ Ϡ σημεῖον]· δῆλον δὲ ὅτι ἡ ΒΑ ἐλάσσων ἐστὶν ἢ διπλασίων δυνάμει τῆς ΑΚ, τῆς δὲ ἐκ τοῦ κέντρου μείζων [130] ἢ διπλασίων δυνάμει. Ἔστω δὴ ἡ ΒΑ τῆς ΑΡ διπλασία δυνάμει, ἔστω δὲ καὶ τῇ ἐκ τοῦ κέντρου τοῦ ΑΒΔ κύκλου ἴση ἡ ΓΞ, καὶ ὃν ἔχει λόγον ἡ ΓΞ πρὸς τὴν ΓΚ, τοῦτον ἐχέτω ἡ ΜΑ πρὸς ΑΚ, ἀπὸ δὲ τοῦ κύκλου τοῦ περὶ διάμετρον τὴν ΒΔ κῶνος ἔστω κορυφὴν ἔχων τὸ Μ σημεῖον· ἴσος δή ἐστιν οὗτος τῷ κατὰ τὴν ΒΑΔ περιφέρειαν τμήματι τῆς σφαίρας. Ἔστω καὶ τῇ ΕΛ ἴση ἡ ΕΝ, καὶ ἀπὸ τοῦ κύκλου τοῦ περὶ διάμετρον τὴν ΘΖ κῶνος ἔστω κορυφὴν ἔχων τὸ Ν σημεῖον· ἴσος δὴ καὶ οὗτός ἐστι τῷ κατὰ τὴν ΘΕΖ περιφέρειαν ἡμισφαιρίῳ. Τὸ δὲ περιεχόμενον ὑπὸ τῶν ΑΡΓ μεῖζόν ἐστι τοῦ περιεχομένου ὑπὸ τῶν ΑΚΓ, διότι τὴν ἐλάσσονα πλευρὰν τῆς ἐλάσσονος τοῦ ἑτέρου μείζονα ἔχει, τὸ δὲ ἀπὸ τῆς ΑΡ ἴσον ἐστὶ τῷ περιεχομένῳ ὑπὸ τῶν ΑΚ, ΓΞ· ἥμισυ γάρ ἐστι τοῦ ἀπὸ τῆς ΑΒ· μεῖζον οὖν ἐστι καὶ τὸ συναμφότερον τοῦ συναμφοτέρου [τὸ ἄρα περιεχόμενον ὑπὸ τῶν ΓΑΡ μεῖζόν ἐστι τοῦ ὑπὸ τῶν ΞΚΑ]. Τῷ δὲ ὑπὸ τῶν ΞΚΑ ἴσον ἐστὶ τὸ ὑπὸ τῶν ΜΚΓ [ὥστε μεῖζόν ἐστι τὸ ὑπὸ τῶν ΓΑΡ τοῦ ὑπὸ τῶν ΜΚΓ]· ὥστε μείζονα λόγον [131] ἔχει ἡ ΓΑ πρὸς [τὴν] ΚΓ ἤπερ ἡ ΜΚ πρὸς [τὴν] ΑΡ. Ὃν δὲ λόγον ἔχει ἡ ΑΓ πρὸς [τὴν] ΓΚ, τοῦτον ἔχει τὸ ἀπὸ τῆς ΑΒ πρὸς τὸ ἀπὸ τῆς ΒΚ· δῆλον οὖν ὅτι μείζονα λόγον ἔχει τὸ ἥμισυ τοῦ ἀπὸ τῆς ΑΒ, ὅ ἐστιν ἴσον τῷ ἀπὸ ΑΡ, πρὸς τὸ ἀπὸ τῆς ΒΚ ἤπερ ἡ ΜΚ πρὸς τὴν διπλασίαν τῆς ΑΡ, ἥ ἐστιν ἴση τῇ ΛΝ· μείζονα ἄρα λόγον ἔχει καὶ ὁ κύκλος ὁ περὶ διάμετρον τὴν ΖΘ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΒΔ ἢ ἡ ΜΚ πρὸς [τὴν] ΝΛ. Ὥστε μείζων ἐστὶν ὁ κῶνος ὁ βάσιν μὲν ἔχων τὸν περὶ διάμετρον τὴν ΖΘ κύκλον, κορυφὴν δὲ τὸ Ν σημεῖον, τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος κύκλον τὸν περὶ διάμετρον τὴν ΒΔ, κορυφὴν δὲ τὸ Μ σημεῖον· δῆλον οὖν ὅτι καὶ τὸ ἡμισφαίριον τὸ κατὰ τὴν ΕΖΘ περιφέρειαν μεῖζόν ἐστι τοῦ τμήματος τοῦ κατὰ τὴν ΒΑΔ περιφέρειαν.

---

ΚΥΚΛΟΥ ΜΕΤΡΗΣΙΣ

 

[138]    α΄.

   Πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ ὀρθογωνίῳ, οὗ ἡ μὲν ἐκ τοῦ κέντρου ἴση μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῇ βάσει.

   Ἐχέτω ὁ ΑΒΓΔ κύκλος τριγώνῳ τῷ Ε, ὡς ὑπόκειται· λέγω ὅτι ἴσος ἐστίν.

   Εἰ γὰρ δυνατόν, ἔστω μείζων ὁ κύκλος, καὶ ἐγγεγράφθω τὸ ΑΓ τετράγωνον, καὶ τετμήσθωσαν αἱ περιφέρειαι δίχα, καὶ ἔστω τὰ τμήματα ἤδη ἐλάσσονα τῆς ὑπεροχῆς, ᾗ ὑπερέχει ὁ κύκλος τοῦ τριγώνου· τὸ εὐθύγραμμον ἄρα ἔτι τοῦ τριγώνου ἐστὶ μεῖζον. Εἰλήφθω κέντρον τὸ Ν καὶ κάθετος ἡ ΝΞ· ἐλάσσων ἄρα ἡ ΝΞ τῆς τοῦ τριγώνου πλευρᾶς. Ἔστιν δὲ καὶ ἡ περίμετρος τοῦ εὐθυγράμμου τῆς [139] λοιπῆς ἐλάττων, ἐπεὶ καὶ τῆς τοῦ κύκλου περιμέτρου· ἔλαττον ἄρα τὸ εὐθύγραμμον τοῦ Ε τριγώνου· ὅπερ ἄτοπον.

   Ἔστω δὲ ὁ κύκλος, εἰ δυνατόν, ἐλάσσων τοῦ Ε τριγώνου, καὶ περιγεγράφθω τὸ τετράγωνον, καὶ τετμήσθωσαν αἱ περιφέρειαι δίχα, καὶ ἤχθωσαν ἐφαπτόμεναι διὰ τῶν σημείων· ὀρθὴ ἄρα ἡ ὑπὸ ΟΑΡ. Ἡ ΟΡ ἄρα τῆς ΜΡ ἐστὶν μείζων· ἡ γὰρ ΡΜ τῇ ΡΑ ἴση ἐστί· καὶ τὸ ΡΟΠ τρίγωνον ἄρα τοῦ ΟΖΑΜ σχήματος μεῖζόν ἐστιν ἢ τὸ ἥμισυ. Λελείφθωσαν οἱ τῷ ΠΖΑ τομεῖ ὅμοιοι ἐλάσσους τῆς ὑπεροχῆς, ᾗ ὑπερέχει τὸ Ε τοῦ ΑΒΓΔ κύκλου· ἔτι ἄρα τὸ περιγεγραμμένον εὐθύγραμμον τοῦ Ε ἐστὶν ἔλασσον· ὅπερ ἄτοπον· ἔστιν γὰρ μεῖζον, ὅτι ἡ μὲν ΝΑ ἴση ἐστὶ τῇ καθέτῳ τοῦ τριγώνου, ἡ δὲ περίμετρος μείζων ἐστὶ τῆς βάσεως τοῦ τριγώνου. Ἴσος ἄρα ὁ κύκλος τῷ Ε τριγώνῳ.

   β΄.

   Ὁ κύκλος πρὸς τὸ ἀπὸ τῆς διαμέτρου τετράγωνον λόγον ἔχει, ὃν ια πρὸς ιδ.

   Ἔστω κύκλος, οὗ διάμετρος ἡ ΑΒ, καὶ περιγεγράφθω τετράγωνον τὸ ΓΗ, καὶ τῆς ΓΔ διπλῆ ἡ ΔΕ, ἕβδομον δὲ ἡ ΕΖ τῆς ΓΔ. Ἐπεὶ οὖν τὸ ΑΓΕ πρὸς τὸ ΑΓΔ λόγον ἔχει, ὃν κα πρὸς ζ, πρὸς δὲ τὸ ΑΕΖ τὸ ΑΓΔ λόγον ἔχει, ὃν ἑπτὰ [140] πρὸς ἕν, τὸ ΑΓΖ πρὸς τὸ ΑΓΔ ἐστίν, ὡς κβ πρὸς ζ. Ἀλλὰ τοῦ ΑΓΔ τετραπλάσιόν ἐστι τὸ ΓΗ τετράγωνον, τὸ δὲ ΑΓΔΖ τρίγωνον τῷ ΑΒ κύκλῳ ἴσον ἐστίν [ἐπεὶ ἡ μὲν ΑΓ κάθετος ἴση ἐστὶ τῇ ἐκ τοῦ κέντρου, ἡ δὲ βάσις τῆς διαμέτρου τριπλασίων καὶ τῷ ζ΄ ἔγγιστα ὑπερέχουσα δειχθήσεται]· ὁ κύκλος οὖν πρὸς τὸ ΓΗ τετράγωνον λόγον ἔχει, ὃν ια πρὸς ιδ.

   γ΄.

   Παντὸς κύκλου ἡ περίμετρος τῆς διαμέτρου τριπλασίων ἐστὶ καὶ ἔτι ὑπερέχει ἐλάσσονι μὲν ἢ ἑβδόμῳ μέρει τῆς διαμέτρου, μείζονι δὲ ἢ δέκα ἑβδομηκοστομόνοις.

   Ἔστω κύκλος καὶ διάμετρος ἡ ΑΓ καὶ κέντρον τὸ Ε καὶ ἡ ΓΛΖ ἐφαπτομένη καὶ ἡ ὑπὸ ΖΕΓ τρίτου ὀρθῆς· ἡ ΕΖ ἄρα πρὸς ΖΓ λόγον ἔχει, ὃν τϚ πρὸς ρνγ, ἡ δὲ ΕΓ πρὸς [τὴν] ΓΖ λόγον ἔχει, ὃν σξε πρὸς ρνγ. Τετμήσθω οὖν ἡ ὑπὸ ΖΕΓ δίχα τῇ ΕΗ· ἔστιν ἄρα, ὡς ἡ ΖΕ πρὸς ΕΓ, ἡ ΖΗ [141] πρὸς ΗΓ [καὶ ἐναλλὰξ καὶ συνθέντι]. Ὡς ἄρα συναμφότερος ἡ ΖΕ, ΕΓ πρὸς ΖΓ, ἡ ΕΓ πρὸς ΓΗ· ὥστε ἡ ΓΕ πρὸς ΓΗ μείζονα λόγον ἔχει ἤπερ φοα πρὸς ρνγ. Ἡ ΕΗ ἄρα πρὸς ΗΓ δυνάμει λόγον ἔχει, ὃν Μ λδ Ϛθυν πρὸς Μ β Ϛγυθ· μήκει ἄρα, ὃν φϞα η΄ πρὸς ρνγ. Πάλιν δίχα ἡ ὑπὸ ΗΕΓ τῇ ΕΘ· διὰ τὰ αὐτὰ ἄρα ἡ ΕΓ πρὸς ΓΘ μείζονα λόγον ἔχει ἢ ὃν Ϛαρξβ η΄ πρὸς ρνγ· ἡ ΘΕ ἄρα πρὸς ΘΓ μείζονα λόγον ἔχει ἢ ὃν Ϛαροβ η΄ πρὸς ρνγ. Ἔτι δίχα ἡ ὑπὸ ΘΕΓ τῇ ΕΚ· ἡ ΕΓ ἄρα πρὸς ΓΚ μείζονα λόγον ἔχει ἢ ὃν Ϛβτλδ δ᾿ πρὸς ρνγ· ἡ ΕΚ ἄρα πρὸς ΓΚ μείζονα ἢ ὃν Ϛβτλθ δ᾿ πρὸς ρνγ. Ἔτι δίχα ἡ ὑπὸ ΚΕΓ τῇ ΛΕ· ἡ ΕΓ ἄρα πρὸς ΛΓ μείζονα [μήκει] λόγον ἔχει ἤπερ τὰ Ϛδχογ Ϛ΄ πρὸς ρνγ. Ἐπεὶ οὖν ἡ ὑπὸ ΖΕΓ τρίτου οὖσα ὀρθῆς τέτμηται τετράκις δίχα, ἡ ὑπὸ ΛΕΓ ὀρθῆς ἐστι μη΄. Κείσθω οὖν αὐτῇ ἴση πρὸς τῷ Ε ἡ ὑπὸ ΓΕΜ· ἡ ἄρα ὑπὸ ΛΕΜ ὀρθῆς ἐστι κδ΄. Καὶ ἡ ΛΜ ἄρα εὐθεῖα τοῦ περὶ τὸν κύκλον ἐστὶ πολυγώνου πλευρὰ πλευρὰς ἔχοντος ϞϚ. Ἐπεὶ οὖν ἡ ΕΓ πρὸς τὴν [142] ΓΛ ἐδείχθη μείζονα λόγον ἔχουσα ἤπερ Ϛδχογ Ϛ΄ πρὸς ρνγ, ἀλλὰ τῆς μὲν ΕΓ διπλῆ ἡ ΑΓ, τῆς δὲ ΓΛ διπλασίων ἡ ΛΜ, καὶ ἡ ΑΓ ἄρα πρὸς τὴν τοῦ ϞϚ γώνου περίμετρον μείζονα λόγον ἔχει ἤπερ Ϛδχογ Ϛ΄ πρὸς Μ α Ϛδχπη. Καί ἐστιν τριπλασία, καὶ ὑπερέχουσιν χξζ Ϛ΄, ἅπερ τῶν Ϛδχογ Ϛ΄ ἐλάττονά ἐστιν ἢ τὸ ἕβδομον· ὥστε τὸ πολύγωνον τὸ περὶ τὸν κύκλον τῆς διαμέτρου ἐστὶ τριπλάσιον καὶ ἐλάττονι ἢ τῷ ἑβδόμῳ μέρει μεῖζον· ἡ τοῦ κύκλου ἄρα περίμετρος πολὺ μᾶλλον ἐλάσσων ἐστὶν ἢ τριπλασίων καὶ ἑβδόμῳ μέρει μείζων.

   Ἔστω κύκλος καὶ διάμετρος ἡ ΑΓ, ἡ δὲ ὑπὸ ΒΑΓ τρίτου ὀρθῆς· ἡ ΑΒ ἄρα πρὸς ΒΓ ἐλάσσονα λόγον ἔχει ἢ ὃν Ϛατνα πρὸς ψπ [ἡ δὲ ΑΓ πρὸς ΓΒ, ὃν Ϛαφξ πρὸς ψπ]. Δίχα ἡ ὑπὸ ΒΑΓ τῇ ΑΗ. Ἐπεὶ οὖν ἴση ἐστὶν ἡ ὑπὸ ΒΑΗ τῇ ὑπὸ ΗΓΒ, ἀλλὰ καὶ τῇ ὑπὸ ΗΑΓ, καὶ ἡ ὑπὸ ΗΓΒ τῇ ὑπὸ ΗΑΓ ἐστὶν ἴση. Καὶ κοινὴ ἡ ὑπὸ ΑΗΓ ὀρθή· καὶ τρίτη ἄρα ἡ ὑπὸ ΗΖΓ τρίτῃ τῇ ὑπὸ ΑΓΗ ἴση. Ἰσογώνιον ἄρα τὸ ΑΗΓ τῷ ΓΗΖ τριγώνῳ· ἔστιν ἄρα, ὡς ἡ ΑΗ πρὸς ΗΓ, ἡ ΓΗ πρὸς ΗΖ καὶ ἡ ΑΓ πρὸς ΓΖ. Ἀλλ᾿ ὡς ἡ ΑΓ πρὸς ΓΖ, [καὶ] συναμφότερος ἡ ΓΑΒ πρὸς ΒΓ· καὶ ὡς συναμφότερος ἄρα ἡ ΒΑΓ πρὸς ΒΓ, ἡ ΑΗ πρὸς ΗΓ. Διὰ [143] τοῦτο οὖν ἡ ΑΗ πρὸς [τὴν] ΗΓ ἐλάσσονα λόγον ἔχει ἤπερ βϠια πρὸς ψπ, ἡ δὲ ΑΓ πρὸς τὴν ΓΗ ἐλάσσονα ἢ ὃν Ϛγιγ Ϛ΄ δ΄ πρὸς ψπ. Δίχα ἡ ὑπὸ ΓΑΗ τῇ ΑΘ· ἡ ΑΘ ἄρα διὰ τὰ αὐτὰ πρὸς τὴν ΘΓ ἐλάσσονα λόγον ἔχει ἢ ὃν ϚεϠκδ Ϛ΄ δ΄ πρὸς ψπ ἢ ὃν Ϛαωκγ πρὸς σμ· ἑκατέρα γὰρ ἑκατέρας δ ιγ΄· ὥστε ἡ ΑΓ πρὸς τὴν ΓΘ ἢ ὃν Ϛαωλη θ ια΄ πρὸς σμ. Ἔτι δίχα ἡ ὑπὸ ΘΑΓ τῇ ΚΑ· καὶ ἡ ΑΚ πρὸς τὴν ΚΓ ἐλάσσονα [ἄρα] λόγον ἔχει ἢ ὃν Ϛαζ πρὸς ξϚ· ἑκατέρα γὰρ ἑκατέρας ια μ΄. Ἡ ΑΓ ἄρα πρὸς [τὴν] ΚΓ ἢ ὃν Ϛαθ Ϛ΄ πρὸς ξϚ. Ἔτι δίχα ἡ ὑπὸ ΚΑΓ τῇ ΛΑ· ἡ ΑΛ ἄρα πρὸς [τὴν] ΛΓ ἐλάσσονα λόγον ἔχει ἢ ὃν τὰ βιϚ Ϛ΄ πρὸς ξϚ, ἡ δὲ ΑΓ πρὸς ΓΛ ἐλάσσονα ἢ τὰ Ϛβιζ δ΄ πρὸς ξϚ. Ἀνάπαλιν ἄρα ἡ περίμετρος τοῦ πολυγώνου πρὸς τὴν διάμετρον μείζονα λόγον ἔχει ἤπερ ϚϚτλϚ πρὸς Ϛβιζ δ΄, ἅπερ τῶν Ϛβιζ δ΄ μείζονά ἐστιν ἢ τριπλασίονα καὶ δέκα οα΄· καὶ ἡ περίμετρος ἄρα τοῦ ϞϚγώνου τοῦ ἐν τῷ κύκλῳ τῆς διαμέτρου τριπλασίων ἐστὶ καὶ μείζων ἢ ι οα΄· ὥστε καὶ ὁ κύκλος ἔτι μᾶλλον τριπλασίων ἐστὶ καὶ μείζων ἢ ι οα΄.

   Ἡ ἄρα τοῦ κύκλου περίμετρος τῆς διαμέτρου τριπλασίων ἐστὶ καὶ ἐλάσσονι μὲν ἢ ἑβδόμῳ μέρει, μείζονι δὲ ἢ ι οα΄ μείζων.

---

ΠΕΡΙ ΚΩΝΟΕΙΔΕΩΝ ΚΑΙ ΣΦΑΙΡΟΕΙΔΕΩΝ

Ἀρχιμήδης Δοσιθέῳ εὖ πράττειν.

[152]   Ἀποστέλλω τοι γράψας ἐν τῷδε τῷ βιβλίῳ τῶν τε λοιπῶν θεωρημάτων τὰς ἀποδείξιας, ὧν οὐκ εἶχες ἐν τοῖς πρότερον ἀπεσταλμένοις, καὶ ἄλλων ὕστερον ποτεξευρημένων, ἃ πρότερον μὲν ἤδη πολλάκις ἐγχειρήσας ἐπισκέπτεσθαι δύσκολον ἔχειν τι φανείσας μοι τᾶς εὑρέσιος αὐτῶν ἀπόρησα· διόπερ οὐδὲ συνεξεδόθεν τοῖς ἄλλοις αὐτὰ τὰ προβεβλημένα. Ὕστερον δὲ ἐπιμελέστερον ποτ᾿ αὐτοῖς γενόμενος ἐξεῦρον τὰ ἀπορηθέντα. Ἦν δὲ τὰ μὲν λοιπὰ τῶν προτέρων θεωρημάτων περὶ τοῦ ὀρθογωνίου κωνοειδέος προβεβλημένα, τὰ δὲ νῦν ἐντι ποτεξευρημένα περί τε ἀμβλυγωνίου κωνοειδέος καὶ περὶ σφαιροειδέων σχημάτων, ὧν τὰ μὲν παραμάκεα, τὰ δὲ ἐπιπλατέα καλέω.

Περὶ μὲν οὖν τοῦ ὀρθογωνίου κωνοειδέος ὑπέκειτο τάδε· εἴ κα ὀρθογωνίου κώνου τομὰ μενούσας τᾶς διαμέτρου περιενεχθεῖσα ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, τὸ περιλαφθὲν σχῆμα ὑπὸ τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς ὀρθογώνιον κωνοειδὲς καλεῖσθαι, καὶ ἄξονα μὲν αὐτοῦ τὰν μεμενάκουσαν διάμετρον καλεῖσθαι, κορυφὰν δὲ τὸ σαμεῖον, καθ᾿ ὃ ἅπτεται ὁ ἄξων τᾶς τοῦ κωνοειδέος ἐπιφανείας· καὶ εἴ κα τοῦ ὀρθογωνίου κωνοειδέος σχήματος ἐπίπεδον ἐπιψαύῃ, παρὰ δὲ τὸ ἐπιψαῦον ἐπίπεδον ἄλλο ἐπίπεδον ἀχθὲν ἀποτέμῃ τι τμᾶμα τοῦ κωνοειδέος, βάσιν μὲν καλεῖσθαι τοῦ ἀποτμαθέντος τμάματος τὸ ἐπίπεδον [153] τὸ περιλαφθὲν ὑπὸ τᾶς τοῦ κωνοειδέος τομᾶς ἐν τῷ ἀποτέμνοντι ἐπιπέδῳ, κορυφὰν δὲ τὸ σαμεῖον, καθ᾿ ὃ ἐπιψαύει τὸ ἕτερον ἐπίπεδον τοῦ κωνοειδέος, ἄξονα δὲ τὰν ἐναπολαφθεῖσαν εὐθεῖαν ἐν τῷ τμάματι ἀπὸ τᾶς ἀχθείσας διὰ τᾶς κορυφᾶς τοῦ τμάματος παρὰ τὸν ἄξονα τοῦ κωνοειδέος.
   Προεβάλλετο δὲ τάδε θεωρῆσαι· διὰ τί, εἴ κα τοῦ ὀρθογωνίου κωνοειδέος τμάματα ἀποτμαθῇ ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα, τὸ ἀποτμαθὲν τμᾶμα ἡμιόλιον ἐσσεῖται τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· καὶ διὰ τί, εἴ κα ἀπὸ τοῦ ὀρθογωνίου κωνοειδέος δύο τμάματα ἀποτμαθέωντι ἐπιπέδοις ὁπωσοῦν ἀγμένοις, τὰ ἀποτμαθέντα τμάματα διπλάσιον λόγον ἑξοῦντι ποτ᾿ ἄλλαλα τῶν ἀξόνων.
   Περὶ δὲ τοῦ ἀμβλυγωνίου κωνοειδέος ὑποτιθέμεθα μὲν τάδε· εἴ κα ἐν ἐπιπέδῳ ἔωντι ἀμβλυγωνίου κώνου τομὰ καὶ ἁ διάμετρος αὐτᾶς καὶ αἱ ἔγγιστα τᾶς τοῦ ἀμβλυγωνίου κώνου τομᾶς, μενούσας δὲ τᾶς διαμέτρου περιενεχθὲν τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ εἰρημέναι γραμμαί, ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, αἱ μὲν ἔγγιστα εὐθεῖαι τᾶς τοῦ ἀμβλυγωνίου κώνου τομᾶς δῆλον ὡς κῶνον ἰσοσκελέα περιλαψοῦνται, οὗ κορυφὰ ἐσσεῖται τὸ σαμεῖον, καθ᾿ ὃ αἱ ἔγγιστα συμπίπτοντι, ἄξων δὲ ἁ μεμενάκουσα διάμετρος· τὸ δὲ ὑπὸ τᾶς τοῦ ἀμβλυγωνίου κώνου τομᾶς σχῆμα περιλαφθὲν ἀμβλυγώνιον κωνοειδὲς καλεῖσθαι, ἄξονα δὲ αὐτοῦ τὰν μεμενάκουσαν διάμετρον, κορυφὰν δὲ τὸ σαμεῖον, καθ᾿ ὃ ἅπτεται ὁ ἄξων τᾶς ἐπιφανείας τοῦ κωνοειδέος· τὸν δὲ κῶνον τὸν περιλαφθέντα ὑπὸ τᾶν ἔγγιστα τᾶς τοῦ ἀμβλυγωνίου κώνου τομᾶς περιέχοντα τὸ κωνοειδὲς καλεῖσθαι, τὰν δὲ μεταξὺ εὐθεῖαν τᾶς τε κορυφᾶς τοῦ [154] κωνοειδέος καὶ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδὲς ποτεοῦσαν τῷ ἄξονι καλεῖσθαι· καὶ εἴ κα τοῦ ἀμβλυγωνίου κωνοειδέος ἐπίπεδον ἐπιψαύῃ, παρὰ δὲ τὸ ἐπιψαῦον ἐπίπεδον ἄλλο ἐπίπεδον ἀχθὲν ἀποτέμῃ τμᾶμα τοῦ κωνοειδέος, βάσιν μὲν καλεῖσθαι τοῦ ἀποτμαθέντος τμάματος τὸ ἐπίπεδον τὸ περιλαφθὲν ὑπὸ τᾶς τοῦ κωνοειδέος τομᾶς ἐν τῷ ἀποτέμνοντι ἐπιπέδῳ, κορυφὰν δὲ τὸ σαμεῖον, καθ᾿ ὃ ἅπτεται τὸ ἐπίπεδον τὸ ἐπιψαῦον τοῦ κωνοειδέος, ἄξονα δὲ τὰν ἀπολαφθεῖσαν ἐν τῷ τμάματι ἀπὸ τᾶς διαχθείσας διὰ τᾶς κορυφᾶς τοῦ τμάματος καὶ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδές, καὶ τὰν μεταξὺ τᾶν εἰρημενᾶν κορυφᾶν εὐθεῖαν ποτεοῦσαν τῷ ἄξονι καλεῖσθαι.
   Τὰ μὲν οὖν ὀρθογώνια κωνοειδέα πάντα ὁμοῖά ἐντι, τῶν δὲ ἀμβλυγωνίων κωνοειδέων ὁμοῖα καλείσθω, ὧν κα οἱ κῶνοι οἱ περιέχοντες τὰ κωνοειδέα ὁμοῖοι ἔωντι. Προβάλλεται δὲ τάδε θεωρῆσαι· διὰ τί, εἴ κα τοῦ ἀμβλυγωνίου κωνοειδέος ἀποτμαθῇ τμάματα ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα, τὸ ἀποτμαθὲν τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ τριπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι ποτὶ τὰν ἴσαν ἀμφοτέραις τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ διπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι· καὶ διὰ τί, εἴ κα τοῦ ἀμβλυγωνίου κωνοειδέος τμᾶμα ἀποτμαθῇ ἐπιπέδῳ μὴ ὀρθῷ ποτὶ τὸν ἄξονα, τὸ ἀποτμαθὲν τμᾶμα ποτὶ τὸ σχῆμα τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, ὃ γίγνεται ἀπότμαμα κώνου, τοῦτον ἕξει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ [155] τριπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι ποτὶ τὰν ἴσαν ἀμφοτέραις τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ διπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι.
   Περὶ δὲ τῶν σφαιροειδέων σχημάτων ὑποτιθέμεθα τάδε· εἴ κα ὀξυγωνίου κώνου τομὰ μενούσας τᾶς μείζονος διαμέτρου περιενεχθεῖσα ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, τὸ περιλαφθὲν σχῆμα ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς παραμᾶκες σφαιροειδὲς καλεῖσθαι· εἰ δέ κα τᾶς ἐλάσσονος διαμέτρου μενούσας περιενεχθεῖσα ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, τὸ περιλαφθὲν σχῆμα ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἐπιπλατὺ σφαιροειδὲς καλεῖσθαι· ἑκατέρου δὲ τῶν σφαιροειδέων ἄξονα μὲν καλεῖσθαι τὰν μεμενάκουσαν διάμετρον, κορυφὰν δὲ τὸ σαμεῖον, καθ᾿ ὃ ἅπτεται ὁ ἄξων τᾶς ἐπιφανείας τοῦ σφαιροειδέος, κέντρον δὲ καλεῖσθαι τὸ μέσον τοῦ ἄξονος καὶ διάμετρον τὰν διὰ τοῦ κέντρου ποτ᾿ ὀρθὰς ἀγομέναν τῷ ἄξονι· καὶ εἴ κα τῶν σφαιροειδέων σχημάτων ὁποτερουοῦν ἐπίπεδα παράλληλα ἐπιψαύωντι μὴ τέμνοντα, παρὰ δὲ τὰ ἐπίπεδα τὰ ψαύοντα ἄλλο ἐπίπεδον ἀχθῇ τέμνον τὸ σφαιροειδές, τῶν γενομένων τμαμάτων βάσιν μὲν καλεῖσθαι τὸ περιλαφθὲν ὑπὸ τᾶς τοῦ σφαιροειδέος τομᾶς ἐν τῷ τέμνοντι ἐπιπέδῳ, κορυφὰς δὲ τὰ σημεῖα, καθ᾿ ἃ ἐπιψαύοντι τοῦ σφαιροειδέος τὰ παράλληλα ἐπίπεδα, ἄξονας δὲ τὰς ἐναπολαφθείσας εὐθείας ἐν τοῖς τμαμάτεσσιν ἀπὸ τᾶς εὐθείας τᾶς τὰς κορυφὰς αὐτῶν ἐπιζευγνυούσας· ὅτι δὲ τά τε ἐπιψαύοντα ἐπίπεδα τοῦ σφαιροειδέος καθ᾿ ἓν μόνον ἅπτονται σαμεῖον τᾶς ἐπιφανείας αὐτοῦ, καὶ ὅτι ἁ τὰς ἁφὰς ἐπιζευγνύουσα εὐθεῖα διὰ τοῦ κέντρου τοῦ σφαιροειδέος πορεύεται, δειξοῦμες· ὁμοῖα δὲ καλεῖσθαι τῶν σφαιροειδέων σχημάτων, [156] ὧν κα οἱ ἄξονες ποτὶ τὰς διαμέτρους τὸν αὐτὸν λόγον ἔχωντι. Τμάματα δὲ σφαιροειδέων σχημάτων καὶ κωνοειδέων ὁμοῖα καλείσθω, εἴ κα ἀφ᾿ ὁμοίων σχημάτων ἀφαιρημένα ἔωντι καὶ τάς τε βάσεις ὁμοίας ἔχωντι, καὶ οἱ ἄξονες αὐτῶν ἤτοι ὀρθοὶ ἐόντες ποτὶ τὰ ἐπίπεδα τῶν βάσιων ἢ γωνίας ἴσας ποιοῦντες ποτὶ τὰς ὁμολόγους διαμέτρους τῶν βάσιων τὸν αὐτὸν ἔχωντι λόγον ποτ᾿ ἀλλάλους ταῖς ὁμολόγοις διαμέτροις τῶν βάσιων.
   Προβάλλεται δὲ περὶ τῶν σφαιροειδέων τάδε θεωρῆσαι· διὰ τί, εἴ κά τι τῶν σφαιροειδέων σχημάτων ἐπιπέδῳ τμαθῇ διὰ τοῦ κέντρου ὀρθῷ ποτὶ τὸν ἄξονα, τῶν γεναμένων τμαμάτων ἑκάτερον διπλάσιον ἐσσεῖται τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, εἰ δέ κα ὀρθῷ μὲν ποτὶ τὸν ἄξονα τῷ ἐπιπέδῳ τμαθῇ, μὴ διὰ τοῦ κέντρου δέ, τῶν γεναμένων τμαμάτων τὸ μὲν μεῖζον ποτὶ τὸν κῶνον τὸν τὰν αὐτὰν βάσιν ἔχοντα τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισείᾳ τᾶς εὐθείας, ἅ ἐστιν ἄξων τοῦ σφαιροειδέος, καὶ τῷ ἄξονι τῷ τοῦ ἐλάσσονος τμάματος ποτὶ τὸν ἄξονα τοῦ ἐλάσσονος τμάματος, τὸ δὲ ἔλασσον τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισείᾳ τᾶς εὐθείας, ἅ ἐστιν ἄξων τοῦ σφαιροειδέος, καὶ τῷ ἄξονι τῷ τοῦ μείζονος τμάματος ποτὶ τὸν ἄξονα τοῦ μείζονος τμάματος· καὶ διὰ τί, εἴ κα τῶν σφαιροειδέων τι ἐπιπέδῳ τμαθῇ διὰ τοῦ κέντρου μὴ ὀρθῷ ποτὶ τὸν ἄξονα, τῶν γεναμένων τμαμάτων ἑκάτερον διπλάσιον ἐσσεῖται τοῦ σχήματος τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· [157] γίγνεται δὲ τὸ σχῆμα ἀπότμαμα κώνου· εἰ δέ κα μήτε διὰ τοῦ κέντρου μήτε ὀρθῷ ποτὶ τὸν ἄξονα τῷ ἐπιπέδῳ τμαθῇ τὸ σφαιροειδές, τῶν γεναμένων τμαμάτων τὸ μὲν μεῖζον ποτὶ τὸ σχῆμα τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισέᾳ αὐτᾶς τᾶς ἐπιζευγνυούσας τὰς κορυφὰς τῶν τμαμάτων καὶ τῷ ἄξονι τῷ τοῦ ἐλάσσονος τμάματος ποτὶ τὸν ἄξονα τὸν τοῦ ἐλάσσονος τμάματος, τὸ δὲ ἔλασσον τμᾶμα ποτὶ τὸ σχῆμα τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἔχει ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισέᾳ τᾶς ἐπιζευγνυούσας τὰς κορυφὰς τῶν τμαμάτων καὶ τῷ ἄξονι τοῦ μείζονος τμάματος ποτὶ τὸν ἄξονα τὸν τοῦ μείζονος τμάματος· γίνεται δὲ καὶ ἐν τούτοις τὸ σχῆμα ἀπότμαμα κώνου.
   Ἀποδειχθέντων δὲ τῶν εἰρημένων θεωρημάτων διὰ τούτων εὑρίσκονται θεωρήματά τε πολλὰ καὶ προβλήματα, οἷον καὶ τόδε· ὅτι τὰ ὁμοῖα σφαιροειδέα καὶ τὰ ὁμοῖα τμάματα τῶν τε σφαιροειδέων σχημάτων καὶ τῶν κωνοειδέων τριπλασίονα λόγον ἔχοντι ποτ᾿ ἄλλαλα τῶν ἀξόνων, καὶ διότι τῶν ἴσων σφαιροειδέων σχημάτων τὰ τετράγωνα τὰ ἀπὸ τῶν διαμέτρων ἀντιπεπόνθασι τοῖς ἀξόνεσσιν, καὶ εἴ κα τῶν σφαιροειδέων σχημάτων τὰ τετράγωνα τὰ ἀπὸ τῶν διαμέτρων ἀντιπεπόνθωντι τοῖς ἀξόνεσσιν, ἴσα ἐντὶ τὰ σφαιροειδέα· πρόβλημα δὲ οἷον καὶ τόδε· ἀπὸ τοῦ δοθέντος σφαιροειδέος σχήματος ἢ κωνοειδέος τμᾶμα ἀποτεμεῖν ἐπιπέδῳ παρὰ δοθὲν ἐπίπεδον ἀγμένῳ, εἶμεν δὲ τὸ ἀποτμαθὲν τμᾶμα ἴσον τῷ δοθέντι κώνῳ ἢ κυλίνδρῳ ἢ σφαίρᾳ τᾷ δοθείσᾳ.
   Προγράψαντες οὖν τά τε θεωρήματα καὶ τὰ ἐπιτάγματα
[158]τὰ χρεῖαν ἔχοντα εἰς τὰς ἀποδείξιας αὐτῶν μετὰ ταῦτα γραψοῦμές τοι τὰ προκείμενα. Εὐτύχει.

‹ΟΡΟΙ›

   Εἴ κα κῶνος ἐπιπέδῳ τμαθῇ συμπίπτοντι πάσαις ταῖς τοῦ κώνου πλευραῖς, ἁ τομὰ ἐσσεῖται ἤτοι κύκλος ἢ ὀξυγωνίου κώνου τομά. Εἰ μὲν οὖν κύκλος ἁ τομά, δῆλον ὅτι τὸ ἀπολαφθὲν ἀπ᾿ αὐτοῦ τμᾶμα ἐπὶ τὰ αὐτὰ τᾷ τοῦ κώνου κορυφᾷ κῶνος ἐσσεῖται· εἰ δέ κα ἁ τομὰ γένηται ὀξυγωνίου κώνου τομά, τὸ ἀπολαφθὲν ἀπὸ τοῦ κώνου σχῆμα ἐπὶ τὰ αὐτὰ τᾷ τοῦ κώνου κορυφᾷ ἀπότμαμα κώνου καλείσθω, τοῦ δὲ ἀποτμάματος βάσις μὲν καλείσθω τὸ ἐπίπεδον τὸ περιλαφθὲν ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, κορυφὰ δὲ τὸ σαμεῖον, ὃ καὶ τοῦ κώνου κορυφά, ἄξων δὲ ἁ ἀπὸ τᾶς κορυφᾶς τοῦ κώνου ἐπὶ τὸ κέντρον τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἐπιζευχθεῖσα εὐθεῖα.

Καὶ εἴ κα κύλινδρος δυοῖς ἐπιπέδοις παραλλήλοις τμαθῇ συμπιπτόντεσσι πάσαις ταῖς τοῦ κυλίνδρου πλευραῖς, αἱ τομαὶ ἐσσοῦνται ἤτοι κύκλοι ἢ ὀξυγωνίων κώνων τομαὶ ἴσαι καὶ ὁμοῖαι ἀλλάλαις. Εἰ μὲν οὖν κα αἱ τομαὶ κύκλοι γένωνται, δῆλον ὅτι τὸ ἀποτμαθὲν ἀπὸ τοῦ κυλίνδρου σχῆμα μεταξὺ τῶν παραλλήλων ἐπιπέδων κύλινδρος ἐσσεῖται· εἰ δέ κα αἱ τομαὶ γένωνται ὀξυγωνίων κώνων τομαί, τὸ ἀπολαφθὲν ἀπὸ τοῦ κυλίνδρου σχῆμα μεταξὺ τῶν παραλλήλων ἐπιπέδων τόμος κυλίνδρου καλείσθω, τοῦ δὲ τόμου βάσις μὲν καλείσθω τὰ ἐπίπεδα τὰ περιλαφθέντα ὑπὸ τᾶν τῶν ὀξυγωνίων κώνων τομᾶν, ἄξων δὲ ἁ ἐπιζευγνύουσα εὐθεῖα τὰ κέντρα τᾶν τῶν ὀξυγωνίων [159] κώνων τομᾶν· ἐσσεῖται δὲ αὕτα ἐπὶ τᾶς αὐτᾶς εὐθείας τῷ ἄξονι τοῦ κυλίνδρου.

‹ΛΗΜΜΑ›

   Εἴ κα ἔωντι μεγέθεα ὁποσαοῦν τῷ ἴσῳ ἀλλάλων ὑπερέχοντα, ᾖ δὲ ἁ ὑπεροχὰ ἴσα τῷ ἐλαχίστῳ, καὶ ἄλλα μεγέθεα τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον τῷ μεγίστῳ, πάντα τὰ μεγέθεα, ὧν ἐστιν ἕκαστον ἴσον τῷ μεγίστῳ, πάντων μὲν τῶν τῷ ἴσῳ ὑπερεχόντων ἐλάσσονα ἐσσοῦνται ἢ διπλάσια, τῶν δὲ λοιπῶν χωρὶς τοῦ μεγίστου μείζονα ἢ διπλάσια. Ἁ δὲ ἀπόδειξις τούτου φανερά.

α΄.
   Εἴ κα μεγέθεα ὁποσαοῦν τῷ πλήθει ἄλλοις μεγέθεσιν ἴσοις τῷ πλήθει κατὰ δύο τὸν αὐτὸν λόγον ἔχωντι τὰ ὁμοίως τεταγμένα, λέγηται δὲ τά τε πρῶτα μεγέθεα ποτ᾿ ἄλλα μεγέθεα ἢ πάντα ἤ τινα αὐτῶν ἐν λόγοις ὁποιοισοῦν, καὶ τὰ ὕστερον ποτ᾿ ἄλλα μεγέθεα τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, πάντα τὰ πρῶτα μεγέθεα ποτὶ πάντα, ἃ λέγονται, τὸν αὐτὸν ἑξοῦντι λόγον, ὃν ἔχοντι πάντα τὰ ὕστερον μεγέθεα ποτὶ πάντα, ἃ λέγονται.

[160]    Ἔστω τινὰ μεγέθεα τὰ Α, Β, Γ, Δ, Ε, Ζ ἄλλοις μεγέθεσιν ἴσοις τῷ πλήθει τοῖς Η, Θ, Ι, Κ, Λ, Μ κατὰ δύο τὸν αὐτὸν ἔχοντα λόγον, καὶ ἐχέτω τὸ μὲν Α ποτὶ τὸ Β τὸν αὐτὸν λόγον, ὃν τὸ Η ποτὶ τὸ Θ, τὸ δὲ Β ποτὶ τὸ Γ, ὃν τὸ Θ ποτὶ τὸ Ι, καὶ τὰ ἄλλα ὁμοίως τούτοις, λεγέσθω δὲ τὰ μὲν Α, Β, Γ, Δ, Ε, Ζ μεγέθεα ποτ᾿ ἄλλα μεγέθεα τὰ Ν, Ξ, Ο, Π, Ρ, Σ ἐν λόγοις ὁποιοισοῦν, τὰ δὲ Η, Θ, Ι, Κ, Λ, Μ ποτ᾿ ἄλλα τὰ Τ, Υ, Φ, Χ, Ψ, Ω τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, καὶ ὃν μὲν ἔχει λόγον τὸ Α ποτὶ τὸ Ν, τὸ Η ἐχέτω ποτὶ τὸ Τ, ὃν δὲ λόγον ἔχει τὸ Β ποτὶ τὸ Ξ, τὸ Θ ἐχέτω ποτὶ τὸ Υ, καὶ τὰ ἄλλα ὁμοίως τούτοις· δεικτέον ὅτι πάντα τὰ Α, Β, Γ, Δ, Ε, Ζ ποτὶ πάντα τὰ Ν, Ξ, Ο, Π, Ρ, Σ τὸν αὐτὸν ἔχοντι λόγον, ὃν πάντα τὰ Η, Θ, Ι, Κ, Λ, Μ ποτὶ πάντα τὰ Τ, Υ, Φ, Χ, Ψ, Ω.
   Ἐπεὶ γὰρ τὸ μὲν Ν ποτὶ τὸ Α τὸν αὐτὸν ἔχει λόγον, ὃν τὸ Τ ποτὶ τὸ Η, τὸ δὲ Α ποτὶ τὸ Β, ὃν τὸ Η ποτὶ τὸ Θ, τὸ δὲ Β ποτὶ τὸ Ξ, ὃν τὸ Θ ποτὶ τὸ Υ, τὸν αὐτὸν ἕξει λόγον τὸ Ν ποτὶ τὸ Ξ, ὃν τὸ Τ ποτὶ τὸ Υ· διὰ τὰ αὐτὰ δὲ καὶ τὸ Ξ ποτὶ τὸ Ο, ὃν τὸ Υ ποτὶ τὸ Φ, καὶ τούτοις τὰ ἄλλα ὁμοίως. Ἔχοντι δὴ τὰ μὲν Α, Β, Γ, Δ, Ε, Ζ πάντα ποτὶ τὸ Α τὸν αὐτὸν λόγον, ὃν ἔχοντι τὰ Η, Θ, Ι, Κ, Λ, Μ πάντα ποτὶ τὸ Η, τὸ δὲ Α ποτὶ τὸ Ν, ὃν τὸ Η ποτὶ τὸ Τ, τὸ δὲ Ν ποτὶ πάντα τὰ Ν, Ξ, Ο, Π, Ρ, Σ τὸν αὐτὸν λόγον, ὃν τὸ Τ ποτὶ πάντα τὰ Τ, Υ, Φ, Χ, Ψ, Ω· δῆλον οὖν, ὅτι πάντα τὰ Α, Β, Γ, Δ, Ε, Ζ ποτὶ πάντα τὰ Ν, Ξ, Ο, Π, Ρ, Σ τὸν αὐτὸν ἔχοντι λόγον, ὃν πάντα τὰ Η, Θ, Ι, Κ, Λ, Μ ποτὶ πάντα τὰ Τ, Υ, Φ, Χ, Ψ, Ω.
   Φανερὸν δὲ ὅτι καὶ εἴ κα τῶν τε Α, Β, Γ, Δ, Ε, Ζ μεγεθέων τὰ μὲν Α, Β, Γ, Δ, Ε λέγωνται ποτὶ τὰ Ν, Ξ, Ο, Π, Ρ, τὸ

[161] δὲ Ζ μηδὲ ποθ᾿ ἓν λέγηται, καὶ τῶν Η, Θ, Ι, Κ, Λ, Μ τὰ μὲν Η, Θ, Ι, Κ, Λ λέγωνται ποτὶ τὰ Τ, Υ, Φ, Χ, Ψ, τὰ ὁμοῖα ἐν τοῖς αὐτοῖς λόγοις, τὸ δὲ Μ μηδὲ ποθ᾿ ἓν λέγηται, ὁμοίως πάντα τὰ Α, Β, Γ, Δ, Ε, Ζ ποτὶ πάντα τὰ Ν, Ξ, Ο, Π, Ρ τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ Η, Θ, Ι, Κ, Λ, Μ ποτὶ πάντα τὰ Τ, Υ, Φ, Χ, Ψ.
   β΄.
   Εἴ κα γραμμαὶ ἴσαι ἀλλάλαις ἔωντι ὁποσαιοῦν τῷ πλήθει, καὶ παρ᾿ ἑκάσταν αὐτᾶν παραπέσῃ τι χωρίον ὑπερβάλλον εἴδει τετραγώνῳ, ἔωντι δὲ αἱ πλευραὶ τῶν ὑπερβλημάτων τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι καὶ ἁ ὑπεροχὰ ἴσα τᾷ ἐλαχίστᾳ, ἔωντι δὲ καὶ ἄλλα χωρία τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον τῷ μεγίστῳ, ποτὶ μὲν πάντα τὰ ἕτερα χωρία ἐλάσσονα λόγον ἑξοῦντι τοῦ ὃν ἔχει ἁ ἴσα συναμφοτέραις τᾷ τε τοῦ μεγίστου ὑπερβλήματος πλευρᾷ καὶ μιᾷ τᾶν ἰσᾶν ἐουσᾶν ποτὶ τὰν ἴσαν συναμφοτέραις τῷ τε τρίτῳ μέρει τᾶς τοῦ μεγίστου ὑπερβλήματος πλευρᾶς καὶ τᾷ ἡμισέᾳ μιᾶς τᾶν ἰσᾶν ἐουσᾶν, ποτὶ δὲ τὰ λοιπὰ χωρία ἄνευ τοῦ μεγίστου μείζονα λόγον ἑξοῦντι τοῦ αὐτοῦ λόγου.

[162]    Ἔστωσαν γὰρ ἴσαι εὐθεῖαι ὁποσαιοῦν τῷ πλήθει, ἐφ᾿ ἇν τὰ Α, καὶ παραπεπτωκέτω παρ᾿ ἑκάσταν αὐτᾶν χωρίον ὑπερβάλλον εἴδει τετραγώνῳ, ἔστων δὲ τῶν ὑπερβλημάτων πλευραὶ αἱ Β, Γ, Δ, Ε, Ζ, Η τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, καὶ ἁ ὑπεροχὰ ἔστω ἴσα τᾷ ἐλαχίστᾳ, καὶ μεγίστα μὲν ἔστω ἁ Β, ἐλαχίστα δὲ ἁ Η· ἔστω δὲ καὶ ἄλλα χωρία, ἐφ᾿ ὧν ἕκαστον τῶν Θ, Ι, Κ, Λ, τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον ἔστω τῷ μεγίστῳ τῷ παρὰ τὰν ΑΒ παρακειμένῳ, ἔστω δὲ ἁ μὲν ΘΙ γραμμὰ ἴσα τᾷ Α, ἁ δὲ ΚΛ ἴσα τᾷ Β, καὶ τᾶν μὲν ΘΙ γραμμᾶν ἑκάστα ἔστω διπλασία τᾶς Ι, τᾶν δὲ ΚΛ ἑκάστα τριπλασία τᾶς Κ· δεικτέον ὅτι τὰ χωρία πάντα, ἐν οἷς τὰ Θ, Ι, Κ, Λ, ποτὶ μὲν πάντα τὰ ἕτερα χωρία τὰ ΑΒ, ΑΓ, ΑΔ, ΑΕ, ΑΖ, ΑΗ ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἁ ΘΙΚΛ εὐθεῖα ποτὶ τὰν ΙΚ, ποτὶ δὲ τὰ λοιπὰ ἄνευ τοῦ μεγίστου τοῦ ΑΒ μείζονα λόγον ἔχοντι τοῦ αὐτοῦ λόγου.
   Ἔστι γάρ τινα χωρία, ἐν οἷς τὰ Α, τῷ ἴσῳ ἀλλάλων ὑπερέχοντα, καὶ ἁ ὑπεροχὰ ἴσα τῷ ἐλαχίστῳ [ἐπεί τε [163] τὰ παραβλήματα καὶ τὰ πλάτη τῷ ἴσῳ ὑπερέχουσιν], καὶ ἄλλα χωρία, ἐν οἷς τὰ Θ, Ι, τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον τῷ μεγίστῳ· σύμπαντα οὖν τὰ χωρία, ἐν οἷς τὰ Θ, Ι, πάντων μὲν τῶν ἐν οἷς τὰ Α ἐλάσσονά ἐντι ἢ διπλασίονα, τῶν δὲ λοιπῶν χωρὶς τοῦ μεγίστου μείζονα ἢ διπλασίονα. Αὐτὰ οὖν τὰ χωρία, ἐν οἷς τὰ Ι, πάντων μὲν τῶν ἐν οἷς τὰ Α ἐλάσσονά ἐντι, τῶν δὲ λοιπῶν ἄνευ τοῦ μεγίστου μείζονα. Πάλιν ἐντὶ γραμμαί τινες αἱ Β, Γ, Δ, Ε, Ζ, Η τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, καὶ ἁ ὑπεροχὰ ἴσα τᾷ ἐλαχίστᾳ, καὶ ἄλλαι γραμμαί, ἐφ᾿ ἇν τὰ Κ, Λ, τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ· τὰ οὖν τετράγωνα τὰ ἀπὸ πασᾶν τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ πάντων μὲν τῶν τετραγώνων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἐλάσσονά ἐντι ἢ τριηλάσια, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονα ἢ τριπλάσια· δέδεικται γὰρ τοῦτο ἐν τοῖς περὶ τᾶν ἑλίκων ἐκδεδομένοις. Τὰ οὖν χωρία, ἐν οἷς τὸ Κ, πάντων μὲν τῶν χωρίων, ἐν οἷς τὰ Β, Γ, Δ, Ε, Ζ, Η, ἐλάσσονά ἐστιν, αὐτῶν δὲ τῶν ἐν οἷς τὰ Γ, Δ, Ε, Ζ, Η, μείζονα· ὥστε καὶ πάντα τὰ χωρία, ἐν οἷς τὰ Ι, Κ, πάντων μὲν τῶν ἐν οἷς τὰ ΑΒ, ΑΓ, ΑΔ, ΑΕ, ΑΖ, ΑΗ, ἐλάσσονά ἐστι, τῶν δὲ ἐν οἷς τὰ ΑΓ, ΑΔ, ΑΕ, ΑΖ, ΑΗ, μείζονα. Δῆλον οὖν ὅτι πάντα τὰ χωρία, ἐν οἷς τὰ Θ, Ι, Κ, Λ ποτὶ μὲν τὰ χωρία, [164] ἐν οἷς τὰ ΑΒ, ΑΓ, ΑΔ, ΑΕ, ΑΖ, ΑΗ, ἐλάσσονα λόγον ἔχοντι τοῦ ὃν ἔχει ἁ ΘΛ ποτὶ τὰν ΙΚ, ποτὶ δὲ τὰ λοιπὰ χωρὶς τοῦ ἐν ᾧ τὸ ΑΒ μείζονα τοῦ αὐτοῦ λόγου.
   γ΄.
   Εἴ κα κώνου τομᾶς ὁποιασοῦν εὐθεῖαι ἐπιψαύωντι ἀπὸ τοῦ αὐτοῦ σαμείου ἀγμέναι, ἔωντι δὲ καὶ ἄλλαι εὐθεῖαι ἐν τᾷ τοῦ κώνου τομᾷ παρὰ τὰς ἐπιψαυούσας ἀγμέναι καὶ τέμνουσαι ἀλλάλας, τὰ περιεχόμενα ὑπὸ τῶν τμαμάτων τὸν αὐτὸν ἑξοῦντι λόγον ποτ᾿ ἄλλαλα, ὃν τὰ τετράγωνα τὰ ἀπὸ τᾶν ἐπιψαυουσᾶν· ὁμόλογον δὲ ἐσσεῖται τὸ περιεχόμενον ὑπὸ τῶν τᾶς ἑτέρας γραμμᾶς τμαμάτων τῷ τετραγώνῳ τῷ ἀπὸ τᾶς ἐπιψαυούσας τᾶς παραλλήλου αὐτᾷ. Ἀποδέδεικται δὲ τοῦτο ἐν τοῖς κωνικοῖς στοιχείοις.
   Εἴ κα ἀπὸ τᾶς αὐτᾶς ὀρθογωνίου κώνου τομᾶς δύο τμάματα ἀποτμαθέωντι ὁπωσοῦν ἴσας ἔχοντα τὰς διαμέτρους, αὐτὰ δὲ τὰ τμάματα ἴσα ἐσσοῦνται καὶ τὰ τρίγωνα τὰ ἐγγραφόμενα εἰς αὐτὰ τὰν αὐτὰν βάσιν ἔχοντα τοῖς τμαμάτεσσι καὶ ὕψος τὸ αὐτό· διάμετρον δὲ καλέω παντὸς τμάματος τὰν δίχα τέμνουσαν τὰς εὐθείας πάσας τὰς παρὰ τὰν βάσιν αὐτοῦ ἀγομένας.
   Ἔστω ὀρθογωνίου κώνου τομὰ ἁ ΑΒΓ, καὶ ἀποτετμήσθω ἀπ᾿ αὐτᾶς δύο τμάματα τό τε ΑΔΕ καὶ τὸ ΘΒΓ, ἔστω δὲ τοῦ μὲν ΑΔΕ τμάματος διάμετρος ἁ ΔΖ, τοῦ δὲ ΘΒΓ ἁ ΒΗ, καὶ ἔστων ἴσαι αἱ ΔΖ, ΒΗ· δεικτέον ὅτι τὰ τμάματα ἴσα ἐστὶ τὰ ΑΔΕ, ΘΒΓ καὶ τὰ τρίγωνα τὰ ἐγγραφόμενα τὸν εἰρημένον τρόπον ἐν αὐτοῖς.

[165]    Ἔστω δὴ πρῶτον ἁ ἀποτέμνουσα τὸ ἕτερον τμᾶμα ἁ ΘΓ ποτ᾿ ὀρθὰς τᾷ διαμέτρῳ τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς, λελάφθω δὲ παρ᾿ ἃν δύνανται αἱ ἀπὸ τᾶς τομᾶς, ἁ διπλασία τᾶς μέχρι τοῦ ἄξονος, καὶ ἔστω ἐφ᾿ ᾇ τὸ Μ, ἀπὸ δὲ τοῦ Α κάθετος ἄχθω ἐπὶ τὰν ΔΖ ἁ ΑΚ. Ἐπεὶ οὖν διάμετρός ἐντι ἁ ΔΖ τοῦ τμάματος, ἁ δὲ ΑΕ δίχα τέμνεται κατὰ τὸ Ζ, καὶ ἁ ΔΖ παρὰ τὰν διάμετρόν ἐστι τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς· οὕτω γὰρ δίχα τέμνει πάσας τὰς παρὰ τὰν ΑΕ ἀγομένας. Ὃν δὴ λόγον ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΖ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΚ, τοῦτον ἐχέτω ἁ Ν ποτὶ τὰν Μ· αἱ δὴ ἀπὸ τᾶς τομᾶς ἐπὶ τὰν ΔΖ ἀγόμεναι παρὰ τὰν ΑΕ δύνανται τὰ παρὰ τὰν ἴσαν τᾷ Ν παραπίπτοντα πλάτος ἔχοντα, ἃς αὐτοὶ ἀπολαμβάνοντι ἀπὸ τᾶς ΔΖ ποτὶ τὸ Δ πέρας· δέδεικται γὰρ ἐν τοῖς κωνικοῖς· δύναται οὖν καὶ ἁ ΑΖ ἴσον τῷ περιεχομένῳ ὑπὸ τᾶς Ν καὶ τᾶς ΔΖ. Δύναται δὲ καὶ ἁ ΘΗ ἴσον τῷ περιεχομένῳ ὑπό τε τᾶς Μ καὶ τᾶς ΒΗ, ἐπεὶ κάθετός ἐστιν ἁ ΘΗ ἐπὶ τὰν διάμετρον· ἔχοι οὖν κα τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΖ [166] ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΗ τὸν αὐτὸν λόγον, ὃν ἁ Ν ποτὶ τὰν Μ, ἐπεὶ ἴσαι ὑπέκειντο αἱ ΔΖ, ΒΗ. Ἔχει δὲ τὸ ἀπὸ τᾶς ΑΖ τετράγωνον καὶ ποτὶ τὸ ἀπὸ τᾶς ΑΚ τὸν αὐτὸν λόγον, ὃν ἁ Ν ποτὶ τὰν Μ· ἴσαι ἄρα ἐντὶ αἱ ΘΗ, ΑΚ. Ἐντὶ δὲ ἴσαι καὶ αἱ ΒΗ, ΔΖ· ὥστε ἴσον ἐστὶ τὸ ὑπὸ τᾶν ΘΗ, ΒΗ περιεχόμενον τῷ ὑπὸ τᾶν ΑΚ, ΔΖ. Ἴσον ἄρα ἐστὶν καὶ τὸ ΘΗΒ τρίγωνον τῷ ΔΑΖ τριγώνῳ· ὥστε καὶ τὰ διπλάσια. Ἔστι δὲ τοῦ μὲν ΑΔΕ τριγώνου ἐπίτριτον τὸ ΑΔΕ τμᾶμα, τοῦ δὲ ΘΒΓ τριγώνου ἐπίτριτον τὸ ΘΒΓ τμᾶμα· δῆλον οὖν ὅτι τά τε τμάματά ἐστιν ἴσα καὶ τὰ τρίγωνα τὰ ἐγγραφόμενα εἰς αὐτά.
   Εἰ δὲ μηδετέρα τᾶν τὰ τμάματα ἀποτεμνουσᾶν ποτ᾿ ὀρθάς ἐντι τᾷ διαμέτρῳ τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς, ἀπολαφθείσας ἀπὸ τᾶς διαμέτρου τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς ἴσας τᾷ διαμέτρῳ τᾷ τοῦ ἑνὸς τμάματος καὶ ἀπὸ τοῦ πέρατος τᾶς ἀπολαφθείσας ποτ᾿ ὀρθὰς ἀχθείσας τᾷ διαμέτρῳ, τὸ γενόμενον τμᾶμα ἑκατέρῳ τῶν τμαμάτων ἴσον ἐσσεῖται. Δῆλον οὖν ἐστι τὸ προτεθέν.
   δ΄.
   Πᾶν χωρίον τὸ περιεχόμενον ὑπὸ ὀξυγωνίου κώνου τομᾶς ποτὶ τὸν κύκλον τὸν ἔχοντα τὰν διάμετρον ἴσαν τᾷ μείζονι διαμέτρῳ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ἐλάσσων διάμετρος αὐτᾶς ποτὶ τὰν μείζω ἢ ποτὶ τὰν τοῦ κύκλου διάμετρον.
   Ἔστω γὰρ ὀξυγωνίου κώνου τομά, ἐφ᾿ ἇς τὰ Α, Β, Γ, Δ, διάμετρος δὲ αὐτᾶς ἁ μὲν μείζων ἔστω, ἐφ᾿ ἇς τὰ Α, Γ, ἁ δὲ ἐλάσσων, ἐφ᾿ ἇς τὰ Β, Δ, ἔστω δὲ κύκλος περὶ διάμετρον τὰν ΑΓ· δεικτέον ὅτι τὸ περιεχόμενον χωρίον ὑπὸ τᾶς τοῦ [167] ὀξυγωνίου κώνου τομᾶς ποτὶ τὸν κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΒΔ ποτὶ τὰν ΓΑ, τουτέστι τὰν ΕΖ. Ὃν δὴ λόγον ἔχει ἁ ΒΔ ποτὶ τὰν ΕΖ, τοῦτον ἐχέτω ὁ κύκλος, ἐν ᾧ τὸ Ψ, ποτὶ τὸν ΑΕΓΖ κύκλον· λέγω ὅτι ἴσος ἐστὶν ὁ Ψ κύκλος τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ.
   Εἰ γὰρ μή ἐστιν ἴσος ὁ Ψ κύκλος τῷ περιεχομένῳ χωρίῳ ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, ἔστω πρῶτον, εἰ δυνατόν, μείζων. Δυνατὸν δή ἐστιν εἰς τὸν Ψ κύκλον πολύγωνον ἐγγράψαι ἀρτιόγωνον μεῖζον τοῦ ΑΒΓΔ χωρίου. Νοείσθω δὴ ἐγγεγραμμένον, ἐγγεγράφθω δὲ καὶ εἰς τὸν ΑΕΓΖ κύκλον εὐθύγραμμον ὁμοῖον τῷ ἐν τῷ Ψ κύκλῳ ἐγγεγραμμένῳ, καὶ ἀπὸ τᾶν γωνιᾶν αὐτοῦ κάθετοι ἄχθωσαν ἐπὶ τὰν ΑΓ διάμετρον, ἐπὶ δὲ τὰ σαμεῖαι καθ᾿ ἃ τέμνοντι αἱ κάθετοι τὰν τοῦ ὀξυγωνίου κώνου τομάν, εὐθεῖαι ἐπεζεύχθωσαν· ἐσσεῖται δή τι ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ ἐγγεγραμμένον εὐθύγραμμον, καὶ ἕξει αὐτὸ ποτὶ τὸ εὐθύγραμμον τὸ ἐν τῷ ΑΕΓΖ κύκλῳ ἐγγεγραμμένον τὸν αὐτὸν λόγον, ὃν ἁ ΒΔ ποτὶ τὰν ΕΖ. Ἐπεὶ γὰρ αἱ ΕΘ, [168] ΚΛ κάθετοι εἰς τὸν αὐτὸν λόγον τέτμηνται κατὰ τὰ Μ, Β, δῆλον ὅτι τὸ ΛΕ τραπέζιον ποτὶ τὸ ΘΜ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΘΕ ποτὶ τὰν ΒΘ. Διὰ ταὐτὰ δὲ καὶ τῶν ἄλλων τραπεζίων ἕκαστον τῶν ἐν τῷ κύκλῳ ποθ᾿ ἕκαστον τῶν τραπεζίων τῶν ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΕΘ ποτὶ τὰν ΒΘ. Ἔχοντι δὲ καὶ τὰ τρίγωνα τὰ ποτὶ τοῖς Α, Γ τὰ ἐν τῷ κύκλῳ ποτὶ τὰ ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ τοῦτον τὸν λόγον· ἕξει οὖν καὶ ὅλον τὸ εὐθύγραμμον τὸ ἐν τῷ ΑΕΓΖ κύκλῳ ἐγγεγραμμένον ποτὶ ὅλον τὸ ἐγγεγραμμένον εὐθύγραμμον ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ τὸν αὐτὸν λόγον, ὃν ἁ ΕΖ ποτὶ τὰν ΒΔ. Ἔχει δὲ τὸ αὐτὸ εὐθύγραμμον καὶ ποτὶ τὸ ἐν τῷ Ψ κύκλῳ ἐγγεγραμμένον τοῦτον τὸν λόγον, διότι καὶ οἱ κύκλοι τοῦτον εἶχον τὸν λόγον· ἴσον ἄρα ἐστὶν τὸ εὐθύγραμμον τὸ ἐν τῷ Ψ κύκλῳ ἐγγεγραμμένον τῷ εὐθυγράμμῳ τῷ ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ ἐγγεγραμμένῳ· ὅπερ ἀδύνατον· μεῖζον γὰρ ἦν ὅλου τοῦ περιεχομένου χωρίου ὑπὸ τᾶς τοῦ ὀξυγωνίου τομᾶς.
   Ἀλλ᾿ ἔστω, εἰ δυνατόν, ἐλάσσων. Πάλιν δὴ δυνατὸν εἰς τὰν τοῦ ὀξυγωνίου κώνου τομὰν ἐγγράψαι πολύγωνον ἀρτιόπλευρον μεῖζον τοῦ Ψ κύκλου. Ἐγγεγράφθω οὖν, καὶ ἀπὸ τᾶν γωνιᾶν αὐτοῦ κάθετοι ἀχθεῖσαι ἐπὶ τὰν ΑΓ ἐκβεβλήσθωσαν ποτὶ τὰν τοῦ κύκλου περιφέρειαν· πάλιν οὖν ἐσσεῖταί τι ἐν τῷ ΑΕ κύκλῳ εὐθύγραμμον ἐγγεγραμμένον, ὃ ἕξει ποτὶ τὸ ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ ἐγγεγραμμένον τὸν αὐτὸν λόγον, ὃν ἁ ΕΖ ποτὶ τὰν ΒΔ. Ἐγγραφέντος δὴ καὶ εἰς τὸν Ψ κύκλον ὁμοίου αὐτῷ δειχθήσεται τὸ ἐν τῷ Ψ κύκλῳ ἐγγεγραμμένον ἴσον ἐὸν τῷ ἐν τᾷ τοῦ ὀξυγωνίου κώνου τομᾷ ἐγγεγραμμένῳ· ὅπερ ἀδύνατον· οὐκ ἔστιν οὖν οὐδὲ ἐλάσσων ὁ Ψ κύκλος τοῦ χωρίου τοῦ [169] περιεχομένου ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς. Δῆλον οὖν ὅτι τὸ εἰρημένον χωρίον ποτὶ τὸν ΑΕΓΖ κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΒΔ ποτὶ τὰν ΕΖ.
   ε΄.
   Πᾶν χωρίον περιεχόμενον ὑπὸ ὀξυγωνίου κώνου τομᾶς ποτὶ πάντα κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν διαμέτρων τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ποτὶ τὸ ἀπὸ τᾶς τοῦ κύκλου διαμέτρου τετράγωνον.
   Ἔστω γάρ τι χωρίον περιεχόμενον ὑπὸ ὀξυγωνίου κώνου τομᾶς, ἐν ᾧ τὸ Χ, διάμετροι δὲ ἔστωσαν τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς αἱ ΑΓ, ΒΔ, μείζων δὲ ἁ ΑΓ, καὶ κύκλος ἔστω, ἐν ᾧ Ψ, διάμετρος δὲ αὐτοῦ ἁ ΕΖ· δεικτέον ὅτι τὸ Χ χωρίον ποτὶ τὸν Ψ κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΑΓ, ΒΔ ποτὶ τὸ ἀπὸ τᾶς ΕΖ τετράγωνον. Περιγεγράφθω δὴ κύκλος περὶ διάμετρον τὰν ΑΓ· τὸ δὴ Χ χωρίον ποτὶ τὸν κύκλον, οὗ διάμετρος ἁ ΑΓ, τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΑΓ, ΒΔ ποτὶ τὸ [170] ἀπὸ τᾶς ΑΓ τετράγωνον· δέδεικται γὰρ ἔχον ὃν ἁ ΒΔ ποτὶ τὰν ΑΓ. Ἔχει δὲ καὶ ὁ κύκλος, οὗ διάμετρος ἁ ΑΓ, ποτὶ τὸν κύκλον, οὗ διάμετρος ἁ ΕΖ, τὸν αὐτὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΑΓ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΕΖ· δῆλον οὖν ὅτι τὸ Χ χωρίον ποτὶ τὸν Ψ κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ὑπὸ τᾶν ΑΓ, ΒΔ περιεχόμενον ποτὶ τὸ ἀπὸ τᾶς ΕΖ τετράγωνον.
   Ϛ΄.
   Τὰ περιεχόμενα χωρία ὑπὸ ὀξυγωνίου κώνου τομᾶς τὸν αὐτὸν ἔχοντι λόγον ποτ᾿ ἄλλαλα, ὃν τὰ περιεχόμενα ὑπὸ τᾶν διαμέτρων τᾶν τῶν ὀξυγωνίων κώνων τομᾶν ποτ᾿ ἄλλαλα.
   Ἔστω περιεχόμενα χωρία ὑπὸ ὀξυγωνίου κώνου τομᾶς, ἐν οἷς τὰ Α, Β, ἔστω δὲ καὶ τὸ μὲν ΓΔ περιεχόμενον ὑπὸ τᾶν διαμέτρων τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τᾶς περιεχούσας τὸ Α χωρίον, τὸ δὲ ΕΖ περιεχόμενον ὑπὸ τᾶν διαμέτρων τᾶς ἑτέρας τομᾶς· δεικτέον ὅτι τὸ Α χωρίον ποτὶ τὸ Β τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ΓΔ ποτὶ τὸ ΕΖ.

[171]    Λελάφθω δὴ κύκλος τις, ἐν ᾧ τὸ Ψ, ἀπὸ δὲ τᾶς διαμέτρου αὐτοῦ τετράγωνον ἔστω τὸ ΚΛ. Ἔχει δὴ τὸ μὲν Α χωρίον ποτὶ τὸν Ψ κύκλον τὸν αὐτὸν λόγον, ὃν τὸ ΓΔ ποτὶ τὸ ΚΛ, ὁ δὲ Ψ κύκλος ποτὶ τὸ Β χωρίον τὸν αὐτὸν λόγον, ὃν τὸ ΚΛ ποτὶ τὸ ΕΖ· δῆλον οὖν ὅτι τὸ Α χωρίον ποτὶ τὸ Β τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ΓΔ ποτὶ τὸ ΕΖ.

ΠΟΡΙΣΜΑ.

   Ἐκ τούτου δὲ φανερὸν ὅτι τὰ περιεχόμενα χωρία ὑπὸ ὁμοιᾶν ὀξυγωνίου κώνου τομᾶν τὸν αὐτὸν λόγον ἔχοντι ποτ᾿ ἄλλαλα, ὃν ἔχοντι δυνάμει ποτ᾿ ἀλλάλας αἱ ὁμόλογοι διάμετροι τᾶν τομᾶν.

ζ΄.
   Ὀξυγωνίου κώνου τομᾶς δοθείσας καὶ γραμμᾶς ἀπὸ τοῦ κέντρου τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἀνεστακούσας ὀρθᾶς ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, δυνατόν ἐστι κῶνον εὑρεῖν κορυφὰν ἔχοντα τὸ πέρας τᾶς ἀνεστακούσας εὐθείας, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ δοθεῖσα τοῦ ὀξυγωνίου κώνου τομά.
   Δεδόσθω τις ὀξυγωνίου κώνου τομά, καὶ ἀπὸ τοῦ κέντρου αὐτᾶς εὐθεῖα γραμμὰ ἀνεστάκουσα ὀρθὰ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, διὰ δὲ τᾶς ἀνεστακούσας εὐθείας καὶ τᾶς ἐλάσσονος διαμέτρου ἐπίπεδόν τι ἐκβεβλήσθω, καὶ ἔστω ἐν αὐτῷ ἁ μὲν ἐλάσσων διάμετρος ἁ ΑΒ, τὸ δὲ κέντρον τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τὸ Δ, ἁ δὲ ἀπὸ τοῦ κέντρου ἀνεστάκουσα ὀρθὰ ἁ ΓΔ, πέρας δὲ αὐτᾶς τὸ Γ, ἁ δὲ τοῦ ὀξυγωνίου κώνου τομὰ νοείσθω περὶ διάμετρον τὰν ΑΒ γεγραμμένα ἐν ἐπιπέδῳ [172] ὀρθῷ ποτὶ τὰν ΓΔ· δεῖ δὴ κῶνον εὑρεῖν κορυφὰν ἔχοντα τὸ Γ σαμεῖον, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Ἀπὸ δὴ τοῦ Γ ἐπὶ τὰ Α, Β εὐθεῖαι ἀχθεῖσαι ἐκβεβλήσθων, καὶ ἀπὸ τοῦ Α διάχθω ἁ ΑΖ, ὥστε τὸ περιεχόμενον ὑπὸ τᾶν ΑΕ, ΕΖ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΕΓ τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ἡμισείας τᾶς μείζονος διαμέτρου ποτὶ τὸ ἀπὸ ΔΓ τετράγωνον· δυνατὸν δέ ἐστιν, ἐπεὶ μείζων ἐστὶν ὁ λόγος τοῦ ὃν ἔχει τὸ ὑπὸ τᾶν ΑΔ, ΔΒ περιεχόμενον ποτὶ τὸ ἀπὸ τᾶς ΔΓ τετράγωνον· ἀπὸ δὲ τᾶς ΑΖ ἐπίπεδον ἀνεστακέτω ὀρθὸν ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΑΓ, ΑΖ, ἐν δὲ τῷ ἐπιπέδῳ τούτῳ κύκλος γεγράφθω περὶ διάμετρον τὰν ΑΖ, καὶ ἀπὸ τοῦ κύκλου τούτου κῶνος ἔστω κορυφὰν ἔχων τὸ Γ σαμεῖον· ἐν δὴ τᾷ ἐπιφανείᾳ τοῦ κώνου τούτου δειχθήσεται ἐοῦσα ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Εἰ γὰρ μή ἐστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου, ἀναγκαῖον εἶμέν τι σαμεῖον ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, ὃ μή ἐστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου. Νοείσθω δή τι σαμεῖον [173] λελαμμένον ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τὸ Θ, ὃ οὐκ ἔστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου, καὶ ἀπὸ τοῦ Θ κάθετος ἄχθω ἁ ΘΚ ἐπὶ τὰν ΑΒ· ἐσσεῖται δὴ αὕτα ὀρθὰ ποτὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐντι αἱ ΑΓ, ΓΖ· ἀπὸ δὲ τοῦ Γ ἐπὶ τὸ Κ εὐθεῖα ἀχθεῖσα ἐκβεβλήσθω· συμπιπτέτω δὴ αὕτα τᾷ ΑΖ κατὰ τὸ Λ, καὶ ἀπὸ τοῦ Λ ἄχθω ποτ᾿ ὀρθὰς τᾷ ΖΑ ἁ ΛΜ ἐν τῷ κύκλῳ τῷ περὶ τὰν ΑΖ, τὸ δὲ Μ νοείσθω μετέωρον ἐπὶ τᾶς περιφερείας αὐτοῦ, ἄχθω δὲ καὶ παρὰ τὰν ΑΒ διὰ μὲν τοῦ Λ ἁ ΞΟ, διὰ δὲ τοῦ Ε ἁ ΠΡ. Ἐπεὶ οὖν τὸ μὲν ὑπὸ τᾶν ΕΑ, ΕΖ περιεχόμενον ποτὶ τὸ ἀπὸ τᾶς ΕΓ τετράγωνον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ἡμισείας τᾶς μείζονος διαμέτρου ποτὶ τὸ ἀπὸ τᾶς ΔΓ, τὸ δὲ ἀπὸ τᾶς ΕΓ ποτὶ τὸ ὑπὸ τᾶν ΕΠ, ΕΡ, ὃν τὸ ἀπὸ τᾶς ΔΓ ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ, τὸν αὐτὸν ἔχει λόγον τὸ ὑπὸ τᾶν ΑΕ, ΕΖ ποτὶ τὸ ὑπὸ τᾶν ΕΠ, ΕΡ, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ἡμισείας τᾶς μείζονος διαμέτρου ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ. Ἔστιν δέ, ὡς μὲν τὸ ὑπὸ τᾶν ΑΕ, ΕΖ ποτὶ τὸ ὑπὸ τᾶν ΕΠ, ΕΡ, οὕτω τὸ ὑπὸ τᾶν ΑΛ, ΛΖ ποτὶ τὸ ὑπὸ τᾶν ΛΞ, ΛΟ, ὡς δὲ τὸ ἀπὸ τᾶς ἡμισείας τᾶς μείζονος διαμέτρου ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ, οὕτως τὸ ἀπὸ τᾶς ΘΚ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ· τὸν αὐτὸν ἄρα ἔχει λόγον τὸ ὑπὸ τᾶν ΑΛ, ΛΖ ποτὶ τὸ ὑπὸ τᾶν ΞΛ, ΛΟ, ὃν τὸ ἀπὸ τᾶς ΘΚ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ. Ἔχει δὲ καὶ τὸ ὑπὸ τᾶν ΞΛ, ΛΟ ποτὶ τὸ ἀπὸ τᾶς ΓΛ τετράγωνον τὸν αὐτὸν λόγον, ὃν τὸ ὑπὸ ΑΚ, ΚΒ ποτὶ τὸ ἀπὸ τᾶς ΚΓ τετράγωνον· ἔχει ἄρα καὶ τὸ ὑπὸ τᾶν ΑΛ, ΛΖ περιεχόμενον ποτὶ τὸ ἀπὸ τᾶς ΓΛ τετράγωνον τὸν αὐτὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΚ ποτὶ τὸ ἀπὸ τᾶς ΚΓ. Τῷ δὲ ὑπὸ τᾶν ΑΛ, ΛΖ περιεχομένῳ ἴσον ἐστὶ τὸ ἀπὸ τᾶς ΛΜ τετράγωνον· ἐν ἡμικυκλίῳ γὰρ τῷ περὶ τὰν ΑΖ κάθετος ἄχθη ἁ ΛΜ· τὸν αὐτὸν ἄρα ἔχει λόγον τὸ ἀπὸ τᾶς ΛΜ τετράγωνον [174] ποτὶ τὸ ἀπὸ τᾶς ΛΓ, ὃν τὸ ἀπὸ τᾶς ΘΚ ποτὶ τὸ ἀπὸ τᾶς ΚΓ· ὥστε ἐπ᾿ εὐθείας ἐστὶν τὰ Γ, Θ, Μ σαμεῖα. Ἁ δὲ ΓΜ ἐν τᾷ ἐπιφανείᾳ ἐστὶ τοῦ κώνου· δῆλον οὖν ὅτι καὶ τὸ Θ σαμεῖον ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται τοῦ κώνου. Ὑπέκειτο δὲ μὴ εἶμεν· οὐκ ἄρα ἐστὶ σαμεῖον οὐδὲν ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, ὃ οὐκ ἔστιν ἐν τᾷ ἐπιφανείᾳ τοῦ προειρημένου κώνου. Ὅλα οὖν ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἐν τᾷ ἐπιφανείᾳ ἐστὶν τοῦ αὐτοῦ κώνου.
   η΄.
   Ὀξυγωνίου κώνου τομᾶς δοθείσας καὶ γραμμᾶς μὴ ὀρθᾶς ἀνεστακούσας ἀπὸ τοῦ κέντρου τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἐν ἐπιπέδῳ, ὅ ἐστιν ὀρθὸν ἀνεστακὸς διὰ τᾶς ἑτέρας διαμέτρου ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, δυνατόν ἐστι κῶνον εὑρεῖν κορυφὰν ἔχοντα τὸ πέρας τᾶς ἀνεστακούσας εὐθείας, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ δοθεῖσα τοῦ ὀξυγωνίου κώνου τομά.

[175]    Ἔστω δὴ διάμετρος μὲν τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἁ ΒΑ, κέντρον δὲ τὸ Δ, καὶ ἁ ΔΓ ἀπὸ τοῦ κέντρου ἀνεστάκουσα, ὡς εἴρηται, ἁ δὲ τοῦ ὀξυγωνίου κώνου τομὰ νοείσθω περὶ διάμετρον τὰν ΑΒ ἐν ἐπιπέδῳ ὀρθῷ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΑΒ, ΓΔ· δεῖ δὴ κῶνον εὑρεῖν κορυφὰν ἔχοντα τὸ Γ σαμεῖον, οὗ ἐν τῇ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Οὐ δή ἐντι ἴσαι αἱ ΑΓ, ΓΒ, ἐπεὶ ἁ ΓΔ οὐκ ἔστιν ὀρθὰ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά. Ἔστω οὖν ἴσα ἁ ΕΓ τᾷ ΓΒ, ἁ δὲ Ν εὐθεῖα ἴσα ἔστῳ τᾷ ἡμισείᾳ τᾶς ἑτέρας διαμέτρου, ᾇ ἐστι συζυγὴς ἁ ΑΒ, καὶ διὰ τοῦ Δ ἄχθω ἁ ΖΗ παρὰ τὰν ΕΒ, ἀπὸ δὲ τᾶς ΕΒ ἐπίπεδον ἀνεστακέτω ὀρθὸν ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΑΓ, ΓΒ, καὶ ἐν τῷ ἐπιπέδῳ τούτῳ γεγράφθω περὶ διάμετρον τὰν ΕΒ, εἰ μὲν ἴσον ἐστὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς Ν τῷ περιεχομένῳ ὑπὸ τᾶν ΖΔ, ΔΗ, κύκλος, εἰ δὲ μή ἐστιν ἴσον, ὀξυγωνίου κώνου τομὰ τοιαύτα, ὥστε τὸ τετράγωνον τὸ ἀπὸ τᾶς ἑτέρας διαμέτρου ποτὶ τὸ ἀπὸ τᾶς ΕΒ τὸν αὐτὸν ἔχειν λόγον, ὃν ἔχει τὸ ἀπὸ τᾶς Ν τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΖΔ, ΔΗ· κῶνος δὲ λελάφθω κορυφὰν ἔχων τὸ Γ σαμεῖον, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ὁ κύκλος ἢ ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΕΒ· δυνατὸν δέ ἐστι τοῦτο, ἐπεὶ ἁ ἀπὸ τοῦ Γ ἐπὶ μέσαν τὰν ΕΒ ἀχθεῖσα ὀρθά ἐντι ποτὶ τὸ ἐπίπεδον τὸ κατὰ τὰν ΕΒ· ἐν ταύτᾳ δὴ τᾷ ἐπιφανείᾳ ἐστὶ καὶ ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΒ.
   Εἰ γὰρ μή ἐστιν, ἐσσεῖταί τι σαμεῖον ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, ὃ οὐκ ἐσσεῖται ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου. Νοείσθω τι σαμεῖον λελαμμένον τὸ Θ, ὃ οὐκ ἔστιν ἐν τᾷ [176] ἐπιφανείᾳ τοῦ κώνου, καὶ ἀπὸ τοῦ Θ κάθετος ἄχθω ἁ ΘΚ ἐπὶ τὰν ΑΒ, ἁ δὲ ΓΚ ἐπιζευχθεῖσα ἐκβεβλήσθω καὶ συμπιπτέτω τᾷ ΕΒ κατὰ τὸ Λ, διὰ δὲ τοῦ Λ ἄχθω τις ἐν τῷ ὀρθῷ ἐπιπέδῳ τῷ κατὰ τὰν ΕΒ ποτ᾿ ὀρθὰς τᾷ ΕΒ ἁ ΛΜ, τὸ δὲ Μ νοείσθω μετέωρον ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου, ἄχθω δὲ καὶ διὰ τοῦ Λ παρὰ τὰν ΑΒ ἁ ΠΡ· ἔστιν δή, ὡς μὲν τὸ ἀπὸ τᾶς Ν τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΖΔ, ΔΗ, οὕτως τὸ ἀπὸ τᾶς ΛΜ ποτὶ τὸ ὑπὸ τᾶν ΕΛ, ΛΒ, ὡς δὲ τὸ ὑπὸ τᾶν ΖΔ, ΔΗ ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ, οὕτως τὸ ὑπὸ ΕΛ, ΛΒ ποτὶ τὸ ὑπὸ τᾶν ΠΛ, ΛΡ· ἐσσεῖται οὖν, ὡς τὸ ἀπὸ τᾶς Ν τετράγωνον ποτὶ τὸ ὑπὸ ΑΔ, ΔΒ περιεχόμενον, οὕτως τὸ ἀπὸ τᾶς ΛΜ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΠΛ, ΛΡ. Ἔχει δέ, ὡς τὸ ἀπὸ τᾶς Ν τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ, οὕτως τὸ ἀπὸ τᾶς ΘΚ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ, ἐπεὶ ἐν τᾷ αὐτᾷ ὀξυγωνίου κώνου τομᾷ κάθετοί ἐντι ἀγμέναι ἐπὶ διάμετρον τὰν ΑΒ· τὸν αὐτὸν ἄρα ἔχει λόγον τὸ ἀπὸ τᾶς ΛΜ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΠΛ, ΛΡ, ὃν τὸ ἀπὸ τᾶς ΘΚ ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ. Ἔχει δὲ καὶ τὸ ὑπὸ τᾶν ΠΛ, ΛΡ ποτὶ τὸ ἀπὸ τᾶς ΓΔ τετράγωνον τὸν αὐτὸν λόγον, ὃν τὸ ὑπὸ τᾶν ΑΚ, ΚΒ ποτὶ τὸ ἀπὸ τᾶς ΚΓ· τὸν αὐτὸν οὖν λόγον ἔχει τὸ ἀπὸ τᾶς ΛΜ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΛΓ τετράγωνον, ὃν τὸ ἀπὸ τᾶς ΘΚ ποτὶ τὸ ἀπὸ τᾶς ΚΓ· ὥστε ἐπ᾿ εὐθείας ἐντὶ τὰ Γ, Θ, Μ σαμεῖα. Ἁ δὲ ΓΜ ἐν τᾷ ἐπιφανείᾳ τοῦ κώνου· δῆλον οὖν ὅτι καὶ τὸ Θ σαμεῖον ἐν τᾷ ἐπιφανείᾳ ἐστὶ τοῦ κώνου. Ὑπέκειτο δὲ μὴ εἶμεν· φανερὸν οὖν ἐστιν ὃ ἔδει δεῖξαι.
   θ΄.
   Ὀξυγωνίου κώνου τομᾶς δοθείσας καὶ γραμμᾶς ἀπὸ τοῦ κέντρου τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς μὴ ὀρθᾶς [177] ἀνεστακούσας ἐν ἐπιπέδῳ, ὅ ἐστιν ἀπὸ τᾶς ἑτέρας διαμέτρου ὀρθὸν ἀνεστακὸς ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, δυνατόν ἐντι κύλινδρον εὑρεῖν τὸν ἄξονα ἔχοντα ἐπ᾿ εὐθείας τᾷ ἀνεστακούσᾳ γραμμᾷ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ δοθεῖσα τοῦ ὀξυγωνίου κώνου τομά.
   Ἔστω τᾶς δοθείσας τοῦ ὀξυγωνίου κώνου τομᾶς ἑτέρα διάμετρος ἁ ΒΑ, κέντρον δὲ τὸ Δ, ἁ δὲ ΓΔ γραμμὰ ἔστω ἀνεστάκουσα ἀπὸ τοῦ κέντρου, ὡς εἴρηται, ἁ δὲ τοῦ ὀξυγωνίου κώνου τομὰ νοείσθω περὶ διάμετρον τὰν ΑΒ ἐν ἐπιπέδῳ ὀρθῷ ποτὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐντι αἱ ΑΒ, ΓΔ· δεῖ δὴ κύλινδρον εὑρεῖν τὸν ἄξονα ἔχοντα ἐπ᾿ εὐθείας τᾷ ΓΔ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ δοθεῖσα τοῦ ὀξυγωνίου κώνου τομά.
   Ἀπὸ δὴ τῶν Α, Β σαμείων ἄχθων παρὰ τὰν ΓΔ αἱ ΑΖ, ΒΗ· ἁ δὴ ἑτέρα διάμετρος τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἤτοι ἴσα ἐντὶ τῷ διαστήματι τᾶν ΑΖ, ΒΗ ἢ μείζων ἢ ἐλάσσων. Ἔστω δὴ πρότερον ἴσα τᾷ ΖΗ, ἁ δὲ ΖΗ ἔστω ποτ᾿ ὀρθὰς τᾷ ΓΔ, ἀπὸ δὲ τᾶς ΖΗ ἀνεστακέτω ἐπίπεδον ὀρθὸν ποτὶ τὰν ΓΔ, καὶ ἐν τῷ ἐπιπέδῳ τούτῳ κύκλος ἔστω περὶ διάμετρον [178] τὰν ΖΗ, καὶ ἀπὸ τοῦ κύκλου τούτου κύλινδρος ἔστω ἄξονα ἔχων τὰν ΓΔ· ἐν δὴ τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου τούτου ἐστὶν ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Εἰ γὰρ μή ἐστιν, ἐσσεῖταί τι σαμεῖον ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς, ὃ οὐκ ἔστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου. Νοείσθω δή τι σαμεῖον λελαμμένον ἐπὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τὸ Θ, ὃ οὐκ ἔστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου, καὶ ἀπὸ τοῦ Θ ἁ ΘΚ κάθετος ἄχθω ἐπὶ τὰν ΑΒ· ἐσσεῖται δὲ αὕτα ὀρθὰ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΒΑ, ΓΔ· ἀπὸ δὲ τοῦ Κ ἄχθω παρὰ τὰν ΓΔ ἁ ΚΛ, καὶ ἀπὸ τοῦ Λ ἀνεστακέτω ἁ ΛΜ ποτ᾿ ὀρθὰς τᾷ ΖΗ ἐν τῷ κύκλῳ τῷ περὶ τὰν ΖΗ, τὸ δὲ Μ νοείσθω μετέωρον ἐν τᾷ περιφερείᾳ τοῦ ἡμικυκλίου τοῦ περὶ διάμετρον τὰν ΖΗ· τὸν αὐτὸν δὴ ἔχει λόγον τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΚ καθέτου ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ περιεχόμενον καὶ τὸ ἀπὸ ΖΓ ποτὶ τὸ ὑπὸ τᾶν ΑΔ, ΔΒ περιεχόμενον, ἐπεὶ ἴσα ἐστὶν ἁ ΖΗ τᾷ ἑτέρᾳ διαμέτρῳ. Ἔχει δὲ καὶ τὸ ὑπὸ τᾶν ΖΛ, ΛΗ περιεχόμενον ποτὶ τὸ ὑπὸ ΑΚ, ΚΒ περιεχόμενον, ὃν τὸ ἀπὸ τᾶς ΖΓ τετράγωνον ποτὶ τὸ ἀπὸ ΑΔ· ἴσον οὖν ἐντι τὸ ὑπὸ τᾶν ΖΛ, ΛΗ περιεχόμενον τῷ ἀπὸ τᾶς ΘΚ τετραγώνῳ. Ἔστιν δὲ ἴσον καὶ τῷ ἀπὸ ΛΜ· ἴσαι ἄρα ἐντὶ αἱ ΘΚ, ΜΛ κάθετοι. Παράλληλοι οὖν ἐντι αἱ ΛΚ, ΜΘ· ὥστε καὶ αἱ ΔΓ, ΜΘ παράλληλοι ἐσσοῦνται. Καὶ ἐν τᾷ ἐπιφανείᾳ ἄρα ἐστὶ τοῦ κυλίνδρου ἁ ΘΜ, ἐπεὶ ἀπὸ τοῦ Μ ἐν τᾷ ἐπιφανείᾳ ἐόντος ἆκται παρὰ τὸν ἄξονα· δῆλον οὖν ὅτι καὶ τὸ Θ ἐν τᾷ ἐπιφανείᾳ ἐστὶν αὐτοῦ. Ὑπέκειτο δὲ μὴ εἶμεν· φανερὸν οὖν ἐστιν, ὃ ἔδει δεῖξαι.
   Δῆλον δὴ ὅτι καὶ ὁ κύλινδρος ὁ περιλαμβάνων ὀρθὸς
[179]ἐσσεῖται, εἴ κα ᾖ ἁ ἑτέρα διάμετρος ἴσα τῷ διαστήματι τᾶν ἀπὸ τῶν περάτων τᾶς ἑτέρας διαμέτρου ἀγμενᾶν παρὰ τὰν ἀνεστάκουσαν εὐθεῖαν.
   Ἔστω πάλιν ἁ ἑτέρα διάμετρος μείζων τᾶς ΖΗ, καὶ ἴσα ἔστω ἁ ΠΖ τᾷ ἑτέρᾳ διαμέτρῳ, ἀπὸ δὲ τᾶς ΠΖ ἐπίπεδον ἀνεστακέτω ὀρθὸν ποτὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐντι αἱ ΒΑ, ΓΔ, καὶ ἐν τῷ ἐπιπέδῳ τούτῳ κύκλος ἔστω περὶ διάμετρον τὰν ΠΖ, ἀπὸ δὲ τοῦ κύκλου τούτου κύλινδρος ἔστω ἄξονα ἔχων τὰν ΔΡ· ἐν δὴ τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου τούτου διὰ τῶν αὐτῶν δειχθήσεται ἐοῦσα ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Ἀλλ᾿ ἔστω ἐλάσσων ἁ ἑτέρα διάμετρος τᾶς ΖΗ. Ὧι δὴ μεῖζον δύναται ἁ ΖΓ τᾶς ἡμισείας τᾶς ἑτέρας διαμέτρου ἔστω τὸ ἀπὸ τᾶς ΓΞ τετράγωνον, καὶ ἀπὸ τοῦ Ξ ἀνεστακέτω γραμμὰ ἴσα τᾷ ἡμισείᾳ τᾶς ἑτέρας διαμέτρου ὀρθὰ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΑΒ, ΓΔ, ἁ ΞΝ, τὸ δὲ Ν νοείσθω μετέωρον· ἁ οὖν ΓΝ ἴσα ἐντὶ τᾷ ΓΖ. Ἐν δὴ τῷ ἐπιπέδῳ, ἐν ᾧ ἐντι αἱ ΖΗ, ΓΝ, κύκλος γεγράφθω περὶ διάμετρον τὰν ΖΗ· ἥξει δὲ οὗτος διὰ τοῦ Ν· καὶ ἀπὸ τοῦ κύκλου κύλινδρος [180] ἔστω ἄξονα ἔχων τὰν ΓΔ· ἐν δὴ τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου τούτου ἐστὶν ἁ τοῦ ὀξυγωνίου κώνου τομά.
   Εἰ γὰρ μή ἐστιν, ἐσσεῖταί τι σαμεῖον ἐπ᾿ αὐτᾶς, ὃ οὐκ ἔστιν ἐν τᾷ ἐπιφανείᾳ τοῦ κυλίνδρου. Λελάφθω δή τι σαμεῖον ἐπ᾿ αὐτᾶς τὸ Θ, καὶ ἁ ΘΚ κάθετος ἄχθω ἐπὶ τὰν ΑΒ, καὶ ἀπὸ τοῦ Κ παρὰ τὰν ΓΔ ἔστω ἁ ΚΛ, καὶ ἀπὸ τοῦ Λ ἄχθω ποτ᾿ ὀρθὰς τᾷ ΖΗ ἐν τῷ ἡμικυκλίῳ τῷ περὶ διάμετρον τὰν ΖΗ ἁ ΛΜ, νοείσθω δὲ τὸ Μ ἐπὶ τᾶς περιφερείας τᾶς τοῦ ἡμικυκλίου τοῦ περὶ τὰν ΖΗ, καὶ ἀπὸ τοῦ Μ κάθετος ἄχθω ἐπὶ τὰν ΚΛ ἐκβληθεῖσαν ἁ ΜΟ· ἐσσεῖται δὲ αὕτα ὀρθὰ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐντι αἱ ΑΒ, ΓΔ, ἐπεὶ ποτ᾿ ὀρθάς ἐντι ἁ ΚΛ τᾷ ΖΗ· ἔστιν δή, ὡς μὲν τὸ ἀπὸ τᾶς ΜΟ ποτὶ τὸ ἀπὸ τᾶς ΜΛ, οὕτως τὸ ἀπὸ τᾶς ΞΝ ποτὶ τὸ ἀπὸ τᾶς ΝΓ, ὡς δὲ τὸ ἀπὸ τᾶς ΜΛ ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ, οὕτως τὸ ἀπὸ ΓΝ ποτὶ τὸ ἀπὸ τᾶς ΑΔ, ἐπεὶ τὸ μὲν ἀπὸ τᾶς ΜΛ ἴσον ἐστὶ τῷ ὑπὸ τᾶν ΛΖ, ΛΗ περιεχομένῳ, τὸ δὲ ἀπὸ τᾶς ΓΝ τῷ ἀπὸ τᾶς ΓΖ· ἔστιν ἄρα, ὡς τὸ ἀπὸ τᾶς ΜΟ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ, [181] οὕτως τὸ ἀπὸ τᾶς ΞΝ ποτὶ τὸ ἀπὸ τᾶς ΑΔ. Ἐντὶ δὲ καὶ τὸ ἀπὸ τᾶς ΚΘ τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΚ, ΚΒ, ὡς τὸ ἀπὸ τᾶς ΞΝ ποτὶ τὸ ἀπὸ τᾶς ΑΔ, ἐπεὶ ἴσα ἐστὶν ἁ ΞΝ τᾷ ἡμισέᾳ τᾶς ἑτέρας διαμέτρου· δῆλον οὖν ὅτι ἴσαι ἐντὶ αἱ ΜΟ, ΘΚ κάθετοι· ὥστε παράλληλοι αἱ ΚΟ, ΘΜ. Ἐπεὶ δὲ ἁ ΜΘ παρὰ τὸν ἄξονά ἐντι τοῦ κυλίνδρου καὶ τὸ Μ σαμεῖον ἐν τᾷ ἐπιφανείᾳ αὐτοῦ, ἀναγκαῖον καὶ τὰν ΜΘ ἐν τᾷ ἐπιφανείᾳ εἶμεν τοῦ κυλίνδρου· φανερὸν οὖν ὅτι καὶ τὸ Θ ἐν τᾷ ἐπιφανείᾳ ἐντὶ αὐτοῦ. Οὐκ ἦν δέ· δῆλον οὖν ὅτι ἀναγκαῖόν ἐστι τὰν τοῦ ὀξυγωνίου κώνου τομὰν ἐν τᾷ ἐπιφανείᾳ εἶμεν τοῦ κυλίνδρου.
   ι΄.
   Ὅτι μὲν πᾶς κῶνος ποτὶ κῶνον τὸν συγκείμενον ἔχει λόγον ἔκ τε τοῦ τῶν βάσιων λόγου καὶ ἐκ τοῦ τῶν ὑψέων ἀποδείκνυται ὑπὸ τῶν πρότερον, ἁ αὐτὰ δὲ ἀπόδειξίς ἐντι καὶ διότι πᾶν ἀπότμαμα κώνου ποτὶ ἀπότμαμα κώνου τὸν συγκείμενον λόγον ἔχει ἔκ τε τοῦ τῶν βάσιων λόγου καὶ ἐκ τοῦ τῶν ὑψέων.
   Καὶ ὅτι πᾶς τόμος κυλίνδρου τριπλασίων ἐστὶ τοῦ ἀποτμάματος τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τόμῳ καὶ ὕψος ἴσον, ἁ αὐτὰ ἀπόδειξις, ἅπερ καὶ ὅτι ὁ κύλινδρος τριπλάσιός ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ κυλίνδρῳ καὶ ὕψος ἴσον.
   ια΄.
   Εἴ κα τὸ ὀρθογώνιον κωνοειδὲς ἐπιπέδῳ τμαθῇ διὰ τοῦ ἄξονος ἢ παρὰ τὸν ἄξονα, ἁ τομὰ ἐσσεῖται ὀρθογωνίου [182] κώνου τομὰ ἁ αὐτὰ τᾷ περιλαμβανούσᾳ τὸ σχῆμα, διάμετρος δὲ αὐτᾶς ἐσσεῖται ἁ κοινὰ τομὰ τῶν ἐπιπέδων τοῦ τέμνοντος τὸ σχῆμα καὶ τοῦ διὰ τοῦ ἄξονος ἀχθέντος ὀρθοῦ ποτὶ τὸ ἐπίπεδον τὸ τέμνον.
   Εἰ δέ κα τμαθῇ τῷ ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα, ἁ τομὰ κύκλος ἐσσεῖται τὸ κέντρον ἔχων ἐπὶ τοῦ ἄξονος.
   Εἴ κα τὸ ἀμβλυγώνιον κωνοειδὲς ἐπιπέδῳ τμαθῇ διὰ τοῦ ἄξονος ἢ παρὰ τὸν ἄξονα ἢ διὰ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδές, ἁ τομὰ ἐσσεῖται ἀμβλυγωνίου κώνου τομά, εἰ μέν κα διὰ τοῦ ἄξονος, ἁ αὐτὰ τᾷ περιλαμβανούσᾳ τὸ σχῆμα, εἰ δέ κα παρὰ τὸν ἄξονα, ὁμοία αὐτᾷ, εἰ δέ κα διὰ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδές, οὐχ ὁμοία, διάμετρος δὲ τᾶς τομᾶς ἐσσεῖται ἁ κοινὰ τομὰ τῶν ἐπιπέδων τοῦ τέμνοντος τὸ σχῆμα καὶ τοῦ ἀχθέντος διὰ τοῦ ἄξονος ὀρθοῦ ποτὶ τὸ τέμνον ἐπίπεδον.
   Εἰ δέ κα τμαθῇ ὀρθῷ τῷ ἐπιπέδῳ ποτὶ τὸν ἄξονα, ἁ τομὰ κύκλος ἐσσεῖται τὸ κέντρον ἔχων ἐπὶ τοῦ ἄξονος.
   Εἴ κα τῶν σφαιροειδέων σχημάτων ὁποτερονοῦν ἐπιπέδῳ τμαθῇ διὰ τοῦ ἄξονος ἢ παρὰ τὸν ἄξονα, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, εἰ μέν κα διὰ τοῦ ἄξονος, αὐτὰ ἁ περιλαμβάνουσα τὸ σχῆμα, εἰ δέ κα παρὰ τὸν ἄξονα, ὁμοία αὐτᾷ, διάμετρος δὲ τᾶς τομᾶς ἐσσεῖται ἁ κοινὰ τομὰ τῶν ἐπιπέδων τοῦ τέμνοντος τὸ σχῆμα καὶ τοῦ ἀχθέντος διὰ τοῦ ἄξονος ὀρθοῦ ποτὶ τὸ τέμνον ἐπίπεδον.
   Εἰ δέ κα τμαθῇ τῷ ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα, ἁ τομὰ κύκλος ἐσσεῖται τὸ κέντρον ἔχων ἐπὶ τοῦ ἄξονος.
   Εἴ κα τῶν εἰρημένων σχημάτων ὁποιονοῦν ἐπιπέδῳ
[183]τμαθῇ διὰ τοῦ ἄξονος, αἱ ἀπὸ τῶν σαμείων τῶν ἐν τᾷ ἐπιφανείᾳ τοῦ σχήματος μὴ ἐπὶ τᾶς τομᾶς ἐόντων κάθετοι ἀγόμεναι ἐπὶ τὸ τέμνον ἐπίπεδον ἐντὸς πεσοῦνται τᾶς τοῦ σχήματος τομᾶς.
   Τούτων δὲ πάντων φανεραί ἐντι αἱ ἀποδείξιες.
   ιβ΄.
   Εἴ κα τὸ ὀρθογώνιον κωνοειδὲς ἐπιπέδῳ τμαθῇ μήτε διὰ τοῦ ἄξονος μήτε παρὰ τὸν ἄξονα μήτε ποτ᾿ ὀρθὰς τῷ ἄξονι, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ μείζων ἐσσεῖται ἁ ἐναπολαφθεῖσα ἐν τῷ κωνοειδεῖ ἀπὸ τᾶς γενομένας τομᾶς τῶν ἐπιπέδων τοῦ τέμνοντος τὸ σχῆμα καὶ τοῦ ἀχθέντος διὰ τοῦ ἄξονος ὀρθοῦ ποτὶ τὸ τέμνον ἐπίπεδον, ἁ δὲ ἐλάσσων διάμετρος ἴσα ἐσσεῖται τῷ διαστήματι τᾶν ἀχθεισᾶν παρὰ τὸν ἄξονα ἀπὸ τῶν περάτων τᾶς μείζονος διαμέτρου.    Τετμάσθω γὰρ τὸ ὀρθογώνιον κωνοειδὲς ἐπιπέδῳ, ὡς εἴρηται, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον ἔστω τοῦ μὲν κωνοειδέος τομὰ ἁ ΑΒΓ, τοῦ δὲ ἐπιπέδου τοῦ τέμνοντος τὸ σχῆμα ἁ ΓΑ εὐθεῖα, ἄξων δὲ ἔστω τοῦ κωνοειδέος καὶ διάμετρος τᾶς τομᾶς ἁ ΒΔ· δεικτέον ὅτι ἁ τομὰ τοῦ κωνοειδέος ἁ ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὰν ΑΓ ὀξυγωνίου ἐστὶ κώνου τομά, καὶ διάμετρος αὐτᾶς ἁ μείζων ἐστὶν ἁ ΑΓ, ἁ δὲ ἐλάσσων διάμετρος ἴσα ἐντὶ τᾷ ΛΑ τᾶς μὲν ΓΛ παρὰ τὰν ΒΔ ἐούσας, τᾶς δὲ ΑΛ καθέτου ἐπὶ τὰν ΓΛ.
   Νοείσθω τι σαμεῖον ἐπὶ τᾶς τομᾶς λελαμμένον τὸ Κ, καὶ ἀπὸ τοῦ Κ κάθετος ἄχθω ἐπὶ τὰν ΓΑ ἁ ΚΘ· ἐσσεῖται

[184] οὖν ἁ ΚΘ κάθετος ἐπὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐστιν ἁ ΑΓΒ ὀρθογωνίου κώνου τομά, διότι καὶ τὸ τέμνον ἐπίπεδον ὀρθόν ἐστιν ποτὶ τὸ αὐτὸ ἐπίπεδον· διὰ δὲ τοῦ Θ ἄχθω ἁ ΕΖ ὀρθὰς ποιοῦσα γωνίας ποτὶ τὰν ΒΔ, καὶ διὰ τᾶν ΕΖ, ΚΘ εὐθειᾶν ἐπίπεδον ἐκβεβλήσθω· ἐσσεῖται δὲ τοῦτο ὀρθὸν ποτὶ τὰν ΒΔ· τετμήσεται δὴ τὸ κωνοειδὲς σχῆμα ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα· ὥστε ἁ τομὰ κύκλος ἐσσεῖται, κέντρον δὲ αὐτοῦ τὸ Δ· ἁ ἄρα ΚΘ ἴσον δυνασεῖται τῷ ὑπὸ ΖΘ, ΘΕ [ἡμικύκλιον γάρ ἐστι τὸ ἐπὶ τῆς ΕΖ, καὶ ἁ ΚΘ κάθετος οὖσα μέση γίνεται ἀνάλογον τῷ ὑπὸ τᾶν ΕΘ, ΘΖ περιεχομένῳ]. Ἄχθω δὲ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς ἁ μὲν ΜΝ παρὰ τὰν ΑΓ, ἐπιψαυέτω δὲ κατὰ τὸ Ν, ἁ δὲ ΒΤ παρὰ τὰν ΕΖ· τὸ δὴ περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΓ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΕΘ, ΘΖ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΝΤ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΤ· δέδεικται γὰρ τοῦτο. Τᾷ δὲ ΝΤ ἴσα ἐντὶ ἁ ΤΜ, διότι καὶ ἁ ΒΡ τᾷ ΒΜ· ἔχει οὖν καὶ τὸ περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΓ ποτὶ τὸ ἀπὸ τᾶς ΚΘ τὸν αὐτὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΤΜ ποτὶ τὸ ἀπὸ τᾶς ΤΒ· [185] ὥστε καὶ τὸ ἀπὸ τᾶς ΘΚ καθέτου τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΘ, ΘΓ περιεχόμενον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΒΤ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΤΜ. Ἐπεὶ οὖν ὁμοῖά ἐντι τὰ ΓΑΛ, ΤΜΒ τρίγωνα, τὸ ἀπὸ τᾶς ΘΚ καθέτου τετράγωνον ποτὶ τὸ ὑπὸ τᾶν ΑΘ, ΘΓ περιεχόμενον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΑΛ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΑΓ τετράγωνον. Ὁμοίως δειχθήσονται καὶ τὰ ἀπὸ τᾶν ἀλλᾶν καθέτων τετράγωνα τᾶν ἀγομενᾶν ἀπὸ τᾶς τομᾶς ἐπὶ τὰν ΑΓ ποτὶ τὰ περιεχόμενα ὑπὸ τῶν τᾶς ΑΓ τμαμάτων τὸν αὐτὸν ἔχοντα λόγον, ὃν τὸ ἀπὸ τᾶς ΑΛ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΑΓ· δῆλον οὖν ὅτι ἁ τομά ἐστιν ὀξυγωνίου κώνου τομά, διάμετροι δὲ αὐτᾶς ἐντι ἁ μὲν μείζων ἁ ΑΓ, ἁ δὲ ἐλάσσων ἴσα τᾷ ΑΛ.
   ιγ΄.
   Εἴ κα τὸ ἀμβλυγώνιον κωνοειδὲς ἐπιπέδῳ τμαθῇ συμπίπτοντι πάσαις ταῖς τοῦ κώνου πλευραῖς τοῦ περιέχοντος τὸ κωνοειδὲς μὴ ποτ᾿ ὀρθὰς τῷ ἄξονι, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ μείζων ἐσσεῖται ἁ ἐναπολαφθεῖσα ἐν τῷ κωνοειδεῖ ἀπὸ τᾶς γενομένας τομᾶς τῶν ἐπιπέδων τοῦ τε τέμνοντος τὸ σχῆμα καὶ τοῦ ἀχθέντος διὰ τοῦ ἄξονος ὀρθοῦ ποτὶ τὸ τέμνον ἐπίπεδον.
   Τεμνέσθω γὰρ τὸ ἀμβλυγώνιον κωνοειδὲς ἐπιπέδῳ, ὡς εἴρηται, καὶ ἄλλῳ ἐπιπέδῳ τμαθέντος αὐτοῦ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον τοῦ μὲν κωνοειδέος τομὰ ἔστω ἁ ΑΒΓ ἀμβλυγωνίου κώνου τομά, τοῦ δὲ τέμνοντος τὸ σχῆμα ἐπιπέδου ἁ ΑΓ εὐθεῖα, ἄξων δὲ τοῦ

[186] κωνοειδέος καὶ διάμετρος τᾶς τομᾶς ἁ ΒΔ. Νοείσθω δή τι ἐπὶ τᾶς τομᾶς λελαμμένον σαμεῖον τὸ Κ, καὶ ἀπὸ τοῦ Κ κάθετος ἄχθω ἐπὶ τὰν ΑΓ ἁ ΚΘ· ἐσσεῖται δὴ αὕτα ὀρθὰ ποτὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐντι ἁ ΑΒΓ κώνου τομά. Διὰ δὲ τοῦ Θ ἄχθω ἁ ΕΖ ποτ᾿ ὀρθὰς τᾷ ΒΔ, καὶ διὰ τᾶν ΕΖ, ΚΘ εὐθειᾶν ἐπίπεδον ἄχθω τέμνον τὸ κωνοειδές· τετμήσεται δὴ ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα· ὥστε ἁ τομὰ κύκλος ἐσσεῖται, κέντρον δὲ αὐτοῦ τὸ Δ· ἁ ἄρα κάθετος ἁ ΚΘ ἴσον δυνασεῖται τῷ περιεχομένῳ ὑπὸ τᾶν ΕΘ, ΘΖ. Ἄχθω δὴ πάλιν ἁ μὲν ΜΝ παρὰ τὰν ΑΓ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Ν, ἁ δὲ ΒΤ παρὰ τὰν ΕΖ· τὸ δὴ περιεχόμενον ὑπὸ ΕΘ, ΘΖ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΓ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΤ ποτὶ τὸ ἀπὸ τᾶς ΤΝ· ὥστε τὸ ἀπὸ τᾶς ΚΘ καθέτου τετράγωνον ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΓ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΒΤ ποτὶ τὸ ἀπὸ τᾶς ΤΝ. Ὁμοίως οὖν δειχθησοῦνται καὶ τὰ ἀπὸ τᾶν ἀλλᾶν καθέτων τᾶν ἀπὸ τᾶς τομᾶς ἀγομενᾶν ἐπὶ τὰν ΑΓ ποτὶ τὰ περιεχόμενα ὑπὸ τῶν τμαμάτων τᾶς ΑΓ, ὧν αἱ κάθετοι ποιοῦντι, τὸν αὐτὸν ἔχοντα λόγον, ὃν τὸ ἀπὸ τᾶς ΒΤ τετράγωνον [187] ποτὶ τὸ ἀπὸ τᾶς ΤΝ. Καί ἐστιν ἐλάσσων ἁ ΒΤ τᾶς ΤΝ, διότι καὶ ἁ ΜΤ ἐλάσσων ἐστὶν τᾶς ΤΝ· καὶ γὰρ ἁ ΜΒ ἐλάσσων τᾶς ΒΡ· τοῦτο γάρ ἐστιν ἐν ταῖς τοῦ ἀμβλυγωνίου κώνου τομαῖς σύμπτωμα· δῆλον οὖν ὅτι ἁ τομὰ ὀξυγωνίου κώνου τομὰ καὶ διάμετρος αὐτᾶς μείζων ἁ ΑΓ [ὁμοίως καθέτου οὔσης τᾶς ΝΡ ἐν τᾷ τοῦ ἀμβλυγωνίου κώνου τομᾷ διάμετρος ταύτας μείζων ἐστὶν ἁ ΓΛ].
   ιδ΄.
   Εἴ κα τὸ παραμᾶκες σφαιροειδὲς ἐπιπέδῳ τμαθῇ μὴ ποτ᾿ ὀρθὰς τῷ ἄξονι, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ μείζων ἐσσεῖται ἁ ἐναπολαφθεῖσα ἐν τῷ σφαιροειδεῖ ἀπὸ τᾶς γενομένας τομᾶς τῶν ἐπιπέδων τοῦ τέμνοντος τὸ σχῆμα καὶ τοῦ ἀχθέντος διὰ τοῦ ἄξονος ὀρθοῦ ποτὶ τὸ τέμνον ἐπίπεδον.
   Εἰ μὲν οὖν κα τμαθῇ διὰ τοῦ ἄξονος ἢ παρὰ τὸν ἄξονα δῆλον· τετμάσθω δὲ ἄλλῳ ἐπιπέδῳ, τμαθέντος δὲ αὐτοῦ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον τοῦ μὲν σφαιραειδέος τομὰ ἔστω ἁ ΑΒΓΔ ὀξυγωνίου κώνου τομά, τοῦ δὲ τέμνοντος αὐτὸ ἐπιπέδου ἁ ΓΑ εὐθεῖα, ἄξων δὲ ἔστω τοῦ σφαιροειδέος καὶ διάμετρος τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἁ ΒΔ, κέντρον δὲ τὸ Χ, καὶ ἐλάσσων διάμετρος ἔστω ἁ ΠΡ. [188] Ἄχθω δὲ ἁ μὲν ΒΤ ποτ᾿ ὀρθὰς τᾷ ΒΔ, ἁ δὲ ΗΝ παρὰ τὰν ΑΓ ἐπιψαύουσα τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς κατὰ τὸ Ν, ἄχθω δὲ καὶ ἁ ΜΛ διὰ τοῦ Χ παρὰ τὰν ΑΓ· ὁμοίως δὴ τοῖς πρότερον δειχθησοῦντι τὰ τετράγωνα τὰ ἀπὸ τᾶν καθέτων τᾶν ἀπὸ τᾶς τομᾶς ἐπὶ τὰν ΑΓ ἀγμενᾶν ποτὶ τὰ περιεχόμενα ὑπὸ τῶν τᾶς ΑΓ τμαμάτων τὸν αὐτὸν ἔχοντα λόγον, ὃν τὸ ἀπὸ τᾶς ΒΤ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΤΝ. Ὅτι μὲν οὖν ἁ τομά ἐστιν ὀξυγωνίου κώνου τομὰ καὶ διάμετρος αὐτᾶς ἁ ΓΑ δῆλον· ὅτι δὲ μείζων δεικτέον. Τὸ γὰρ ὑπὸ τᾶν ΠΧ, ΧΡ περιεχόμενον ποτὶ τὸ ὑπὸ ΜΧ, ΧΛ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΒΤ ποτὶ τὸ ἀπὸ τᾶς ΝΤ, ἐπεὶ παρὰ τὰς ἐπιψαυούσας ἐντὶ αἱ ΠΡ, ΜΛ. Ἔλασσον δέ ἐστι τὸ ὑπὸ τᾶν ΠΧ, ΧΡ περιεχόμενον τοῦ ὑπὸ τᾶν ΜΧ, ΧΛ, ἐπεὶ καὶ ἁ ΧΠ τᾶς ΧΛ· ἔλασσον ἄρα ἐστὶν καὶ τὸ ἀπὸ τᾶς ΒΤ τετράγωνον τοῦ ἀπὸ τᾶς ΤΝ· ὥστε καὶ τὰ ἀπὸ τᾶν καθέτων τετράγωνα τᾶν ἀπὸ τᾶς τομᾶς ἐπὶ τὰν ΑΓ ἀγομενᾶν ἐλάσσονά ἐντι τῶν ὑπὸ τῶν τμαμάτων τᾶς ΑΓ περιεχομένων. Δῆλον οὖν ὅτι μείζων ἐντὶ διάμετρος ἁ ΓΑ.
   Εἴ κα τὸ ἐπιπλατὺ σφαιροειδὲς ἐπιπέδῳ τμαθῇ, τὰ μὲν ἄλλα τὰ αὐτὰ ἐσσεῖται, τᾶν δὲ διαμέτρων ἐλάσσων ἐσσεῖται ἁ ἐναπολαφθεῖσα ἐν τῷ σφαιροειδεῖ.
   Ἐξ αὐτῶν δὲ φανερὸν ἐν πάντεσσι τοῖς σχημάτεσσιν ὅτι, εἴ κα παραλλήλοις ἐπιπέδοις τμαθῇ, αἱ αὐτῶν τομαὶ ὁμοῖαι ἐσσοῦνται· τὰ γὰρ τετράγωνα τὰ ἀπὸ τᾶν καθέτων ποτὶ τὰ περιεχόμενα ὑπὸ τῶν τμαμάτων τοὺς αὐτοὺς λόγους ἑξοῦντι.

[189]    ιε΄.
   Ἐν τῷ ὀρθογωνίῳ κωνοειδεῖ ἀπὸ παντὸς ὁτουοῦν σαμείου τῶν ἐν τᾷ ἐπιφανείᾳ τοῦ κωνοειδέος τᾶν ἀγομενᾶν εὐθειᾶν παρὰ τὸν ἄξονα αἱ μὲν ἐπὶ τὰ αὐτὰ ἀγόμεναι, ἐφ᾿ ἅ ἐντι τὰ κυρτὰ αὐτοῦ, ἐκτὸς πεσοῦνται τοῦ κωνοειδέος, αἱ δὲ ἐπὶ θάτερα ἐντός.
   Ἀχθέντος γὰρ ἐπιπέδου διά τε τοῦ ἄξονος καὶ τοῦ σαμείου, ἀφ᾿ οὗ ἁ παράλληλος ἄγεται τῷ ἄξονι, ἁ τομὰ ἐσσεῖται ὀρθογωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ὁ ἄξων τοῦ κωνοειδέος· ἐν δὲ τᾷ τοῦ ὀρθογωνίου κώνου τομᾷ ἀπὸ παντὸς σαμείου τοῦ ἐπὶ τᾶς τομᾶς ἀγομενᾶν παρὰ τὰν διάμετρον εὐθειᾶν αἱ μὲν ἐπὶ τὰ αὐτὰ ἀγόμεναι, ἐφ᾿ ἅ ἐντι τὰ κυρτὰ αὐτᾶς, ἐκτὸς πίπτοντι, αἱ δὲ ἐπὶ θάτερα ἐντός· δῆλον οὖν τὸ προτεθέν.
   Ἐν τῷ ἀμβλυγωνίῳ κωνοειδεῖ ἀπὸ παντὸς σαμείου τῶν ἐν τᾷ ἐπιφανείᾳ αὐτοῦ τᾶν ἀγομενᾶν εὐθειᾶν παρά τινα γραμμάν, ἅ ἐστιν ἐν τῷ κωνοειδεῖ ἀγομένα διὰ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδές, αἱ μὲν ἐπὶ τὰ αὐτὰ ἀγόμεναι, ἐφ᾿ ἅ ἐντι τὰ κυρτὰ αὐτοῦ, ἐκτὸς πεσοῦνται τοῦ κωνοειδέος, αἱ δὲ ἐπὶ θάτερα ἐντός.
   Ἀχθέντος γὰρ ἐπιπέδου διά τε τᾶς εὐθείας τᾶς ἐν τῷ κωνοειδεῖ ἀγομένας διὰ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδὲς καὶ διὰ τοῦ σαμείου, ἀφ᾿ οὗ ἄγεται ἁ ἐς αὐτό, ἁ τομὰ ἐσσεῖται ἀμβλυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ ἀπὸ τᾶς κορυφᾶς τοῦ κώνου ἐν τῷ κωνοειδεῖ ἀγομένα· ἐν δὲ τᾷ τοῦ ἀμβλυγωνίου κώνου τομᾷ ἀπὸ παντὸς σαμείου τοῦ ἐπὶ τᾶς τομᾶς τᾶν ἀγομενᾶν εὐθειᾶν παρὰ τὰν οὕτως ἀγμέναν γραμμὰν αἱ [190] μὲν ἐπὶ τὰ αὐτὰ ἀγόμεναι, ἐφ᾿ ἅ ἐστιν αὐτᾶς τὰ κυρτά, ἐκτὸς πίπτοντι, αἱ δὲ ἐπὶ θάτερα ἐντός.
   Εἴ κα τῶν κωνοειδέων σχημάτων ἐπίπεδον ἐφάπτηται μὴ τέμνον τὸ κωνοειδές, καθ᾿ ἓν μόνον ἅψεται σαμεῖον, καὶ τὸ διὰ τᾶς ἁφᾶς καὶ τοῦ ἄξονος ἐπίπεδον ἀχθὲν ὀρθὸν ἐσσεῖται ποτὶ τὸ ἐπιψαῦον ἐπίπεδον.
   Ἐφαπτέσθω γάρ, εἰ δυνατόν, κατὰ πλείονα σαμεῖα. Λαφθέντων δὴ δύο σαμείων, καθ᾿ ἃ ἅπτεται τὸ ἐπιψαῦον ἐπίπεδον τοῦ κωνοειδέος, καὶ ἀφ᾿ ἑκατέρου παρὰ τὸν ἄξονα εὐθειᾶν ἀχθεισᾶν ἀπὸ τᾶν ἀχθεισᾶν παρὰ τὸν ἄξονα ἐπίπεδον ἐκβληθὲν ἤτοι διὰ τοῦ ἄξονος ἢ παρὰ τὸν ἄξονα ἐσσεῖται ἀγμένον· ὥστε τὰν τομὰν ποιήσει κώνου τομάν, καὶ τὰ σημεῖα ἐσσοῦνται ἐν τᾷ τοῦ κώνου τομᾷ, ἐπεὶ ἔν τε τᾷ ἐπιφανείᾳ ἐντὶ καὶ ἐν τῷ ἐπιπέδῳ. Ἁ οὖν μεταξὺ τῶν σαμείων εὐθεῖα ἐντὸς ἐσσεῖται τᾶς τοῦ κώνου τομᾶς· ὥστε καὶ τᾶς τοῦ κωνοειδέος ἐπιφανείας ἐντὸς ἐσσεῖται. Ἔστιν δὲ ἁ εὐθεῖα αὕτα ἐν τῷ ἐπιψαύοντι ἐπιπέδῳ, διότι καὶ τὰ σαμεῖα· τοῦ ἄρα ἐπιψαύοντος ἐπιπέδου ἐσσεῖταί τι ἐντὸς τοῦ κωνοειδέος· ὅπερ ἀδύνατον· ὑπέκειτο γὰρ μὴ τέμνειν. Καθ᾿ ἓν ἄρα μόνον ἅψεται σαμεῖον.

[191]    Ὅτι δὲ καὶ τὸ διὰ τᾶς ἁφᾶς καὶ τοῦ ἄξονος ἐπίπεδον ἀχθὲν ὀρθὸν ἐσσεῖται ποτὶ τὸ ἐπιψαῦον, εἰ μὲν κατὰ τὰν κορυφὰν τοῦ κωνοειδέος ἐφάπτεται, δῆλον. Ἀχθέντων γὰρ διὰ τοῦ ἄξονος δύο ἐπιπέδων τοῦ κωνοειδέος αἱ τομαὶ ἐσσοῦνται κώνων τομαὶ διάμετρον ἔχουσαι τὸν ἄξονα, τοῦ δὲ ἐπιψαύοντος ἐπιπέδου εὐθεῖαι ἐπιψαύουσαι τᾶν τῶν κώνων τομᾶν κατὰ τὸ πέρας τᾶς διαμέτρου. Αἱ δὲ εὐθεῖαι αἱ ἐπιψαύουσαι τᾶν τῶν κώνων τομᾶν κατὰ τὸ πέρας τᾶς διαμέτρου ὀρθὰς ποιοῦντι γωνίας ποτὶ τὰν διάμετρον· ἐσσοῦνται οὖν ἐν τῷ ἐπιψαύοντι ἐπιπέδῳ δύο εὐθεῖαι ποτ᾿ ὀρθὰς τῷ ἄξονι. Ὀρθὸν οὖν ἐσσεῖται ποτὶ τὸν ἄξονα τὸ ἐπίπεδον· ὥστε καὶ ποτὶ τὸ διὰ τοῦ ἄξονος. Ἀλλὰ ἔστω μὴ κατὰ τὰν κορυφὰν τοῦ κωνοειδέος ἐπιψαῦον τὸ ἐπίπεδον. Ἄχθω δὴ ἐπίπεδον διὰ τᾶς ἁφᾶς καὶ τοῦ ἄξονος, καὶ τοῦ μὲν κωνοειδέος τομὰ ἔστω ἁ ΑΒΓ κώνου τομά, ἄξων δὲ ἔστω καὶ διάμετρος τᾶς τομᾶς ἁ ΒΔ, τοῦ δὲ ἐπιψαύοντος ἐπιπέδου τομὰ ἔστω ἁ ΕΘΖ εὐθεῖα τᾶς τοῦ κώνου τομᾶς ἁπτομένα κατὰ τὸ Θ, ἀπὸ δὲ τοῦ Θ κάθετος ἄχθω ἐπὶ τὰν ΒΔ ἁ ΘΚ, καὶ ἐπίπεδον ἀνεστακέτω ὀρθὸν ποτὶ τὸν ἄξονα· ποιήσει δὴ τοῦτο τὰν τομὰν κύκλον, οὗ κέντρον τὸ Κ. Ἁ δὲ τομὰ τούτου τοῦ ἐπιπέδου καὶ τοῦ ἐπιψαύοντος ἐσσεῖται ἐπιψαύουσα τοῦ κύκλου· ὀρθὰς ἄρα ποιήσει γωνίας ποτὶ τὰν ΘΚ· ὥστ᾿ ὀρθὰ ἐσσεῖται ποτὶ τὸ ἐπίπεδον τὸ ἐν ᾧ ἐντι αἱ ΚΘ, ΒΔ. Δῆλον οὖν ὅτι τὸ ἐπιψαῦον ἐπίπεδον ὀρθόν ἐστι ποτὶ τὸ αὐτὸ ἐπίπεδον, ἐπεὶ καὶ αἱ ἐν αὐτῷ εὐθεῖαι.

[192]    ιϚ΄.
   Εἴ κα τῶν σφαιροειδέων σχημάτων ὁποτερουοῦν ἐπίπεδον ἅπτηται μὴ τέμνον τὸ σχῆμα, καθ᾿ ἓν μόνον ἅψεται σαμεῖον, καὶ τὸ διὰ τᾶς ἁφᾶς καὶ τοῦ ἄξονος ἐπίπεδον ἀχθὲν ὀρθὸν ἐσσεῖται ποτὶ τὸ ἐπιψαῦον ἐπίπεδον.
   Ἁπτέσθω γὰρ κατὰ πλείονα σαμεῖα. Λαφθέντων δὴ τῶν σαμείων, καθ᾿ ἃ ἅπτεται τὸ ἐπίπεδον τοῦ σφαιροειδέος, καὶ ἀφ᾿ ἑκατέρου αὐτῶν παρὰ τὸν ἄξονα εὐθειᾶν ἀχθεισᾶν καὶ διὰ τᾶν ἀχθεισᾶν ἐπιπέδου ἐκβληθέντος ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, καὶ τὰ σαμεῖα ἐσσοῦνται ἐν τᾷ τοῦ κώνου τομᾷ. Ἁ οὖν μεταξὺ τῶν σαμείων εὐθεῖα ἐντὸς ἐσσεῖται τᾶς τοῦ κώνου τομᾶς· ὥστε καὶ τᾶς τοῦ σφαιροειδέος ἐπιφανείας ἐντὸς ἐσσεῖται. Ἔστιν δὲ ἁ εὐθεῖα ἐν τῷ ἐπιψαύοντι ἐπιπέδῳ, διότι καὶ τὰ σαμεῖα· τοῦ οὖν ἐπιψαύοντος ἐπιπέδου ἐσσεῖταί τι ἐντὸς τοῦ σφαιροειδέος. Οὐκ ἔστιν δέ· ὑπέκειτο γὰρ μὴ τέμνειν. Δῆλον οὖν, ὅτι καθ᾿ ἓν σαμεῖον μόνον ἅψεται. Ὅτι δὲ τὸ διὰ τᾶς ἁφᾶς καὶ τοῦ ἄξονος ἐπίπεδον ἀχθὲν ὀρθὸν ἐσσεῖται ποτὶ τὸ ἐπίπεδον τὸ ἐπιψαῦον, ὁμοίως τοῖς περὶ τῶν κωνοειδέων σχημάτων.
   Εἴ κα τῶν κωνοειδέων ἢ τῶν σφαιροειδέων σχημάτων ὁποιονοῦν ἐπιπέδῳ τμαθῇ διὰ τοῦ ἄξονος, καὶ τᾶς γενομένας τομᾶς ἐπιψαύουσά τις ἀχθῇ εὐθεῖα, καὶ διὰ τᾶς ἐπιψαυούσας ἐπίπεδον ἀνασταθῇ ὀρθὸν ποτὶ τὸ τέμνον, ἐπιψαύει τοῦ σχήματος κατὰ τὸ αὐτὸ σαμεῖον, καθ᾿ ὃ καὶ ἁ εὐθεῖα ἐπιψαύει τᾶς τοῦ κώνου τομᾶς.
   Οὐ γὰρ ἅψεται κατ᾿ ἄλλο σαμεῖον τᾶς ἐπιφανείας αὐτοῦ. Εἰ δὲ μή, ἁ ἀπὸ τοῦ σαμείου κάθετος ἀγομένα ἐπὶ τὸ τέμνον ἐπίπεδον πεσεῖται ἐκτὸς τᾶς τοῦ κώνου τομᾶς· [193] ἐπὶ γὰρ τὰν ἐπιψαύουσαν πεσεῖται, ἐπεὶ ὀρθὰ ποτ᾿ ἄλλαλά ἐντι τὰ ἐπίπεδα· ὅπερ ἀδύνατον· ἐδείχθη γάρ, ὅτι ἐντὸς πεσεῖται.
   Εἴ κα τῶν σφαιροειδέων τινὸς σχημάτων δύο ἐπίπεδα παράλληλα ἐπιψαύωντι, ἁ τὰς ἁφὰς ἐπιζευγνύουσα εὐθεῖα διὰ τοῦ κέντρου τοῦ σφαιροειδέος πορεύσεται.
   Εἰ μὲν οὖν κα ποτ᾿ ὀρθὰς τῷ ἄξονι τὰ ἐπίπεδα ἔωντι, δῆλον· ἄλλ᾿ ἔστω μὴ ποτ᾿ ὀρθάς. Τὸ δὴ ἐπίπεδον τὸ ἀχθὲν διὰ τοῦ ἄξονος καὶ τᾶς ἁφᾶς τᾶς ἑτέρας ὀρθὸν ἐσσεῖται ποτὶ τὸ ἐπιψαῦον ἐπίπεδον· ὥστε καὶ ποτὶ τὸ παράλληλον αὐτῷ. Ἀναγκαῖον ἄρα τὸ αὐτὸ εἶμεν ἐπίπεδον τὸ διὰ τοῦ ἄξονος καὶ ἑκατερᾶν τᾶν ἁφᾶν ἀγμένον. Εἰ δὲ μή, ἐσσοῦνται δύο ἐπίπεδα ποτὶ τὸ αὐτὸ ἐπίπεδον ὀρθὰ διὰ τᾶς αὐτᾶς γραμμᾶς ἀγμένα οὐκ ἐούσας ὀρθᾶς ποτὶ τὸ ἐπίπεδον· ὑπέκειτο γὰρ ὁ ἄξων μὴ εἶμεν ὀρθὸς ποτὶ τὰ παράλληλα ἐπίπεδα· ἐν τῷ αὐτῷ ἄρα ἐσσοῦνται ἐπιπέδῳ ὅ τε ἄξων καὶ αἱ ἁφαί, καὶ τετμακὸς ἐσσεῖται τὸ σφαιροειδὲς διὰ τοῦ ἄξονος. Ἁ οὖν τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, αἱ δὲ τῶν ἐπιψαυόντων ἐπιπέδων τομαὶ [194] παράλληλοι ἐσσοῦνται καὶ ἐπιψαύουσαι τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς κατὰ τὰς ἁφὰς τῶν ἐπιπέδων· εἰ δέ κα δύο εὐθεῖαι ὀξυγωνίου κώνου τομᾶς ἐπιψαύωντι παράλληλοι ἐοῦσαι, τό τε κέντρον τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς καὶ αἱ ἁφαὶ ἐπ᾿ εὐθείας ἐσσοῦνται.
   ιζ΄.
   Εἴ κα τῶν σφαιροειδέων σχημάτων ὁποτερουοῦν δύο παράλληλα ἐπίπεδα ἀχθῇ ἐπιψαύοντα, ἀχθῇ δέ τι ἐπίπεδον διὰ τοῦ κέντρου τοῦ σφαιροειδέος παρὰ τὰ ἐπιψαύοντα, αἱ διὰ τᾶς γενομένας τομᾶς ἀγόμεναι εὐθεῖαι παρὰ τὰν τὰς ἁφὰς ἐπιζευγνύουσαν ἐκτὸς πεσοῦνται τοῦ σφαιροειδέος.

Ὑποκείσθω τὰ εἰρημένα, καὶ λελάφθω τι σαμεῖον ἐπὶ τᾶς γενομένας τομᾶς, διὰ δὲ τοῦ γενομένου σαμείου καὶ τᾶς εὐθείας τᾶς τὰς ἁφὰς ἐπιζευγνυούσας ἐπίπεδον ἄχθω· τεμεῖ δὴ τοῦτο τό τε σφαιροειδὲς καὶ τὰ παράλλαλα ἐπίπεδα. Ἔστω οὖν ἁ μὲν τοῦ σφαιροειδέος τομὰ ἁ ΑΒΓΔ [ὀξυγωνίου κώνου τομά], αἱ δὲ τῶν ἐπιπέδων τῶν ψαυόντων τομαὶ αἱ ΕΖ, ΗΘ εὐθεῖαι, τὸ δὲ λαφθὲν σαμεῖον τὸ Α, ἁ δὲ [195] τὰς ἁφὰς ἐπιζευγνύουσα ἔστω ἁ ΒΔ· πεσεῖται δὲ αὕτα διὰ τοῦ κέντρου· ἁ δὲ τοῦ παραλλήλου ἐπιπέδου τοῖς ἐπιψαυόντεσσιν ἐπιπέδοις τομὰ ἁ ΓΑ· ἐσσεῖται δὲ αὕτα διὰ τοῦ κέντρου ἀγμένα, ἐπεὶ καὶ τὸ ἐπίπεδον. Ἐπεὶ οὖν ἐστιν ἁ ΑΒΓΔ ἤτοι κύκλος ἢ ὀξυγωνίου κώνου τομά, καὶ ἐπιψαύοντι αὐτᾶς δύο εὐθεῖαι αἱ ΕΖ, ΗΘ, διὰ δὲ τοῦ κέντρου ἆκται παράλληλος αὐταῖς ἁ ΑΓ, δῆλον ὡς αἱ ἀπὸ τῶν Α, Γ ἀγόμεναι σαμείων παρὰ τὰν ΒΔ ἐπιψαύοντι τᾶς τομᾶς καὶ ἐκτὸς πεσοῦνται τοῦ σφαιροειδέος.

Εἰ δέ κα τὸ παράλληλον ἐπίπεδον τοῖς ἐπιψαυόντεσσι μὴ διὰ τοῦ κέντρου ἀγμένον ᾖ, ὡς τὸ ΚΛ, δῆλον ὡς τᾶν ἀπὸ τᾶς τομᾶς ἀγομενᾶν εὐθειᾶν αἱ μὲν ἐπὶ τὰ αὐτὰ γενόμενα τῷ ἐλάσσονι τμάματι ἐκτὸς πεσοῦνται τοῦ σφαιροειδέος, αἱ δὲ ἐπὶ θάτερα ἐντός.
   ιη΄.
   Πᾶν σχῆμα σφαιροειδὲς ἐπιπέδῳ τμαθὲν διὰ τοῦ κέντρου δίχα τέμνεται ὑπὸ τοῦ ἐπιπέδου καὶ αὐτὸ καὶ ἁ ἐπιφάνεια αὐτοῦ.
   Τετμάσθω γὰρ τὸ σφαιροειδὲς ἐπιπέδῳ διὰ τοῦ κέντρου· ἤτοι δὴ καὶ διὰ τοῦ ἄξονος ἐσσεῖται τετμαμένον ἢ ποτ᾿ ὀρθὰς ἢ μὴ ποτ᾿ ὀρθὰς τῷ ἄξονι. Εἰ μὲν οὖν διὰ τοῦ ἄξονος τέμνεται ἢ ποτ᾿ ὀρθᾶς τῷ ἄξονι, δῆλον ὡς δίχα τέμνεταί τε αὐτὸ καὶ ἁ ἐπιφάνεια αὐτοῦ· φανερὸν γὰρ ὅτι ἐφαρμόζει τὸ ἕτερον μέρος αὐτοῦ ἐπὶ τὸ ἕτερον καὶ ἁ ἐπιφάνεια τοῦ ἑτέρου μέρους ἐπὶ τὰν τοῦ ἑτέρου.

[196]    Ἀλλ᾿ ἔστω μὴ διὰ τοῦ ἄξονος τετμαμένον μήτε ποτ᾿ ὀρθὰς τῷ ἄξονι. Τμαθέντος δὴ τοῦ σφαιροειδέος ἐπιπέδῳ ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον διὰ τοῦ ἄξονος αὐτοῦ μὲν τοῦ σχήματος τομὰ ἔστω ἁ ΑΒΓΔ ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἔστω καὶ ἄξων τοῦ σφαιροειδέος ἁ ΒΔ καὶ κέντρον τὸ Θ, τοῦ δὲ ἐπιπέδου τοῦ τετμακότος διὰ τοῦ κέντρου τὸ σφαιροειδὲς ἔστω τομὰ ἁ ΑΓ εὐθεῖα. Λελάφθω δή τι καὶ ἄλλο σφαιροειδὲς ἴσον καὶ ὁμοῖον τούτῳ, καὶ τμαθέντος αὐτοῦ διὰ τοῦ ἄξονος ἐπιπέδῳ τομὰ ἔστω ἁ ΕΖΗΝ ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς καὶ ἄξων τοῦ σφαιροειδέος ἁ ΕΗ καὶ κέντρον τὸ Κ, καὶ διὰ τοῦ Κ ἄχθω ἁ ΖΝ γωνίαν ποιοῦσα τὰν Κ ἴσαν τᾷ Θ, ἀπὸ δὲ τᾶς ΖΝ ἐπίπεδον ἔστω ἀνεστακὸς ὀρθὸν ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ ΕΖΗΝ τομά· ἐντὶ δὴ δύο ὀξυγωνίων κώνων τομαὶ αἱ ΑΒΓΔ, ΕΖΗΝ ἴσαι καὶ ὁμοῖαι ἀλλάλαις· ἐφαρμόζοντι οὖν ἐπ᾿ ἀλλάλας τεθείσας τᾶς ΕΗ ἐπὶ τὰν ΒΔ καὶ τᾶς ΖΝ ἐπὶ τὰν ΑΓ. Ἐφαρμόζει δὲ καὶ τὸ ἐπίπεδον τὸ κατὰ τὰν ΝΖ τῷ ἐπιπέδῳ τῷ κατὰ τὰν ΑΓ, ἐπεὶ ἀπὸ τᾶς αὐτᾶς γραμμᾶς ποτὶ τὸ [197] αὐτὸ ἐπίπεδον ἀμφότερα ὀρθά ἐντι· ἐφαρμόζει οὖν καὶ τὸ τμᾶμα τὸ ὑπὸ τοῦ ἐπιπέδου ἀποτεμνόμενον τοῦ κατὰ τὰν ΝΖ ἀπὸ τοῦ σφαιροειδέος τὸ ἐπὶ τὰ αὐτὰ τῷ Ε τῷ ἑτέρῳ τμάματι τῷ ἀποτεμνομένῳ ἀπὸ τοῦ ἑτέρου σφαιροειδέος ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὰν ΑΓ ἐπὶ τὰ αὐτὰ τῷ Β καὶ τὸ λοιπὸν τμᾶμα ἐπὶ τὸ λοιπὸν καὶ αἱ ἐπιφάνειαι τῶν τμαμάτων ἐπὶ τὰς ἐπιφανείας. Πάλιν δὲ καὶ τεθείσας τᾶς ΕΗ ἐπὶ τὰν ΒΔ οὕτως, ὥστε τὸ μὲν Ε κατὰ τὸ Δ κεῖσθαι, τὸ δὲ Η κατὰ τὸ Β, τὰν δὲ μεταξὺ τῶν Ν, Ζ σαμείων γραμμὰν ἐπὶ τὰν μεταξὺ τῶν Α, Γ σαμείων, δῆλον ὡς αἵ τε τῶν ὀξυγωνίων κώνων τομαὶ ἐφαρμοξοῦντι ἐπ᾿ ἀλλάλας, καὶ τὸ μὲν Ζ ἐπὶ τὸ Γ πεσεῖται, τὸ δὲ Ν ἐπὶ τὸ Α. Ὁμοίως καὶ τὸ ἐπίπεδον τὸ κατὰ τὰν ΝΖ ἐφαρμόζει τῷ ἐπιπέδῳ τῷ κατὰ τὰν ΑΓ, καὶ τῶν τμαμάτων τῶν ἀποτεμνομένων ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὰν ΝΖ τὸ μὲν ἐπὶ τὰ αὐτὰ τῷ Η ἐφαρμόζει τῷ τμάματι τῷ ἀποτεμνομένῳ ὑπὸ τοῦ ἐπιπέδου τοῦ κατὰ τὰν ΑΓ ἐπὶ τὰ αὐτὰ τῷ Β, τὸ δὲ ἐπὶ τὰ αὐτὰ τῷ Ε τῷ ἐπὶ τὰ αὐτὰ τῷ Δ. Ἐπεὶ δὲ τὸ αὐτὸ τμᾶμα ἐφ᾿ ἑκάτερον τῶν τμαμάτων ἐφαρμόζει, δῆλον ὅτι ἴσα ἐντὶ τὰ τμάματα· διὰ ταὐτὰ δὲ καὶ αἱ ἐπιφάνειαι.
   ιθ΄.
   Τμάματος δοθέντος ὁποτερουοῦν τῶν κωνοειδέων ἀποτετμαμένου ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα ἢ τῶν σφαιροειδέων ὁποτερουοῦν μὴ μείζονος ἡμίσους τοῦ σφαιροειδέος ὁμοίως ἀποτεμνομένου δυνατόν ἐστι σχῆμα στερεὸν ἐγγράψαι καὶ ἄλλο περιγράψαι ἐκ κυλίνδρων ἴσον ὕψος ἐχόντων συγκείμενον, ὥστε τὸ περιγραφόμενον σχῆμα τοῦ [198] ἐγγραφέντος ἐλάσσονι ὑπερέχειν παντὸς τοῦ προτεθέντος στερεοῦ μεγέθεος.
   Δεδόσθω τμᾶμα, οἷον τὸ ΑΒΓ, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος τοῦ μὲν τμάματος τομὰ ἔστω ἁ ΑΒΓ κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμακότος τὸ τμᾶμα ἁ ΑΓ εὐθεῖα, ἄξων δὲ ἔστω τοῦ τμάματος καὶ διάμετρος τᾶς τομᾶς ἁ ΒΔ. Ἐπεὶ οὖν ὑπόκειται τὸ ἀποτέμνον ἐπίπεδον ὀρθὸν εἶμεν ποτὶ τὸν ἄξονα, ἁ τομὰ κύκλος ἐστί, διάμετρος δὲ αὐτοῦ ἁ ΓΑ. Ἀπὸ δὲ τοῦ κύκλου τούτου κύλινδρος ἔστω ἄξονα ἔχων τὰν ΒΔ· πεσεῖται δὲ ἁ ἐπιφάνεια αὐτοῦ ἐκτὸς τοῦ τμάματος, ἐπεί ἐστιν ἤτοι κωνοειδὲς ἢ σφαιροειδὲς μὴ μεῖζον τοῦ ἡμίσεος τοῦ σφαιροειδέος. Τοῦ δὴ κυλίνδρου τούτου ἀεὶ δίχα τεμνομένου ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα ἐσσεῖταί ποτε τὸ καταλειπόμενον ἔλασσον τοῦ προτεθέντος στερεοῦ μεγέθεος· ἔστω δὴ τὸ καταλελειμμένον [199] ἀπ᾿ αὐτοῦ κύλινδρος ὁ ἔχων βάσιν τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΕΔ, ἐλάσσων τοῦ προτεθέντος στερεοῦ μεγέθεος. Διαιρήσθω δὴ ἁ ΒΔ ἐς τὰς ἴσας τᾷ ΕΔ κατὰ τὰ Ρ, Ο, Π, Ξ, καὶ ἀπὸ τᾶν διαιρέσιων ἄχθων εὐθεῖαι παρὰ τὰν ΑΓ ἔστε ποτὶ τὰν τοῦ κώνου τομάν, ἀπὸ δὲ τᾶν ἀχθεισᾶν ἐπίπεδα ἀνεστακέτω ὀρθὰ ποτὶ τὰν ΒΔ· ἐσσοῦνται δὴ αἱ τομαὶ κύκλοι τὰ κέντρα ἔχοντες ἐπὶ τᾶς ΒΔ, Ἀφ᾿ ἑκάστου δὴ τῶν κύκλων δύο κύλινδροι ἀναγεγράφθων ἑκάτερος ἔχων ἄξονα ἴσον τῷ ΕΔ, ὁ μὲν ἐπὶ τὰ αὐτὰ τοῦ κύκλου, ἐφ᾿ ἅ ἐστι τὸ Δ, ὁ δὲ ἐπὶ τὰ αὐτά, ἐφ᾿ ἅ ἐστι τὸ Β· ἐσσεῖται δή τι ἐν τῷ τμάματι σχῆμα στερεὸν ἐγγεγραμμένον ἐκ τῶν κυλίνδρων συγκείμενον τῶν ἐπὶ τὰ αὐτὰ ἀναγραφέντων, ἐφ᾿ ἅ ἐστι τὸ Δ, καὶ ἄλλο περιγεγραμμένον συγκείμενον ἐκ τῶν κυλίνδρων τῶν ἐπὶ τὰ αὐτὰ ἀναγραφέντων, ἐφ᾿ ἃ τὸ Β ἐστίν. Λοιπὸν δέ ἐστι δεῖξαι ὅτι τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου ὑπερέχει ἐλάσσονι τοῦ προτεθέντος στερεοῦ μεγέθεος. Ἕκαστος δὴ τῶν κυλίνδων τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι ἴσος ἐστὶ τῷ κυλίνδρῳ τῷ ἀπὸ τοῦ αὐτοῦ κύκλου ἀναγραφομένῳ ἐπὶ τὰ αὐτὰ τῷ Β, ὡς ὁ μὲν ΘΗ τῷ ΘΙ, ὁ δὲ ΚΛ τῷ ΚΜ, καὶ οἱ ἄλλοι ὡσαύτως· καὶ πάντες δὴ οἱ κύλινδροι πάντεσσιν ἴσοι ἐντί. Δῆλον οὖν ὅτι τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου ὑπερέχει τῷ κυλίνδρῳ τῷ βάσιν ἔχοντι τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΕΔ· οὗτος δέ ἐστιν ἐλάσσων τοῦ προτεθέντος στερεοῦ μεγέθεος.

[200]    κ΄.    Τμάματος δοθέντος ὁποτερουοῦν τῶν κωνοειδέων ἀποτετμαμένου ἐπιπέδῳ μὴ ὀρθῷ ποτὶ τὸν ἄξονα ἢ τῶν σφαιροειδέων ὁποτερουοῦν μὴ μείζονος ἡμίσεος τοῦ σφαιροειδέος ὁμοίως ἀποτετμαμένου δυνατόν ἐστιν εἰς τὸ τμᾶμα σχῆμα στερεὸν ἐγγράψαι καὶ ἄλλο περιγράψαι ἐκ κυλίνδρων τόμων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφομένου ὑπερέχειν ἐλάσσονι παντὸς τοῦ προτεθέντος στερεοῦ μεγέθεος.
   Δεδόσθω τμᾶμα, οἷον εἴρηται, τμαθέντος δὲ τοῦ σχήματος ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ ἐπίπεδον τὸ ἀποτετμακὸς τὸ δοθὲν τμᾶμα τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμακότος τὸ τμᾶμα ἁ ΓΑ εὐθεῖα. Ἐπεὶ οὖν ὑπόκειται τὸ ἐπίπεδον τὸ ἀποτετμακὸς τὸ τμᾶμα μὴ εἶμεν ὀρθὸν ποτὶ τὸν [201] ἄξονα, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ ΑΓ. Ἔστω δὴ παράλληλος τᾷ ΑΓ ἁ ΦΥ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς, ἐπιψαυέτω δὲ κατὰ τὸ Β, καὶ ἀπὸ τᾶς ΦΥ ἀνεστακέτω ἐπίπεδον παράλληλον τῷ κατὰ τὰν ΑΓ· ἐπιψαύσει δὲ τοῦτο τοῦ σχήματος κατὰ τὸ Β· καὶ εἰ μέν ἐστι τὸ τμᾶμα ὀρθογωνίου κωνοειδέος, ἀπὸ τοῦ Β ἄχθω παρὰ τὸν ἄξονα ἁ ΒΔ, εἰ δὲ ἀμβλυγωνίου, ἀπὸ τᾶς κορυφᾶς τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδὲς εὐθεῖα ἀχθεῖσα ἐπὶ τὸ Β ἐκβεβλήσθω ἁ ΒΔ, εἰ δὲ σφαιροειδέος, ἐπὶ τὸ Β ἀχθεῖσα εὐθεῖα ἀπολελάφθω ἁ ΒΔ· δῆλον δὲ ὅτι τέμνει ἁ ΒΔ δίχα τὰν ΑΓ· ἐσσεῖται οὖν τὸ μὲν Β κορυφὰ τοῦ τμάματος, ἁ δὲ ΒΔ ἄξων. Ἔστιν δή τις ὀξυγωνίου κώνου τομὰ περὶ διάμετρον τὰν ΑΓ, καὶ γραμμὰ ἁ ΒΔ ἀπὸ τοῦ κέντρου ἀνεστάκουσα ἐν ὀρθῷ ἐπιπέδῳ ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, διὰ τᾶς ἑτέρας διαμέτρου ἐόντος τοῦ ἐπιπέδου· δυνατὸν οὖν ἐστιν κύλινδρον εὑρεῖν ἄξονα ἔχοντα τὰν ΒΔ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ περὶ διάμετρον τὰν ΑΓ· πεσεῖται δὲ ἁ ἐπιφάνεια αὐτοῦ ἐκτὸς τοῦ τμάματος, ἐπεί ἐστιν ἤτοι κωνοειδέος ἢ σφαιροειδέος τμᾶμα καὶ οὐ μεῖζόν ἐστιν ἡμίσεος τοῦ σφαιροειδέος. Ἐσσεῖται δή τις κυλίνδρου τόμος βάσιας μὲν ἔχων τὰν τοῦ ὀξυγωνίου κώνου τομὰν τὰν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ· τοῦ οὖν τόμου δίχα τεμνομένου ἐπιπέδοις παραλλήλοις τῷ ἐπιπέδῳ τῷ κατὰ τὰν ΑΓ ἐσσεῖται τὸ καταλειπόμενον ἔλασσον τοῦ προτεθέντος στερεοῦ μεγέθεος. Ἔστω τόμος βάσιν μὲν ἔχων τὰν τοῦ ὀξυγωνίου κώνου τομὰν τὰν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΕΔ, ἐλάσσων τοῦ προτεθέντος στερεοῦ μεγέθεος. Διῃρήσθω δὴ ἁ ΔΒ ἐς τὰς ἴσας τᾷ ΔΕ, καὶ ἀπὸ τᾶν διαιρέσιων ἄχθων [202] εὐθεῖαι παρὰ τὰν ΑΓ ἔστε ποτὶ τὰν τοῦ κώνου τομάν, ἀπὸ δὲ τᾶν ἀχθεισᾶν ἐπίπεδα ἀνεστακότων παράλληλα τῷ κατὰ τὰν ΑΓ ἐπιπέδῳ· τέμνοντι δὴ ταῦτα τὰν ἐπιφάνειαν τοῦ τμάματος, καὶ ἐσσοῦνται ὀξυγωνίων κώνων τομαὶ ὁμοῖαι τᾷ περὶ τὰν ΑΓ διάμετρον, ἐπεὶ παράλληλά ἐντι τὰ ἐπίπεδα. Ἀφ᾿ ἑκάστας δὴ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἀναγεγράφθων κυλίνδρου τόμοι δύο, ὁ μὲν ἐπὶ τὰ αὐτὰ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τῷ Δ, ὁ δὲ ἐπὶ τὰ αὐτὰ τῷ Β, ἄξονα ἔχοντες ἴσον τῷ ΔΕ· ἐσσοῦνται δή τινα σχήματα στερεά, τὸ μὲν ἐγγεγραμμένον ἐν τῷ τμάματι, τὸ δὲ περιγεγραμμένον, ἐκ κυλίνδρου τόμων ἴσον ὕψος ἐχόντων συγκείμενα. Λοιπὸν δέ ἐστι δεῖξαι ὅτι τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου ἐλάσσονι ὑπερέχει τοῦ προτεθέντος στερεοῦ μεγέθεος. Δειχθήσεται δὲ ὁμοίως τῷ προτέρῳ ὅτι τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου ὑπερέχει τῷ τόμῳ τῷ βάσιν μὲν ἔχοντι τὰν τοῦ ὀξυγωνίου κώνου τομὰν τὰν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΕΔ· οὗτος δέ ἐστιν ἐλάσσων τοῦ προτεθέντος στερεοῦ μεγέθεος.
   κα΄.
   Τούτων προγεγραμμένων ἀποδεικνύωμες τὰ προβεβλημένα τῶν σχημάτων.
   Πᾶν τμᾶμα ὀρθογωνίου κωνοειδέος ἀποτετμαμένον ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα ἡμιόλιόν ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   Ἔστω γὰρ τμᾶμα ὀρθογωνίου κωνοειδέος ἀποτετμαμένον ὀρθῷ ἐπιπέδῳ ποτὶ τὸν ἄξονα, καὶ τμαθέντος αὐτοῦ [203] ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος τᾶς μὲν ἐπιφανείας τομὰ ἔστω ἁ ΑΒΓ ὀρθογωνίου κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτέμνοντος τὸ τμᾶμα ἁ ΓΑ εὐθεῖα, ἄξων δὲ ἔστω τοῦ τμάματος ἁ ΒΔ, ἔστω δὲ καὶ κῶνος τὰν αὐτὰν βάσιν ἔχων τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, οὗ κορυφὰ τὸ Β. Δεικτέον ὅτι τὸ τμᾶμα τοῦ κωνοειδέος ἡμιόλιόν ἐστι τοῦ κώνου τούτου.
   Ἐκκείσθω γὰρ κῶνος ὁ Ψ ἡμιόλιος ἐὼν τοῦ κώνου, οὗ βάσις ὁ περὶ διάμετρον τὰν ΑΓ, ἄξων δὲ ἁ ΒΔ, ἔστω δὲ καὶ κύλινδρος βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ· ἐσσεῖται οὖν ὁ Ψ κῶνος ἡμίσεος τοῦ κυλίνδρου [ἐπείπερ ἡμιόλιός ἐστιν ὁ Ψ κῶνος τοῦ αὐτοῦ κώνου]· λέγω ὅτι τὸ τμᾶμα τοῦ κωνοειδέος ἴσον ἐστὶ τῷ Ψ κώνῳ.
   Εἰ γὰρ μή ἐστιν ἴσον, ἤτοι μεῖζόν ἐντι ἢ ἔλασσον. Ἔστω δὴ πρότερον, εἰ δυνατόν, μεῖζον. Ἐγγεγράφθω δὴ σχῆμα στερεὸν εἰς τὸ τμᾶμα, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι [204] ἢ ἁλίκῳ ὑπερέχει τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου, καὶ ἔστω τῶν κυλίνδρων, ἐξ ὧν σύγκειται τὸ περιγραφὲν σχῆμα, μέγιστος μὲν ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΕΔ, ἐλάχιστος δὲ ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΣΤ, ἄξονα δὲ τὰν ΒΙ, τῶν δὲ κυλίνδρων, ἐξ ὧν σύγκειται τὸ ἐγγραφὲν σχῆμα, μέγιστος μὲν ἔστω ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΚΛ, ἄξονα δὲ τὰν ΔΕ, ἐλάχιστος δὲ ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΣΤ, ἄξονα δὲ τὰν ΘΙ, ἐκβεβλήσθω δὲ τὰ ἐπίπεδα πάντων τῶν κυλίνδρων ποτὶ τὰν ἐπιφάνειαν τοῦ κυλίνδρου τοῦ βάσιν ἔχοντος τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ· ἐσσεῖται δὴ ὁ ὅλος κύλινδρος διῃρημένος εἰς κυλίνδρους τῷ μὲν πλήθει ἴσους τοῖς κυλίνδροις τοῖς ἐν τῷ περιγεγραμμένῳ σχήματι, τῷ δὲ μεγέθει ἴσους τῷ μεγίστῳ αὐτῶν. Καὶ ἐπεὶ τὸ περιγεγραμμένον σχῆμα περὶ τὸ τμᾶμα ἐλάσσονι ὑπερέχει τοῦ ἐγγεγραμμένου σχήματος ἢ τὸ τμᾶμα τοῦ κώνου, δῆλον ὅτι καὶ τὸ ἐγγεγραμμένον [205] σχῆμα ἐν τῶ τμάματι μεῖζόν ἐστι τοῦ Ψ κώνου. Ὁ δὴ πρῶτος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΚΕ δυνάμει· οὗτος δέ ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει ἁ ΒΔ ποτὶ τὰν ΒΕ καὶ τῷ ὃν ἔχει ἁ ΔΑ ποτὶ τὰν ΕΞ. Ὁμοίως δὲ δειχθήσεται καὶ ὁ δεύτερος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΕΖ ποτὶ τὸν δεύτερον κύλινδρον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΠΕ, τουτέστιν ἁ ΔΑ, ποτὶ τὰν ΖΟ, καὶ τῶν ἄλλων κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἐχόντων ἴσον τᾷ ΔΕ ποτὶ ἕκαστον τῶν κυλίνδρων τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι ἄξονα ἐχόντων τὸν αὐτὸν ἕξει τοῦτον τὸν λόγον, ὃν ἁ ἡμίσεια τᾶς διαμέτρου τᾶς βάσιος αὐτοῦ ποτὶ τὰν ἀπολελαμμέναν ἀπ᾿ αὐτᾶς μεταξὺ τᾶν ΑΒ, ΒΔ εὐθειᾶν· καὶ πάντες οὖν οἱ κύλινδροι οἱ ἐν τῷ κυλίνδρῳ, οὗ βάσις μέν ἐστιν ὁ κύκλος ὁ περὶ διάμετρον τὰν ΑΓ, ἄξων δὲ [ἐστὶν] ἁ ΔΒ εὐθεῖα, ποτὶ πάντας τοὺς κυλίνδρους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πᾶσαι αἱ εὐθεῖαι αἱ ἐκ τῶν κέντρων τῶν κύκλων, οἵ ἐντι βάσιες τῶν εἰρημένων κυλίνδρων, ποτὶ πάσας τὰς εὐθείας τὰς ἀπολελαμμένας ἀπ᾿ αὐτᾶν μεταξὺ τᾶν ΑΒ, ΒΔ. Αἱ δὲ εἰρημέναι εὐθεῖαι τῶν εἰρημένων χωρὶς τᾶς ΑΔ μείζονές ἐντι ἢ διπλάσιαι· ὥστε καὶ οἱ κύλινδροι πάντες οἱ ἐν τῷ [206] κυλίνδρῳ, οὗ ἄξων ἁ ΔΒ, μείζονές ἐντι ἢ διπλάσιοι τοῦ ἐγγεγραμμένου σχήματος· πολλῷ ἄρα καὶ ὁ ὅλος κύλινδρος, οὗ ἄξων ἁ ΔΒ, μείζων ἐντὶ ἢ διπλασίων τοῦ ἐγγεγραμμένου σχήματος. Τοῦ δὲ Ψ κώνου ἦν διπλασίων· ἔλασσον ἄρα τὸ ἐγγεγραμμένον σχῆμα τοῦ Ψ κώνου· ὅπερ ἀδύνατον· ἐδείχθη γὰρ μεῖζον. Οὐκ ἄρα ἐστὶν μεῖζον τὸ κωνοειδὲς τοῦ Ψ κώνου. Ὁμοίως δὲ οὐδὲ ἔλασσον· πάλιν γὰρ ἐγγεγράφθω τὸ σχῆμα καὶ περιγεγράφθω, ὥστε ὑπερέχειν [ἕκαστον] ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ Ψ κῶνος τοῦ κωνοειδέος, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Ἐπεὶ οὖν ἔλασσόν ἐστι τὸ ἐγγεγραμμένον σχῆμα τοῦ τμάματος, καὶ τὸ ἐγγραφὲν τοῦ περιγραφέντος ἐλάσσονι λείπεται ἢ τὸ τμᾶμα τοῦ Ψ κώνου, δῆλον ὡς ἔλασσόν ἐστι τὸ περιγραφὲν σχῆμα τοῦ Ψ κώνου. Πάλιν δὲ ὁ πρῶτος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν τὸν αὐτὸν ἔχοντα ἄξονα τὰν ΕΔ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΑΔ τετράγωνον ποτὶ τὸ αὐτό, ὁ δὲ δεύτερος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΕΖ ποτὶ τὸν δεύτερον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΕΖ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΚΕ δυνάμει· οὗτος δέ ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει ἁ ΒΔ ποτὶ τὰν ΒΕ, καὶ τῷ ὃν ἔχει ἁ ΔΑ ποτὶ τὰν ΕΞ· καὶ τῶν ἄλλων κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἐχόντων ἴσον τᾷ ΔΕ ποτὶ ἕκαστον τῶν κυλίνδρων τῶν ἐν τῷ περιγεγραμμένῳ σχήματι [207] ἄξονα ἐχόντων τὸν αὐτὸν ἕξει τοῦτον τὸν λόγον, ὃν ἁ ἡμίσεια τᾶς διαμέτρου τᾶς βάσιος αὐτοῦ ποτὶ τὰν ἀπολελαμμέναν ἀπ᾿ αὐτᾶς μεταξὺ τᾶν ΑΒ, ΒΔ εὐθειᾶν· καὶ πάντες οὖν οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ, οὗ ἄξων ἐστὶν ἁ ΒΔ εὐθεῖα, ποτὶ πάντας τοὺς κυλίνδρους τοὺς ἐν τῷ περιγεγραμμένῳ σχήματι τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πᾶσαι αἱ εὐθεῖαι ποτὶ πάσας τὰς εὐθείας. Αἱ δὲ εὐθεῖαι πᾶσαι αἱ ἐκ τῶν κέντρων τῶν κύκλων, οἳ βάσιές ἐντι τῶν κυλίνδρων, τᾶν εὐθειᾶν πασᾶν τᾶν ἀπολελαμμενᾶν ἀπ᾿ αὐτᾶν σὺν τᾷ ΑΔ ἐλάσσονές ἐντι ἢ διπλάσιαι· δῆλον οὖν ὅτι καὶ οἱ κύλινδροι πάντες οἱ ἐν τῷ ὅλῳ κυλίνδρῳ ἐλάσσονές ἐντι ἢ διπλάσιοι τῶν κυλίνδρων τῶν ἐν τῷ περιγεγραμμένῳ σχήματι· ὁ ἄρα κύλινδρος ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ, ἐλάσσων ἐστὶν ἢ διπλασίων τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων ἢ διπλάσιος· τοῦ γὰρ Ψ κώνου διπλασίων ἐστί, τὸ δὲ περιγεγραμμένον σχῆμα ἔλαττον ἐδείχθη τοῦ Ψ κώνου. Οὐκ ἄρα ἐστὶν οὐδὲ ἔλασσον τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου. Ἐδείχθη δὲ ὅτι οὐδὲ μεῖζον· ἡμιόλιον ἄρα ἐστὶν τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   κβ΄.
   Καὶ τοίνυν εἴ κα μὴ ὀρθῷ ποτὶ τὸν ἄξονα ἐπιπέδῳ ἀποτμαθῇ τὸ τμᾶμα ἀπὸ τοῦ ὀρθογωνίου κωνοειδέος, ὁμοίως ἡμιόλιον ἐσσεῖται τοῦ ἀποτμάματος τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   Ἔστω τμᾶμα ὀρθογωνίου κωνοειδέος ἀποτετμαμένον, ὡς εἴρηται, καὶ τμαθέντος αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος [208] ὀρθῷ ποτὶ τὸ ἐπίπεδον τὸ ἀποτετμακὸς τὸ τμᾶμα τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ ὀρθογωνίου κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμακότος τὸ τμᾶμα ἁ ΑΓ εὐθεῖα, παρὰ δὲ τὰν ΑΓ ἁ ΦΥ ἐπιψαύουσα τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς κατὰ τὸ Β, καὶ ἁ ΒΔ ἄχθω παρὰ τὸν ἄξονα· τεμεῖ δὴ αὕτα δίχα τὰν ΑΓ· ἀπὸ δὲ τᾶς ΦΥ ἐπίπεδον ἀνεστακέτω παράλληλον τῷ κατὰ τὰν ΑΔ· ἐπιψαύσει δὴ τοῦτο τὸ κωνοειδὲς κατὰ τὸ Β, καὶ ἐσσεῖται τοῦ τμάματος κορυφὰ τὸ Β σαμεῖον, ἄξων δὲ ἁ ΒΔ. Ἐπεὶ οὖν τὸ ἐπίπεδον τὸ κατὰ τὰν ΑΓ οὐ ποτ᾿ ὀρθὰς ἐὸν τῷ ἄξονι τετμάκει τὸ κωνοειδές, ἁ τομά ἐστιν ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ μείζων ἁ ΑΓ. Ἐούσας δὴ ὀξυγωνίου κώνου τομᾶς περὶ διάμετρον τὰν ΓΑ καὶ γραμμᾶς τᾶς ΒΔ, ἅ ἐστιν ἀπὸ τοῦ κέντρου τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς ἀνεστάκουσα ἐν ἐπιπέδῳ ὀρθῷ ἀνεστακότι ἀπὸ τᾶς διαμέτρου ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, δυνατόν ἐστι κύλινδρον εὑρεῖν τὸν ἄξονα ἔχοντα ἐπ᾿ εὐθείας τᾷ ΒΔ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομά· δυνατὸν δέ ἐστι καὶ κῶνον εὑρεῖν κορυφὰν ἔχοντα τὸ Β σαμεῖον, οὗ ἐν τᾷ ἐπιφανείᾳ ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἐσσεῖται· ὥστε ἐσσεῖται τόμος κυλίνδρου τις βάσιν ἔχων τὰν τοῦ ὀξυγωνίου κώνου τομὰν τὰν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ, καὶ ἀπότμαμα κώνου βάσιν ἔχον τὰν αὐτὰν τῷ τε τόμῳ καὶ τῷ τμάματι, ἄξονα δὲ τὸν αὐτόν. Δεικτέον, ὅτι τὸ τοῦ κωνοειδέος τμᾶμα ἡμιόλιόν ἐστι τούτου τοῦ κώνου.
   Ἔστω δὴ ὁ Ψ κῶνος ἡμιόλιος τοῦ ἀποτμάματος τούτου· ἐσσεῖται δὴ ὁ τόμος τοῦ κυλίνδρου ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν διπλάσιος τοῦ Ψ

[209] κώνου· οὗτος γὰρ ἡμιόλιός ἐστι τοῦ ἀποτμάματος τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, τὸ δὲ ἀπότμαμα τοῦ κώνου τὸ εἰρημένον τρίτον μέρος ἐστὶ τοῦ τόμου τοῦ κυλίνδρου τοῦ βάσιν μὲν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν. Ἀναγκαῖον δή ἐστι τὸ τοῦ κωνοειδέος τμᾶμα ἴσον εἶμεν τῷ Ψ κώνῳ.
   Εἰ γὰρ μή ἐστιν ἴσον, ἤτοι μεῖζόν ἐστι ἢ ἔλασσον. Ἔστω δὴ πρότερον, εἰ δυνατόν, μεῖζον. Ἐγγεγράφθω δή τι εἰς τὸ τμᾶμα σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων τόμων ὕψος ἴσον ἐχόντων συγκείμενα, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου, καὶ διάχθω τὰ ἐπίπεδα τῶν τόμων ἔστε ποτὶ τὰν ἐπιφάνειαν τοῦ τόμου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν. Πάλιν δὴ ὁ πρῶτος τόμος τῶν ἐν τῷ ὅλῳ τόμῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον τόμον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ἀπὸ τᾶς ΑΔ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΚΕ· οἱ γὰρ τόμοι οἱ ἴσον ὕψος ἔχοντες

[210] τὸν αὐτὸν ἔχοντι λόγον ποτ᾿ ἀλλάλους ταῖς βάσεσιν, αἱ δέ βάσιες αὐτῶν, ἐπεὶ ὁμοῖαί ἐντι ὀξυγωνίων κώνων τομαί, τὸν αὐτὸν ἔχοντι λόγον, ὃν αἱ ὁμόλογοι διάμετροι αὐτῶν δυνάμει, ἡμίσειαι δέ ἐντι τῶν ὁμολόγων διαμέτρων αἱ ΑΔ, ΚΕ. Ὃν δὲ λόγον ἔχει ἁ ΑΔ ποτὶ τὰν ΚΕ δυνάμει, τοῦτον ἔχει ἁ ΒΔ ποτὶ τὰν ΒΕ μάκει, ἐπεὶ ἁ μὲν ΒΔ παρὰ τὰν διάμετρόν ἐστιν, αἱ δὲ ΑΔ, ΚΕ παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσαν· ὃν δὲ λόγον ἔχει ἁ ΒΔ ποτὶ τὰν ΒΕ, τοῦτον ἔχει ἁ ΑΔ ποτὶ τὰν ΕΞ· ἕξει οὖν ὁ πρῶτος τόμος τῶν ἐν τῷ ὅλῳ τόμῳ ποτὶ τὸν πρῶτον τόμον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν λόγον, ὃν ἁ ΑΔ ποτὶ τὰν ΕΞ· καὶ τῶν ἄλλων τόμων ἕκαστος τῶν ἐν τῷ ὅλῳ τόμῳ ἄξονα ἴσον ἐχόντων τᾷ ΔΕ ποτὶ ἕκαστον τῶν τόμων τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν ἄξονα ἐχόντων τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ἡμίσεια τᾶς διαμέτρου τᾶν βάσιων αὐτοῦ ποτὶ τὰν ἀπολελαμμέναν ἀπ᾿ αὐτᾶς μεταξὺ τᾶν ΑΒ, ΒΔ. Δειχθήσεται οὖν ὁμοίως τοῖς πρότερον τὸ μὲν ἐγγεγραμμένον [211] σχῆμα μεῖζον ἐὸν τοῦ Ψ κώνου, ὁ δὲ τοῦ κυλίνδρου τόμος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν μείζων ἐὼν ἢ διπλασίων τοῦ ἐγγεγραμμένου σχήματος· ὥστε καὶ τοῦ Ψ κώνου μείζων ἐσσεῖται ἢ διπλασίων. Οὐκ ἔστι δέ, ἀλλὰ διπλασίων. Οὐκ ἄρα ἐστὶ μεῖζον τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου. Διὰ τῶν αὐτῶν δὲ δειχθήσεται ὅτι οὐδὲ ἔλασσόν ἐστιν· δῆλον οὖν ὅτι ἴσον. Ἡμιόλιον ἄρα ἐστὶ τὸ τοῦ κωνοειδέος τμᾶμα τοῦ ἀποτμάματος τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   κγ΄.
   Εἴ κα τοῦ ὀρθογωνίου κωνοειδέος δύο τμάματα ἀποτμαθέωντι ἐπιπέδοις, τὸ μὲν ἕτερον ὀρθῷ ποτὶ τὸν ἄξονα, τὸ δὲ ἕτερον μὴ ὀρθῷ, ἔωντι δὲ οἱ τῶν τμαμάτων ἄξονες ἴσοι, ἴσα ἐσσοῦνται τὰ τμάματα.
   Ἀποτετμάσθω γὰρ ὀρθογωνίου κωνοειδέος δύο τμάματα, ὡς εἴρηται, τμαθέντος δὲ τοῦ κωνοειδέος ἐπιπέδῳ διὰ τοῦ ἄξονος [καὶ ἄλλῳ ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα] τοῦ μὲν κωνοειδέος ἔστω τομὰ ἁ ΑΒΓ ὀρθογωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ ΒΔ, τῶν δὲ ἐπιπέδων αἱ ΑΖ, ΕΓ εὐθεῖαι, τοῦ μὲν ὀρθοῦ ποτὶ τὸν ἄξονα ἁ ΕΓ, τοῦ δὲ μὴ ὀρθοῦ ἁ ΖΑ, ἄξονες δὲ ἔστων τῶν τμαμάτων αἱ ΒΘ, ΚΛ ἴσαι ἀλλάλαις, κορυφαὶ δὲ τὰ Β, Λ· δεικτέον ὅτι ἴσον ἐστὶ τὸ τμᾶμα τοῦ κωνοειδέος, οὗ κορυφὰ τὸ Β, τῷ τμάματι τοῦ κωνοειδέος, οὗ κορυφὰ τὸ Λ.
   Ἐπεὶ γὰρ ἀπὸ τᾶς αὐτᾶς ὀρθογωνίου κώνου τομᾶς δύο τμάματά ἐντι ἀφῃρημένα τό τε ΑΛΖ καὶ τὸ ΕΒΓ, καί ἐντι αὐτῶν αἱ διάμετροι ἴσαι αἱ ΚΛ, ΒΘ, ἴσον ἐστὶ τὸ τρίγω    νον [212] τὸ ΑΛΚ τῷ ΕΘΒ· δέδεικται γὰρ ὅτι τὸ ΑΛΖ τρίγωνον ἴσον ἐστὶ τῷ ΕΒΓ τριγώνῳ. Ἄχθω δὴ ἁ ΑΧ κάθετος ἐπὶ τὰν ΚΛ ἐκβληθεῖσαν. Καὶ ἐπεὶ ἴσαι αἱ ΒΘ, ΚΛ, ἴσαι καὶ αἱ ΕΘ, ΑΧ. Ἔστω δὴ ἐν τῷ τμάματι, οὗ κορυφὰ τὸ Β, κῶνος ἐγγεγραμμένος τὰν αὐτὰν βάσιν ἔχων τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, ἐν δὲ τῷ τμάματι, οὗ κορυφὰ τὸ Λ, ἀπότμαμα κώνου τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, ἄχθω δὲ ἀπὸ τοῦ Λ κάθετος ἐπὶ τὰν ΑΖ ἁ ΛΝ· ἐσσεῖται δὴ αὕτα ὕψος τοῦ ἀποτμάματος τοῦ κώνου, οὗ κορυφὰ τὸ Λ. Τὸ δὲ ἀπότμαμα τοῦ κώνου, οὗ κορυφὰ τὸ Λ, καὶ ὁ κῶνος, οὗ κορυφὰ τὸ Β, τὸν συγκείμενον λόγον ἔχοντι ποτ᾿ ἄλλαλα ἔκ τε τοῦ τῶν βάσιων λόγου καὶ ἐκ τοῦ τῶν ὑψέων· τὸν συγκείμενον οὖν ἔχοντι λόγον ἔκ τε τοῦ ὃν ἔχει τὸ περιεχόμενον χωρίον ὑπὸ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τᾶς περὶ διάμετρον τὰν ΑΖ ποτὶ τὸν κύκλον τὸν περὶ διάμετρον τὰν ΕΓ, καὶ ἐκ τοῦ ὃν ἔχει ἁ ΝΛ ποτὶ τὰν ΒΘ. Τὸ δὲ χωρίον τὸ περιεχόμενον ὑπὸ τᾶς τοῦ ὀξυγωνίου [213] κώνου τομᾶς ποτὶ τὸν αὐτὸν κύκλον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν διαμέτρων ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΕΓ [ἔχει καὶ τὸ ἀπότμαμα τοῦ κώνου, οὗ κορυφὰ τὸ Λ, πρὸς τὸν κῶνον, οὗ κορυφὰ τὸ Β, τὸν συγκείμενον λόγον ἔκ τε τοῦ ὃν ἔχει ἁ ΚΑ ποτὶ τὰν ΕΘ, καὶ τοῦ ὃν ἔχει ἁ ΝΛ ποτὶ τὰν ΒΘ· ἁ μὲν γὰρ ΚΑ ἡμισέα ἐντὶ τᾶς διαμέτρου τᾶς βάσιος τᾶς τοῦ ἀποτμήματος τοῦ κώνου, οὗ κορυφὰ τὸ Λ, ἁ δὲ ΕΘ ἡμισέα τᾶς διαμέτρου τᾶς βάσεως τοῦ κώνου, αἱ δὲ ΛΝ, ΒΘ ὕψεά ἐντι αὐτῶν. Ἔχει δὲ ἁ ΛΝ ποτὶ τὰν ΒΘ τὸν αὐτὸν λόγον, ὃν καὶ ποτὶ τὰν ΚΛ, ἐπεὶ ἁ ΒΘ ἴση ἐστὶ τᾷ ΚΛ. Ἔχει δὲ καὶ ἁ ΛΝ ποτὶ τὰν ΚΛ, ὃν ἁ ΧΑ ποτὶ τὰν ΑΚ]· ἔχοι οὖν κα καὶ τὸ ἀπότμαμα τοῦ κώνου ποτὶ τὸν κῶνον τὸν συγκείμενον λόγον ἔκ τε τοῦ ὃν ἔχει ἁ ΑΚ ποτὶ τὰν ΑΧ· ἴσα γάρ ἐστιν ἁ ΑΧ τᾷ ΕΘ, καὶ ἐκ τοῦ ὃν ἔχει ἁ ΛΝ ποτὶ τὰν ΒΘ. Ὁ δὲ [ἐκ] τῶν εἰρημένων λόγων, ὁ τᾶς ΑΚ ποτὶ ΑΧ, ὁ αὐτός ἐστι τῷ τᾶς ΛΚ ποτὶ ΛΝ· τὸ ἄρα ἀπότμαμα ποτὶ τὸν κῶνον λόγον ἔχει, ὃν ἁ ΛΚ ποτὶ τὰν ΛΝ, καὶ ὃν ἔχει ἁ ΛΝ ποτὶ τὰν ΒΘ. Ἴσα δὲ ἁ ΒΘ τᾷ ΚΛ· δῆλον οὖν ὅτι ἴσον ἐστὶ τὸ ἀπότμαμα τοῦ κώνου, οὗ κορυφὰ τὸ Λ, τῷ κώνῳ, οὗ κορυφὰ τὸ Β. Φανερὸν οὖν ὅτι καὶ τὰ τμάματα ἴσα ἐντί, ἐπεὶ τὸ μὲν ἕτερον αὐτῶν ἡμιόλιόν ἐστι τοῦ κώνου, τὸ δὲ ἕτερον ἡμιόλιον τοῦ ἀποτμάματος τοῦ κώνου ἴσων ἐόντων.
   κδ΄.
   Εἴ κα τοῦ ὀρθογωνίου κωνοειδέος δύο τμάματα ἀποτμαθέωντι ἐπιπέδοις ὁπωσοῦν ἀγμένοις, τὰ τμάματα ποτ᾿ ἄλλαλα τὸν αὐτὸν ἑξοῦντι λόγον τοῖς τετραγώνοις τοῖς ἀπὸ τῶν ἀξόνων αὐτῶν.

[214]    Ἀποτετμάσθω γὰρ τοῦ ὀρθογωνίου κωνοειδέος δύο τμάματα, ὡς ἔτυχεν, ἔστω δὲ τῷ μὲν τοῦ ἑτέρου τμάματος ἄξονι ἴσα ἁ Κ, τῷ δὲ τοῦ ἑτέρου ἴσα ἁ Λ· δεικτέον ὅτι τὰ τμάματα τὸν αὐτὸν ἔχοντι λόγον ποτ᾿ ἄλλαλα τοῖς ἀπὸ τᾶν Κ, Λ τετραγώνοις.
   Τμαθέντος δὴ τοῦ κωνοειδέος ἐπιπέδῳ διὰ τοῦ ἄξονος τοῦ τμάματος ἔστω τομὰ ἁ ΑΒΓ ὀρθογωνίου κώνου τομά, ἄξων δὲ ἁ ΒΔ, καὶ ἀπολελάφθω ἁ ΒΔ τᾷ Κ ἴσα, καὶ διὰ τοῦ Δ ἐπίπεδον ἐκβεβλήσθω ὀρθὸν ποτὶ τὸν ἄξονα· τὸ δὴ τμᾶμα τοῦ κωνοειδέος τὸ βάσιν μὲν ἔχον τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ ἴσον ἐστὶ τῷ τμάματι τῷ ἄξονα ἔχοντι ἴσον τᾷ Κ. Εἰ μὲν οὖν καὶ ἁ Κ ἴσα ἐστὶ τᾷ Λ, φανερὸν ὅτι καὶ τὰ τμάματα ἴσα ἐσσοῦνται ἀλλάλοις· ἑκάτερον γὰρ αὐτῶν ἴσον τῷ αὐτῷ· καὶ τὰ τετράγωνα τὰ ἀπὸ τᾶν Κ, Λ ἴσα· ὥστε τὸν αὐτὸν ἑξοῦντι λόγον τὰ τμάματα τοῖς τετραγώνοις τοῖς ἀπὸ τῶν ἀξόνων. [215] Εἰ δὲ μὴ ἴσα ἐστὶν ἁ Λ τᾷ Κ, ἔστω ἁ Λ ἴσα τᾷ ΒΘ, καὶ διὰ τοῦ Θ ἐπίπεδον ἄχθω ὀρθὸν ποτὶ τὸν ἄξονα· τὸ δὴ τμᾶμα τὸ βάσιν ἔχον τὸν κύκλον τὸν περὶ διάμετρον τὰν ΕΖ, ἄξονα δὲ τὰν ΒΘ, ἴσον ἐστὶ τῷ τμάματι τῷ ἔχοντι ἄξονα ἴσον τᾷ Λ. Ἐγγεγράφθωσαν δὴ κῶνοι βάσιας μὲν ἔχοντες τοὺς κύκλους τοὺς περὶ διαμέτρους τὰς ΑΓ, ΕΖ, κορυφὰν δὲ τὸ Β σαμεῖον· ὁ δὴ κῶνος ὁ ἔχων ἄξονα τὰν ΒΔ ποτὶ τὸν κῶνον τὸν ἔχοντα ἄξονα τὰν ΒΘ τὸν συγκείμενον ἔχει λόγον ἔκ τε τοῦ ὃν ἔχει ἁ ΑΔ ποτὶ τὰν ΘΕ δυνάμει, καὶ ἐκ τοῦ ὃν ἔχει ἁ ΔΒ ποτὶ τὰν ΒΘ μάκει. Ὃν δὲ λόγον ἔχει ἁ ΔΑ ποτὶ τὰν ΘΕ δυνάμει, τοῦτον ἔχει ἁ ΒΔ ποτὶ τὰν ΒΘ μάκει· ὁ ἄρα κῶνος ὁ ἔχων ἄξονα τὰν ΒΔ ποτὶ τὸν κῶνον τὸν ἔχοντα ἄξονα τὰν ΒΘ τὸν συγκείμενον ἔχει λόγον ἔκ τε τοῦ ὃν ἔχει ἁ ΔΒ ποτὶ τὰν ΘΒ, καὶ ἐκ τοῦ ὃν ἔχει ἁ ΔΒ ποτὶ τὰν ΒΘ· οὗτος δέ ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΔΒ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΒ. Ὃν δὲ λόγον ἔχει ὁ κῶνος ὁ ἄξονα ἔχων τὰν ΒΔ ποτὶ τὸν κῶνον τὸν ἄξονα ἔχοντα τὰν ΘΒ, τοῦτον ἔχει τὸν λόγον τὸ τμᾶμα τοῦ κωνοειδέος τὸ ἄξονα ἔχον τὰν ΔΒ ποτὶ τὸ τμᾶμα τὸ ἄξονα ἔχον τὰν ΘΒ [ἑκάτερον γὰρ ἡμιόλιόν ἐστιν]. Καὶ ἔστιν τῷ μὲν τμάματι τῷ ἄξονα ἔχοντι τὰν ΒΔ ἴσον τὸ τμᾶμα τοῦ κωνοειδέος τὸ ἄξονα ἔχον ἴσον τᾷ Κ, τῷ δὲ τμάματι τῷ ἄξονα ἔχοντι τὰν ΘΒ ἴσον τὸ τμᾶμα τοῦ κωνοειδέος τὸ ἄξονα ἔχον ἴσον τᾷ Λ, καὶ τᾷ μὲν ΒΔ ἴσα ἁ Κ, τᾷ δὲ ΘΒ ἴσα ἁ Λ· δῆλον οὖν ὅτι τὸ τμᾶμα τοῦ κωνοειδέος τὸ ἄξονα ἔχον ἴσον τᾷ Κ τὸν αὐτὸν ἔχει λόγον ποτὶ τὸ τμᾶμα τοῦ κωνοειδέος τὸ ἄξονα ἔχον ἴσον τᾷ Λ, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς Κ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς Λ.

[216]    κε΄.
   Πᾶν τμᾶμα ἀμβλυγωνίου κωνοειδέος ἀποτετμαμένον ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον τοῦτον ἔχει τὸν λόγον, ὃν ἔχει ἁ συναμφοτέραις ἴσα τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ τριπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι ποτὶ τὰν ἴσαν ἀμφοτέραις τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ διπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι.
   Ἔστω τι τμᾶμα ἀμβλυγωνίου κωνοειδέος ἀποτετμαμένον ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα, καὶ τμαθέντος αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ἁ τομὰ ἔστω αὐτοῦ μὲν τοῦ κωνοειδέος ἁ ΑΒΓ ἀμβλυγωνίου κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτέμνοντος τὸ τμᾶμα ἁ ΑΓ εὐθεῖα, ἄξων δὲ ἔστω τοῦ τμάματος ἁ ΒΔ, ἁ δὲ ποτεοῦσα τῷ ἄξονι ἔστω ἁ ΒΘ καὶ τᾷ ΒΘ ἴσα ἁ ΖΘ καὶ ἁ ΖΗ. Δεικτέον ὅτι τὸ τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν λόγον ἔχει, ὃν ἁ ΗΔ ποτὶ τὰν ΖΔ.
   Ἔστω δὴ κύλινδρος τὰν αὐτὰν βάσιν ἔχων τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, πλευραὶ δὲ αὐτοῦ ἔστωσαν αἱ ΦΑ, ΓΥ, ἔστω δὲ καὶ κῶνός τις, ἐν ᾧ τὸ Ψ, καὶ ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὰν ΒΔ τοῦτον ἐχέτω τὸν λόγον, ὃν ἔχει ἁ ΗΔ ποτὶ τὰν ΔΖ· φαμὶ δὴ τὸ τμᾶμα τοῦ κωνοειδέος ἴσον εἶμεν τῷ Ψ κώνῳ.
   Εἰ γὰρ μή ἐστιν ἴσον, ἤτοι μεῖζον ἢ ἔλασσόν ἐστιν. Ἔστω πρότερον, εἰ δυνατόν, μεῖζον. Ἐγγεγράφθω δὴ εἰς τὸ τμᾶμα σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ

[217] κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου, διάχθω δὲ τὰ ἐπίπεδα πάντων τῶν κυλίνδρων ποτὶ τὰν ἐπιφάνειαν τοῦ κυλίνδρου τοῦ βάσιν μὲν ἔχοντος τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΔ· ἐσσεῖται δὴ ὅλος ὁ κύλινδρος διῃρημένος εἰς κυλίνδρους τῷ μὲν πλήθει ἴσους τοῖς κυλίνδροις τοῖς ἐν τῷ περιγεγραμμένῳ σχήματι, τῷ δὲ μεγέθει ἴσους τῷ μεγίστῳ αὐτῶν. Καὶ ἐπεὶ ἐλάσσονι ὑπερέχει τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου ἢ τὸ τμᾶμα τοῦ Ψ κώνου, καὶ μεῖζόν ἐστι τὸ περιγεγραμμένον σχῆμα τοῦ τμάματος, δῆλον ὅτι καὶ τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστι τοῦ Ψ κώνου. Ἔστω δὴ τρίτον μέρος τᾶς ΒΔ ἁ ΒΡ· ἐσσεῖται οὖν ἁ ΗΔ τριπλασία τᾶς ΘΡ. Καὶ ἐπεὶ ὁ μὲν κύλινδρος ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα [218] δὲ τὰν ΒΔ, ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΗΔ ποτὶ τὰν ΘΡ, ἔχει δὲ καὶ ὁ εἰρημένος κῶνος ποτὶ τὸν Ψ κῶνον, ὃν ἁ ΖΔ ποτὶ τὰν ΗΔ, ἕξει ἄρα μεγεθέων τριῶν ἀνομοίως τῶν λόγων τεταγμένων τὸν αὐτὸν λόγον ὁ κύλινδρος ὁ εἰρημένος ποτὶ τὸν Ψ κῶνον, ὃν ἁ ΖΔ ποτὶ τὰν ΘΡ. Ἔστωσαν δὲ γραμμαὶ κείμεναι, ἐφ᾿ ἇν τὰ Ξ, τῷ μὲν πλήθει ἴσαι τοῖς τμαμάτεσσιν τοῖς ἐν τᾷ ΒΔ εὐθείᾳ, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ ΖΒ, καὶ παρ᾿ ἑκάσταν αὐτᾶν παραπεπτωκέτω χωρίον ὑπερβάλλον εἴδει τετραγώνῳ, καὶ τὸ μὲν μέγιστον ἔστω ἴσον τῷ ὑπὸ ΖΔΒ, τὸ δὲ ἐλάχιστον ἴσον τῷ ὑπὸ ΖΙΒ, αἱ δὲ πλευραὶ τῶν ὑπερβλημάτων τῷ ἴσῳ ἀλλαλᾶν ὑπερεχόντων [καὶ γὰρ αἱ ἴσαι αὐταῖς αἱ ἐπὶ τᾶς ΒΔ εὐθείας τῷ ἴσῳ ἀλλάλων ὑπερέχουσιν], καὶ ἔστω ἁ μὲν τοῦ μεγίστου ὑπερβλήματος πλευρά, ἐφ᾿ ἇς τὸ Ν, ἴσα τᾷ ΒΔ, ἁ δὲ τοῦ ἐλαχίστου ἴσα τᾷ ΒΙ, ἔστω δὲ καὶ ἄλλα χωρία, ἐν οἷς τὸ Ω, τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον τῷ μεγίστῳ τῷ ὑπὸ τᾶν ΖΔΒ· ὁ δὴ κύλινδρος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΔΕ, ποτὶ τὸν κύλινδρον τὸν βάσιν μὲν ἔχοντα τὸν κύκλον τὸν περὶ διάμετρον τὰν ΚΛ, ἄξονα δὲ τὰν ΔΕ, τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΚΕ δυνάμει· οὗτος δέ ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει τὸ περιεχόμενον ὑπὸ τᾶν ΖΔ, ΒΔ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΖΕ, ΒΕ· ἐν πάσᾳ γὰρ τοῦ ἀμβλυγωνίου κώνου τομᾷ τοῦτο συμβαίνει [ἁ γὰρ διπλασία τᾶς ποτεούσας, τουτέστι τᾶς ἐκ τοῦ κέντρου, πλαγία ἐστὶ τοῦ εἴδους πλευρά]. Καὶ ἔστι τῷ μὲν [219] ὑπὸ τᾶν ΖΔ, ΒΔ περιεχομένῳ ἴσον τὸ ΞΝ χωρίον, τῷ δὲ ὑπὸ τᾶν ΖΕ, ΒΕ ἴσον ἐστὶ τὸ ΞΜ· ἁ γὰρ Ξ ἴσα ἐστὶ τᾷ ΖΒ, ἁ δὲ Μ τᾷ ΒΕ, ἁ δὲ Ν τᾷ ΒΔ· ὁ ἄρα κύλινδρος ὁ βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΔΕ, ποτὶ τὸν κύλινδρον τὸν βάσιν ἔχοντα τὸν κύκλον τὸν περὶ διάμετρον τὰν ΚΛ, ἄξονα δὲ τὰν ΔΕ, τὸν αὐτὸν ἕξει λόγον, ὃν τὸ Ω χωρίον ποτὶ τὸ ΞΜ. Ὁμοίως δὲ δειχθήσεται καὶ τῶν ἄλλων κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἔχων τὰν ἴσαν τᾷ ΔΕ ποτὶ τὸν κύλινδρον τὸν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα τὸν αὐτὸν ἄξονα τοῦτον ἔχων τὸν λόγον, ὃν ἔχει τὸ Ω χωρίον ποτὶ τὸ ὁμόλογον τῶν παρὰ τὰν Ξ παραπεπτωκότων ὑπερβαλλόντων τετραγώνῳ. Ἔστιν δή τινα μεγέθεα, οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ, ὧν ἕκαστος ἄξονα ἔχει ἴσον τᾷ ΔΕ, καὶ ἄλλα μεγέθεα, τὰ χωρία, ἐν οἷς τὸ Ω, ἴσα τούτοις τῷ πλήθει, κατὰ δύο μεγέθεα τὸν αὐτὸν ἔχοντα λόγον, ἐπεὶ οἵ τε κύλινδροι ἴσοι ἐντὶ ἀλλάλοις καὶ τὰ Ω χωρία ἴσα ἀλλάλοις, λέγονται δὲ τῶν τε κυλίνδρων τινὲς ποτὶ ἄλλους κυλίνδρους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι, ὁ δὲ ἔσχατος οὐδὲ ποθ᾿ ἓν λέγεται, καὶ τῶν χωρίων, ἐν οἷς τὰ Ω, ποτ᾿ ἄλλα χωρία τὰ παρὰ τὰν Ξ παραπεπτωκότα ὑπερβάλλοντα εἴδει τετραγώνῳ, τὰ [δὲ] ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, τὸ δὲ ἔσχατον οὐδὲ ποθ᾿ ἓν λέγεται· δῆλον οὖν ὅτι καὶ πάντες οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ ποτὶ πάντας τοὺς κυλίνδρους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν ἑξοῦντι λόγον, ὃν [220] πάντα τὰ Ω χωρία ποτὶ πάντα τὰ παραβλήματα χωρὶς τοῦ μεγίστου. Δέδεικται δὲ ὅτι πάντα τὰ Ω χωρία ποτὶ πάντα τὰ παραβλήματα χωρὶς τοῦ μεγίστου μείζω λόγον ἔχοντι ἢ ὃν ἁ ΝΞ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισείᾳ τᾶς Ξ καὶ τῷ τρίτῳ μέρει τᾶς Ν· ὥστε καὶ ὅλος ὁ κύλινδρος ποτὶ τὸ ἐγγεγραμμένον σχῆμα μείζονα ἔχει λόγον ἢ ὃν ἁ ΖΔ ποτὶ τὰν ΘΡ· ὃν ὁ ὅλος κύλινδρος ἔχων ἐδείχθη ποτὶ τὸν Ψ κῶνον· μείζονα οὖν ἔχει λόγον ὁ ὅλος κύλινδρος ποτὶ τὸ ἐγγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ψ κῶνον. Ὥστε μείζων ἐστὶν ὁ Ψ κῶνος τοῦ ἐγγεγραμμένου σχήματος· ὅπερ ἀδύνατον· ἐδείχθη γὰρ τὸ ἐγγεγραμμένον σχῆμα μεῖζον τοῦ Ψ κώνου· οὐκ ἄρα μεῖζον τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου.
   Οὐδὲ τοίνυν ἔλασσον. Ἔστω γάρ, εἰ δυνατόν, ἔλασσον. Πάλιν οὖν ἐγγεγράφθω εἰς τὸ τμᾶμα σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ κῶνος τοῦ τμάματος, καὶ τὰ ἄλλα τὰ αὐτὰ κατεσκευάσθω. Ἐπεὶ οὖν ἔλασσόν ἐστι τὸ ἐγγεγραμμένον σχῆμα τοῦ τμάματος, καὶ ἐλάσσονι ὑπερέχει τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου ἢ ὁ Ψ κῶνος τοῦ τμάματος, δῆλον ὅτι καὶ τὸ περιγεγραμμένον σχῆμα ἔλασσόν ἐστι τοῦ Ψ κώνου. Πάλιν δὴ ὅ τε κύλινδρος ὁ πρῶτος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ Ω χωρίον ποτὶ τὸ ΞΝ [ἴσον γὰρ ἑκάτερον], καὶ τῶν ἄλλων κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἐχόντων τὰν ἴσαν τᾷ ΔΕ ποτὶ τὸν κύλινδρον τὸν ἐν τῷ περιγεγραμμένῳ σχήματι κατ᾿ αὐτὸν ἐόντα καὶ ἄξονα [221] ἔχοντα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν τὸ Ω χωρίον ποτὶ τὸ ὁμόλογον τῶν παρὰ τὰν Ξ παραβλημάτων σὺν τῷ ὑπερβλήματι, διὰ τὸ ἕκαστον τῶν περιγεγραμμένων χωρὶς τοῦ μεγίστου ἴσον εἶμεν ἑκάστῳ τῶν ἐγγεγραμμένων σὺν τῷ μεγίστῳ· ἕξει οὖν καὶ ὁ ὅλος κύλινδρος ποτὶ τὸ περιγεγραμμένον σχῆμα τὸν αὐτὸν λόγον, ὃν πάντα τὰ Ω χωρία ποτὶ τὰ παραβλήματα σὺν τοῖς ὑπερβλημάτεσσιν. Δέδεικται δὲ πάλιν πάντα τὰ Ω χωρία ποτὶ πάντα τὰ ἕτερα ἐλάσσω λόγον ἔχοντα τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισέᾳ τᾶς Ξ καὶ τῷ τρίτῳ μέρει τᾶς Ν· ὥστε καὶ ὅλος ὁ κύλινδρος ποτὶ τὸ περιγεγραμμένον σχῆμα ἐλάσσονα λόγον ἕξει ἢ ἁ ΖΔ ποτὶ τὰν ΘΡ. Ἀλλ᾿ ὡς ἁ ΖΔ ποτὶ τὰν ΘΡ, ὁ ὅλος κύλινδρος ποτὶ τὸν Ψ κῶνον· ἐλάσσονα οὖν λόγον ἔχει ὁ αὐτὸς κύλινδρος ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ψ. Ὥστε μεῖζόν ἐστι τὸ περιγεγραμμένον τοῦ Ψ κώνου· ὅπερ ἀδύνατον· ἐδείχθη γὰρ ἔλαττον ἐὸν τὸ περιγεγραμμένον σχῆμα τοῦ Ψ κώνου. Οὐκ ἄρα ἔλασσόν ἐστι τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου. Ἐπεὶ δὲ οὔτε μεῖζον οὔτε ἔλασσόν ἐστιν, δέδεικται οὖν τὸ προτεθέν.
   κϚ΄.
   Καὶ τοίνυν εἴ κα μὴ ὀρθῷ ποτὶ τὸν ἄξονα τῷ ἐπιπέδῳ ἀποτμαθῇ τὸ τμᾶμα τοῦ ἀμβλυγωνίου κωνοειδέος, ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τῷ τε ἄξονι τοῦ τμάματος καὶ τᾷ τριπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι ποτὶ τὰν ἴσαν συναμφοτέραις τῷ τε ἄξονι καὶ τᾷ διπλασίᾳ τᾶς ποτεούσας τῷ ἄξονι.

[222]    Ἔστω γὰρ τμᾶμα ἀμβλυγωνίου κωνοειδέος ἀποτετμαμένον ἐπιπέδῳ, ὡς εἴρηται, τμαθέντος δὲ ἐπιπέδῳ τοῦ σχήματος ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ ἐπίπεδον τὸ ἀποτετμακὸς τὸ τμᾶμα τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ ἀμβλυγωνίου κώνου τομά, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμακότος τὸ τμᾶμα ἁ ΓΑ εὐθεῖα, κορυφὰ δὲ ἔστω τοῦ κώνου τοῦ περιέχοντος τὸ κωνοειδὲς τὸ Θ σαμεῖον, καὶ ἄχθω διὰ τοῦ Β παρὰ τὰν ΑΓ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς ἁ ΦΥ, ἐπιψαυέτω δὲ κατὰ τὸ Β, καὶ ἀπὸ τοῦ Θ ἐπὶ τὸ Β ἐπιζευχθεῖσα ἐκβεβλήσθω· τεμεῖ δὴ αὕτα δίχα τὰν ΑΓ, καὶ ἐσσεῖται κορυφὰ μὲν τοῦ τμάματος τὸ Β σαμεῖον, ἄξων δὲ ἁ ΒΔ, ἁ δὲ ποτεοῦσα τῷ ἄξονι ἁ ΒΘ· τᾷ δὲ ΒΘ ἴσα ἔστω ἅ τε ΘΖ καὶ ἁ ΖΗ, ἀπὸ δὲ τᾶς ΦΥ ἐπίπεδον ἀνεστακέτω τι παράλληλον τῷ κατὰ τὰν ΑΓ· ἐπιψαύσει δὴ τοῦ κωνοειδέος κατὰ τὸ Β. Καὶ ἐπεὶ τὸ ἐπίπεδον τὸ κατὰ τὰν ΑΓ οὐκ ἐὸν ὀρθὸν ποτὶ τὸν ἄξονα τετμάκει τὸ κωνοειδές, ἁ τομὰ ἐσσεῖται ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς ἁ μείζων ἁ ΓΑ· ἐούσας δὴ ὀξυγωνίου κώνου τομᾶς περὶ διάμετρον τὰν ΑΓ καὶ τᾶς ΒΔ γραμμᾶς ἀπὸ τοῦ κέντρου ἀνεστακούσας ἐν ἐπιπέδῳ, ὅ ἐστιν ἀπὸ τᾶς διαμέτρου ὀρθὸν ποτὶ τὸ ἐπίπεδον, ἐν ᾧ ἐστιν ἁ τοῦ ὀξυγωνίου κώνου τομά, δυνατόν ἐστι κύλινδρον εὑρεῖν τὸν ἄξονα ἔχοντα ἐπ᾿ εὐθείας τᾷ ΒΔ, οὗ ἐν τᾷ [223] ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΓ. Εὑρεθέντος οὖν ἐσσεῖταί τις κυλίνδρου τόμος τὰν αὐτὰν βάσιν ἔχων τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, ἁ δὲ ἑτέρα βάσις αὐτοῦ ἐσσεῖται τὸ ἐπίπεδον τὸ κατὰ τὰν ΦΥ. Πάλιν δὲ καὶ κῶνον εὑρεῖν δυνατόν ἐστι κορυφὰν ἔχοντα τὸ Β σαμεῖον, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΓ. Εὑρεθέντος οὖν καὶ ἀπότμαμά τι ἐσσεῖται κώνου βάσιν ἔχον τὰν αὐτὰν τῷ τε τόμῳ καὶ τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· δεικτέον ὅτι τὸ τοῦ κωνοειδέος τμᾶμα ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ εἰρημένον τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΗΔ ποτὶ τὰν ΔΖ.
   Ὃν γὰρ ἔχει λόγον ἁ ΗΔ ποτὶ τὰν ΔΖ, τοῦτον ἐχέτω ὁ Ψ κῶνος ποτὶ τὸ ἀπότμαμα τοῦ κώνου. Εἰ οὖν μή ἐστιν ἴσον τὸ τοῦ κωνοειδέος τμᾶμα τῷ κώνῳ τῷ Ψ, ἔστω, εἰ δυνατόν ἐστιν, μεῖζον. Ἐγγεγράφθω δὴ εἰς τὸ τοῦ κωνοειδέος τμᾶμα σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρου τόμων ἴσον ὕψος ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου. Ἐπεὶ οὖν τὸ περιγεγραμμένον σχῆμα μεῖζον ἐὸν τοῦ τμάματος ἐλάσσονι ὑπερέχει τοῦ ἐγγεγραμμένου σχήματος ἢ τὸ τμᾶμα τοῦ Ψ κώνου, δῆλον ὅτι μεῖζόν ἐστι τὸ ἐγγεγραμμένον σχῆμα τοῦ Ψ κώνου. Διάχθω δὴ τὰ ἐπίπεδα τῶν τόμων τῶν ἐγγεγραμμένων ἐν τῷ τμάματι πάντων ἔστε [224] ποτὶ τὰν ἐπιφάνειαν τοῦ τόμου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, καὶ ἅ τε ΒΡ τρίτον μέρος ἔστω τᾶς ΒΔ, καὶ τἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Πάλιν δὴ ὁ πρῶτος τόμος τῶν ἐν τῷ ὅλῳ τόμῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον τόμον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΑΔ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΚΕ· οἱ γὰρ τόμοι οἱ ἴσον ὕψος ἔχοντες τὸν αὐτὸν ἔχοντι λόγον ποτ᾿ ἀλλάλους, ὅνπερ αἱ βάσιες αὐτῶν, αἱ δὲ βάσιες αὐτῶν, ἐπεὶ ὁμοῖαί ἐντι ὀξυγωνίων κώνων τομαί, τὸν αὐτὸν [οὖν] λόγον ἔχοντι ποτ᾿ ἀλλάλας, ὃν αἱ ὁμόλογοι διάμετροι αὐτᾶν δυνάμει. Ὃν δὲ λόγον ἔχει τὸ ἀπὸ τᾶς ΑΔ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΚΕ, τοῦτον ἔχει τὸ ὑπὸ τᾶν ΖΔΒ περιεχόμενον ποτὶ τὸ ὑπὸ τᾶν ΖΕΒ, ἐπεί ἐστιν ἁ μὲν ΖΔ ἀγμένα διὰ τοῦ Θ, καθ᾿ ὃ αἱ ἔγγιστα συμπίπτοντι, αἱ δὲ ΑΔ, ΚΕ παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσαν· ἔστιν δὲ τὸ μὲν ὑπὸ τᾶν ΖΔΒ περιεχόμενον ἴσον τῷ Ω χωρίῳ, τὸ δὲ ὑπὸ τᾶν ΖΕΒ τῷ ΞΜ· ἔχει οὖν ὁ πρῶτος τόμος τῶν ἐν τῷ ὅλῳ τόμῳ ὁ ἔχων ἄξονα τὰν [225] ΔΕ ποτὶ τὸν πρῶτον τόμον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τὸν αὐτὸν λόγον, ὃν τὸ Ω χωρίον ποτὶ τὸ ΞΜ· καὶ τῶν ἄλλων δὲ τόμων ἕκαστος τῶν ἐν τῷ ὅλῳ τόμῳ ἄξονα ἐχόντων τὰν ἴσαν τᾷ ΔΕ ποτὶ τὸν τόμον τὸν ἐν τῷ ἐγγεγραμμένῳ σχήματι κατ᾿ αὐτὸν ἐόντα καὶ ἄξονα ἔχοντα τὰν ἴσαν τᾷ ΔΕ τοῦτον ἔχει τὸν λόγον, ὃν τὸ Ω χωρίον ποτὶ τὸ ὁμόλογον τῶν παρὰ τὰν Ξ παραπεπτωκότων ὑπερβαλλόντων εἴδει τετραγώνῳ. Πάλιν οὖν ἐντί τινα μεγέθεα, οἱ τόμοι οἱ ἐν τῷ ὅλῳ τόμῳ, καὶ ἄλλα μεγέθεα, τὰ χωρία, ἐν οἷς τὸ Ω, ἴσα τῷ πλήθει τοῖς τόμοις καὶ κατὰ δύο τὸν αὐτὸν λόγον ἔχοντα αὐτοῖς, λέγονται δὲ οἱ τόμοι ποτ᾿ ἄλλους τόμους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι, ὁ δὲ ἔσχατος τόμος οὐδὲ ποθ᾿ ἓν λέγεται, τὰ δὲ Ω χωρία ποτ᾿ ἄλλα χωρία τὰ παρὰ τὰν Ξ παραπεπτωκότα ὑπερβάλλοντα εἴδεσι τετραγώνοις, τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, τὸ δὲ ἔσχατον οὐδὲ ποθ᾿ ἓν λέγεται· δῆλον οὖν ὅτι καὶ πάντες οἱ τόμοι ποτὶ πάντας τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ Ω χωρία ποτὶ πάντα τὰ παραβλήματα χωρὶς τοῦ μεγίστου. Πάντα δὲ τὰ Ω χωρία ποτὶ πάντα τὰ παραβλήματα χωρὶς τοῦ μεγίστου μείζονα λόγον ἔχοντι ἢ ὃν ἁ ΞΝ ποτὶ τὰν ἴσαν ἀμφοτέραις τᾷ τε ἡμισέᾳ τᾶς Ξ καὶ τῷ τρίτῳ μέρει τᾶς Ν· μείζονα οὖν λόγον ἔχει ὅλος ὁ τόμος ποτὶ τὸ ἐγγεγραμμένον σχῆμα τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν ἀμφοτέραις τᾷ τε ἡμισέᾳ τᾶς Ξ καὶ τῷ τρίτῳ μέρει τᾶς Ν· ὥστε καὶ τοῦ ὃν ἔχει ἁ ΖΔ ποτὶ τὰν ΘΡ. Μείζονα οὖν ἔχει λόγον ὁ ὅλος τόμος ποτὶ τὸ ἐγγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ψ κῶνον· [226] ὅπερ ἀδύνατον· ἐδείχθη γὰρ μεῖζον ἐὸν τὸ ἐγγεγραμμένον σχῆμα τοῦ Ψ κώνου. Οὐκ ἔστιν οὖν μεῖζον τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου.
   Εἰ δὲ ἔλασσόν ἐστι τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου, ἐγγραφέντος εἰς τὸ τμᾶμα σχήματος στερεοῦ καὶ ἄλλου περιγραφέντος ἐκ κυλίνδρου τόμων ἴσον ὕψος ἐχόντων συγκειμένου, ὥστε τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ Ψ κῶνος τοῦ τμάματος, πάλιν ὁμοίως δειχθήσεται τὸ περιγεγραμμένον σχῆμα ἔλασσον ἐὸν τοῦ Ψ κώνου καὶ ὁ τοῦ κυλίνδρου τόμος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ περιγεγραμμένον σχῆμα ἐλάσσονα λόγον ἔχων ἢ ποτὶ τὸν Ψ κῶνον· ὅπερ ἐστὶν ἀδύνατον. Οὐκ ἔστιν οὖν οὐδ᾿ ἔλασσον τὸ τοῦ κωνοειδέος τμᾶμα τοῦ Ψ κώνου. Δῆλον οὖν τὸ προτεθέν.
   κζ΄.
   Παντὸς σχήματος σφαιροειδέος ἐπιπέδῳ τμαθέντος διὰ τοῦ κέντρου ὀρθῷ ποτὶ τὸν ἄξονα τὸ ἁμίσεον τοῦ σφαιροειδέος διπλάσιόν ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   Ἔστω σφαιροειδὲς σχῆμα ἐπιπέδῳ τετμαμένον διὰ τοῦ κέντρου ὀρθῷ ποτὶ τὸν ἄξονα, τμαθέντος δὲ αὐτοῦ ἄλλῳ ἐπιπέδῳ διὰ τοῦ ἄξονος τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓΔ ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς καὶ ἄξων τοῦ σφαιροειδέος ἁ ΒΔ, κέντρον δὲ τὸ Θ· διοίσει δὲ οὐδέν, εἴτε ἁ μείζων ἐστὶ διάμετρος ἁ ΒΔ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς εἴτε ἁ ἐλάσσων· τοῦ δὲ τετμακότος ἐπιπέδου τὸ σχῆμα τομὰ ἔστω ἁ ΓΑ εὐθεῖα· ἐσσεῖται δὴ αὕτα διὰ

[227] τοῦ Θ καὶ ὀρθὰς ποιήσει γωνίας ποτὶ τὰν ΒΔ, ἐπεὶ τὸ ἐπίπεδον ὑπόκειται διὰ τοῦ κέντρου τε ἄχθαι καὶ ὀρθὸν εἶμεν ποτὶ τὸν ἄξονα. Δεικτέον ὅτι τὸ ἁμίσεον τοῦ σφαιροειδέος τμᾶμα τὸ βάσιν μὲν ἔχον τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, κορυφὰν δὲ τὸ Β σαμεῖον, διπλάσιόν ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   Ἔστω γὰρ κῶνός τις, ἐν ᾧ τὸ Ψ, διπλασίων τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τὰν ΘΒ· φαμὶ δὴ τὸ ἁμίσεον τοῦ σφαιροειδέος ἴσον εἶμεν τῷ Ψ κώνῳ.
   Εἰ οὖν μή ἐστιν ἴσον τὸ ἁμίσεον τοῦ σφαιροειδέος τῷ Ψ κώνῳ, ἔστω πρῶτον, εἰ δυνατόν, μεῖζον. Ἐγγεγράφθω δὴ εἰς τὸ τμᾶμα τὸ ἁμίσεον τοῦ σφαιροειδέος σχῆμα [228] στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ ἁμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου. Ἐπεὶ οὖν μεῖζον ἐὸν τὸ περιγεγραμμένον σχῆμα τοῦ ἁμίσεος τοῦ σφαιροειδέος ἐλάσσονι ὑπερέχει τοῦ ἐγγεγραμμένου σχήματος ἢ τὸ ἁμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου, δῆλον οὖν ὅτι καὶ τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ τμάματι τῷ ἁμισέῳ τοῦ σφαιροειδέος μεῖζόν ἐστι τοῦ Ψ κώνου. Ἔστω δὴ κύλινδρος βάσιν μὲν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, ἄξονα δὲ τὰν ΒΘ. Ἐπεὶ οὖν οὗτος ὁ κύλινδρος τριπλάσιός ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν, ὁ δὲ Ψ κῶνος διπλάσιός ἐστι τοῦ αὐτοῦ κώνου, δῆλον ὡς ὁ κύλινδρος ἡμιόλιός ἐστι τοῦ Ψ κώνου. Ἐκβεβλήσθω δὴ τὰ ἐπίπεδα τῶν κυλίνδρων πάντων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, ἔστε ποτὶ τὰν ἐπιφάνειαν τοῦ κυλίνδρου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· ἐσσεῖται δὴ ὁ ὅλος κύλινδρος διαιρημένος εἰς κυλίνδρους τῷ μὲν πλήθει ἴσους τοῖς κυλίνδροις τοῖς ἐν τῷ περιγεγραμμένῳ σχήματι, τῷ δὲ μεγέθει ἴσους τῷ μεγίστῳ αὐτῶν. Ἔστων [δὴ] οὖν γραμμαὶ κείμεναι, ἐφ᾿ ἇν τὰ Ξ, τῷ πλήθει ἴσαι τοῖς τμαμάτεσσι τοῖς τᾶς ΒΘ εὐθείας, τῷ δὲ μεγέθει ἴσα ἑκάστᾳ τᾷ ΒΘ, καὶ ἀπὸ ἑκάστας τετράγωνον ἀναγεγράφθω, ἀφαιρήσθω δὲ ἀπὸ μὲν τοῦ ἐσχάτου τετραγώνου γνώμων πλάτος ἔχων ἴσον τᾷ ΒΙ· ἐσσεῖται δὴ οὗτος ἴσος τῷ περιεχομένῳ ὑπὸ τᾶν ΒΙ, ΙΔ· ἀπὸ δὲ τοῦ παρ᾿ αὐτῷ [229] τετραγώνου γνώμων ἀφαιρήσθω πλάτος ἔχων διπλάσιον τᾶς ΒΙ· ἐσσεῖται δὴ οὗτος ἴσος τῷ περιεχομένῳ ὑπὸ τᾶν ΒΧ, ΧΔ· καὶ ἀεὶ ἀπὸ τοῦ ἐχομένου τετραγώνου γνώμων ἀφαιρήσθω, οὗ πλάτος ἑνὶ τμάματι μεῖζον τοῦ πλάτεος τοῦ πρὸ αὐτοῦ ἀφαιρημένου γνώμονος· ἐσσεῖται δὴ ἕκαστος αὐτῶν ἴσος τῷ περιεχομένῳ ὑπὸ τῶν τᾶς ΒΔ τμαμάτων, ὧν τὸ ἕτερον τμᾶμα ἴσον ἐστὶ τῷ πλάτει τοῦ γνώμονος. Ἐσσεῖται δὴ καὶ [ἀπὸ] τοῦ τετραγώνου τοῦ δευτέρου τὸ λοιπὸν τετράγωνον τὰν πλευρὰν ἔχον ἴσαν τᾷ ΘΕ. Ὁ δὲ κύλινδρος ὁ πρῶτος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΘΕ ποτὶ τὸν κύλινδρον τὸν πρῶτον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν αὐτὸν ἔχοντα ἄξονα τὰν ΘΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΘ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΚΕ· ὥστε καὶ ὃν τὸ ὑπὸ τᾶν ΒΘ, ΘΔ περιεχόμενον ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ περιεχόμενον· ἔχει οὖν ὁ κύλινδρος ποτὶ τὸν κύλινδρον τὸν αὐτὸν λόγον, ὃν τὸ πρῶτον τετράγωνον ποτὶ τὸν γνώμονα τὸν ἀπὸ τοῦ δευτέρου τετραγώνου ἀφαιρημένον. Ὁμοίως δὲ καὶ τῶν ἄλλων κυλίνδρων ἕκαστος ἄξονα ἐχόντων ἴσον τᾷ ΘΕ ποτὶ τὸν κύλινδρον τὸν ἐν τῷ ἐγγεγραμμένῳ σχήματι καὶ ἔχοντα ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ τετράγωνον τὸ ὁμοίως τεταγμένον αὐτῷ ποτὶ τὸν γνώμονα τὸν ἀπὸ τοῦ ἑπομένου αὐτῷ τετραγώνου ἀφαιρημένον. Ἐντὶ δή τινα μεγέθεα, οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ, καὶ ἄλλα, τὰ τετράγωνα τὰ ἀπὸ τᾶν Ξ, ἴσα τῷ πλήθει τοῖς κυλίνδροις καὶ κατὰ δύο τὸν αὐτὸν λόγον ἔχοντα, λέγονται δὲ οἱ κύλινδροι ποτ᾿ ἄλλα μεγέθεα, τοὺς κυλίνδρους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι, ὁ δὲ [230] ἔσχατος οὐδὲ ποθ᾿ ἓν λέγεται, καὶ τὰ τετράγωνα ποτ᾿ ἄλλα μεγέθεα, τοὺς ἀπὸ τῶν τετραγώνων ἀφαιρημένους, τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, τὸ δὲ ἔσχατον τετράγωνον οὐδὲ ποθ᾿ ἓν λέγεται· πάντες οὖν οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ ποτὶ πάντας τοὺς ἑτέρους κυλίνδρους τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ τετράγωνα ποτὶ πάντας τοὺς γνώμονας τοὺς ἀφαιρημένους ἀπ᾿ αὐτῶν· ὁ ἄρα κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ ἐγγεγραμμένον σχῆμα τὸν αὐτὸν ἔχει λόγον, ὃν πάντα τὰ τετράγωνα ποτὶ πάντας τοὺς γνώμονας τοὺς ἀφαιρημένους ἀπ᾿ αὐτῶν. Τὰ δὲ τετράγωνα πάντων τῶν γνωμόνων τῶν ἀφαιρημένων ἀπ᾿ αὐτῶν μείζονά ἐντι ἢ ἡμιόλια· ἐντὶ γάρ τινες γραμμαὶ κείμεναι αἱ ΞΡ, ΞΣ, ΞΤ, ΞΥ, ΞΦ [ΞΨ, ΞΩ] τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, καὶ ἁ ἐλαχίστα ἴσα τᾷ ὑπεροχᾷ, ἐντὶ δὲ καὶ ἄλλαι γραμμαί, ἐφ᾿ ἇν τὰ δύο Ξ, Ξ, τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ· τὰ οὖν τετράγωνα τὰ ἀπὸ πασᾶν, ἇν ἐστιν ἑκάστα ἴσα τᾷ μεγίστᾳ, πάντων μὲν τῶν τετραγώνων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἐλάσσονά ἐντι ἢ τριπλάσια, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα ἢ τριπλάσια· τοῦτο γὰρ ἐν τοῖς περὶ τᾶν ἑλίκων ἐκδεδομένοις δέδεικται. Ἐπεὶ δὲ πάντα τὰ τετράγωνα ἐλάσσονά ἐντι ἢ τριπλάσια τῶν ἑτέρων τετραγώνων, ἅ ἐντι ἀφαιρημένα ἀπ᾿ αὐτῶν, δῆλον ὅτι τῶν λοιπῶν μείζονά ἐντι ἢ ἡμιόλια· τῶν οὖν γνωμόνων μείζονά ἐντι ἢ ἡμιόλια. Ὥστε καὶ ὁ κύλινδρος ὁ βάσιν ἔχων τὰν [231] αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν μείζων ἐστὶν ἢ ἡμιόλιος τοῦ ἐγγεγραμμένου σχήματος· ὅπερ ἀδύνατον· τοῦ γὰρ Ψ κώνου ἡμιόλιός ἐστι, τὸ δὲ ἐγγεγραμμένον σχῆμα μεῖζον ἐδείχθη τοῦ Ψ κώνου. Οὐκ ἄρα ἐστὶ μεῖζον τὸ ἡμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου.
   Οὐδὲ τοίνυν ἔλασσον. Ἔστω γὰρ, εἰ δυνατόν, ἔλασσον. Πάλιν δὴ ἐγγεγράφθω εἰς τὸ ἁμίσεον τοῦ σφαιροειδέος σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ᾧ ὑπερέχει ὁ Ψ κῶνος τοῦ ἡμίσεος τοῦ σφαιροειδέος, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Ἐπεὶ οὖν ἔλασσόν ἐστι τὸ ἐγγραφὲν σχῆμα τοῦ τμάματος, δῆλον ὅτι καὶ τὸ περιγραφὲν σχῆμα ἔλασσόν ἐστι τοῦ Ψ κώνου. Πάλιν δὴ ὁ πρῶτος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΘΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΘΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ πρῶτον τετράγωνον ποθ᾿ αὑτό, ὁ δὲ δεύτερος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΕΠ ποτὶ τὸν δεύτερον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΕΠ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ δεύτερον τετράγωνον ποτὶ τὸν γνώμονα τὸν ἀπ᾿ αὐτοῦ ἀφαιρημένον· καὶ τῶν ἄλλων δὲ κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἐχόντων τὰν ἴσαν τᾷ ΘΕ ποτὶ τὸν κύλινδρον τὸν ἐν τῷ περιγεγραμμένῳ σχήματι κατ᾿ αὐτὸν ἐόντα καὶ ἄξοντα ἔχοντα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ ὁμοίως τεταγμένον αὐτῷ τετράγωνον ποτὶ τὸν γνώμονα τὸν ἀπ᾿ αὐτοῦ ἀφαιρημένον· καὶ πάντες [232] οὖν οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ ποτὶ πάντας τοὺς κυλίνδρους τοὺς ἐν τῷ περιγεγραμμένῳ σχήματι τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ τετράγωνα ποτὶ τὸ ἴσον τῷ πρώτῳ τετραγώνῳ καὶ τοῖς γνωμόνεσσι τοῖς ἀπὸ τῶν λοιπῶν τετραγώνων ἀφαιρημένοις. Καὶ τὰ τετράγωνα πάντα ἐλάσσονά ἐντι ἢ ἡμιόλια τοῦ ἴσου τῷ τε πρώτῳ τετραγώνῳ καὶ τοῖς γνωμόνεσσιν τοῖς ἀπὸ τῶν λοιπῶν ἀφαιρημένοις, διότι τῶν τετραγώνων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονά ἐντι ἢ τριπλάσια· ὁ ἄρα κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ἐλάσσων ἢ ἡμιόλιός ἐστι τοῦ περιγεγραμμένου σχήματος· ὅπερ ἀδύνατον· τοῦ γὰρ Ψ κώνου ἡμιόλιός ἐστι, τὸ δὲ περιγεγραμμένον σχῆμα ἔλαττον ἐδείχθη τοῦ Ψ κώνου. Οὐκ ἄρα ἐστὶν ἔλασσον τὸ ἡμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου. Ἐπεὶ δὲ οὔτε μεῖζόν ἐστι οὔτε ἔλασσον, ἴσον ἄρα ἐστίν.
   κη΄.
   Καὶ τοίνυν εἴ κα τὸ σφαιροειδὲς μὴ ὀρθῷ ποτὶ τὸν ἄξονα τῷ ἐπιπέδῳ διὰ τοῦ κέντρου τμαθῇ, ὁμοίως τὸ ἁμίσεον τοῦ σφαιροειδέος διπλάσιον ἐσσεῖται τοῦ ἀποτμάματος τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν.
   Τετμάσθω γὰρ σχῆμα σφαιροειδές, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓΔ ὀξυγωνίου κώνου τομά, κέντρον δὲ αὐτᾶς τὸ Θ, τοῦ δὲ τετμακότος ἐπιπέδου τὸ σχῆμα ἔστω ἁ ΑΓ εὐθεῖα· ἐσσεῖται δ᾿ αὕτα διὰ τοῦ Θ ἀγμένα, ἐπεὶ τὸ ἐπίπεδον ὑπέκειτο διὰ τοῦ κέντρου ἄχθαι. [233] Ἐσσεῖται οὖν τις ὀξυγωνίου κώνου τομὰ περὶ διάμετρον τὰν ΑΓ, ἐπεὶ τὸ ἐπίπεδον τὸ ἀποτέμνον ὑπέκειτο οὐ ποτ᾿ ὀρθὰς εἶμεν τῷ ἄξονι ἀγμένον. Ἄχθων δή τινες αἱ ΚΛ, ΜΝ παρὰ τὰν ΑΓ ἐπιψαύουσαι τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς κατὰ τὰ Β, Δ, ἀπὸ δὲ τᾶν ΚΛ, ΜΝ ἐπίπεδα ἀνεστακέτω παράλληλα τῷ κατὰ τὰν ΑΓ· ἐπιψαύοντι δὴ ταῦτα τοῦ σφαιροειδέος κατὰ τὰ Β, Δ, καὶ ἁ ΒΔ ἐπιζευχθεῖσα πεσεῖται διὰ τοῦ Θ, καὶ ἐσσοῦνται τῶν τμαμάτων κορυφαὶ μὲν τὰ Β, Δ σαμεῖα, ἄξονες δὲ αἱ ΒΘ, ΘΔ. Δυνατὸν δή ἐστιν κύλινδρον εὑρεῖν ἄξονα ἔχοντα τὰν ΒΘ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΓ, εὑρεθέντος δὲ ἐσσεῖταί τις κυλίνδρου τόμος τὰν αὐτὰν βάσιν ἔχων τῷ ἡμισέῳ τοῦ σφαιροειδέος καὶ ἄξονα τὸν αὐτόν· πάλιν δὲ καὶ κῶνον εὑρεῖν δυνατόν ἐστι κορυφὰν ἔχοντα τὸ Β σαμεῖον, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ ἀπὸ διαμέτρου τᾶς ΑΓ. Εὑρεθέντος δὴ ἐσσεῖταί τι ἀπότμαμα κώνου τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· λέγω δὴ ὅτι τοῦ σφαιροειδέος τὸ ἡμίσεον διπλάσιόν ἐστι τοῦ κώνου τούτου.
   Ἔστω δὴ ὁ Ψ κῶνος διπλάσιος τοῦ ἀποτμάματος τοῦ κώνου. Εἰ οὖν μή ἐστιν ἴσον τὸ ἡμίσεον τοῦ σφαιροειδέος τῷ Ψ κώνῳ, ἔστω πρῶτον, εἰ δυνατόν, μεῖζον. Ἐνέγραψα δή τι εἰς τὸ ἡμίσεον τοῦ σφαιροειδέος σχῆμα στερεὸν καὶ ἄλλο περιέγραψα ἐκ κυλίνδρου τόμων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος

[234] ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ ἁμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου. Ὁμοίως δὴ τοῖς πρότερον δειχθήσεται τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος μεῖζον ἐὸν τοῦ Ψ κώνου καὶ ὁ τόμος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦ μὲν Ψ κώνου ἡμιόλιος ἐών, τοῦ δὲ ἐγγεγραμμένου σχήματος ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος μείζων ἢ ἡμιόλιος· ὅπερ ἀδύνατον. Οὐκ ἐσσεῖται οὖν μεῖζον τὸ ἡμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου.
   Εἰ δὲ ἔλασσόν ἐστι τὸ ἡμίσεον τοῦ σφαιροειδέος τοῦ Ψ κώνου, ἐγγεγράφθω εἰς τὸ ἡμίσεον τοῦ σφαιροειδέος σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων τόμων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ Ψ κῶνος τοῦ ἡμίσεος τοῦ σφαιροειδέος. Πάλιν οὖν ὁμοίως τοῖς πρότερον δειχθήσεται τὸ περιγεγραμμένον [235] σχῆμα ἔλασσον ἐὸν τοῦ Ψ κώνου καὶ ὁ τόμος τοῦ κυλίνδρου ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦ μὲν Ψ κώνου ἡμιόλιος ἐών, τοῦ δὲ περιγεγραμμένου σχήματος ἐλάσσων ἢ ἁμιόλιος· ὅπερ ἀδύνατον. Οὐκ ἐσσεῖται οὖν οὐδὲ ἔλασσον τὸ ἥμισυ τοῦ σφαιροειδέος τοῦ Ψ κώνου. Ἐπεὶ δὲ οὔτε μεῖζόν ἐστιν οὔτε ἔλασσον, ἴσον ἐστί. Φανερὸν οὖν ἐστιν ὃ ἔδει δεῖξαι.
   κθ΄.
   Παντὸς σχήματος σφαιροειδέος ἐπιπέδῳ τμαθέντος μὴ διὰ τοῦ κέντρου ὀρθῷ ποτὶ τὸν ἄξονα τὸ ἔλαττον τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν συναμφότερα τό τε ἡμίσεον τοῦ ἄξονος τοῦ σφαιροειδέος καὶ ὁ ἄξων τοῦ μείζονος τμάματος ποτὶ τὸν ἄξονα τὸν τοῦ μείζονος τμάματος.
   Ἔστω γάρ τι τμᾶμα σφαιροειδέος σχήματος ἀποτετμαμένον ἐπιπέδῳ ὀρθῷ ποτὶ τὸν ἄξονα μὴ διὰ τοῦ κέντρου, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ ὀξυγωνίου κώνου τομά, διάμετρος δὲ τᾶς τομᾶς καὶ ἄξων τοῦ σφαιροειδέος ἔστω ἁ ΒΖ, κέντρον δὲ τὸ Θ, τοῦ δὲ ἐπιπέδου τοῦ ἀποτέμνοντος τὸ τμᾶμα τομὰ ἔστω ἁ ΑΓ εὐθεῖα· ποιήσει δὲ αὕτα ὀρθὰς γωνίας ποτὶ τὰν ΒΖ, ἐπεὶ τὸ ἐπίπεδον ὀρθὸν εἶμεν ποτὶ τὸν ἄξονα ὑπέκειτο· ἔστω δὲ τὸ τμᾶμα τὸ ἀποτετμαμένον, οὗ κορυφὰ τὸ Β σαμεῖον, ἔλασσον ἢ ἁμίσεον τοῦ σφαιροειδέος σχήματος, καὶ τᾷ ΒΘ ἴσα ἔστω ἁ ΖΗ. Δεικτέον ὅτι τὸ τμᾶμα, οὗ κορυφὰ [236] τὸ Β σαμεῖον, ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΔΗ ποτὶ τὰν ΔΖ.
   Ἔστω δὴ κύλινδρος τὰν αὐτὰν βάσιν ἔχων τῷ ἐλάσσονι τμάματι καὶ ἄξονα τὸν αὐτόν, ἔστω δὲ καὶ κῶνος, ἐν ᾧ τὸ Ψ, ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τοῦτον ἔχων τὸν λόγον, ὃν ἔχει ἁ ΔΗ ποτὶ τὰν ΔΖ· φαμὶ δὴ τὸν Ψ κῶνον ἴσον εἶμεν τῷ τμάματι τῷ κορυφὰν ἔχοντι τὸ Β σαμεῖον.
   Εἰ γὰρ μή ἐστιν ἴσος, ἔστω πρῶτον, εἰ δυνατόν, ἐλάσσων. Ἐνέγραψα δὴ εἰς τὸ τμᾶμα σχῆμα στερεὸν καὶ ἄλλο περιέγραψα ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ μεῖζόν ἐστι τὸ τοῦ σφαιροειδέος τμᾶμα τοῦ Ψ κώνου. Ἐπεὶ οὖν μεῖζον ἐὸν τὸ περιγεγραμμένον σχῆμα τοῦ τμάματος [237] ἐλάσσονι ὑπερέχει τοῦ ἐγγεγραμμένου ἢ τὸ τμᾶμα τοῦ κώνου, δῆλον ὅτι μεῖζόν ἐστι καὶ τὸ ἐγγεγραμμένον σχῆμα τοῦ Ψ κώνου. Ἔστω δὴ τρίτον μέρος τᾶς ΒΔ ἁ ΒΡ. Ἐπεὶ οὖν ἁ μὲν ΒΗ τριπλασία ἐστὶν τᾶς ΒΘ, ἁ δὲ ΒΔ τᾶς ΒΡ, δῆλον ὅτι τριπλασία ἐστὶν ἁ ΔΗ τᾶς ΘΡ· ἔχει δὴ ὁ μὲν κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὰν ΒΔ ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν καὶ ἄξονα τὸν αὐτὸν τοῦτον τὸν λόγον, ὃν ἔχει ἁ ΔΗ ποτὶ τὰν ΘΡ. Ὁ δὲ κῶνος ὁ εἰρημένος ποτὶ τὸν Ψ κῶνον τὸν αὐτὸν λόγον ἔχει, ὃν ἁ ΔΖ ποτὶ τὰν ΔΗ· ἕξει οὖν ἀνομοίως τῶν λόγων τεταγμένων ὁ κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸν Ψ κῶνον τὸν αὐτὸν λόγον, ὃν ἁ ΔΖ ποτὶ τὰν ΘΡ. Ἔστων δὴ γραμμαὶ κείμεναι, ἐφ᾿ ἇν τὰ Ξ, Ν, τῷ μὲν πλήθει ἴσαι τοῖς τμαμάτεσσιν τοῖς τᾶς ΒΔ, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ ΖΔ, ἔστω δὲ καὶ τᾶν ΞΟ ἑκάστα ἴσα τᾷ ΒΔ· τᾶν οὖν ΝΟ ἑκάστα διπλασία ἐσσεῖται τᾶς ΘΔ. Παραπεπτωκέτω δὴ παρ᾿ ἑκάσταν αὐτᾶν χωρίον τι πλάτος ἔχον ἴσον τᾷ ΒΔ, ὥστε εἶμεν ἕκαστον τῶν ἐχόντων τὰς διαμέτρους τετράγωνον. Ἀφαιρήσθω δὴ ἀπὸ μὲν τοῦ πρώτου γνώμων πλάτος ἔχων ἴσον τᾷ ΒΕ, ἀπὸ δὲ τοῦ δευτέρου πλάτος ἔχων ἴσον τᾷ ΒΧ, καὶ ἀφ᾿ ἑκάστου τὸν αὐτὸν τρόπον εἷς ἀπὸ τοῦ ἑπομένου χωρίου γνώμων ἀφαιρήσθω πλάτος ἔχων ἑνὶ τμάματι ἔλασσον τοῦ πλατέος τοῦ πρὸ αὐτοῦ γνώμονος ἀφαιρημένου· ἐσσεῖται δὴ ὁ μὲν ἀπὸ τοῦ πρώτου χωρίου γνώμων ἀφαιρημένος ἴσος τῷ περιεχομένῳ ὑπὸ τᾶν ΒΕ, ΕΖ, καὶ τὸ λοιπὸν χωρίον παραπεπτωκὸς παρὰ τὰν [238] ΝΟ ὑπερβάλλον εἴδει τετραγώνῳ τὰν τοῦ ὑπερβλήματος πλευρὰν ἔχον ἴσαν τᾷ ΔΕ, ὁ δὲ ἀπὸ τοῦ δευτέρου χωρίου γνώμων ἀφαιρημένος ἴσος τῷ περιεχομένῳ ὑπὸ τᾶν ΖΧ, ΧΒ, καὶ τὸ λοιπὸν χωρίον παρὰ τὰν ΝΟ παραπεπτωκὸς ὑπερβάλλον εἴδει τετραγώνῳ, καὶ τὰ λοιπὰ ὁμοίως τούτοις ἑξοῦντι. Διάχθω δὲ τὰ ἐπίπεδα πάντων τῶν κυλίνδρων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ τμάματι, ποτὶ τὰν ἐπιφάνειαν τοῦ κυλίνδρου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· ἐσσεῖται δὴ ὁ ὅλος κύλινδρος διαιρημένος εἰς κυλίνδρους τῷ μὲν πλήθει ἴσους τοῖς ἐν τῷ περιγεγραμμένῳ σχήματι, τῷ δὲ μεγέθει ἴσους τῷ μεγίστῳ αὐτῶν. Ὁ δὴ πρῶτος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὰν ΔΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΔΓ ποτὶ τὸ ἀπὸ τᾶς ΚΕ. Οὗτος δέ ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει τὸ ὑπὸ τᾶν ΒΔ, ΔΖ περιεχόμενον ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΖ· ἔχει οὖν ὁ κύλινδρος ποτὶ τὸν κύλινδρον τὸν αὐτὸν λόγον, ὃν τὸ πρῶτον χωρίον ποτὶ τὸν γνώμονα τὸν ἀπ᾿ αὐτοῦ ἀφαιρημένον· ὁμοίως δὲ καὶ τῶν ἄλλων κυλίνδρων τῶν ἐν τῶ ὅλῳ κυλίνδρῳ ἕκαστος ἄξονα ἔχων τὰν ἴσαν τᾷ ΔΕ ποτὶ τὸν κατ᾿ αὐτὸν κύλινδρον τὸν ἐν τῷ ἐγγεγραμμένῳ σχήματι ἄξονα ἔχοντα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν τὸ ὁμοίως τεταγμένον αὐτῷ χωρίον ποτὶ τὸν γνώμονα τὸν ἀπ᾿ αὐτοῦ ἀφαιρημένον. Ἐντὶ οὖν μεγέθεά τινα οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ καὶ ἄλλα μεγέθεα τὰ χωρία τὰ παρὰ τὰν ΞΝ παραπεπτωκότα πλάτος ἔχοντα [239] τὰν ἴσαν τᾷ ΒΔ, τῷ δὲ πλήθει ἴσα τοῖς κυλίνδροις καὶ κατὰ δύο τὸν αὐτὸν ἔχοντα λόγον, λέγονται δὲ οἵ τε κύλινδροι ποτ᾿ ἄλλους κυλίνδρους τοὺς ἐν τῷ ἐγγεγραμμένῳ σχήματι, ὁ δὲ ἔσχατος οὐδὲ ποθ᾿ ἓν λέγεται, καὶ τὰ χωρία ποτ᾿ ἄλλα χωρία, τοὺς ἀπ᾿ αὐτῶν ἀφαιρημένους, τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις, τὸ δὲ ἔσχατον χωρίον οὐδὲ ποθ᾿ ἓν λέγεται· δῆλον οὖν ὅτι καὶ πάντες οἱ κύλινδροι ποτὶ πάντας τοὺς ἑτέρους τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ χωρία ποτὶ πάντας τοὺς γνώμονας· ὁ ἄρα κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ σχῆμα τὸ ἐγγεγραμμένον ἐν τῷ τμάματι τὸν αὐτὸν ἕξει λόγον, ὃν πάντα τὰ χωρία ποτὶ πάντας τοὺς γνώμονας. Καὶ ἐπεί ἐντί τινες γραμμαὶ ἴσαι κείμεναι, ἐφ᾿ ἇν τὰ Ν, Ο, καὶ παρ᾿ ἑκάσταν παραπέπτωκέν τι χωρίον ὑπερβάλλον εἴδει τετραγώνῳ, αἱ δὲ πλευραὶ τῶν ὑπερβλημάτων τῷ ἴσῳ ἀλλαλᾶν ὑπερέχοντι, καὶ ἁ ὑπεροχὰ ἴσα ἐστὶ τᾷ ἐλαχίστᾳ, καὶ ἄλλα ἐντὶ χωρία παρὰ τὰν ΞΝ παραπεπτωκότα, πλάτος δὲ ἔχοντα τὰς ἴσας τᾷ ΒΔ, τῷ μὲν πλήθει ἴσα τούτοις, τῷ δὲ μεγέθει ἕκαστον ἴσον τῷ μεγίστῳ, δῆλον ὡς σύμπαντα τὰ χωρία, ὧν ἐστιν ἕκαστον ἴσον τῷ μεγίστῳ, ποτὶ πάντα τὰ ἕτερα χωρία ἐλάσσω λόγον ἔχοντι τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέρᾳ τᾷ τε ἡμισέᾳ τᾶς ΝΟ καὶ τῷ τρίτῳ μέρει τᾶς ΞΟ. Φανερὸν οὖν ὅτι τὰ αὐτὰ χωρία ποτὶ πάντας τοὺς γνώμονας μείζονα λόγον ἑξοῦντι τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισέᾳ τᾶς ΝΟ καὶ δυοῖς τριταμορίοις τᾶς ΞΟ· ὁ ἄρα κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ σχῆμα τὸ ἐγγεγραμμένον ἐν τῷ τμάματι μείζονα λόγον ἔχει ἢ ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισέᾳ τᾶς ΝΟ καὶ δυοῖς τριταμορίοις τᾶς [240] ΞΟ. Ἔστιν δὲ τᾷ μὲν ΞΝ ἴσα ἁ ΔΖ, τᾷ δὲ ἡμισέᾳ τᾶς ΝΟ ἁ ΔΘ, τὰ δὲ δύο τριταμόρια τᾶς ΞΟ ἁ ΔΡ· ὅλος ἄρα ὁ κύλινδρος ποτὶ τὸ σχῆμα τὸ ἐγγεγραμμένον ἐν τῷ τμάματι μείζονα λόγον ἔχει ἢ ὃν ἔχει ἁ ΔΖ ποτὶ τὰν ΘΡ. Ὃν δὲ λόγον ἔχει ἁ ΔΖ ποτὶ τὰν ΘΡ, τοῦτον ἐδείχθη ἔχων ὁ αὐτὸς κύλινδρος ποτὶ τὸν Ψ κῶνον· μείζονα οὖν ἕξει λόγον ποτὶ τὸ ἐγγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ψ κῶνον· ὅπερ ἀδύνατον· ἐδείχθη γὰρ μεῖζον ἐὸν τὸ ἐγγεγραμμένον σχῆμα τοῦ Ψ κώνου. Οὐκ ἄρα ἐστὶ μεῖζον τὸ τοῦ σφαιροειδέος τμᾶμα τοῦ Ψ κώνου.
   Ἀλλ᾿ ἔστω, εἰ δυνατόν, ἔλασσον. Πάλιν δὴ ἐγγεγράφθω τι εἰς τὸ τμᾶμα σχῆμα στερεόν, καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ μείζων ἐστὶν ὁ Ψ κῶνος τοῦ τμάματος, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Ἐπεὶ οὖν ἔλασσόν ἐστι τὸ ἐγγεγραμμένον σχῆμα τοῦ τμάματος, καὶ ἐλάσσονι ὑπερέχει τὸ περιγραφὲν ἢ ὁ Ψ κῶνος τοῦ τμάματος, δῆλον ὅτι καὶ τὸ περιγραφὲν σχῆμα ἔλασσόν ἐστι τοῦ Ψ κώνου. Πάλιν δὴ ὁ πρῶτος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ὁ ἔχων ἄξονα τὰν ΔΕ ποτὶ τὸν πρῶτον κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν ἔχοντα ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἔσχατον χωρίον τῶν παρὰ τὰν ΞΝ παραπεπτωκότων πλάτος ἐχόντων ἴσον τᾷ ΒΔ ποθ᾿ αὑτό· ἑκάτερα γὰρ ἴσα ἐστίν· ὁ δὲ δεύτερος κύλινδρος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἔχων ἴσον τᾷ ΔΕ ποτὶ τὸν κύλινδρον τὸν κατ᾿ αὐτὸν ἐόντα τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν αὐτὸν ἔχει λόγον, ὃν τὸ πρῶτον χωρίον τῶν [241] παρὰ τὰν ΞΝ παραπεπτωκότων πλάτος ἐχόντων ἴσον τᾷ ΒΔ ποτὶ τὸν γνώμονα τὸν ἀφαιρημένον ἀπ᾿ αὐτοῦ, καὶ τῶν ἄλλων δὲ κυλίνδρων ἕκαστος τῶν ἐν τῷ ὅλῳ κυλίνδρῳ ἄξονα ἐχόντων ἴσον τᾷ ΔΕ ποτὶ τὸν κατ᾿ αὐτὸν κύλινδρον τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τὸν αὐτὸν λόγον, ὃν τὸ ὁμόλογον χωρίον αὐτῷ τῶν παρὰ τὰν ΞΝ παραπεπτωκότων ποτὶ τὸν γνώμονα τὸν ἀπ᾿ αὐτοῦ ἀφαιρημένον πρώτου λεγομένου τοῦ ἐσχάτου· καὶ πάντες οὖν οἱ κύλινδροι οἱ ἐν τῷ ὅλῳ κυλίνδρῳ ποτὶ πάντας τοὺς κυλίνδρους τοὺς ἐν τῷ περιγεγραμμένῳ σχήματι τὸν αὐτὸν ἑξοῦντι λόγον, ὃν πάντα τὰ χωρία τὰ παρὰ τὰν ΞΝ παραπεπτωκότα ποτὶ τὸ ἴσον τῷ τε ἐσχάτῳ κειμένῳ χωρίῳ καὶ τοῖς γνωμόνεσσι τοῖς ἀφαιρημένοις ἀπὸ τῶν ἄλλων διὰ τὰ αὐτὰ τοῖς πρότερον. Ἐπεὶ οὖν δέδεικται ὅτι τὰ χωρία πάντα τὰ παρὰ τὰν ΞΝ παραπεπτωκότα ποτὶ τὰ χωρία πάντα τὰ παρὰ τὰν ΝΟ παραπεπτωκότα ὑπερβάλλοντα εἴδει τετραγώνῳ χωρὶς τοῦ μεγίστου μείζονα λόγον ἔχοντι τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισέᾳ τᾶς ΝΟ καὶ τῷ τρίτῳ μέρει τᾶς ΞΟ, δῆλον ὅτι τὰ αὐτὰ χωρία ποτὶ τὰ λοιπά, ἅ ἐντι ἴσα τῷ ἐσχάτῳ χωρίῳ κειμένῳ καὶ τοῖς γνωμόνεσσι τοῖς ἀπὸ τῶν λοιπῶν ἀφαιρουμένοις, ἐλάσσονα λόγον ἔχοντι τοῦ ὃν ἔχει ἁ ΞΝ ποτὶ τὰν ἴσαν συναμφοτέραις τᾷ τε ἡμισέᾳ τᾶς ΝΟ καὶ δυσὶ τριταμορίοις τᾶς ΞΟ· δῆλον οὖν ὅτι καὶ ὁ κύλινδρος ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ σχῆμα τὸ περιγεγραμμένον ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἁ ΖΔ ποτὶ τὰν ΘΡ. Ὃν δὲ λόγον ἔχει ἁ ΔΖ ποτὶ τὰν ΘΡ, τοῦτον ἔχει ὁ εἰρημένος κύλινδρος ποτὶ τὸν Ψ κῶνον· ἐλάσσονα [242] ἄρα λόγον ἔχει ὁ αὐτὸς κύλινδρος ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ψ κῶνον· ὅπερ ἀδύνατον· ἐδείχθη γὰρ ἔλασσον ἐὸν τὸ περιγεγραμμένον σχῆμα τοῦ Ψ κώνου. Οὐκ ἄρα ἐστὶν ἔλασσον τοῦ κώνου. Ἐπεὶ δὲ οὔτε μεῖζον οὔτε ἔλασσον, ἴσον ἄρα ἐστίν.
   λ΄.
   Καὶ τοίνυν εἴ κα μὴ ὀρθῷ ποτὶ τὸν ἄξονα τμαθῇ τὸ σφαιροειδὲς μηδὲ διὰ τοῦ κέντρου, τὸ ἔλασσον αὐτοῦ τμᾶμα ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ ἴσα συναμφοτέρᾳ τᾷ τε ἡμισέᾳ τᾶς ἐπιζευγνυούσας τὰς κορυφὰς τῶν γενομένων τμαμάτων καὶ τῷ ἄξονι τοῦ μείζονος τμάματος ποτὶ τὸν ἄξονα τοῦ μείζονος τμάματος.
   Τετμάσθω γάρ τι σχῆμα σφαιροειδές, ὡς εἴρηται, καὶ τμαθέντος αὐτοῦ ἄλλῳ ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ ὀξυγωνίου κώνου [243] τομά, τοῦ δὲ τέμνοντος ἐπιπέδου τὸ σχῆμα ἁ ΓΑ εὐθεῖα, καὶ παρὰ τὰν ΑΓ ἄχθων αἱ ΠΡ, ΣΤ ἐπιψαύουσαι τᾶς τοῦ κώνου τομᾶς κατὰ τὰ Β, Ζ, καὶ ἀνεστακέτω ἀπ᾿ αὐτᾶν ἐπίπεδα παράλληλα τῷ κατὰ τὰν ΑΓ· ἐπιψαυσοῦντι δὲ ταῦτα τοῦ σφαιροειδέος κατὰ τὰ Β, Ζ, καὶ ἐσσοῦνται κορυφαὶ τῶν τμαμάτων τὰ Β, Ζ. Ἄχθω οὖν ἁ τὰς κορυφὰς τῶν τμαμάτων ἐπιζευγνύουσα καὶ ἔστω ἁ ΒΖ· πεσεῖται δὲ αὕτα διὰ τοῦ κέντρου· καὶ ἔστω κέντρον τοῦ σφαιροειδέος καὶ τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς τὸ Θ. Ἐπεὶ οὖν ὑπέκειτο μὴ ὀρθῷ ποτὶ τὸν ἄξονα τετμᾶσθαι τῷ ἐπιπέδῳ τὸ σχῆμα, ἁ τομά ἐστιν ὀξυγωνίου κώνου τομὰ καὶ διάμετρος αὐτᾶς ἁ ΓΑ. Λελάφθω οὖν ὅ τε κύλινδρος ὁ ἄξονα ἔχων ἐπ᾿ εὐθείας τᾷ ΒΔ, οὗ ἐν τᾷ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΓ, καὶ ὁ κῶνος ὁ κορυφὰν ἔχων τὸ Β σαμεῖον, οὗ ἐν τᾶ ἐπιφανείᾳ ἐσσεῖται ἁ τοῦ ὀξυγωνίου κώνου τομὰ ἁ περὶ διάμετρον τὰν ΑΓ· ἐσσεῖται δὴ τόμος τις κυλίνδρου τὰν αὐτὰν βάσιν ἔχων τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν καὶ ἀπότμαμα κώνου τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ἄξονα τὸν αὐτόν. Δεικτέον ὅτι τὸ τμᾶμα τοῦ σφαιροειδέος, οὗ κορυφὰ τὸ Β, ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ ΔΗ ποτὶ τὰν ΔΖ· ἴσα δὲ ἔστω ἁ ΖΗ τᾷ ΘΖ.
   Λελάφθω δή τις κῶνος, ἐν ᾧ τὸ Ψ, ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχων τὸν λόγον, ὃν ἔχει ἁ ΔΗ ποτὶ τὰν ΔΖ. Εἰ οὖν μή ἐστιν ἴσον τὸ τμᾶμα τοῦ σφαιροειδέος τῷ [244] Ψ κώνῳ, ἔστω πρῶτον, εἰ δυνατόν, μεῖζον. Ἐνέγραψα δὴ εἰς τὸ τμᾶμα τοῦ σφαιροειδέος σχῆμα στερεὸν καὶ ἄλλο περιέγραψα ἐκ κυλίνδρων τόμων ὕψος ἴσον ἐχόντων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ τμᾶμα τοῦ σφαιροειδέος τοῦ Ψ κώνου. Ὁμοίως δὴ τῷ προτέρῳ δειχθήσεται τὸ ἐγγεγραμμένον σχῆμα μεῖζον ἐὸν τοῦ Ψ κώνου καὶ ὁ τόμος τοῦ κυλίνδρου ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ ἐγγεγραμμένον σχῆμα μείζονα λόγον ἔχων ἢ ποτὶ τὸν Ψ κῶνον· ὅ ἐστιν ἀδύνατον. Οὐκ ἐσσεῖται οὖν τὸ τοῦ σφαιροειδέος τμᾶμα τοῦ Ψ κώνου μεῖζον.
   Ἀλλ᾿ ἔστω, εἰ δυνατόν, ἔλασσον. Ἐγγεγράφθω δὴ πάλιν εἰς τὸ τμᾶμα σχῆμα στερεὸν καὶ ἄλλο περιγεγράφθω ἐκ κυλίνδρου τόμων ὕψος ἴσον ἐχόντων συγκείμενα, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ Ψ κῶνος τοῦ τμάματος. Πάλιν δὴ διὰ τῶν αὐτῶν δειχθήσεται τὸ περιγεγραμμένον σχῆμα ἔλασσον τοῦ Ψ κώνου καὶ ὁ τόμος τοῦ κυλίνδρου ὁ βάσιν ἔχων τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν ποτὶ τὸ περιγεγραμμένον σχῆμα ἐλάσσονα λόγον ἔχων ἢ ποτὶ τὸν Ψ κῶνον· ὅ ἐστιν ἀδύνατον. Οὐκ ἐσσεῖται οὖν οὐδὲ ἔλασσον τὸ τμᾶμα τοῦ κώνου. Φανερὸν οὖν ὃ ἔδει δεῖξαι.
   λα΄.
   Παντὸς σχήματος σφαιροειδέος ἐπιπέδῳ τμαθέντος ὀρθῷ ποτὶ τὸν ἄξονα μὴ διὰ τοῦ κέντρου τὸ μεῖζον τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι [245] καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ἴσα συναμφοτέραις τᾷ τε ἡμισέᾳ τοῦ ἄξονος τοῦ σφαιροειδέος καὶ τῷ τοῦ ἐλάσσονος τμάματος ἄξονι ποτὶ τὸν τοῦ ἐλάσσονος τμάματος ἄξονα.
   Τετμάσθω τι σφαιροειδές, ὡς εἴρηται, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓ ὀξυγωνίου κώνου τομά, διάμετρος δὲ αὐτᾶς καὶ ἄξων τοῦ σχήματος ἁ ΒΔ, τοῦ δὲ τέμνοντος ἐπιπέδου ἁ ΓΑ εὐθεῖα· ἐσσεῖται δὲ αὕτα ποτ᾿ ὀρθὰς τᾷ ΒΔ· ἔστω δὲ μεῖζον τῶν τμαμάτων, οὗ κορυφὰ τὸ Β, καὶ κέντρον τοῦ σφαιροειδέος τὸ Θ. Ποτικείσθω δὴ ἁ ΔΗ τᾷ ΔΘ ἴσα καὶ ἁ ΒΖ τᾷ αὐτᾷ ἴσα· δεικτέον ὅτι τὸ τμᾶμα τοῦ σφαιροειδέος, οὗ κορυφὰ τὸ Β, ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἔχει ἁ ΕΗ ποτὶ τὰν ΕΔ.

[246]    Τετμάσθω δὴ τὸ σφαιροειδὲς ἐπιπέδῳ διὰ τοῦ κέντρου ὀρθῷ ποτὶ τὸν ἄξονα, καὶ ἀπὸ τοῦ γενομένου κύκλου κῶνος ἔστω κορυφὰν ἔχων τὸ Δ σαμεῖον· ἔστιν δὴ τὸ μὲν ὅλον σφαιροειδὲς διπλάσιον τοῦ τμάματος τοῦ βάσιν ἔχοντος τὸν κύκλον τὸν περὶ διάμετρον τὰν ΚΛ, κορυφὰν δὲ τὸ Δ σαμεῖον, τὸ δὲ εἰρημένον τμᾶμα διπλάσιον τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτόν· δέδεικται γὰρ ταῦτα· τὸ ὅλον οὖν σφαιροειδὲς τετραπλάσιόν ἐστι τοῦ κώνου τοῦ εἰρημένου. Ὁ δὲ κῶνος οὗτος ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, κορυφὰν δὲ τὸ Δ σαμεῖον, τὸν συγκείμενον ἔχει λόγον ἔκ τε τοῦ ὃν ἔχει ἁ ΘΔ ποτὶ τὰν ΕΔ, καὶ ἐκ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΚΘ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΕΑ· ὃν δὲ λόγον ἔχει τὸ ἀπὸ τᾶς ΚΘ ποτὶ τὸ ἀπὸ τᾶς ΕΑ, ὁ αὐτός ἐστι τῷ ὃν ἔχει τὸ ὑπὸ ΒΘ, ΘΔ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ. Ὃν δὴ λόγον ἔχει ἁ ΘΔ ποτὶ τὰν ΕΔ, τοῦτον ἐχέτω ἁ ΞΔ ποτὶ τὰν ΘΔ· ἕξει οὖν καὶ τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΒΘ, ΘΔ, ὃν ἁ ΔΘ ποτὶ τὰν ΔΕ. Ὁ δὲ συγκείμενος λόγος ἔκ τε τοῦ ὃν ἔχει τὸ ὑπὸ ΞΔ, ΘΒ ποτὶ τὸ ὑπὸ ΒΘΔ, καὶ ἐκ τοῦ ὃν ἔχει τὸ ὑπὸ τᾶν ΒΘ, ΘΔ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ ὁ αὐτός ἐστι τῷ ὃν ἔχει τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ· ἔχει οὖν ὁ μὲν κῶνος ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΚΛ, κορυφὰν δὲ τὸ Δ σαμεῖον, ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, κορυφὰν δὲ τὸ Δ σαμεῖον, τὸν αὐτὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ. Ὁ δὲ κῶνος ὁ βάσιν ἔχων τὸν κύκλον τὸν περὶ διάμετρον τὰν ΑΓ, κορυφὰν δὲ τὸ Δ σαμεῖον, ποτὶ [247] τὸ τμᾶμα τοῦ σφαιροειδέος τὸ βάσιν ἔχον τὰν αὐτὰν αὐτῷ καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΒΕ, ΕΔ ποτὶ τὸ περιεχόμενον ὑπὸ ΖΕ, ΕΔ [τουτέστιν ἁ ΒΕ ποτὶ ΕΖ· τὸ γὰρ ἔλασσον ἢ ἡμίσεον τοῦ σφαιροειδέος ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν δέδεικται τοῦτον ἔχον τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισέᾳ τοῦ ἄξονος τοῦ σφαιροειδέος καὶ τῷ ἄξονι τῷ τοῦ μείζονος τμάματος ποτὶ τὸν ἄξονα τὸν τοῦ μείζονος τμάματος, οὗτος δέ ἐστιν ὃν ἔχει ἁ ΖΕ ποτὶ τὰν ΒΕ]· ὁ ἄρα κῶνος ὁ ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος ποτὶ τὸ τμᾶμα τοῦ σφαιροειδέος τὸ ἔλασσον τοῦ ἡμίσεος τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ. Ἐπεὶ οὖν τὸ μὲν ὅλον σφαιροειδὲς ποτὶ τὸν κῶνον τὸν ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ ποτὶ τὸ ὑπὸ τᾶν ΒΘ, ΞΔ [τετραπλάσιον γὰρ ἑκάτερον], ὁ δὲ κῶνος ὁ ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος ποτὶ τὸ τμᾶμα τὸ ἔλασσον ἢ τὸ ἡμίσεον τοῦ σφαιροειδέος τοῦτον ἔχει τὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ, ἔχοι κα καὶ τὸ ὅλον σφαιροειδὲς ποτὶ τὸ τμᾶμα τὸ ἔλασσον αὐτοῦ τὸν αὐτὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ ποτὶ τὸ ὑπὸ τᾶν ΖΕΔ· ὥστε καὶ τὸ μεῖζον τμᾶμα τοῦ σφαιροειδέος ποτὶ τὸ ἔλασσον τὸν αὐτὸν λόγον ἔχει, ὃν ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ τοῦ ὑπὸ τᾶν ΖΕ, ΕΔ, ποτὶ τὸ ὑπὸ τᾶν ΖΕΔ. Ὑπερέχει δὲ τὸ ὑπὸ τᾶν ΖΗ, ΞΔ τοῦ ὑπὸ τᾶν ΖΕ, ΕΔ τῷ τε ὑπὸ τᾶν ΞΔ, ΕΗ περιεχομένῳ καὶ τῷ [248] ὑπὸ τᾶν ΖΕ, ΞΕ· ἔχει ἄρα τὸ μεῖζον τμᾶμα τοῦ σφαιροειδέος ποτὶ τὸ ἔλασσον τὸν αὐτὸν λόγον, ὃν τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπὸ τᾶν ΞΔ, ΕΗ καὶ τῷ ὑπὸ τᾶν ΖΕ, ΞΕ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΖΕ, ΕΔ. Τὸ δὲ ἔλασσον τμᾶμα τοῦ σφαιροειδέος ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν αὐτῷ καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΖΕ, ΕΔ ποτὶ τὸ ὑπὸ τᾶν ΒΕΔ [τὸν γὰρ αὐτὸν ἔχει λόγον, ὃν ἁ ΖΕ ποτὶ τὰν ΒΕ], ὁ δὲ κῶνος ὁ ἐν τῷ ἐλάσσονι τμάματι ποτὶ τὸν κῶνον τὸν ἐν τῷ μείζονι τμάματι τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΒΕ, ΕΔ ποτὶ τὸ ἀπὸ τᾶς ΒΕ τετράγωνον· τὸν γὰρ τῶν ὑψέων λόγον ἔχοντι οἱ κῶνοι, ἐπεὶ βάσιν ἔχοντι τὰν αὐτάν· ἔχοι οὖν κα τὸ μεῖζον τμᾶμα τοῦ σφαιροειδέος ποτὶ τὸν κῶνον τὸν ἐν αὐτῷ ἐγγεγραμμένον ὃν τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπὸ τᾶν ΞΔ, ΕΗ καὶ τῷ ὑπὸ τᾶν ΖΕ, ΞΕ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΕ. Οὗτος δὲ ὁ αὐτός ἐστι τῷ ὃν ἔχει ἁ ΕΗ ποτὶ τὰν ΕΔ· τὸ γὰρ ὑπὸ τᾶν ΞΔ, ΕΗ ποτὶ τὸ ὑπὸ τᾶν ΞΔ, ΕΔ τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ, καὶ τὸ ὑπὸ τᾶν ΞΕ, ΖΕ περιεχόμενον ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΘΕ τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ· ἁ γὰρ ΞΕ ποτὶ τὰν ΘΕ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ διὰ τὸ ἀνάλογόν τε εἶμεν τὰς ΞΔ, ΘΔ, ΔΕ, καὶ τὰν ΘΔ ἴσαν εἶμεν τᾷ ΗΔ· καὶ τὸ ἴσον οὖν ἀμφοτέροις τῷ τε περιεχομένῳ ὑπὸ τᾶν ΞΔ, ΕΗ καὶ τῷ ὑπὸ τᾶν ΖΕ, ΞΕ ποτὶ τὸ ἴσον συναμφοτέροις τῷ τε ὑπὸ τᾶν ΞΔ, ΕΔ καὶ τῷ ὑπὸ τᾶν ΖΕ, ΘΕ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ. Τὸ δὲ ἀπὸ τᾶς ΕΒ τετράγωνον ἴσον ἐντὶ ἀμφοτέροις [249] τῷ τε περιεχομένῳ ὑπὸ τᾶν ΞΔ, ΕΔ καὶ τῷ ὑπὸ τᾶν ΖΕ, ΘΕ· τὸ μὲν γὰρ ἀπὸ τᾶς ΒΘ τετράγωνον ἴσον τῷ ὑπὸ τᾶν ΞΔ, ΕΔ περιεχομένῳ, ἁ δὲ ὑπεροχά, ᾇ μεῖζόν ἐστι τὸ ἀπὸ τᾶς ΒΕ τετράγωνον τοῦ ἀπὸ τᾶς ΒΘ, ἴσον ἐστὶ τῷ περιεχομένῳ ὑπὸ τᾶν ΖΕ, ΘΕ, ἐπεὶ ἴσαι αἱ ΒΘ, ΒΖ· δῆλον οὖν ὅτι τὸ μεῖζον τοῦ σφαιροειδέος τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ.
   λβ΄.
   Καὶ τοίνυν εἴ κα μὴ ὀρθῷ ποτὶ τὸν ἄξονα τῷ ἐπιπέδῳ τμαθῇ τὸ σφαιροειδὲς μηδὲ διὰ τοῦ κέντρου, τὸ μεῖζον τμᾶμα αὐτοῦ ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἕξει τὸν λόγον, ὃν ἁ συναμφοτέραις ἴσα τᾷ τε ἡμισέᾳ τᾶς ἐπιζευγνυούσας τὰς κορυφὰς τῶν γενομένων τμαμάτων καὶ τῷ ἄξονι τῷ τοῦ ἐλάσσονος τμάματος ποτὶ τὸν ἄξονα τὸν τοῦ ἐλάσσονος τμάματος.
   Τετμάσθω τὸ σφαιροειδὲς ἐπιπέδῳ, ὡς εἴρηται, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ ἄλλῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ τέμνον ἐπίπεδον τοῦ μὲν σχήματος τομὰ ἔστω ἁ ΑΒΓΔ ὀξυγωνίου κώνου τομά, τοῦ δὲ τέμνοντος ἐπιπέδου τὸ σχῆμα ἁ ΓΑ εὐθεῖα, παρὰ δὲ τὰν ΑΓ ἄχθωσαν αἱ ΠΡ, ΣΤ ἐπιψαύουσαι τᾶς τοῦ ὀξυγωνίου κώνου τομᾶς κατὰ τὰ Β, Δ, καὶ ἀνεστακέτω ἀπ᾿ αὐτᾶν ἐπίπεδα παράλληλα τῷ κατὰ τὰν ΑΓ· ἐπιψαυσοῦντι δὲ ταῦτα τοῦ σφαιροειδέος κατὰ τὰ Β, Δ, καὶ ἐσσοῦνται κορυφαὶ τῶν τμαμάτων τὰ [250] Β, Δ. Ἄχθω οὖν ἁ τὰς κορυφὰς ἐπιζευγνύουσα τῶν γενομένων τμαμάτων ἁ ΒΔ· πεσεῖται δ᾿ αὕτα διὰ τοῦ κέντρου· καὶ ἔστω κέντρον τὸ Θ, μεῖζον δὲ ἢ τὸ ἡμίσεον τοῦ σφαιροειδέος τὸ τμᾶμα, οὗ κορυφὰ τὸ Β, ποτικείσθω δὲ ἁ ΔΗ ἴσα τᾷ ΔΘ καὶ ἁ ΒΖ τᾷ αὐτᾷ. Δεικτέον ὅτι τὸ τμᾶμα τοῦ σφαιροειδέος τὸ μεῖζον ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ βάσιν ἔχον τὰν αὐτὰν τῷ τμάματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΕΗ ποτὶ τὰν ΕΔ.    Τετμάσθω γὰρ τὸ σφαιροειδὲς ἐπιπέδῳ διὰ τοῦ κέντρου παραλλήλῳ τῷ κατὰ τὰν ΑΓ ἐπιπέδῳ, καὶ ἐγγεγράφθω εἰς τὸ ἡμίσεον τοῦ σφαιροειδέος ἀπότμαμα κώνου κορυφὰν ἔχον τὸ Δ σαμεῖον, καὶ ὃν ἔχει λόγον ἁ ΔΘ ποτὶ τὰν ΕΔ, τοῦτον ἐχέτω ἁ ΞΔ ποτὶ τὰν ΘΔ. Ὁμοίως δὴ τῷ πρότερον δειχθήσεται τό τε ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἡμισέῳ [251] τοῦ σφαιροειδέος ἐγγεγραμμένον ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἐλάσσονι ἐγγεγραμμένον τὸν αὐτὸν ἔχον λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ, καὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἐλάσσονι τμάματι ἐγγεγραμμένον ποτὶ τὸ τμᾶμα τὸ ἐν ᾧ ἐγγέγραπται τὸν αὐτὸν ἔχον λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΒΕ, ΕΔ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ· ἕξει οὖν τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος ἐγγεγραμμένον ποτὶ τὸ ἔλασσον τμᾶμα τοῦ σφαιροειδέος ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ. Ἕξει οὖν τὸ μὲν ὅλον σφαιροειδὲς ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἡμισέῳ τοῦ σφαιροειδέος ἐγγεγραμμένον τὸν αὐτὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ ποτὶ τὸ ὑπὸ τᾶν ΒΘ, ΞΔ· τετραπλάσιον γὰρ ἑκατέρου ἑκάτερον· τὸ δὲ ἀπότμαμα τοῦ κώνου τὸ εἰρημένον ποτὶ τὸ ἔλασσον τμᾶμα τοῦ σφαιροειδέος τὸν αὐτὸν ἔχει λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΞΔ, ΒΘ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ· ἕξει οὖν τὸ ὅλον σφαιροειδὲς ποτὶ τὸ ἔλασσον τμᾶμα αὐτοῦ [τοῦ σφαιροειδέος] τὸν αὐτὸν λόγον, ὃν τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ· αὐτὸ δὲ τὸ μεῖζον τμᾶμα ποτὶ τὸ ἔλασσον τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ περιεχόμενον ὑπὸ τᾶν ΖΗ, ΞΔ τοῦ περιεχομένου ὑπὸ τᾶν ΖΕ, ΕΔ, ποτὶ τὸ ὑπὸ τᾶν ΖΕ, ΕΔ. Τὸ δὲ ἔλασσον τμᾶμα ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν αὐτῷ ἐγγεγραμμένον τὸν αὐτὸν ἔχει [252] λόγον, ὃν τὸ ὑπὸ τᾶν ΖΕ, ΕΔ ποτὶ τὸ ὑπὸ τᾶν ΒΕ, ΕΔ [δέδεικται γὰρ τοῦτον ἔχον τὸν λόγον, ὃν ἁ ΖΕ ποτὶ τὰν ΒΕ]· τὸ δὲ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ ἐλάσσονι τμάματι ἐγγεγραμμένον ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν τῷ μείζονι τμάματι ἐγγεγραμμένον τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ὑπὸ τᾶν ΒΕ, ΕΔ ποτὶ τὸ ἀπὸ τᾶς ΒΕ τετράγωνον· τὰ γὰρ ἀποτμάματα τῶν κώνων τὰ εἰρημένα τὸν τῶν ὑψέων λόγον ἔχοντι, ἐπεὶ βάσιν ἔχοντι τὰν αὐτάν, τὰ δὲ ὕψεα αὐτῶν τὸν αὐτὸν λόγον ἔχοντι τῷ τᾶς ΔΕ ποτὶ τὰν ΕΒ· ἔχει οὖν καὶ τὸ μεῖζον τμᾶμα τοῦ σφαιροειδέος ποτὶ τὸ ἀπότμαμα τοῦ κώνου τὸ ἐν αὐτῷ ἐγγεγραμμένον τὸν αὐτὸν λόγον, ὃν ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ περιεχόμενον ὑπὸ τᾶν ΗΖ, ΞΔ τοῦ ὑπὸ τᾶν ΖΕΔ, ποτὶ τὸ ἀπὸ τᾶς ΒΕ τετράγωνον· ὁ δὲ λόγος οὗτος ὁμοίως τῷ πρότερον δειχθείη κα ὁ αὐτὸς ἐὼν τῷ ὃν ἔχει ἁ ΕΗ ποτὶ τὰν ΕΔ.

---

ΠΕΡΙ ΕΛΙΚΩΝ

 

Ἀρχιμήδης Δοσιθέῳ χαίρειν

[8]   Τῶν ποτὶ Κόνωνα ἀποσταλέντων θεωρημάτων, ὑπὲρ ὧν ἀεὶ τὰς ἀποδείξιας ἐπιστέλλεις μοι γράψαι, τῶν μὲν πλείστων ἐν τοῖς ὑπὸ Ἡρακλείδα κομισθέντεσσιν ἔχεις γεγραμμένας, τινὰς δὲ αὐτῶν καὶ ἐν τῷδε τῷ βιβλίῳ γράψας ἐπιστέλλω τοι. Μὴ θαυμάσῃς δὲ εἰ πλείονα χρόνον ποιήσαντες ἐκδίδομες τὰς ἀποδείξιας αὐτῶν· συμβαίνει γὰρ τοῦτο γεγενῆσθαι διὰ τὸ βούλεσθαί με πρότερον διδόμεν τοῖς περὶ τὰ μαθήματα πραγματευομένοις καὶ μαστεύειν αὐτὰ προαιρουμένοις. Πόσα γὰρ τῶν ἐν γεωμετρίᾳ θεωρημάτων οὐκ εὐμέθοδα ἐν ἀρχᾷ φανέντα χρόνῳ τὰν ἐξεργασίαν λαμβάνοντι; Κόνων μὲν οὖν οὐχ ἱκανὸν λαβὼν ἐς τὰν μάστευσιν αὐτῶν χρόνον μετάλλαξεν τὸν βίον· ἢ δῆλα ἐποίησέν κα ταῦτα πάντα εὑρὼν καὶ ἄλλα πολλὰ ἐξευρὼν καὶ ἐπὶ τὸ πλεῖον προάγαγεν γεωμετρίαν· ἐπιστάμεθα γὰρ ὑπάρξασαν αὐτῷ σύνεσιν οὐ τὰν τυχοῦσαν περὶ τὸ μάθημα καὶ φιλοπονίαν ὑπερβάλλουσαν. Μετὰ δὲ τὰν Κόνωνος τελευτὰν πολλῶν ἐτέων ἐπιγεγενημένων οὐδ' ὑφ᾿ ἑνὸς οὐδὲν τῶν προβλημάτων αἰσθανόμεθα κεκινημένον. Βούλομαι δὲ καθ᾿ ἓν ἕκαστον αὐτῶν προενέγκασθαι· καὶ γὰρ συμβαίνει δύο τινὰ τῶν ἐμαυτῷ μήπω πεπερασμένων διὰ [9] τέλους ποτιτεθῆμεν, ὅπως οἱ φάμενοι μὲν πάντα εὑρίσκειν, ἀπόδειξιν δὲ αὐτῶν οὐδεμίαν ἐκφέροντες ἐλέγχωνται ποθωμολογηκότες εὑρίσκειν τὰ ἀδύνατα. Ταῦτα δὴ ποῖα τῶν προβλημάτων ἐντί, καὶ τίνων τὰς ἀποδείξιας ἔχεις ἀπεσταλμένας, καὶ ποίων ἐν τῷδε τῷ βιβλίῳ κομίζομες, δοκιμάζομες ἐμφανίξαι τοι. Πρῶτον δὴ τῶν προβλημάτων ἦν· σφαίρας δοθείσας ἐπίπεδον χωρίον εὑρεῖν ἴσον τᾷ ἐπιφανείᾳ τᾶς σφαίρας. Ὃ δὴ καὶ πρῶτον ἐγένετο φανερὸν ἐκδοθέντος τοῦ περὶ τὰν σφαῖραν βιβλίου· δειχθέντος γὰρ ὅτι πάσας σφαίρας ἁ ἐπιφάνεια τετραπλασία ἐστὶ τοῦ μεγίστου κύκλου τῶν ἐν τᾷ σφαίρᾳ δῆλον ὡς δυνατόν ἐστι χωρίον ἐπίπεδον εὑρεῖν ἴσον τᾷ ἐπιφανείᾳ τᾶς σφαίρας. Δεύτερον δέ· κώνου δοθέντος ἢ κυλίνδρου σφαῖραν εὑρεῖν ἴσαν τῷ κώνῳ ἢ τῷ κυλίνδρῳ. Τρίτον δέ· τὰν δοθεῖσαν σφαῖραν ἐπιπέδῳ τεμεῖν, ὥστε τὰ τμάματα αὐτᾶς ποτ' ἄλλαλα τὸν ταχθέντα λόγον ἔχειν. Τέταρτον δέ· τὰν δοθεῖσαν σφαῖραν ἐπιπέδῳ τεμεῖν, ὥστε τὰ τμάματα τᾶς ἐπιφανείας τὸν ταχθέντα λόγον ἔχειν ποτ' ἄλλαλα. Πέμπτον δέ· τὸ δοθὲν τμᾶμα σφαίρας τῷ δοθέντι τμάματι σφαίρας ὁμοιῶσαι. Ἕκτον δέ· δύο δοθέντων τμαμάτων σφαίρας εἴτε τᾶς αὐτᾶς εἴτε ἄλλας εὑρεῖν τι τμᾶμα σφαίρας, ὃ ἐσσεῖται αὐτὸ μὲν ὁμοῖον τῷ ἑτέρῳ τῶν τμαμάτων, τὰν δὲ ἐπιφάνειαν ἴσαν ἕξει τᾷ ἐπιφανείᾳ τοῦ ἑτέρου τμάματος. Ἕβδομον· ἀπὸ τᾶς δοθείσας σφαίρας τμᾶμα ἀποτεμεῖν ἐπιπέδῳ, ὥστε τὸ τμᾶμα ποτὶ τὸν κῶνον τὸν βάσιν ἔχοντα τὰν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον τὸν ταχθέντα λόγον ἔχειν μείζονα τοῦ ὃν ἔχει τὰ τρία ποτὶ τὰ δύο. Τούτων μὲν οὖν τῶν εἰρημένων πάντων τὰς [10] ἀποδείξιας Ἡρακλείδας ἐκόμιξεν· τὸ δὲ μετὰ ταῦτα κεχωρισμένον ψεῦδος ἦν. Ἔστι δέ· εἴ κα σφαῖρα ἐπιπέδῳ τμαθῇ εἰς ἄνισα, τὸ μεῖζον τμᾶμα ποτὶ τὸ ἔλασσον διπλασίονα λόγον ἕξει ἢ ἁ μείζων ἐπιφάνεια ποτὶ τὰν ἐλάσσονα. Ὅτι δὲ τοῦτο ψεῦδός ἐστι, διὰ τῶν προαπεσταλμένων φανερόν ἐστι· κεχώρισται γὰρ ἐν αὐτοῖς τόδε· εἴ κα σφαῖρα ἐπιπέδῳ τμαθῇ εἰς ἄνισα ποτ' ὀρθὰς διαμέτρῳ τινὶ τῶν ἐν τᾷ σφαίρᾳ, τᾶς μὲν ἐπιφανείας τὸ μεῖζον τμᾶμα ποτὶ τὸ ἔλασσον τὸν αὐτὸν ἕξει λόγον, ὃν τὸ τμᾶμα τὸ μεῖζον τᾶς διαμέτρου ποτὶ τὸ ἔλασσον, τὸ δὲ μεῖζον τμᾶμα τᾶς σφαίρας ποτὶ τὸ ἔλασσον ἐλάσσονα μὲν ἢ διπλάσιον λόγον ἔχει τοῦ ὃν ἔχει ἁ μείζων ἐπιφάνεια ποτὶ τὰν ἐλάσσονα, μείζονα δὲ ἢ ἡμιόλιον. Ἦν δὲ καὶ τὸ ἔσχατον κεχωρισμένον τῶν προβλημάτων ψεῦδος, ὅτι, εἴ κα σφαίρας τινὸς ἁ διάμετρος τμαθῇ, ὥστε τὸ ἀπὸ τοῦ μείζονος τμάματος τετράγωνον τριπλάσιον εἶμεν τοῦ τετραγώνου τοῦ ἀπὸ τοῦ ἐλάσσονος τμάματος, καὶ διὰ τοῦ σαμείου ἐπίπεδον ἀχθὲν ποτ' ὀρθὰς τᾷ διαμέτρῳ τέμνῃ τὰν σφαῖραν, τὸ τοιοῦτον τῷ εἴδει σχῆμα, οἷόν ἐστι τὸ μεῖζον τᾶς σφαίρας τμᾶμα, μέγιστόν ἐστι τῶν ἄλλων τμαμάτων τῶν ἐχόντων ἴσαν τὰν ἐπιφάνειαν. Ὅτι δὲ τοῦτο ψεῦδός ἐστι δῆλον διὰ τῶν προαπεσταλμένων θεωρημάτων· δέδεικται γὰρ ὅτι τὸ ἡμισφαίριον μέγιστόν ἐστι τῶν περιεχομένων ὑπὸ ἴσας ἐπιφανείας σφαίρας τμαμάτων. Μετὰ δὲ ταῦτα περὶ τοῦ κώνου προβεβλημένα ἐστὶ τάδε· εἴ κα ὀρθογωνίου κώνου τομὰ μενούσας τᾶς διαμέτρου περιενεχθῆ ὥστε εἶμεν ἄξονα τὰν διάμετρον, τὸ περιγραφὲν σχῆμα ὑπὸ τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς κωνοειδὲς καλείσθω, καὶ εἴ κα τοῦ κωνοειδέος [11] σχήματος ἐπίπεδον ἐπιψαύῃ, παρὰ δὲ τὸ ἐπιψαῦον ἐπίπεδον ἄλλο ἐπίπεδον ἀχθὲν ἀποτέμνῃ τι τμᾶμα τοῦ κωνοειδέος, τοῦ ἀποτμαθέντος τμάματος βάσις μὲν καλείσθω τὸ ἀποτέμνον ἐπίπεδον, κορυφὰ δὲ τὸ σαμεῖον, καθ᾿ ὃ ἐπιψαύει τὸ ἕτερον ἐπίπεδον τοῦ κωνοειδέος. Εἰ δή κα τὸ εἰρημένον σχῆμα ἐπιπέδῳ τμαθῆ ποτ' ὀρθὰς τῷ ἄξονι, ὅτι μὲν ἁ τομὰ κύκλος ἐσσεῖται δῆλον, ὅτι δὲ τὸ ἀποτμαθὲν τμᾶμα ἡμιόλιον ἐσσεῖται τοῦ κώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον, δεῖξαι δεῖ. Καὶ εἴ κα τοῦ κωνοειδέος δύο τμάματα ἀποτμαθέωντι ἐπιπέδοις ὁπωσοῦν ἀγμένοις, ὅτι μὲν οὖν αἱ τομαὶ ἐσσοῦνται ὀξυγωνίων κώνων τομαὶ δῆλον, εἴ κα τὰ ἀποτέμνοντα ἐπίπεδα μὴ ὀρθὰ ἔωντι ποτὶ τὸν ἄξονα, ὅτι δὲ τὰ τμάματα ποτ' ἄλλαλα τοῦτον ἑξοῦντι τὸν λόγον, ὃν ἔχοντι δυνάμει ποτ' ἀλλάλας αἱ ἀπὸ τᾶν κορυφᾶν αὐτῶν ἀγμέναι παρὰ τὸν ἄξονα μέχρι ἐπὶ τὰ ἐπίπεδα τὰ τέμνοντα, δεῖξαι δεῖ· τούτων δ' αἱ ἀποδείξιες οὔπω τοι ἀποστέλλονται. Μετὰ δὲ ταῦτα περὶ τᾶς ἕλικος ἦν προβεβλημένα ταῦτα· ἐντὶ δ' ὥσπερ ἄλλο τι γένος προβλημάτων οὐδὲν ἐπικοινωνέοντα τοῖς προειρημένοις· ὑπὲρ ὧν ἐν τῷδε τῷ βιβλίῳ τὰς ἀποδείξιας γεγραφήκαμές τοι. Ἔστιν δὲ τάδε· εἴ κα εὐθεῖα γραμμὰ ἐν ἐπιπέδῳ μένοντος τοῦ ἑτέρου πέρατος ἰσοταχέως περιενεχθεῖσα ἀποκατασταθῇ πάλιν ὅθεν ὥρμασεν, ἅμα δὲ τᾷ γραμμᾷ περιφερομένᾳ φέρηταί τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ κατὰ τᾶς εὐθείας ἀρξάμενον ἀπὸ τοῦ μένοντος πέρατος, τὸ σαμεῖον ἕλικα γράψει ἐν τῷ ἐπιπέδῳ. Φαμὶ δὴ τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος καὶ τᾶς εὐθείας τᾶς ἀποκατασταθείσας ὅθεν ὥρμασεν τρίτον μέρος εἶμεν τοῦ κύκλου [12] τοῦ γραφέντος κέντρῳ μὲν τῷ μένοντι σαμείῳ, διαστήματι δὲ τᾷ εὐθείᾳ τᾷ διανυσθείσᾳ ὑπὸ τοῦ σαμείου ἐν τᾷ μιᾷ περιφορᾷ τᾶς εὐθείας. Καὶ εἴ κα τᾶς ἕλικος ἐπιψαύῃ τις εὐθεῖα κατὰ τὸ πέρας τᾶς ἕλικος τὸ ἔσχατον γενόμενον, ἄλλα δέ τις εὐθεῖα τᾷ περιαχθείσᾳ καὶ ἀποκατασταθείσᾳ γραμμᾷ ποτ' ὀρθὰς ἀχθῇ ἀπὸ τοῦ μένοντος πέρατος αὐτᾶς ὥστε ἐμπεσεῖν τᾷ ἐπιψαυούσᾳ, φαμὶ τὰν ποταχθεῖσαν εὐθεῖαν ἴσαν εἶμεν τᾷ τοῦ κύκλου περιφερείᾳ. Καὶ εἴ κα ἁ περιαγομένα γραμμὰ καὶ τὸ σαμεῖον τὸ φερόμενον κατ' αὐτᾶς πλείονας περιφορὰς περιενεχθέωντι καὶ ἀποκατασταθέωντι πάλιν ὅθεν ὥρμασαν, φαμὶ τοῦ χωρίου τοῦ ἐν τᾷ δευτέρᾳ περιφορᾷ ποτιλαφθέντος ὑπὸ τᾶς ἕλικος τὸ μὲν ἐν τᾷ τρίτᾳ ποτιλαφθὲν διπλάσιον ἐσσεῖσθαι, τὸ δὲ ἐν τᾷ τετάρτᾳ τριπλάσιον, τὸ δὲ ἐν τᾷ πέμπτᾳ τετραπλάσιον, καὶ ἀεὶ τὰ ἐν ταῖς ὕστερον περιφοραῖς ποτιλαμβανόμενα χωρία κατὰ τοὺς ἑξῆς ἀριθμοὺς πολλαπλάσια ἐσσεῖσθαι τοῦ ἐν τᾷ δευτέρᾳ περιφορᾷ ποτιλαφθέντος, τὸ δὲ ἐν τᾷ πρώτᾳ περιφορᾷ περιλαφθὲν χωρίον ἕκτον μέρος εἶμεν τοῦ ἐν τᾷ δευτέρᾳ περιφορᾷ ποτιλαφθέντος χωρίου. Καὶ εἴ κα ἐπὶ τᾶς ἕλικος τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας δύο σαμεῖα λαφθέωντι, καὶ ἀπ' αὐτῶν ἐπιζευχθέωντι εὐθεῖαι ἐπὶ τὸ μεμενακὸς πέρας τᾶς περιενεχθείσας γραμμᾶς, καὶ κύκλοι δύο γραφέωντι κέντρῳ μὲν τῷ μεμενακότι σαμείῳ, διαστημάτεσσι δὲ ταῖς ἐπιζευχθείσαις ἐπὶ τὸ μεμενακὸς πέρας τᾶς εὐθείας, καὶ ἁ ἐλάσσων τᾶν ἐπιζευχθεισᾶν ἐπεκβληθῇ, φαμὶ τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς τοῦ μείζονος κύκλου περιφερείας τᾶς ἐπὶ τὰ αὐτὰ τᾷ ἕλικι μεταξὺ τᾶν εὐθειᾶν ἐούσας καὶ τᾶς ἕλικος καὶ τᾶς εὐθείας τᾶς [13] ἐκβληθείσας ποτὶ τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς τοῦ ἐλάσσονος κύκλου περιφερείας καὶ τᾶς αὐτᾶς ἕλικος καὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ πέρατα αὐτᾶν τοῦτον ἕξειν τὸν λόγον, ὃν ἔχει ἁ ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ δύο τριταμορίων τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τᾶς ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ ἑνὸς τριταμορίου τᾶς εἰρημένας ὑπεροχᾶς. Τούτων δή μοι καὶ ἄλλων περὶ τᾶς ἕλικος αἱ ἀποδείξιες ἐν τῷδε τῷ βιβλίῳ γράφονται, πρόκεινται δέ, ὡς καὶ τῶν ἄλλων τῶν γεωμετρουμένων, τὰ χρείαν ἔχοντα εἰς τὰν ἀπόδειξιν αὐτῶν. Λαμβάνω δὲ καὶ ἐν τούτοις τῶν ἐν τοῖς πρότερον ἐκδεδομένοις βιβλίοις λῆμμα τόδε· τᾶν ἀνισᾶν γραμμᾶν καὶ τῶν ἀνίσων χωρίων τὰν ὑπεροχάν, ᾇ ὑπερέχει τὸ μεῖζον τοῦ ἐλάσσονος, αὐτὰν ἑαυτᾷ συντιθεμέναν δυνατὸν εἶμεν παντὸς ὑπερίσχειν τοῦ προτεθέντος τῶν ποτ' ἄλλαλα λεγομένων.

   α΄.

   Εἴ κα κατά τινος γραμμᾶς ἐνεχθῇ τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ φερόμενον, καὶ λαφθέωντι ἐν αὐτᾷ δύο γραμμαί, αἱ ἀπολαφθεῖσαι τὸν αὐτὸν ἑξοῦντι λόγον ποτ' ἀλλάλας ὅνπερ οἱ χρόνοι, ἐν οἷς τὸ σαμεῖον τὰς γραμμὰς ἐπορεύθη.

   Ἐνηνέχθω γάρ τι σαμεῖον κατὰ τᾶς ΑΒ γραμμᾶς ἰσοταχέως, καὶ λελάφθωσαν ἐν αὐτᾷ δύο γραμμαὶ αἱ ΓΔ, ΔΕ, ἔστω δὲ ὁ χρόνος, ἐν ᾧ τὰν ΓΔ γραμμὰν τὸ [14] σαμεῖον διεπορεύθη, ὁ ΖΗ, ἐν ᾧ δὲ τὰν ΔΕ, ὁ ΗΘ. Δεικτέον ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΓΔ γραμμὰ ποτὶ τὰν ΔΕ γραμμάν, ὃν ὁ χρόνος ὁ ΖΗ ποτὶ τὸν ΗΘ.

   Συγκείσθωσαν γὰρ ἐκ τᾶν ΓΔ, ΔΕ γραμμᾶν αἱ ΑΔ, ΔΒ γραμμαὶ καθ᾿ ἁντινοῦν σύνθεσιν οὕτως, ὥστε ὑπερέχειν τὰν ΑΔ τᾶς ΔΒ, καὶ ὁσάκις μὲν σύγκειται ἁ ΓΔ γραμμὰ ἐν τᾷ ΑΔ, τοσαυτάκις συγκείσθω ὁ χρόνος ὁ ΖΗ ἐν τῷ χρόνῳ τῷ ΛΗ, ὁσάκις δὲ σύγκειται ἁ ΔΕ γραμμὰ ἐν τᾷ ΔΒ, τοσαυτάκις συγκείσθω ὁ ΘΗ χρόνος ἐν τῷ ΚΗ χρόνῳ. Ἐπεὶ οὖν ὑπόκειται τὸ σαμεῖον ἰσοταχέως ἐνηνέχθαι κατὰ τᾶς ΑΒ γραμμᾶς, δῆλον ὡς, ἐν ὅσῳ χρόνῳ τὰν ΓΔ ἐνήνεκται, ἐν τοσούτῳ καὶ ἑκάσταν ἐνήνεκται τᾶν ἰσᾶν τᾷ ΓΔ· φανερὸν οὖν ὅτι καὶ συγκειμέναν τὰν ΑΔ γραμμὰν ἐν τοσούτῳ χρόνῳ ἐνήνεκται, ὅσος ἐστὶν ὁ ΛΗ χρόνος, ἐπειδὴ τοσαυτάκις σύγκειται ἅ τε ΓΔ γραμμὰ ἐν τᾷ ΑΔ γραμμᾷ καὶ ὁ ΖΗ χρόνος ἐν τῷ ΛΗ χρόνῳ. Διὰ ταὐτὰ δὴ καὶ τὰν ΒΔ γραμμὰν ἐν τοσούτῳ χρόνῳ τὸ σαμεῖον ἐνήνεκται, ὅσος ἐστὶν ὁ ΚΗ χρόνος. Ἐπεὶ οὖν μείζων ἐστὶν ἁ ΑΔ γραμμὰ τᾶς ΒΔ, δῆλον ὅτι ἐν πλείονι χρόνῳ τὸ σαμεῖον τὰν ΔΑ διαπορεύεται γραμμὰν ἢ τὰν ΒΔ· ὥστε ὁ χρόνος ὁ ΛΗ μείζων ἐστὶ τοῦ ΚΗ χρόνου. Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα ἐκ τῶν χρόνων τῶν ΖΗ, ΗΘ συντεθέωντι χρόνοι καθ᾿ ἁντινοῦν σύνθεσιν, ὥστε ὑπερέχειν τὸν ἕτερον τοῦ ἑτέρου, ὅτι καὶ τᾶν ἐκ τᾶν γραμμᾶν τᾶν ΓΔ, ΔΕ κατὰ τὰν αὐτὰν σύνθεσιν συντεθεισᾶν [15] ὑπερέξει ἁ ὁμόλογος τῷ ὑπερέχοντι χρόνῳ· δῆλον οὖν ὅτι τὸν αὐτὸν ἕξει λόγον ἁ ΓΔ ποτὶ τὰν ΔΕ, ὃν ὁ χρόνος ὁ ΖΗ ποτὶ τὸν χρόνον τὸν ΗΘ.

   β΄.

   Εἴ κα δύο σαμείων ἑκατέρου κατά τινος γραμμᾶς ἐνεχθέντος μὴ τᾶς αὐτᾶς ἰσοταχέως αὐτοῦ ἑαυτῷ φερομένου λαφθέωντι ἐν ἑκατέρᾳ τᾶν γραμμᾶν δύο γραμμαί, ἇν αἵ τε πρῶται ἐν ἴσοις χρόνοις ὑπὸ τῶν σαμείων διανυέσθων καὶ αἱ δεύτεραι, τὸν αὐτὸν ἑξοῦντι λόγον ποτ' ἀλλάλας αἱ λαφθεῖσαι γραμμαί.

   Ἔστω κατὰ τᾶς ΑΒ γραμμᾶς ἐνηνεγμένον τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ καὶ ἄλλο κατὰ τᾶς ΚΛ, λελάφθωσαν δὲ ἐν τᾷ ΑΒ δύο αἱ ΓΔ, ΔΕ γραμμαί, καὶ ἐν τᾷ ΚΛ αἱ ΖΗ, ΗΘ, ἐν ἴσῳ δὲ χρόνῳ τὸ κατὰ τᾶς ΑΒ γραμμᾶς ἐνηνεγμένον σαμεῖον τὰν ΓΔ γραμμὰν διαπορευέσθω, ἐν ὅσῳ τὸ ἕτερον κατὰ τᾶς ΚΛ ἐνηνεγμένον τὰν ΖΗ, ὁμοίως δὲ καὶ τὰν ΔΕ γραμμὰν ἐν ἴσῳ διαπορευέσθω τὸ σαμεῖον, ἐν ὅσῳ τὸ ἕτερον τὰν ΗΘ. Δεικτέον ὅτι τὸν αὐτὸν ἔχει λόγον ἁ ΓΔ ποτὶ τὰν ΔΕ, ὃν ἁ ΖΗ ποτὶ τὰν ΗΘ.

   Ἔστω δὴ ὁ χρόνος, ἐν ᾧ τὰν ΓΔ γραμμὰν διεπορεύετο τὸ σαμεῖον, ὁ ΜΝ· ἐν τούτῳ δὴ τῷ χρόνῳ καὶ τὸ ἕτερον σαμεῖον διαπορεύεται τὰν ΖΗ. Πάλιν δὴ καὶ ἐν ᾧ τὰν [16] ΔΕ γραμμὰν διεπορεύετο τὸ σαμεῖον, ἔστω ὁ ΝΞ χρόνος· ἐν τούτῳ δὴ καὶ τὸ ἕτερον σαμεῖον διαπορεύεται τὰν ΗΘ· τὸν αὐτὸν δὴ λόγον ἑξοῦντι ἅ τε ΓΔ ποτὶ τὰν ΔΕ γραμμάν, ὃν ὁ χρόνος ὁ ΜΝ ποτὶ ΝΞ, καὶ ἁ ΖΗ ποτὶ τὰν ΗΘ, ὃν ὁ χρόνος ὁ ΜΝ ποτὶ τὸν ΝΞ. Δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΓΔ ποτὶ τὰν ΔΕ, ὃν ἁ ΖΗ ποτὶ τὰν ΗΘ.

   γ΄.

   Κύκλων δοθέντων ὁποσωνοῦν τῷ πλήθει δυνατόν ἐστιν εὐθεῖαν λαβεῖν μείζονα ἐοῦσαν τᾶν τῶν κύκλων περιφερειᾶν.

   Περιγραφέντος γὰρ περὶ ἕκαστον τῶν κύκλων πολυγώνου δῆλον ὡς ἁ ἐκ πασᾶν συγκειμένα τᾶν περιμέτρων εὐθεῖα μείζων ἐσσεῖται πασᾶν τᾶν τῶν κύκλων περιφερειᾶν.

   δ΄.

   Δύο γραμμᾶν δοθεισᾶν ἀνισᾶν, εὐθείας τε καὶ κύκλου περιφερείας, δυνατόν ἐστι λαβεῖν εὐθεῖαν τᾶς μὲν μείζονος τᾶν δοθεισᾶν γραμμᾶν ἐλάσσονα, τᾶς δὲ ἐλάσσονος μείζονα.

   Ὁσάκις γὰρ ἁ ὑπεροχά, ᾇ ὑπερέχει ἁ μείζων γραμμὰ τᾶς ἐλάσσονος, αὐτὰ ἑαυτᾷ συντιθεμένα ὑπερέξει τᾶς εὐθείας, εἰς τοσαῦτα ἴσα διαιρεθείσας τᾶς εὐθείας τὸ ἓν τμᾶμα ἔλασσον ἐσσεῖται τᾶς ὑπεροχᾶς. Εἰ μὲν οὖν κα ᾖ ἁ περιφέρεια μείζων τᾶς εὐθείας, ἑνὸς τμάματος ποτιτεθέντος ποτὶ τὰν εὐθεῖαν τᾶς μὲν ἐλάσσονος τᾶν δοθεισᾶν δῆλον ὡς μείζων ἐσσεῖται, τᾶς δὲ μείζονος [17] ἐλάσσων· εἰ δέ κα ἐλάσσων, ἑνὸς τμάματος ποτιτεθέντος ποτὶ τὰν περιφέρειαν ὁμοίως τᾶς μὲν ἐλάσσονος μείζων ἐσσεῖται, τᾶς δὲ μείζονος ἐλάσσων· καὶ γὰρ ἁ ποτικειμένα ἐλάσσων ἐστὶ τᾶς ὑπεροχᾶς.

   ε΄.

   Κύκλου δοθέντος καὶ εὐθείας ἐπιψαυούσας τοῦ κύκλου δυνατόν ἐστιν ἀπὸ τοῦ κέντρου τοῦ κύκλου ἀγαγεῖν εὐθεῖαν ἐπὶ τὰν ἐπιψαύουσαν, ὥστε τὰν μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς τοῦ κύκλου περιφερείας εὐθεῖαν ποτὶ τὰν ἐκ τοῦ κέντρου ἐλάσσονα λόγον ἔχειν ἢ ἁ περιφέρεια τοῦ κύκλου ἁ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς διαχθείσας ποτὶ τὰν δοθεῖσαν ὁποιανοῦν κύκλου περιφέρειαν.

   Δεδόσθω κύκλος ὁ ΑΒΓ, κέντρον δὲ αὐτοῦ τὸ Κ, καὶ ἐπιψαυέτω τοῦ κύκλου ἁ ΔΖ κατὰ τὸ Β, δεδόσθω δὲ καὶ κύκλου περιφέρεια ὁποιαοῦν· δυνατὸν δέ ἐστι τᾶς δοθείσας περιφερείας λαβεῖν τινα εὐθεῖαν μείζονα, καὶ ἔστω ἁ Ε εὐθεῖα μείζων τᾶς δοθείσας περιφερείας· ἄχθω δὲ ἀπὸ τοῦ Κ κέντρου παρὰ τὰν ΔΖ ἁ ΑΗ, καὶ κείσθω ἁ ΗΘ ἴσα τᾷ Ε νεύουσα ἐπὶ τὸ Β. Ἀπὸ δὴ τοῦ Κ κέντρου ἐπὶ τὸ Θ [18] ἐπιζευχθεῖσα ἐκβεβλήσθω· τὸν αὐτὸν δὴ λόγον ἔχει ἁ ΘΖ ποτὶ τὰν ΘΚ, ὃν ἁ ΒΘ ποτὶ τὰν ΘΗ. Ἁ ἄρα ΖΘ ποτὶ τὰν ΘΚ ἐλάσσονα λόγον ἔχει τοῦ ὃν ἁ ΒΘ περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν, διότι ἁ μὲν ΒΘ εὐθεῖα ἐλάσσων ἐστὶ τᾶς ΒΘ περιφερείας, ἁ δὲ ΘΗ μείζων τᾶς δοθείσας περιφερείας· ἐλάσσονα οὖν λόγον ἔχει καὶ ἁ ΖΘ ποτὶ τὰν ἐκ τοῦ κέντρου ἢ ἁ ΒΘ περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν.

   Ϛ΄.

   Κύκλου δοθέντος καὶ ἐν τῷ κύκλῳ γραμμᾶς ἐλάσσονος τᾶς διαμέτρου δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτὶ τὰν περιφέρειαν αὐτοῦ ποτιβαλεῖν εὐθεῖαν τέμνουσαν τὰν ἐν τῷ κύκλῳ δεδομέναν γραμμάν, ὥστε τὰν ἀπολαφθεῖσαν εὐθεῖαν μεταξὺ τᾶς περιφερείας καὶ τᾶς εὐθείας τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἐπιζευχθεῖσαν ἀπὸ τοῦ πέρατος τᾶς ποτιπεσούσας τοῦ ἐπὶ τᾶς περιφερείας ποτὶ τὸ ἕτερον πέρας τᾶς ἐν τῷ κύκλῳ δεδομένας εὐθείας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος ἐλάσσων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[19]    Δεδόσθω κύκλος ὁ ΑΒΓ, κέντρον δὲ αὐτοῦ τὸ Κ, καὶ ἐν αὐτῷ δεδόσθω εὐθεῖα ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ Η, ἐλάσσων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΚΘ, καθέτου ἐούσας τᾶς ΚΘ· ἄχθω δὲ ἀπὸ τοῦ κέντρου παρὰ τὰν ΑΓ ἁ ΚΝ καὶ τᾷ ΚΓ πρὸς ὀρθὰς ἁ ΓΛ· ὁμοῖα δή ἐστι τὰ ΓΘΚ, ΓΚΛ τρίγωνα. Ἔστιν οὖν ὡς ἁ ΓΘ ποτὶ τὰν ΘΚ οὕτως ἁ ΚΓ ποτὶ τὰν ΓΛ· ἐλάσσονα ἄρα λόγον ἔχει ἁ Ζ ποτὶ τὰν Η ἢ ἁ ΚΓ ποτὶ τὰν ΓΛ. Ὃν δὴ λόγον ἔχει ἁ Ζ ποτὶ τὰν Η, τοῦτον ἐχέτω ἁ ΚΓ ποτὶ μείζονα τᾶς ΓΛ. Ἐχέτω ποτὶ τὰν ΒΝ, κείσθω δὲ ἁ ΒΝ μεταξὺ τᾶς περιφερείας καὶ τᾶς εὐθείας διὰ τοῦ Γ· δυνατὸν δέ ἐστιν οὕτως τέμνειν· καὶ πεσεῖται ἐκτός, ἐπεὶ μείζων ἐστὶν τᾶς ΓΛ. Ἐπεὶ οὖν ἁ ΚΒ ποτὶ ΒΝ τὸν αὐτὸν ἔχει λόγον ὃν ἁ Ζ ποτὶ Η, καὶ ἁ ΕΒ ποτὶ ΒΓ τὸν αὐτὸν ἕξει λόγον ὃν ἁ Ζ ποτὶ Η.

   ζ΄.

   Τῶν αὐτῶν δεδομένων καὶ τᾶς ἐν τῷ κύκλῳ εὐθείας ἐκβεβλημένας δυνατόν ἐστιν ἀπὸ τοῦ κέντρου ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας ποτὶ τὰν ἐπιζευχθεῖσαν ἀπὸ τοῦ πέρατος τᾶς ἐναπολαφθείσας ποτὶ τὸ πέρας τᾶς ἐκβεβλημένας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος μείζων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[20]    Δεδόσθω τὰ αὐτά, καὶ ἔστω ἁ ἐν τῷ κύκλῳ γραμμὰ ἐκβεβλημένα, ὁ δὲ δοθεὶς λόγος ἔστω, ὃν ἔχει ἁ Ζ ποτὶ τὰν Η, μείζων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΘΚ· μείζων οὖν ἐσσεῖται καὶ τοῦ ὃν ἔχει ἁ ΚΓ ποτὶ ΓΛ. Ὃν δὴ λόγον ἔχει ἁ Ζ ποτὶ Η, τοῦτον ἕξει ἁ ΚΓ ποτὶ ἐλάσσονα τᾶς ΓΛ. Ἐχέτω ποτὶ ΙΝ νεύουσαν ἐπὶ τὸ Γ· δυνατὸν δέ ἐστιν οὕτως τέμνειν· καὶ πεσεῖται ἐντὸς τᾶς ΓΛ, ἐπειδὴ ἐλάσσων ἐστὶ τᾶς ΓΛ. Ἐπεὶ οὖν τὸν αὐτὸν ἔχει λόγον ἁ ΚΓ ποτὶ ΙΝ ὃν ἁ Ζ ποτὶ Η, καὶ ἁ ΕΙ ποτὶ ΙΓ τὸν αὐτὸν ἕξει λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   η΄.

   Κύκλου δοθέντος καὶ ἐν τῷ κύκλῳ γραμμᾶς ἐλάσσονος τᾶς διαμέτρου καὶ ἄλλας ἐπιψαυούσας τοῦ κύκλου κατὰ τὸ πέρας τᾶς ἐν τῷ κύκλῳ δεδομένας δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτιβαλεῖν τινα εὐθεῖαν ποτὶ τὰν εὐθεῖαν, ὥστε τὰν ἀπολαφθεῖσαν ἀπ' αὐτᾶς μεταξὺ τᾶς τοῦ κύκλου περιφερείας καὶ τᾶς ἐν τῷ κύκλῳ δεδομένας γραμμᾶς ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος ἐλάσσων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου τοῦ κύκλου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[21]    Ἔστω κύκλος δεδομένος ὁ ΑΒΓΔ, καὶ ἐν τῷ κύκλῳ εὐθεῖα δεδόσθω ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ, καὶ ἁ ΞΛ ἐπιψαυέτω τοῦ κύκλου κατὰ τὸ Γ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ Η, ἐλάσσων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ ΘΚ· ἐσσεῖται δὴ ἐλάσσων καὶ τοῦ ὃν ἔχει ἁ ΓΚ ποτὶ ΓΛ, εἴ κα παράλληλος ἀχθῇ ἁ ΚΛ τᾷ ΘΓ· ἐχέτω δὴ ἁ ΚΓ ποτὶ ΓΞ τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ Η· μείζων δή ἐστιν ἁ ΞΓ τᾶς ΓΛ. Γεγράφθω κύκλου περιφέρεια περὶ τὰ Κ, Λ, Ξ. Ἐπεὶ οὖν ἐστι μείζων ἁ ΞΓ τᾶς ΓΛ, καὶ ποτ' ὀρθάς ἐντι ἀλλάλαις αἱ ΚΓ, ΞΛ, δυνατόν ἐστι τᾷ ΜΓ ἴσαν ἄλλαν θέμεν τὰν ΙΝ νεύουσαν ἐπὶ τὸ Κ. Τὸ δὴ περιεχόμενον ὑπὸ τᾶν ΞΙΛ ποτὶ τὸ ὑπὸ τᾶν ΚΕ, ΙΛ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΞΙ ποτὶ ΚΕ, καὶ τὸ ὑπὸ τᾶν ΚΙΝ ποτὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΙΝ ποτὶ ΓΛ· ὥστε καὶ ἁ ΙΝ ποτὶ ΓΛ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ· ὥστε καὶ ἁ ΓΜ ποτὶ ΓΛ καὶ ἁ ΞΓ ποτὶ ΚΓ καὶ ποτὶ ΚΒ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ, καὶ λοιπὰ ἁ ΙΓ ποτὶ ΒΕ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΞΓ ποτὶ τὰν ΓΚ καὶ ὃν ἁ Η ποτὶ Ζ. Πέπτωκεν οὖν ἁ ΚΝ ποτὶ τὰν ἐπιψαύουσαν, καὶ ἔχει ἁ μεταξὺ τᾶς περιφερείας [22] καὶ τᾶς εὐθείας ἁ ΒΕ ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   θ΄.

   Τῶν αὐτῶν δεδομένων καὶ τᾶς ἐν τῷ κύκλῳ δεδομένας γραμμᾶς ἐκβεβλημένας δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν εὐθεῖαν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας ποτὶ τὰν ἁφὰν τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος μείζων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγομέναν.

   Δεδόσθω κύκλος ὁ ΑΒΓΔ, καὶ ἐν τῷ κύκλῳ εὐθεῖα ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ διάχθω, καὶ ἐπιψαυέτω τοῦ κύκλου ἁ ΞΓ κατὰ τὸ Γ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ τὰν Η, μείζων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΘΚ· ἐσσεῖται δὴ μείζων καὶ τοῦ ὃν ἔχει ἁ ΚΓ ποτὶ τὰν ΓΛ. Ἐχέτω οὖν ἁ ΚΓ ποτὶ τὰν ΓΞ τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ τὰν Η· ἐλάσσων ἄρα ἐστὶν αὕτα τᾶς ΓΛ.

[23]    Πάλιν δὴ γεγράφθω κύκλος διὰ τῶν Ξ, Κ, Λ σαμείων. Ἐπεὶ οὖν ἐλάσσων ἐστὶν ἁ ΞΓ τᾶς ΓΛ, καὶ ποτ' ὀρθάς ἐντι ἀλλάλαις αἱ ΚΜ, ΞΓ, δυνατὸν τᾷ ΓΜ ἴσαν θέμεν τὰν ΙΝ νεύουσαν ἐπὶ τὸ Κ. Ἐπεὶ οὖν τὸ ὑπὸ τᾶν ΞΙΛ ποτὶ τὸ ὑπὸ τᾶν ΛΙ, ΚΕ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ, ἀλλὰ τῷ μὲν ὑπὸ τᾶν ΞΙΛ ἴσον ἐστὶ τὸ ὑπὸ τᾶν ΚΙΝ, τῷ δὲ ὑπὸ τᾶν ΛΙ, ΚΕ ἴσον ἐστὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ διὰ τὸ εἶμεν ὡς τὰν ΚΕ ποτὶ ΙΚ οὕτως τὰν ΛΓ ποτὶ ΛΙ, καὶ ὡς ἄρα ἁ ΞΙ ποτὶ ΚΕ, οὕτως τὸ ὑπὸ τᾶν ΚΙΝ ποτὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ, τουτέστιν ὡς ἁ ΝΙ ποτὶ ΓΛ, τουτέστιν ἁ ΓΜ ποτὶ ΓΛ. Ἔστιν δὲ καὶ, ὡς ἁ ΓΜ ποτὶ ΓΛ, ἁ ΞΓ ποτὶ ΚΓ, τουτέστι ποτὶ ΚΒ· ἔστιν ἄρα, ὡς ἁ ΞΙ ποτὶ ΚΕ, ἁ ΞΓ ποτὶ ΚΒ, καὶ λοιπὰ ἁ ΙΓ ποτὶ λοιπὰν τὰν ΒΕ ἐστὶν ὡς ἁ ΞΓ ποτὶ ΓΚ. Ὃν δὲ λόγον ἔχει ἁ ΞΓ ποτὶ ΓΚ, τοῦτον ἔχει ἁ Η ποτὶ Ζ· ποτιπέπτωκεν δὴ ἁ ΚΕ ποτὶ τὰν ἐκβεβλημέναν, καὶ ἁ μεταξὺ τᾶς ἐκβεβλημένας καὶ τᾶς περιφερειὰς ἁ ΒΕ ποτὶ τὰν ΓΙ τὰν ἀπὸ τᾶς ἐπιψαυούσας ἀπολαφθεῖσαν τὸν αὐτὸν ἔχει λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   ι΄.

   Εἴ κα γραμμαὶ ἑξῆς τεθέωντι ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, ᾖ δὲ ἁ ὑπεροχὰ ἴσα τᾷ ἐλαχίστᾳ, καὶ ἄλλαι γραμμαὶ τεθέωντι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα τᾷ μεγίστᾳ, τὰ τετράγωνα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτιλαμβάνοντα τό τε ἀπὸ τᾶς μεγίστας τετράγωνον καὶ τὸ περιεχόμενον ὑπό τε τᾶς ἐλαχίστας καὶ τᾶς ἴσας πάσαις ταῖς τῷ ἴσῳ ἀλλαλᾶν ὑπερεχούσαις τριπλάσια ἐσσοῦνται τῶν τετραγώνων πάντων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν.

[24]    Ἔστων γραμμαὶ ὁποσαιοῦν ἐφεξῆς κείμεναι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ Α, Β, Γ, Δ, Ε, Ζ, Η, Θ, ἁ δὲ Θ ἴσα ἔστω τᾷ ὑπεροχᾷ, ποτικείσθω δὲ ποτὶ τὰν Β ἴσα τᾷ Θ ἁ Ι, ποτὶ δὲ τὰν Γ ἁ Κ ἴσα τᾷ Η, ποτὶ δὲ τὰν Δ ἁ Λ ἴσα τᾷ Ζ, ποτὶ δὲ τὰν Ε ἁ Μ ἴσα τᾷ Ε, ποτὶ δὲ τὰν Ζ ἁ Ν ἴσα τᾷ Δ, ποτὶ δὲ τὰν Η ἁ Ξ ἴσα τᾷ Γ, ποτὶ δὲ τὰν Θ ἁ Ο ἴσα τᾷ Β· ἐσσοῦνται δὴ αἱ γενόμεναι ἴσαι ἀλλάλαις καὶ τᾷ μεγίστᾳ. Δεικτέον οὖν ὅτι τὰ τετράγωνα τὰ ἀπὸ πασᾶν τᾶς τε Α καὶ τᾶν γενομενᾶν ποτιλαβόντα τό τε ἀπὸ τᾶς Α τεράγωνον καὶ τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τριπλάσιά ἐντι τῶν τετραγώνων πάντων τῶν ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ.

   Ἔστιν δὴ τὸ μὲν ἀπὸ τᾶς ΒΙ τετράγωνον ἴσον τοῖς ἀπὸ τᾶν Ι, Β τετραγώνοις καὶ δύο τοῖς ὑπὸ τᾶν Β, Ι περιεχομένοις, τὸ δὲ ἀπὸ τᾶς ΚΓ ἴσον τοῖς ἀπὸ τᾶν Κ, Γ τετραγώνοις καὶ δύο τοῖς ὑπὸ τᾶν Κ, Γ περιεχομένοις· ὁμοίως δὲ καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τᾶν ἰσᾶν τᾷ Α τετράγωνα ἴσα ἐντὶ τοῖς ἀπὸ τῶν τμαμάτων τετραγώνοις καὶ δυσὶ τοῖς ὑπὸ τῶν τμαμάτων περιεχομένοις. Τὰ μὲν οὖν ἀπὸ [25] τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ καὶ τὰ ἀπὸ τᾶν Ι, Κ, Λ, Μ, Ν, Ξ, Ο ποτιλαβόντα τὸ ἀπὸ τᾶς Α τετράγωνον διπλάσιά ἐντι τῶν ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τετραγώνων· λοιπὸν δὲ ἐπιδειξοῦμες ὅτι τὰ διπλάσια τῶν περιεχομένων ὑπὸ τῶν τμαμάτων τῶν ἐν ἑκάστᾳ γραμμᾷ τᾶν ἰσᾶν τᾷ Α ποτιλαβόντα τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ ἴσα ἐντὶ τοῖς ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ. Καὶ ἐπεὶ δύο μὲν τὰ ὑπὸ Β, Ι περιεχόμενα ἴσα δυσὶ τοῖς ὑπὸ τᾶν Β, Θ περιεχομένοις, δύο δὲ τὰ ὑπὸ τᾶν Κ, Γ ἴσα τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς τετραπλασίας τᾶς Γ διὰ τὸ τὰν Κ διπλασίονα εἶμεν τᾶς Θ, δύο δὲ τὰ ὑπὸ τᾶν Δ, Λ ἴσα τῷ ὑπὸ τᾶς Θ καὶ τᾶς ἑξαπλασίας τᾶς Δ διὰ τὸ τὰν Λ τριπλασίαν εἶμεν τᾶς Θ, ὁμοίως δὲ καὶ τὰ ἄλλα τὰ διπλάσια τὰ περιεχόμενα ὑπὸ τῶν τμαμάτων ἴσα ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς πολλαπλασίας ἀεὶ κατὰ τοὺς ἑξῆς ἀριθμοὺς ἀρτίους τᾶς ἑπομένας γραμμᾶς, τὰ οὖν σύμπαντα ποτιλαβόντα τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ ἐσσοῦνται ἴσα τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις τᾷ τε Α καὶ τᾷ τριπλασίᾳ τᾶς Β καὶ τᾷ πενταπλασίᾳ τᾶς Γ καὶ ἀεὶ τᾷ [περισσᾷ] κατὰ τοὺς ἑξῆς ἀριθμοὺς περισσοὺς πολλαπλασίᾳ τᾶς ἑπομένας γραμμᾶς. Ἐντὶ δὲ καὶ τὰ ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τετράγωνα ἴσα τῷ περιεχομένῳ ὑπὸ τᾶν αὐτᾶν γραμμᾶν. Ἔστι γὰρ τὸ ἀπὸ τᾶς Α τετράγωνον ἴσον τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας [πάσαις] τᾷ τε Α καὶ τᾷ ἴσᾳ ταῖς λοιπαῖς, ἇν ἑκάστα ἴσα τᾷ Α· ἰσάκις γὰρ μετρεῖ ἅ τε Θ τὰν Α καὶ ἁ Α τὰς ἴσας αὐτᾷ πάσας σὺν τᾷ Α· ὥστε ἴσον ἐστὶ [26] τὸ ἀπὸ Α τετράγωνον τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ Α καὶ τᾷ διπλασίᾳ τᾶν Β, Γ, Δ, Ε, Ζ, Η, Θ· αἱ γὰρ ἴσαι τᾷ Α πᾶσαι χωρὶς τᾶς Α διπλάσιαί ἐντι τᾶν Β, Γ, Δ, Ε, Ζ, Η, Θ. Ὁμοίως δὲ καὶ τὸ ἀπὸ τᾶς Β τετράγωνον ἴσον ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ τε Β καὶ τᾷ διπλασίᾳ τᾶν Γ, Δ, Ε, Ζ, Η, Θ, καὶ πάλιν τὸ ἀπὸ τᾶς Γ τετράγωνον ἴσον τῷ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ τε Γ καὶ τᾷ διπλασίᾳ τᾶν Δ, Ε, Ζ, Η, Θ, ὁμοίως δὲ καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τετράγωνα ἴσα ἐντὶ τοῖς περιεχομένοις ὑπό τε τᾶς Θ καὶ τᾶς ἴσας αὐτᾷ τε καὶ τᾷ διπλασίᾳ τᾶν λοιπᾶν. Δῆλον οὖν ὅτι τὰ ἀπὸ πασᾶν τετράγωνα ἴσα ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις τᾷ τε Α καὶ τᾷ τριπλασίᾳ τᾶς Β καὶ τᾷ πενταπλασίᾳ τᾶς Γ καὶ τᾷ κατὰ τοὺς ἑξῆς ἀριθμοὺς περισσοὺς πολλαπλασίᾳ τᾶς ἑπομένας.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου οὖν φανερὸν ὅτι τὰ τετράγωνα πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ τῶν μὲν τετραγώνων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἐλάσσονά ἐστιν ἢ τριπλάσια, ἐπειδὴ ποτιλαβόντα τινὰ τριπλάσιά ἐντι, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονα ἢ τριπλάσια, ἐπειδὴ τὰ ποτιλαφθέντα ἐλάσσονά ἐντι ἢ τριπλάσια τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου. Καὶ τοίνυν, εἴ κα ὁμοῖα εἴδεα ἀναγραφέωντι ἀπὸ πασᾶν, ἀπὸ τὲ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ, τὰ εἴδεα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ τῶν μὲν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν εἰδέων [27] ἐλάσσονα ἐσσοῦνται ἢ τριπλάσια, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας εἴδεος μείζονα ἢ τριπλάσια· τὸν γὰρ αὐτὸν ἑξοῦντι λόγον τὰ ὁμοῖα εἴδεα τοῖς τετραγώνοις.

   ια΄.

   Εἴ κα γραμμαὶ ἑξῆς τεθέωντι ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, καὶ ἄλλαι γραμμαὶ τεθέωντι τῷ μὲν πλήθει μιᾷ ἐλάσσονες τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ, τὰ τετράγωνα πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ μὲν τὰ τετράγωνα τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τᾶς ἐλαχίστας ἐλάσσονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπό τε τᾶς μεγίστας καὶ τᾶς ἐλαχίστας καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ὑπεροχᾶς τετραγώνου, ᾇ ὑπερέχει ἁ μεγίστα τᾶς ἐλαχίστας, ποτὶ δὲ τὰ τετράγωνα τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονα τοῦ αὐτοῦ λόγου.

[28]    Ἔστωσαν γὰρ γραμμαὶ ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι ἑξῆς κείμεναι, ἁ μὲν ΑΒ τᾶς ΓΔ, ἁ δὲ ΓΔ τᾶς ΕΖ, ἁ δὲ ΕΖ τᾶς ΗΘ, ἁ δὲ ΗΘ τᾶς ΙΚ, ἁ δὲ ΙΚ τᾶς ΛΜ, ἁ δὲ ΛΜ τᾶς ΝΞ, ποτικείσθω δὲ ποτὶ μὲν τὰν ΓΔ ἴσα μιᾷ ὑπεροχᾷ ἁ ΓΟ, ποτὶ δὲ τὰν ΕΖ ἴσα δυσὶν ὑπεροχαῖς ἁ ΕΠ, ποτὶ δὲ τὰν ΗΘ ἴσα τρισὶν ὑπεροχαῖς ἁ ΗΡ, καὶ ποτὶ τὰς ἄλλας τὸν αὐτὸν τρόπον· ἐσσοῦνται δὴ αἱ γενόμεναι ἀλλάλαις ἴσαι καὶ ἑκάστα τᾷ μεγίστᾳ. Δεικτέον οὖν ὅτι τὰ ἀπὸ πασᾶν τᾶν γενομενᾶν τετράγωνα ποτὶ μὲν πάντα τὰ τετράγωνα τὰ ἀπὸ πασᾶν τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ΝΞ τετραγώνου ἐλάσσονα λόγον ἔχει ἢ τὸ ἀπὸ τᾶς ΑΒ τετράγωνον ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπὸ τᾶν ΑΒ, ΝΞ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΝΥ τετραγώνου, ποτὶ δὲ τὰ τετράγωνα τὰ ἀπὸ τᾶν αὐτᾶν χωρὶς τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου μείζονα λόγον ἔχει τοῦ αὐτοῦ λόγου.

   Ἀπολελάφθω ἀφ' ἑκάστας τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἴσα τᾷ ὑπεροχᾷ· ὃν δὴ λόγον ἔχει τὸ ἀπὸ τᾶς ΑΒ ποτὶ συναμφότερα τό τε ὑπὸ τᾶν ΑΒ, ΦΒ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΦ τετραγώνου, τοῦτον ἔχει τὸν λόγον τό τε ἀπὸ τᾶς ΟΔ τετράγωνον ποτί τε τὸ περιεχόμενον ὑπὸ τᾶν ΟΔ, ΔΧ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΧΟ τετραγώνου καὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΖ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΠΖ, ΨΖ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΨΠ τετραγώνου καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τετράγωνα ποτὶ τὰ ὁμοίως λαμβανόμενα χωρία· καὶ τὰ πάντα δὴ τὰ ἀπὸ πασᾶν τᾶν ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ ποτί τε πάντα τὰ περιεχόμενα ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς εἰρημέναις γραμμαῖς καὶ τὰ [29] τριταμόρια τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τὸν αὐτὸν ἑξοῦντι λόγον, ὃν τὸ ἀπὸ τᾶς ΑΒ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΒ, ΦΒ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ ΦΑ τετραγώνου. Εἰ οὖν κα δειχθῇ τό τε περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ καὶ τὰ τρίτα μέρεα τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τῶν μὲν τετραγώνων τῶν ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ ἐλάττονα, τῶν δὲ τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ μείζονα, δεδειγμένον ἐσσεῖται τὸ προτεθέν.

   Ἐντὶ δὴ τὸ μὲν περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ καὶ τὰ τρίτα μέρεα τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ ἴσα τοῖς τετραγώνοις τοῖς ἀπὸ ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ, ΝΞ καὶ τῷ περιεχομένῳ ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ καὶ τῷ τρίτῳ μέρει τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ, τὰ δὲ ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ τετράγωνα ἴσα τοῖς ἀπὸ τᾶν ΒΦ, ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ τετραγώνοις καὶ τοῖς ἀπὸ τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ καὶ τῷ περιεχομένῳ ὑπὸ τᾶς ΒΦ καὶ τᾶς διπλασίας τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ. Κοινὰ μὲν οὖν ἐντι ἑκατέρων τὰ τετράγωνα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ ΝΞ, τὸ δὲ περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας ταῖς ΟΧ, ΠΨ, ΩΡ, ϠΣ, ϞΤ, ΥΝ ἔλασσόν ἐστι τοῦ περιεχομένου ὑπό τε τᾶς ΒΦ καὶ τᾶς διπλασίας τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ διὰ τὸ τὰς νῦν εἰρημένας γραμμὰς ταῖς μὲν ΓΟ, ΕΠ, ΡΗ, ΙΣ, ΛΤ, ΥΝ ἴσας εἶμεν, τᾶν δὲ λοιπᾶν [30] μείζονας, καὶ τὰ τετράγωνα δὲ τὰ ἀπὸ τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ μείζονά ἐντι τοῦ τρίτου μέρεος τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ· δέδεικται γὰρ τοῦτο ἐν τοῖς ἐπάνω· ἐλάττονα ἄρα ἐντὶ τὰ ῥηθέντα χωρία τῶν τετραγώνων τῶν ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ.

   Λοιπὸν δὲ δειξοῦμες ὅτι μείζονά ἐντι τῶν τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ. Πάλιν δὴ τὰ τετράγωνα τὰ ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ ἴσα ἐντὶ τοῖς τε ἀπὸ τᾶν ΧΓ, ΕΨ, ΗΩ, ΙϠ, ΛϞ καὶ τοῖς ἀπὸ τᾶν ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ, ΝΞ καὶ τῷ περιεχομένῳ ὑπό τε τᾶς ΝΞ καὶ τᾶς διπλασίας πασᾶν τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ. Καί ἐστι κοινὰ μὲν τὰ ἀπὸ τᾶν ΧΔ, ΨΖ, ΩΘ, ϠΚ, ΜϞ, ΝΞ, μεῖζον δὲ τὸ ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τοῦ ὑπὸ τᾶς ΝΞ καὶ τᾶς διπλασίας πασᾶν τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ, ἐντὶ δὲ καὶ τὰ τετράγωνα τὰ ἀπὸ τᾶν ΧΟ, ΨΠ, ΩΡ, ϠΣ, ϞΤ, ΥΝ τῶν ἀπὸ τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ μείζονα ἢ τριπλάσια· δέδεικται γὰρ καὶ τοῦτο· μείζονα ἄρα ἐντὶ τὰ ῥηθέντα χωρία τῶν τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ.

ΠΟΡΙΣΜΑ

   Καὶ τοίνυν εἴ κα ὁμοῖα ἀναγραφέωντι ἀπὸ πασᾶν, ἀπό τε τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ, εἴδεα, πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς [31] τοῦ ἀπὸ τᾶς ἐλαχίστας εἴδεος ἐλάσσονα λόγον ἑξοῦντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπό τε τᾶς μεγίστας καὶ τᾶς ἐλαχίστας καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ μεγίστα τᾶς ἐλαχίστας, ποτὶ δὲ τὰ ἀπὸ τᾶν αὐτᾶν εἴδεα χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα τοῦ αὐτοῦ λόγου· τὸν αὐτὸν γὰρ ἑξοῦντι λόγον τὰ ὁμοῖα εἴδεα τοῖς τετραγώνοις.

ΟΡΟΙ

   α΄. Εἴ κα εὐθεῖα ἐπιζευχθῇ γραμμὰ ἐν ἐπιπέδῳ καὶ μένοντος τοῦ ἑτέρου πέρατος αὐτᾶς ἰσοταχέως περιενεχθεῖσα ὁσακισοῦν ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, ἅμα δὲ τᾷ γραμμᾷ περιαγομένᾳ φέρηταί τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ κατὰ τᾶς εὐθείας ἀρξάμενον ἀπὸ τοῦ μένοντος πέρατος, τὸ σαμεῖον ἕλικα γράψει ἐν τῷ ἐπιπέδῳ.

   β΄. Καλείσθω οὖν τὸ μὲν πέρας τᾶς εὐθείας τὸ μένον περιαγομένας αὐτᾶς ἀρχὰ τᾶς ἕλικος.

   γ΄. Ἁ δὲ θέσις τᾶς γραμμᾶς, ἀφ' ἇς ἄρξατο ἁ εὐθεῖα περιφέρεσθαι, ἀρχὰ τᾶς περιφορᾶς.

   δ΄. Εὐθεῖα, ἃν μὲν ἐν τᾷ πρώτᾳ περιφορᾷ διαπορευθῇ τὸ σαμεῖον τὸ κατὰ τᾶς εὐθείας φερόμενον, πρώτα καλείσθω, ἃν δ' ἐν τᾷ δευτέρᾳ περιφορᾷ τὸ αὐτὸ σαμεῖον διανύσῃ, δευτέρα, καὶ αἱ ἄλλαι ὁμοίως ταύταις ὁμωνύμως ταῖς περιφοραῖς καλείσθωσαν.

[32]    ε΄. Τὸ δὲ χωρίον τὸ περιλαφθὲν ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γραφείσας καὶ τᾶς εὐθείας, ἅ ἐστιν πρώτα, πρῶτον καλείσθω, τὸ δὲ περιλαφθὲν ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γραφείσας καὶ τᾶς εὐθείας τᾶς δευτέρας δεύτερον καλείσθω, καὶ τὰ ἄλλα ἑξῆς οὕτω καλείσθω.

   Ϛ. Καὶ εἴ κα ἀπὸ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ἀχθῇ τις εὐθεῖα γραμμά, τᾶς εὐθείας ταύτας τὰ ἐπὶ τὰ αὐτά, ἐφ' ἅ κα ἁ περιφορὰ γένηται, προαγουμένα καλείσθω, τὰ δὲ ἐπὶ θάτερα ἑπόμενα.

   ζ΄. Ὅ τε γραφεὶς κύκλος κέντρῳ μὲν τῷ σαμείῳ, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, διαστήματι δὲ τᾷ εὐθείᾳ, ἅ ἐστιν πρώτα, πρῶτος καλείσθω, ὁ δὲ γραφεὶς κέντρῳ μὲν τῷ αὐτῷ, διαστήματι δὲ τᾷ διπλασίᾳ εὐθείᾳ δεύτερος καλείσθω, καὶ οἱ ἄλλοι δὲ ἑξῆς τούτοις τὸν αὐτὸν τρόπον.

   ιβ΄.

   Εἴ κα ποτὶ τὰν ἕλικα τὰν ἐν μιᾷ περιφορᾷ ὁποιᾳοῦν γεγραμμέναν ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος εὐθεῖαι ἐμπεσῶντι ὁποιαιοῦν ἴσας ποιοῦσαι γωνίας ποτ' ἀλλάλας, τῷ ἴσῳ ὑπερέχοντι ἀλλαλᾶν.

[33]    Ἔστω ἕλιξ, ἐφ' ἇς αἱ ΑΒ, ΑΓ, ΑΔ, ΑΕ, ΑΖ ἴσας γωνίας ποιοῦσαι ποτ' ἀλλάλας. Δεικτέον ὅτι τῷ ἴσῳ ὑπερέχει ἁ ΑΓ τᾶς ΑΒ καὶ ἁ ΑΔ τᾶς ΑΓ καὶ αἱ ἄλλαι ὁμοίως.

   Ἐν ᾧ γὰρ χρόνῳ ἁ περιαγομένα γραμμὰ ἀπὸ τᾶς ΑΒ ἐπὶ τὰν ΑΓ ἀφικνεῖται, ἐν τούτῳ τῷ χρόνῳ τὸ σαμεῖον τὸ κατὰ τᾶς εὐθείας φερόμενον τὰν ὑπεροχὰν διαπορεύεται, ᾇ ὑπερέχει ἁ ΓΑ τᾶς ΑΒ, ἐν ᾧ δὲ χρόνῳ ἀπὸ τᾶς ΑΓ ἐπὶ τὰν ΑΔ, ἐν τούτῳ διαπορεύεται τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΑΔ τᾶς ΑΓ. Ἐν ἴσῳ δὲ χρόνῳ ἁ περιαγομένα γραμμὰ ἀπό τε τᾶς ΑΒ ἐπὶ τὰν ΑΓ ἀφικνεῖται καὶ ἀπὸ τᾶς ΑΓ ἐπὶ τὰν ΑΔ, ἐπειδὴ αἱ γωνίαι ἴσαι ἐντί· ἐν ἴσῳ ἄρα χρόνῳ τὸ κατὰ τᾶς εὐθείας φερόμενον σαμεῖον διαπορεύεται τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΓΑ τᾶς ΑΒ, καὶ τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΑΔ τᾶς ΑΓ. Τῷ ἴσῳ ἄρα ὑπερέχει ἅ τε ΑΓ τᾶς ΑΒ καὶ ἁ ΑΔ τᾶς ΑΓ, καὶ αἱ λοιπαί.

   ιγ΄.

   Εἴ κα εὐθεῖα γραμμὰ τᾶς ἕλικος ἐπιψαύῃ, καθ᾿ ἓν μόνον ἐπιψαύσει σαμεῖον.

   Ἔστω ἕλιξ, ἐφ' ἇς τὰ Α, Β, Γ, Δ, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Α σαμεῖον, ἀρχὰ δὲ τᾶς περιφορᾶς ἁ ΑΔ [34] εὐθεῖα, καὶ ἐπιψαυέτω τᾶς ἕλικος εὐθεῖά τις ἁ ΖΕ. Φαμὶ δὴ καθ᾿ ἓν μόνον σαμεῖον ἐπιψαύειν αὐτᾶς.

   Ἐπιψαυέτω γάρ, εἰ δυνατόν, κατὰ δύο σαμεῖα τὰ Γ, Η, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΑΗ, καὶ ἁ γωνία δίχα τετμάσθω ἁ περιεχόμενα ὑπὸ τᾶν ΑΗ, ΑΓ, καθ᾿ ὃ δὲ σαμεῖον ἁ δίχα τέμνουσα τὰν γωνίαν τᾷ ἕλικι ποτιπίπτει, ἔστω τὸ Θ. Τῷ δὴ ἴσῳ ὑπερέχει ἅ τε ΑΗ τᾶς ΑΘ καὶ ἁ ΑΘ τᾶς ΑΓ, ἐπειδὴ ἴσας γωνίας περιέχοντι ποτ' ἀλλάλας· ὥστε διπλάσιαί ἐντι αἱ ΑΗ, ΑΓ τᾶς ΑΘ. Ἀλλὰ τᾶς ἐν τῷ τριγώνῳ [τᾶς ΑΘ] δίχα τεμνούσας τὰν γωνίαν μείζονές ἐντι ἢ διπλάσιαι· δῆλον οὖν ὅτι, καθ᾿ ὃ συμπίπτει σαμεῖον τᾷ ΓΗ εὐθείᾳ ἁ ΑΘ, μεταξὺ τῶν Θ, Α ἐντὶ σαμείων· τέμνει ἄρα ἁ ΕΖ τὰν ἕλικα, ἐπειδή τι τῶν ἐν τᾷ ΓΘΗ σαμείων ἐντός ἐστι τᾶς ἕλικος. Ὑπέκειτο δὲ ἐπιψαύουσα· καθ᾿ ἓν ἄρα μόνον ἅπτεται ἁ ΕΖ τᾶς ἕλικος.

   ιδ΄.

   Εἴ κα ποτὶ τὰν ἕλικα τὰν ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμέναν ποτιπεσέωντι δύο εὐθεῖαι ἀπὸ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, καὶ ἐκβληθέωντι ποτὶ τὰν τοῦ πρώτου κύκλου περιφέρειαν, τὸν αὐτὸν ἑξοῦντι λόγον αἱ ποτὶ τὰν ἕλικα ποτιπίπτουσαι ποτ' ἀλλάλας, ὃν αἱ περιφέρειαι τοῦ κύκλου αἱ μεταξὺ τοῦ πέρατος τᾶς ἕλικος καὶ τῶν περάτων τᾶν ἐκβληθεισᾶν εὐθειᾶν τῶν ἐπὶ τᾶς περιφερείας γινομένων, ἐπὶ τὰ προαγούμενα λαμβανομενᾶν τᾶν περιφερειᾶν ἀπὸ τοῦ πέρατος τᾶς ἕλικος.

   Ἔστω ἕλιξ ἁ ΑΒΓΔΕΘ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἀρχὰ δὲ τᾶς μὲν ἕλικος ἔστω τὸ Α σαμεῖον, ἁ δὲ

[35] ΘΑ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς ἔστω, καὶ κύκλος ὁ ΘΚΗ ἔστω ὁ πρῶτος, ποτιπιπτόντων δὲ ἀπὸ τοῦ Α σαμείου ποτὶ τὰν ἕλικα αἱ ΑΕ, ΑΔ καὶ ἐκπιπτόντων ποτὶ τὰν τοῦ κύκλου περιφέρειαν ἐπὶ τὰ Ζ, Η. Δεικτέον ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΕ ποτὶ τὰν ΑΔ, ὃν ἁ ΘΚΖ περιφέρεια ποτὶ τὰν ΘΚΗ περιφέρειαν.

   Περιαγομένας γὰρ τᾶς ΑΘ γραμμᾶς δῆλον ὡς τὸ μὲν Θ σαμεῖον κατὰ τᾶς τοῦ ΘΚΗ κύκλου περιφερείας ἐνηνεγμένον ἐστὶν ἰσοταχέως, τὸ δὲ Α κατὰ τᾶς εὐθείας φερόμενον τὰν ΑΘ γραμμὰν πορεύεται, καὶ τὸ Θ σαμεῖον κατὰ τᾶς τοῦ κύκλου περιφερείας φερόμενον τὰν ΘΚΖ περιφέρειαν, τὸ δὲ Α τὰν ΑΕ εὐθεῖαν, καὶ πάλιν τό τε Α σαμεῖον τὰν ΑΔ γραμμὰν καὶ τὸ Θ τὰν ΘΚΗ περιφέρειαν, ἑκάτερον ἰσοταχέως αὐτὸ ἑαυτῷ φερόμενον· δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΕ ποτὶ τὰν ΑΔ, ὃν ἁ ΘΚΖ περιφέρεια ποτὶ τὰν ΘΚΗ περιφέρειαν [δέδεικται γὰρ τοῦτο ἔξω ἐν τοῖς πρώτοις].

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα ἁ ἑτέρα τᾶν ποτιπιπτουσᾶν ἐπὶ τὸ πέρας τᾶς ἕλικος ποτιπίπτῃ, ὅτι τὸ αὐτὸ συμβαίνει.

[36]    ιε΄.

   Εἰ δέ κα ποτὶ τὰν ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμέναν ἕλικα ποτιπίπτωντι εὐθεῖαι ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος, τὸν αὐτὸν ἑξοῦντι λόγον αἱ εὐθεῖαι ποτ' ἀλλάλας, ὃν αἱ εἰρημέναι περιφέρειαι μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας λαμβανομένας.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔΘ, ἁ μὲν ΑΒΓΔΘ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἁ δὲ ΘΛΕΜ ἐν τᾷ δευτέρᾳ, καὶ ποτιπιπτόντων εὐθεῖαι αἱ ΑΕ, ΑΛ. Δεικτέον ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΛ ποτὶ τὰν ΑΕ, ὃν ἁ ΘΚΖ περιφέρεια μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ ΘΚΗ μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας.

   Ἐν ἴσῳ γὰρ χρόνῳ τὸ Α σαμεῖον κατὰ τᾶς εὐθείας φερόμενον τὰν ΑΛ γραμμὰν διαπορεύεται, καὶ τὸ Θ σαμεῖον κατὰ τᾶς τοῦ κύκλου περιφερείας φερόμενον ὅλαν τε τὰν τοῦ κύκλου περιφέρειαν καὶ ἔτι τὰν ΘΚΖ περιφέρειαν διαπορεύεται, καὶ πάλιν τὸ Α σαμεῖον τὰν ΑΕ εὐθεῖαν καὶ τὸ Θ ὅλαν τε τὰν τοῦ κύκλου περιφέρειαν καὶ ἔτι τὰν ΘΚΗ, ἑκάτερον ἰσοταχέως αὐτὸ ἑαυτῷ φερόμενον· [37] δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΛ γραμμὰ ποτὶ τὰν ΑΕ, ὃν ἁ ΘΚΖ περιφέρεια μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν ΘΚΗ περιφέρειαν μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας.

   Τὸν αὐτὸν δὲ τρόπον δειχθήσεται, καὶ εἴ κα ποτὶ τὰν ἐν τᾷ τρίτᾳ περιφορᾷ γεγραμμέναν ἕλικα ποτιπεσέωντι εὐθεῖαι, ὅτι τὸν αὐτὸν λόγον ἑξοῦντι ποτ' ἀλλάλας, ὃν αἱ εἰρημέναι περιφέρειαι μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας δὶς λαμβανομένας· ὁμοίως δὲ καὶ αἱ ποτὶ τὰς ἄλλας ἕλικας ποτιπίπτουσαι δείκνυνται ὅτι τὸν αὐτὸν ἔχοντι λόγον, ὃν αἱ εἰρημέναι περιφέρειαι μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας τοσαυτάκις λαμβανομένας, ὅσος ἐστὶν ὁ ἑνὶ ἐλάσσων ἀριθμὸς τᾶν περιφορᾶν, καὶ εἴ κα ἁ ποτιπίπτουσα ἁ ἑτέρα ποτὶ τὸ πέρας τᾶς ἕλικος πίπτῃ.

   ιϚ΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ, καὶ ἀπὸ τᾶς ἁφᾶς εὐθεῖα γραμμὰ ἐπιζευχθῇ ἐπὶ τὸ σαμεῖον, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ἃς ποιεῖ γωνίας ἁ ἐφαπτομένα ποτὶ τὰν ἐπιζευχθεῖσαν, ἀνίσοι ἐσσοῦνται καὶ ἁ μὲν ἐν τοῖς προαγουμένοις ἀμβλεῖα, ἁ δὲ ἐν τοῖς ἑπομένοις ὀξεῖα.

   Ἔστω ἕλιξ, ἐφ' ἇς τὰ Α, Β, Γ, Δ, Θ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, καὶ ἔστω τὸ μὲν Α σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΑΘ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς, ὅ τε πρῶτος κύκλος ὁ ΘΚΗ, ἐπιψαυέτω δέ τις εὐθεῖα γραμμὰ τᾶς ἕλικος ἁ ΕΔΖ κατὰ τὸ Δ, καὶ ἀπὸ τοῦ Δ ἐπὶ τὸ Α ἐπεζεύχθω ἁ ΔΑ. Δεικτέον ὅτι ἁ ΔΖ ποτὶ τὰν ΑΔ ἀμβλεῖαν ποιεῖ γωνίαν.

[38]    Γεγράφθω κύκλος ὁ ΔΤΝ κέντρῳ μὲν τῷ Α, διαστήματι δὲ τᾷ ΑΔ· ἀναγκαῖον δὴ τούτου τοῦ κύκλου τὰν μὲν ἐν τοῖς προαγουμένοις περιφέρειαν ἐντὸς πίπτειν τᾶς ἕλικος, τὰν δὲ ἐν τοῖς ἑπομένοις ἐκτὸς διὰ τὸ τᾶν ἀπὸ τοῦ Α ποτὶ τὰν ἕλικα ποτιπιπτουσᾶν εὐθειᾶν τὰς μὲν ἐν τοῖς προαγουμένοις μείζονας εἶμεν τᾶς ΑΔ, τὰς δὲ ἐν τοῖς ἑπομένοις ἐλάσσονας. Ὅτι μὲν οὖν ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ οὐκ ἔστιν ὀξεῖα δῆλον, ἐπειδὴ μείζων ἐστὶ τᾶς τοῦ ἡμικυκλίου, ὅτι δὲ ὀρθὰ οὐκ ἔστι δεικτέον οὕτως· ἔστω γὰρ, εἰ δυνατόν, ὀρθά· ἁ ἄρα ΕΔΖ ἐπιψαύει τοῦ ΔΤΝ κύκλου. Δυνατὸν δή ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν εὐθεῖαν ποτὶ τὰν ἐπιψαύουσαν, ὥστε τὰν μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς τοῦ κύκλου περιφερείας εὐθεῖαν ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ κύκλου ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ἁ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς ποτιπιπτούσας περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν. Ποτιπιπτέτω δὴ ἁ ΑΙ· τεμεῖ δὴ αὕτα τὰν μὲν ἕλικα κατὰ τὸ Λ, τὰν δὲ τοῦ ΔΝΤ κύκλου περιφέρειαν κατὰ τὸ Ρ· καὶ ἐχέτω [39] ἁ ΡΙ εὐθεῖα ποτὶ τὰν ΑΡ ἐλάσσονα λόγον τοῦ ὃν ἔχει ἁ ΔΡ περιφέρεια ποτὶ τὰν ΔΝΤ περιφέρειαν· καὶ ὅλα ἄρα ἁ ΙΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΡΔΝΤ περιφέρεια ποτὶ τὰν ΔΝΤ περιφέρειαν, τουτέστιν ὃν ἔχει ἁ ΣΗΚΘ περιφέρεια ποτὶ τὰν ΗΚΘ περιφέρειαν. Ὃν δὲ ἁ ΣΗΚΘ περιφέρεια ποτὶ τὰν ΗΚΘ περιφέρειαν, τοῦτον ἔχει ἁ ΑΛ εὐθεῖα ποτὶ τὰν ΑΔ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΑΙ ποτὶ τὰν ΑΡ ἤπερ ἁ ΛΑ ποτὶ τὰν ΑΔ· ὅπερ ἀδύνατον· ἴσα γὰρ ἁ ΡΑ τᾷ ΑΔ. Οὐκ ἄρα ἐστὶν ὀρθὰ ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ. Δέδεικται δὲ ὅτι οὐδὲ ὀξεῖα· ἀμβλεῖα ἄρα ἐστίν. Ὥστε ἁ λοιπὰ ὀξεῖά ἐστιν.

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα ἁ ἐπιψαύουσα τᾶς ἕλικος κατὰ τὸ πέρας ἐπιψαύῃ, ὅτι τὸ αὐτὸ συμβήσεται.

   ιζ΄.

   Καὶ τοίνυν, εἴ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ ἁ εὐθεῖα, τὸ αὐτὸ συμβήσεται.

[40]    Ἐπιψαυέτω γὰρ ἁ ΕΖ εὐθεῖα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος κατὰ τὸ Δ, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Ὁμοίως δὴ τᾶς τοῦ ΡΝΔ κύκλου περιφερείας τὰ μὲν ἐν τοῖς προαγουμένοις τᾶς ἕλικος ἐντὸς πεσοῦνται, τὰ δὲ ἐν τοῖς ἑπομένοις ἐκτός· ἁ οὖν γωνία ἁ ὑπὸ τᾶν ΑΔΖ οὐκ ἔστιν ὀρθά, ἀλλὰ ἀμβλεῖα. Ἔστω γάρ, εἰ δυνατόν, ὀρθά· ἐπιψαύσει δὴ ἁ ΕΖ τοῦ ΡΝΔ κύκλου κατὰ τὸ Δ. Ἄχθω δὴ πάλιν ποτὶ τὰν ἐπιψαύουσαν ἁ ΑΙ καὶ τεμνέτω τὰν μὲν ἕλικα κατὰ τὸ Χ, τὰν δὲ τοῦ ΡΝΔ κύκλου περιφέρειαν κατὰ τὸ Ρ, ἐχέτω δὲ ἁ ΡΙ ποτὶ ΡΑ ἐλάσσονα λόγον τοῦ ὃν ἔχει ἁ ΔΡ περιφέρεια ποτὶ ὅλαν τὰν τοῦ ΔΡΝ κύκλου περιφέρειαν καὶ [ποτὶ] τὰν ΔΝΤ· δέδεικται γὰρ τοῦτο δυνατὸν ἐόν· καὶ ὅλα ἄρα ἁ ΙΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΡΔΝΤ περιφέρεια μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν ΔΝΤ περιφέρειαν μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας. Ἀλλ' ὃν ἔχει λόγον ἁ ΡΔΝΤ περιφέρεια μεθ' ὅλας τᾶς τοῦ ΔΝΤΡ κύκλου περιφερείας ποτὶ τὰν ΔΝΤ περιφέρειαν μεθ' ὅλας τᾶς τοῦ ΔΝΤΡ κύκλου περιφερείας, τοῦτον ἔχει τὸν λόγον ἁ ΣΗΚΘ περιφέρεια μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας τᾶς ΘΣΗΚ ποτὶ τὰν ΗΚΘ περιφέρειαν μεθ' ὅλας τᾶς τοῦ ΘΣΗΚ κύκλου περιφερείας, ὃν δὲ λόγον ἔχοντι αἱ ὕστερον εἰρημέναι περιφέρειαι, τοῦτον ἔχει τὸν λόγον ἁ ΧΑ εὐθεῖα ποτὶ τὰν ΑΔ εὐθεῖαν· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΙΑ ποτὶ τὰν ΑΡ ἢ ἁ ΑΧ ποτὶ τὰν ΑΔ· ὅπερ ἀδύνατον [ἴση μὲν γὰρ ἡ ΡΑ τῇ ΑΔ, μείζων δὲ ἡ ΙΑ τῆς ΑΧ]. Δῆλον οὖν ὅτι ἀμβλεῖά ἐστιν ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ· ὥστε ἁ λοιπὰ ὀξεῖά ἐστι.

[41]    Τὰ δ' αὐτὰ συμβήσεται, καὶ εἴ κα ἁ ἐπιψαύουσα κατὰ τὸ πέρας τᾶς ἕλικος ἐπιψαύῃ.

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ τις εὐθεῖα, καὶ εἴ κα κατὰ τὸ πέρας αὐτᾶς, ὅτι ἀνίσους ποιήσει τὰς γωνίας ποτὶ τὰν ἀπὸ τᾶς ἁφᾶς ἐπιζευχθεῖσαν ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος καὶ τὰν μὲν ἐν τοῖς προαγουμένοις ἀμβλεῖαν, τὰν δὲ ἐν τοῖς ἑπομένοις ὀξεῖαν.

   ιη΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ κατὰ τὸ πέρας τᾶς ἕλικος, ἀπὸ δὲ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ποτ' ὀρθὰς ἀχθῇ τις τᾷ ἀρχᾷ τᾶς περιφορᾶς, ἁ ἀχθεῖσα συμπεσεῖται τᾷ ἐπιψαυούσᾳ, καὶ ἁ μεταξὺ εὐθεῖα τᾶς ἐπιψαυούσας καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα ἐσσεῖται τᾷ τοῦ πρώτου κύκλου περιφερείᾳ.

   Ἔστω ἕλιξ ἁ ΑΒΓΔΘ, ἔστω δὲ τὸ Α σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΑ γραμμὰ ἀρχὰ τᾶς περιφορᾶς, ὁ δὲ ΘΗΚ κύκλος ὁ πρῶτος, ἐπιψαυέτω δέ τις τᾶς ἕλικος κατὰ τὸ Θ ἁ ΘΖ, καὶ ἀπὸ τοῦ Α ἄχθω ποτ' ὀρθὰς τᾷ ΘΑ ἁ ΑΖ· συμπεσεῖται δὴ αὕτα ποτὶ τὰν ΘΖ, ἐπεὶ αἱ ΖΘ, ΘΑ ὀξεῖαν [42] γωνίαν περιέχοντι. Συμπιπτέτω κατὰ τὸ Ζ. Δεικτέον ὅτι ἁ ΖΑ ἴσα ἐστὶ τᾷ τοῦ ΘΚΗ κύκλου περιφερείᾳ.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω πρότερον, εἰ δυνατόν, μείζων. Ἔλαβον δή τινα εὐθεῖαν τὰν ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσονα, τᾶς δὲ τοῦ ΘΗΚ κύκλου περιφερείας μείζονα. Ἔστιν δὴ κύκλος τις ὁ ΘΗΚ καὶ ἐν τῷ κύκλῳ γραμμὰ ἐλάσσων τᾶς διαμέτρου ἁ ΘΗ καὶ λόγος, ὃν ἔχει ἁ ΘΑ ποτὶ ΑΛ, μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΗΘ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὸν ἀγμέναν, διότι καὶ τοῦ ὃν ἔχει ἁ ΘΑ ποτὶ ΑΖ· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν τὰν ΑΝ, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας τὰν ΝΡ ποτὶ ΘΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΘΑ ποτὶ τὰν ΑΛ· ἕξει οὖν ἁ ΝΡ ποτὶ τὰν ΡΑ λόγον, ὃν ἁ ΘΡ εὐθεῖα ποτὶ τὰν ΑΛ. Ἁ δὲ ΘΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· ἁ μὲν γὰρ ΘΡ εὐθεῖα ἐλάσσων ἐστὶ τᾶς ΘΡ περιφερείας, ἁ δὲ ΑΛ εὐθεῖα τᾶς τοῦ ΘΗΚ κύκλου περιφερείας μείζων· ἐλάσσονα οὖν λόγον ἕξει καὶ ἁ ΝΡ ποτὶ ΡΑ ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· καὶ ὅλα οὖν ἁ ΝΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἤπερ ἁ ΘΡ περιφέρεια μεθ' ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ ΘΡ περιφέρεια μεθ' ὅλας τᾶς τοῦ ΘΗΚ κύκλου περιφερείας ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν, τοῦτον ἔχει ἁ ΧΑ ποτὶ τὰν ΑΘ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΝΑ ποτὶ τὰν ΑΡ ἤπερ ἁ ΧΑ ποτὶ τὰν ΑΘ· ὅπερ ἀδύνατον· ἁ μὲν γὰρ ΝΑ μείζων ἐστὶ τᾶς ΑΧ, ἁ δὲ ΑΡ ἴσα ἐστὶ τᾷ ΘΑ. Οὐκ ἄρα μείζων ἁ ΖΑ τᾶς τοῦ κύκλου περιφερείας τοῦ ΘΗΚ.

[43]    Ἔστω δὴ πάλιν, εἰ δυνατόν, ἐλάσσων ἁ ΖΑ τᾶς τοῦ ΘΗΚ κύκλου περιφερείας. Ἔλαβον δή τινα εὐθεῖαν πάλιν τὰν ΑΛ τᾶς μὲν ΑΖ μείζονα, τᾶς δὲ τοῦ ΘΗΚ κύκλου περιφερείας ἐλάσσονα, καὶ ἄγω ἀπὸ τοῦ Θ τὰν ΘΜ παράλληλον τᾷ ΑΖ. Πάλιν οὖν κύκλος ἐστὶν ὁ ΘΗΚ καὶ ἐν αὐτῷ ἐλάσσων γραμμὰ τᾶς διαμέτρου ἁ ΘΗ καὶ ἄλλα ἐπιψαύουσα τοῦ κύκλου κατὰ τὸ Θ καὶ λόγος, ὃν ἔχει ἁ ΑΘ ποτὶ τὰν ΑΛ, ἐλάσσων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΗΘ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν, ἐπειδὴ καὶ τοῦ ὃν ἔχει ἁ ΘΑ ποτὶ ΑΖ ἐλάσσων ἐστί· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ἀγαγεῖν τὰν ΑΠ ποτὶ τὰν ἐπιψαύουσαν, ὥστε τὰν ΡΝ τὰν μεταξὺ τᾶς ἐν τῷ κύκλῳ εὐθείας καὶ τᾶς περιφερείας ποτὶ τὰν ΘΠ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει ἁ ΘΑ ποτὶ τὰν ΑΛ· τεμεῖ δὴ ἁ ΑΠ τὸν μὲν κύκλον κατὰ τὸ Ρ, τὰν δὲ ἕλικα κατὰ τὸ Χ· καὶ ἕξει καὶ ἐναλλὰξ τὸν αὐτὸν λόγον ἁ ΝΡ ποτὶ ΡΑ, ὃν ἁ ΘΠ ποτὶ ΑΛ. Ἁ δὲ ΘΠ ποτὶ τὰν ΑΛ μείζονα λόγον ἔχει ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· ἁ μὲν γὰρ ΘΠ εὐθεῖα μείζων ἐστὶν τᾶς ΘΡ περιφερείας, ἁ δὲ ΑΛ ἐλάσσων τᾶς τοῦ ΘΗΚ κύκλου περιφερείας· μείζονα ἄρα λόγον ἔχει ἁ ΠΡ ποτὶ τὰν ΑΡ ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ [44] κύκλου περιφέρειαν· ὥστε καὶ ἁ ΡΑ ποτὶ τὰν ΑΝ μείζονα λόγον ἔχει ἢ ἁ τοῦ ΘΗΚ κύκλου περιφέρεια ποτὶ τὰν ΘΚΡ περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ τοῦ ΘΗΚ κύκλου περιφέρεια ποτὶ τὰν ΘΚΡ περιφέρειαν, τοῦτον ἔχει ἁ ΘΑ εὐθεῖα ποτὶ τὰν ΑΧ· δέδεικται γὰρ τοῦτο· μείζονα ἄρα λόγον ἔχει ἁ ΡΑ ποτὶ τὰν ΑΝ ἢ ἁ ΘΑ ποτὶ τὰν ΑΧ· ὅπερ ἀδύνατον. Οὐκ ἄρα μείζων ἐστὶν οὐδὲ ἐλάσσων ἁ ΖΑ τᾶς τοῦ ΘΗΚ κύκλου περιφερείας· ἴσα ἄρα.

   ιθ΄.

   Εἰ δέ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος κατὰ τὸ πέρας ἐπιψαύῃ εὐθεῖα, καὶ ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος ἀχθῇ τις ποτ' ὀρθὰς τᾷ ἀρχᾷ τᾶς περιφορᾶς, συμπεσεῖται αὕτα ποτὶ τὰν ἐπιψαύουσαν, καὶ ἐσσεῖται ἁ εὐθεῖα ἁ μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς ἀρχᾶς τᾶς ἕλικος διπλασία τᾶς τοῦ δευτέρου κύκλου περιφερείας.

   Ἔστω γὰρ ἁ μὲν ΑΒΓΘ ἕλιξ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἁ δὲ ΘΕΤ ἐν τᾷ δευτέρᾳ, καὶ ὁ μὲν ΘΚΗ κύκλος ὁ πρῶτος, ὁ δὲ ΤΜΝ ὁ δεύτερος, ἔστω δέ τις [45] γραμμὰ ἐπιψαύουσα τᾶς ἕλικος κατὰ τὸ Θ ἁ ΤΖ, ἁ δὲ ΖΑ ποτ' ὀρθὰς ἄχθῳ τᾷ ΤΑ· συμπεσεῖται δὲ αὕτα τᾷ ΤΖ διὰ τὸ δεδεῖχθαι τὰν γωνίαν ὀξεῖαν ἐοῦσαν τὰν ὑπὸ τᾶν ΑΤΖ. Δεικτέον ὅτι ἁ ΖΑ εὐθεῖα διπλασία ἐντὶ τᾶς τοῦ ΤΜΝ κύκλου περιφερείας.

   Εἰ γὰρ μή ἐστιν διπλασία, ἤτοι μείζων ἐστὶν ἢ διπλασία ἢ ἐλάσσων ἐστὶν ἢ διπλασία. Ἔστω πρότερον, εἰ δυνατόν, μείζων ἢ διπλασία, καὶ λελάφθω τις εὐθεῖα ἁ ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσων, τᾶς δὲ τοῦ ΤΜΝ κύκλου περιφερείας μείζων ἢ διπλασία. Ἔστιν δή τις κύκλος ὁ ΤΜΝ καὶ ἐν τῷ κύκλῳ γραμμὰ δεδομένα ἐλάσσων τᾶς διαμέτρου ἁ ΤΝ, καὶ ὃν ἔχει ἁ ΤΑ ποτὶ τὰν ΑΛ μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΤΝ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν τὰν ΑΣ ποτὶ τὰν ΤΝ ἐκβεβλημέναν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας τὰν ΡΣ ποτὶ τὰν ΤΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΤΑ ποτὶ τὰν ΑΛ· τεμεῖ δὴ ἁ ΑΣ τὸν μὲν κύκλον κατὰ τὸ Ρ, τὰν δὲ ἕλικα κατὰ τὸ Χ· καὶ ἐναλλὰξ τὸν αὐτὸν ἕξει λόγον ἁ ΡΣ ποτὶ τὰν ΤΑ, ὃν ἁ ΤΡ ποτὶ τὰν ΑΛ. Ἁ δὲ ΤΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΤΡ περιφέρεια ποτὶ τὰν διπλασίαν τοῦ ΤΜΝ κύκλου περιφέρειαν· ἔστιν γὰρ ἁ μὲν ΤΡ εὐθεῖα ἐλάσσων τᾶς ΤΡ περιφερείας, ἁ δὲ ΑΛ εὐθεῖα μείζων ἢ διπλασία τᾶς τοῦ ΤΜΝ κύκλου περιφερείας· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΡΣ ποτὶ τὰν ΑΡ ἢ ἁ ΤΡ περιφέρεια ποτὶ τὰν διπλασίαν τᾶς τοῦ ΤΜΝ κύκλου περιφερείας· ὅλα οὖν ἁ ΣΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΤΡ περιφέρεια μετὰ τᾶς τοῦ ΤΜΝ κύκλου περιφερείας δὶς εἰρημένας ποτὶ τὰν τοῦ ΤΜΝ κύκλου περιφέρειαν [46] δὶς εἰρημέναν. Ὃν δὲ λόγον ἔχοντι αἱ εἰρημέναι περιφέρειαι, τοῦτον ἔχει τὸν λόγον ἁ ΧΑ ποτὶ τὰν ΑΤ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΑΣ ποτὶ τὰν ΑΡ ἢ ἁ ΧΑ ποτὶ τὰν ΤΑ· ὅπερ ἀδύνατον. Οὐκ ἄρα μείζων ἐστὶν ἢ διπλασία ἁ ΖΑ εὐθεῖα τᾶς τοῦ ΤΜΝ κύκλου περιφερείας. Ὁμοίως δὲ δειχθήσεται ὅτι οὐδὲ ἐλάσσων ἢ διπλασία. Δῆλον οὖν ὅτι διπλασία ἐστίν.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δεικτέον, καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ τις εὐθεῖα κατὰ τὸ πέρας τᾶς ἕλικος, καὶ ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος ποτ' ὀρθὰς ἀχθεῖσα τᾷ ἀρχᾷ τᾶς περιφορᾶς συμπίπτῃ ποτὶ τὰν ἐπιψαύουσαν, ὅτι πολλαπλασία ἐστὶν τᾶς τοῦ κύκλου περιφερείας τοῦ κατὰ τὸν ἀριθμὸν τᾶς περιφορᾶς λεγομένου τῷ αὐτῷ ἀριθμῷ.

   κ΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ μὴ κατὰ τὸ πέρας τᾶς ἕλικος, ἀπὸ δὲ τᾶς ἁφᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος εὐθεῖα ἐπιζευχθῇ, καὶ κέντρῳ μὲν τᾷ ἀρχᾷ τᾶς ἕλικος, διαστήματι δὲ τᾷ ἐπιζευχθείσᾳ κύκλος γραφῇ, ἀπὸ δὲ τᾶς ἀρχᾶς τᾶς ἕλικος ἀχθῇ τις ποτ' ὀρθὰς τᾷ ἀπὸ τᾶς ἁφᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπιζευχθείσᾳ, συμπεσεῖται αὕτα ποτὶ τὰν ἐπιψαύουσαν, καὶ ἐσσεῖται ἁ μεταξὺ εὐθεῖα τᾶς τε συμπτώσιος καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα τᾷ περιφερείᾳ τοῦ γραφέντος κύκλου τᾷ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς τομᾶς, καθ᾿ ἃν τέμνει ὁ γραφεὶς κύκλος τὰν ἀρχὰν τᾶς περιφορᾶς, ἐπὶ τὰ προαγούμενα λαμβανομένας τᾶς περιφερείας ἀπὸ τοῦ σαμείου τοῦ ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς.

[47]    Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, καὶ ἐπιψαυέτω τις αὐτᾶς εὐθεῖα ἁ ΕΖ κατὰ τὸ Δ, ἀπὸ δὲ τοῦ Δ ποτὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπεζεύχθω ἁ ΑΔ, καὶ κέντρῳ μὲν τῷ Α, διαστήματι δὲ τῷ ΑΔ κύκλος γεγράφθω ὁ ΔΜΝ, τεμνέτω δ' οὗτος τὰν ἀρχὰν τᾶς περιφορᾶς κατὰ τὸ Κ, ἄχθω δὲ ἁ ΖΑ ποτὶ τὰν ΑΔ ὀρθά. Ὅτι μὲν οὖν αὕτα συμπίπτει δῆλον· ὅτι δὲ καὶ ἴσα ἐστὶν ἁ ΖΑ εὐθεῖα τᾷ ΚΜΝΔ περιφερείᾳ δεικτέον.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω, εἰ δυνατόν, πρότερον μείζων, λελάφθω δέ τις ἁ ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσων, τᾶς δὲ ΚΜΝΔ περιφερείας μείζων. Πάλιν δὴ κύκλος ἐστὶν ὁ ΚΜΝ καὶ ἐν τῷ κύκλῳ γραμμὰ ἐλάσσων τᾶς διαμέτρου ἁ ΔΝ καὶ λόγος, ὃν ἔχει ἁ ΔΑ ποτὶ ΑΛ, μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΔΝ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν τὰν ΑΕ ποτὶ τὰν ΝΔ ἐκβεβλημέναν, ὥστε τὰν ΕΡ ποτὶ τὰν ΔΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΑΛ· δέδεικται γὰρ τοῦτο δυνατὸν ἐόν· ἕξει οὖν καὶ ἁ ΕΡ ποτὶ τὰν ΑΡ τὸν αὐτὸν λόγον, ὃν ἁ ΔΡ ποτὶ τὰν ΑΛ. Ἁ δὲ ΔΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΔΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν, ἐπεὶ ἁ μὲν ΔΡ ἐλάσσων ἐστὶ τᾶς ΔΡ [48] περιφερείας, ἁ δὲ ΑΛ μείζων τᾶς ΚΜΔ περιφερείας· ἐλάσσονα οὖν λόγον ἔχει ἁ ΕΡ εὐθεῖα ποτὶ ΡΑ ἢ ἁ ΔΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν· ὥστε καὶ ἁ ΑΕ ποτὶ ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΚΜΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ ΚΜΡ ποτὶ τὰν ΚΜΔ περιφέρειαν, τοῦτον ἔχει ἁ ΧΑ ποτὶ ΑΔ· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΕΑ ποτὶ ΑΡ ἢ ἁ ΑΧ ποτὶ ΔΑ· ὅπερ ἐστὶν ἀδύνατον. Οὐκ ἄρα μείζων ἁ ΖΑ τᾶς ΚΜΔ περιφερείας. Ὁμοίως δὲ τοῖς πρότερον δειχθήσεται ὅτι οὐδὲ ἐλάσσων ἐστίν· ἴσα ἄρα.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δειχθήσεται, καὶ εἴ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ εὐθεῖα μὴ κατὰ τὸ πέρας τᾶς ἕλικος, τὰ δὲ ἄλλα τὰ αὐτὰ κατασκευασθέωντι, ὅτι ἁ μεταξὺ εὐθεῖα τᾶς ποτὶ τὰν ἐπιψαύουσαν συμπτώσιος καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα ἐστὶν ὅλᾳ τᾷ τοῦ γραφέντος κύκλου περιφερείᾳ καὶ ἔτι τᾷ μεταξὺ τῶν εἰρημένων σαμείων, ὡσαύτως τᾶς περιφερείας λαμβανομένας· καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν γεγραμμένας περιφορᾷ ἕλικος ἐπιψαύῃ τις εὐθεῖα μὴ κατὰ τὸ πέρας τᾶς ἕλικος, τὰ δὲ ἄλλα τὰ αὐτὰ κατασκευασθέωντι, ὅτι ἁ μεταξὺ εὐθεῖα τῶν εἰρημένων σαμείων πολλαπλασία τίς ἐστι τᾶς τοῦ γραφέντος κύκλου περιφερείας κατὰ τὸν ἑνὶ ἐλάσσονα ἀριθμὸν τοῦ καθ᾿ ὃν αἱ περιφοραὶ λέγονται, καὶ ἔτι ἴσα τᾷ μεταξὺ τῶν εἰρημένων σαμείων ὁμοίως λαμβανομένᾳ.

[49]    κα΄.

   Λαμβάνοντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς πρώτας ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς δυνατόν ἐστι περὶ αὐτὸ σχῆμα ἐπίπεδον περιγράψαι καὶ ἄλλο ἐγγράψαι ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Θ σαμεῖον, ἀρχὰ δὲ τᾶς περιφορᾶς ἁ ΘΑ, ὁ δὲ πρῶτος κύκλος ὁ ΖΗΙΑ, αἱ δὲ ΑΗ, ΖΙ διάμετροι αὐτοῦ ποτ' ὀρθὰς ἀλλάλαις. Ἀεὶ δὴ τᾶς ὀρθᾶς γωνίας δίχα τεμνομένας καὶ τοῦ τομέως τοῦ τὰν ὀρθὰν γωνίαν περιέχοντος ἐσσεῖται τὸ καταλειπόμενον τοῦ τομέως ἔλασσον τοῦ προτεθέντος· καὶ ἔστω γεγενημένος ὁ τομεὺς ὁ ΑΘΚ ἐλάσσων τοῦ προτεθέντος χωρίου. Διαιρήσθωσαν δὴ αἱ γωνίαι αἱ τέσσαρες ὀρθαὶ εἰς τὰς ἴσας γωνίας τᾷ περιεχομένᾳ ὑπὸ τᾶν ΑΘ, [50] ΘΚ, καὶ αἱ ποιοῦσαι τὰς γωνίας εὐθεῖαι ἔστε ποτὶ τὰν ἕλικα ἄχθωσαν. Καθ' ὃ δὴ τέμνει σαμεῖον ἁ ΘΚ τὰν ἕλικα, ἔστω τὸ Λ, καὶ κέντρῳ τῷ Θ, διαστήματι δὲ τῷ ΘΛ κύκλος γεγράφθω· πεσεῖται δὲ αὐτοῦ ἁ μὲν εἰς τὰ προαγούμενα περιφέρεια ἐντὸς τᾶς ἕλικος, ἁ δὲ εἰς τὰ ἑπόμενα ἐκτός. Γεγράφθω δὴ ἁ περιφέρεια, ἔστε κα συμπέσῃ τᾷ ΘΑ [κατὰ τὸ Ο ἁ ΟΜ] καὶ τᾷ μετὰ τὰν ΘΚ εὐθεῖαν ποτὶ τὰν ἕλικα ποτιπιπτούσᾳ. Πάλιν δὴ καὶ καθ᾿ ὃ τέμνει τὰν ἕλικα σαμεῖον ἁ ΘΜ, ἔστω τὸ Ν, καὶ κέντρῳ τῷ Θ, διαστήματι δὲ τῷ ΘΝ κύκλος γεγράφθω, ἔστε κα συμπέσῃ ἁ περιφέρεια τοῦ κύκλου τᾷ ΘΚ καὶ τᾷ μετὰ τὰν ΘΜ ποτιπιπτούσᾳ ποτὶ τὰν ἕλικα, ὁμοίως δὲ καὶ διὰ τῶν ἄλλων πάντων, καθ᾿ ἃ τέμνοντι τὰν ἕλικα αἱ τὰς ἴσας γωνίας ποιοῦσαι, κύκλοι γεγράφθωσαν κέντρῳ τῷ Θ, ἔστ' ἂν συμπέσῃ ἑκάστα ἁ περιφέρεια τᾷ τε προαγουμένᾳ εὐθείᾳ καὶ τᾷ ἑπομένᾳ· ἐσσεῖται δή τι περὶ τὸ λαφθὲν χωρίον περιγεγραμμένον ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγεγραμμένον. Ὅτι δὲ τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου μεῖζόν ἐστιν ἐλάσσονι τοῦ προτεθέντος χωρίου δειχθήσεται. Ἔστιν γὰρ ὁ μὲν ΘΛΟ τομεὺς ἴσος τῷ ΘΜΛ, ὁ δὲ ΘΝΠ τῷ ΘΝΡ, ὁ δὲ ΘΧΣ τῷ ΘΧΤ, ἔστιν δὲ καὶ τῶν ἄλλων τομέων ἕκαστος τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι ἴσος τῷ κοινὰν ἔχοντι πλευρὰν τομεῖ τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τομέων. Δῆλον οὖν ὅτι καὶ πάντες οἱ τομέες πάντεσσιν ἴσοι ἐσσοῦνται· [51] ἴσον ἄρα ἐστὶν τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ χωρίῳ τῷ περιγεγραμμένῳ περὶ τὸ χωρίον σχήματι χωρὶς τοῦ ΘΑΚ τομέως· μόνος γὰρ οὗτος οὐ λέλαπται τῶν ἐν τῷ περιγεγραμμένῳ σχήματι. Δῆλον οὖν ὅτι τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου μεῖζόν ἐστι τῷ ΑΚΘ τομεῖ, ὃς ἐλάσσων ἐστὶν τοῦ προτεθέντος.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου δὲ φανερὸν ὅτι δυνατόν ἐστι περὶ τὸ εἰρημένον χωρίον σχῆμα, οἷον εἴρηται, γράφειν, ὥστε τὸ περιγεγραμμένον σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράφειν, ὥστε τὸ χωρίον ὁμοίως μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κβ΄.

   Λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπὸ τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας, ἅ ἐστι δευτέρα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, δυνατόν ἐστι περὶ αὐτὸ σχῆμα ἐπίπεδον περιγράψαι ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγράψαι, ὥστε τὸ περιγραφὲν τοῦ ἐγγραφέντος μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ' ᾇ ἁ ΑΒΓΔΕ, ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένα, καὶ ἔστω τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΑΘ ἀρχὰ τᾶς περιφορᾶς, ἁ δὲ ΕΑ ἁ δευτέρα εὐθεῖα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, ὁ δὲ ΑΖΗ κύκλος ἔστω δεύτερος καὶ αἱ ΑΓΗ, ΖΙ διάμετροι αὐτοῦ ποτ' ὀρθὰς

[52] ἀλλάλαις. Πάλιν οὖν δίχα τεμνομένας τᾶς ὀρθᾶς γωνίας καὶ τοῦ τομέως τοῦ τὰν ὀρθὰν γωνίαν περιέχοντος ἐσσεῖται τὸ καταλειπόμενον ἔλασσον τοῦ προτεθέντος· καὶ ἔστω γεγενημένος ὁ ΘΚΑ τομεὺς ἐλάσσων τοῦ προτεθέντος χωρίου. Διαιρεθεισᾶν δὴ τᾶν ὀρθᾶν γωνιᾶν εἰς τὰς ἴσας γωνίας τᾷ ὑπὸ τᾶν ΚΘΑ καὶ τῶν ἄλλων κατεσκευασθέντων κατὰ τὰ αὐτὰ τοῖς πρότερον ἐσσεῖται τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου σχήματος μεῖζον ἐλάσσονι ἢ ὁ τομεὺς ὁ ΘΚΑ· μεῖζον γὰρ ἐσσεῖται τᾷ ὑπεροχᾷ, ᾇ ὑπερέχει ὁ ΘΚΑ τομεὺς τοῦ ΘΕΡ.

ΠΟΡΙΣΜΑ

   Δῆλον οὖν ὅτι δυνατόν ἐστιν καὶ τὸ περιγραφὲν σχῆμα τοῦ λαφθέντος χωρίου μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν τὸ λαφθὲν χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου φανερὸν διότι δυνατὸν λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος [53] τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς κατὰ τὸν αὐτὸν ἀριθμὸν λεγομένας περιγράψαι σχῆμα, οἷον εἴρηται, ἐπίπεδον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ λαφθέντος χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράψαι, ὥστε τὸ λαφθὲν χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κγ΄.

   Λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος, ἅ ἐστιν ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, οὐκ ἐχούσας πέρας τὰν ἀρχὰν τᾶς ἕλικος, καὶ τᾶν εὐθειᾶν τᾶν ἀπὸ τῶν περάτων τᾶς ἕλικος ἀγομενᾶν δυνατόν ἐστι περὶ τὸ χωρίον σχῆμα ἐπίπεδον περιγράψαι ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγράψαι, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔΕ, πέρατα δὲ αὐτᾶς τὰ Α, Ε, ἔστω δὲ ἀρχὰ τᾶς ἕλικος τὸ Θ, καὶ ἐπεζεύχθωσαν αἱ ΑΘ, [54] ΘΕ. Γεγράφθω δὴ κύκλος κέντρῳ μὲν τῷ Θ, διαστήματι δὲ τῷ ΘΑ, καὶ συμπιπτέτω τᾷ ΘΕ κατὰ τὸ Ζ. Ἀεὶ δὲ τᾶς γωνίας τᾶς ποτὶ τῷ Θ καὶ τοῦ τομέως τοῦ ΘΑΖ δίχα τεμνομένων ἐσσεῖται τὸ καταλειπόμενον τοῦ προτεθέντος ἔλασσον. Ἔστω ἐλάσσων ὁ τομεὺς ὁ ΘΑΚ τοῦ προτεθέντος. Ὁμοίως δὴ τοῖς πρότερον γεγράφθωσαν κύκλοι διὰ τῶν σαμείων, καθ᾿ ἃ τέμνοντι τὰν ἕλικα αἱ τὰς ἴσας γωνίας ποιοῦσαι ποτὶ τῷ Θ, ὥστε τᾶν περιφερειᾶν ἑκάσταν συμπίπτειν τᾷ τε προαγουμένᾳ καὶ τᾷ ἑπομένᾳ· ἐσσεῖται δή τι περὶ τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν περιγεγραμμένον σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγεγραμμένον, καὶ τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου ἐλάσσονι ὑπερέχει τοῦ προτεθέντος χωρίου· ἐλάσσων γάρ ἐστιν ὁ ΘΑΚ τομεύς.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου φανερόν ἐστιν ὅτι δυνατόν ἐστιν περὶ τὸ εἰρημένον χωρίον σχῆμα ἐπίπεδον, οἷον εἴρηται, περιγράψαι, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράψαι, ὥστε τὸ εἰρημένον χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κδ΄.

   Τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς πρώτας [55] τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς τρίτον μέρος ἐστὶ τοῦ κύκλου τοῦ πρώτου.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔΕΘ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΑ εὐθεῖα πρώτα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, ὁ δὲ ΑΚΖΗΙ κύκλος πρῶτος, οὗ τρίτον μέρος ἔστω ὁ ἐν ᾧ Ϟ κύκλος. Δεικτέον ὅτι ἴσον ἐστὶ τὸ προειρημένον χωρίον τῷ Ϟ κύκλῳ.

   Εἰ γὰρ μή, ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. Ἔστω πρότερον, εἰ δυνατόν, ἔλασσον. Δυνατὸν δή ἐστιν περὶ τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ὁ Ϟ κύκλος τοῦ εἰρημένου χωρίου. Περιγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ εἰρημένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ, ἐλάχιστος δὲ ὁ ΘΕΟ· δῆλον οὖν [56] ὅτι τὸ περιγεγραμμένον σχῆμα ἔλασσόν ἐστι τοῦ Ϟ κύκλου. Ἐκβεβλήσθωσαν δὴ αἱ εὐθεῖαι αἱ ποτὶ τῷ Θ ποιοῦσαι τὰς ἴσας γωνίας, ἔστ' ἂν ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι· ἐντὶ δή τινες γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, καὶ ἁ ἐλαχίστα ἴσα τᾷ ὑπεροχᾷ, ἐντὶ δὲ καὶ ἄλλαι τινὲς γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ πασᾶν ὁμοῖοι τομέες, ἀπό τε τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ἐλάσσονές ἐντι ἢ τριπλάσιοι τῶν τομέων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ οἱ μὲν τομέες οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσοι τῷ ΑΖΗΙ κύκλῳ, οἱ δὲ τομέες οἱ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἴσοι τῷ περιγεγραμμένῳ σχήματι· ἐλάσσων ἄρα ὁ ΑΖΗΙ κύκλος τοῦ περιγεγραμμένου σχήματος ἢ τριπλασίων. Τοῦ δὲ Ϟ κύκλου τριπλασίων· ἐλάσσων ἄρα ὁ Ϟ κύκλος τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα ἐστὶν τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ ἔλασσον τοῦ Ϟ χωρίου.

   Οὐδὲ τοίνυν μεῖζον. Ἔστω γάρ, εἰ δυνατόν, μεῖζον. Ἔστι δὴ πάλιν δυνατὸν εἰς τὸ χωρίον τὸ περιεχόμενον

[57] ὑπὸ τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας ἐγγράψαι σχῆμα, ὥστε τὸ εἰρημένον χωρίον τοῦ ἐγγραφέντος σχήματος μεῖζον εἶμεν ἐλάσσονι ἢ ᾧ ὑπερέχει τὸ εἰρημένον χωρίον τοῦ Ϟ κύκλου. Ἐγγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΡΞ, ἐλάχιστος δὲ ὁ ΟΘΕ· δῆλον οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστιν τοῦ Ϟ κύκλου. Ἐκβεβλήστωσαν δὴ αἱ ποιοῦσαι τὰς ἴσας γωνίας ποτὶ τῷ Θ, ἔστε κα ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, καί ἐστιν ἁ ἐλαχίστα ἴσα τᾷ ὑπεροχᾷ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΖΗΙ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα [58] τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ πασᾶν ὁμοῖοι τομέες ἀπό τε τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ μείζονές ἐντι ἢ τριπλάσιοι τῶν τομέων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ οἱ μὲν τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ἴσοι τῷ ΑΖΗΙ κύκλῳ, οἱ δὲ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας ἴσοι τῷ ἐγγεγραμμένῳ σχήματι· μείζων ἄρα ὁ ΑΖΗΙ κύκλος ἢ τριπλασίων τοῦ ἐγγεγραμμένου σχήματος. Τοῦ δὲ Ϟ κύκλου τριπλασίων· μείζων ἄρα ἐστὶν ὁ Ϟ κύκλος τοῦ ἐγγεγραμμένου σχήματος. Οὐκ ἔστιν δέ, ἀλλὰ ἐλάσσων· οὐκ ἄρα ἐστὶν οὐδὲ μεῖζον τὸ χωρίον τὸ ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας τοῦ Ϟ κύκλου. Ἴσον ἄρα ἐστίν [τῷ περιλαφθέντι ὑπὸ τᾶς ἕλικος καὶ τᾶς ΑΘ εὐθείας].

   κε΄.

   Τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς δευτέρας τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ποτὶ τὸν δεύτερον κύκλον τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὰ ζ ποτὶ τὰ ιβ, ὅς ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει τὰ συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶς ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου καὶ τᾶς ἐκ τοῦ κέντρου τοῦ πρώτου κύκλου καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου τᾶς ἐκ τοῦ κέντρου τοῦ πρώτου κύκλου ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου.

[59]    Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔΕ, ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΕ εὐθεῖα ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ἁ πρώτα, ἁ δὲ ΑΕ ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ἁ δευτέρα, ὁ δὲ κύκλος ὁ ΑΖΗΙ ὁ δεύτερος ἔστω, καὶ αἱ ΑΗ, ΙΖ διάμετροι ποτ' ὀρθὰς ἀλλάλαις. Δεικτέον ὅτι τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας ποτὶ τὸν ΑΖΗΙ κύκλον λόγον ἔχει, ὃν τὰ ζ ποτὶ ιβ.

   Ἔστω δή τις κύκλος ὁ Ϟ, ἁ δὲ ἐκ τοῦ κέντρου τοῦ Ϟ κύκλου δυνάμει ἴσα τῷ τε ὑπὸ τᾶν ΑΘ, ΘΕ περιεχομένῳ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου· ἕξει δὴ ὁ Ϟ κύκλος ποτὶ τὸν ΑΗΖΙ ὡς ζ ποτὶ ιβ, διότι καὶ ἁ ἐκ τοῦ κέντρου αὐτοῦ ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ΑΖΗΙ κύκλου τοῦτον ἔχει δυνάμει τὸν λόγον. Δειχθήσεται οὖν ἴσος ὁ Ϟ κύκλος τῷ περιεχομένῳ χωρίῳ ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάττων. Ἔστω δὴ πρότερον, εἰ δυνατόν, μείζων. Δυνατὸν δή ἐστι περὶ τὸ [60] χωρίον περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι ἢ ᾧ ὑπερέχει ὁ Ϟ κύκλος τοῦ χωρίου. Περιγεγράφθω, καὶ ἔστω, ἐξ ὧν σύγκειται τὸ περιγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ τομεύς, ἐλάχιστος δὲ ὁ ΘΟΔ· δῆλον οὖν ὅτι τὸ περιγραφὲν σχῆμα ἔλασσόν ἐστιν τοῦ κύκλου. Ἐκβεβλήσθωσαν αἱ εὐθεῖαι αἱ ποιοῦσαι ποτὶ τῷ Θ ἴσας γωνίας, ἔστ' ἂν ποτὶ τὰν τοῦ δευτέρου κύκλου περιφέρειαν πέσωντι. Ἐντὶ δή τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΖΗΙ κύκλου περιφέρειαν ποτιπίπτουσαι, τῷ μὲν πλήθει μιᾷ ἐλάσσονες ταυτᾶν, τῷ δὲ μεγέθει ἀλλάλαις τε ἴσαι καὶ τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ὁμοῖοι τομέες ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, ἀπὸ δὲ τᾶς ἐλαχίστας οὐκ ἀναγράφεται· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας ἐλάσσονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΑ τετραγώνου· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ τοῖς μὲν τομέεσσι τοῖς ἀπὸ τᾶν ἰσᾶν ἀλλάλαις καὶ τᾷ μεγίστᾳ ἴσος ὁ ΑΖΗΙ κύκλος, τοῖς δὲ τομέεσσι τοῖς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας ἴσον τὸ περιγεγραμμένον σχῆμα· ἐλάσσονα ἄρα λόγον ἔχει ὁ κύκλος ποτὶ τὸ περιγεγραμμένον σχῆμα [61] ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΘ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου. Ὃν δὲ ἔχει λόγον τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου, τοῦτον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸν Ϟ κύκλον· ἐλάσσονα οὖν λόγον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ϟ κύκλον· ὥστε ἐλάσσων ἐστὶν ὁ Ϟ κύκλος τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα μείζων ἐστὶν ὁ Ϟ κύκλος τοῦ χωρίου τοῦ περιεχομένου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΖ εὐθείας.

   Οὐδὲ τοίνυν ἐλάσσων. Ἔστω γάρ, εἰ δυνατόν, ἐλάσσων. Πάλιν οὖν δυνατόν ἐστιν εἰς τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος καὶ τᾶς ΑΕ εὐθείας ἐγγράψαι σχῆμα ἐπίπεδον ὑπὸ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας μεῖζον εἶμεν τοῦ ἐγγεγραμμένου σχήματος [62] ἐλάσσονι, ἢ ᾧ ὑπερέχει τὸ αὐτὸ χωρίον τοῦ Ϟ κύκλου. Ἐγγεγράφθω οὖν, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΚΡ τομεύς, ἐλάχιστος δὲ ὁ ΘΕΟ· δῆλον οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστι τοῦ Ϟ κύκλου. Ἐκβεβλήσθωσαν αἱ ποιοῦσαι ἴσας γωνίας ποτὶ τῷ Θ, ἔστ' ἂν ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει μιᾷ ἐλάσσους ταυτᾶν, τῷ δὲ μεγέθει ἴσαι ἀλλάλαις τε καὶ τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ὁμοῖοι τομέες καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον τοῦ ἀπὸ τᾶς ΕΑ τετραγώνου. Ἔστιν δὲ τοῖς μὲν τομέεσσιν τοῖς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας ἴσον τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ χωρίῳ, τοῖς δὲ ἑτέροις ὁ κύκλος· μείζονα οὖν λόγον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸ ἐγγεγραμμένον σχῆμα ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου, τουτέστιν ὁ ΑΖΗΙ κύκλος ποτὶ τὸν Ϟ κύκλον. Μείζων ἄρα ἐστὶν ὁ Ϟ κύκλος τοῦ ἐγγεγραμμένου σχήματος· ὅπερ ἀδύνατον· [63] ἦν γὰρ ἐλάσσων. Οὐκ ἄρα ἐστὶν οὐδὲ ἐλάσσων ὁ Ϟ κύκλος τοῦ περιεχομένου χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας· ὥστε ἴσος.

ΠΟΡΙΣΜΑ

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δειχθήσεται καὶ διότι τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς κατὰ τὸν αὐτὸν ἀριθμὸν ταῖς περιφοραῖς λεγομένας ποτὶ τὸν κύκλον τὸν κατὰ τὸν αὐτὸν ἀριθμὸν λεγόμενον ταῖς περιφοραῖς λόγον ἔχει, ὃν συναμφότερον τό τε ὑπὸ τᾶς ἐκ τοῦ κέντρου τοῦ κατὰ τὸν αὐτὸν ἀριθμὸν κύκλου καὶ τᾶς ἐκ τοῦ κέντρου τοῦ κατὰ τὸν ἑνὶ ἐλάσσονα τᾶν περιφορᾶν λεγομένου καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τῶν εἰρημένων τᾶς ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου τῶν εἰρημένων, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τῶν εἰρημένων.

   κϚ΄.

   Τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ἕλικος, ἅ ἐστιν ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, οὐκ ἐχούσας πέρας τὰν ἀρχὰν τᾶς ἕλικος, καὶ τᾶν εὐθειᾶν τᾶν ἀπὸ τῶν περάτων αὐτᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν ποτὶ τὸν τομέα τὸν ἔχοντα τὰν μὲν ἐκ τοῦ κέντρου ἴσαν τᾷ μείζονι τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν, τὰν δὲ περιφέρειαν, ἅ ἐστι μεταξὺ τᾶν εἰρημενᾶν εὐθειᾶν ἐπὶ τὰ αὐτὰ τᾷ ἕλικι, τοῦτον ἔχει [64] τὸν λόγον, ὃν ἔχει συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ μείζων τᾶν εἰρημενᾶν εὐθειᾶν τᾶς ἐλάσσονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς μείζονος τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπιζευχθεισᾶν.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔΕ, ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, πέρατα δὲ αὐτᾶς ἔστω τὰ Α, Ε, ἔστω δὲ ἀρχὰ τᾶς ἕλικος τὸ Θ σαμεῖον, καὶ κέντρῳ μὲν τῷ Θ, διαστήματι δὲ τῷ ΘΑ κύκλος γεγράφθω, καὶ συμπιπτέτω τᾷ περιφερείᾳ αὐτοῦ ἁ ΘΕ κατὰ τὸ Ζ. Δεικτέον ὅτι τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν εὐθειᾶν τᾶν ΑΘ, ΘΕ ποτὶ τὸν τομέα τὸν ΑΘΖ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ.

[65]    Ἔστω δὴ κύκλος, ἐν ᾧ ϞΧ, τὰν ἐκ τοῦ κέντρου ἔχων ἴσαν δυνάμει τῷ τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΕΖ, ποτὶ δὲ τῷ κέντρῳ αὐτοῦ γωνία ἴσα τᾷ ποτὶ τῷ Θ· ὁ δὴ τομεὺς ὁ ϞΧ ποτὶ τὸν τομέα τὸν ΘΑΖ τὸν αὐτὸν ἔχει λόγον, ὃν ἔχει τὸ ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΘΑ τετράγωνον· αἱ γὰρ ἐκ τῶν κέντρων τοῦτον ἔχοντι τὸν λόγον δυνάμει ποτ' ἀλλάλας. Δειχθήσεται δὴ ὁ ΧϞ τομεὺς ἴσος ἐὼν τῷ χωρίῳ τῷ περιεχομένῳ ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν.

   Εἰ γὰρ μή, ἤτοι μείζων ἢ ἐλάττων ἐστίν. Ἔστω πρότερον, εἰ δυνατόν, μείζων. Δυνατὸν οὖν ἐστιν περὶ τὸ εἰρημένον χωρίον περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφόμενον σχῆμα μεῖζον εἶμεν τοῦ εἰρημένου χωρίου ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ ϞΧ τομεὺς τοῦ εἰρημένου χωρίου. Περιγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ περιγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ, ἐλάχιστος δὲ ὁ ΘΟΔ· δῆλον οὖν ὅτι τὸ περιγεγραμμένον σχῆμα ἔλασσόν ἐστι τοῦ ΧϞ τομέως. Διάχθωσαν δὴ αἱ εὐθεῖαι αἱ ποιοῦσαι τὰς ἴσας γωνίας ποτὶ τῷ Θ, ἔστ' ἂν ποτὶ τὰν περιφέρειαν τοῦ ΘΑΖ τομέως πέσωντι. Ἐντὶ δή τινες εὐθεῖαι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι εὐθεῖαι τῷ μὲν πλήθει μιᾷ ἐλάσσονες ταυτᾶν, τῷ δὲ μεγέθει ἴσαι ἀλλάλαις τε καὶ τᾷ μεγίστᾳ, αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΘΖ τομέως περιφέρειαν ποτιπίπτουσαι χωρὶς τᾶς ΘΖ, καὶ ἀναγεγράφαται ὁμοῖοι τομέες [66] ἀπὸ πασᾶν, ἀπό τε τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, ἀπὸ δὲ τᾶς ΘΕ οὐκ ἀναγέγραπται· τομέες οὖν οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας τομέως ἐλάσσονα λόγον ἔχοντι ἢ τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ τετραγώνου. Ἔστιν δὲ τοῖς μὲν τομέεσσιν τοῖς ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσος ὁ ΘΑΖ τομεύς, τοῖς δὲ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν τὸ περιγεγραμμένον· ἐλάσσονα οὖν λόγον ἔχει ὁ ΘΑΖ τομεὺς ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΖΕ. Ὃν δὲ λόγον ἔχει τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ εἰρημένα, τοῦτον τὸν λόγον ἔχει ὁ ΘΑΖ τομεὺς ποτὶ τὸν ΧϞ τομέα· ὥστε ἐλάσσων ἐστὶν ὁ ΧϞ τομεὺς τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα ἐσσεῖται ὁ ΧϞ τομεὺς μείζων τοῦ περιεχομένου Χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν.

   Οὐδὲ τοίνυν ἐλάσσων. Ἔστω γὰρ ἐλάσσων, καὶ τὰ ἄλλα τὰ αὐτὰ κατεσκευάσθω. Πάλιν δὴ δυνατόν ἐστιν εἰς τὸ χωρίον ἐγγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ εἰρημένον χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ αὐτὸ χωρίον τοῦ ΧϞ τομέως. Ἐγγεγράφθω οὖν, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΒΓ, ἐλάχιστος δὲ ὁ ΟΘΕ· δῆλον

[67] οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστι τοῦ ΧϞ τομέως. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΘΑΖ τομέως περιφέρειαν ποτιπίπτουσαι χωρὶς τᾶς ΘΑ τῷ μὲν πλήθει μιᾷ ἐλάσσονες τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, τῷ δὲ μεγέθει ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσαι, καὶ ἀναγεγράφαται ἀπὸ ἑκάστας ὁμοῖοι τομέες, ἀπὸ δὲ τᾶς μεγίστας τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν οὐκ ἀναγέγραπται· οἱ τομέες οὖν οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ· ὥστε καὶ [68] ὁ ΘΑΖ τομεὺς ποτὶ τὸ ἐγγεγραμμένον σχῆμα μείζονα λόγον ἔχει ἤπερ ποτὶ τὸν ΧϞ τομέα· ὥστε μείζων ὁ ΧϞ τομεὺς τοῦ ἐγγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ ἐλάσσων· οὐκ ἄρα ἐστὶν οὐδὲ ἐλάσσων ὁ ΧϞ τομεὺς τοῦ περιεχομένου χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν· ἴσος ἄρα.

   κζ΄.

   Τῶν χωρίων τῶν περιεχομένων ὑπό τε τᾶν ἑλίκων καὶ τᾶν εὐθειᾶν τᾶν ἐν τᾷ περιφορᾷ τὸ μὲν τρίτον τοῦ δευτέρου διπλάσιόν ἐστι, τὸ δὲ τέταρτον τριπλάσιον, τὸ δὲ πέμπτον τετραπλάσιον, καὶ ἀεὶ τὸ ἑπόμενον κατὰ τοὺς ἑξῆς ἀριθμοὺς πολλαπλάσιον τοῦ δευτέρου χωρίου, τὸ δὲ πρῶτον χωρίον ἕκτον μέρος ἐστὶ τοῦ δευτέρου.

   Ἔστω ἁ προκειμένα ἕλιξ ἔν τε τᾷ πρώτᾳ περιφορᾷ γεγραμμένα καὶ ἐν τᾷ δευτέρᾳ καὶ ἐν ταῖς ἑπομέναις ὁποσαισοῦν, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Θ σαμεῖον, ἁ δὲ ΘΕ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς, τῶν δὲ χωρίων [69] ἔστω τὸ μὲν Κ τὸ πρῶτον, τὸ δὲ Λ τὸ δεύτερον, τὸ δὲ Μ τὸ τρίτον, τὸ δὲ Ν τὸ τέταρτον, τὸ δὲ Ξ τὸ πέμπτον. Δεικτέον ὅτι τὸ μὲν Κ χωρίον Ϛ΄ μέρος ἐστὶ τοῦ ἑπομένου, τὸ δὲ Μ διπλάσιον τοῦ Λ, τὸ δὲ Ν τριπλάσιον τοῦ Λ, καὶ τῶν ἑξῆς ἀεὶ τὸ ἑπόμενον πολλαπλάσιον τοῦ Λ κατὰ τοὺς ἑξῆς ἀριθμούς.

   Ὅτι μὲν οὖν τὸ Κ Ϛ΄ μέρος ἐστὶ τοῦ Λ, ὧδε δείκνυται. Ἐπεὶ τὸ ΚΛ χωρίον ποτὶ τὸν δεύτερον κύκλον δέδεικται τοῦτον ἔχον τὸν λόγον, ὃν ἔχει τὰ ζ ποτὶ τὰ ιβ, ὁ δὲ δεύτερος κύκλος ποτὶ τὸν πρῶτον κύκλον ὡς ιβ ποτὶ τὰ γ· δῆλον γάρ ἐστιν· ὁ δὲ πρῶτος κύκλος ποτὶ τὸ Κ χωρίον ἔχει ὡς γ ποτὶ α, Ϛ΄ ἄρα ἐστὶ τὸ Κ χωρίον τοῦ Λ. Πάλιν δὲ καὶ τὸ ΚΛΜ χωρίον ποτὶ τὸν τρίτον κύκλον δέδεικται ὅτι τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΓΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ τετραγώνου ποτὶ τὸ ἀπὸ ΓΘ τετράγωνον. Ὁ δὲ τρίτος κύκλος ἔχει ποτὶ τὸν δεύτερον κύκλον ὃν τὸ ἀπὸ τᾶς ΓΘ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΘΒ, ὁ δὲ δεύτερος κύκλος ἔχει ποτὶ τὸ ΚΛ χωρίον ὃν τὸ ἀπὸ ΒΘ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΒΘ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου· καὶ τὸ ΚΛΜ ἄρα ποτὶ τὸ ΚΛ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΓΘ, ΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ ποτὶ τὸ ὑπὸ τᾶν ΒΘ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου. Ταῦτα δὲ ἔχει ποτὶ ἄλλαλα λόγον, ὃν ιθ ποτὶ τὰ ζ· ὥστε καὶ τὸ ΚΛΜ χωρίον ποτὶ τὸ ΛΚ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν ιθ ποτὶ τὰ ζ· αὐτὸ οὖν τὸ Μ ποτὶ τὸ ΚΛ λόγον ἔχει, ὃν τὰ ιβ ποτὶ τὰ ζ. Τὸ δὲ ΚΛ ποτὶ τὸ Λ λόγον ἔχει, ὃν τὰ ζ ποτὶ τὰ Ϛ· δῆλον οὖν ὅτι διπλάσιόν ἐστι τὸ Μ τοῦ Λ.

[70]    Ὅτι δὲ τὰ ἑπόμενα τὸν τῶν ἑξῆς ἀριθμῶν λόγον ἔχει, δειχθήσεται. Τὸ γὰρ ΚΛΜΝΞ ποτὶ τὸν κύκλον, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΕ, τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ τᾶν ΕΘ, ΘΔ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΕ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΘΕ τετράγωνον. Ὁ δὲ κύκλος, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΕ, ποτὶ τὸν κύκλον, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΔ, τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΕ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΘΔ τετράγωνον, ὁ δὲ κύκλος, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΔΘ, ποτὶ τὸ ΚΛΜΝ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΔ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΘΔ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ τετραγώνου· καὶ τὸ ΚΛΜΝΞ ἄρα ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΘΕ, ΘΔ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΕ ποτὶ τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ· διελόντι καὶ τὸ Ξ χωρίον ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν ἁ ὑπεροχὰ τοῦ τε ὑπὸ ΕΘ, ΘΔ μετὰ τοῦ τρίτου μέρεος τοῦ ἀπὸ τᾶς ΕΔ καὶ τοῦ ὑπὸ τᾶν ΔΘ, ΘΓ μετὰ τοῦ τρίτου μέρεος τοῦ ἀπὸ τᾶς ΓΔ ποτί τε τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ· ὑπερέχει δὲ τὰ συναμφότερα τῶν συναμφοτέρων ᾧ καὶ τὸ ὑπὸ τᾶν ΕΘΔ τοῦ ὑπὸ τᾶν ΔΘΓ, ὑπερέχει δὲ τῷ ὑπὸ τᾶν ΔΘ, ΓΕ· τὸ Ξ ἄρα ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου. Διὰ δὲ τῶν αὐτῶν δειχθήσεται καὶ τὸ Ν ποτὶ τὸ ΚΛΜ χωρίον λόγον ἔχον τοῦτον, ὃν τὸ ὑπὸ τᾶν ΘΓ, ΒΔ ποτὶ τὰ συναμφότερα τό τε ὑπὸ ΓΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ ΓΒ τετραγώνου· [71] τὸ Ν ἄρα ποτὶ τὸ ΚΛΜΝ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν τὸ ὑπὸ ΘΓ, ΒΔ ποτὶ τὸ ὑπὸ ΘΓ, ΒΔ καὶ τὸ ὑπὸ ΘΓ, ΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ [καὶ ἀνάπαλιν]· ταῦτα δὲ ἴσα ἐντὶ τῷ τε ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου. Ἐπεὶ οὖν τὸ μὲν Ξ χωρίον ποτὶ τὸ ΚΛΜΝ τοῦτον ἔχει τὸν λόγον, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΔΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου, τὸ δὲ ΚΛΜΝ ποτὶ τὸ Ν ὃν τὰ συναμφότερα τό τε ὑπὸ τᾶν ΔΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ τετραγώνου ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ, ἔχει ἄρα καὶ τὸ Ξ ποτὶ τὸ Ν τὸν αὐτὸν λόγον, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ. Τὸ δὲ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΘΔ ποτὶ τὰν ΘΓ, ἐπεὶ ἴσαι ἐντὶ αἱ ΓΕ, ΒΔ· δῆλον οὖν ὅτι καὶ τὸ Ξ ποτὶ τὸ Ν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΘΔ ποτὶ τὰν ΘΓ.

   Ὁμοίως δὲ καὶ δειχθήσεται καὶ τὸ Ν ποτὶ τὸ Μ τοῦτον ἔχον τὸν λόγον, ὃν ἁ ΘΓ ποτὶ τὰν ΘΒ, καὶ τὸ Μ ποτὶ τὸ Λ, ὃν ἁ ΒΘ ποτὶ τὰν ΑΘ· αἱ δὲ [ΕΘ] ΔΘ, ΓΘ, ΒΘ, ΑΘ εὐθεῖαι τὸν τῶν ἑξῆς ἀριθμῶν λόγον ἔχοντι.

   κη΄.

   Εἴ κα ἐπὶ τᾶς ἕλικος τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας δύο σαμεῖα λαφθέωντι μὴ τὰ πέρατα, ἀπὸ δὲ τῶν λαφθέντων σαμείων ἐπιζευχθέωντι εὐθεῖαι ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος, καὶ κέντρῳ μὲν τᾷ ἀρχᾷ τᾶς ἕλικος, διαστημάτεσσι δὲ τοῖς ἀπὸ τῶν σαμείων ἐπὶ τὰν ἀρχὰν [72] τᾶς ἕλικος, κύκλοι γραφέωντι, τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς μείζονος τᾶν περιφερειᾶν τᾶν μεταξὺ τᾶν εὐθειᾶν καὶ τᾶς ἕλικος τᾶς μεταξὺ τᾶν αὐτᾶν εὐθειᾶν καὶ τᾶς εὐθείας τᾶς ἐκβληθείσας τοῦτον ἕξει τὸν λόγον ποτὶ τὸ ἀπολαφθὲν χωρίον ὑπό τε τᾶς ἐλάσσονος περιφερείας καὶ τᾶς αὐτᾶς ἕλικος καὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ πέρατα αὐτᾶν, ὃν ἁ ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ δύο τριταμορίων τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τᾶς ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ ἑνὸς τριταμορίου τᾶς αὐτᾶς ὑπεροχᾶς.

   Ἔστω ἕλιξ, ἐφ' ἇς ἁ ΑΒΓΔ, ἐν μιᾷ περιφορᾷ γεγραμμένα, καὶ λελάφθω ἐπ᾿ αὐτᾶς δύο σαμεῖα τὰ Α, Γ, ὥστε τὸ Θ σαμεῖον ἀρχὰν εἶμεν τᾶς ἕλικος, καὶ ἀπὸ τῶν Α, Γ ἐπεζεύχθωσαν ἐπὶ τὸ Θ, καὶ κέντρῳ τῷ Θ, διαστημάτεσσι δὲ τοῖς ΘΑ, ΘΓ, κύκλοι γεγράφθωσαν. Δεικτέον ὅτι τὸ Ξ χωρίον ποτὶ τὸ Π τὸν αὐτὸν ἔχει λόγον, ὃν ἔχει συναμφότερος [73] ἅ τε ΑΘ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΑΘ καὶ ἓν τριταμόριον τᾶς ΗΑ.

   Τὸ γὰρ χωρίον τὸ ΝΠ ποτὶ τὸν ΗΓΘ τομέα δέδεικται τοῦτον ἔχον τὸν λόγον, ὃν ἔχει τό τε ὑπὸ τᾶν ΗΘ, ΑΘ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΗ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΗΘ τετράγωνον· αὐτὸ ἄρα τὸ Ξ ποτὶ τὸ ΝΠ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὸ ὑπὸ τᾶν ΘΑΗ μετὰ δύο τριταμορίων τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ. Καὶ ἐπεὶ τὸ ΝΠ χωρίον ποτὶ τὸν ΝΠΞ τομέα τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ τᾶν ΘΑ, ΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ τὸ ἀπὸ τᾶς ΘΗ τετράγωνον, ὁ δὲ ΝΠΞ τομεὺς ποτὶ τὸν Ν τομέα τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΗ ποτὶ τὸ ἀπὸ τᾶς ΘΑ, ἕξει καὶ τὸ ΝΠ χωρίον ποτὶ τὸν Ν τὸν αὐτὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΘΑ, ΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ τὸ ἀπὸ ΘΑ· τὸ ἄρα ΝΠ ποτὶ τὸ Π λόγον ἔχει, ὃν συναμφότερα τό τε ὑπὸ τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΗΑ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου. Ἐπεὶ οὖν τὸ Ξ χωρίον ποτὶ τὸ ΝΠ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ, τὸ δὲ ΝΠ χωρίον ποτὶ τὸ Π τοῦτον ἔχει τὸν λόγον, ὃν τὰ συναμφότερα τό τε ὑπὸ [74] τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΗΑΘ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου, ἕξει καὶ τὸ Ξ ποτὶ τὸ Π τοῦτον τὸν λόγον, ὃν ἔχει συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΘΑΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ. Τὰ δὲ συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερα ἅ τε ΘΑ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΘΑ καὶ τὸ τρίτον μέρος τᾶς ΗΑ· δῆλον οὖν ὅτι καὶ τὸ Ξ χωρίον ποτὶ τὸ Π χωρίον τοῦτον ἔχει τὸν λόγον, ὃν συναμφότερα ἅ τε ΘΑ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΘΑ καὶ τὸ τρίτον μέρος τᾶς ΗΑ. ω

 

---

ΜΗΧΑΝΙΚΑ Β΄ 

    

Ἐπιπέδων ἰσορροπιῶν ἢ κέντρα βαρῶν ἐπιπέδων β΄.

   Εἴ κα δύο σαμείων ἑκατέρου κατά τινος γραμμᾶς ἐνεχθέντος μὴ τᾶς αὐτᾶς ἰσοταχέως αὐτοῦ ἑαυτῷ φερομένου λαφθέωντι ἐν ἑκατέρᾳ τᾶν γραμμᾶν δύο γραμμαί, ἇν αἵ τε πρῶται ἐν ἴσοις χρόνοις ὑπὸ τῶν σαμείων διανυέσθων καὶ αἱ δεύτεραι, τὸν αὐτὸν ἑξοῦντι λόγον ποτ᾿ ἀλλάλας αἱ λαφθεῖσαι γραμμαί.

   Ἔστω κατὰ τᾶς ΑΒ γραμμᾶς ἐνηνεγμένον τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ καὶ ἄλλο κατὰ τᾶς ΚΛ, λελάφθωσαν δὲ ἐν τᾷ ΑΒ δύο αἱ ΓΔ, ΔΕ γραμμαί, καὶ ἐν τᾷ ΚΛ αἱ ΖΗ, ΗΘ, ἐν ἴσῳ δὲ χρόνῳ τὸ κατὰ τᾶς ΑΒ γραμμᾶς ἐνηνεγμένον σαμεῖον τὰν ΓΔ γραμμὰν διαπορευέσθω, ἐν ὅσῳ τὸ ἕτερον κατὰ τᾶς ΚΛ ἐνηνεγμένον τὰν ΖΗ, ὁμοίως δὲ καὶ τὰν ΔΕ γραμμὰν ἐν ἴσῳ διαπορευέσθω τὸ σαμεῖον, ἐν ὅσῳ τὸ ἕτερον τὰν ΗΘ. Δεικτέον ὅτι τὸν αὐτὸν ἔχει λόγον ἁ ΓΔ ποτὶ τὰν ΔΕ, ὃν ἁ ΖΗ ποτὶ τὰν ΗΘ.

   Ἔστω δὴ ὁ χρόνος, ἐν ᾧ τὰν ΓΔ γραμμὰν διεπορεύετο τὸ σαμεῖον, ὁ ΜΝ· ἐν τούτῳ δὴ τῷ χρόνῳ καὶ τὸ ἕτερον σαμεῖον διαπορεύεται τὰν ΖΗ. Πάλιν δὴ καὶ ἐν ᾧ τὰν [16] ΔΕ γραμμὰν διεπορεύετο τὸ σαμεῖον, ἔστω ὁ ΝΞ χρόνος· ἐν τούτῳ δὴ καὶ τὸ ἕτερον σαμεῖον διαπορεύεται τὰν ΗΘ· τὸν αὐτὸν δὴ λόγον ἑξοῦντι ἅ τε ΓΔ ποτὶ τὰν ΔΕ γραμμάν, ὃν ὁ χρόνος ὁ ΜΝ ποτὶ ΝΞ, καὶ ἁ ΖΗ ποτὶ τὰν ΗΘ, ὃν ὁ χρόνος ὁ ΜΝ ποτὶ τὸν ΝΞ. Δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΓΔ ποτὶ τὰν ΔΕ, ὃν ἁ ΖΗ ποτὶ τὰν ΗΘ.

   γ΄.

   Κύκλων δοθέντων ὁποσωνοῦν τῷ πλήθει δυνατόν ἐστιν εὐθεῖαν λαβεῖν μείζονα ἐοῦσαν τᾶν τῶν κύκλων περιφερειᾶν.

   Περιγραφέντος γὰρ περὶ ἕκαστον τῶν κύκλων πολυγώνου δῆλον ὡς ἁ ἐκ πασᾶν συγκειμένα τᾶν περιμέτρων εὐθεῖα μείζων ἐσσεῖται πασᾶν τᾶν τῶν κύκλων περιφερειᾶν.

   δ΄.

   Δύο γραμμᾶν δοθεισᾶν ἀνισᾶν, εὐθείας τε καὶ κύκλου περιφερείας, δυνατόν ἐστι λαβεῖν εὐθεῖαν τᾶς μὲν μείζονος τᾶν δοθεισᾶν γραμμᾶν ἐλάσσονα, τᾶς δὲ ἐλάσσονος μείζονα.

   Ὁσάκις γὰρ ἁ ὑπεροχά, ᾇ ὑπερέχει ἁ μείζων γραμμὰ τᾶς ἐλάσσονος, αὐτὰ ἑαυτᾷ συντιθεμένα ὑπερέξει τᾶς εὐθείας, εἰς τοσαῦτα ἴσα διαιρεθείσας τᾶς εὐθείας τὸ ἓν τμᾶμα ἔλασσον ἐσσεῖται τᾶς ὑπεροχᾶς. Εἰ μὲν οὖν κα ᾖ ἁ περιφέρεια μείζων τᾶς εὐθείας, ἑνὸς τμάματος ποτιτεθέντος ποτὶ τὰν εὐθεῖαν τᾶς μὲν ἐλάσσονος τᾶν δοθεισᾶν δῆλον ὡς μείζων ἐσσεῖται, τᾶς δὲ μείζονος [17] ἐλάσσων· εἰ δέ κα ἐλάσσων, ἑνὸς τμάματος ποτιτεθέντος ποτὶ τὰν περιφέρειαν ὁμοίως τᾶς μὲν ἐλάσσονος μείζων ἐσσεῖται, τᾶς δὲ μείζονος ἐλάσσων· καὶ γὰρ ἁ ποτικειμένα ἐλάσσων ἐστὶ τᾶς ὑπεροχᾶς.

   ε΄.

   Κύκλου δοθέντος καὶ εὐθείας ἐπιψαυούσας τοῦ κύκλου δυνατόν ἐστιν ἀπὸ τοῦ κέντρου τοῦ κύκλου ἀγαγεῖν εὐθεῖαν ἐπὶ τὰν ἐπιψαύουσαν, ὥστε τὰν μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς τοῦ κύκλου περιφερείας εὐθεῖαν ποτὶ τὰν ἐκ τοῦ κέντρου ἐλάσσονα λόγον ἔχειν ἢ ἁ περιφέρεια τοῦ κύκλου ἁ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς διαχθείσας ποτὶ τὰν δοθεῖσαν ὁποιανοῦν κύκλου περιφέρειαν.

   Δεδόσθω κύκλος ὁ ΑΒΓ, κέντρον δὲ αὐτοῦ τὸ Κ, καὶ ἐπιψαυέτω τοῦ κύκλου ἁ ΔΖ κατὰ τὸ Β, δεδόσθω δὲ καὶ κύκλου περιφέρεια ὁποιαοῦν· δυνατὸν δέ ἐστι τᾶς δοθείσας περιφερείας λαβεῖν τινα εὐθεῖαν μείζονα, καὶ ἔστω ἁ Ε εὐθεῖα μείζων τᾶς δοθείσας περιφερείας· ἄχθω δὲ ἀπὸ τοῦ Κ κέντρου παρὰ τὰν ΔΖ ἁ ΑΗ, καὶ κείσθω ἁ ΗΘ ἴσα τᾷ Ε νεύουσα ἐπὶ τὸ Β. Ἀπὸ δὴ τοῦ Κ κέντρου ἐπὶ τὸ Θ [18] ἐπιζευχθεῖσα ἐκβεβλήσθω· τὸν αὐτὸν δὴ λόγον ἔχει ἁ ΘΖ ποτὶ τὰν ΘΚ, ὃν ἁ ΒΘ ποτὶ τὰν ΘΗ. Ἁ ἄρα ΖΘ ποτὶ τὰν ΘΚ ἐλάσσονα λόγον ἔχει τοῦ ὃν ἁ ΒΘ περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν, διότι ἁ μὲν ΒΘ εὐθεῖα ἐλάσσων ἐστὶ τᾶς ΒΘ περιφερείας, ἁ δὲ ΘΗ μείζων τᾶς δοθείσας περιφερείας· ἐλάσσονα οὖν λόγον ἔχει καὶ ἁ ΖΘ ποτὶ τὰν ἐκ τοῦ κέντρου ἢ ἁ ΒΘ περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν.

   Ϛ΄.

   Κύκλου δοθέντος καὶ ἐν τῷ κύκλῳ γραμμᾶς ἐλάσσονος τᾶς διαμέτρου δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτὶ τὰν περιφέρειαν αὐτοῦ ποτιβαλεῖν εὐθεῖαν τέμνουσαν τὰν ἐν τῷ κύκλῳ δεδομέναν γραμμάν, ὥστε τὰν ἀπολαφθεῖσαν εὐθεῖαν μεταξὺ τᾶς περιφερείας καὶ τᾶς εὐθείας τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἐπιζευχθεῖσαν ἀπὸ τοῦ πέρατος τᾶς ποτιπεσούσας τοῦ ἐπὶ τᾶς περιφερείας ποτὶ τὸ ἕτερον πέρας τᾶς ἐν τῷ κύκλῳ δεδομένας εὐθείας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος ἐλάσσων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[19]    Δεδόσθω κύκλος ὁ ΑΒΓ, κέντρον δὲ αὐτοῦ τὸ Κ, καὶ ἐν αὐτῷ δεδόσθω εὐθεῖα ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ Η, ἐλάσσων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΚΘ, καθέτου ἐούσας τᾶς ΚΘ· ἄχθω δὲ ἀπὸ τοῦ κέντρου παρὰ τὰν ΑΓ ἁ ΚΝ καὶ τᾷ ΚΓ πρὸς ὀρθὰς ἁ ΓΛ· ὁμοῖα δή ἐστι τὰ ΓΘΚ, ΓΚΛ τρίγωνα. Ἔστιν οὖν ὡς ἁ ΓΘ ποτὶ τὰν ΘΚ οὕτως ἁ ΚΓ ποτὶ τὰν ΓΛ· ἐλάσσονα ἄρα λόγον ἔχει ἁ Ζ ποτὶ τὰν Η ἢ ἁ ΚΓ ποτὶ τὰν ΓΛ. Ὃν δὴ λόγον ἔχει ἁ Ζ ποτὶ τὰν Η, τοῦτον ἐχέτω ἁ ΚΓ ποτὶ μείζονα τᾶς ΓΛ. Ἐχέτω ποτὶ τὰν ΒΝ, κείσθω δὲ ἁ ΒΝ μεταξὺ τᾶς περιφερείας καὶ τᾶς εὐθείας διὰ τοῦ Γ· δυνατὸν δέ ἐστιν οὕτως τέμνειν· καὶ πεσεῖται ἐκτός, ἐπεὶ μείζων ἐστὶν τᾶς ΓΛ. Ἐπεὶ οὖν ἁ ΚΒ ποτὶ ΒΝ τὸν αὐτὸν ἔχει λόγον ὃν ἁ Ζ ποτὶ Η, καὶ ἁ ΕΒ ποτὶ ΒΓ τὸν αὐτὸν ἕξει λόγον ὃν ἁ Ζ ποτὶ Η.

   ζ΄.

   Τῶν αὐτῶν δεδομένων καὶ τᾶς ἐν τῷ κύκλῳ εὐθείας ἐκβεβλημένας δυνατόν ἐστιν ἀπὸ τοῦ κέντρου ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας ποτὶ τὰν ἐπιζευχθεῖσαν ἀπὸ τοῦ πέρατος τᾶς ἐναπολαφθείσας ποτὶ τὸ πέρας τᾶς ἐκβεβλημένας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος μείζων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[20]    Δεδόσθω τὰ αὐτά, καὶ ἔστω ἁ ἐν τῷ κύκλῳ γραμμὰ ἐκβεβλημένα, ὁ δὲ δοθεὶς λόγος ἔστω, ὃν ἔχει ἁ Ζ ποτὶ τὰν Η, μείζων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΘΚ· μείζων οὖν ἐσσεῖται καὶ τοῦ ὃν ἔχει ἁ ΚΓ ποτὶ ΓΛ. Ὃν δὴ λόγον ἔχει ἁ Ζ ποτὶ Η, τοῦτον ἕξει ἁ ΚΓ ποτὶ ἐλάσσονα τᾶς ΓΛ. Ἐχέτω ποτὶ ΙΝ νεύουσαν ἐπὶ τὸ Γ· δυνατὸν δέ ἐστιν οὕτως τέμνειν· καὶ πεσεῖται ἐντὸς τᾶς ΓΛ, ἐπειδὴ ἐλάσσων ἐστὶ τᾶς ΓΛ. Ἐπεὶ οὖν τὸν αὐτὸν ἔχει λόγον ἁ ΚΓ ποτὶ ΙΝ ὃν ἁ Ζ ποτὶ Η, καὶ ἁ ΕΙ ποτὶ ΙΓ τὸν αὐτὸν ἕξει λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   η΄.

   Κύκλου δοθέντος καὶ ἐν τῷ κύκλῳ γραμμᾶς ἐλάσσονος τᾶς διαμέτρου καὶ ἄλλας ἐπιψαυούσας τοῦ κύκλου κατὰ τὸ πέρας τᾶς ἐν τῷ κύκλῳ δεδομένας δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτιβαλεῖν τινα εὐθεῖαν ποτὶ τὰν εὐθεῖαν, ὥστε τὰν ἀπολαφθεῖσαν ἀπ᾿ αὐτᾶς μεταξὺ τᾶς τοῦ κύκλου περιφερείας καὶ τᾶς ἐν τῷ κύκλῳ δεδομένας γραμμᾶς ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος ἐλάσσων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου τοῦ κύκλου κάθετον ἐπ᾿ αὐτὰν ἀγμέναν.

[21]    Ἔστω κύκλος δεδομένος ὁ ΑΒΓΔ, καὶ ἐν τῷ κύκλῳ εὐθεῖα δεδόσθω ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ, καὶ ἁ ΞΛ ἐπιψαυέτω τοῦ κύκλου κατὰ τὸ Γ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ Η, ἐλάσσων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ ΘΚ· ἐσσεῖται δὴ ἐλάσσων καὶ τοῦ ὃν ἔχει ἁ ΓΚ ποτὶ ΓΛ, εἴ κα παράλληλος ἀχθῇ ἁ ΚΛ τᾷ ΘΓ· ἐχέτω δὴ ἁ ΚΓ ποτὶ ΓΞ τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ Η· μείζων δή ἐστιν ἁ ΞΓ τᾶς ΓΛ. Γεγράφθω κύκλου περιφέρεια περὶ τὰ Κ, Λ, Ξ. Ἐπεὶ οὖν ἐστι μείζων ἁ ΞΓ τᾶς ΓΛ, καὶ ποτ᾿ ὀρθάς ἐντι ἀλλάλαις αἱ ΚΓ, ΞΛ, δυνατόν ἐστι τᾷ ΜΓ ἴσαν ἄλλαν θέμεν τὰν ΙΝ νεύουσαν ἐπὶ τὸ Κ. Τὸ δὴ περιεχόμενον ὑπὸ τᾶν ΞΙΛ ποτὶ τὸ ὑπὸ τᾶν ΚΕ, ΙΛ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΞΙ ποτὶ ΚΕ, καὶ τὸ ὑπὸ τᾶν ΚΙΝ ποτὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΙΝ ποτὶ ΓΛ· ὥστε καὶ ἁ ΙΝ ποτὶ ΓΛ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ· ὥστε καὶ ἁ ΓΜ ποτὶ ΓΛ καὶ ἁ ΞΓ ποτὶ ΚΓ καὶ ποτὶ ΚΒ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ, καὶ λοιπὰ ἁ ΙΓ ποτὶ ΒΕ τὸν αὐτὸν ἔχει λόγον ὃν ἁ ΞΓ ποτὶ τὰν ΓΚ καὶ ὃν ἁ Η ποτὶ Ζ. Πέπτωκεν οὖν ἁ ΚΝ ποτὶ τὰν ἐπιψαύουσαν, καὶ ἔχει ἁ μεταξὺ τᾶς περιφερείας [22] καὶ τᾶς εὐθείας ἁ ΒΕ ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   θ΄.

   Τῶν αὐτῶν δεδομένων καὶ τᾶς ἐν τῷ κύκλῳ δεδομένας γραμμᾶς ἐκβεβλημένας δυνατὸν ἀπὸ τοῦ κέντρου τοῦ κύκλου ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν εὐθεῖαν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας ποτὶ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας ποτὶ τὰν ἁφὰν τὸν ταχθέντα λόγον ἔχειν, εἴ κα ὁ δοθεὶς λόγος μείζων ᾖ τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ἐν τῷ κύκλῳ δεδομένας ποτὶ τὰν ἀπὸ τοῦ κέντρου κάθετον ἐπ᾿ αὐτὰν ἀγομέναν.

   Δεδόσθω κύκλος ὁ ΑΒΓΔ, καὶ ἐν τῷ κύκλῳ εὐθεῖα ἐλάσσων τᾶς διαμέτρου ἁ ΓΑ διάχθω, καὶ ἐπιψαυέτω τοῦ κύκλου ἁ ΞΓ κατὰ τὸ Γ, καὶ λόγος, ὃν ἔχει ἁ Ζ ποτὶ τὰν Η, μείζων τοῦ ὃν ἔχει ἁ ΓΘ ποτὶ τὰν ΘΚ· ἐσσεῖται δὴ μείζων καὶ τοῦ ὃν ἔχει ἁ ΚΓ ποτὶ τὰν ΓΛ. Ἐχέτω οὖν ἁ ΚΓ ποτὶ τὰν ΓΞ τὸν αὐτὸν λόγον ὃν ἁ Ζ ποτὶ τὰν Η· ἐλάσσων ἄρα ἐστὶν αὕτα τᾶς ΓΛ.

[23]    Πάλιν δὴ γεγράφθω κύκλος διὰ τῶν Ξ, Κ, Λ σαμείων. Ἐπεὶ οὖν ἐλάσσων ἐστὶν ἁ ΞΓ τᾶς ΓΛ, καὶ ποτ᾿ ὀρθάς ἐντι ἀλλάλαις αἱ ΚΜ, ΞΓ, δυνατὸν τᾷ ΓΜ ἴσαν θέμεν τὰν ΙΝ νεύουσαν ἐπὶ τὸ Κ. Ἐπεὶ οὖν τὸ ὑπὸ τᾶν ΞΙΛ ποτὶ τὸ ὑπὸ τᾶν ΛΙ, ΚΕ ἐστὶν ὡς ἁ ΞΙ ποτὶ ΚΕ, ἀλλὰ τῷ μὲν ὑπὸ τᾶν ΞΙΛ ἴσον ἐστὶ τὸ ὑπὸ τᾶν ΚΙΝ, τῷ δὲ ὑπὸ τᾶν ΛΙ, ΚΕ ἴσον ἐστὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ διὰ τὸ εἶμεν ὡς τὰν ΚΕ ποτὶ ΙΚ οὕτως τὰν ΛΓ ποτὶ ΛΙ, καὶ ὡς ἄρα ἁ ΞΙ ποτὶ ΚΕ, οὕτως τὸ ὑπὸ τᾶν ΚΙΝ ποτὶ τὸ ὑπὸ τᾶν ΚΙ, ΓΛ, τουτέστιν ὡς ἁ ΝΙ ποτὶ ΓΛ, τουτέστιν ἁ ΓΜ ποτὶ ΓΛ. Ἔστιν δὲ καὶ, ὡς ἁ ΓΜ ποτὶ ΓΛ, ἁ ΞΓ ποτὶ ΚΓ, τουτέστι ποτὶ ΚΒ· ἔστιν ἄρα, ὡς ἁ ΞΙ ποτὶ ΚΕ, ἁ ΞΓ ποτὶ ΚΒ, καὶ λοιπὰ ἁ ΙΓ ποτὶ λοιπὰν τὰν ΒΕ ἐστὶν ὡς ἁ ΞΓ ποτὶ ΓΚ. Ὃν δὲ λόγον ἔχει ἁ ΞΓ ποτὶ ΓΚ, τοῦτον ἔχει ἁ Η ποτὶ Ζ· ποτιπέπτωκεν δὴ ἁ ΚΕ ποτὶ τὰν ἐκβεβλημέναν, καὶ ἁ μεταξὺ τᾶς ἐκβεβλημένας καὶ τᾶς περιφερειὰς ἁ ΒΕ ποτὶ τὰν ΓΙ τὰν ἀπὸ τᾶς ἐπιψαυούσας ἀπολαφθεῖσαν τὸν αὐτὸν ἔχει λόγον ὃν ἁ Ζ ποτὶ τὰν Η.

   ι΄.

   Εἴ κα γραμμαὶ ἑξῆς τεθέωντι ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, ᾖ δὲ ἁ ὑπεροχὰ ἴσα τᾷ ἐλαχίστᾳ, καὶ ἄλλαι γραμμαὶ τεθέωντι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα τᾷ μεγίστᾳ, τὰ τετράγωνα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτιλαμβάνοντα τό τε ἀπὸ τᾶς μεγίστας τετράγωνον καὶ τὸ περιεχόμενον ὑπό τε τᾶς ἐλαχίστας καὶ τᾶς ἴσας πάσαις ταῖς τῷ ἴσῳ ἀλλαλᾶν ὑπερεχούσαις τριπλάσια ἐσσοῦνται τῶν τετραγώνων πάντων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν.

[24]    Ἔστων γραμμαὶ ὁποσαιοῦν ἐφεξῆς κείμεναι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ Α, Β, Γ, Δ, Ε, Ζ, Η, Θ, ἁ δὲ Θ ἴσα ἔστω τᾷ ὑπεροχᾷ, ποτικείσθω δὲ ποτὶ τὰν Β ἴσα τᾷ Θ ἁ Ι, ποτὶ δὲ τὰν Γ ἁ Κ ἴσα τᾷ Η, ποτὶ δὲ τὰν Δ ἁ Λ ἴσα τᾷ Ζ, ποτὶ δὲ τὰν Ε ἁ Μ ἴσα τᾷ Ε, ποτὶ δὲ τὰν Ζ ἁ Ν ἴσα τᾷ Δ, ποτὶ δὲ τὰν Η ἁ Ξ ἴσα τᾷ Γ, ποτὶ δὲ τὰν Θ ἁ Ο ἴσα τᾷ Β· ἐσσοῦνται δὴ αἱ γενόμεναι ἴσαι ἀλλάλαις καὶ τᾷ μεγίστᾳ. Δεικτέον οὖν ὅτι τὰ τετράγωνα τὰ ἀπὸ πασᾶν τᾶς τε Α καὶ τᾶν γενομενᾶν ποτιλαβόντα τό τε ἀπὸ τᾶς Α τεράγωνον καὶ τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τριπλάσιά ἐντι τῶν τετραγώνων πάντων τῶν ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ.

   Ἔστιν δὴ τὸ μὲν ἀπὸ τᾶς ΒΙ τετράγωνον ἴσον τοῖς ἀπὸ τᾶν Ι, Β τετραγώνοις καὶ δύο τοῖς ὑπὸ τᾶν Β, Ι περιεχομένοις, τὸ δὲ ἀπὸ τᾶς ΚΓ ἴσον τοῖς ἀπὸ τᾶν Κ, Γ τετραγώνοις καὶ δύο τοῖς ὑπὸ τᾶν Κ, Γ περιεχομένοις· ὁμοίως δὲ καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τᾶν ἰσᾶν τᾷ Α τετράγωνα ἴσα ἐντὶ τοῖς ἀπὸ τῶν τμαμάτων τετραγώνοις καὶ δυσὶ τοῖς ὑπὸ τῶν τμαμάτων περιεχομένοις. Τὰ μὲν οὖν ἀπὸ [25] τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ καὶ τὰ ἀπὸ τᾶν Ι, Κ, Λ, Μ, Ν, Ξ, Ο ποτιλαβόντα τὸ ἀπὸ τᾶς Α τετράγωνον διπλάσιά ἐντι τῶν ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τετραγώνων· λοιπὸν δὲ ἐπιδειξοῦμες ὅτι τὰ διπλάσια τῶν περιεχομένων ὑπὸ τῶν τμαμάτων τῶν ἐν ἑκάστᾳ γραμμᾷ τᾶν ἰσᾶν τᾷ Α ποτιλαβόντα τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ ἴσα ἐντὶ τοῖς ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ. Καὶ ἐπεὶ δύο μὲν τὰ ὑπὸ Β, Ι περιεχόμενα ἴσα δυσὶ τοῖς ὑπὸ τᾶν Β, Θ περιεχομένοις, δύο δὲ τὰ ὑπὸ τᾶν Κ, Γ ἴσα τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς τετραπλασίας τᾶς Γ διὰ τὸ τὰν Κ διπλασίονα εἶμεν τᾶς Θ, δύο δὲ τὰ ὑπὸ τᾶν Δ, Λ ἴσα τῷ ὑπὸ τᾶς Θ καὶ τᾶς ἑξαπλασίας τᾶς Δ διὰ τὸ τὰν Λ τριπλασίαν εἶμεν τᾶς Θ, ὁμοίως δὲ καὶ τὰ ἄλλα τὰ διπλάσια τὰ περιεχόμενα ὑπὸ τῶν τμαμάτων ἴσα ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς πολλαπλασίας ἀεὶ κατὰ τοὺς ἑξῆς ἀριθμοὺς ἀρτίους τᾶς ἑπομένας γραμμᾶς, τὰ οὖν σύμπαντα ποτιλαβόντα τὸ περιεχόμενον ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις ταῖς Α, Β, Γ, Δ, Ε, Ζ, Η, Θ ἐσσοῦνται ἴσα τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις τᾷ τε Α καὶ τᾷ τριπλασίᾳ τᾶς Β καὶ τᾷ πενταπλασίᾳ τᾶς Γ καὶ ἀεὶ τᾷ [περισσᾷ] κατὰ τοὺς ἑξῆς ἀριθμοὺς περισσοὺς πολλαπλασίᾳ τᾶς ἑπομένας γραμμᾶς. Ἐντὶ δὲ καὶ τὰ ἀπὸ τᾶν Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τετράγωνα ἴσα τῷ περιεχομένῳ ὑπὸ τᾶν αὐτᾶν γραμμᾶν. Ἔστι γὰρ τὸ ἀπὸ τᾶς Α τετράγωνον ἴσον τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας [πάσαις] τᾷ τε Α καὶ τᾷ ἴσᾳ ταῖς λοιπαῖς, ἇν ἑκάστα ἴσα τᾷ Α· ἰσάκις γὰρ μετρεῖ ἅ τε Θ τὰν Α καὶ ἁ Α τὰς ἴσας αὐτᾷ πάσας σὺν τᾷ Α· ὥστε ἴσον ἐστὶ [26] τὸ ἀπὸ Α τετράγωνον τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ Α καὶ τᾷ διπλασίᾳ τᾶν Β, Γ, Δ, Ε, Ζ, Η, Θ· αἱ γὰρ ἴσαι τᾷ Α πᾶσαι χωρὶς τᾶς Α διπλάσιαί ἐντι τᾶν Β, Γ, Δ, Ε, Ζ, Η, Θ. Ὁμοίως δὲ καὶ τὸ ἀπὸ τᾶς Β τετράγωνον ἴσον ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ τε Β καὶ τᾷ διπλασίᾳ τᾶν Γ, Δ, Ε, Ζ, Η, Θ, καὶ πάλιν τὸ ἀπὸ τᾶς Γ τετράγωνον ἴσον τῷ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας τᾷ τε Γ καὶ τᾷ διπλασίᾳ τᾶν Δ, Ε, Ζ, Η, Θ, ὁμοίως δὲ καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τετράγωνα ἴσα ἐντὶ τοῖς περιεχομένοις ὑπό τε τᾶς Θ καὶ τᾶς ἴσας αὐτᾷ τε καὶ τᾷ διπλασίᾳ τᾶν λοιπᾶν. Δῆλον οὖν ὅτι τὰ ἀπὸ πασᾶν τετράγωνα ἴσα ἐντὶ τῷ περιεχομένῳ ὑπό τε τᾶς Θ καὶ τᾶς ἴσας πάσαις τᾷ τε Α καὶ τᾷ τριπλασίᾳ τᾶς Β καὶ τᾷ πενταπλασίᾳ τᾶς Γ καὶ τᾷ κατὰ τοὺς ἑξῆς ἀριθμοὺς περισσοὺς πολλαπλασίᾳ τᾶς ἑπομένας.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου οὖν φανερὸν ὅτι τὰ τετράγωνα πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ τῶν μὲν τετραγώνων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἐλάσσονά ἐστιν ἢ τριπλάσια, ἐπειδὴ ποτιλαβόντα τινὰ τριπλάσιά ἐντι, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονα ἢ τριπλάσια, ἐπειδὴ τὰ ποτιλαφθέντα ἐλάσσονά ἐντι ἢ τριπλάσια τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου. Καὶ τοίνυν, εἴ κα ὁμοῖα εἴδεα ἀναγραφέωντι ἀπὸ πασᾶν, ἀπὸ τὲ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ, τὰ εἴδεα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ τῶν μὲν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν εἰδέων [27] ἐλάσσονα ἐσσοῦνται ἢ τριπλάσια, τῶν δὲ λοιπῶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας εἴδεος μείζονα ἢ τριπλάσια· τὸν γὰρ αὐτὸν ἑξοῦντι λόγον τὰ ὁμοῖα εἴδεα τοῖς τετραγώνοις.

   ια΄.

   Εἴ κα γραμμαὶ ἑξῆς τεθέωντι ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, καὶ ἄλλαι γραμμαὶ τεθέωντι τῷ μὲν πλήθει μιᾷ ἐλάσσονες τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ, τὰ τετράγωνα πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ μὲν τὰ τετράγωνα τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τᾶς ἐλαχίστας ἐλάσσονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπό τε τᾶς μεγίστας καὶ τᾶς ἐλαχίστας καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ὑπεροχᾶς τετραγώνου, ᾇ ὑπερέχει ἁ μεγίστα τᾶς ἐλαχίστας, ποτὶ δὲ τὰ τετράγωνα τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας τετραγώνου μείζονα τοῦ αὐτοῦ λόγου.

[28]    Ἔστωσαν γὰρ γραμμαὶ ὁποσαιοῦν τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι ἑξῆς κείμεναι, ἁ μὲν ΑΒ τᾶς ΓΔ, ἁ δὲ ΓΔ τᾶς ΕΖ, ἁ δὲ ΕΖ τᾶς ΗΘ, ἁ δὲ ΗΘ τᾶς ΙΚ, ἁ δὲ ΙΚ τᾶς ΛΜ, ἁ δὲ ΛΜ τᾶς ΝΞ, ποτικείσθω δὲ ποτὶ μὲν τὰν ΓΔ ἴσα μιᾷ ὑπεροχᾷ ἁ ΓΟ, ποτὶ δὲ τὰν ΕΖ ἴσα δυσὶν ὑπεροχαῖς ἁ ΕΠ, ποτὶ δὲ τὰν ΗΘ ἴσα τρισὶν ὑπεροχαῖς ἁ ΗΡ, καὶ ποτὶ τὰς ἄλλας τὸν αὐτὸν τρόπον· ἐσσοῦνται δὴ αἱ γενόμεναι ἀλλάλαις ἴσαι καὶ ἑκάστα τᾷ μεγίστᾳ. Δεικτέον οὖν ὅτι τὰ ἀπὸ πασᾶν τᾶν γενομενᾶν τετράγωνα ποτὶ μὲν πάντα τὰ τετράγωνα τὰ ἀπὸ πασᾶν τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ΝΞ τετραγώνου ἐλάσσονα λόγον ἔχει ἢ τὸ ἀπὸ τᾶς ΑΒ τετράγωνον ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπὸ τᾶν ΑΒ, ΝΞ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΝΥ τετραγώνου, ποτὶ δὲ τὰ τετράγωνα τὰ ἀπὸ τᾶν αὐτᾶν χωρὶς τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου μείζονα λόγον ἔχει τοῦ αὐτοῦ λόγου.

   Ἀπολελάφθω ἀφ᾿ ἑκάστας τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἴσα τᾷ ὑπεροχᾷ· ὃν δὴ λόγον ἔχει τὸ ἀπὸ τᾶς ΑΒ ποτὶ συναμφότερα τό τε ὑπὸ τᾶν ΑΒ, ΦΒ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΦ τετραγώνου, τοῦτον ἔχει τὸν λόγον τό τε ἀπὸ τᾶς ΟΔ τετράγωνον ποτί τε τὸ περιεχόμενον ὑπὸ τᾶν ΟΔ, ΔΧ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΧΟ τετραγώνου καὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΖ ποτὶ τὸ περιεχόμενον ὑπὸ τᾶν ΠΖ, ΨΖ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΨΠ τετραγώνου καὶ τὰ ἀπὸ τᾶν ἀλλᾶν τετράγωνα ποτὶ τὰ ὁμοίως λαμβανόμενα χωρία· καὶ τὰ πάντα δὴ τὰ ἀπὸ πασᾶν τᾶν ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ ποτί τε πάντα τὰ περιεχόμενα ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς εἰρημέναις γραμμαῖς καὶ τὰ [29] τριταμόρια τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τὸν αὐτὸν ἑξοῦντι λόγον, ὃν τὸ ἀπὸ τᾶς ΑΒ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΒ, ΦΒ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ ΦΑ τετραγώνου. Εἰ οὖν κα δειχθῇ τό τε περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ καὶ τὰ τρίτα μέρεα τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τῶν μὲν τετραγώνων τῶν ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ ἐλάττονα, τῶν δὲ τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ μείζονα, δεδειγμένον ἐσσεῖται τὸ προτεθέν.

   Ἐντὶ δὴ τὸ μὲν περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΔ, ΠΖ, ΡΘ, ΣΚ, ΤΜ, ΥΞ καὶ τὰ τρίτα μέρεα τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ ἴσα τοῖς τετραγώνοις τοῖς ἀπὸ ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ, ΝΞ καὶ τῷ περιεχομένῳ ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ καὶ τῷ τρίτῳ μέρει τῶν τετραγώνων τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ, τὰ δὲ ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ τετράγωνα ἴσα τοῖς ἀπὸ τᾶν ΒΦ, ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ τετραγώνοις καὶ τοῖς ἀπὸ τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ καὶ τῷ περιεχομένῳ ὑπὸ τᾶς ΒΦ καὶ τᾶς διπλασίας τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ. Κοινὰ μὲν οὖν ἐντι ἑκατέρων τὰ τετράγωνα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ ΝΞ, τὸ δὲ περιεχόμενον ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας ταῖς ΟΧ, ΠΨ, ΩΡ, ϠΣ, ϞΤ, ΥΝ ἔλασσόν ἐστι τοῦ περιεχομένου ὑπό τε τᾶς ΒΦ καὶ τᾶς διπλασίας τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ διὰ τὸ τὰς νῦν εἰρημένας γραμμὰς ταῖς μὲν ΓΟ, ΕΠ, ΡΗ, ΙΣ, ΛΤ, ΥΝ ἴσας εἶμεν, τᾶν δὲ λοιπᾶν [30] μείζονας, καὶ τὰ τετράγωνα δὲ τὰ ἀπὸ τᾶν ΑΦ, ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ μείζονά ἐντι τοῦ τρίτου μέρεος τῶν ἀπὸ τᾶν ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ· δέδεικται γὰρ τοῦτο ἐν τοῖς ἐπάνω· ἐλάττονα ἄρα ἐντὶ τὰ ῥηθέντα χωρία τῶν τετραγώνων τῶν ἀπὸ τᾶν ΑΒ, ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ.

   Λοιπὸν δὲ δειξοῦμες ὅτι μείζονά ἐντι τῶν τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ. Πάλιν δὴ τὰ τετράγωνα τὰ ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ ἴσα ἐντὶ τοῖς τε ἀπὸ τᾶν ΧΓ, ΕΨ, ΗΩ, ΙϠ, ΛϞ καὶ τοῖς ἀπὸ τᾶν ΧΔ, ΨΖ, ΩΘ, ϠΚ, ϞΜ, ΝΞ καὶ τῷ περιεχομένῳ ὑπό τε τᾶς ΝΞ καὶ τᾶς διπλασίας πασᾶν τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ. Καί ἐστι κοινὰ μὲν τὰ ἀπὸ τᾶν ΧΔ, ΨΖ, ΩΘ, ϠΚ, ΜϞ, ΝΞ, μεῖζον δὲ τὸ ὑπό τε τᾶς ΝΞ καὶ τᾶς ἴσας πάσαις ταῖς ΟΧ, ΠΨ, ΡΩ, ΣϠ, ΤϞ, ΥΝ τοῦ ὑπὸ τᾶς ΝΞ καὶ τᾶς διπλασίας πασᾶν τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ, ἐντὶ δὲ καὶ τὰ τετράγωνα τὰ ἀπὸ τᾶν ΧΟ, ΨΠ, ΩΡ, ϠΣ, ϞΤ, ΥΝ τῶν ἀπὸ τᾶν ΓΧ, ΕΨ, ΗΩ, ΙϠ, ΛϞ μείζονα ἢ τριπλάσια· δέδεικται γὰρ καὶ τοῦτο· μείζονα ἄρα ἐντὶ τὰ ῥηθέντα χωρία τῶν τετραγώνων τῶν ἀπὸ τᾶν ΓΔ, ΕΖ, ΗΘ, ΙΚ, ΛΜ, ΝΞ.

ΠΟΡΙΣΜΑ

   Καὶ τοίνυν εἴ κα ὁμοῖα ἀναγραφέωντι ἀπὸ πασᾶν, ἀπό τε τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ, εἴδεα, πάντα τὰ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τὰ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς [31] τοῦ ἀπὸ τᾶς ἐλαχίστας εἴδεος ἐλάσσονα λόγον ἑξοῦντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας ποτὶ τὸ ἴσον ἀμφοτέροις τῷ τε περιεχομένῳ ὑπό τε τᾶς μεγίστας καὶ τᾶς ἐλαχίστας καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ μεγίστα τᾶς ἐλαχίστας, ποτὶ δὲ τὰ ἀπὸ τᾶν αὐτᾶν εἴδεα χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα τοῦ αὐτοῦ λόγου· τὸν αὐτὸν γὰρ ἑξοῦντι λόγον τὰ ὁμοῖα εἴδεα τοῖς τετραγώνοις.

ΟΡΟΙ

   α΄. Εἴ κα εὐθεῖα ἐπιζευχθῇ γραμμὰ ἐν ἐπιπέδῳ καὶ μένοντος τοῦ ἑτέρου πέρατος αὐτᾶς ἰσοταχέως περιενεχθεῖσα ὁσακισοῦν ἀποκατασταθῇ πάλιν, ὅθεν ὥρμασεν, ἅμα δὲ τᾷ γραμμᾷ περιαγομένᾳ φέρηταί τι σαμεῖον ἰσοταχέως αὐτὸ ἑαυτῷ κατὰ τᾶς εὐθείας ἀρξάμενον ἀπὸ τοῦ μένοντος πέρατος, τὸ σαμεῖον ἕλικα γράψει ἐν τῷ ἐπιπέδῳ.

   β΄. Καλείσθω οὖν τὸ μὲν πέρας τᾶς εὐθείας τὸ μένον περιαγομένας αὐτᾶς ἀρχὰ τᾶς ἕλικος.

   γ΄. Ἁ δὲ θέσις τᾶς γραμμᾶς, ἀφ᾿ ἇς ἄρξατο ἁ εὐθεῖα περιφέρεσθαι, ἀρχὰ τᾶς περιφορᾶς.

   δ΄. Εὐθεῖα, ἃν μὲν ἐν τᾷ πρώτᾳ περιφορᾷ διαπορευθῇ τὸ σαμεῖον τὸ κατὰ τᾶς εὐθείας φερόμενον, πρώτα καλείσθω, ἃν δ᾿ ἐν τᾷ δευτέρᾳ περιφορᾷ τὸ αὐτὸ σαμεῖον διανύσῃ, δευτέρα, καὶ αἱ ἄλλαι ὁμοίως ταύταις ὁμωνύμως ταῖς περιφοραῖς καλείσθωσαν.

[32]    ε΄. Τὸ δὲ χωρίον τὸ περιλαφθὲν ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γραφείσας καὶ τᾶς εὐθείας, ἅ ἐστιν πρώτα, πρῶτον καλείσθω, τὸ δὲ περιλαφθὲν ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γραφείσας καὶ τᾶς εὐθείας τᾶς δευτέρας δεύτερον καλείσθω, καὶ τὰ ἄλλα ἑξῆς οὕτω καλείσθω.

   Ϛ. Καὶ εἴ κα ἀπὸ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ἀχθῇ τις εὐθεῖα γραμμά, τᾶς εὐθείας ταύτας τὰ ἐπὶ τὰ αὐτά, ἐφ᾿ ἅ κα ἁ περιφορὰ γένηται, προαγουμένα καλείσθω, τὰ δὲ ἐπὶ θάτερα ἑπόμενα.

   ζ΄. Ὅ τε γραφεὶς κύκλος κέντρῳ μὲν τῷ σαμείῳ, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, διαστήματι δὲ τᾷ εὐθείᾳ, ἅ ἐστιν πρώτα, πρῶτος καλείσθω, ὁ δὲ γραφεὶς κέντρῳ μὲν τῷ αὐτῷ, διαστήματι δὲ τᾷ διπλασίᾳ εὐθείᾳ δεύτερος καλείσθω, καὶ οἱ ἄλλοι δὲ ἑξῆς τούτοις τὸν αὐτὸν τρόπον.

   ιβ΄.

   Εἴ κα ποτὶ τὰν ἕλικα τὰν ἐν μιᾷ περιφορᾷ ὁποιᾳοῦν γεγραμμέναν ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος εὐθεῖαι ἐμπεσῶντι ὁποιαιοῦν ἴσας ποιοῦσαι γωνίας ποτ᾿ ἀλλάλας, τῷ ἴσῳ ὑπερέχοντι ἀλλαλᾶν.

[33]    Ἔστω ἕλιξ, ἐφ᾿ ἇς αἱ ΑΒ, ΑΓ, ΑΔ, ΑΕ, ΑΖ ἴσας γωνίας ποιοῦσαι ποτ᾿ ἀλλάλας. Δεικτέον ὅτι τῷ ἴσῳ ὑπερέχει ἁ ΑΓ τᾶς ΑΒ καὶ ἁ ΑΔ τᾶς ΑΓ καὶ αἱ ἄλλαι ὁμοίως.

   Ἐν ᾧ γὰρ χρόνῳ ἁ περιαγομένα γραμμὰ ἀπὸ τᾶς ΑΒ ἐπὶ τὰν ΑΓ ἀφικνεῖται, ἐν τούτῳ τῷ χρόνῳ τὸ σαμεῖον τὸ κατὰ τᾶς εὐθείας φερόμενον τὰν ὑπεροχὰν διαπορεύεται, ᾇ ὑπερέχει ἁ ΓΑ τᾶς ΑΒ, ἐν ᾧ δὲ χρόνῳ ἀπὸ τᾶς ΑΓ ἐπὶ τὰν ΑΔ, ἐν τούτῳ διαπορεύεται τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΑΔ τᾶς ΑΓ. Ἐν ἴσῳ δὲ χρόνῳ ἁ περιαγομένα γραμμὰ ἀπό τε τᾶς ΑΒ ἐπὶ τὰν ΑΓ ἀφικνεῖται καὶ ἀπὸ τᾶς ΑΓ ἐπὶ τὰν ΑΔ, ἐπειδὴ αἱ γωνίαι ἴσαι ἐντί· ἐν ἴσῳ ἄρα χρόνῳ τὸ κατὰ τᾶς εὐθείας φερόμενον σαμεῖον διαπορεύεται τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΓΑ τᾶς ΑΒ, καὶ τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ ΑΔ τᾶς ΑΓ. Τῷ ἴσῳ ἄρα ὑπερέχει ἅ τε ΑΓ τᾶς ΑΒ καὶ ἁ ΑΔ τᾶς ΑΓ, καὶ αἱ λοιπαί.

   ιγ΄.

   Εἴ κα εὐθεῖα γραμμὰ τᾶς ἕλικος ἐπιψαύῃ, καθ᾿ ἓν μόνον ἐπιψαύσει σαμεῖον.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς τὰ Α, Β, Γ, Δ, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Α σαμεῖον, ἀρχὰ δὲ τᾶς περιφορᾶς ἁ ΑΔ [34] εὐθεῖα, καὶ ἐπιψαυέτω τᾶς ἕλικος εὐθεῖά τις ἁ ΖΕ. Φαμὶ δὴ καθ᾿ ἓν μόνον σαμεῖον ἐπιψαύειν αὐτᾶς.

   Ἐπιψαυέτω γάρ, εἰ δυνατόν, κατὰ δύο σαμεῖα τὰ Γ, Η, καὶ ἐπεζεύχθωσαν αἱ ΑΓ, ΑΗ, καὶ ἁ γωνία δίχα τετμάσθω ἁ περιεχόμενα ὑπὸ τᾶν ΑΗ, ΑΓ, καθ᾿ ὃ δὲ σαμεῖον ἁ δίχα τέμνουσα τὰν γωνίαν τᾷ ἕλικι ποτιπίπτει, ἔστω τὸ Θ. Τῷ δὴ ἴσῳ ὑπερέχει ἅ τε ΑΗ τᾶς ΑΘ καὶ ἁ ΑΘ τᾶς ΑΓ, ἐπειδὴ ἴσας γωνίας περιέχοντι ποτ᾿ ἀλλάλας· ὥστε διπλάσιαί ἐντι αἱ ΑΗ, ΑΓ τᾶς ΑΘ. Ἀλλὰ τᾶς ἐν τῷ τριγώνῳ [τᾶς ΑΘ] δίχα τεμνούσας τὰν γωνίαν μείζονές ἐντι ἢ διπλάσιαι· δῆλον οὖν ὅτι, καθ᾿ ὃ συμπίπτει σαμεῖον τᾷ ΓΗ εὐθείᾳ ἁ ΑΘ, μεταξὺ τῶν Θ, Α ἐντὶ σαμείων· τέμνει ἄρα ἁ ΕΖ τὰν ἕλικα, ἐπειδή τι τῶν ἐν τᾷ ΓΘΗ σαμείων ἐντός ἐστι τᾶς ἕλικος. Ὑπέκειτο δὲ ἐπιψαύουσα· καθ᾿ ἓν ἄρα μόνον ἅπτεται ἁ ΕΖ τᾶς ἕλικος.

   ιδ΄.

   Εἴ κα ποτὶ τὰν ἕλικα τὰν ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμέναν ποτιπεσέωντι δύο εὐθεῖαι ἀπὸ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, καὶ ἐκβληθέωντι ποτὶ τὰν τοῦ πρώτου κύκλου περιφέρειαν, τὸν αὐτὸν ἑξοῦντι λόγον αἱ ποτὶ τὰν ἕλικα ποτιπίπτουσαι ποτ᾿ ἀλλάλας, ὃν αἱ περιφέρειαι τοῦ κύκλου αἱ μεταξὺ τοῦ πέρατος τᾶς ἕλικος καὶ τῶν περάτων τᾶν ἐκβληθεισᾶν εὐθειᾶν τῶν ἐπὶ τᾶς περιφερείας γινομένων, ἐπὶ τὰ προαγούμενα λαμβανομενᾶν τᾶν περιφερειᾶν ἀπὸ τοῦ πέρατος τᾶς ἕλικος.

   Ἔστω ἕλιξ ἁ ΑΒΓΔΕΘ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἀρχὰ δὲ τᾶς μὲν ἕλικος ἔστω τὸ Α σαμεῖον, ἁ δὲ

[35] ΘΑ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς ἔστω, καὶ κύκλος ὁ ΘΚΗ ἔστω ὁ πρῶτος, ποτιπιπτόντων δὲ ἀπὸ τοῦ Α σαμείου ποτὶ τὰν ἕλικα αἱ ΑΕ, ΑΔ καὶ ἐκπιπτόντων ποτὶ τὰν τοῦ κύκλου περιφέρειαν ἐπὶ τὰ Ζ, Η. Δεικτέον ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΕ ποτὶ τὰν ΑΔ, ὃν ἁ ΘΚΖ περιφέρεια ποτὶ τὰν ΘΚΗ περιφέρειαν.

   Περιαγομένας γὰρ τᾶς ΑΘ γραμμᾶς δῆλον ὡς τὸ μὲν Θ σαμεῖον κατὰ τᾶς τοῦ ΘΚΗ κύκλου περιφερείας ἐνηνεγμένον ἐστὶν ἰσοταχέως, τὸ δὲ Α κατὰ τᾶς εὐθείας φερόμενον τὰν ΑΘ γραμμὰν πορεύεται, καὶ τὸ Θ σαμεῖον κατὰ τᾶς τοῦ κύκλου περιφερείας φερόμενον τὰν ΘΚΖ περιφέρειαν, τὸ δὲ Α τὰν ΑΕ εὐθεῖαν, καὶ πάλιν τό τε Α σαμεῖον τὰν ΑΔ γραμμὰν καὶ τὸ Θ τὰν ΘΚΗ περιφέρειαν, ἑκάτερον ἰσοταχέως αὐτὸ ἑαυτῷ φερόμενον· δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΕ ποτὶ τὰν ΑΔ, ὃν ἁ ΘΚΖ περιφέρεια ποτὶ τὰν ΘΚΗ περιφέρειαν [δέδεικται γὰρ τοῦτο ἔξω ἐν τοῖς πρώτοις].

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα ἁ ἑτέρα τᾶν ποτιπιπτουσᾶν ἐπὶ τὸ πέρας τᾶς ἕλικος ποτιπίπτῃ, ὅτι τὸ αὐτὸ συμβαίνει.

[36]    ιε΄.

   Εἰ δέ κα ποτὶ τὰν ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμέναν ἕλικα ποτιπίπτωντι εὐθεῖαι ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος, τὸν αὐτὸν ἑξοῦντι λόγον αἱ εὐθεῖαι ποτ᾿ ἀλλάλας, ὃν αἱ εἰρημέναι περιφέρειαι μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας λαμβανομένας.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔΘ, ἁ μὲν ΑΒΓΔΘ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἁ δὲ ΘΛΕΜ ἐν τᾷ δευτέρᾳ, καὶ ποτιπιπτόντων εὐθεῖαι αἱ ΑΕ, ΑΛ. Δεικτέον ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΛ ποτὶ τὰν ΑΕ, ὃν ἁ ΘΚΖ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ ΘΚΗ μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας.

   Ἐν ἴσῳ γὰρ χρόνῳ τὸ Α σαμεῖον κατὰ τᾶς εὐθείας φερόμενον τὰν ΑΛ γραμμὰν διαπορεύεται, καὶ τὸ Θ σαμεῖον κατὰ τᾶς τοῦ κύκλου περιφερείας φερόμενον ὅλαν τε τὰν τοῦ κύκλου περιφέρειαν καὶ ἔτι τὰν ΘΚΖ περιφέρειαν διαπορεύεται, καὶ πάλιν τὸ Α σαμεῖον τὰν ΑΕ εὐθεῖαν καὶ τὸ Θ ὅλαν τε τὰν τοῦ κύκλου περιφέρειαν καὶ ἔτι τὰν ΘΚΗ, ἑκάτερον ἰσοταχέως αὐτὸ ἑαυτῷ φερόμενον· [37] δῆλον οὖν ὅτι τὸν αὐτὸν ἔχοντι λόγον ἁ ΑΛ γραμμὰ ποτὶ τὰν ΑΕ, ὃν ἁ ΘΚΖ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν ΘΚΗ περιφέρειαν μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας.

   Τὸν αὐτὸν δὲ τρόπον δειχθήσεται, καὶ εἴ κα ποτὶ τὰν ἐν τᾷ τρίτᾳ περιφορᾷ γεγραμμέναν ἕλικα ποτιπεσέωντι εὐθεῖαι, ὅτι τὸν αὐτὸν λόγον ἑξοῦντι ποτ᾿ ἀλλάλας, ὃν αἱ εἰρημέναι περιφέρειαι μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας δὶς λαμβανομένας· ὁμοίως δὲ καὶ αἱ ποτὶ τὰς ἄλλας ἕλικας ποτιπίπτουσαι δείκνυνται ὅτι τὸν αὐτὸν ἔχοντι λόγον, ὃν αἱ εἰρημέναι περιφέρειαι μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας τοσαυτάκις λαμβανομένας, ὅσος ἐστὶν ὁ ἑνὶ ἐλάσσων ἀριθμὸς τᾶν περιφορᾶν, καὶ εἴ κα ἁ ποτιπίπτουσα ἁ ἑτέρα ποτὶ τὸ πέρας τᾶς ἕλικος πίπτῃ.

   ιϚ΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ, καὶ ἀπὸ τᾶς ἁφᾶς εὐθεῖα γραμμὰ ἐπιζευχθῇ ἐπὶ τὸ σαμεῖον, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ἃς ποιεῖ γωνίας ἁ ἐφαπτομένα ποτὶ τὰν ἐπιζευχθεῖσαν, ἀνίσοι ἐσσοῦνται καὶ ἁ μὲν ἐν τοῖς προαγουμένοις ἀμβλεῖα, ἁ δὲ ἐν τοῖς ἑπομένοις ὀξεῖα.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς τὰ Α, Β, Γ, Δ, Θ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, καὶ ἔστω τὸ μὲν Α σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΑΘ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς, ὅ τε πρῶτος κύκλος ὁ ΘΚΗ, ἐπιψαυέτω δέ τις εὐθεῖα γραμμὰ τᾶς ἕλικος ἁ ΕΔΖ κατὰ τὸ Δ, καὶ ἀπὸ τοῦ Δ ἐπὶ τὸ Α ἐπεζεύχθω ἁ ΔΑ. Δεικτέον ὅτι ἁ ΔΖ ποτὶ τὰν ΑΔ ἀμβλεῖαν ποιεῖ γωνίαν.

[38]    Γεγράφθω κύκλος ὁ ΔΤΝ κέντρῳ μὲν τῷ Α, διαστήματι δὲ τᾷ ΑΔ· ἀναγκαῖον δὴ τούτου τοῦ κύκλου τὰν μὲν ἐν τοῖς προαγουμένοις περιφέρειαν ἐντὸς πίπτειν τᾶς ἕλικος, τὰν δὲ ἐν τοῖς ἑπομένοις ἐκτὸς διὰ τὸ τᾶν ἀπὸ τοῦ Α ποτὶ τὰν ἕλικα ποτιπιπτουσᾶν εὐθειᾶν τὰς μὲν ἐν τοῖς προαγουμένοις μείζονας εἶμεν τᾶς ΑΔ, τὰς δὲ ἐν τοῖς ἑπομένοις ἐλάσσονας. Ὅτι μὲν οὖν ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ οὐκ ἔστιν ὀξεῖα δῆλον, ἐπειδὴ μείζων ἐστὶ τᾶς τοῦ ἡμικυκλίου, ὅτι δὲ ὀρθὰ οὐκ ἔστι δεικτέον οὕτως· ἔστω γὰρ, εἰ δυνατόν, ὀρθά· ἁ ἄρα ΕΔΖ ἐπιψαύει τοῦ ΔΤΝ κύκλου. Δυνατὸν δή ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν εὐθεῖαν ποτὶ τὰν ἐπιψαύουσαν, ὥστε τὰν μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς τοῦ κύκλου περιφερείας εὐθεῖαν ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ κύκλου ἐλάσσονα λόγον ἔχειν τοῦ ὃν ἔχει ἁ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς ποτιπιπτούσας περιφέρεια ποτὶ τὰν δοθεῖσαν περιφέρειαν. Ποτιπιπτέτω δὴ ἁ ΑΙ· τεμεῖ δὴ αὕτα τὰν μὲν ἕλικα κατὰ τὸ Λ, τὰν δὲ τοῦ ΔΝΤ κύκλου περιφέρειαν κατὰ τὸ Ρ· καὶ ἐχέτω [39] ἁ ΡΙ εὐθεῖα ποτὶ τὰν ΑΡ ἐλάσσονα λόγον τοῦ ὃν ἔχει ἁ ΔΡ περιφέρεια ποτὶ τὰν ΔΝΤ περιφέρειαν· καὶ ὅλα ἄρα ἁ ΙΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΡΔΝΤ περιφέρεια ποτὶ τὰν ΔΝΤ περιφέρειαν, τουτέστιν ὃν ἔχει ἁ ΣΗΚΘ περιφέρεια ποτὶ τὰν ΗΚΘ περιφέρειαν. Ὃν δὲ ἁ ΣΗΚΘ περιφέρεια ποτὶ τὰν ΗΚΘ περιφέρειαν, τοῦτον ἔχει ἁ ΑΛ εὐθεῖα ποτὶ τὰν ΑΔ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΑΙ ποτὶ τὰν ΑΡ ἤπερ ἁ ΛΑ ποτὶ τὰν ΑΔ· ὅπερ ἀδύνατον· ἴσα γὰρ ἁ ΡΑ τᾷ ΑΔ. Οὐκ ἄρα ἐστὶν ὀρθὰ ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ. Δέδεικται δὲ ὅτι οὐδὲ ὀξεῖα· ἀμβλεῖα ἄρα ἐστίν. Ὥστε ἁ λοιπὰ ὀξεῖά ἐστιν.

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα ἁ ἐπιψαύουσα τᾶς ἕλικος κατὰ τὸ πέρας ἐπιψαύῃ, ὅτι τὸ αὐτὸ συμβήσεται.

   ιζ΄.

   Καὶ τοίνυν, εἴ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ ἁ εὐθεῖα, τὸ αὐτὸ συμβήσεται.

[40]    Ἐπιψαυέτω γὰρ ἁ ΕΖ εὐθεῖα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος κατὰ τὸ Δ, καὶ τὰ ἄλλα τὰ αὐτὰ τοῖς πρότερον κατεσκευάσθω. Ὁμοίως δὴ τᾶς τοῦ ΡΝΔ κύκλου περιφερείας τὰ μὲν ἐν τοῖς προαγουμένοις τᾶς ἕλικος ἐντὸς πεσοῦνται, τὰ δὲ ἐν τοῖς ἑπομένοις ἐκτός· ἁ οὖν γωνία ἁ ὑπὸ τᾶν ΑΔΖ οὐκ ἔστιν ὀρθά, ἀλλὰ ἀμβλεῖα. Ἔστω γάρ, εἰ δυνατόν, ὀρθά· ἐπιψαύσει δὴ ἁ ΕΖ τοῦ ΡΝΔ κύκλου κατὰ τὸ Δ. Ἄχθω δὴ πάλιν ποτὶ τὰν ἐπιψαύουσαν ἁ ΑΙ καὶ τεμνέτω τὰν μὲν ἕλικα κατὰ τὸ Χ, τὰν δὲ τοῦ ΡΝΔ κύκλου περιφέρειαν κατὰ τὸ Ρ, ἐχέτω δὲ ἁ ΡΙ ποτὶ ΡΑ ἐλάσσονα λόγον τοῦ ὃν ἔχει ἁ ΔΡ περιφέρεια ποτὶ ὅλαν τὰν τοῦ ΔΡΝ κύκλου περιφέρειαν καὶ [ποτὶ] τὰν ΔΝΤ· δέδεικται γὰρ τοῦτο δυνατὸν ἐόν· καὶ ὅλα ἄρα ἁ ΙΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΡΔΝΤ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν ΔΝΤ περιφέρειαν μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας. Ἀλλ᾿ ὃν ἔχει λόγον ἁ ΡΔΝΤ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ ΔΝΤΡ κύκλου περιφερείας ποτὶ τὰν ΔΝΤ περιφέρειαν μεθ᾿ ὅλας τᾶς τοῦ ΔΝΤΡ κύκλου περιφερείας, τοῦτον ἔχει τὸν λόγον ἁ ΣΗΚΘ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας τᾶς ΘΣΗΚ ποτὶ τὰν ΗΚΘ περιφέρειαν μεθ᾿ ὅλας τᾶς τοῦ ΘΣΗΚ κύκλου περιφερείας, ὃν δὲ λόγον ἔχοντι αἱ ὕστερον εἰρημέναι περιφέρειαι, τοῦτον ἔχει τὸν λόγον ἁ ΧΑ εὐθεῖα ποτὶ τὰν ΑΔ εὐθεῖαν· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΙΑ ποτὶ τὰν ΑΡ ἢ ἁ ΑΧ ποτὶ τὰν ΑΔ· ὅπερ ἀδύνατον [ἴση μὲν γὰρ ἡ ΡΑ τῇ ΑΔ, μείζων δὲ ἡ ΙΑ τῆς ΑΧ]. Δῆλον οὖν ὅτι ἀμβλεῖά ἐστιν ἁ περιεχομένα ὑπὸ τᾶν ΑΔΖ· ὥστε ἁ λοιπὰ ὀξεῖά ἐστι.

[41]    Τὰ δ᾿ αὐτὰ συμβήσεται, καὶ εἴ κα ἁ ἐπιψαύουσα κατὰ τὸ πέρας τᾶς ἕλικος ἐπιψαύῃ.

   Ὁμοίως δὲ δειχθήσεται, καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ τις εὐθεῖα, καὶ εἴ κα κατὰ τὸ πέρας αὐτᾶς, ὅτι ἀνίσους ποιήσει τὰς γωνίας ποτὶ τὰν ἀπὸ τᾶς ἁφᾶς ἐπιζευχθεῖσαν ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος καὶ τὰν μὲν ἐν τοῖς προαγουμένοις ἀμβλεῖαν, τὰν δὲ ἐν τοῖς ἑπομένοις ὀξεῖαν.

   ιη΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ κατὰ τὸ πέρας τᾶς ἕλικος, ἀπὸ δὲ τοῦ σαμείου, ὅ ἐστιν ἀρχὰ τᾶς ἕλικος, ποτ᾿ ὀρθὰς ἀχθῇ τις τᾷ ἀρχᾷ τᾶς περιφορᾶς, ἁ ἀχθεῖσα συμπεσεῖται τᾷ ἐπιψαυούσᾳ, καὶ ἁ μεταξὺ εὐθεῖα τᾶς ἐπιψαυούσας καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα ἐσσεῖται τᾷ τοῦ πρώτου κύκλου περιφερείᾳ.

   Ἔστω ἕλιξ ἁ ΑΒΓΔΘ, ἔστω δὲ τὸ Α σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΑ γραμμὰ ἀρχὰ τᾶς περιφορᾶς, ὁ δὲ ΘΗΚ κύκλος ὁ πρῶτος, ἐπιψαυέτω δέ τις τᾶς ἕλικος κατὰ τὸ Θ ἁ ΘΖ, καὶ ἀπὸ τοῦ Α ἄχθω ποτ᾿ ὀρθὰς τᾷ ΘΑ ἁ ΑΖ· συμπεσεῖται δὴ αὕτα ποτὶ τὰν ΘΖ, ἐπεὶ αἱ ΖΘ, ΘΑ ὀξεῖαν [42] γωνίαν περιέχοντι. Συμπιπτέτω κατὰ τὸ Ζ. Δεικτέον ὅτι ἁ ΖΑ ἴσα ἐστὶ τᾷ τοῦ ΘΚΗ κύκλου περιφερείᾳ.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω πρότερον, εἰ δυνατόν, μείζων. Ἔλαβον δή τινα εὐθεῖαν τὰν ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσονα, τᾶς δὲ τοῦ ΘΗΚ κύκλου περιφερείας μείζονα. Ἔστιν δὴ κύκλος τις ὁ ΘΗΚ καὶ ἐν τῷ κύκλῳ γραμμὰ ἐλάσσων τᾶς διαμέτρου ἁ ΘΗ καὶ λόγος, ὃν ἔχει ἁ ΘΑ ποτὶ ΑΛ, μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΗΘ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὸν ἀγμέναν, διότι καὶ τοῦ ὃν ἔχει ἁ ΘΑ ποτὶ ΑΖ· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν ποτὶ τὰν ἐκβεβλημέναν τὰν ΑΝ, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας τὰν ΝΡ ποτὶ ΘΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΘΑ ποτὶ τὰν ΑΛ· ἕξει οὖν ἁ ΝΡ ποτὶ τὰν ΡΑ λόγον, ὃν ἁ ΘΡ εὐθεῖα ποτὶ τὰν ΑΛ. Ἁ δὲ ΘΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· ἁ μὲν γὰρ ΘΡ εὐθεῖα ἐλάσσων ἐστὶ τᾶς ΘΡ περιφερείας, ἁ δὲ ΑΛ εὐθεῖα τᾶς τοῦ ΘΗΚ κύκλου περιφερείας μείζων· ἐλάσσονα οὖν λόγον ἕξει καὶ ἁ ΝΡ ποτὶ ΡΑ ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· καὶ ὅλα οὖν ἁ ΝΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἤπερ ἁ ΘΡ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ κύκλου περιφερείας ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ ΘΡ περιφέρεια μεθ᾿ ὅλας τᾶς τοῦ ΘΗΚ κύκλου περιφερείας ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν, τοῦτον ἔχει ἁ ΧΑ ποτὶ τὰν ΑΘ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΝΑ ποτὶ τὰν ΑΡ ἤπερ ἁ ΧΑ ποτὶ τὰν ΑΘ· ὅπερ ἀδύνατον· ἁ μὲν γὰρ ΝΑ μείζων ἐστὶ τᾶς ΑΧ, ἁ δὲ ΑΡ ἴσα ἐστὶ τᾷ ΘΑ. Οὐκ ἄρα μείζων ἁ ΖΑ τᾶς τοῦ κύκλου περιφερείας τοῦ ΘΗΚ.

[43]    Ἔστω δὴ πάλιν, εἰ δυνατόν, ἐλάσσων ἁ ΖΑ τᾶς τοῦ ΘΗΚ κύκλου περιφερείας. Ἔλαβον δή τινα εὐθεῖαν πάλιν τὰν ΑΛ τᾶς μὲν ΑΖ μείζονα, τᾶς δὲ τοῦ ΘΗΚ κύκλου περιφερείας ἐλάσσονα, καὶ ἄγω ἀπὸ τοῦ Θ τὰν ΘΜ παράλληλον τᾷ ΑΖ. Πάλιν οὖν κύκλος ἐστὶν ὁ ΘΗΚ καὶ ἐν αὐτῷ ἐλάσσων γραμμὰ τᾶς διαμέτρου ἁ ΘΗ καὶ ἄλλα ἐπιψαύουσα τοῦ κύκλου κατὰ τὸ Θ καὶ λόγος, ὃν ἔχει ἁ ΑΘ ποτὶ τὰν ΑΛ, ἐλάσσων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΗΘ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν, ἐπειδὴ καὶ τοῦ ὃν ἔχει ἁ ΘΑ ποτὶ ΑΖ ἐλάσσων ἐστί· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ἀγαγεῖν τὰν ΑΠ ποτὶ τὰν ἐπιψαύουσαν, ὥστε τὰν ΡΝ τὰν μεταξὺ τᾶς ἐν τῷ κύκλῳ εὐθείας καὶ τᾶς περιφερείας ποτὶ τὰν ΘΠ τὰν ἀπολαφθεῖσαν ἀπὸ τᾶς ἐπιψαυούσας τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει ἁ ΘΑ ποτὶ τὰν ΑΛ· τεμεῖ δὴ ἁ ΑΠ τὸν μὲν κύκλον κατὰ τὸ Ρ, τὰν δὲ ἕλικα κατὰ τὸ Χ· καὶ ἕξει καὶ ἐναλλὰξ τὸν αὐτὸν λόγον ἁ ΝΡ ποτὶ ΡΑ, ὃν ἁ ΘΠ ποτὶ ΑΛ. Ἁ δὲ ΘΠ ποτὶ τὰν ΑΛ μείζονα λόγον ἔχει ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ κύκλου περιφέρειαν· ἁ μὲν γὰρ ΘΠ εὐθεῖα μείζων ἐστὶν τᾶς ΘΡ περιφερείας, ἁ δὲ ΑΛ ἐλάσσων τᾶς τοῦ ΘΗΚ κύκλου περιφερείας· μείζονα ἄρα λόγον ἔχει ἁ ΠΡ ποτὶ τὰν ΑΡ ἢ ἁ ΘΡ περιφέρεια ποτὶ τὰν τοῦ ΘΗΚ [44] κύκλου περιφέρειαν· ὥστε καὶ ἁ ΡΑ ποτὶ τὰν ΑΝ μείζονα λόγον ἔχει ἢ ἁ τοῦ ΘΗΚ κύκλου περιφέρεια ποτὶ τὰν ΘΚΡ περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ τοῦ ΘΗΚ κύκλου περιφέρεια ποτὶ τὰν ΘΚΡ περιφέρειαν, τοῦτον ἔχει ἁ ΘΑ εὐθεῖα ποτὶ τὰν ΑΧ· δέδεικται γὰρ τοῦτο· μείζονα ἄρα λόγον ἔχει ἁ ΡΑ ποτὶ τὰν ΑΝ ἢ ἁ ΘΑ ποτὶ τὰν ΑΧ· ὅπερ ἀδύνατον. Οὐκ ἄρα μείζων ἐστὶν οὐδὲ ἐλάσσων ἁ ΖΑ τᾶς τοῦ ΘΗΚ κύκλου περιφερείας· ἴσα ἄρα.

   ιθ΄.

   Εἰ δέ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος κατὰ τὸ πέρας ἐπιψαύῃ εὐθεῖα, καὶ ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος ἀχθῇ τις ποτ᾿ ὀρθὰς τᾷ ἀρχᾷ τᾶς περιφορᾶς, συμπεσεῖται αὕτα ποτὶ τὰν ἐπιψαύουσαν, καὶ ἐσσεῖται ἁ εὐθεῖα ἁ μεταξὺ τᾶς ἐπιψαυούσας καὶ τᾶς ἀρχᾶς τᾶς ἕλικος διπλασία τᾶς τοῦ δευτέρου κύκλου περιφερείας.

   Ἔστω γὰρ ἁ μὲν ΑΒΓΘ ἕλιξ ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἁ δὲ ΘΕΤ ἐν τᾷ δευτέρᾳ, καὶ ὁ μὲν ΘΚΗ κύκλος ὁ πρῶτος, ὁ δὲ ΤΜΝ ὁ δεύτερος, ἔστω δέ τις [45] γραμμὰ ἐπιψαύουσα τᾶς ἕλικος κατὰ τὸ Θ ἁ ΤΖ, ἁ δὲ ΖΑ ποτ᾿ ὀρθὰς ἄχθῳ τᾷ ΤΑ· συμπεσεῖται δὲ αὕτα τᾷ ΤΖ διὰ τὸ δεδεῖχθαι τὰν γωνίαν ὀξεῖαν ἐοῦσαν τὰν ὑπὸ τᾶν ΑΤΖ. Δεικτέον ὅτι ἁ ΖΑ εὐθεῖα διπλασία ἐντὶ τᾶς τοῦ ΤΜΝ κύκλου περιφερείας.

   Εἰ γὰρ μή ἐστιν διπλασία, ἤτοι μείζων ἐστὶν ἢ διπλασία ἢ ἐλάσσων ἐστὶν ἢ διπλασία. Ἔστω πρότερον, εἰ δυνατόν, μείζων ἢ διπλασία, καὶ λελάφθω τις εὐθεῖα ἁ ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσων, τᾶς δὲ τοῦ ΤΜΝ κύκλου περιφερείας μείζων ἢ διπλασία. Ἔστιν δή τις κύκλος ὁ ΤΜΝ καὶ ἐν τῷ κύκλῳ γραμμὰ δεδομένα ἐλάσσων τᾶς διαμέτρου ἁ ΤΝ, καὶ ὃν ἔχει ἁ ΤΑ ποτὶ τὰν ΑΛ μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΤΝ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν τὰν ΑΣ ποτὶ τὰν ΤΝ ἐκβεβλημέναν, ὥστε τὰν μεταξὺ τᾶς περιφερείας καὶ τᾶς ἐκβεβλημένας τὰν ΡΣ ποτὶ τὰν ΤΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΤΑ ποτὶ τὰν ΑΛ· τεμεῖ δὴ ἁ ΑΣ τὸν μὲν κύκλον κατὰ τὸ Ρ, τὰν δὲ ἕλικα κατὰ τὸ Χ· καὶ ἐναλλὰξ τὸν αὐτὸν ἕξει λόγον ἁ ΡΣ ποτὶ τὰν ΤΑ, ὃν ἁ ΤΡ ποτὶ τὰν ΑΛ. Ἁ δὲ ΤΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΤΡ περιφέρεια ποτὶ τὰν διπλασίαν τοῦ ΤΜΝ κύκλου περιφέρειαν· ἔστιν γὰρ ἁ μὲν ΤΡ εὐθεῖα ἐλάσσων τᾶς ΤΡ περιφερείας, ἁ δὲ ΑΛ εὐθεῖα μείζων ἢ διπλασία τᾶς τοῦ ΤΜΝ κύκλου περιφερείας· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΡΣ ποτὶ τὰν ΑΡ ἢ ἁ ΤΡ περιφέρεια ποτὶ τὰν διπλασίαν τᾶς τοῦ ΤΜΝ κύκλου περιφερείας· ὅλα οὖν ἁ ΣΑ ποτὶ τὰν ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΤΡ περιφέρεια μετὰ τᾶς τοῦ ΤΜΝ κύκλου περιφερείας δὶς εἰρημένας ποτὶ τὰν τοῦ ΤΜΝ κύκλου περιφέρειαν [46] δὶς εἰρημέναν. Ὃν δὲ λόγον ἔχοντι αἱ εἰρημέναι περιφέρειαι, τοῦτον ἔχει τὸν λόγον ἁ ΧΑ ποτὶ τὰν ΑΤ· δέδεικται γὰρ τοῦτο· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΑΣ ποτὶ τὰν ΑΡ ἢ ἁ ΧΑ ποτὶ τὰν ΤΑ· ὅπερ ἀδύνατον. Οὐκ ἄρα μείζων ἐστὶν ἢ διπλασία ἁ ΖΑ εὐθεῖα τᾶς τοῦ ΤΜΝ κύκλου περιφερείας. Ὁμοίως δὲ δειχθήσεται ὅτι οὐδὲ ἐλάσσων ἢ διπλασία. Δῆλον οὖν ὅτι διπλασία ἐστίν.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δεικτέον, καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ τις εὐθεῖα κατὰ τὸ πέρας τᾶς ἕλικος, καὶ ἀπὸ τᾶς ἀρχᾶς τᾶς ἕλικος ποτ᾿ ὀρθὰς ἀχθεῖσα τᾷ ἀρχᾷ τᾶς περιφορᾶς συμπίπτῃ ποτὶ τὰν ἐπιψαύουσαν, ὅτι πολλαπλασία ἐστὶν τᾶς τοῦ κύκλου περιφερείας τοῦ κατὰ τὸν ἀριθμὸν τᾶς περιφορᾶς λεγομένου τῷ αὐτῷ ἀριθμῷ.

   κ΄.

   Εἴ κα τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας εὐθεῖα γραμμὰ ἐπιψαύῃ μὴ κατὰ τὸ πέρας τᾶς ἕλικος, ἀπὸ δὲ τᾶς ἁφᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος εὐθεῖα ἐπιζευχθῇ, καὶ κέντρῳ μὲν τᾷ ἀρχᾷ τᾶς ἕλικος, διαστήματι δὲ τᾷ ἐπιζευχθείσᾳ κύκλος γραφῇ, ἀπὸ δὲ τᾶς ἀρχᾶς τᾶς ἕλικος ἀχθῇ τις ποτ᾿ ὀρθὰς τᾷ ἀπὸ τᾶς ἁφᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπιζευχθείσᾳ, συμπεσεῖται αὕτα ποτὶ τὰν ἐπιψαύουσαν, καὶ ἐσσεῖται ἁ μεταξὺ εὐθεῖα τᾶς τε συμπτώσιος καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα τᾷ περιφερείᾳ τοῦ γραφέντος κύκλου τᾷ μεταξὺ τᾶς ἁφᾶς καὶ τᾶς τομᾶς, καθ᾿ ἃν τέμνει ὁ γραφεὶς κύκλος τὰν ἀρχὰν τᾶς περιφορᾶς, ἐπὶ τὰ προαγούμενα λαμβανομένας τᾶς περιφερείας ἀπὸ τοῦ σαμείου τοῦ ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς.

[47]    Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, καὶ ἐπιψαυέτω τις αὐτᾶς εὐθεῖα ἁ ΕΖ κατὰ τὸ Δ, ἀπὸ δὲ τοῦ Δ ποτὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπεζεύχθω ἁ ΑΔ, καὶ κέντρῳ μὲν τῷ Α, διαστήματι δὲ τῷ ΑΔ κύκλος γεγράφθω ὁ ΔΜΝ, τεμνέτω δ᾿ οὗτος τὰν ἀρχὰν τᾶς περιφορᾶς κατὰ τὸ Κ, ἄχθω δὲ ἁ ΖΑ ποτὶ τὰν ΑΔ ὀρθά. Ὅτι μὲν οὖν αὕτα συμπίπτει δῆλον· ὅτι δὲ καὶ ἴσα ἐστὶν ἁ ΖΑ εὐθεῖα τᾷ ΚΜΝΔ περιφερείᾳ δεικτέον.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάσσων. Ἔστω, εἰ δυνατόν, πρότερον μείζων, λελάφθω δέ τις ἁ ΛΑ τᾶς μὲν ΖΑ εὐθείας ἐλάσσων, τᾶς δὲ ΚΜΝΔ περιφερείας μείζων. Πάλιν δὴ κύκλος ἐστὶν ὁ ΚΜΝ καὶ ἐν τῷ κύκλῳ γραμμὰ ἐλάσσων τᾶς διαμέτρου ἁ ΔΝ καὶ λόγος, ὃν ἔχει ἁ ΔΑ ποτὶ ΑΛ, μείζων τοῦ ὃν ἔχει ἁ ἡμίσεια τᾶς ΔΝ ποτὶ τὰν ἀπὸ τοῦ Α κάθετον ἐπ᾿ αὐτὰν ἀγμέναν· δυνατὸν οὖν ἐστιν ἀπὸ τοῦ Α ποτιβαλεῖν τὰν ΑΕ ποτὶ τὰν ΝΔ ἐκβεβλημέναν, ὥστε τὰν ΕΡ ποτὶ τὰν ΔΡ τὸν αὐτὸν ἔχειν λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΑΛ· δέδεικται γὰρ τοῦτο δυνατὸν ἐόν· ἕξει οὖν καὶ ἁ ΕΡ ποτὶ τὰν ΑΡ τὸν αὐτὸν λόγον, ὃν ἁ ΔΡ ποτὶ τὰν ΑΛ. Ἁ δὲ ΔΡ ποτὶ τὰν ΑΛ ἐλάσσονα λόγον ἔχει ἢ ἁ ΔΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν, ἐπεὶ ἁ μὲν ΔΡ ἐλάσσων ἐστὶ τᾶς ΔΡ [48] περιφερείας, ἁ δὲ ΑΛ μείζων τᾶς ΚΜΔ περιφερείας· ἐλάσσονα οὖν λόγον ἔχει ἁ ΕΡ εὐθεῖα ποτὶ ΡΑ ἢ ἁ ΔΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν· ὥστε καὶ ἁ ΑΕ ποτὶ ΑΡ ἐλάσσονα λόγον ἔχει ἢ ἁ ΚΜΡ περιφέρεια ποτὶ τὰν ΚΜΔ περιφέρειαν. Ὃν δὲ λόγον ἔχει ἁ ΚΜΡ ποτὶ τὰν ΚΜΔ περιφέρειαν, τοῦτον ἔχει ἁ ΧΑ ποτὶ ΑΔ· ἐλάσσονα ἄρα λόγον ἔχει ἁ ΕΑ ποτὶ ΑΡ ἢ ἁ ΑΧ ποτὶ ΔΑ· ὅπερ ἐστὶν ἀδύνατον. Οὐκ ἄρα μείζων ἁ ΖΑ τᾶς ΚΜΔ περιφερείας. Ὁμοίως δὲ τοῖς πρότερον δειχθήσεται ὅτι οὐδὲ ἐλάσσων ἐστίν· ἴσα ἄρα.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δειχθήσεται, καὶ εἴ κα τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας ἕλικος ἐπιψαύῃ εὐθεῖα μὴ κατὰ τὸ πέρας τᾶς ἕλικος, τὰ δὲ ἄλλα τὰ αὐτὰ κατασκευασθέωντι, ὅτι ἁ μεταξὺ εὐθεῖα τᾶς ποτὶ τὰν ἐπιψαύουσαν συμπτώσιος καὶ τᾶς ἀρχᾶς τᾶς ἕλικος ἴσα ἐστὶν ὅλᾳ τᾷ τοῦ γραφέντος κύκλου περιφερείᾳ καὶ ἔτι τᾷ μεταξὺ τῶν εἰρημένων σαμείων, ὡσαύτως τᾶς περιφερείας λαμβανομένας· καὶ εἴ κα τᾶς ἐν ὁποιᾳοῦν γεγραμμένας περιφορᾷ ἕλικος ἐπιψαύῃ τις εὐθεῖα μὴ κατὰ τὸ πέρας τᾶς ἕλικος, τὰ δὲ ἄλλα τὰ αὐτὰ κατασκευασθέωντι, ὅτι ἁ μεταξὺ εὐθεῖα τῶν εἰρημένων σαμείων πολλαπλασία τίς ἐστι τᾶς τοῦ γραφέντος κύκλου περιφερείας κατὰ τὸν ἑνὶ ἐλάσσονα ἀριθμὸν τοῦ καθ᾿ ὃν αἱ περιφοραὶ λέγονται, καὶ ἔτι ἴσα τᾷ μεταξὺ τῶν εἰρημένων σαμείων ὁμοίως λαμβανομένᾳ.

[49]    κα΄.

   Λαμβάνοντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς πρώτας ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς δυνατόν ἐστι περὶ αὐτὸ σχῆμα ἐπίπεδον περιγράψαι καὶ ἄλλο ἐγγράψαι ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Θ σαμεῖον, ἀρχὰ δὲ τᾶς περιφορᾶς ἁ ΘΑ, ὁ δὲ πρῶτος κύκλος ὁ ΖΗΙΑ, αἱ δὲ ΑΗ, ΖΙ διάμετροι αὐτοῦ ποτ᾿ ὀρθὰς ἀλλάλαις. Ἀεὶ δὴ τᾶς ὀρθᾶς γωνίας δίχα τεμνομένας καὶ τοῦ τομέως τοῦ τὰν ὀρθὰν γωνίαν περιέχοντος ἐσσεῖται τὸ καταλειπόμενον τοῦ τομέως ἔλασσον τοῦ προτεθέντος· καὶ ἔστω γεγενημένος ὁ τομεὺς ὁ ΑΘΚ ἐλάσσων τοῦ προτεθέντος χωρίου. Διαιρήσθωσαν δὴ αἱ γωνίαι αἱ τέσσαρες ὀρθαὶ εἰς τὰς ἴσας γωνίας τᾷ περιεχομένᾳ ὑπὸ τᾶν ΑΘ, [50] ΘΚ, καὶ αἱ ποιοῦσαι τὰς γωνίας εὐθεῖαι ἔστε ποτὶ τὰν ἕλικα ἄχθωσαν. Καθ᾿ ὃ δὴ τέμνει σαμεῖον ἁ ΘΚ τὰν ἕλικα, ἔστω τὸ Λ, καὶ κέντρῳ τῷ Θ, διαστήματι δὲ τῷ ΘΛ κύκλος γεγράφθω· πεσεῖται δὲ αὐτοῦ ἁ μὲν εἰς τὰ προαγούμενα περιφέρεια ἐντὸς τᾶς ἕλικος, ἁ δὲ εἰς τὰ ἑπόμενα ἐκτός. Γεγράφθω δὴ ἁ περιφέρεια, ἔστε κα συμπέσῃ τᾷ ΘΑ [κατὰ τὸ Ο ἁ ΟΜ] καὶ τᾷ μετὰ τὰν ΘΚ εὐθεῖαν ποτὶ τὰν ἕλικα ποτιπιπτούσᾳ. Πάλιν δὴ καὶ καθ᾿ ὃ τέμνει τὰν ἕλικα σαμεῖον ἁ ΘΜ, ἔστω τὸ Ν, καὶ κέντρῳ τῷ Θ, διαστήματι δὲ τῷ ΘΝ κύκλος γεγράφθω, ἔστε κα συμπέσῃ ἁ περιφέρεια τοῦ κύκλου τᾷ ΘΚ καὶ τᾷ μετὰ τὰν ΘΜ ποτιπιπτούσᾳ ποτὶ τὰν ἕλικα, ὁμοίως δὲ καὶ διὰ τῶν ἄλλων πάντων, καθ᾿ ἃ τέμνοντι τὰν ἕλικα αἱ τὰς ἴσας γωνίας ποιοῦσαι, κύκλοι γεγράφθωσαν κέντρῳ τῷ Θ, ἔστ᾿ ἂν συμπέσῃ ἑκάστα ἁ περιφέρεια τᾷ τε προαγουμένᾳ εὐθείᾳ καὶ τᾷ ἑπομένᾳ· ἐσσεῖται δή τι περὶ τὸ λαφθὲν χωρίον περιγεγραμμένον ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγεγραμμένον. Ὅτι δὲ τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου μεῖζόν ἐστιν ἐλάσσονι τοῦ προτεθέντος χωρίου δειχθήσεται. Ἔστιν γὰρ ὁ μὲν ΘΛΟ τομεὺς ἴσος τῷ ΘΜΛ, ὁ δὲ ΘΝΠ τῷ ΘΝΡ, ὁ δὲ ΘΧΣ τῷ ΘΧΤ, ἔστιν δὲ καὶ τῶν ἄλλων τομέων ἕκαστος τῶν ἐν τῷ ἐγγεγραμμένῳ σχήματι ἴσος τῷ κοινὰν ἔχοντι πλευρὰν τομεῖ τῶν ἐν τῷ περιγεγραμμένῳ σχήματι τομέων. Δῆλον οὖν ὅτι καὶ πάντες οἱ τομέες πάντεσσιν ἴσοι ἐσσοῦνται· [51] ἴσον ἄρα ἐστὶν τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ χωρίῳ τῷ περιγεγραμμένῳ περὶ τὸ χωρίον σχήματι χωρὶς τοῦ ΘΑΚ τομέως· μόνος γὰρ οὗτος οὐ λέλαπται τῶν ἐν τῷ περιγεγραμμένῳ σχήματι. Δῆλον οὖν ὅτι τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου μεῖζόν ἐστι τῷ ΑΚΘ τομεῖ, ὃς ἐλάσσων ἐστὶν τοῦ προτεθέντος.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου δὲ φανερὸν ὅτι δυνατόν ἐστι περὶ τὸ εἰρημένον χωρίον σχῆμα, οἷον εἴρηται, γράφειν, ὥστε τὸ περιγεγραμμένον σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράφειν, ὥστε τὸ χωρίον ὁμοίως μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κβ΄.

   Λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπὸ τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας, ἅ ἐστι δευτέρα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, δυνατόν ἐστι περὶ αὐτὸ σχῆμα ἐπίπεδον περιγράψαι ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγράψαι, ὥστε τὸ περιγραφὲν τοῦ ἐγγραφέντος μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ᾿ ᾇ ἁ ΑΒΓΔΕ, ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένα, καὶ ἔστω τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΑΘ ἀρχὰ τᾶς περιφορᾶς, ἁ δὲ ΕΑ ἁ δευτέρα εὐθεῖα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, ὁ δὲ ΑΖΗ κύκλος ἔστω δεύτερος καὶ αἱ ΑΓΗ, ΖΙ διάμετροι αὐτοῦ ποτ᾿ ὀρθὰς

[52] ἀλλάλαις. Πάλιν οὖν δίχα τεμνομένας τᾶς ὀρθᾶς γωνίας καὶ τοῦ τομέως τοῦ τὰν ὀρθὰν γωνίαν περιέχοντος ἐσσεῖται τὸ καταλειπόμενον ἔλασσον τοῦ προτεθέντος· καὶ ἔστω γεγενημένος ὁ ΘΚΑ τομεὺς ἐλάσσων τοῦ προτεθέντος χωρίου. Διαιρεθεισᾶν δὴ τᾶν ὀρθᾶν γωνιᾶν εἰς τὰς ἴσας γωνίας τᾷ ὑπὸ τᾶν ΚΘΑ καὶ τῶν ἄλλων κατεσκευασθέντων κατὰ τὰ αὐτὰ τοῖς πρότερον ἐσσεῖται τὸ περιγεγραμμένον σχῆμα τοῦ ἐγγεγραμμένου σχήματος μεῖζον ἐλάσσονι ἢ ὁ τομεὺς ὁ ΘΚΑ· μεῖζον γὰρ ἐσσεῖται τᾷ ὑπεροχᾷ, ᾇ ὑπερέχει ὁ ΘΚΑ τομεὺς τοῦ ΘΕΡ.

ΠΟΡΙΣΜΑ

   Δῆλον οὖν ὅτι δυνατόν ἐστιν καὶ τὸ περιγραφὲν σχῆμα τοῦ λαφθέντος χωρίου μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν τὸ λαφθὲν χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Διὰ δὲ τοῦ αὐτοῦ τρόπου φανερὸν διότι δυνατὸν λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος [53] τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς κατὰ τὸν αὐτὸν ἀριθμὸν λεγομένας περιγράψαι σχῆμα, οἷον εἴρηται, ἐπίπεδον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ λαφθέντος χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράψαι, ὥστε τὸ λαφθὲν χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κγ΄.

   Λαβόντα τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος, ἅ ἐστιν ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, οὐκ ἐχούσας πέρας τὰν ἀρχὰν τᾶς ἕλικος, καὶ τᾶν εὐθειᾶν τᾶν ἀπὸ τῶν περάτων τᾶς ἕλικος ἀγομενᾶν δυνατόν ἐστι περὶ τὸ χωρίον σχῆμα ἐπίπεδον περιγράψαι ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγράψαι, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος μεῖζον εἶμεν ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔΕ, πέρατα δὲ αὐτᾶς τὰ Α, Ε, ἔστω δὲ ἀρχὰ τᾶς ἕλικος τὸ Θ, καὶ ἐπεζεύχθωσαν αἱ ΑΘ, [54] ΘΕ. Γεγράφθω δὴ κύκλος κέντρῳ μὲν τῷ Θ, διαστήματι δὲ τῷ ΘΑ, καὶ συμπιπτέτω τᾷ ΘΕ κατὰ τὸ Ζ. Ἀεὶ δὲ τᾶς γωνίας τᾶς ποτὶ τῷ Θ καὶ τοῦ τομέως τοῦ ΘΑΖ δίχα τεμνομένων ἐσσεῖται τὸ καταλειπόμενον τοῦ προτεθέντος ἔλασσον. Ἔστω ἐλάσσων ὁ τομεὺς ὁ ΘΑΚ τοῦ προτεθέντος. Ὁμοίως δὴ τοῖς πρότερον γεγράφθωσαν κύκλοι διὰ τῶν σαμείων, καθ᾿ ἃ τέμνοντι τὰν ἕλικα αἱ τὰς ἴσας γωνίας ποιοῦσαι ποτὶ τῷ Θ, ὥστε τᾶν περιφερειᾶν ἑκάσταν συμπίπτειν τᾷ τε προαγουμένᾳ καὶ τᾷ ἑπομένᾳ· ἐσσεῖται δή τι περὶ τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν περιγεγραμμένον σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον καὶ ἄλλο ἐγγεγραμμένον, καὶ τὸ περιγεγραμμένον τοῦ ἐγγεγραμμένου ἐλάσσονι ὑπερέχει τοῦ προτεθέντος χωρίου· ἐλάσσων γάρ ἐστιν ὁ ΘΑΚ τομεύς.

ΠΟΡΙΣΜΑ

   Ἐκ τούτου φανερόν ἐστιν ὅτι δυνατόν ἐστιν περὶ τὸ εἰρημένον χωρίον σχῆμα ἐπίπεδον, οἷον εἴρηται, περιγράψαι, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου, καὶ πάλιν ἐγγράψαι, ὥστε τὸ εἰρημένον χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι παντὸς τοῦ προτεθέντος χωρίου.

   κδ΄.

   Τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς πρώτας [55] τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς τρίτον μέρος ἐστὶ τοῦ κύκλου τοῦ πρώτου.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔΕΘ, ἐν τᾷ πρώτᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΑ εὐθεῖα πρώτα τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς, ὁ δὲ ΑΚΖΗΙ κύκλος πρῶτος, οὗ τρίτον μέρος ἔστω ὁ ἐν ᾧ Ϟ κύκλος. Δεικτέον ὅτι ἴσον ἐστὶ τὸ προειρημένον χωρίον τῷ Ϟ κύκλῳ.

   Εἰ γὰρ μή, ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. Ἔστω πρότερον, εἰ δυνατόν, ἔλασσον. Δυνατὸν δή ἐστιν περὶ τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ὁ Ϟ κύκλος τοῦ εἰρημένου χωρίου. Περιγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ εἰρημένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ, ἐλάχιστος δὲ ὁ ΘΕΟ· δῆλον οὖν [56] ὅτι τὸ περιγεγραμμένον σχῆμα ἔλασσόν ἐστι τοῦ Ϟ κύκλου. Ἐκβεβλήσθωσαν δὴ αἱ εὐθεῖαι αἱ ποτὶ τῷ Θ ποιοῦσαι τὰς ἴσας γωνίας, ἔστ᾿ ἂν ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι· ἐντὶ δή τινες γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, καὶ ἁ ἐλαχίστα ἴσα τᾷ ὑπεροχᾷ, ἐντὶ δὲ καὶ ἄλλαι τινὲς γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ πασᾶν ὁμοῖοι τομέες, ἀπό τε τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν καὶ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ἐλάσσονές ἐντι ἢ τριπλάσιοι τῶν τομέων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ οἱ μὲν τομέες οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσοι τῷ ΑΖΗΙ κύκλῳ, οἱ δὲ τομέες οἱ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ἴσοι τῷ περιγεγραμμένῳ σχήματι· ἐλάσσων ἄρα ὁ ΑΖΗΙ κύκλος τοῦ περιγεγραμμένου σχήματος ἢ τριπλασίων. Τοῦ δὲ Ϟ κύκλου τριπλασίων· ἐλάσσων ἄρα ὁ Ϟ κύκλος τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα ἐστὶν τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ ἔλασσον τοῦ Ϟ χωρίου.

   Οὐδὲ τοίνυν μεῖζον. Ἔστω γάρ, εἰ δυνατόν, μεῖζον. Ἔστι δὴ πάλιν δυνατὸν εἰς τὸ χωρίον τὸ περιεχόμενον

[57] ὑπὸ τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας ἐγγράψαι σχῆμα, ὥστε τὸ εἰρημένον χωρίον τοῦ ἐγγραφέντος σχήματος μεῖζον εἶμεν ἐλάσσονι ἢ ᾧ ὑπερέχει τὸ εἰρημένον χωρίον τοῦ Ϟ κύκλου. Ἐγγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΡΞ, ἐλάχιστος δὲ ὁ ΟΘΕ· δῆλον οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστιν τοῦ Ϟ κύκλου. Ἐκβεβλήστωσαν δὴ αἱ ποιοῦσαι τὰς ἴσας γωνίας ποτὶ τῷ Θ, ἔστε κα ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, καί ἐστιν ἁ ἐλαχίστα ἴσα τᾷ ὑπεροχᾷ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΖΗΙ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει ἴσαι ταύταις, τῷ δὲ μεγέθει ἑκάστα ἴσα [58] τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ πασᾶν ὁμοῖοι τομέες ἀπό τε τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ μείζονές ἐντι ἢ τριπλάσιοι τῶν τομέων τῶν ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ οἱ μὲν τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ἴσοι τῷ ΑΖΗΙ κύκλῳ, οἱ δὲ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας ἴσοι τῷ ἐγγεγραμμένῳ σχήματι· μείζων ἄρα ὁ ΑΖΗΙ κύκλος ἢ τριπλασίων τοῦ ἐγγεγραμμένου σχήματος. Τοῦ δὲ Ϟ κύκλου τριπλασίων· μείζων ἄρα ἐστὶν ὁ Ϟ κύκλος τοῦ ἐγγεγραμμένου σχήματος. Οὐκ ἔστιν δέ, ἀλλὰ ἐλάσσων· οὐκ ἄρα ἐστὶν οὐδὲ μεῖζον τὸ χωρίον τὸ ὑπό τε τᾶς ΑΒΓΔΕΘ ἕλικος καὶ τᾶς ΑΘ εὐθείας τοῦ Ϟ κύκλου. Ἴσον ἄρα ἐστίν [τῷ περιλαφθέντι ὑπὸ τᾶς ἕλικος καὶ τᾶς ΑΘ εὐθείας].

   κε΄.

   Τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς δευτέρας τᾶν ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ποτὶ τὸν δεύτερον κύκλον τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὰ ζ ποτὶ τὰ ιβ, ὅς ἐστιν ὁ αὐτὸς τῷ ὃν ἔχει τὰ συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶς ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου καὶ τᾶς ἐκ τοῦ κέντρου τοῦ πρώτου κύκλου καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου τᾶς ἐκ τοῦ κέντρου τοῦ πρώτου κύκλου ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ἐκ τοῦ κέντρου τοῦ δευτέρου κύκλου.

[59]    Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔΕ, ἐν τᾷ δευτέρᾳ περιφορᾷ γεγραμμένα, ἔστω δὲ τὸ μὲν Θ σαμεῖον ἀρχὰ τᾶς ἕλικος, ἁ δὲ ΘΕ εὐθεῖα ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ἁ πρώτα, ἁ δὲ ΑΕ ἐν τᾷ ἀρχᾷ τᾶς περιφορᾶς ἁ δευτέρα, ὁ δὲ κύκλος ὁ ΑΖΗΙ ὁ δεύτερος ἔστω, καὶ αἱ ΑΗ, ΙΖ διάμετροι ποτ᾿ ὀρθὰς ἀλλάλαις. Δεικτέον ὅτι τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας ποτὶ τὸν ΑΖΗΙ κύκλον λόγον ἔχει, ὃν τὰ ζ ποτὶ ιβ.

   Ἔστω δή τις κύκλος ὁ Ϟ, ἁ δὲ ἐκ τοῦ κέντρου τοῦ Ϟ κύκλου δυνάμει ἴσα τῷ τε ὑπὸ τᾶν ΑΘ, ΘΕ περιεχομένῳ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου· ἕξει δὴ ὁ Ϟ κύκλος ποτὶ τὸν ΑΗΖΙ ὡς ζ ποτὶ ιβ, διότι καὶ ἁ ἐκ τοῦ κέντρου αὐτοῦ ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ΑΖΗΙ κύκλου τοῦτον ἔχει δυνάμει τὸν λόγον. Δειχθήσεται οὖν ἴσος ὁ Ϟ κύκλος τῷ περιεχομένῳ χωρίῳ ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας.

   Εἰ γὰρ μή, ἤτοι μείζων ἐστὶν ἢ ἐλάττων. Ἔστω δὴ πρότερον, εἰ δυνατόν, μείζων. Δυνατὸν δή ἐστι περὶ τὸ [60] χωρίον περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφὲν σχῆμα μεῖζον εἶμεν τοῦ χωρίου ἐλάσσονι ἢ ᾧ ὑπερέχει ὁ Ϟ κύκλος τοῦ χωρίου. Περιγεγράφθω, καὶ ἔστω, ἐξ ὧν σύγκειται τὸ περιγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ τομεύς, ἐλάχιστος δὲ ὁ ΘΟΔ· δῆλον οὖν ὅτι τὸ περιγραφὲν σχῆμα ἔλασσόν ἐστιν τοῦ κύκλου. Ἐκβεβλήσθωσαν αἱ εὐθεῖαι αἱ ποιοῦσαι ποτὶ τῷ Θ ἴσας γωνίας, ἔστ᾿ ἂν ποτὶ τὰν τοῦ δευτέρου κύκλου περιφέρειαν πέσωντι. Ἐντὶ δή τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΖΗΙ κύκλου περιφέρειαν ποτιπίπτουσαι, τῷ μὲν πλήθει μιᾷ ἐλάσσονες ταυτᾶν, τῷ δὲ μεγέθει ἀλλάλαις τε ἴσαι καὶ τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ὁμοῖοι τομέες ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, ἀπὸ δὲ τᾶς ἐλαχίστας οὐκ ἀναγράφεται· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας ἐλάσσονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς μεγίστας τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΑ τετραγώνου· δέδεικται γὰρ τοῦτο. Ἐντὶ δὲ τοῖς μὲν τομέεσσι τοῖς ἀπὸ τᾶν ἰσᾶν ἀλλάλαις καὶ τᾷ μεγίστᾳ ἴσος ὁ ΑΖΗΙ κύκλος, τοῖς δὲ τομέεσσι τοῖς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας ἴσον τὸ περιγεγραμμένον σχῆμα· ἐλάσσονα ἄρα λόγον ἔχει ὁ κύκλος ποτὶ τὸ περιγεγραμμένον σχῆμα [61] ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΑΘ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου. Ὃν δὲ ἔχει λόγον τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου, τοῦτον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸν Ϟ κύκλον· ἐλάσσονα οὖν λόγον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ ποτὶ τὸν Ϟ κύκλον· ὥστε ἐλάσσων ἐστὶν ὁ Ϟ κύκλος τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα μείζων ἐστὶν ὁ Ϟ κύκλος τοῦ χωρίου τοῦ περιεχομένου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΖ εὐθείας.

   Οὐδὲ τοίνυν ἐλάσσων. Ἔστω γάρ, εἰ δυνατόν, ἐλάσσων. Πάλιν οὖν δυνατόν ἐστιν εἰς τὸ χωρίον τὸ περιεχόμενον ὑπό τε τᾶς ἕλικος καὶ τᾶς ΑΕ εὐθείας ἐγγράψαι σχῆμα ἐπίπεδον ὑπὸ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας μεῖζον εἶμεν τοῦ ἐγγεγραμμένου σχήματος [62] ἐλάσσονι, ἢ ᾧ ὑπερέχει τὸ αὐτὸ χωρίον τοῦ Ϟ κύκλου. Ἐγγεγράφθω οὖν, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΚΡ τομεύς, ἐλάχιστος δὲ ὁ ΘΕΟ· δῆλον οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστι τοῦ Ϟ κύκλου. Ἐκβεβλήσθωσαν αἱ ποιοῦσαι ἴσας γωνίας ποτὶ τῷ Θ, ἔστ᾿ ἂν ποτὶ τὰν τοῦ κύκλου περιφέρειαν πέσωντι. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ κύκλου περιφέρειαν ποτιπίπτουσαι τῷ μὲν πλήθει μιᾷ ἐλάσσους ταυτᾶν, τῷ δὲ μεγέθει ἴσαι ἀλλάλαις τε καὶ τᾷ μεγίστᾳ, καὶ ἀναγεγράφαται ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν ὁμοῖοι τομέες καὶ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ· οἱ ἄρα τομέες οἱ ἀπὸ τᾶν ἰσᾶν τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον τοῦ ἀπὸ τᾶς ΕΑ τετραγώνου. Ἔστιν δὲ τοῖς μὲν τομέεσσιν τοῖς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας ἴσον τὸ ἐγγεγραμμένον σχῆμα ἐν τῷ χωρίῳ, τοῖς δὲ ἑτέροις ὁ κύκλος· μείζονα οὖν λόγον ἔχει ὁ ΑΖΗΙ κύκλος ποτὶ τὸ ἐγγεγραμμένον σχῆμα ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΕ τετραγώνου, τουτέστιν ὁ ΑΖΗΙ κύκλος ποτὶ τὸν Ϟ κύκλον. Μείζων ἄρα ἐστὶν ὁ Ϟ κύκλος τοῦ ἐγγεγραμμένου σχήματος· ὅπερ ἀδύνατον· [63] ἦν γὰρ ἐλάσσων. Οὐκ ἄρα ἐστὶν οὐδὲ ἐλάσσων ὁ Ϟ κύκλος τοῦ περιεχομένου χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶς ΑΕ εὐθείας· ὥστε ἴσος.

ΠΟΡΙΣΜΑ

   Διὰ δὲ τοῦ αὐτοῦ τρόπου δειχθήσεται καὶ διότι τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς ἕλικος τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας καὶ τᾶς εὐθείας τᾶς κατὰ τὸν αὐτὸν ἀριθμὸν ταῖς περιφοραῖς λεγομένας ποτὶ τὸν κύκλον τὸν κατὰ τὸν αὐτὸν ἀριθμὸν λεγόμενον ταῖς περιφοραῖς λόγον ἔχει, ὃν συναμφότερον τό τε ὑπὸ τᾶς ἐκ τοῦ κέντρου τοῦ κατὰ τὸν αὐτὸν ἀριθμὸν κύκλου καὶ τᾶς ἐκ τοῦ κέντρου τοῦ κατὰ τὸν ἑνὶ ἐλάσσονα τᾶν περιφορᾶν λεγομένου καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τῶν εἰρημένων τᾶς ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου τῶν εἰρημένων, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τῶν εἰρημένων.

   κϚ΄.

   Τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ἕλικος, ἅ ἐστιν ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, οὐκ ἐχούσας πέρας τὰν ἀρχὰν τᾶς ἕλικος, καὶ τᾶν εὐθειᾶν τᾶν ἀπὸ τῶν περάτων αὐτᾶς ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν ποτὶ τὸν τομέα τὸν ἔχοντα τὰν μὲν ἐκ τοῦ κέντρου ἴσαν τᾷ μείζονι τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν, τὰν δὲ περιφέρειαν, ἅ ἐστι μεταξὺ τᾶν εἰρημενᾶν εὐθειᾶν ἐπὶ τὰ αὐτὰ τᾷ ἕλικι, τοῦτον ἔχει [64] τὸν λόγον, ὃν ἔχει συναμφότερα τό τε περιεχόμενον ὑπὸ τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἀγμενᾶν καὶ τὸ τρίτον μέρος τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ μείζων τᾶν εἰρημενᾶν εὐθειᾶν τᾶς ἐλάσσονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς μείζονος τᾶν ἀπὸ τῶν περάτων ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος ἐπιζευχθεισᾶν.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔΕ, ἐλάσσων τᾶς ἐν μιᾷ περιφορᾷ γεγραμμένας, πέρατα δὲ αὐτᾶς ἔστω τὰ Α, Ε, ἔστω δὲ ἀρχὰ τᾶς ἕλικος τὸ Θ σαμεῖον, καὶ κέντρῳ μὲν τῷ Θ, διαστήματι δὲ τῷ ΘΑ κύκλος γεγράφθω, καὶ συμπιπτέτω τᾷ περιφερείᾳ αὐτοῦ ἁ ΘΕ κατὰ τὸ Ζ. Δεικτέον ὅτι τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν εὐθειᾶν τᾶν ΑΘ, ΘΕ ποτὶ τὸν τομέα τὸν ΑΘΖ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ.

[65]    Ἔστω δὴ κύκλος, ἐν ᾧ ϞΧ, τὰν ἐκ τοῦ κέντρου ἔχων ἴσαν δυνάμει τῷ τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΕΖ, ποτὶ δὲ τῷ κέντρῳ αὐτοῦ γωνία ἴσα τᾷ ποτὶ τῷ Θ· ὁ δὴ τομεὺς ὁ ϞΧ ποτὶ τὸν τομέα τὸν ΘΑΖ τὸν αὐτὸν ἔχει λόγον, ὃν ἔχει τὸ ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΘΑ τετράγωνον· αἱ γὰρ ἐκ τῶν κέντρων τοῦτον ἔχοντι τὸν λόγον δυνάμει ποτ᾿ ἀλλάλας. Δειχθήσεται δὴ ὁ ΧϞ τομεὺς ἴσος ἐὼν τῷ χωρίῳ τῷ περιεχομένῳ ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν.

   Εἰ γὰρ μή, ἤτοι μείζων ἢ ἐλάττων ἐστίν. Ἔστω πρότερον, εἰ δυνατόν, μείζων. Δυνατὸν οὖν ἐστιν περὶ τὸ εἰρημένον χωρίον περιγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ περιγραφόμενον σχῆμα μεῖζον εἶμεν τοῦ εἰρημένου χωρίου ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει ὁ ϞΧ τομεὺς τοῦ εἰρημένου χωρίου. Περιγεγράφθω δή, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ περιγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΑΚ, ἐλάχιστος δὲ ὁ ΘΟΔ· δῆλον οὖν ὅτι τὸ περιγεγραμμένον σχῆμα ἔλασσόν ἐστι τοῦ ΧϞ τομέως. Διάχθωσαν δὴ αἱ εὐθεῖαι αἱ ποιοῦσαι τὰς ἴσας γωνίας ποτὶ τῷ Θ, ἔστ᾿ ἂν ποτὶ τὰν περιφέρειαν τοῦ ΘΑΖ τομέως πέσωντι. Ἐντὶ δή τινες εὐθεῖαι τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι, αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι εὐθεῖαι τῷ μὲν πλήθει μιᾷ ἐλάσσονες ταυτᾶν, τῷ δὲ μεγέθει ἴσαι ἀλλάλαις τε καὶ τᾷ μεγίστᾳ, αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΑΘΖ τομέως περιφέρειαν ποτιπίπτουσαι χωρὶς τᾶς ΘΖ, καὶ ἀναγεγράφαται ὁμοῖοι τομέες [66] ἀπὸ πασᾶν, ἀπό τε τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ καὶ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, ἀπὸ δὲ τᾶς ΘΕ οὐκ ἀναγέγραπται· τομέες οὖν οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς ἐλαχίστας τομέως ἐλάσσονα λόγον ἔχοντι ἢ τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ τετραγώνου. Ἔστιν δὲ τοῖς μὲν τομέεσσιν τοῖς ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσος ὁ ΘΑΖ τομεύς, τοῖς δὲ ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν τὸ περιγεγραμμένον· ἐλάσσονα οὖν λόγον ἔχει ὁ ΘΑΖ τομεὺς ποτὶ τὸ περιγεγραμμένον σχῆμα ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΖΕ. Ὃν δὲ λόγον ἔχει τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὰ εἰρημένα, τοῦτον τὸν λόγον ἔχει ὁ ΘΑΖ τομεὺς ποτὶ τὸν ΧϞ τομέα· ὥστε ἐλάσσων ἐστὶν ὁ ΧϞ τομεὺς τοῦ περιγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ μείζων· οὐκ ἄρα ἐσσεῖται ὁ ΧϞ τομεὺς μείζων τοῦ περιεχομένου Χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν.

   Οὐδὲ τοίνυν ἐλάσσων. Ἔστω γὰρ ἐλάσσων, καὶ τὰ ἄλλα τὰ αὐτὰ κατεσκευάσθω. Πάλιν δὴ δυνατόν ἐστιν εἰς τὸ χωρίον ἐγγράψαι σχῆμα ἐπίπεδον ἐξ ὁμοίων τομέων συγκείμενον, ὥστε τὸ εἰρημένον χωρίον μεῖζον εἶμεν τοῦ ἐγγραφέντος σχήματος ἐλάσσονι ἢ ἁλίκῳ ὑπερέχει τὸ αὐτὸ χωρίον τοῦ ΧϞ τομέως. Ἐγγεγράφθω οὖν, καὶ ἔστω τῶν τομέων, ἐξ ὧν σύγκειται τὸ ἐγγεγραμμένον σχῆμα, μέγιστος μὲν ὁ ΘΒΓ, ἐλάχιστος δὲ ὁ ΟΘΕ· δῆλον

[67] οὖν ὅτι τὸ ἐγγεγραμμένον σχῆμα μεῖζόν ἐστι τοῦ ΧϞ τομέως. Πάλιν οὖν ἐντί τινες γραμμαὶ τῷ ἴσῳ ἀλλαλᾶν ὑπερέχουσαι αἱ ἀπὸ τοῦ Θ ποτὶ τὰν ἕλικα ποτιπίπτουσαι, ἇν ἐστι μεγίστα μὲν ἁ ΘΑ, ἐλαχίστα δὲ ἁ ΘΕ, ἐντὶ δὲ καὶ ἄλλαι γραμμαὶ αἱ ἀπὸ τοῦ Θ ποτὶ τὰν τοῦ ΘΑΖ τομέως περιφέρειαν ποτιπίπτουσαι χωρὶς τᾶς ΘΑ τῷ μὲν πλήθει μιᾷ ἐλάσσονες τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν, τῷ δὲ μεγέθει ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ἴσαι, καὶ ἀναγεγράφαται ἀπὸ ἑκάστας ὁμοῖοι τομέες, ἀπὸ δὲ τᾶς μεγίστας τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν οὐκ ἀναγέγραπται· οἱ τομέες οὖν οἱ ἀπὸ τᾶν ἰσᾶν ἀλλάλαις τε καὶ τᾷ μεγίστᾳ ποτὶ τοὺς τομέας τοὺς ἀπὸ τᾶν τῷ ἴσῳ ἀλλαλᾶν ὑπερεχουσᾶν χωρὶς τοῦ ἀπὸ τᾶς μεγίστας μείζονα λόγον ἔχοντι ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΘΑ ποτὶ τὸ ὑπὸ τᾶν ΘΑ, ΘΕ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΕΖ· ὥστε καὶ [68] ὁ ΘΑΖ τομεὺς ποτὶ τὸ ἐγγεγραμμένον σχῆμα μείζονα λόγον ἔχει ἤπερ ποτὶ τὸν ΧϞ τομέα· ὥστε μείζων ὁ ΧϞ τομεὺς τοῦ ἐγγεγραμμένου σχήματος. Οὐκ ἔστι δέ, ἀλλὰ ἐλάσσων· οὐκ ἄρα ἐστὶν οὐδὲ ἐλάσσων ὁ ΧϞ τομεὺς τοῦ περιεχομένου χωρίου ὑπό τε τᾶς ΑΒΓΔΕ ἕλικος καὶ τᾶν ΑΘ, ΘΕ εὐθειᾶν· ἴσος ἄρα.

   κζ΄.

   Τῶν χωρίων τῶν περιεχομένων ὑπό τε τᾶν ἑλίκων καὶ τᾶν εὐθειᾶν τᾶν ἐν τᾷ περιφορᾷ τὸ μὲν τρίτον τοῦ δευτέρου διπλάσιόν ἐστι, τὸ δὲ τέταρτον τριπλάσιον, τὸ δὲ πέμπτον τετραπλάσιον, καὶ ἀεὶ τὸ ἑπόμενον κατὰ τοὺς ἑξῆς ἀριθμοὺς πολλαπλάσιον τοῦ δευτέρου χωρίου, τὸ δὲ πρῶτον χωρίον ἕκτον μέρος ἐστὶ τοῦ δευτέρου.

   Ἔστω ἁ προκειμένα ἕλιξ ἔν τε τᾷ πρώτᾳ περιφορᾷ γεγραμμένα καὶ ἐν τᾷ δευτέρᾳ καὶ ἐν ταῖς ἑπομέναις ὁποσαισοῦν, ἔστω δὲ ἀρχὰ μὲν τᾶς ἕλικος τὸ Θ σαμεῖον, ἁ δὲ ΘΕ εὐθεῖα ἀρχὰ τᾶς περιφορᾶς, τῶν δὲ χωρίων [69] ἔστω τὸ μὲν Κ τὸ πρῶτον, τὸ δὲ Λ τὸ δεύτερον, τὸ δὲ Μ τὸ τρίτον, τὸ δὲ Ν τὸ τέταρτον, τὸ δὲ Ξ τὸ πέμπτον. Δεικτέον ὅτι τὸ μὲν Κ χωρίον Ϛ΄ μέρος ἐστὶ τοῦ ἑπομένου, τὸ δὲ Μ διπλάσιον τοῦ Λ, τὸ δὲ Ν τριπλάσιον τοῦ Λ, καὶ τῶν ἑξῆς ἀεὶ τὸ ἑπόμενον πολλαπλάσιον τοῦ Λ κατὰ τοὺς ἑξῆς ἀριθμούς.

   Ὅτι μὲν οὖν τὸ Κ Ϛ΄ μέρος ἐστὶ τοῦ Λ, ὧδε δείκνυται. Ἐπεὶ τὸ ΚΛ χωρίον ποτὶ τὸν δεύτερον κύκλον δέδεικται τοῦτον ἔχον τὸν λόγον, ὃν ἔχει τὰ ζ ποτὶ τὰ ιβ, ὁ δὲ δεύτερος κύκλος ποτὶ τὸν πρῶτον κύκλον ὡς ιβ ποτὶ τὰ γ· δῆλον γάρ ἐστιν· ὁ δὲ πρῶτος κύκλος ποτὶ τὸ Κ χωρίον ἔχει ὡς γ ποτὶ α, Ϛ΄ ἄρα ἐστὶ τὸ Κ χωρίον τοῦ Λ. Πάλιν δὲ καὶ τὸ ΚΛΜ χωρίον ποτὶ τὸν τρίτον κύκλον δέδεικται ὅτι τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΓΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ τετραγώνου ποτὶ τὸ ἀπὸ ΓΘ τετράγωνον. Ὁ δὲ τρίτος κύκλος ἔχει ποτὶ τὸν δεύτερον κύκλον ὃν τὸ ἀπὸ τᾶς ΓΘ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΘΒ, ὁ δὲ δεύτερος κύκλος ἔχει ποτὶ τὸ ΚΛ χωρίον ὃν τὸ ἀπὸ ΒΘ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΒΘ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου· καὶ τὸ ΚΛΜ ἄρα ποτὶ τὸ ΚΛ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΓΘ, ΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ ποτὶ τὸ ὑπὸ τᾶν ΒΘ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΒ τετραγώνου. Ταῦτα δὲ ἔχει ποτὶ ἄλλαλα λόγον, ὃν ιθ ποτὶ τὰ ζ· ὥστε καὶ τὸ ΚΛΜ χωρίον ποτὶ τὸ ΛΚ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν ιθ ποτὶ τὰ ζ· αὐτὸ οὖν τὸ Μ ποτὶ τὸ ΚΛ λόγον ἔχει, ὃν τὰ ιβ ποτὶ τὰ ζ. Τὸ δὲ ΚΛ ποτὶ τὸ Λ λόγον ἔχει, ὃν τὰ ζ ποτὶ τὰ Ϛ· δῆλον οὖν ὅτι διπλάσιόν ἐστι τὸ Μ τοῦ Λ.

[70]    Ὅτι δὲ τὰ ἑπόμενα τὸν τῶν ἑξῆς ἀριθμῶν λόγον ἔχει, δειχθήσεται. Τὸ γὰρ ΚΛΜΝΞ ποτὶ τὸν κύκλον, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΕ, τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ τᾶν ΕΘ, ΘΔ περιεχόμενον καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΕ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΘΕ τετράγωνον. Ὁ δὲ κύκλος, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΕ, ποτὶ τὸν κύκλον, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΘΔ, τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΕ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΘΔ τετράγωνον, ὁ δὲ κύκλος, οὗ ἐστιν ἐκ τοῦ κέντρου ἁ ΔΘ, ποτὶ τὸ ΚΛΜΝ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΔ τετράγωνον ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΘΔ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ τετραγώνου· καὶ τὸ ΚΛΜΝΞ ἄρα ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΘΕ, ΘΔ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΕ ποτὶ τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ· διελόντι καὶ τὸ Ξ χωρίον ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν ἁ ὑπεροχὰ τοῦ τε ὑπὸ ΕΘ, ΘΔ μετὰ τοῦ τρίτου μέρεος τοῦ ἀπὸ τᾶς ΕΔ καὶ τοῦ ὑπὸ τᾶν ΔΘ, ΘΓ μετὰ τοῦ τρίτου μέρεος τοῦ ἀπὸ τᾶς ΓΔ ποτί τε τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ· ὑπερέχει δὲ τὰ συναμφότερα τῶν συναμφοτέρων ᾧ καὶ τὸ ὑπὸ τᾶν ΕΘΔ τοῦ ὑπὸ τᾶν ΔΘΓ, ὑπερέχει δὲ τῷ ὑπὸ τᾶν ΔΘ, ΓΕ· τὸ Ξ ἄρα ποτὶ τὸ ΚΛΜΝ λόγον ἔχει, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου. Διὰ δὲ τῶν αὐτῶν δειχθήσεται καὶ τὸ Ν ποτὶ τὸ ΚΛΜ χωρίον λόγον ἔχον τοῦτον, ὃν τὸ ὑπὸ τᾶν ΘΓ, ΒΔ ποτὶ τὰ συναμφότερα τό τε ὑπὸ ΓΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ ΓΒ τετραγώνου· [71] τὸ Ν ἄρα ποτὶ τὸ ΚΛΜΝ χωρίον τοῦτον ἔχει τὸν λόγον, ὃν τὸ ὑπὸ ΘΓ, ΒΔ ποτὶ τὸ ὑπὸ ΘΓ, ΒΔ καὶ τὸ ὑπὸ ΘΓ, ΘΒ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΒ [καὶ ἀνάπαλιν]· ταῦτα δὲ ἴσα ἐντὶ τῷ τε ὑπὸ τᾶν ΔΘ, ΘΓ καὶ τῷ τρίτῳ μέρει τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου. Ἐπεὶ οὖν τὸ μὲν Ξ χωρίον ποτὶ τὸ ΚΛΜΝ τοῦτον ἔχει τὸν λόγον, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΔΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΓΔ τετραγώνου, τὸ δὲ ΚΛΜΝ ποτὶ τὸ Ν ὃν τὰ συναμφότερα τό τε ὑπὸ τᾶν ΔΘΓ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΔΓ τετραγώνου ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ, ἔχει ἄρα καὶ τὸ Ξ ποτὶ τὸ Ν τὸν αὐτὸν λόγον, ὃν τὸ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ. Τὸ δὲ ὑπὸ τᾶν ΘΔ, ΓΕ ποτὶ τὸ ὑπὸ τᾶν ΘΓ, ΔΒ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΘΔ ποτὶ τὰν ΘΓ, ἐπεὶ ἴσαι ἐντὶ αἱ ΓΕ, ΒΔ· δῆλον οὖν ὅτι καὶ τὸ Ξ ποτὶ τὸ Ν τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΘΔ ποτὶ τὰν ΘΓ.

   Ὁμοίως δὲ καὶ δειχθήσεται καὶ τὸ Ν ποτὶ τὸ Μ τοῦτον ἔχον τὸν λόγον, ὃν ἁ ΘΓ ποτὶ τὰν ΘΒ, καὶ τὸ Μ ποτὶ τὸ Λ, ὃν ἁ ΒΘ ποτὶ τὰν ΑΘ· αἱ δὲ [ΕΘ] ΔΘ, ΓΘ, ΒΘ, ΑΘ εὐθεῖαι τὸν τῶν ἑξῆς ἀριθμῶν λόγον ἔχοντι.

   κη΄.

   Εἴ κα ἐπὶ τᾶς ἕλικος τᾶς ἐν ὁποιᾳοῦν περιφορᾷ γεγραμμένας δύο σαμεῖα λαφθέωντι μὴ τὰ πέρατα, ἀπὸ δὲ τῶν λαφθέντων σαμείων ἐπιζευχθέωντι εὐθεῖαι ἐπὶ τὰν ἀρχὰν τᾶς ἕλικος, καὶ κέντρῳ μὲν τᾷ ἀρχᾷ τᾶς ἕλικος, διαστημάτεσσι δὲ τοῖς ἀπὸ τῶν σαμείων ἐπὶ τὰν ἀρχὰν [72] τᾶς ἕλικος, κύκλοι γραφέωντι, τὸ περιλαφθὲν χωρίον ὑπό τε τᾶς μείζονος τᾶν περιφερειᾶν τᾶν μεταξὺ τᾶν εὐθειᾶν καὶ τᾶς ἕλικος τᾶς μεταξὺ τᾶν αὐτᾶν εὐθειᾶν καὶ τᾶς εὐθείας τᾶς ἐκβληθείσας τοῦτον ἕξει τὸν λόγον ποτὶ τὸ ἀπολαφθὲν χωρίον ὑπό τε τᾶς ἐλάσσονος περιφερείας καὶ τᾶς αὐτᾶς ἕλικος καὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ πέρατα αὐτᾶν, ὃν ἁ ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ δύο τριταμορίων τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ ἐκ τοῦ κέντρου τοῦ μείζονος κύκλου τᾶς ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ἐλάσσονος κύκλου μετὰ ἑνὸς τριταμορίου τᾶς αὐτᾶς ὑπεροχᾶς.

   Ἔστω ἕλιξ, ἐφ᾿ ἇς ἁ ΑΒΓΔ, ἐν μιᾷ περιφορᾷ γεγραμμένα, καὶ λελάφθω ἐπ᾿ αὐτᾶς δύο σαμεῖα τὰ Α, Γ, ὥστε τὸ Θ σαμεῖον ἀρχὰν εἶμεν τᾶς ἕλικος, καὶ ἀπὸ τῶν Α, Γ ἐπεζεύχθωσαν ἐπὶ τὸ Θ, καὶ κέντρῳ τῷ Θ, διαστημάτεσσι δὲ τοῖς ΘΑ, ΘΓ, κύκλοι γεγράφθωσαν. Δεικτέον ὅτι τὸ Ξ χωρίον ποτὶ τὸ Π τὸν αὐτὸν ἔχει λόγον, ὃν ἔχει συναμφότερος [73] ἅ τε ΑΘ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΑΘ καὶ ἓν τριταμόριον τᾶς ΗΑ.

   Τὸ γὰρ χωρίον τὸ ΝΠ ποτὶ τὸν ΗΓΘ τομέα δέδεικται τοῦτον ἔχον τὸν λόγον, ὃν ἔχει τό τε ὑπὸ τᾶν ΗΘ, ΑΘ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΑΗ τετραγώνου ποτὶ τὸ ἀπὸ τᾶς ΗΘ τετράγωνον· αὐτὸ ἄρα τὸ Ξ ποτὶ τὸ ΝΠ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὸ ὑπὸ τᾶν ΘΑΗ μετὰ δύο τριταμορίων τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΑΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ. Καὶ ἐπεὶ τὸ ΝΠ χωρίον ποτὶ τὸν ΝΠΞ τομέα τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ τᾶν ΘΑ, ΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ τὸ ἀπὸ τᾶς ΘΗ τετράγωνον, ὁ δὲ ΝΠΞ τομεὺς ποτὶ τὸν Ν τομέα τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΘΗ ποτὶ τὸ ἀπὸ τᾶς ΘΑ, ἕξει καὶ τὸ ΝΠ χωρίον ποτὶ τὸν Ν τὸν αὐτὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΘΑ, ΘΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ τὸ ἀπὸ ΘΑ· τὸ ἄρα ΝΠ ποτὶ τὸ Π λόγον ἔχει, ὃν συναμφότερα τό τε ὑπὸ τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΗΑ, ΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου. Ἐπεὶ οὖν τὸ Ξ χωρίον ποτὶ τὸ ΝΠ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερον τό τε ὑπὸ ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ τὰ συναμφότερα τό τε ὑπὸ τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ, τὸ δὲ ΝΠ χωρίον ποτὶ τὸ Π τοῦτον ἔχει τὸν λόγον, ὃν τὰ συναμφότερα τό τε ὑπὸ [74] τᾶν ΗΘΑ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΗΑΘ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου, ἕξει καὶ τὸ Ξ ποτὶ τὸ Π τοῦτον τὸν λόγον, ὃν ἔχει συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερον τό τε ὑπὸ τᾶν ΘΑΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ. Τὰ δὲ συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ δύο τριταμόρια τοῦ ἀπὸ τᾶς ΗΑ ποτὶ συναμφότερα τό τε ὑπὸ τᾶν ΘΑΗ καὶ τὸ τρίτον μέρος τοῦ ἀπὸ τᾶς ΗΑ τετραγώνου τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερα ἅ τε ΘΑ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΘΑ καὶ τὸ τρίτον μέρος τᾶς ΗΑ· δῆλον οὖν ὅτι καὶ τὸ Ξ χωρίον ποτὶ τὸ Π χωρίον τοῦτον ἔχει τὸν λόγον, ὃν συναμφότερα ἅ τε ΘΑ καὶ δύο τριταμόρια τᾶς ΗΑ ποτὶ συναμφότερον τάν τε ΘΑ καὶ τὸ τρίτον μέρος τᾶς ΗΑ. ω

 

---

ΜΗΧΑΝΙΚΑ Α΄ 

    

Ἐπιπέδων ἰσορροπιῶν ἢ κέντρα βαρῶν ἐπιπέδων α΄

[80]

   α΄. Αἰτούμεθα τὰ ἴσα βάρεα ἀπὸ ἴσων μακέων ἰσορροπεῖν, τὰ δὲ ἴσα βάρεα ἀπὸ τῶν ἀνίσων μακέων μὴ ἰσορροπεῖν, ἀλλὰ ῥέπειν ἐπὶ τὸ βάρος τὸ ἀπὸ τοῦ μείζονος μάκεος.

   β΄. Εἴ κα βαρέων ἰσορροπεόντων ἀπό τινων μακέων ποτὶ τὸ ἕτερον τῶν βαρέων ποτιτεθῇ, μὴ ἰσορροπεῖν, ἀλλὰ ῥέπειν ἐπὶ τὸ βάρος ἐκεῖνο, ᾧ ποτετέθη.

   γ΄. Ὁμοίως δὲ καί, εἴ κα ἀπὸ τοῦ ἑτέρου τῶν βαρέων ἀφαιρεθῇ τι, μὴ ἰσορροπεῖν, ἀλλὰ ῥέπειν ἐπὶ τὸ βάρος, ἀφ᾿ οὗ οὐκ ἀφῃρέθη.

   δ΄. Τῶν ἴσων καὶ ὁμοίων σχημάτων ἐπιπέδων ἐφαρμοζομένων ἐπ᾿ ἄλλαλα καὶ τὰ κέντρα τῶν βαρέων ἐφαρμόζει ἐπ᾿ ἄλλαλα.

   ε΄. Τῶν δὲ ἀνίσων, ὁμοίων δέ, τὰ κέντρα τῶν βαρέων ὁμοίως ἐσσεῖται κείμενα. Ὁμοίως δὲ λέγομες σαμεῖα κέεσθαι ποτὶ τὰ ὁμοῖα σχήματα, ἀφ᾿ ὧν ἐπὶ τὰς ἴσας γωνίας ἀγόμεναι εὐθεῖαι ποιέοντι γωνίας ἴσας ποτὶ τὰς ὁμολόγους πλευράς.

   Ϛ΄. Εἴ κα μεγέθεα ἀπό τινων μακέων ἰσορροπέωντι, καὶ τὰ ἴσα αὐτοῖς ἀπὸ τῶν αὐτῶν μακέων ἰσορροπήσει.

   ζ΄. Παντὸς σχήματος, οὗ κα ἁ περίμετρος ἐπὶ τὰ

[81]αὐτὰ κοῖλα ᾖ, τὸ κέντρον τοῦ βάρεος ἐντὸς εἶμεν δεῖ τοῦ σχήματος.

   Τούτων δὲ ὑποκειμένων

   α΄.

   Τὰ ἀπὸ ἴσων μακέων ἰσορροπέοντα βάρεα ἴσα ἐντί.

   Εἴπερ γὰρ ἄνισα ἐσσεῖται, ἀφαιρεθείσας ἀπὸ τοῦ μείζονος τᾶς ὑπεροχᾶς τὰ λοιπὰ οὐκ ἰσορροπησοῦντι, ἐπειδὴ ἰσορροπεόντων ἀπὸ τοῦ ἑτέρου ἀφῄρηται. Ὥστε τὰ ἀπὸ τῶν ἴσων μακέων βάρεα ἰσορροπέοντα ἴσα ἐντί.

   β΄.

   Τὰ ἀπὸ τῶν ἴσων μακέων ἄνισα βάρεα οὐκ ἰσορροπέοντι, ἀλλὰ ῥέψει ἐπὶ τὸ μεῖζον.

   Ἀφαιρεθείσας γὰρ τᾶς ὑπεροχᾶς ἰσορροπησοῦντι, ἐπειδὴ τὰ ἴσα ἀπὸ τῶν ἴσων μακέων ἰσορροπέοντι. Ποτιτεθέντος οὖν τοῦ ἀφαιρεθέντος ῥέψει ἐπὶ τὸ μεῖζον, ἐπεὶ ἰσορροπεόντων τῷ ἑτέρῳ ποτετέθη.

   γ΄.

   Τὰ ἄνισα βάρεα ἀπὸ τῶν ἀνίσων μακέων ἰσορροπησοῦντι, καὶ τὸ μεῖζον ἀπὸ τοῦ ἐλάσσονος.

[82]    Ἔστω ἄνισα βάρεα τὰ Α, Β, καὶ ἔστω μεῖζον τὸ Α, καὶ ἰσορροπεόντων ἀπὸ τῶν ΑΓ, ΓΒ μακέων. Δεικτέον ὅτι ἐλάσσων ἐστὶν ἁ ΑΓ τᾶς ΓΒ.

   Μὴ γὰρ ἔστω ἐλάσσων. Ἀφαιρεθείσας δὴ τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει τὸ Α τοῦ Β, ἐπειδὴ ἰσορροπεόντων ἀπὸ τοῦ ἑτέρου ἀφῄρηται, ῥέψει ἐπὶ τὸ Β. Οὐ ῥέψει δέ· εἴτε γὰρ ἴσα ἐστὶν ἁ ΓΑ τᾷ ΓΒ, ἰσορροπησοῦντι [τὰ γὰρ ἴσα ἀπὸ τῶν ἴσων μακέων], εἴτε μείζων ἁ ΓΑ τᾶς ΓΒ, ῥέπει ἐπὶ τὸ Α· τὰ γὰρ ἴσα ἀπὸ τῶν ἀνίσων μακέων οὐκ ἰσορροπέοντι, ἀλλὰ ῥέπει ἐπὶ τὸ ἀπὸ τοῦ μείζονος μάκεος. Διὰ δὴ ταῦτα ἐλάσσων ἐστὶν ἁ ΑΓ τᾶς ΓΒ.

   Φανερὸν δὲ ὅτι καὶ τὰ ἀπὸ τῶν ἀνίσων μακέων ἰσορροπέοντα ἄνισά ἐντι, καὶ μεῖζόν ἐστι τὸ ἀπὸ τοῦ ἐλάσσονος.

   δ΄.

   Εἴ κα δύο ἴσα μεγέθεα μὴ τὸ αὐτὸ κέντρον τοῦ βάρεος ἔχωντι, τοῦ ἐξ ἀμφοτέρων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον ἐσσεῖται τοῦ βάρεος τὸ μέσον τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τῶν μεγεθέων τὰ κέντρα τοῦ βάρεος.

   Ἔστω τοῦ μὲν Α κέντρον τοῦ βάρεος τὸ Α, τοῦ δὲ Β τὸ Β, καὶ ἐπιζευχθεῖσα ἁ ΑΒ τετμάσθω δίχα κατὰ τὸ Γ· λέγω ὅτι τοῦ ἐξ ἀμφοτέρων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον ἐστὶ τὸ Γ.

[83]    Εἰ γὰρ μή, ἔστω [τοῦ ἐξ ἀμφοτέρων τῶν Α, Β μεγεθῶν] κέντρον τοῦ βάρεος τὸ Δ, εἰ δυνατόν [ὅτι γὰρ ἔστιν ἐπὶ τῆς ΑΒ προδέδεικται]. Ἐπεὶ οὖν τὸ Δ σαμεῖον κέντρον ἐστὶν τοῦ βάρεος τοῦ ἐκ τῶν Α, Β συγκειμένου μεγέθεος, κατεχομένου τοῦ Δ ἰσορροπήσει· τὰ ἄρα Α, Β μεγέθεα ἰσορροπησοῦντι ἀπὸ τῶν ΑΔ, ΔΒ μακέων· ὅπερ ἀδύνατον [τὰ γὰρ ἴσα ἀπὸ τῶν ἀνίσων μακέων οὐκ ἰσορροπέοντι]. Δῆλον οὖν ὅτι τὸ Γ κέντρον ἐστὶ τοῦ βάρεος τοῦ ἐκ τῶν Α, Β συγκειμένου μεγέθεος.

   ε΄.

   Εἴ κα τριῶν μεγεθέων τὰ κέντρα τοῦ βάρεος ἐπ᾿ εὐθείας ἔωντι κείμενα, καὶ τὰ μεγέθεα ἴσον βάρος ἔχωντι, καὶ αἱ μεταξὺ τῶν κέντρων εὐθεῖαι ἴσαι ἔωντι, τοῦ ἐκ πάντων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον ἐσσεῖται τοῦ βάρεος τὸ σαμεῖον, ὃ καὶ τοῦ μέσου τὸ αὐτὸ κέντρον ἐστὶ τοῦ βάρεος.

   Ἔστω τρία μεγέθεα τὰ Α, Β, Γ, κέντρα δὲ αὐτῶν τοῦ βάρεος τὰ Α, Β, Γ σαμεῖα ἐπ᾿ εὐθείας κείμενα, ἔστω δὲ τά τε Α, Β, Γ ἴσα καὶ αἱ ΑΓ, ΓΒ ἴσαι εὐθεῖαι· λέγω ὅτι τοῦ ἐκ πάντων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον τοῦ βάρεός ἐστι τὸ Γ σαμεῖον.

   Ἐπεὶ γὰρ τὰ Α, Β μεγέθεα ἴσον βάρος ἔχει, κέντρον ἐσσεῖται τοῦ βάρεος τὸ Γ σαμεῖον, ἐπειδὴ ἴσαι ἐντὶ αἱ [84] ΑΓ, ΓΒ. Ἔστιν δὲ καὶ τοῦ Γ κέντρον τοῦ βάρεος τὸ Γ σαμεῖον· δῆλον οὖν ὅτι καὶ τοῦ ἐκ πάντων συγκειμένου μεγέθεος κέντρον ἐσσεῖται τοῦ βάρεος τὸ σαμεῖον, ὃ καὶ τοῦ μέσου κέντρον ἐστὶ τοῦ βάρεος.

ΠΟΡΙΣΜΑ Α΄

   Ἐκ δὴ τούτων φανερὸν ὅτι, ὁπόσων κα τῷ πλήθει περισσῶν μεγεθέων τὰ κέντρα τοῦ βάρεος ἐπ᾿ εὐθείας ἔωντι κείμενα, εἴ κα τά τε ἴσον ἀπέχοντα ἀπὸ τοῦ μέσου μεγέθεα ἴσον βάρος ἔχωντι, καὶ αἱ εὐθεῖαι αἱ μεταξὺ τῶν κέντρων αὐτῶν ἴσαι ἔωντι, τοῦ ἐκ πάντων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον ἐσσεῖται τοῦ βάρεος τὸ σαμεῖον, ὃ καὶ τοῦ μέσου αὐτῶν κέντρον ἐστὶ τοῦ βάρεος.

ΠΟΡΙΣΜΑ Β΄

   Εἴ κα καὶ ἄρτια ἔωντι τῷ πλήθει τὰ μεγέθεα, καὶ τὰ κέντρα τοῦ βάρεος αὐτῶν ἐπ᾿ εὐθείας ἔωντι κείμενα, καὶ τὰ μέσα αὐτῶν καὶ τὰ ἴσα ἀπέχοντα ἀπ᾿ αὐτῶν ἴσον βάρος ἔχωντι, καὶ αἱ μεταξὺ τῶν κέντρων εὐθεῖαι ἴσαι ἔωντι, τοῦ ἐκ πάντων τῶν μεγεθέων συγκειμένου μεγέθεος κέντρον ἐσσεῖται τοῦ βάρεος τὸ μέσον τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ κέντρα τοῦ βάρεος τῶν μεγεθέων, ὡς ὑπογέγραπται.

[85]    Ϛ΄.

   Τὰ σύμμετρα μεγέθεα ἰσορροπέοντι ἀπὸ μακέων ἀντιπεπονθότως τὸν αὐτὸν λόγον ἐχόντων τοῖς βάρεσιν.

   Ἔστω σύμμετρα μεγέθεα τὰ Α, Β, ὧν κέντρα τὰ Α, Β, καὶ μᾶκος ἔστω τι τὸ ΕΔ, καὶ ἔστω ὡς τὸ Α ποτὶ τὸ Β, οὕτως τὸ ΔΓ μᾶκος ποτὶ τὸ ΓΕ μᾶκος· δεικτέον ὅτι τοῦ ἐξ ἀμφοτέρων τῶν Α, Β συγκειμένου μεγέθεος κέντρον ἐστὶ τοῦ βάρεος τὸ Γ.

   Ἐπεὶ γάρ ἐστιν, ὡς τὸ Α ποτὶ τὸ Β, οὕτως τὸ ΔΓ ποτὶ τὸ ΓΕ, τὸ δὲ Α τῷ Β σύμμετρον, καὶ τὸ ΓΔ ἄρα τῷ ΓΕ σύμμετρον, τουτέστιν εὐθεῖα τᾷ εὐθείᾳ· ὥστε τῶν ΕΓ, ΓΔ ἐστὶ κοινὸν μέτρον. Ἔστω δὴ τὸ Ν, καὶ κείσθω τᾷ μὲν ΕΓ ἴσα ἑκατέρα τᾶν ΔΗ, ΔΚ, τᾷ δὲ ΔΓ ἴσα ἁ ΕΛ. Καὶ ἐπεὶ ἴσα ἁ ΔΗ τᾷ ΓΕ, ἴσα καὶ ἁ ΔΓ τᾷ ΕΗ· ὥστε καὶ ἁ ΛΕ ἴσα τᾷ ΕΗ. Διπλασία ἄρα ἁ μὲν ΛΗ τᾶς ΔΓ, ἁ δὲ ΗΚ τᾶς ΓΕ· ὥστε τὸ Ν καὶ ἑκατέραν τᾶν ΛΗ, ΗΚ μετρεῖ, ἐπειδήπερ καὶ τὰ ἡμίσεα αὐτᾶν. Καὶ ἐπεί ἐστιν, ὡς τὸ Α ποτὶ τὸ Β, οὕτως ἁ ΔΓ ποτὶ ΓΕ, ὡς δὲ ἁ ΔΓ ποτὶ ΓΕ, οὕτως ἁ ΛΗ ποτὶ ΗΚ· διπλασία γὰρ ἑκατέρα ἑκατέρας· [86] καὶ ὡς ἄρα τὸ Α ποτὶ τὸ Β, οὕτως ἁ ΛΗ ποτὶ ΗΚ. Ὁσαπλασίων δέ ἐστιν ἁ ΛΗ τᾶς Ν, τοσαυταπλασίων ἔστω καὶ τὸ Α τοῦ Ζ· ἔστιν ἄρα ὡς ἁ ΛΗ ποτὶ Ν, οὕτως τὸ Α ποτὶ Ζ. Ἔστι δὲ καὶ ὡς ἁ ΚΗ ποτὶ ΛΗ, οὕτως τὸ Β ποτὶ Α· δι᾿ ἴσου ἄρα ἐστὶν ὡς ἁ ΚΗ ποτὶ Ν, οὕτως τὸ Β ποτὶ Ζ· ἰσάκις ἄρα πολλαπλασίων ἐστὶν ἁ ΚΗ τᾶς Ν καὶ τὸ Β τοῦ Ζ. Ἐδείχθη δὲ τοῦ Ζ καὶ τὸ Α πολλαπλάσιον ἐόν· ὥστε τὸ Ζ τῶν Α, Β κοινόν ἐστι μέτρον. Διαιρεθείσας οὖν τᾶς μὲν ΛΗ εἰς τὰς τᾷ Ν ἴσας, τοῦ δὲ Α εἰς τὰ τῷ Ζ ἴσα, τὰ ἐν τᾷ ΛΗ τμάματα ἰσομεγέθεα τᾷ Ν ἴσα ἐσσεῖται τῷ πλήθει τοῖς ἐν τῷ Α τμαμάτεσσιν ἴσοις ἐοῦσιν τῷ Ζ. Ὥστε, ἂν ἐφ᾿ ἕκαστον τῶν τμαμάτων τῶν ἐν τᾷ ΛΗ ἐπιτεθῇ μέγεθος ἴσον τῷ Ζ τὸ κέντρον τοῦ βάρεος ἔχον ἐπὶ μέσου τοῦ τμάματος, τά τε πάντα μεγέθεα ἴσα ἐντὶ τῷ Α, καὶ τοῦ ἐκ πάντων συγκειμένου κέντρον ἐσσεῖται τοῦ βάρεος τὸ Ε· ἄρτιά τε γάρ ἐστι τὰ πάντα τῷ πλήθει, καὶ τὰ ἐφ᾿ ἑκάτερα τοῦ Ε ἴσα τῷ πλήθει διὰ τὸ ἴσαν εἶμεν τὰν ΛΕ τᾷ ΗΕ. Ὁμοίως δὲ δειχθήσεται ὅτι κἄν, εἴ κα ἐφ᾿ ἕκαστον τῶν ἐν τᾷ ΚΗ τμαμάτων ἐπιτεθῇ μέγεθος ἴσον τῷ Ζ κέντρον τοῦ βάρεος ἔχον ἐπὶ τοῦ μέσου τοῦ τμάματος, τά τε πάντα μεγέθεα ἴσα ἐσσεῖται τῷ Β, καὶ τοῦ ἐκ πάντων συγκειμένου κέντρον τοῦ βάρεος ἐσσεῖται τὸ Δ· ἐσσεῖται οὖν τὸ μὲν Α ἐπικείμενον κατὰ τὸ Ε, τὸ δὲ Β κατὰ τὸ Δ. Ἐσσεῖται δὴ μεγέθεα ἴσα ἀλλάλοις ἐπ᾿ εὐθείας κείμενα, ὧν τὰ κέντρα τοῦ βάρεος ἴσα ἀπ᾿ ἀλλάλων διέστακεν, [συγκείμενα] ἄρτια τῷ πλήθει· δῆλον οὖν ὅτι τοῦ ἐκ πάντων συγκειμένου μεγέθεος κέντρον ἐστὶ τοῦ βάρεος ἁ διχοτομία τᾶς εὐθείας τᾶς [87] ἐχούσας τὰ κέντρα τῶν μέσων μεγεθέων. Ἐπεὶ δ᾿ ἴσαι ἐντὶ ἁ μὲν ΛΕ τᾷ ΓΔ, ἁ δὲ ΕΓ τᾷ ΔΚ, καὶ ὅλα ἄρα ἁ ΛΓ ἴσα τᾷ ΓΚ· ὥστε τοῦ ἐκ πάντων μεγέθεος κέντρον τοῦ βάρεος τὸ Γ σαμεῖον. Τοῦ μὲν ἄρα Α κειμένου κατὰ τὸ Ε, τοῦ δὲ Β κατὰ τὸ Δ, ἰσορροπησοῦντι κατὰ τὸ Γ.

   ζ΄.

   Καὶ τοίνυν, εἴ κα ἀσύμμετρα ἔωντι τὰ μεγέθεα, ὁμοίως ἰσορροπησοῦντι ἀπὸ μακέων ἀντιπεπονθότως τὸν αὐτὸν λόγον ἐχόντων τοῖς μεγέθεσιν.

   Ἔστω ἀσύμμετρα μεγέθεα τὰ ΑΒ, Γ, μάκεα δὲ τὰ ΔΕ, ΕΖ, ἐχέτω δὲ τὸ ΑΒ ποτὶ τὸ Γ τὸν αὐτὸν λόγον, ὃν καὶ τὸ ΕΔ ποτὶ τὸ ΕΖ μᾶκος· λέγω ὅτι τοῦ ἐξ ἀμφοτέρων τῶν ΑΒ, Γ κέντρον τοῦ βάρεός ἐστι τὸ Ε.

   Εἰ γὰρ μὴ ἰσορροπήσει τὸ ΑΒ τεθὲν ἐπὶ τῷ Ζ τῷ Γ τεθέντι ἐπὶ τῷ Δ, ἤτοι μεῖζόν ἐστι τὸ ΑΒ τοῦ Γ ἢ ὥστε ἰσορροπεῖν [τῷ Γ] ἢ οὔ. Ἔστω μεῖζον, καὶ ἀφῃρήσθω ἀπὸ τοῦ ΑΒ ἔλασσον τᾶς ὑπεροχᾶς, ᾇ μεῖζόν ἐστι τὸ ΑΒ τοῦ Γ ἢ ὥστε ἰσορροπεῖν, ὥστε [τὸ] λοιπὸν τὸ Α σύμμετρον εἶμεν τῷ Γ. Ἐπεὶ οὖν σύμμετρά ἐστι τὰ Α, Γ μεγέθεα, [88] καὶ ἐλάσσονα λόγον ἔχει τὸ Α ποτὶ τὸ Γ ἢ ἁ ΔΕ ποτὶ ΕΖ, οὐκ ἰσορροπησοῦντι τὰ Α, Γ ἀπὸ τῶν ΔΕ, ΕΖ μακέων, τεθέντος τοῦ μὲν Α ἐπὶ τῷ Ζ, τοῦ δὲ Γ ἐπὶ τῷ Δ. Διὰ ταὐτὰ δ᾿, οὐδ᾿ εἰ τὸ Γ μεῖζόν ἐστιν ἢ ὥστε ἰσορροπεῖν τῷ ΑΒ.

   η΄.

   Εἴ κα ἀπό τινος μεγέθεος ἀφαιρεθῇ τι μέγεθος μὴ τὸ αὐτὸ κέντρον ἔχον τῷ ὅλῳ, τοῦ λοιποῦ μεγέθεος κέντρον ἐστὶ τοῦ βάρεος, ἐκβληθείσας τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ κέντρα τῶν βαρέων τοῦ τε ὅλου μεγέθεος καὶ τοῦ ἀφῃρημένου ἐπὶ τὰ αὐτά, ἐφ᾿ ἃ τὸ κέντρον τοῦ ὅλου μεγέθεος, καὶ ἀπολαφθείσας τινὸς ἀπὸ [τᾶς] ἐκβληθείσας τᾶς ἐπιζευγνυούσας τὰ εἰρημένα κέντρα, ὥστε τὸν αὐτὸν ἔχειν λόγον ποτὶ τὰν μεταξὺ τῶν κέντρων, ὃν ἔχει τὸ βάρος τοῦ ἀφῃρημένου μεγέθεος ποτὶ τὸ τοῦ λοιποῦ βάρος, τὸ πέρας τᾶς ἀπολαφθείσας.

   Ἔστω μεγέθεός τινος τοῦ ΑΒ κέντρον τοῦ βάρεος τὸ Γ, καὶ ἀφῃρήσθω ἀπὸ τοῦ ΑΒ τὸ ΑΔ, οὗ κέντρον τοῦ βάρεος ἔστω τὸ Ε, ἐπιζευχθείσας δὲ τᾶς ΕΓ καὶ ἐκβληθείσας ἀπολελάφθω ἁ ΓΖ ποτὶ τὰν ΓΕ λόγον ἔχουσα τὸν αὐτόν, [89] ὃν ἔχει τὸ ΑΔ μέγεθος ποτὶ τὸ ΔΗ· δεικτέον ὅτι τοῦ ΔΗ μεγέθεος κέντρον τοῦ βάρεός ἐστι τὸ Ζ σαμεῖον.

   Μὴ γάρ, ἀλλ᾿, εἰ δυνατόν, ἔστω τὸ Θ σαμεῖον. Ἐπεὶ οὖν τοῦ μὲν ΑΔ μεγέθεος κέντρον τοῦ βάρεός ἐστι τὸ Ε, τοῦ δὲ ΔΗ τὸ Θ σαμεῖον, τοῦ ἐξ ἀμφοτέρων τῶν ΑΔ, ΔΗ μεγεθέων κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς ΕΘ τμαθείσας, ὥστε τὰ τμάματα αὐτᾶς ἀντιπεπονθέμεν κατὰ τὸν αὐτὸν λόγον τοῖς μεγέθεσιν· ὥστε οὐκ ἐσσεῖται τὸ Γ σαμεῖον κατὰ τὰν ἀνάλογον τομὰν τᾷ εἰρημένᾳ. Οὐκ ἄρα ἐστὶ τὸ Γ κέντρον τοῦ ἐκ τῶν ΑΔ, ΔΗ συγκειμένου μεγέθεος, τουτέστι τοῦ ΑΒ. Ἔστι δέ· ὑπέκειτο γάρ· οὐκ ἄρα ἐστὶ τὸ Θ κέντρον βάρεος τοῦ ΔΗ μεγέθεος.

   θ΄.

   Παντὸς παραλληλογράμμου τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰς διχοτομίας τᾶν κατ᾿ ἐναντίον τοῦ παραλληλογράμμου πλευρᾶν.

   Ἔστω παραλληλόγραμμον τὸ ΑΒΓΔ, ἐπὶ δὲ τὰν διχοτομίαν τᾶν ΑΒ, ΓΔ ἁ ΕΖ· φαμὶ δὴ ὅτι τοῦ ΑΒΓΔ παραλληλογράμμου τὸ κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς ΕΖ.

[90]    Μὴ γάρ, ἀλλ᾿, εἰ δυνατόν, ἔστω τὸ Θ, καὶ ἄχθω παρὰ τὰν ΑΒ ἁ ΘΙ. Τᾶς [δὲ] δὴ ΕΒ διχοτομουμένας αἰεὶ ἐσσεῖταί ποκα ἁ καταλειπομένα ἐλάσσων τᾶς ΙΘ· καὶ διῃρήσθω ἑκατέρα τᾶν ΑΕ, ΕΒ εἰς τὰς τᾷ ΕΚ ἴσας, καὶ ἀπὸ τῶν κατὰ τὰς διαιρέσιας σαμείων ἄχθωσαν παρὰ τὰν ΕΖ· διαιρεθήσεται δὴ τὸ ὅλον παραλληλόγραμμον εἰς παραλληλόγραμμα τὰ ἴσα καὶ ὁμοῖα τῷ ΚΖ. Τῶν οὖν παραλληλογράμμων τῶν ἴσων καὶ ὁμοίων τῷ ΚΖ ἐφαρμοζομένων ἐπ᾿ ἄλλαλα καὶ τὰ κέντρα τοῦ βάρεος αὐτῶν ἐπ᾿ ἄλλαλα πεσοῦνται. Ἐσσοῦνται δὴ μεγέθεά τινα, παραλληλόγραμμα ἴσα τῷ ΚΖ, ἄρτια τῷ πλήθει, καὶ τὰ κέντρα τοῦ βάρεος αὐτῶν ἐπ᾿ εὐθείας κείμενα, καὶ τὰ μέσα ἴσα, καὶ πάντα τὰ ἐφ᾿ ἑκάτερα τῶν μέσων αὐτά τε ἴσα ἐντὶ καὶ αἱ μεταξὺ τῶν κέντρων εὐθεῖαι ἴσαι· τοῦ ἐκ πάντων αὐτῶν ἄρα συγκειμένου μεγέθεος τὸ κέντρον ἐσσεῖται τοῦ βάρεος ἐπὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ κέντρα τοῦ βάρεος τῶν μέσων χωρίων. Οὐκ ἔστι δέ· τὸ γὰρ Θ ἐκτός ἐστι τῶν μέσων παραλληλογράμμων. Φανερὸν οὖν ὅτι ἐπὶ τᾶς ΕΖ εὐθείας τὸ κέντρον ἐστὶ τοῦ βάρεος τοῦ ΑΒΓΔ παραλληλογράμμου.

   ι΄.

   Παντὸς παραλληλογράμμου τὸ κέντρον τοῦ βάρεός ἐστι τὸ σαμεῖον, καθ᾿ ὃ αἱ διάμετροι συμπίπτοντι.

[91]    Ἔστω παραλληλόγραμμον τὸ ΑΒΓΔ καὶ ἐν αὐτῷ ἁ ΕΖ δίχα τέμνουσα τὰς ΑΒ, ΓΔ, ἁ δὲ ΚΛ τὰς ΑΓ, ΒΔ· ἔστιν δὴ τοῦ ΑΒΓΔ παραλληλογράμμου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΕΖ· δέδεικται γὰρ τοῦτο· διὰ ταὐτὰ δὲ καὶ ἐπὶ τᾶς ΚΛ· τὸ Θ ἄρα σαμεῖον κέντρον τοῦ βάρεος. Κατὰ δὲ τὸ Θ αἱ διάμετροι τοῦ παραλληλογράμμου συμπίπτοντι· ὥστε δέδεικται τὸ προτεθέν.

ΑΛΛΩΣ

   Ἔστιν δὲ καὶ ἄλλως τὸ αὐτὸ δεῖξαι.

   Ἔστω παραλληλόγραμμον τὸ ΑΒΓΔ, διάμετρος δὲ αὐτοῦ ἔστω ἁ ΔΒ. Τὰ ἄρα ΑΒΔ, ΒΔΓ τρίγωνα ἴσα ἐντὶ καὶ ὁμοῖα ἀλλάλοις· ὥστε ἐφαρμοζομένων ἐπ᾿ ἄλλαλα τῶν τριγώνων καὶ τὰ κέντρα τοῦ βάρεος αὐτῶν ἐπ᾿ ἄλλαλα πεσοῦνται. Ἔστω δὴ τοῦ ΑΒΔ τριγώνου κέντρον τοῦ βάρεος τὸ Ε σαμεῖον, καὶ τετμάσθω δίχα ἁ ΔΒ κατὰ τὸ Θ, καὶ ἐπεζεύχθω ἁ ΕΘ καὶ ἐκβεβλήσθω, καὶ ἀπολελάφθω ἁ ΖΘ ἴσα τᾷ ΘΕ. Ἐφαρμοζομένου δὴ τοῦ ΑΒΔ τριγώνου ἐπὶ τὸ ΒΔΓ τρίγωνον καὶ τιθεμένας τᾶς μὲν ΑΒ πλευρᾶς ἐπὶ τὰν ΔΓ, τᾶς δὲ ΑΔ ἐπὶ τὰν ΒΓ, ἐφαρμόξει καὶ ἁ ΘΕ εὐθεῖα ἐπὶ τὰν ΖΘ, καὶ τὸ Ε σαμεῖον ἐπὶ τὸ Ζ πεσεῖται. [92] Ἀλλὰ καὶ ἐπὶ τὸ κέντρον τοῦ βάρεος τοῦ ΒΔΓ τριγώνου. Ἐπεὶ οὖν τοῦ μὲν ΑΒΔ τριγώνου κέντρον τοῦ βάρεος τὸ Ε σαμεῖον, τοῦ δὲ ΔΒΓ τὸ Ζ, δῆλον ὡς τοῦ ἐξ ἀμφοτέρων τῶν τριγώνων συγκειμένου μεγέθεος κέντρον τοῦ βάρεός ἐστι τὸ μέσον τᾶς ΕΖ εὐθείας, ὅπερ ἐστὶ τὸ Θ σαμεῖον.

   ια΄.

   Ἐὰν δύο τρίγωνα ὁμοῖα ἀλλάλοις ᾖ καὶ ἐν αὐτοῖς σαμεῖα ὁμοίως κείμενα ποτὶ τὰ τρίγωνα, καὶ τὸ ἓν σαμεῖον τοῦ ἐν ᾧ ἐστι τριγώνου κέντρον ᾖ τοῦ βάρεος, καὶ τὸ λοιπὸν σαμεῖον κέντρον ἐστὶ τοῦ βάρεος τοῦ ἐν ᾧ ἐστι τριγώνου [ὁμοίως δὲ λέγομεν σαμεῖα κέεσθαι ποτὶ τὰ ὁμοῖα σχήματα, ἀφ᾿ ὧν αἱ ἐπὶ τὰς ἴσας γωνίας ἀγόμεναι εὐθεῖαι ἴσας ποιοῦσιν γωνίας πρὸς ταῖς ὁμολόγοις πλευραῖς].

   Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ, καὶ ἔστω ὡς ἁ ΑΓ ποτὶ ΔΖ, οὕτως ἅ τε ΑΒ ποτὶ ΔΕ καὶ ἁ ΒΓ ποτὶ ΕΖ, καὶ ἐν τοῖς εἰρημένοις τριγώνοις σαμεῖα ὁμοίως κείμενα ἔστω τὰ Θ, Ν [πρὸς τὰ ΑΒΓ, ΔΕΖ τρίγωνα], καὶ ἔστω τὸ Θ κέντρον τοῦ βάρεος τοῦ ΑΒΓ τριγώνου· λέγω ὅτι καὶ τὸ Ν κέντρον βάρεός ἐστι τοῦ ΔΕΖ τριγώνου.

[93]    Μὴ γάρ, ἀλλ᾿, εἰ δυνατόν, ἔστω τὸ Η κέντρον βάρεος τοῦ ΔΕΖ τριγώνου, καὶ ἐπεζεύχθωσαν αἱ ΘΑ, ΘΒ, ΘΓ, ΔΝ, ΕΝ, ΖΝ, ΔΗ, ΕΗ, ΖΗ. Ἐπεὶ οὖν ὁμοῖόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΔΕΖ τριγώνῳ, καὶ κέντρα τῶν βαρέων ἐστὶ τὰ Θ, Η σαμεῖα, τῶν δὲ ὁμοίων σχημάτων τὰ κέντρα τῶν βαρέων ὁμοίως ἐντὶ κείμενα [ὥστε ἴσας ποιησοῦντι γωνίας ποτὶ ταῖς ὁμολόγοις πλευραῖς ἕκαστον ἑκάσταις], ἴσα ἄρα ἁ ὑπὸ ΗΔΕ γωνία τᾷ ὑπὸ ΘΑΒ. Ἀλλὰ ἁ ὑπὸ ΘΑΒ γωνία ἴσα ἐστὶ τᾷ ὑπὸ ΕΔΝ [διὰ τὸ ὁμοίως κεῖσθαι τὰ Θ, Ν σαμεῖα]· καὶ ἁ ὑπὸ ΕΔΝ γωνία ἄρα ἴσα ἐστὶ τᾷ ὑπὸ ΕΔΗ, ἁ μείζων τᾷ ἐλάσσονι· ὅπερ ἀδύνατον. Οὐκ ἄρα οὐκ ἔστι κέντρον τοῦ βάρεος τοῦ ΔΕΖ τριγώνου τὸ Ν σαμεῖον· ἔστιν ἄρα.

   ιβ΄.

   Εἴ κα δύο τρίγωνα ὁμοῖα ἔωντι, τοῦ δὲ ἑνὸς τριγώνου κέντρον ᾖ τοῦ βάρεος ἐπὶ τᾶς εὐθείας, ἅ ἐντι ἀπό τινος γωνίας ἐπὶ μέσαν τὰν βάσιν ἀγομένα, καὶ τοῦ λοιποῦ τριγώνου τὸ κέντρον ἐσσεῖται τοῦ βάρεος ἐπὶ τᾶς ὁμοίως ἀγομένας γραμμᾶς.

[94]    Ἔστω δύο τρίγωνα τὰ ΑΒΓ, ΔΕΖ, καὶ ἔστω ὡς ἁ ΑΓ ποτὶ ΔΖ, οὕτως ἅ τε ΑΒ ποτὶ ΔΕ καὶ ἁ ΒΓ ποτὶ ΖΕ, καὶ τμαθείσας τᾶς ΑΓ δίχα κατὰ τὸ Η ἐπεζεύχθω ἁ ΒΗ, καὶ ἔστω τὸ κέντρον τοῦ βάρεος τοῦ ΑΒΓ τριγώνου ἐπὶ τᾶς ΒΗ τὸ Θ· λέγω ὅτι καὶ τοῦ ΕΔΖ τριγώνου τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ὁμοίως ἀγομένας εὐθείας.

   Τετμάσθω ἁ ΔΖ δίχα κατὰ τὸ Μ, καὶ ἐπεζεύχθω ἁ ΕΜ, καὶ πεποιήσθω ὡς ἁ ΒΗ ποτὶ ΒΘ, οὕτως ἁ ΜΕ ποτὶ ΕΝ, καὶ ἐπεζεύχθωσαν αἱ ΑΘ, ΘΓ, ΔΝ, ΝΖ. Ἐπεί ἐστι τᾶς μὲν ΓΑ ἡμίσεια ἁ ΑΗ, τᾶς δὲ ΔΖ ἡμίσεια ἁ ΔΜ, ἔστιν ἄρα καὶ ὡς ἁ ΒΑ ποτὶ ΕΔ, οὕτως ἁ ΑΗ ποτὶ ΔΜ. Καὶ περὶ ἴσας γωνίας αἱ πλευραὶ ἀνάλογόν ἐντι· ἴσα τε ἄρα ἐστὶν ἁ ὑπὸ ΑΗΒ γωνία τᾷ ὑπὸ ΔΜΕ, καί ἐστιν ὡς ἁ ΑΗ ποτὶ ΔΜ, οὕτως ἁ ΒΗ ποτὶ ΕΜ. Ἔστιν δὲ καὶ ὡς ἁ ΒΗ ποτὶ ΒΘ, οὕτως ἁ ΜΕ ποτὶ ΕΝ· καὶ δι᾿ ἴσου ἄρα ἐστὶν ὡς ἁ ΑΒ ποτὶ ΔΕ, οὕτως ἁ ΒΘ ποτὶ ΕΝ. Καὶ περὶ ἴσας γωνίας αἱ πλευραὶ ἀνάλογόν ἐντι· εἰ δὲ τοῦτο, ἴσα ἐστὶν ἁ ὑπὸ ΒΑΘ γωνία τᾷ ὑπὸ ΕΔΝ· ὥστε καὶ λοιπὰ ἁ ὑπὸ ΘΑΓ γωνία ἴσα ἐστὶ τᾷ ὑπὸ ΝΔΖ γωνίᾳ. Διὰ τὰ αὐτὰ δὲ ἁ μὲν ὑπὸ ΒΓΘ γωνία ἴσα ἐστὶ τᾷ ὑπὸ ΕΖΝ, ἁ δὲ ὑπὸ ΘΓΗ τᾷ ὑπὸ ΝΖΜ ἴσα. Ἐδείχθη δὲ καὶ ἁ ὑπὸ ΑΒΘ τᾷ ὑπὸ ΔΕΜ ἴσα· ὥστε καὶ λοιπὰ ἁ ὑπὸ ΘΒΓ γωνία ἴσα ἐστὶ τᾷ ὑπὸ ΝΕΖ. Διὰ ταῦτα δὴ πάντα ὁμοίως κεῖται τὰ Θ, Ν σαμεῖα [ποτὶ τὰς ὁμολόγους πλευρὰς ἴσας γωνίας ποιεῖ]. Ἐπεὶ οὖν ὁμοίως κεῖται τὰ Θ, Ν σαμεῖα, καί ἐστι τὸ Θ κέντρον τοῦ βάρεος τοῦ ΑΒΓ τριγώνου, καὶ τὸ Ν ἄρα κέντρον βάρεος τοῦ ΔΕΖ.

[95]    ιγ΄.

   Παντὸς τριγώνου τὸ κέντρον ἐστὶ τοῦ βάρεος ἐπὶ τᾶς εὐθείας, ἅ ἐστιν ἐκ τᾶς γωνίας ἐπὶ μέσαν ἀγομένα τὰν βάσιν.

   Ἔστω τρίγωνον τὸ ΑΒΓ καὶ ἐν αὐτῷ ἁ ΑΔ ἐπὶ μέσαν τὰν ΒΓ βάσιν· δεικτέον ὅτι ἐπὶ τᾶς ΑΔ τὸ κέντρον ἐστὶ τοῦ βάρεος τοῦ ΑΒΓ.

   Μὴ γάρ, ἀλλ᾿, εἰ δυνατόν, ἔστω τὸ Θ, καὶ δι᾿ αὐτοῦ παρὰ τὰν ΒΓ ἄχθω ἁ ΘΙ. Ἀεὶ δὴ δίχα τεμνομένας τᾶς ΔΓ ἐσσεῖταί ποκα ἁ καταλειπομένα ἐλάσσων τᾶς ΘΙ· καὶ διῃρήσθω ἑκατέρα τᾶν ΒΔ, ΔΓ ἐς τὰς ἴσας, καὶ διὰ τᾶν τομᾶν παρὰ τὰν ΑΔ ἄχθωσαν, καὶ ἐπεζεύχθωσαν αἱ ΕΖ, ΗΚ, ΛΜ· ἐσσοῦνται δὴ αὗται παρὰ τὰν ΒΓ. Τοῦ δὴ παραλληλογράμμου τοῦ μὲν ΜΝ τὸ κέντρον ἐστὶ τοῦ βάρεος ἐπὶ τᾶς ΥΣ, τοῦ δὲ ΚΞ τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΤΥ, τοῦ δὲ ΖΟ ἐπὶ τᾶς ΤΔ· τοῦ ἄρα ἐκ πάντων συγκειμένου μεγέθεος τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ [96] τᾶς ΣΔ εὐθείας. Ἔστω δὴ τὸ Ρ, καὶ ἐπεζεύχθω ἁ ΡΘ καὶ ἐκβεβλήσθω, καὶ ἄχθω παρὰ τὰν ΑΔ ἁ ΓΦ. Τὸ δὴ ΑΔΓ [τρίγωνον] ποτὶ πάντα τὰ τρίγωνα τὰ ἀπὸ τᾶν ΑΜ, ΜΚ, ΚΖ, ΖΓ ἀναγεγραμμένα ὁμοῖα τῷ ΑΔΓ τοῦτον ἔχει τὸν λόγον, ὃν ἔχει ἁ ΓΑ ποτὶ ΑΜ, διὰ τὸ ἴσας εἶμεν τὰς ΑΜ, ΜΚ, ΖΓ, ΚΖ. Ἐπεὶ δὲ καὶ τὸ ΑΔΒ τρίγωνον ποτὶ πάντα τὰ ἀπὸ τᾶν ΑΛ, ΛΗ, ΗΕ, ΕΒ ἀναγεγραμμένα ὁμοῖα τρίγωνα τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΒΑ ποτὶ ΑΛ, τὸ ἄρα ΑΒΓ τρίγωνον ποτὶ πάντα τὰ εἰρημένα τρίγωνα τοῦτον ἔχει τὸν λόγον, ὃν ἔχει ἁ ΓΑ ποτὶ ΑΜ. Ἀλλὰ ἁ ΓΑ ποτὶ ΑΜ μείζονα λόγον ἔχει ἤπερ ἁ ΦΡ ποτὶ ΡΘ· ὁ γὰρ τᾶς ΓΑ ποτὶ ΑΜ λόγος ὁ αὐτός ἐστι τῷ [ὅλας] τᾶς ΦΡ ποτὶ ΡΠ [διὰ τὸ ὁμοῖα εἶμεν τὰ τρίγωνα]· καὶ τὸ ΑΒΓ ἄρα τρίγωνον ποτὶ τὰ εἰρημένα μείζονα λόγον ἔχει ἤπερ ἁ ΦΡ ποτὶ ΡΘ· ὥστε καὶ διελόντι τὰ ΜΝ, ΚΞ, ΖΟ παραλληλόγραμμα ποτὶ τὰ καταλειπόμενα τρίγωνα μείζονα λόγον ἔχει ἤπερ ἁ ΦΘ ποτὶ ΘΡ. Γεγονέτω οὖν ἐν τῷ τῶν παραλληλογράμμων ποτὶ τὰ τρίγωνα λόγῳ ἁ ΧΘ ποτὶ ΘΡ. Ἐπεὶ οὖν ἔστι τι μέγεθος τὸ ΑΒΓ, οὗ τὸ κέντρον τοῦ βάρεός ἐστι τὸ Θ, καὶ ἀφῄρηται ἀπ᾿ αὐτοῦ μέγεθος τὸ συγκείμενον ἐκ τῶν ΜΝ, ΚΞ, ΖΟ παραλληλογράμμων, καί ἐστιν τοῦ ἀφῃρημένου μεγέθεος κέντρον τοῦ βάρεος τὸ Ρ σαμεῖον, τοῦ ἄρα λοιποῦ μεγέθεος τοῦ συγκειμένου ἐκ τῶν περιλειπομένων τριγώνων κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΡΘ εὐθείας ἐκβληθείσας καὶ ἀπολαφθείσας ποτὶ τὰν ΘΡ τοῦτον ἐχούσας τὸν λόγον, ὃν ἔχει τὸ ἀφαιρεθὲν μέγεθος ποτὶ τὸ λοιπόν. Τὸ ἄρα Χ σαμεῖον κέντρον ἐστὶ τοῦ βάρεος τοῦ συγκειμένου μεγέθεος ἐκ [97] τῶν περιλειπομένων· ὅπερ ἀδύνατον· τᾶς γὰρ διὰ τοῦ Χ εὐθείας παρὰ τὰν ΑΔ ἀγομένας ἐν τῷ ἐπιπέδῳ ἐπὶ ταὐτὰ πάντα ἐντί [τουτέστιν ἐπὶ θάτερον μέρος]. Δῆλον οὖν τὸ προτεθέν.

ΑΛΛΩΣ ΤΟ ΑΥΤΟ

   Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ ἄχθω ἁ ΑΔ ἐπὶ μέσαν τὰν ΒΓ· λέγω ὅτι ἐπὶ τᾶς ΑΔ τὸ κέντρον ἐστὶ τοῦ βάρεος τοῦ ΑΒΓ τριγώνου.

   Μὴ γάρ, ἀλλ᾿, εἰ δυνατόν, ἔστω τὸ Θ, καὶ ἐπεζεύχθωσαν αἵ τε ΑΘ, ΘΒ, ΘΓ καὶ αἱ ΕΔ, ΖΕ ἐπὶ μέσας τὰς ΒΑ, ΑΓ, καὶ παρὰ τὰν ΑΘ ἄχθωσαν αἱ ΕΚ, ΖΛ, καὶ ἐπεζεύχθωσαν αἱ ΚΛ, ΛΔ, ΔΚ, ΔΘ, ΜΝ. Ἐπεὶ ὁμοῖόν ἐστι τὸ ΑΒΓ τρίγωνον τῷ ΔΖΓ τριγώνῳ διὰ τὸ παράλληλον εἶμεν τὰν ΒΑ τᾷ ΖΔ, καί ἐστι τοῦ ΑΒΓ τριγώνου κέντρον τοῦ βάρεος τὸ Θ σαμεῖον, καὶ τοῦ ΖΔΓ ἄρα τριγώνου κέντρον τοῦ βάρεός ἐστι τὸ Λ σαμεῖον· ὁμοίως γάρ ἐντι κείμενα τὰ Θ, Λ σαμεῖα ἐν ἑκατέρῳ τῶν τριγώνων [ἐπειδήπερ ποτὶ τὰς ὁμολόγους πλευρὰς ἴσας ποιέοντι γωνίας· φανερὸν γὰρ τοῦτο]. Διὰ τὰ αὐτὰ δὴ καὶ τοῦ ΕΒΔ κέντρον τοῦ [98] βάρεός ἐστι τὸ Κ σαμεῖον· ὥστε τοῦ ἐξ ἀμφοτέρων τῶν ΕΒΔ, ΖΔΓ τριγώνων συγκειμένου μεγέθεος κέντρον τοῦ βάρεός ἐστιν ἐπὶ μέσας τᾶς ΚΛ εὐθείας [ἐπειδήπερ ἴσα ἐντὶ τὰ ΕΒΔ, ΖΔΓ τρίγωνα]. Καί ἐστιν τᾶς ΚΛ μέσον τὸ Ν, ἐπεί ἐστιν ὡς ἁ ΒΕ ποτὶ ΕΑ, οὕτως ἁ ΒΚ ποτὶ ΘΚ, ὡς δὲ ἁ ΓΖ ποτὶ ΖΑ, οὕτως ἁ ΓΛ ποτὶ ΛΘ· εἰ δὲ τοῦτο, ἔστιν ἁ ΒΓ τᾷ ΚΛ παράλληλος. Καὶ ἐπέζευκται ἁ ΔΘ· ἔστιν ἄρα ὡς ἁ ΒΔ ποτὶ ΔΓ, οὕτως ἁ ΚΝ ποτὶ τὰν ΝΛ· ὥστε τοῦ ἐξ ἀμφοτέρων τῶν εἰρημένων τριγώνων συγκειμένου μεγέθεος κέντρον ἐστὶ τὸ Ν. Ἔστιν δὲ καὶ τοῦ ΑΕΔΖ παραλληλογράμμου κέντρον τοῦ βάρεος τὸ Μ σαμεῖον· ὥστε τοῦ ἐκ πάντων συγκειμένου μεγέθεος τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΜΝ εὐθείας. Ἔστιν δὲ καὶ τοῦ ΑΒΓ κέντρον τοῦ βάρεος τὸ Θ σαμεῖον· ἁ ΜΝ ἄρα ἐκβαλλομένα πορεύεται διὰ τοῦ Θ σαμείου· ὅπερ ἀδύνατον. Οὐκ ἄρα τὸ κέντρον τοῦ βάρεος τοῦ ΑΒΓ τριγώνου οὐκ ἔστιν ἐπὶ τᾶς ΑΔ εὐθείας· ἔστιν ἄρα ἐπ᾿ αὐτᾶς.

   ιδ΄

   Παντὸς τριγώνου κέντρον ἐστὶ τοῦ βάρεος τὸ σαμεῖον, καθ᾿ ὃ συμπίπτοντι τοῦ τριγώνου αἱ ἐκ τᾶν γωνιᾶν ἐπὶ μέσας τὰς πλευρὰς ἀγόμεναι εὐθεῖαι.

[99]    Ἔστω τρίγωνον τὸ ΑΒΓ, καὶ ἄχθω ἁ μὲν ΑΔ ἐπὶ μέσαν τὰν ΒΓ, ἁ δὲ ΒΕ ἐπὶ μέσαν τὰν ΑΓ· ἐσσεῖται δὴ τοῦ ΑΒΓ τριγώνου κέντρον τοῦ βάρεος ἐφ᾿ ἑκατέρας τᾶν ΑΔ, ΒΕ· δέδεικται γὰρ τοῦτο. Ὥστε τὸ Θ σαμεῖον κέντρον τοῦ βάρεός ἐστιν.

   ιε΄.

   Παντὸς τραπεζίου τὰς δύο πλευρὰς ἔχοντος παραλλήλους ἀλλάλαις τὸ κέντρον ἐστὶ τοῦ βάρεος ἐπὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰς διχοτομίας τᾶν παραλλήλων διαιρεθείσας, ὥστε τὸ τμᾶμα αὐτᾶς τὸ πέρας ἔχον τὰν διχοτομίαν τᾶς ἐλάσσονος τᾶν παραλλήλων ποτὶ τὸ λοιπὸν τμᾶμα τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει συναμφότερος ἁ ἴσα τᾷ διπλασίᾳ τᾶς μείζονος μετὰ τᾶς ἐλάσσονος ποτὶ τὰν διπλασίαν τᾶς ἐλάσσονος μετὰ τᾶς μείζονος τᾶν παραλλήλων.

   Ἔστω τραπέζιον τὸ ΑΒΓΔ παραλλήλους ἔχον τὰς ΑΔ, ΒΓ, ἁ δὲ ΕΖ ἐπιζευγνυέτω τὰς διχοτομίας τᾶν ΑΔ, ΒΓ. Ὅτι οὖν ἐπὶ τᾶς ΕΖ ἐστὶ τὸ κέντρον τοῦ τραπεζίου [100] φανερόν. Ἐὰν γὰρ ἐκβάλῃς τὰς ΓΔΗ, ΖΕΗ, ΒΑΗ, δῆλον ὅτι ἐπὶ τὸ αὐτὸ σαμεῖον ἔρχονται, καὶ ἐσσεῖται τοῦ ΗΒΓ τριγώνου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΗΖ, καὶ ὁμοίως τοῦ ΑΗΔ τριγώνου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΕΗ· καὶ λοιποῦ ἄρα τοῦ ΑΒΓΔ τραπεζίου κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς ΕΖ. Ἐπιζευχθεῖσα δὲ ἁ ΒΔ διῃρήσθω εἰς τρία ἴσα κατὰ τὰ Κ, Θ σαμεῖα, καὶ δι᾿ αὐτῶν παρὰ τὰν ΒΓ ἄχθωσαν αἱ ΛΘΜ, ΝΚΤ, καὶ ἐπεζεύχθωσαν αἱ ΔΖ, ΒΕ, ΟΞ· ἐσσεῖται δὴ τοῦ μὲν ΔΒΓ τριγώνου κέντρον τοῦ βάρεος ἐπὶ τᾶς ΘΜ, ἐπειδήπερ τρίτον μέρος ἁ ΘΒ τᾶς ΒΔ [καὶ διὰ τοῦ Θ σαμείου παράλληλος τᾷ βάσει ἆκται ἁ ΜΘ]. Ἔστιν δὲ τὸ κέντρον τοῦ βάρεος τοῦ ΔΒΓ τριγώνου καὶ ἐπὶ τᾶς ΔΖ· ὥστε τὸ Ξ κέντρον τοῦ βάρεος τοῦ εἰρημένου τριγώνου. Διὰ ταὐτὰ δὲ καὶ τὸ Ο σαμεῖον κέντρον ἐστὶ τοῦ βάρεος τοῦ ΑΒΔ τριγώνου· τοῦ ἄρα ἐξ ἀμφοτέρων τῶν ΑΒΔ, ΒΔΓ τριγώνων συγκειμένου μεγέθεος, ὅπερ ἐστὶ τὸ τραπέζιον, κέντρον τοῦ βάρεος ἐπὶ τᾶς ΟΞ εὐθείας. Ἔστιν δὲ τοῦ εἰρημένου τραπεζίου κέντρον τοῦ βάρεος καὶ ἐπὶ τᾶς ΕΖ· ὥστε τοῦ ΑΒΓΔ τραπεζίου κέντρον ἐστὶ τοῦ βάρεος τὸ Π σαμεῖον. Ἔχοι δ᾿ ἂν τὸ ΒΔΓ τρίγωνον ποτὶ τὸ ΑΒΔ λόγον, ὃν ἁ ΟΠ ποτὶ ΠΞ. Ἀλλ᾿ ὡς τὸ ΒΔΓ τρίγωνον ποτὶ τὸ ΑΒΔ τρίγωνον, οὕτως ἐντὶ ἁ ΒΓ ποτὶ ΑΔ, ὡς δὲ ἁ ΟΠ ποτὶ ΠΞ, οὕτως ἁ ΡΠ ποτὶ ΠΣ· καὶ ὡς ἄρα ἁ ΒΓ ποτὶ ΑΔ, οὕτως ἁ ΡΠ ποτὶ ΠΣ· ὥστε καὶ ὡς δύο αἱ ΒΓ μετὰ τᾶς ΑΔ ποτὶ δύο τὰς ΑΔ μετὰ τᾶς ΒΓ, οὕτως δύο αἱ ΡΠ μετὰ τᾶς ΠΣ ποτὶ δύο τὰς ΠΣ μετὰ τᾶς ΠΡ. Ἀλλὰ δύο μὲν αἱ ΡΠ μετὰ τᾶς ΠΣ συναμφότερός ἐστιν ἁ ΣΡΠ, τουτέστιν ἁ ΠΕ, δύο δὲ αἱ ΠΣ μετὰ τᾶς ΠΡ συναμφότερός ἐστιν ἁ ΡΣΠ, τουτέστιν ἁ ΠΖ· δέδεικται ἄρα τὰ προτεθέντα. [101]

Ἰσορροπικῶν β΄

   α΄.

   Εἴ κα δύο χωρία περιεχόμενα ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, ἃ δυνάμεθα παρὰ τὰν δοθεῖσαν εὐθεῖαν παραβαλεῖν, μὴ τὸ αὐτὸ κέντρον τοῦ βάρεος ἔχωντι, τοῦ ἐξ ἀμφοτέρων αὐτῶν συγκειμένου μεγέθεος τὸ κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ κέντρα τοῦ βάρεος αὐτῶν διαιρέον οὕτως τὰν εἰρημέναν εὐθεῖαν, ὥστε τὰ τμάματα αὐτᾶς ἀντιπεπονθότως τὸν αὐτὸν λόγον ἔχειν τοῖς χωρίοις.

   Ἔστω δύο χωρία τὰ ΑΒ, ΓΔ, οἷα εἴρηται, κέντρα δὲ αὐτῶν τοῦ βάρεος ἔστω τὰ Ε, Ζ σαμεῖα, καὶ ὃν ἔχει λόγον τὸ ΑΒ ποτὶ τὸ ΓΔ, τοῦτον ἐχέτω ἁ ΖΘ ποτὶ ΘΕ. Δεικτέον ὅτι τοῦ ἐξ ἀμφοτέρων τῶν ΑΒ, ΓΔ χωρίων συγκειμένου μεγέθεος κέντρον τοῦ βάρεός ἐστι τὸ Θ σαμεῖον.

   Ἔστω δὴ τᾷ μὲν ΕΘ ἑκατέρα ἴσα τᾶν ΖΗ, ΖΚ, τᾷ δὲ

[102]ΖΘ, τουτέστι τᾷ ΗΕ, ἴσα ἁ ΕΛ· ἐσσεῖται ἄρα καὶ ἁ ΛΘ τᾷ ΚΘ ἴσα, καὶ ἔτι ὡς ἁ ΛΗ ποτὶ ΗΚ, οὕτως τὸ ΑΒ ποτὶ ΓΔ· διπλασία γὰρ ἑκατέρα ἑκατέρας. Παραβεβλήσθω δὴ παρὰ τὰν ΛΗ τὸ χωρίον τοῦ ΑΒ ἐφ᾿ ἑκάτερα τᾶς ΛΗ, ὥστε εἶμεν τὸ ΜΝ ἴσον τῷ ΑΒ· ἐσσεῖται δὴ τοῦ ΜΝ κέντρον τοῦ βάρεος τὸ Ε σαμεῖον. Συμπεπληρώσθω δὴ τὸ ΝΞ, ἕξει δὲ τὸ ΜΝ ποτὶ τὸ ΝΞ λόγον, ὃν ἁ ΛΗ ποτὶ ΗΚ. Ἔχει δὲ καὶ τὸ ΑΒ ποτὶ τὸ ΓΔ τὸν τᾶς ΛΗ ποτὶ ΗΚ λόγον· καὶ ὡς ἄρα τὸ ΑΒ ποτὶ ΓΔ, οὕτως τὸ ΜΝ ποτὶ ΝΞ. Καὶ ἐναλλάξ· ἴσον δὲ τὸ ΑΒ τῷ ΜΝ· ἴσον ἄρα καὶ τὸ ΓΔ τῷ ΝΞ, καὶ κέντρον ἐστὶν αὐτοῦ τοῦ βάρεος τὸ Ζ σαμεῖον. Καὶ ἐπεὶ ἴσα ἐστὶν ἁ ΛΘ τᾷ ΘΚ, καὶ ὅλα ἁ ΛΚ τὰς ἀπεναντίον πλευρὰς δίχα τέμνει, [τοῦ] ὅλου τοῦ ΠΜ κέντρον τοῦ βάρεός ἐστι τὸ Θ σαμεῖον. Ἀλλὰ τὸ ΜΠ ἴσον τῷ ἐξ ἀμφοτέρων τῶν ΜΝ, ΝΞ· ὥστε καὶ τοῦ ἐξ ἀμφοτέρων τῶν ΑΒ, ΓΔ κέντρον ἐστὶ τοῦ βάρεος τὸ Θ σαμεῖον.

   β΄.

   Εἴ κα εἰς τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τρίγωνον ἐγγραφῇ τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ὕψος ἴσον, καὶ πάλιν εἰς τὰ παραλειπόμενα τμάματα τρίγωνα ἐγγραφέωντι τὰς αὐτὰς βάσιας ἔχοντα τοῖς τμαμάτεσσιν καὶ ὕψος ἴσον, καὶ ἀεὶ εἰς τὰ παραλειπόμενα τμάματα τρίγωνα ἐγγραφέωντι τὸν αὐτὸν τρόπον, τὸ γενόμενον σχῆμα ἐν τῷ τμάματι γνωρίμως ἐγγράφεσθαι [103] λεγέσθω. Φανερὸν δὲ ὅτι τοῦ οὕτως ἐγγραφέντος σχήματος αἱ τὰς γωνίας ἐπιζευγνύουσαι τάς τε ἔγγιστα ἀπὸ τᾶς κορυφᾶς τοῦ τμάματος καὶ τὰς ἑξῆς παρὰ τὰν βάσιν ἐσσοῦνται τοῦ τμάματος καὶ δίχα τμαθήσονται ὑπὸ τᾶς τοῦ τμάματος διαμέτρου καὶ τὰν διάμετρον τεμοῦντι εἰς τοὺς τῶν ἑξῆς περισσῶν ἀριθμῶν λόγους ἑνὸς λεγομένου ποτὶ τᾷ κορυφᾷ τοῦ τμάματος. Ταῦτα δὲ δεικτέον ἐν ταῖς τάξεσιν.

   Εἰ δέ κα εἰς τμᾶμα περιεχόμενον ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς εὐθύγραμμον γνωρίμως ἐγγραφῇ, τοῦ ἐγγραφέντος κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς τοῦ τμάματος διαμέτρου.

   Ἔστω τμᾶμα τὸ ΑΒΓ οἷον εἴρηται, καὶ ἐγγεγράφθω εἰς αὐτὸ εὐθύγραμμον γνωρίμως τὸ ΑΕΖΗΒΘΙΚΓ. Δεικτέον ὅτι τὸ κέντρον τοῦ βάρεος τοῦ εὐθυγράμμου ἐστὶν ἐπὶ τᾶς ΒΔ.

   Ἐπεὶ γὰρ τοῦ μὲν ΑΕΚΓ τραπεζίου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΛΔ ἐστί, τοῦ δὲ ΕΖΙΚ τραπεζίου τὸ κέντρον [104] ἐπὶ τᾶς ΜΛ, τοῦ δὲ ΖΗΘΙ τραπεζίου τὸ κέντρον ἐπὶ τᾶς ΜΝ, ἔτι δὲ καὶ τοῦ ΗΒΘ τριγώνου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΒΝ, δῆλον ὅτι καὶ τοῦ ὅλου εὐθυγράμμου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΒΔ ἐστίν.

   γ΄

   Εἴ κα δύο τμαμάτων ὁμοίων περιεχομένων ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς εἰς ἑκάτερον εὐθύγραμμον ἐγγραφῇ γνωρίμως, ἔχωντι δὲ τὰ ἐγγραφέντα εὐθύγραμμα τὰς πλευρὰς ἴσας τῷ πλήθει ἀλλάλαις, τῶν εὐθυγράμμων τὰ κέντρα τῶν βαρέων ὁμοίως τέμνοντι τὰς διαμέτρους τῶν τμαμάτων.

   Ἔστω δύο τμάματα τὰ ΑΒΓ, ΞΟΠ, καὶ ἐγγεγράφθω εἰς αὐτὰ εὐθύγραμμα γνωρίμως, καὶ τᾶν πασᾶν πλευρᾶν [105] τὸν ἀριθμὸν ἐχόντων ἀλλάλοις ἴσον, διάμετροι δὲ ἔστωσαν τῶν τμαμάτων αἱ ΒΔ, ΟΡ, καὶ ἐπεζεύχθωσαν αἱ ΕΚ, ΖΙ, ΗΘ καὶ αἱ ΣΤ, ΥΦ, ΧΨ. Ἐπεὶ οὖν ἅ τε ΒΔ διαιρεῖται ὑπὸ τᾶν παραλλήλων εἰς τοὺς τῶν ἑξῆς ἀριθμῶν περισσῶν λόγους καὶ ἁ ΡΟ, καὶ τῷ πλήθει τὰ τμάματα αὐτᾶν ἴσα ἐντί, δῆλον ὡς τά τε τμάματα τᾶν διαμέτρων ἐν τοῖς αὐτοῖς λόγοις ἐσσεῖται, καὶ αἱ παράλληλοι τοὺς αὐτοὺς λόγους ἑξοῦντι. Καὶ τῶν τραπεζίων τοῦ τε ΑΕΚΓ καὶ τοῦ ΞΣΤΠ τὰ κέντρα τῶν βαρέων ἐσσεῖται ἐπὶ τᾶν ΛΔ, ΩΡ εὐθειᾶν ὁμοίως κείμενα, ἐπεὶ τὸν αὐτὸν ἔχοντι λόγον αἱ ΑΓ, ΕΚ ταῖς ΞΠ, ΣΤ· πάλιν δὲ καὶ τῶν ΕΖΙΚ, ΣΥΦΤ τραπεζίων τὰ κέντρα τῶν βαρέων ἐσσοῦνται ὁμοίως διαιρέοντα τὰς ΛΜ, ΩϠ, καὶ τῶν ΖΗΘΙ, ΥΧΨΦ τραπεζίων τὰ κέντρα τῶν βαρέων ἐσσοῦνται ὁμοίως διαιρέοντα τὰς ΜΝ, ϞϠ, ἐσσεῖται δὲ καὶ τῶν ΗΒΘ, ΧΟΨ τριγώνων τὰ κέντρα τῶν βαρέων ἐπὶ τᾶν ΒΝ, ΟϞ ὁμοίως κείμενα· ἔχοντι δὴ τὸν αὐτὸν λόγον τὰ τραπέζια καὶ τὰ τρίγωνα. Δῆλον οὖν ὅτι τοῦ ὅλου εὐθυγράμμου τοῦ ἐν τῷ ΑΒΓ τμάματι ἐγγεγραμμένου τὸ κέντρον τοῦ βάρεος ὁμοίως διαιρεῖ τὰν ΒΔ καὶ τοῦ ἐν τῷ ΞΟΠ τμάματι ἐγγεγραμμένου τὸ κέντρον τοῦ βάρεος τὰν ΟΡ· ὅπερ ἔδει δεῖξαι.

[106]    δ΄.

   Παντὸς τμάματος περιεχομένου ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς τοῦ τμάματος διαμέτρου.

   Ἔστω τμᾶμα ὡς εἴρηται τὸ ΑΒΓ, οὗ διάμετρος ἔστω ἁ ΒΔ. Δεικτέον ὅτι τοῦ εἰρημένου τμάματος τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΒΔ.

   Εἰ γὰρ μή, ἔστω τὸ Ε, καὶ δι᾿ αὐτοῦ ἄχθω παρὰ τὰν ΒΔ ἁ ΕΖ, καὶ ἐγγεγράφθω εἰς τὸ τμᾶμα τρίγωνον τὸ ΑΒΓ τὰν αὐτὰν βάσιν ἔχον καὶ ὕψος ἴσον, καὶ ὃν ἔχει λόγον ἁ ΓΖ ποτὶ ΖΔ, τοῦτον ἐχέτω τὸ ΑΒΓ τρίγωνον ποτὶ τὸ Κ χωρίον· ἐγγεγράφθω δὲ καὶ εὐθύγραμμον εἰς τὸ τμᾶμα γνωρίμως, ὥστε τὰ περιλειπόμενα τμάματα ἐλάσσονα εἶμεν τοῦ Κ· τοῦ δὴ ἐγγραφομένου εὐθυγράμμου τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΒΔ. Ἔστω τὸ Θ, καὶ ἐπεζεύχθω ἁ ΘΕ καὶ ἐκβεβλήσθω, καὶ παρὰ τὰν ΒΔ ἄχθω ἁ ΓΛ· δῆλον δὴ ὅτι μείζονα λόγον ἔχει τὸ ἐγγεγραμμένον εὐθύγραμμον ἐν τῷ τμάματι ποτὶ τὰ λειπόμενα τμάματα [107] ἢ τὸ ΑΒΓ τρίγωνον ποτὶ τὸ Κ. Ἀλλ᾿ ὡς τὸ ΑΒΓ τρίγωνον ποτὶ τὸ Κ, οὕτως ἁ ΓΖ ποτὶ ΖΔ· καὶ τὸ ἐγγεγραμμένον ἄρα εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα μείζονα λόγον ἔχει ἢ ἁ ΓΖ ποτὶ ΖΔ, τουτέστιν ἁ ΛΕ ποτὶ ΕΘ. Ἐχέτω οὖν ἁ ΜΕ ποτὶ ΕΘ τὸν αὐτὸν λόγον τὸν τοῦ εὐθυγράμμου ποτὶ τὰ τμάματα. Ἐπεὶ οὖν τὸ μὲν Ε κέντρον τοῦ ὅλου τμάματος, τοῦ δὲ ἐγγεγραμμένου ἐν αὐτῷ εὐθυγράμμου τὸ Θ, δῆλον ὅτι λοιποῦ τοῦ συγκειμένου μεγέθεος ἐκ τῶν περιλειπομένων τμαμάτων τὸ κέντρον τοῦ βάρεός ἐστιν ἐκβληθείσας τᾶς ΘΕ καὶ ἀπολαφθείσας τινὸς εὐθείας, ἃ λόγον ἔχει ποτὶ τὰν ΘΕ ὃν τὸ ἐγγεγραμμένον εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα. Ὥστε εἴη κα τοῦ συγκειμένου μεγέθεος ἐκ τῶν περιλειπομένων τμαμάτων κέντρον τοῦ βάρεος τὸ Μ σαμεῖον· ὅπερ ἄτοπον· τᾶς γὰρ διὰ τοῦ Μ παρὰ τὰν ΒΔ ἀγομένας ἐπὶ ταὐτὰ ἐσσοῦνται πάντα τὰ περιλειπόμενα τμάματα. Δῆλον οὖν ὅτι ἐπὶ τᾶς ΒΔ τὸ κέντρον ἐστὶ τοῦ βάρεος.

   ε΄.

   Εἴ κα εἰς τμᾶμα περιεχόμενον ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς εὐθύγραμμον ἐγγραφῇ γνωρίμως, τοῦ ὅλου τμάματος τὸ κέντρον τοῦ βάρεος ἐγγύτερόν ἐστι τᾶς κορυφᾶς τοῦ τμάματος ἢ τὸ τοῦ ἐγγραφέντος εὐθυγράμμου κέντρον.

[108]    Ἔστω τὸ ΑΒΓ τμᾶμα οἷον εἴρηται, διάμετρος δὲ αὐτοῦ ἁ ΔΒ, καὶ ἐγγεγράφθω εἰς αὐτὸ τρίγωνον πρῶτον γνωρίμως τὸ ΑΒΓ, καὶ τετμάσθω ἁ ΒΔ κατὰ τὸ Ε, ὥστε εἶμεν διπλασίαν τὰν ΒΕ τᾶς ΕΔ· ἔστιν οὖν τοῦ ΑΒΓ τριγώνου κέντρον τοῦ βάρεος τὸ Ε σαμεῖον. Τετμάσθω δὴ δίχα ἑκατέρα τᾶν ΑΒ, ΒΓ κατὰ τὰ Ζ, Η, καὶ διὰ τῶν Ζ, Η παρὰ τὰν ΒΔ ἄχθωσαν αἱ ΖΚ, ΛΗ· ἐσσεῖται ἄρα τοῦ μὲν ΑΚΒ τμάματος τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΖΚ, τοῦ ΒΓΛ τμάματος τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΗΛ. Ἔστω δὲ τὰ Θ, Ι, καὶ ἐπεζεύχθω ἁ ΘΙ. Καὶ ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΘΖΗΙ, καὶ ἴσα ἐστὶ τᾷ ΖΝ ἁ ΝΗ, ἔστιν ἄρα καὶ ἁ ΧΘ ἴσα τᾷ ΧΙ· ὥστε τοῦ ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τμαμάτων συγκειμένου μεγέθεος κέντρον τοῦ βάρεός ἐστιν ἐπὶ μέσας τᾶς ΘΙ [ἐπειδήπερ ἴσα ἐντὶ τμάματα], τουτέστιν τὸ Χ σαμεῖον. Ἐπεὶ δὲ τοῦ μὲν ΑΒΓ τριγώνου [109] κέντρον τοῦ βάρεός ἐστι τὸ Ε σαμεῖον, τοῦ δὲ συγκειμένου ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τὸ Χ, δῆλον οὖν ὅτι ὅλου τοῦ τμάματος τοῦ ΑΒΓ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΧΕ, τουτέστι μεταξὺ τῶν Χ, Ε σαμείων· ὥστ᾿ εἴη κα ἐγγύτερον τᾶς τοῦ τμάματος κορυφᾶς τὸ κέντρον τοῦ ὅλου τμάματος ἢ τὸ τοῦ ἐγγραφομένου τριγώνου γνωρίμως.

   Ἐγγεγράφθω πάλιν εἰς τὸ τμᾶμα πεντάγωνον εὐθύγραμμον γνωρίμως τὸ ΑΚΒΛΓ, καὶ ἔστω τοῦ μὲν ὅλου τμάματος διάμετρος ἁ ΒΔ, ἑκατέρου δὲ τῶν τμαμάτων ἑκατέρα τᾶν ΚΖ, ΛΗ διάμετρος [καὶ ἐπεὶ ἐν τῷ ΑΚΒ τμάματι ἐγγέγραπται εὐθύγραμμον γνωρίμως, τοῦ ὅλου τμάματος κέντρον τοῦ βάρεός ἐστιν ἐγγύτερον τᾶς κορυφᾶς ἢ τὸ τοῦ εὐθυγράμμου]. Ἔστω οὖν τοῦ μὲν τμάματος τὸ κέντρον τοῦ βάρεος τὸ Θ, τοῦ δὲ τριγώνου τὸ Ι, πάλιν δὲ ἔστω τοῦ μὲν ΒΛΓ τμάματος τὸ κέντρον τοῦ βάρεος τὸ Μ, τοῦ δὲ τριγώνου τὸ Ν· ἐσσεῖται δὴ τοῦ μὲν ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τμαμάτων συγκειμένου [110] μεγέθεος κέντρον τοῦ βάρεος τὸ Χ, τοῦ δὲ ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τριγώνων τὸ Τ. Πάλιν οὖν, ἐπεὶ τοῦ ΑΒΓ τριγώνου κέντρον τοῦ βάρεός ἐστι τὸ Ε, τοῦ δὲ ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τμαμάτων τὸ Χ, δῆλον ὡς [τοῦ] ὅλου τοῦ ΑΒΓ τμάματος τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΧΕ τμαθείσας οὕτως ὥστε ὃν ἔχει λόγον τὸ ΑΒΓ τρίγωνον ποτὶ τὰ συναμφότερα τὰ ΑΚΒ, ΒΛΓ τμάματα, τὸν αὐτὸν λόγον ἔχειν τὸ τμᾶμα αὐτᾶς τὸ πέρας ἔχον τὸ Χ ποτὶ τὸ ἔλασσον τμᾶμα. Τοῦ δὲ ΑΚΒΛΓ πενταγώνου κέντρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΕΤ εὐθείας τμαθείσας οὕτως, ὥστε ὃν ἔχει λόγον τὸ ΑΒΓ τρίγωνον ποτὶ τὰ ΑΚΒ, ΒΛΓ τρίγωνα, τοῦτον ἔχειν τὸν λόγον τὸ τμᾶμα αὐτᾶς τὸ πέρας ἔχον τὸ Τ ποτὶ τὸ λοιπόν. Ἐπεὶ οὖν μείζονα λόγον ἔχει τὸ ΑΒΓ τρίγωνον ποτὶ τὰ ΚΑΒ, ΛΒΓ τρίγωνα ἢ ποτὶ τὰ τμάματα, δῆλον οὖν ὅτι τοῦ ΑΒΓ τμάματος τὸ κέντρον τοῦ βάρεος ἐγγύτερόν ἐστι τᾶς Β κορυφᾶς ἢ τὸ τοῦ ἐγγραφομένου εὐθυγράμμου. Καὶ ἐπὶ πάντων εὐθυγράμμων τῶν ἐγγραφομένων ἐς τὰ τμάματα γνωρίμως ὁ αὐτὸς λόγος.

   Ϛ΄.

   Τμάματος δοθέντος περιεχομένου ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς δυνατόν ἐστιν ἐς τὸ τμᾶμα εὐθύγραμμον γνωρίμως ἐγγράψαι, ὥστε τὰν μεταξὺ εὐθεῖαν τῶν κέντρων τοῦ βάρεος τοῦ τμάματος καὶ τοῦ ἐγγραφέντος εὐθυγράμμου ἐλάσσονα εἶμεν πάσας τᾶς προτεθείσας εὐθείας.

[111]    Δεδόσθω τμᾶμα τὸ ΑΒΓ οἷον εἴρηται, οὗ κέντρον ἔστω τοῦ βάρεος τὸ Θ, καὶ ἐγγεγράφθω εἰς αὐτὸ τρίγωνον γνωρίμως τὸ ΑΒΓ, καὶ ἔστω ἁ προτεθεῖσα εὐθεῖα ἁ Ζ, καὶ ὃν λόγον ἔχει ἁ ΒΘ ποτὶ Ζ, τοῦτον τὸν λόγον ἐχέτω τὸ ΑΒΓ τρίγωνον ποτὶ τὸ Χ χωρίον. Ἐγγεγράφθω δὴ εἰς τὸ ΑΒΓ τμᾶμα εὐθύγραμμον γνωρίμως τὸ ΑΚΒΛΓ, ὥστε τὰ περιλειπόμενα τμάματα ἐλάσσονα εἶμεν τοῦ Χ, καὶ ἔστω τοῦ ἐγγραφέντος εὐθυγράμμου κέντρον τοῦ βάρεος τὸ Ε. Φαμὶ δὴ τὰν ΘΕ ἐλάσσονα εἶμεν τᾶς Ζ.

   Εἰ γὰρ μή, ἤτοι ἴσα ἐστὶν ἢ μείζων. Ἐπεὶ δὲ τὸ ΑΚΒΛΓ εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα μείζονα λόγον ἔχει ἢ τὸ ΑΒΓ τρίγωνον ποτὶ Χ, τουτέστιν ἁ ΘΒ ποτὶ Ζ, ἔχει δὲ καὶ ἁ ΒΘ ποτὶ Ζ οὐκ ἐλάσσονα λόγον ἢ ὃν ἔχει ποτὶ ΘΕ, διὰ τὸ μὴ ἐλάσσονα εἶμεν τὰν ΘΕ τᾶς Ζ, πολλῷ ἄρα τὸ ΑΚΒΛΓ εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα μείζονα λόγον ἔχει ἢ ἁ ΒΘ ποτὶ ΘΕ· ὥστε, ἐὰν ποιῶμες ὡς τὸ ΑΚΒΛΓ εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα, οὕτως ἄλλαν τινα ποτὶ ΘΕ [ἐπειδὴ τοῦ ΑΒΓ τμάματος τὸ κέντρον τοῦ βάρεός ἐστι [112] τὸ Θ, ἐκβληθείσας τᾶς ΕΘ καὶ ἀπολαφθείσας τινὸς εὐθείας ἐχούσας λόγον ποτὶ τὰν ΕΘ, ὃν τὸ ΑΚΒΛΓ εὐθύγραμμον ποτὶ τὰ περιλειπόμενα τμάματα], ἐσσεῖται μείζων τᾶς ΘΒ. Ἐχέτω οὖν ἁ ΗΘ ποτὶ ΘΕ. Τὸ Η ἄρα κέντρον τοῦ βάρεος τοῦ συγκειμένου ἐκ τῶν περιλειπομένων τμαμάτων· ὅπερ ἀδύνατον· τᾶς γὰρ διὰ τοῦ Η ἀχθείσας παρὰ τὰν ΑΓ ἐπὶ τὰ αὐτά ἐστιν [τῷ τμήματι]. Δῆλον οὖν ὅτι ἁ ΘΕ ἐλάσσων ἐστὶ τᾶς Ζ· ἔδει δὲ τοῦτο δεῖξαι.

   ζ΄.

   Δύο τμαμάτων ὁμοίων περιεχομένων ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τὰ κέντρα τῶν βαρέων εἰς τὸν αὐτὸν λόγον τέμνοντι τὰς διαμέτρους.

   Ἔστω δύο τμάματα οἷα εἴρηται τὰ ΑΒΓ, ΕΖΗ, ὧν διάμετροι αἱ ΒΔ, ΖΘ, καὶ ἔστω τοῦ μὲν ΑΒΓ τμάματος [113] κέντρον τοῦ βάρεος τὸ Κ σαμεῖον, τοῦ δὲ ΕΖΗ τὸ Λ. Δεικτέον ὅτι εἰς τὸν αὐτὸν λόγον τέμνοντι τὰς διαμέτρους τὰ Κ, Λ.

   Εἰ γὰρ μή, ἔστω ὡς ἁ ΚΒ ποτὶ ΚΔ, οὕτως ἁ ΖΜ ποτὶ ΜΘ, καὶ ἐγγεγράφθω εἰς τὸ ΕΖΗ τμᾶμα εὐθύγραμμον γνωρίμως, ὥστε τὰν μεταξὺ τοῦ κέντρου τοῦ τμάματος καὶ τοῦ ἐγγραφομένου εὐθυγράμμου ἐλάσσονα εἶμεν τᾶς ΛΜ, καὶ ἔστω τοῦ ἐγγραφέντος εὐθυγράμμου κέντρον τοῦ βάρεος τὸ Ξ σαμεῖον, ἐγγεγράφθω δὲ εἰς τὸ ΑΒΓ τμᾶμα τῷ ἐν τῷ ΕΖΗ [ἐγγεγραμμένῳ εὐθυγράμμῳ] ὁμοῖον εὐθύγραμμον [τουτέστιν ὁμοίως γνωρίμως]· οὗ τὸ κέντρον τοῦ βάρεος τᾶς κορυφᾶς ἐγγύτερον ἤπερ τὸ τοῦ τμάματος· ὅπερ ἀδύνατον. Δῆλον οὖν ὅτι τὸν αὐτὸν λόγον ἔχει ἁ ΒΚ ποτὶ ΚΔ, ὃν ἁ ΖΛ ποτὶ ΛΘ.

   η΄.

   Παντὸς τμάματος περιεχομένου ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς τὸ κέντρον τοῦ βάρεος διαιρεῖ τὰν τοῦ τμάματος διάμετρον, ὥστε εἶμεν ἁμιόλιον τὸ μέρος αὐτᾶς τὸ ποτὶ τᾷ κορυφᾷ τοῦ τμάματος τοῦ ποτὶ τᾷ βάσει.

[114]    Ἔστω τὸ ΑΒΓ τμᾶμα οἷον εἴρηται, διάμετρος δὲ αὐτοῦ ἔστω ἁ ΒΔ, κέντρον δὲ τοῦ βάρεος τὸ Θ σαμεῖον. Δεικτέον ὅτι ἁμιολία ἐστὶν ἁ ΒΘ τᾶς ΘΔ.    Ἐγγεγράφθω ἐς τὸ ΑΒΓ τμᾶμα γνωρίμως τρίγωνον τὸ ΑΒΓ, οὗ κέντρον τοῦ βάρεος ἔστω τὸ Ε, καὶ τετμάσθω δίχα ἑκατέρα τᾶν ΑΒ, ΒΓ, καὶ ἄχθων αἱ ΚΖ, ΗΛ· διάμετροι ἄρα ἐντὶ τῶν ΑΚΒ, ΒΛΓ τμαμάτων. Ἔστω οὖν τοῦ μὲν ΑΚΒ τμάματος τὸ κέντρον τοῦ βάρεος τὸ Μ, τοῦ δὲ ΒΛΓ τὸ Ν, καὶ ἐπεζεύχθωσαν αἱ ΖΗ, ΜΝ, ΚΛ· τοῦ ἄρα ἐξ ἀμφοτέρων τῶν τμαμάτων συγκειμένου μεγέθεος τὸ κέντρον τοῦ βάρεός ἐστι τὸ Χ. Καὶ ἐπεί ἐστιν ὡς ἁ ΒΘ ποτὶ ΘΔ, οὕτως ἁ ΚΜ ποτὶ ΜΖ, καὶ συνθέντι καὶ ἐναλλὰξ ὡς ἁ ΒΔ ποτὶ ΚΖ, οὕτως ἁ ΔΘ ποτὶ ΜΖ, τετραπλασία δὲ ἁ ΒΔ τᾶς ΚΖ· τοῦτο γὰρ ἐπὶ τέλει δείκνυται, οὗ σαμεῖον Ϡ· τετραπλασίων ἄρα καὶ ἁ ΔΘ τᾶς ΜΖ· ὥστε καὶ λοιπὰ ἁ ΒΘ λοιπᾶς τᾶς ΚΜ, τουτέστι τᾶς ΣΧ, τετραπλασίων. Καὶ λοιπὰ ἄρα συναμφοτέρα ἁ ΒΣ, ΧΘ τριπλασίων τᾶς ΣΧ. Ἔστω τριπλασία ἁ ΒΣ τᾶς ΣΞ· καὶ ἁ ΧΘ ἄρα τᾶς ΞΧ ἐστὶ τριπλασία. Καὶ ἐπεὶ τετραπλασίων ἐστὶν ἁ ΒΔ τᾶς ΒΣ· καὶ γὰρ τοῦτο δείκνυται· ἁ δὲ ΒΣ τᾶς ΣΞ τριπλασίων, ἁ ΞΒ ἄρα τᾶς ΒΔ τρίτον μέρος ἐστίν. Ἔστιν δὲ καὶ ἁ ΕΔ τᾶς ΔΒ τρίτον μέρος, ἐπειδήπερ κέντρον τοῦ βάρεος τοῦ ΑΒΓ τριγώνου ἐστὶ τὸ Ε· καὶ λοιπὰ ἄρα [115] ἁ ΞΕ τρίτον μέρος τᾶς ΒΔ. Καὶ ἐπεὶ τοῦ μὲν ὅλου τμάματος κέντρον τοῦ βάρεός ἐστι τὸ Θ σαμεῖον, τοῦ δὲ ἐξ ἀμφοτέρων τῶν ΑΚΒ, ΒΛΓ τμαμάτων συγκειμένου μεγέθεος τὸ κέντρον τοῦ βάρεος τὸ Χ, τοῦ δὲ ΑΒΓ τριγώνου τὸ Ε, ἐσσεῖται ὡς τὸ ΑΒΓ τρίγωνον ποτὶ τὰ καταλειπόμενα τμάματα, οὕτως ἁ ΧΘ ποτὶ ΘΕ. Τριπλάσιον δὲ τὸ ΑΒΓ τρίγωνον τῶν τμαμάτων [ἐπειδήπερ τὸ ὅλον τμᾶμα ἐπίτριτόν ἐστι τοῦ ΑΒΓ τριγώνου]· τριπλασία ἄρα καὶ ἁ ΧΘ τᾶς ΘΕ. Ἐδείχθη δὲ ἁ ΧΘ τριπλασία καὶ τᾶς ΧΞ· πενταπλασία ἄρα ἐστὶν ἁ ΞΕ τᾶς ΕΘ, τουτέστιν ἁ ΔΕ τᾶς ΕΘ· ἴσα γάρ ἐστιν αὐτᾷ· ὥστε ἑξαπλασία ἐστὶν ἁ ΔΘ τᾶς ΘΕ. Καί ἐντι τᾶς ΔΕ τριπλασία ἁ ΒΔ· ἁμιολία ἄρα ἐντὶ ἁ ΒΘ τᾶς ΘΔ· ὅπερ ἔδει δεῖξαι.

   θ΄.

   Εἴ κα τέσσαρες γραμμαὶ ἀνάλογον ἔωντι ἐν τᾷ συνεχεῖ ἀναλογίᾳ, καὶ ὃν ἔχει λόγον ἁ ἐλαχίστα ποτὶ τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ μεγίστα τᾶς ἐλαχίστας, τοῦτον ἔχουσά τις λαφθῇ ποτὶ τὰ τρία πεμπταμόρια τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει ἁ μεγίστα τᾶν ἀνάλογον τᾶς τρίτας, ὃν δὲ ἔχει λόγον ἁ ἴσα τᾷ τε διπλασίᾳ τᾶς μεγίστας τᾶν ἀνάλογον καὶ τᾷ τετραπλασίᾳ τᾶς δευτέρας καὶ τᾷ ἑξαπλασίᾳ τᾶς τρίτας καὶ τᾷ τριπλασίᾳ τᾶς τετάρτας ποτὶ τὰν ἴσαν τᾷ τε πενταπλασίᾳ τᾶς μεγίστας καὶ τᾷ δεκαπλασίᾳ τᾶς δευτέρας καὶ τᾷ δεκαπλασίᾳ τᾶς τρίτας καὶ τᾷ πενταπλασίᾳ τᾶς τετάρτας, τοῦτον ἔχουσά τις λαφθῇ ποτὶ τὰν ὑπεροχάν, ᾇ ὑπερέχει ἁ μεγίστα τᾶν ἀνάλογον [116] τᾶς τρίτας, συναμφότεραι αἱ λαφθεῖσαι ἐσσοῦνται δύο πεμπταμόρια τᾶς μεγίστας.

   Ἔστωσαν τέσσαρες γραμμαὶ ἀνάλογον αἱ ΑΒ, ΒΓ, ΒΔ, ΒΕ, καὶ ὃν μὲν ἔχει λόγον ἁ ΒΕ ποτὶ ΕΑ, τοῦτον ἐχέτω ἁ ΖΗ ποτὶ τὰ τρία πέμπτα τᾶς ΑΔ, ὃν δὲ λόγον ἔχει ἁ ἴσα τᾷ διπλασίᾳ τᾶς ΑΒ καὶ τετραπλασίᾳ τᾶς ΒΓ καὶ ἑξαπλασίᾳ τᾶς ΒΔ καὶ τριπλασίᾳ τᾶς ΒΕ ποτὶ τὰν ἴσαν τᾷ πενταπλασίᾳ τᾶς ΑΒ καὶ δεκαπλασίᾳ τᾶς ΓΒ καὶ δεκαπλασίᾳ τᾶς ΒΔ καὶ πενταπλασίᾳ τᾶς ΒΕ, τοῦτον ἐχέτω τὸν λόγον ἁ ΗΘ ποτὶ τὰν ΑΔ. Δεικτέον ὅτι ἁ ΖΘ δύο πενταμόριά ἐντι τᾶς ΑΒ.

   Ἐπεὶ γὰρ ἀνάλογόν ἐντι αἱ ΑΒ, ΒΓ, ΒΔ, ΒΕ, καὶ αἱ ΑΓ, ΓΔ, ΔΕ ἐν τῷ αὐτῷ λόγῳ ἐντί, καὶ συναμφότερος ἁ ΑΒ, ΒΓ ποτὶ τὰν ΒΔ, τουτέστιν ἁ διπλασία συναμφοτέρου τᾶς ΑΒ, ΒΓ ποτὶ τὰν διπλασίαν τᾶς ΒΔ, ἔχει τὸν αὐτὸν λόγον, ὃν ἁ ΑΔ ποτὶ τὰν ΔΕ, καὶ συναμφότερος ἁ ΔΒ, ΒΓ ποτὶ τὰν ΕΒ, καὶ πάντα ποτὶ πάντα· τὸν αὐτὸν ἄρα λόγον ἔχει ἁ ΑΔ ποτὶ τὰν ΔΕ, ὃν ἁ ἴσα τᾷ τε διπλασίᾳ τᾶς ΑΒ καὶ τᾷ τριπλασίᾳ τᾶς ΓΒ καὶ τᾷ ΔΒ ποτὶ τὰν ἴσαν τᾷ τε διπλασίᾳ τᾶς ΒΔ καὶ τᾷ ΒΕ, ὃν δὲ λόγον ἔχει ἁ ἴσα τᾷ τε διπλασίᾳ τᾶς ΑΒ καὶ τᾷ τετραπλασίᾳ τᾶς ΒΓ καὶ τᾷ τετραπλασίᾳ τᾶς ΒΔ καὶ τᾷ διπλασίᾳ τᾶς ΒΕ ποτὶ τὰν ἴσαν τᾷ τε διπλασίᾳ τᾶς ΔΒ καὶ τᾷ ΕΒ, τοῦτον ἕξει ἁ ΔΑ ποτὶ ἐλάσσονα τᾶς ΔΕ. Ἐχέτω οὖν ποτὶ ΔΟ. Καὶ ἀμφότεραι δὲ ποτὶ τὰς πρώτας τὸν αὐτὸν ἑξοῦντι [117] λόγον· ἕξει οὖν ἁ ΟΑ ποτὶ ΑΔ τὸν αὐτὸν λόγον, ὃν ἁ ἴσα τᾷ τε διπλασίᾳ τᾶς ΑΒ καὶ τετραπλασίᾳ τᾶς ΓΒ καὶ ἑξαπλασίᾳ τᾶς ΒΔ καὶ τριπλασίᾳ τᾶς ΒΕ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας συναμφοτέρας τᾶς ΑΒ, ΕΒ καὶ τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ. Ἔχει δὲ καὶ ἁ ΑΔ ποτὶ ΗΘ τὸν αὐτὸν λόγον, ὃν ἁ πενταπλασία συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς δεκαπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΑΒ καὶ τᾶς τετραπλασίας τᾶς ΓΒ καὶ τᾶς τριπλασίας τᾶς ΕΒ καὶ ἑξαπλασίας τᾶς ΒΔ· ἀνομοίως δὲ τῶν λόγων τεταγμένων, τουτέστιν ἐν τεταραγμένᾳ ἀναλογίᾳ, δι᾿ ἴσου τὸν αὐτὸν ἔχει λόγον ἁ ΟΑ ποτὶ ΗΘ, ὃν ἁ πενταπλασία συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς δεκαπλασίας τᾶν ΓΒ, ΒΔ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒ, ΒΕ καὶ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ. Ἀλλ᾿ ἁ συγκειμένα ἔκ τε τᾶς πενταπλασίας συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς δεκαπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒ, ΒΕ καὶ τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ λόγον ἔχει, ὃν πέντε ποτὶ δύο· καὶ ἁ ΑΟ ἄρα ποτὶ ΗΘ λόγον ἔχει, ὃν πέντε ποτὶ δύο. Πάλιν, ἐπεὶ ἁ ΟΔ ποτὶ ΔΑ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ΕΒ μετὰ τᾶς διπλασίας τᾶς ΒΔ ποτὶ τὰν ἴσαν τᾷ συγκειμένᾳ ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ, ἔστιν δὲ καὶ ὡς ἁ ΑΔ ποτὶ ΔΕ, οὕτως ἁ συγκειμένα ἔκ τε τᾶς διπλασίας τᾶς ΑΒ καὶ [118] τριπλασίας τᾶς ΓΒ καὶ τᾶς ΒΔ ποτὶ τὰν ἴσαν τᾷ τε ΕΒ καὶ τᾷ διπλασίᾳ τᾶς ΒΔ, ἀνομοίως οὖν τῶν λόγων τεταγμένων, τουτέστιν τεταραγμένας ἐούσας τᾶς ἀναλογίας, δι᾿ ἴσου ὡς ἁ ΟΔ ποτὶ ΔΕ, οὕτως ἁ διπλασία τᾶς ΑΒ μετὰ τᾶς τριπλασίας τᾶς ΒΓ καὶ ἁ ΒΔ ποτὶ τὰν συγκειμέναν ἐκ τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒ, ΒΕ καὶ τᾶς τετραπλασίας τᾶν ΓΒ, ΒΔ· ὥστε καὶ ὡς ἁ ΟΕ ποτὶ ΕΔ ἐστίν, οὕτως ἁ ΓΒ μετὰ τᾶς τριπλασίας τᾶς ΒΔ καὶ διπλασίας τᾶς ΕΒ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΑΒ, ΒΕ καὶ τετραπλασίαν συναμφοτέρου τᾶς ΓΒ, ΒΔ. Ἔστιν δὲ καὶ ὡς ἁ ΔΕ ποτὶ ΕΒ, οὕτως ἅ τε ΑΓ ποτὶ ΓΒ, ἐπεὶ καὶ κατὰ σύνθεσιν, καὶ ἁ τριπλασία τᾶς ΓΔ ποτὶ τὰν τριπλασίαν τᾶς ΔΒ καὶ ἁ διπλασία τᾶς ΔΕ ποτὶ τὰν διπλασίαν τᾶς ΕΒ· ὥστε καὶ ἁ συγκειμένα ἔκ τε τᾶς ΑΓ καὶ τριπλασίας τᾶς ΓΔ καὶ διπλασίας τᾶς ΔΕ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς ΓΒ καὶ τριπλασίας τᾶς ΔΒ καὶ διπλασίας τᾶς ΕΒ. Ἀνομοίως οὖν πάλιν τῶν λόγων τεταγμένων, τουτέστιν ἐν τεταραγμένᾳ ἀναλογίᾳ, δι᾿ ἴσου τὸν αὐτὸν ἕξει λόγον ἁ ΕΟ ποτὶ ΕΒ, ὃν ἁ ΑΓ μετὰ τᾶς τριπλασίας τᾶς ΓΔ καὶ διπλασίας τᾶς ΔΕ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ· ὅλα οὖν ἁ ΟΒ ποτὶ ΒΕ τὸν αὐτὸν ἔχει λόγον, ὃν ἁ ἴσα τᾷ τε τριπλασίᾳ τᾶς ΑΒ μετὰ τᾶς ἑξαπλασίας τᾶς ΓΒ καὶ τᾷ τριπλασίᾳ τᾶς ΒΔ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΑΒ, ΒΕ μετὰ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΓΒ, ΒΔ. Καὶ ἐπεὶ [119] αἵ τε ΕΔ, ΔΓ, ΓΑ ἐν τῷ αὐτῷ λόγῳ ἐντὶ καὶ συναμφότερος ἑκάστα τᾶν ΕΒ, ΒΔ, ΔΒ, ΒΓ, ΓΒ, ΒΑ, ἐσσεῖται καὶ ὡς ἁ ΕΔ ποτὶ ΔΑ, οὕτως συναμφότερος ἁ ΕΒ, ΒΔ ποτὶ συναμφότερον τὰν ΔΒ, ΒΓ μετὰ τᾶς συναμφοτέρου τᾶς ΓΒ, ΒΑ. Καὶ συνθέντι ἄρα ἐστὶν ὡς ἁ ΑΕ ποτὶ ΑΔ, οὕτως συναμφότερος ἁ ΕΒ, ΒΔ μετὰ συναμφοτέρου τᾶς ΑΒ, ΒΓ καὶ συναμφοτέρου τᾶς ΓΒΔ, ὅ ἐστι συναμφότερος ἁ ΕΒΑ μετὰ τᾶς διπλασίας συναμφοτέρου τᾶς ΔΒΓ ποτὶ συναμφότερον τὰν ΒΔ, ΒΑ μετὰ τᾶς διπλασίας τᾶς ΒΓ· ὥστε καὶ ἁ διπλασία ποτὶ τὰν διπλασίαν τὸν αὐτὸν ἕξει λόγον, τουτέστιν ὡς ἁ ΕΑ ποτὶ ΑΔ, οὕτως ἁ διπλασία συναμφοτέρου τᾶς ΕΒΑ μετὰ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΓΒΔ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΑΒΔ μετὰ τᾶς τετραπλασίας τᾶς ΓΒ· ὥστε καὶ ὡς ἁ ΕΑ ποτὶ τὰ τρία πέμπτα τᾶς ΑΔ, οὕτως ἁ συγκειμένα ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒΕ καὶ τετραπλασίας συναμφοτέρου τᾶς ΓΒΔ ποτὶ τὰ τρία πέμπτα τᾶς συγκειμένας ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒΔ καὶ τετραπλασίας τᾶς ΓΒ. Ἀλλ᾿ ὡς ἁ ΕΑ ποτὶ τὰ τρία πέμπτα τᾶς ΑΔ, οὕτως ἐστὶν ἁ ΕΒ ποτὶ ΖΗ· καὶ ὡς ἄρα ἁ ΕΒ ποτὶ ΖΗ, οὕτως ἁ διπλασία συναμφοτέρου τᾶς ΑΒΕ μετὰ τᾶς τετραπλασίας συναμφοτέρου τᾶς ΔΒΓ ποτὶ τὰ τρία πέμπτα τᾶς συγκειμένας ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒΔ μετὰ τᾶς τετραπλασίας τᾶς ΓΒ. Ἐδείχθη δὲ καὶ ὡς ἁ ΟΒ ποτὶ ΕΒ, οὕτως ἁ τριπλασία συναμφοτέρου τᾶς ΑΒΔ μετὰ τᾶς ἑξαπλασίας τᾶς ΓΒ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΑΒΕ καὶ τετραπλασίαν συναμφοτέρου τᾶς ΓΒΔ. Καὶ δι᾿ ἴσου ἄρα [120] ἐστὶν ὡς ἁ ΟΒ ποτὶ ΖΗ, οὕτως ἁ συγκειμένα ἔκ τε τᾶς τριπλασίας συναμφοτέρου τᾶς ΑΒΔ καὶ ἑξαπλασίας τᾶς ΓΒ ποτὶ τὰ τρία πέμπτα τᾶς συγκειμένας ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒΔ καὶ τετραπλασίας τᾶς ΓΒ. Ἀλλὰ ἁ συγκειμένα ἔκ τε τᾶς τριπλασίας συναμφοτέρου τᾶς ΑΒΔ καὶ ἑξαπλασίας τᾶς ΓΒ ποτὶ μὲν τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας συναμφοτέρου τᾶς ΑΒΔ καὶ τετραπλασίας τᾶς ΓΒ λόγον ἔχει, ὃν τρία ποτὶ δύο, ποτὶ δὲ τὰ τρία πέμπτα τᾶς αὐτᾶς λόγον ἔχει, ὃν πέντε ποτὶ δύο· ἐδείχθη δὲ καὶ ἁ ΑΟ ποτὶ ΗΘ λόγον ἔχουσα, ὃν πέντε ποτὶ δύο· καὶ ὅλα ἄρα ἁ ΒΑ ποτὶ ὅλαν τὰν ΖΘ λόγον ἔχει, ὃν πέντε ποτὶ δύο. Εἰ δὲ τοῦτο, δύο πεμπταμόριά ἐντι ἁ ΖΘ τᾶς ΑΒ· ὅπερ ἔδει δεῖξαι.

   ι΄.

   Παντὸς τόμου ἀπὸ ὀρθογωνίου κώνου τομᾶς ἀφαιρουμένου τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς εὐθείας ἐστίν, ἃ διάμετρός ἐστι τοῦ τόμου, τόνδε τὸν τρόπον κείμενον· διαιρεθείσας τᾶς εὐθείας εἰς ἴσα πέντε ἐπὶ μέσου πεμπταμορίου, ὥστε τὸ τμᾶμα αὐτοῦ τὸ ἐγγύτερον τᾶς ἐλάσσονος βάσιος τοῦ τόμου ποτὶ τὸ λοιπὸν τμᾶμα τὸν αὐτὸν ἔχειν λόγον, ὃν ἔχει τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ τετράγωνον τὸ ἀπὸ τᾶς μείζονος τᾶν βάσιων τοῦ τόμου, ὕψος δὲ τὰν ἴσαν συναμφοτέρᾳ τᾷ τε διπλασίᾳ τᾶς ἐλάσσονος τᾶν βάσιων καὶ τᾷ μείζονι, ποτὶ τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ τετράγωνον τὸ ἀπὸ τᾶς ἐλάσσονος τᾶν βάσιων τοῦ [121] τόμου, ὕψος δὲ τὰν ἴσαν ἀμφοτέρᾳ τᾷ τε διπλασίᾳ τᾶς μείζονος καὶ τᾷ ἐλάσσονι αὐτᾶν.

   Ἔστωσαν ἐν ὀρθογωνίου κώνου τομᾷ δύο εὐθεῖαι αἱ ΑΓ, ΔΕ, διάμετρος δὲ ἔστω τοῦ ΑΒΓ τμάματος ἁ ΒΖ· φανερὸν δὴ ὅτι καὶ τοῦ ΑΔΕΓ τόμου διάμετρός ἐστιν ἁ ΗΖ [καὶ αἱ μὲν ΑΓ, ΔΕ παράλληλοί ἐντι τᾷ κατὰ τὸ Β ἐφαπτομένᾳ τᾶς τομᾶς]· καὶ τᾶς ΗΖ εὐθείας διαιρεθείσας εἰς πέντε ἴσα μέσον ἔστω πεμπταμόριον ἁ ΘΚ, ἁ δὲ ΘΙ ποτὶ τὰν ΙΚ τὸν αὐτὸν ἐχέτω λόγον, ὃν ἔχει τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ τᾶς ΑΖ τετράγωνον, ὕψος δὲ τὰν ἴσαν ἀμφοτέραις τᾷ τε διπλασίᾳ τᾶς ΔΗ καὶ τᾷ ΑΖ, ποτὶ τὸ στερεὸν τὸ βάσιν ἔχον τὸ ἀπὸ τᾶς ΔΗ τετράγωνον, ὕψος δὲ τὰν ἴσαν ἀμφοτέραις τᾷ διπλασίᾳ τᾶς ΑΖ καὶ τᾷ ΔΗ. Δεικτέον ὅτι τοῦ ΑΔΕΓ τόμου κέντρον ἐστὶ τοῦ βάρεος τὸ Ι σαμεῖον.

   Ἔστω δὴ τᾷ μὲν ΖΒ ἴσα ἁ ΜΝ, τᾷ δὲ ΗΒ ἴσα ἁ ΝΟ, καὶ

[122]λελάφθω τᾶν μὲν ΜΝΟ μέσα ἀνάλογον ἁ ΝΞ, τετάρτα δὲ ἀνάλογον ἁ ΤΝ, καὶ ὡς ἁ ΤΜ ποτὶ ΤΝ, οὕτως ἁ ΖΘ ποτί τινα ἀπὸ τοῦ Ι, ὅπου ἂν ἔρχηται τὸ ἕτερον σαμεῖον· οὐδὲν γὰρ διαφέρει εἴτε καὶ μεταξὺ τῶν Ζ, Η εἴτε καὶ μεταξὺ τῶν Η, Β· τὰν ΙΡ. Καὶ ἐπεὶ ἐν ὀρθογωνίου κώνου τομᾷ διάμετρός ἐστι τοῦ τμάματος ἁ ΖΒ, ἁ ΒΖ ἤτοι ἀρχικά ἐστι τᾶς τομᾶς ἢ παρὰ τὰν διάμετρον ἆκται, αἱ δὲ ΑΖ, ΔΗ εἰς αὐτὰν τεταγμένως ἐντὶ καταγμέναι, ἐπειδὴ παράλληλοί ἐντι τᾷ ἐπὶ τοῦ Β τᾶς τομᾶς ἐφαπτομένᾳ. Εἰ δὲ τοῦτο, ἔστιν ὡς ἁ ΑΖ ποτὶ ΔΗ δυνάμει, οὕτως ἁ ΖΒ ποτὶ ΒΗ μάκει, τουτέστιν ἁ ΜΝ ποτὶ ΝΟ. Ὡς δὲ ἁ ΜΝ ποτὶ ΝΟ μάκει, οὕτως ἁ ΜΝ ποτὶ ΝΞ δυνάμει· καὶ ὡς ἄρα ἁ ΑΖ ποτὶ ΔΗ δυνάμει, οὕτως ἁ ΜΝ ποτὶ ΝΞ δυνάμει· ὥστε καὶ μάκει ἐν τῷ αὐτῷ λόγῳ. Καὶ ὡς ἄρα ὁ ἀπὸ ΑΖ κύβος ποτὶ τὸν ἀπὸ ΔΗ κύβον, οὕτως ὁ ἀπὸ ΜΝ κύβος ποτὶ τὸν ἀπὸ ΝΞ κύβον. Ἀλλ᾿ ὡς μὲν ὁ ἀπὸ ΑΖ κύβος ποτὶ τὸν ἀπὸ ΔΗ κύβον, οὕτως τὸ ΑΒΓ τμᾶμα ποτὶ τὸ ΔΒΕ τμᾶμα, ὡς δὲ ὁ ἀπὸ ΜΝ κύβος ποτὶ τὸν ἀπὸ ΝΞ κύβον, οὕτως ἁ ΜΝ ποτὶ ΝΤ· ὥστε καὶ διελόντι ἐστὶν ὡς ὁ ΑΔΕΓ τόμος ποτὶ τὸ ΔΒΕ τμᾶμα, οὕτως ἁ ΜΤ ποτὶ ΝΤ, τουτέστι τὰ γ ε΄ τᾶς ΗΖ ποτὶ ΙΡ. Καὶ ἐπεὶ τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΑΖ τετράγωνον, ὕψος δὲ τὰν [123] συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΔΗ καὶ τᾶς ΑΖ, ποτὶ τὸν ἀπὸ ΑΖ κύβον λόγον ἔχει, ὃν ἁ διπλασία τᾶς ΔΗ μετὰ τᾶς ΑΖ ποτὶ ΖΑ, ὥστε καὶ ὃν ἁ διπλασία τᾶς ΝΞ μετὰ τᾶς ΝΜ ποτὶ ΝΜ, ἔστι δὲ καὶ ὡς ὁ ἀπὸ ΑΖ κύβος ποτὶ τὸν ἀπὸ ΔΗ κύβον, οὕτως ἁ ΜΝ ποτὶ ΝΤ, ὡς δὲ ὁ ἀπὸ ΔΗ κύβος ποτὶ τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΔΗ τετράγωνον, ὕψος δὲ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΑΖ μετὰ τᾶς ΔΗ, οὕτως ἁ ΔΗ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΑΖ καὶ τᾶς ΔΗ, ὥστε καὶ ἁ ΤΝ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΟΝ καὶ τᾶς ΤΝ, γέγονεν οὖν τέσσαρα μεγέθεα, τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΑΖ τετράγωνον, ὕψος δὲ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΔΗ καὶ τᾶς ΑΖ, καὶ ὁ ἀπὸ ΑΖ κύβος καὶ ὁ ἀπὸ ΔΗ κύβος καὶ τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΔΗ τετράγωνον, ὕψος δὲ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΑΖ καὶ τᾶς ΔΗ, τέτταρσι μεγέθεσιν ἀνάλογον σύνδυο λαμβανομένοις, τᾷ τε συγκειμένᾳ ἔκ τε τᾶς διπλασίας τᾶς ΝΞ καὶ τᾶς ΝΜ καὶ ἑτέρῳ μεγέθει τᾷ ΜΝ καὶ ἄλλῳ ἑξῆς τᾷ ΝΤ καὶ τελευταῖον τᾷ συγκειμένᾳ ἔκ τε τᾶς διπλασίας τᾶς ΝΟ καὶ τᾶς ΝΤ· δι᾿ ἴσου ἄρα γενήσεται ὡς τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΑΖ τετράγωνον, ὕψος δὲ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΔΗ καὶ τᾶς ΑΖ, ποτὶ τὸ στερεὸν τὸ βάσιν μὲν ἔχον τὸ ἀπὸ ΔΗ τετράγωνον, ὕψος δὲ τὰν [124] συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΑΖ καὶ τᾶς ΔΗ, οὕτως ἁ συγκειμένα ἔκ τε τᾶς διπλασίας τᾶς ΝΞ καὶ τᾶς ΜΝ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΝΟ καὶ τᾶς ΝΤ. Ἀλλ᾿ ὡς τὸ εἰρημένον στερεὸν ποτὶ τὸ εἰρημένον στερεόν, οὕτως ἁ ΘΙ ποτὶ ΙΚ· καὶ ὡς ἄρα ἁ ΘΙ ποτὶ ΙΚ, οὕτως ἁ συγκειμένα ποτὶ τὰν συγκειμέναν· Ὥστε καὶ συνθέντι καὶ τῶν ἁγουμένων τὰ πενταπλάσια· ἔστιν ἄρα ὡς ἁ ΖΗ ποτὶ ΙΚ, οὕτως ἁ πενταπλασία συναμφοτέρου τᾶς ΜΝΤ καὶ δεκαπλασία συναμφοτέρου τᾶς ΝΞ, ΝΟ ποτὶ τὰν διπλασίαν τᾶς ΟΝ καὶ τὰν ΝΤ. Καὶ ὡς ἁ ΖΗ ποτὶ ΖΚ ἐοῦσαν αὐτᾶς δύο πέμπτα, οὕτως ἁ πενταπλασία συναμφοτέρου τᾶς ΜΝΤ καὶ δεκαπλασία συναμφοτέρου τᾶς ΞΝΟ ποτὶ τὰν διπλασίαν συναμφοτέρου τᾶς ΜΝΤ καὶ τετραπλασίαν συναμφοτέρου τᾶς ΞΝΟ· ἐσσεῖται οὖν ὡς ἁ ΖΗ ποτὶ ΖΙ, οὕτως ἁ πενταπλασία συναμφοτέρου τᾶς ΜΝΤ καὶ δεκαπλασία συναμφοτέρου τᾶς ΞΝΟ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς διπλασίας τᾶς ΜΝ καὶ τετραπλασίας τᾶς ΝΞ καὶ ἑξαπλασίας τᾶς ΟΝ καὶ τριπλασίας τᾶς ΝΤ. Ἐπεὶ οὖν τέσσαρες εὐθεῖαι ἑξῆς ἀνάλογον αἱ ΜΝ, ΝΞ, ΟΝ, ΝΤ, καί ἐστιν, ὡς μὲν ἁ ΝΤ ποτὶ ΤΜ, οὕτως λελαμμένα τις ἁ ΡΙ ποτὶ τὰ τρία πέμπτα τᾶς ΖΗ, τουτέστι τᾶς ΜΟ, ὡς δὲ ἁ συγκειμένα ἔκ τε τᾶς διπλασίας τᾶς ΝΜ καὶ τετραπλασίας τᾶς ΝΞ καὶ ἑξαπλασίας τᾶς ΝΟ καὶ τριπλασίας τᾶς ΝΤ ποτὶ τὰν συγκειμέναν ἔκ τε τᾶς πενταπλασίας συναμφοτέρου τᾶς ΜΝΤ καὶ δεκαπλασίας συναμφοτέρου τᾶς ΞΝΟ, οὕτως ἑτέρα τις [125] λελαμμένα ἁ ΙΖ ποτὶ τὰν ΖΗ, τουτέστιν ποτὶ τὰν ΜΟ, ἐσσεῖται διὰ τὰ πρότερον ἁ ΡΖ δύο πέμπτα τᾶς ΜΝ, τουτέστι τᾶς ΖΒ· ὥστε κέντρον βάρεός ἐστι τοῦ ΑΒΓ τμάματος τὸ Ρ σαμεῖον. Ἔστω δὴ καὶ τοῦ ΔΒΕ τμάματος κέντρον βάρεος τὸ Χ σαμεῖον. Τοῦ ἄρα ΑΔΕΓ τόμου ἐσσεῖται τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ἐπ᾿ εὐθείας τᾷ ΧΡ τὸν αὐτὸν ποτὶ αὐτὰν λόγον ἐχούσας, ὃν ἔχει ὁ τόμος ποτὶ τὸ λοιπὸν τμᾶμα. Ἔστιν δὲ τὸ Ι σαμεῖον. Ἐπεὶ γὰρ τᾶς μὲν ΖΒ τρία πέμπτα ἐστὶν ἁ ΒΡ, τᾶς δὲ ΗΒ τρία πέμπτα ἐστὶν ἁ ΒΧ, καὶ λοιπᾶς ἄρα τᾶς ΗΖ τρία πέμπτα ἐστὶν ἁ ΧΡ. Ἐπεὶ οὖν ἐστιν ὡς μὲν ὁ ΑΔΕΓ τόμος ποτὶ τὸ ΔΒΕ τμᾶμα, οὕτως ἁ ΜΤ ποτὶ ΤΝ, ὡς δὲ ἁ ΜΤ ποτὶ τὰν ΤΝ, οὕτως τὰ τρία πέμπτα τᾶς ΗΖ, ἅτις ἐστὶν ἁ ΧΡ, ποτὶ ΡΙ, ἐσσεῖται ἄρα καὶ ὡς ὁ ΑΔΕΓ τόμος ποτὶ τὸ ΔΒΕ τμᾶμα, οὕτως ἁ ΧΡ ποτὶ ΡΙ. Καί ἐστι τοῦ μὲν ὅλου τμάματος κέντρον τοῦ βάρεος τὸ Ρ σαμεῖον, τοῦ δὲ ΔΒΕ κέντρον βάρεος τὸ Χ· φανερὸν οὖν ὅτι καὶ τοῦ ΑΔΕΓ τόμου τὸ κέντρον τοῦ βάρεος τὸ Ι σαμεῖον.

 

---

     

ΨΑΜΜΙΤΗΣ

[134]    Οἴονταί τινες, βασιλεῦ Γέλων, τοῦ ψάμμου τὸν ἀριθμὸν ἄπειρον εἶμεν τῷ πλήθει· λέγω δὲ οὐ μόνον τοῦ περὶ Συρακούσας τε καὶ τὰν ἄλλαν Σικελίαν ὑπάρχοντος, ἀλλὰ καὶ τοῦ κατὰ πᾶσαν χώραν τάν τε οἰκημέναν καὶ τὰν ἀοίκητον. Ἐντί τινες δέ, οἳ αὐτὸν ἄπειρον μὲν εἶμεν οὐχ ὑπολαμβάνοντι, μηδένα μέντοι ταλικοῦτον κατωνομασμένον ὑπάρχειν ἀριθμόν, ὅστις ὑπερβάλλει τὸ πλῆθος αὐτοῦ. Οἱ δὲ οὕτως δοξάζοντες δῆλον ὡς, εἰ νοήσαιεν ἐκ τοῦ ψάμμου ταλικοῦτον ὄγκον συγκείμενον τὸ μέγεθος, ἁλίκος ὁ τᾶς γᾶς ὄγκος ἀναπεπληρωμένων ἐν αὐτῷ τῶν τε πελάγεων πάντων καὶ τῶν κοιλωμάτων τᾶς γᾶς εἰς ἴσον ὕψος τοῖς ὑψηλοτάτοις τῶν ὀρέων, πολλαπλασίως μὴ γνώσονται μηδένα κα ῥηθῆμεν ἀριθμὸν ὑπερβάλλοντα τὸ πλῆθος αὐτοῦ. Ἐγὼ δὲ πειρασοῦμαί τοι δεικνύειν δι᾿ ἀποδείξιων γεωμετρικᾶν, αἷς παρακολουθήσεις, ὅτι τῶν ὑφ᾿ ἁμῶν κατωνομασμένων ἀριθμῶν καὶ ἐκδεδομένων ἐν τοῖς ποτὶ Ζεύξιππον γεγραμμένοις ὑπερβάλλοντί τινες οὐ μόνον τὸν ἀριθμὸν τοῦ ψάμμου τοῦ μέγεθος ἔχοντος [135] ἴσον τᾷ γᾷ πεπληρωμένᾳ, καθάπερ εἴπαμες, ἀλλὰ καὶ τὸν τοῦ μέγεθος ἴσον ἔχοντος τῷ κόσμῳ. Κατέχεις δὲ διότι καλεῖται κόσμος ὑπὸ μὲν τῶν πλείστων ἀστρολόγων ἁ σφαῖρα, ἇς ἐστι κέντρον μὲν τὸ τᾶς γᾶς κέντρον, ἁ δὲ ἐκ τοῦ κέντρου ἴσα τᾷ εὐθείᾳ τᾷ μεταξὺ τοῦ κέντρου τοῦ ἁλίου καὶ τοῦ κέντρου τᾶς γᾶς· ταῦτα γὰρ ἐν ταῖς γραφομέναις παρὰ τῶν ἀστρολόγων δείξεσι διάκουσας. Ἀρίσταρχος δὲ ὁ Σάμιος ὑποθέσιών τινων ἐξέδωκεν γραφάς, ἐν αἷς ἐκ τῶν ὑποκειμένων συμβαίνει τὸν κόσμον πολλαπλάσιον εἶμεν τοῦ νῦν εἰρημένου. Ὑποτίθεται γὰρ τὰ μὲν ἀπλανέα τῶν ἄστρων καὶ τὸν ἅλιον μένειν ἀκίνητον, τὰν δὲ γᾶν περιφέρεσθαι περὶ τὸν ἅλιον κατὰ κύκλου περιφέρειαν, ὅς ἐστιν ἐν μέσῳ τῷ δρόμῳ κείμενος, τὰν δὲ τῶν ἀπλανέων ἄστρων σφαῖραν περὶ τὸ αὐτὸ κέντρον τῷ ἁλίῳ κειμέναν τῷ μεγέθει τηλικαύταν εἶμεν, ὥστε τὸν κύκλον, καθ᾿ ὃν τὰν γᾶν ὑποτίθεται περιφέρεσθαι, τοιαύταν ἔχειν ἀναλογίαν ποτὶ τὰν τῶν ἀπλανέων ἀποστασίαν, οἵαν ἔχει τὸ κέντρον τᾶς σφαίρας ποτὶ τὰν ἐπιφάνειαν. Τοῦτό γ᾿ εὔδηλον ὡς ἀδύνατόν ἐστιν· ἐπεὶ γὰρ τὸ τᾶς σφαίρας κέντρον οὐδὲν ἔχει μέγεθος, οὐδὲ λόγον ἔχειν οὐδένα ποτὶ τὰν ἐπιφάνειαν τᾶς σφαίρας ὑπολαπτέον αὐτό. Ἐκδεκτέον δὲ τὸν Ἀρίσταρχον διανοεῖσθαι τόδε· ἐπειδὴ τὰν γᾶν ὑπολαμβάνομες ὥσπερ εἶμεν τὸ κέντρον τοῦ κόσμου, ὃν ἔχει λόγον ἁ γᾶ ποτὶ τὸν ὑφ᾿ ἁμῶν εἰρημένον κόσμον, τοῦτον ἔχειν τὸν λόγον τὰν σφαῖραν, ἐν ᾇ ἐστιν ὁ κύκλος, καθ᾿ ὃν τὰν γᾶν ὑποτίθεται περιφέρεσθαι, ποτὶ τὰν τῶν ἀπλανέων ἄστρων [136] σφαῖραν· τὰς γὰρ ἀποδείξιας τῶν φαινομένων οὕτως ὑποκειμένῳ ἐναρμόζει, καὶ μάλιστα φαίνεται τὸ μέγεθος τᾶς σφαίρας, ἐν ᾇ ποιεῖται τὰν γᾶν κινουμέναν, ἴσον ὑποτίθεσθαι τῷ ὑφ᾿ ἁμῶν εἰρημένῳ κόσμῳ. Φαμὲς δή, καὶ εἰ γένοιτο ἐκ τοῦ ψάμμου σφαῖρα τηλικαύτα τὸ μέγεθος, ἁλίκαν Ἀρίσταρχος ὑποτίθεται τὰν τῶν ἀπλανέων ἄστρων σφαῖραν εἶμεν, καὶ οὕτως τινὰς δειχθήσειν τῶν ἐν ἀρχᾷ ἀριθμῶν τῶν κατονομαξίαν ἐχόντων ὑπερβάλλοντας τῷ πλήθει τὸν ἀριθμὸν τὸν τοῦ ψάμμου τοῦ μέγεθος ἔχοντος ἴσον τᾷ εἰρημένᾳ σφαίρᾳ, ὑποκειμένων τῶνδε· πρῶτον μὲν τὰν περίμετρον τᾶς γᾶς εἶμεν ὡς τ μυριάδων σταδίων καὶ μὴ μείζω, καίπερ τινῶν πεπειραμένων ἀποδεικνύειν, καθὼς καὶ τὺ παρακολουθεῖς, ἐοῦσαν αὐτὰν ὡς λ μυριάδων σταδίων. Ἐγὼ δ᾿ ὑπερβαλλόμενος καὶ θεὶς τὸ μέγεθος τᾶς γᾶς ὡς δεκαπλάσιον τοῦ ὑπὸ τῶν προτέρων δεδοξασμένου τὰν περίμετρον αὐτᾶς ὑποτίθεμαι εἶμεν ὡς τ μυριάδων σταδίων καὶ μὴ μείζω· μετὰ δὲ τοῦτο τὰν διάμετρον τᾶς γᾶς μείζονα εἶμεν τᾶς διαμέτρου τᾶς σελήνας, καὶ τὰν διάμετρον τοῦ ἁλίου μείζονα εἶμεν τᾶς διαμέτρου τᾶς γᾶς, ὁμοίως τὰ αὐτὰ λαμβάνων τοῖς πλείστοις τῶν προτέρων ἀστρολόγων· μετὰ δὲ ταῦτα τὰν διάμετρον τοῦ ἁλίου τᾶς διαμέτρου τᾶς σελήνας ὡς τριακονταπλασίαν εἶμεν καὶ μὴ μείζονα, καίπερ τῶν [137] προτέρων ἀστρολόγων Εὐδόξου μὲν ὡς ἐννεαπλασίονα ἀποφαινομένου, Φειδία δὲ τοῦ ἁμοῦ πατρὸς ὡς δὴ δωδεκαπλασίαν, Ἀριστάρχου δὲ πεπειραμένου δεικνύειν ὅτι ἐστὶν ἁ διάμετρος τοῦ ἁλίου τᾶς διαμέτρου τᾶς σελήνας μείζων μὲν ἢ ὀκτωκαιδεκαπλασίων, ἐλάττων δὲ ἢ εἰκοσαπλασίων· ἐγὼ δὲ ὑπερβαλλόμενος καὶ τοῦτον, ὅπως τὸ προκείμενον ἀναμφιλόγως ᾖ δεδειγμένον, ὑποτίθεμαι τὰν διάμετρον τοῦ ἁλίου τᾶς διαμέτρου τᾶς σελήνας ὡς τριακονταπλασίαν εἶμεν καὶ μὴ μείζονα· ποτὶ δὲ τούτοις τὰν διάμετρον τοῦ ἁλίου μείζονα εἶμεν τᾶς τοῦ χιλιαγώνου πλευρᾶς τοῦ εἰς τὸν μέγιστον κύκλον ἐγγραφομένου τῶν ἐν τῷ κόσμῳ. Τοῦτο δὲ ὑποτίθεμαι Ἀριστάρχου μὲν εὑρηκότος τοῦ κύκλου τῶν ζῳδίων τὸν ἅλιον φαινόμενον ὡς τὸ εἰκοστὸν καὶ ἑπτακοσιοστόν, αὐτὸς δὲ ἐπισκεψάμενος τόνδε τὸν τρόπον ἐπειράθην ὀργανικῶς λαβεῖν τὰν γωνίαν, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει. Τὸ μὲν οὖν ἀκριβὲς λαβεῖν οὐκ εὐχερές ἐστι διὰ τὸ μήτε τὰν ὄψιν μήτε τὰς χεῖρας μήτε τὰ ὄργανα, δι᾿ ὧν δεῖ λαβεῖν, ἀξιόπιστα εἶμεν τὸ ἀκριβὲς ἀποφαίνεσθαι· περὶ δὲ τούτων ἐπὶ τοῦ παρόντος οὐκ εὔκαιρον μακύνειν ἄλλως τε καὶ πλεονάκις τοιούτων ἐμπεφανισμένων· ἀποχρὴ δέ μοι ἐς τὰν ἀπόδειξιν τοῦ προκειμένου γωνίαν λαβεῖν, ἅτις ἐστὶ μὴ μείζων τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει, καὶ πάλιν [138] ἄλλαν γωνίαν λαβεῖν, ἅτις ἐστὶν οὐκ ἐλάττων τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει. Τεθέντος οὖν μακροῦ κανόνος ἐπὶ πόδα ὀρθὸν ἐν τόπῳ κείμενον, ὅθεν ἤμελλεν ἀνατέλλων ὁ ἅλιος ὁρᾶσθαι, καὶ κυλίνδρου μικροῦ τορνευθέντος καὶ τεθέντος ἐπὶ τὸν κανόνα ὀρθοῦ εὐθέως μετὰ τὰν ἀνατολὰν τοῦ ἁλίου, ἔπειτ᾿ ἐόντος αὐτοῦ ποτὶ τῷ ὁρίζοντι καὶ δυναμένου ἀντιβλέπεσθαι ἐπεστράφη ὁ κανὼν εἰς τὸν ἅλιον, καὶ ἁ ὄψις κατεστάθη ἐπὶ τὸ ἄκρον τοῦ κανόνος· ὁ δὲ κύλινδρος ἐν μέσῳ κείμενος τοῦ τε ἁλίου καὶ τᾶς ὄψιος ἐπεσκότει τῷ ἁλίῳ. Ἀποχωριζόμενος οὖν [τοῦ κυλίνδρου] ἀπὸ τᾶς ὄψιος, ἐν ᾧ ἄρξατο παραφαίνεσθαι τοῦ ἁλίου μικρὸν ἐφ᾿ ἑκάτερα τοῦ κυλίνδρου, κατεστάθη ὁ κύλινδρος. Εἰ μὲν οὖν συνέβαινεν τὰν ὄψιν ἀφ᾿ ἑνὸς σαμείου βλέπειν, εὐθειᾶν ἀχθεισᾶν ἀπ᾿ ἄκρου τοῦ κανόνος, ἐν ᾧ τόπῳ ἁ ὄψις κατεστάθη, ἐπιψαυουσᾶν τοῦ κυλίνδρου ἁ περιεχομένα γωνία ὑπὸ τᾶν ἀχθεισᾶν ἐλάσσων κα ἦς τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει, διὰ τὸ παραβλέπεσθαί τι τοῦ ἁλίου ἐφ᾿ ἑκάτερα τοῦ κυλίνδρου· ἐπεὶ δ᾿ αἱ ὄψιες οὐκ ἀφ᾿ ἑνὸς σαμείου βλέποντι, ἀλλὰ ἀπό τινος μεγέθεος, ἐλάφθη τι μέγεθος στρογγύλον οὐκ ἔλαττον ὄψιος, καὶ τεθέντος τοῦ μεγέθεος ἐπὶ τὸ [139] ἄκρον τοῦ κανόνος, ἐν ᾧ τόπῳ ἁ ὄψις κατεστάθη, ἀχθεισᾶν εὐθειᾶν ἐπιψαυουσᾶν τοῦ τε μεγέθεος καὶ τοῦ κυλίνδρου ἁ οὖν περιεχομένα γωνία ὑπὸ τᾶν ἀχθεισᾶν ἐλάττων ἦς τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει. Τὸ δὲ μέγεθος τὸ οὐκ ἔλαττον τᾶς ὄψιος τόνδε τὸν τρόπον εὑρίσκεται· δύο κυλίνδρια λαμβάνεται λεπτὰ ἰσοπαχέα ἀλλάλοις, τὸ μὲν λευκόν, τὸ δὲ οὔ, καὶ προτίθενται πρὸ τᾶς ὄψιος, τὸ μὲν λευκὸν ἀφεστακὸς ἀπ᾿ αὐτᾶς, τὸ δὲ οὐ λευκὸν ὡς ἔστιν ἐγγυτάτω τᾶς ὄψιος, ὥστε καὶ θιγγάνειν τοῦ προσώπου. Εἰ μὲν οὖν κα τὰ λαφθέντα κυλίνδρια λεπτότερα ἔωντι τᾶς ὄψιος, περιλαμβάνεται ὑπὸ τᾶς ὄψιος τὸ ἐγγὺς κυλίνδριον καὶ ὁρῆται ὑπὸ αὐτᾶς τὸ λευκόν, εἰ μέν κα παρὰ πολὺ λεπτότερα ἔωντι, πᾶν, εἰ δέ κα μὴ παρὰ πολύ, μέρεά τινα τοῦ λευκοῦ ὁρῶνται ἐφ᾿ ἑκάτερα τοῦ ἐγγὺς τᾶς ὄψιος, λαφθέντων δὲ τῶνδε τῶν κυλινδρίων ἐπιταδείων πως τῷ πάχει ἐπισκοτεῖ τὸ ἕτερον αὐτῶν τῷ ἑτέρῳ καὶ οὐ πλείονι τόπῳ· τὸ δὴ ταλικοῦτον μέγεθος, ἁλίκον ἐστὶ τὸ πάχος τῶν κυλινδρίων τῶν τοῦτο ποιούντων, μάλιστά πώς ἐστιν οὐκ ἔλαττον τᾶς ὄψιος. Ἁ δὲ γωνία ἁ οὐκ ἐλάττων τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει, οὕτως ἐλάφθη· ἀποσταθέντος ἐπὶ τοῦ κανονίου τοῦ κυλίνδρου ἀπὸ τᾶς ὄψιος οὕτως, ὡς ἐπισκοτεῖν τὸν [140] κύλινδρον ὅλῳ τῷ ἁλίῳ, καὶ ἀχθεισᾶν εὐθειᾶν ἀπ᾿ ἄκρου τοῦ κανόνος, ἐν ᾧ τόπῳ ἁ ὄψις κατεστάθη, ἐπιψαυουσᾶν τοῦ κυλίνδρου ἁ περιεχομένα γωνία ὑπὸ τᾶν ἀχθεισᾶν εὐθειᾶν οὐκ ἐλάττων γίνεται τᾶς γωνίας, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει. Ταῖς δὴ γωνίαις ταῖς οὕτως λαφθείσαις καταμετρηθείσας ὀρθᾶς γωνίας ἐγένετο ἁ ἐν στίγῳ διαιρεθείσας τᾶς ὀρθᾶς εἰς ρξδ ἐλάττων ἢ ἓν μέρος τούτων, ἁ δὲ ἐλάττων διαιρεθείσας τᾶς ὀρθᾶς εἰς σ μείζων ἢ ἓν μέρος τούτων· δῆλον οὖν ὅτι καὶ ἁ γωνία, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει, ἐλάττων μέν ἐστιν ἢ διαιρεθείσας τᾶς ὀρθᾶς εἰς ρξδ τούτων ἓν μέρος, μείζων δὲ ἢ διαιρεθείσας τᾶς ὀρθᾶς εἰς σ τούτων ἓν μέρος. Πεπιστευμένων δὲ τούτων δείκνυται ἁ διάμετρος τοῦ ἁλίου μείζων ἐοῦσα τᾶς τοῦ χιλιαγώνου πλευρᾶς τοῦ εἰς τὸν μέγιστον κύκλον ἐγγραφομένου τῶν ἐν τῷ κόσμῳ. Νοείσθω γὰρ ἐπίπεδον ἐκβεβλημένον διά τε τοῦ κέντρου τοῦ ἁλίου καὶ τοῦ κέντρου τᾶς γᾶς καὶ διὰ τᾶς ὄψιος, μικρὸν ὑπὲρ τὸν ὁρίζοντα ἐόντος τοῦ ἁλίου, τεμνέτω δὲ τὸ ἐκβληθὲν ἐπίπεδον τὸν μὲν κόσμον κατὰ τὸν ΑΒΓ κύκλον, τὰν δὲ γᾶν κατὰ τὸν ΔΕΖ, τὸν δὲ ἅλιον κατὰ τὸν ΣΗ κύκλον, κέντρον δὲ ἔστω τᾶς μὲν γᾶς τὸ Θ, τοῦ δὲ ἁλίου τὸ Κ, ὄψις δὲ ἔστω τὸ Δ, καὶ ἄχθωσαν εὐθεῖαι ἐπιψαύουσαι τοῦ ΣΗ κύκλου ἀπὸ μὲν τοῦ Δ αἱ ΔΛ, ΔΞ, ἐπιψαυόντων δὲ κατὰ τὸ Ν καὶ τὸ Τ, ἀπὸ δὲ τοῦ Θ αἱ ΘΜ, ΘΟ, ἐπιψαυόντων δὲ κατὰ τὸ Χ καὶ τὸ Ρ, τὸν δὲ ΑΒΓ κύκλον τεμνόντων αἱ ΘΜ, ΘΟ κατὰ τὸ [141] Α καὶ τὸ Β· ἔστι δὴ μείζων ἁ ΘΚ τᾶς ΔΚ, ἐπεὶ ὑπόκειται ὁ ἅλιος ὑπὲρ τὸν ὁρίζοντα εἶμεν· ὥστε ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΔΛ, ΔΞ μείζων ἐστὶ τᾶς γωνίας τᾶς περιεχομένας ὑπὸ τᾶν ΘΜ, ΘΟ. Ἁ δὲ περιεχομένα γωνία ὑπὸ τᾶν ΔΛ, ΔΞ μείζων μέν ἐστιν ἢ διακοσιοστὸν μέρος ὀρθᾶς, ἐλάττων δὲ ἢ τᾶς ὀρθᾶς διαιρεθείσας εἰς ρξδ τούτων ἓν μέρος· ἴσα γάρ ἐστιν τᾷ γωνίᾳ, εἰς ἃν ὁ ἅλιος ἐναρμόζει τὰν κορυφὰν ἔχουσαν ποτὶ τᾷ ὄψει· ὥστε ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΘΜ, ΘΟ ἐλάττων ἐστὶν ἢ τᾶς ὀρθᾶς διαιρεθείσας εἰς ρξδ τούτων ἓν μέρος, ἁ δὲ ΑΒ εὐθεῖα ἐλάττων ἐστὶ τᾶς ὑποτεινούσας ἓν τμᾶμα διαιρεθείσας τᾶς τοῦ ΑΒΓ κύκλου περιφερείας ἐς χνϚ. Ἁ δὲ τοῦ εἰρημένου πολυγωνίου περίμετρος ποτὶ τὰν ἐκ τοῦ κέντρου τοῦ ΑΒΓ κύκλου ἐλάττονα λόγον ἔχει ἢ τὰ μδ ποτὶ τὰ ζ διὰ τὸ παντὸς πολυγωνίου ἐγγεγραμμένου ἐν κύκλῳ [142] τὰν περίμετρον ποτὶ τὰν ἐκ τοῦ κέντρου ἐλάττονα λόγον ἔχειν ἢ τὰ μδ ποτὶ τὰ ζ· ἐπίστασαι γὰρ δεδειγμένον ὑφ᾿ ἁμῶν ὅτι παντὸς κύκλου ἁ περιφέρεια μείζων ἐστὶν ἢ τριπλασίων τᾶς διαμέτρου ἐλάσσονι ἢ ἑβδόμῳ μέρει, ταύτας δὲ ἐλάττων ἐστὶν ἁ περίμετρος τοῦ ἐγγραφέντος πολυγωνίου· ἐλάττω οὖν λόγον ἔχει ἁ ΒΑ ποτὶ τὰν ΘΚ ἢ τὰ ια ποτὶ τὰ Ϛαρμη· ὥστε ἐλάττων ἐστὶν ἁ ΒΑ τᾶς ΘΚ ἢ ἑκατοστὸν μέρος. Τᾷ δὲ ΒΑ ἴσα ἐστὶν ἁ διάμετρος τοῦ ΣΗ κύκλου, διότι καὶ ἁ ἡμίσεια αὐτᾶς ἁ ΦΑ ἴσα ἐστὶ τᾷ ΚΡ· ἰσᾶν γὰρ ἐουσᾶν τᾶν ΘΚ, ΘΑ ἀπὸ τῶν περάτων κάθετοι ἐπιζεύγνυνται ὑπὸ τὰν αὐτὰν γωνίαν· δῆλον οὖν ὅτι ἁ διάμετρος τοῦ ΣΗ κύκλου ἐλάττων ἐστὶν ἢ ἑκατοστὸν μέρος τᾶς ΘΚ. Καὶ ἁ ΕΘΥ διάμετρος ἐλάττων ἐστὶ τᾶς διαμέτρου τοῦ ΣΗ κύκλου, ἐπεὶ ἐλάττων ἐστὶν ὁ ΔΕΖ κύκλος τοῦ ΣΗ κύκλου· ἐλάττονες ἄρα ἐντὶ ἀμφότεραι αἱ ΘΥ, ΚΣ ἢ ἑκατοστὸν μέρος τᾶς ΘΚ· ὥστε ἁ ΘΚ ποτὶ τὰν ΥΣ ἐλάττονα λόγον ἔχει ἢ τὰ ρ ποτὶ τὰ Ϟθ. Καὶ ἐπεὶ ἁ μὲν ΘΚ οὐκ ἐλάττων ἐστὶ τᾶς ΘΡ, ἁ δὲ ΣΥ ἐλάττων τᾶς ΔΤ, ἐλάττω ἄρα κα λόγον ἔχοι ἁ ΘΡ ποτὶ τὰν ΔΤ ἢ τὰ ρ ποτὶ τὰ Ϟθ. Ἐπεὶ δὲ τῶν ΘΚΡ, ΔΚΤ ὀρθογωνίων ἐόντων αἱ μὲν ΚΡ, ΚΤ πλευραὶ ἴσαι ἐντὶ, αἱ δὲ ΘΡ, ΔΤ ἀνίσοι καὶ μείζων ἁ ΘΡ, ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΔΤ, ΔΚ ποτὶ τὰν γωνίαν τὰν περιεχομέναν ὑπὸ τᾶν ΘΡ, ΘΚ μείζονα μὲν ἔχει λόγον ἢ ἁ ΘΚ ποτὶ τὰν ΔΚ, [143] ἐλάττω δὲ ἢ ἁ ΘΡ ποτὶ τὰν ΔΤ· εἰ γάρ κα δυῶν τριγώνων ὀρθογωνίων αἱ μὲν ἅτεραι πλευραὶ αἱ περὶ τὰν ὀρθὰν γωνίαν ἴσαι ἔωντι, αἱ δὲ ἅτεραι ἄνισοι, ἁ μείζων γωνία τᾶν ποτὶ ταῖς ἀνίσοις πλευραῖς ποτὶ τὰν ἐλάττονα μείζονα μὲν ἔχει λόγον ἢ ἁ μείζων γραμμὰ τᾶν ὑπὸ τὰν ὀρθὰν γωνίαν ὑποτεινουσᾶν ποτὶ τὰν ἐλάττονα, ἐλάττονα δὲ ἢ ἁ μείζων γραμμὰ τᾶν περὶ τὰν ὀρθὰν γωνίαν ποτὶ τὰν ἐλάττονα. Ὥστε ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΔΛ, ΔΞ ποτὶ τὰν γωνίαν τὰν περιεχομέναν ὑπὸ τᾶν ΘΟ, ΘΜ ἐλάττω λόγον ἔχει ἢ ἁ ΘΡ ποτὶ τὰν ΔΤ, ἅτις ἐλάττω λόγον ἔχει ἢ τὰ ρ ποτὶ τὰ Ϟθ· ὥστε καὶ ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΔΛ, ΔΞ ποτὶ τὰν γωνίαν τὰν περιεχομέναν ὑπὸ τᾶν ΘΜ, ΘΟ ἐλάττω λόγον ἔχει ἢ τὰ ρ ποτὶ τὰ Ϟθ. Καὶ ἐπεί ἐστιν ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΔΛ, ΔΞ μείζων ἢ διακοσιοστὸν μέρος ὀρθᾶς, εἴη κα ἁ γωνία ἁ περιεχομένα ὑπὸ τᾶν ΘΜ, ΘΟ μείζων ἢ τᾶς ὀρθᾶς διαιρεθείσας ἐς δισμύρια τούτων Ϟθ μέρεα· ὥστε μείζων ἐστὶν ἢ διαιρεθείσας τᾶς ὀρθᾶς εἰς σ καὶ γ τούτων ἓν μέρος. Ἁ ἄρα ΒΑ μείζων ἐστὶ τᾶς ὑποτεινούσας ἓν τμᾶμα διῃρημένας τᾶς τοῦ ΑΒΓ κύκλου περιφερείας εἰς ωιβ. Τᾷ δὲ ΑΒ ἴσα ἐντὶ ἁ τοῦ ἁλίου διάμετρος· δῆλον οὖν ὅτι μείζων ἐστὶν ἁ τοῦ ἁλίου διάμετρος τᾶς τοῦ χιλιαγώνου πλευρᾶς.

   Τούτων δὲ ὑποκειμένων δείκνυται καὶ τάδε· οἷον ἁ διάμετρος τοῦ κόσμου τᾶς διαμέτρου τᾶς γᾶς ἐλάττων ἐστὶν ἢ μυριοπλασίων, καὶ ἔτι ἁ διάμετρος τοῦ κόσμου ἐλάττων ἐστὶν ἢ σταδίων μυριάκις μυριάδες ρ. Ἐπεὶ γὰρ ὑπόκειται τὰν διάμετρον τοῦ ἁλίου μὴ μείζω εἶμεν ἢ [144] τριακονταπλασίονα τᾶς διαμέτρου τᾶς σελήνας, τὰν δὲ διάμετρον τᾶς γᾶς μείζω εἶμεν τᾶς διαμέτρου τᾶς σελήνας, δῆλον ὡς ἁ διάμετρος τοῦ ἁλίου ἐλάττων ἐστὶν ἢ τριακονταπλασίων τᾶς διαμέτρου τᾶς γᾶς. Πάλιν δέ, ἐπεὶ ἐδείχθη ἁ διάμετρος τοῦ ἁλίου μείζων ἐοῦσα τᾶς τοῦ χιλιαγώνου πλευρᾶς τοῦ εἰς τὸν μέγιστον κύκλον ἐγγραφομένου τῶν ἐν τῷ κόσμῳ, φανερὸν ὅτι ἁ τοῦ χιλιαγώνου περίμετρος τοῦ εἰρημένου ἐλάττων ἐστὶν ἢ χιλιοπλασίων τᾶς διαμέτρου τοῦ ἁλίου. Ἁ δὲ διάμετρος τοῦ ἁλίου ἐλάττων ἐστὶν ἢ τριακονταπλασίων τᾶς διαμέτρου τᾶς γᾶς· ὥστε ἁ περίμετρος τοῦ χιλιαγώνου ἐλάττων ἐστὶν ἢ τρισμυριοπλασίων τᾶς διαμέτρου τᾶς γᾶς. Ἐπεὶ οὖν ἁ περίμετρος τοῦ χιλιαγώνου τᾶς μὲν διαμέτρου τᾶς γᾶς ἐλάττων ἐστὶν ἢ τρισμυριοπλασίων, τᾶς δὲ διαμέτρου τοῦ κόσμου μείζων ἢ τριπλασίων· δέδεικται γάρ τοι διότι παντὸς κύκλου ἁ διάμετρος ἐλάττων ἐστὶν ἢ τρίτον μέρος παντὸς πολυγωνίου τᾶς περιμέτρου, ὅ κα ἰσόπλευρον ᾖ καὶ πολυγωνότερον τοῦ ἑξαγώνου ἐγγεγραμμένον ἐν τῷ κύκλῳ· εἴη κα ἁ διάμετρος τοῦ κόσμου ἐλάττων ἢ μυριοπλασίων τᾶς διαμέτρου τᾶς γᾶς. Ἁ μὲν οὖν διάμετρος τοῦ κόσμου ἐλάττων ἐοῦσα ἢ μυριοπλασίων τᾶς διαμέτρου τᾶς γᾶς δέδεικται· ὅτι δὲ ἐλάττων ἐστὶν ἁ διάμετρος τοῦ κόσμου ἢ σταδίων μυριάκις μυριάδες ρ ἐκ τούτου δῆλον· ἐπεὶ γὰρ ὑπόκειται τὰν περίμετρον τᾶς γᾶς μὴ μείζονα εἶμεν ἢ τριακοσίας μυριάδας σταδίων, ἁ δὲ περίμετρος τᾶς γᾶς μείζων ἐστὶν [145] ἢ τριπλασία τᾶς διαμέτρου διὰ τὸ παντὸς κύκλου τὰν περιφέρειαν μείζονα εἶμεν ἢ τριπλασίονα τᾶς διαμέτρου, δῆλον ὡς ἁ διάμετρος τᾶς γᾶς ἐλάττων ἐστὶν ἢ σταδίων ρ μυριάδες. Ἐπεὶ οὖν ἁ τοῦ κόσμου διάμετρος ἐλάττων ἐστὶν ἢ μυριοπλασίων τᾶς διαμέτρου τᾶς γᾶς, δῆλον ὡς ἁ τοῦ κόσμου διάμετρος ἐλάττων ἐστὶν ἢ σταδίων μυριάκις μυριάδες ρ. Περὶ μὲν οὖν τῶν μεγεθέων καὶ τῶν ἀποστημάτων ταῦτα ὑποτίθεμαι, περὶ δὲ τοῦ ψάμμου τάδε· εἴ κα ᾖ τι συγκείμενον μέγεθος ἐκ τοῦ ψάμμου μὴ μεῖζον μάκωνος, τὸν ἀριθμὸν αὐτοῦ μὴ μείζονα εἶμεν μυρίων, καὶ τὰν διάμετρον τᾶς μάκωνος μὴ ἐλάττονα εἶμεν ἢ τετρωκοστομόριον δακτύλου. Ὑποτίθεμαι δὲ τοῦτο ἐπισκεψάμενος τόνδε τὸν τρόπον· ἐτέθεν ἐπὶ κανόνα λεῖον μάκωνες ἐπ᾿ εὐθείας ἐπὶ μίαν κείμεναι ἁπτόμεναι ἀλλαλᾶν, καὶ ἀνέλαβον αἱ κε μάκωνες πλέονα τόπον δακτυλιαίου μάκεος. Ἐλάττονα οὖν τιθεὶς τὰν διάμετρον τᾶς μάκωνος ὑποτίθεμαι ὡς τετρωκοστομόριον εἶμεν δακτύλου καὶ μὴ ἐλάττονα βουλόμενος καὶ διὰ τούτων ἀναμφιλογώτατα δείκνυσθαι τὸ προκείμενον.

   Ἃ μὲν οὖν ὑποτίθεμαι, ταῦτα· χρήσιμον δὲ εἶμεν ὑπολαμβάνω τὰν κατονόμαξιν τῶν ἀριθμῶν ῥηθῆμεν, ὅπως καὶ τῶν ἄλλων οἱ τῷ βιβλίῳ μὴ περιτετευχότες τῷ ποτὶ Ζεύξιππον γεγραμμένῳ μὴ πλανῶνται διὰ τὸ μηδὲν εἶμεν ὑπὲρ αὐτᾶς ἐν τῷδε τῷ βιβλίῳ προειρημένον, Συμβαίνει δὴ τὰ ὀνόματα τῶν ἀριθμῶν ἐς τὸ μὲν τῶν μυρίων ὑπάρχειν ἁμῖν παραδεδομένα, καὶ ὑπὲρ τὸ τῶν [146] μυρίων [μὲν] ἀποχρεόντως γιγνώσκομες μυριάδων ἀριθμὸν λέγοντες ἔστε ποτὶ τὰς μυρίας μυριάδας. Ἔστων οὖν ἁμῖν οἱ μὲν νῦν εἰρημένοι ἀριθμοὶ ἐς τὰς μυρίας μυριάδας πρῶτοι καλούμενοι, τῶν δὲ πρώτων ἀριθμῶν αἱ μύριαι μυριάδες μονὰς καλείσθω δευτέρων ἀριθμῶν, καὶ ἀριθμείσθων τῶν δευτέρων μονάδες καὶ ἐκ τᾶν μονάδων δεκάδες καὶ ἑκατοντάδες καὶ χιλιάδες καὶ μυριάδες ἐς τὰς μυρίας μυριάδας. Πάλιν δὲ καὶ αἱ μύριαι μυριάδες τῶν δευτέρων ἀριθμῶν μονὰς καλείσθω τρίτων ἀριθμῶν, καὶ ἀριθμείσθων τῶν τρίτων ἀριθμῶν μονάδες καὶ ἀπὸ τᾶν μονάδων δεκάδες καὶ ἑκατοντάδες καὶ χιλιάδες καὶ μυριάδες ἐς τὰς μυρίας μυριάδας. Τὸν αὐτὸν δὲ τρόπον καὶ τῶν τρίτων ἀριθμῶν μύριαι μυριάδες μονὰς καλείσθω τετάρτων ἀριθμῶν, καὶ αἱ τῶν τετάρτων ἀριθμῶν μύριαι μυριάδες μονὰς καλείσθω πέμπτων ἀριθμῶν, καὶ ἀεὶ οὕτως προάγοντες οἱ ἀριθμοὶ τὰ ὀνόματα ἐχόντων ἐς τὰς μυριακισμυριοστῶν ἀριθμῶν μυρίας μυριάδας. Ἀποχρέοντι μὲν οὖν καὶ ἐπὶ τοσοῦτον οἱ ἀριθμοὶ γιγνωσκόμενοι, ἔξεστι δὲ καὶ ἐπὶ πλέον προάγειν. Ἔστων γὰρ οἱ μὲν νῦν εἰρημένοι ἀριθμοὶ πρώτας περιόδου καλούμενοι, ὁ δὲ ἔσχατος ἀριθμὸς τᾶς πρώτας περιόδου μονὰς καλείσθω δευτέρας περιόδου πρώτων ἀριθμῶν. Πάλιν δὲ καὶ αἱ μύριαι μυριάδες τᾶς δευτέρας περιόδου [147] πρώτων ἀριθμῶν μονὰς καλείσθω τᾶς δευτέρας περιόδου δευτέρων ἀριθμῶν. Ὁμοίως δὲ καὶ τούτων ὁ ἔσχατος μονὰς καλείσθω δευτέρας περιόδου τρίτων ἀριθμῶν, καὶ ἀεὶ οὕτως οἱ ἀριθμοὶ προάγοντες τὰ ὀνόματα ἐχόντων τᾶς δευτέρας περιόδου ἐς τὰς μυριακισμυριοστῶν ἀριθμῶν μυρίας μυριάδας. Πάλιν δὲ καὶ ὁ ἔσχατος ἀριθμὸς τᾶς δευτέρας περιόδου μονὰς καλείσθω τρίτας περιόδου πρώτων ἀριθμῶν, καὶ ἀεὶ οὕτως προαγόντων ἐς τὰς μυριακισμυριοστᾶς περιόδου μυριακισμυριοστῶν ἀριθμῶν μυρίας μυριάδας. Τούτων δὲ οὕτως κατωνομασμένων, εἴ κα ἔωντι ἀριθμοὶ ἀπὸ μονάδος ἀνάλογον ἑξῆς κείμενοι, ὁ δὲ παρὰ τὰν μονάδα δεκὰς ᾖ, ὀκτὼ μὲν αὐτῶν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων ἀριθμῶν καλουμένων ἐσσοῦνται, οἱ δὲ μετ᾿ αὐτοὺς ἄλλοι ὀκτὼ τῶν δευτέρων καλουμένων, καὶ οἱ ἄλλοι τὸν αὐτὸν τρόπον τούτοις τῶν συνωνύμων καλουμένων ἐσσοῦνται τᾷ ἀποστάσει τᾶς ὀκτάδος τῶν ἀριθμῶν ἀπὸ τᾶς πρώτας ὀκτάδος τῶν ἀριθμῶν. Τᾶς μὲν οὖν πρώτας ὀκτάδος τῶν ἀριθμῶν ὁ ὄγδοός ἐστιν ἀριθμὸς χίλιαι μυριάδες, τᾶς δὲ δευτέρας ὀκτάδος ὁ πρῶτος, ἐπεὶ δεκαπλασίων ἐστὶν τοῦ πρὸ αὐτοῦ, μύριαι μυριάδες ἐσσεῖται· οὗτος δέ ἐστι μονὰς τῶν δευτέρων ἀριθμῶν. Ὁ δὲ ὄγδοος τᾶς δευτέρας ὀκτάδος ἐστὶ χίλιαι μυριάδες τῶν δευτέρων ἀριθμῶν. Πάλιν δὲ καὶ τᾶς τρίτας ὀκτάδος ὁ πρῶτος, ἐπεὶ δεκαπλασίων ἐστὶ τοῦ πρὸ αὐτοῦ, μύριαι μυριάδες ἐσσεῖται τῶν δευτέρων ἀριθμῶν· οὗτος δέ ἐστιν μονὰς τῶν τρίτων ἀριθμῶν. Φανερὸν δὲ ὅτι καὶ πολλοσταὶ ὀκτάδες ἑξοῦντι ὡς εἴρηται. Χρήσιμον δέ ἐστι καὶ τόδε γιγνωσκόμενον. Εἴ κα ἀριθμῶν ἀπὸ τᾶς [148] μονάδος ἀνάλογον ἐόντων πολλαπλασιάζωντί τινες ἀλλάλους τῶν ἐκ τᾶς αὐτᾶς ἀναλογίας, ὁ γενόμενος ἐσσεῖται ἐκ τᾶς αὐτᾶς ἀναλογίας ἀπέχων ἀπὸ μὲν τοῦ μείζονος τῶν πολλαπλασιαξάντων ἀλλάλους, ὅσους ὁ ἐλάττων τῶν πολλαπλασιαξάντων ἀπὸ μονάδος ἀνάλογον ἀπέχει, ἀπὸ δὲ τᾶς μονάδος ἀφέξει ἑνὶ ἐλάττονας ἢ ὅσος ἐστὶν ὁ ἀριθμὸς συναμφοτέρων, οὓς ἀπέχοντι ἀπὸ μονάδος οἱ πολλαπλασιάξαντες ἀλλάλους. Ἔστων γὰρ ἀριθμοί τινες ἀνάλογον ἀπὸ μονάδος οἱ Α, Β, Γ, Δ, Ε, Ζ, Η, Θ, Ι, Κ, Λ, μονὰς δὲ ἔστω ὁ Α, καὶ πεπολλαπλασιάσθω ὁ Δ τῷ Θ, ὁ δὲ γενόμενος ἔστω ὁ Χ. Λελάφθω δὴ ἐκ τῆς ἀναλογίας ὁ Λ ἀπέχων ἀπὸ τοῦ Θ τοσούτους, ὅσους ὁ Δ ἀπὸ μονάδος ἀπέχει· δεικτέον ὅτι ἴσος ἐστὶν ὁ Χ τῷ Λ. Ἐπεὶ οὖν ἀνάλογον ἐόντων ἀριθμῶν ἴσους ἀπέχει ὅ τε Δ ἀπὸ τοῦ Α καὶ ὁ Λ ἀπὸ τοῦ Θ, τὸν αὐτὸν ἔχει λόγον ὁ Δ ποτὶ τὸν Α, ὃν ὁ Λ ποτὶ τὸν Θ. Πολλαπλασίων δέ ἐστιν ὁ Δ τοῦ Α τῷ Δ· πολλαπλασίων ἄρα ἐστὶν καὶ ὁ Λ τοῦ Θ τῷ Δ· ὥστε ἴσος ἐστὶν ὁ Λ τῷ Χ. Δῆλον οὖν ὅτι ὁ γενόμενος ἐκ τᾶς ἀναλογίας τέ ἐστιν καὶ ἀπὸ τοῦ μείζονος τῶν πολλαπλασιαξάντων ἀλλάλους ἴσους ἀπέχων, ὅσους ὁ ἐλάττων ἀπὸ τᾶς μονάδος ἀπέχει. Φανερὸν δὲ ὅτι καὶ ἀπὸ μονάδος ἀπέχει ἑνὶ ἐλάττονας ἢ ὅσος ἐστὶν ὁ ἀριθμὸς συναμφοτέρων, οὓς ἀπέχοντι ἀπὸ τᾶς μονάδος οἱ Δ, Θ· οἱ μὲν γὰρ Α, Β, Γ, Δ, Ε, Ζ, Η, Θ τοσοῦτοί ἐντι, ὅσους ὁ Θ ἀπὸ μονάδος ἀπέχει, οἱ δὲ Ι, Κ, Λ ἑνὶ ἐλάττονες ἢ ὅσους ὁ Δ ἀπὸ μονάδος ἀπέχει· σὺν γὰρ τῷ Θ τοσοῦτοί ἐντι.

[149]    Τούτων δὲ τῶν μὲν ὑποκειμένων, τῶν δὲ ἀποδεδειγμένων, τὸ προκείμενον δειχθήσεται. Ἐπεὶ γὰρ ὑπόκειται τὰν διάμετρον τᾶς μάκωνος μὴ ἐλάσσονα εἶμεν ἢ τετρωκοστομόριον δακτύλου, δῆλον ὡς ἁ σφαῖρα ἁ δακτυλιαίαν ἔχουσα τὰν διάμετρον οὐ μείζων ἐστὶν ἢ ὥστε χωρεῖν μάκωνας ἑξακισμυρίας καὶ τετρακισχιλίας· τᾶς γὰρ σφαίρας τᾶς ἐχούσας τὰν διάμετρον τετρωκοστομόριον δακτύλου πολλαπλασία ἐστὶν τῷ εἰρημένῳ ἀριθμῷ· δέδεικται γάρ τοι ὅτι αἱ σφαῖραι τριπλάσιον λόγον ἔχοντι ποτὶ ἀλλάλας τᾶν διαμέτρων. Ἐπεὶ δὲ ὑπόκειται καὶ τοῦ ψάμμου τὸν ἀριθμὸν τοῦ εἰς τὸ τᾶς μάκωνος μέγεθος μὴ μείζονα εἶμεν μυρίων, δῆλον ὡς, εἰ πληρωθείη ψάμμου ἁ σφαῖρα ἁ δακτυλιαίαν ἔχουσα τὰν διάμετρον, οὐ μείζων κα εἴη ὁ ἀριθμὸς τοῦ ψάμμου ἢ μυριάκις τὰ ἑξακισμύρια καὶ τετρακισχίλια. Οὗτος δέ ἐστιν ὁ ἀριθμὸς μονάδες τε Ϛ τῶν δευτέρων ἀριθμῶν καὶ τῶν πρώτων μυριάδες τετρακισχίλιαι· ἐλάσσων οὖν ἐστιν ἢ ι μονάδες τῶν δευτέρων ἀριθμῶν. Ἁ δὲ τῶν ρ δακτύλων ἔχουσα τὰν διάμετρον σφαῖρα πολλαπλασία ἐστὶν τᾶς δακτυλιαίαν ἐχούσας τὰν διάμετρον σφαίρας ταῖς ρ μυριάδεσσιν διὰ τὸ τριπλάσιον λόγον ἔχειν ποτ᾿ ἀλλάλας τᾶν διαμέτρων τὰς σφαίρας. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον δακτύλων ρ, δῆλον ὡς ἐλάττων ἐσσεῖται ὁ τοῦ ψάμμου ἀριθμὸς τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν δέκα μονάδων τῶν δευτέρων ἀριθμῶν [150] ταῖς ρ μυριάδεσσιν. Ἐπεὶ δ᾿ αἱ τῶν δευτέρων ἀριθμῶν δέκα μονάδες δέκατός ἐστιν ἀριθμὸς ἀπὸ μονάδος ἀνάλογον ἐν τᾷ τῶν δεκαπλασίων ὅρων ἀναλογίᾳ, αἱ δὲ ἑκατὸν μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὡς ὁ γενόμενος ἀριθμὸς ἐσσεῖται τῶν ἐκ τᾶς αὐτᾶς ἀναλογίας ἑκκαιδέκατος ἀπὸ μονάδος· δέδεικται γὰρ ὅτι ἑνὶ ἐλάσσονας ἀπέχει ἀπὸ τᾶς μονάδος ἢ ὅσος ἐστὶν ὁ ἀριθμὸς συναμφοτέρων, οὓς ἀπέχοντι ἀπὸ μονάδος οἱ πολλαπλασιάξαντες ἀλλάλους. Τῶν δὲ ἑκκαίδεκα τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, οἱ δὲ μετὰ τούτους ὀκτὼ τῶν δευτέρων, καὶ ὁ ἔσχατός ἐστιν αὐτῶν χίλιαι μυριάδες δευτέρων ἀριθμῶν. Φανερὸν οὖν ὅτι τοῦ ψάμμου τὸ πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ρ δακτύλων ἐχούσᾳ ἔλαττόν ἐστιν ἢ χίλιαι μυριάδες τῶν δευτέρων ἀριθμῶν. Πάλιν δὲ καὶ ἁ σφαῖρα ἁ τῶν μυρίων δακτύλων ἔχουσα τὰν διάμετρον πολλαπλασία ἐστὶν τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον ρ δακτύλων ταῖς ρ μυριάδεσσιν. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ ἔχουσα σφαῖρα τὰν διάμετρον μυρίων δακτύλων, δῆλον ὡς ἐλάσσων ἐσσεῖται ὁ τοῦ ψάμμου ἀριθμὸς τοῦ γενομένου πολλαπλασιασθεισᾶν τᾶν χιλιᾶν μυριάδων τῶν δευτέρων ἀριθμῶν ταῖς ρ μυριάδεσσιν. Ἐπεὶ δ᾿ αἱ μὲν τῶν δευτέρων ἀριθμῶν χίλιαι μυριάδες ἑκκαιδέκατός ἐστιν ἀριθμὸς ἀπὸ μονάδος ἀνάλογον, αἱ δὲ ρ μυριάδες ἕβδομος ἀπὸ μονάδος ἐν τᾷ [151] αὐτᾷ ἀναλογίᾳ, δῆλον ὡς ὁ γενόμενος ἐσσεῖται δυοκαιεικοστὸς τῶν ἐκ τᾶς αὐτᾶς ἀναλογίας ἀπὸ μονάδος. Τῶν δὲ δύο καὶ εἴκοσι τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, ὀκτὼ δὲ οἱ μετὰ τούτους τῶν δευτέρων καλουμένων, οἱ δὲ λοιποὶ ἓξ τῶν τρίτων καλουμένων, καὶ ὁ ἔσχατος αὐτῶν ἐστι δέκα μυριάδες τῶν τρίτων ἀριθμῶν. Φανερὸν οὖν ὅτι τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ μυρίων δακτύλων ἔλασσόν ἐστιν ἢ ι μυριάδες τρίτων ἀριθμῶν. Καὶ ἐπεὶ ἐλάσσων ἐστὶν ἁ σταδιαίαν ἔχουσα τὰν διάμετρον σφαῖρα τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον μυρίων δακτύλων, δῆλον ὅτι καὶ τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδιαίαν ἔλασσόν ἐστιν ἢ ι μυριάδες τῶν τρίτων ἀριθμῶν. Πάλιν δὴ ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον ρ σταδίων πολλαπλασίων ἐστὶ τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον σταδιαίαν ταῖς ρ μυριάδεσσιν. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ ἔχουσα τὰν διάμετρον ρ σταδίων, δῆλον ὅτι ἐλάσσων ἐσσεῖται ὁ τοῦ ψάμμου ἀριθμὸς τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν δέκα μυριάδων τρίτων ἀριθμῶν ταῖς ρ μυριάδεσσι. Καὶ ἐπεὶ αἱ μὲν τῶν τρίτων ἀριθμῶν δέκα μυριάδες δυοκαιεικοστός ἐστιν ἀπὸ μονάδος ἀνάλογον, αἱ δὲ ρ μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὡς ὁ γενόμενος ἐσσεῖται ὀκτωκαιεικοστὸς ἐκ τᾶς αὐτᾶς ἀναλογίας ἀπὸ μονάδος. Τῶν δὲ ὀκτὼ καὶ εἴκοσι τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, οἱ δὲ μετὰ τούτους ἄλλοι ὀκτὼ τῶν δευτέρων, καὶ οἱ μετὰ τούτους ὀκτὼ [152] τῶν τρίτων, οἱ δὲ λοιποὶ τέσσαρες τῶν τετάρτων καλουμένων, καὶ ὁ ἔσχατος αὐτῶν ἐστι χίλιαι μονάδες τῶν τετάρτων ἀριθμῶν. Φανερὸν οὖν ὅτι τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδίων ρ ἔλασσόν ἐστιν ἢ χίλιαι μονάδες τῶν τετάρτων ἀριθμῶν. Πάλιν δὴ ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον μυρίων σταδίων πολλαπλασία ἐστὶ τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον σταδίων ρ ταῖς ρ μυριάδεσσιν. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον σταδίων μυρίων, δῆλον ὅτι ἔλασσον ἐσσεῖται τὸ τοῦ ψάμμου πλῆθος τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν χιλιᾶν μονάδων τῶν τετάρτων ἀριθμῶν ταῖς ρ μυριάδεσσιν. Ἐπεὶ δ᾿ αἱ μὲν τῶν τετάρτων ἀριθμῶν χίλιαι μονάδες ὀκτωκαιεικοστός ἐστιν ἀπὸ μονάδος ἀνάλογον, αἱ δ᾿ ἑκατὸν μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὅτι ὁ γενόμενος ἐσσεῖται ἐκ τᾶς αὐτᾶς ἀναλογίας τέταρτος καὶ τριακοστὸς ἀπὸ μονάδος. Τῶν δὲ τεσσάρων καὶ τριάκοντα τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, οἱ δὲ μετὰ τούτους ὀκτὼ τῶν δευτέρων, καὶ οἱ μετὰ τούτους ἄλλοι ὀκτὼ τῶν τρίτων, καὶ οἱ μετὰ τούτους ὀκτὼ τῶν τετάρτων, οἱ δὲ λοιποὶ δύο τῶν πέμπτων καλουμένων ἐσσοῦνται, καὶ ὁ ἔσχατος αὐτῶν ἐστι δέκα μονάδες τῶν πέμπτων ἀριθμῶν. Δῆλον οὖν ὅτι τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδίων μυρίων ἔλασσον ἐσσεῖται ἢ ι μονάδες τῶν πέμπτων ἀριθμῶν. Πάλιν δὴ ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον σταδίων ρ μυριάδων πολλαπλασία [153] ἐστὶ τᾶς σφαίρας τᾶς τὰν διάμετρον ἐχούσας σταδίων μυρίων ταῖς ρ μυριάδεσσιν. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον σταδίων ρ μυριάδων, δῆλον ὡς ἐλάσσων ἐσσεῖται ὁ τοῦ ψάμμου ἀριθμὸς τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν δέκα μονάδων τῶν πέμπτων ἀριθμῶν ταῖς ρ μυριάδεσσιν. Καὶ ἐπεὶ αἱ μὲν τῶν πέμπτων ἀριθμῶν δέκα μονάδες τέταρτός ἐστι καὶ τριακοστὸς ἀπὸ μονάδος ἀνάλογον, αἱ δὲ ρ μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὅτι ὁ γενόμενος ἐκ τᾶς αὐτᾶς ἀναλογίας ἐσσεῖται τετρωκοστὸς ἀπὸ μονάδος. Τῶν δὲ τεσσαράκοντα τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, οἱ δὲ μετὰ ταῦτα ἄλλοι ὀκτὼ τῶν δευτέρων, καὶ οἱ μετὰ τούτους ἄλλοι ὀκτὼ τῶν τρίτων, οἱ δὲ μετὰ τοὺς τρίτους ὀκτὼ τῶν τετάρτων, οἱ δὲ μετὰ τούτους ὀκτὼ τῶν πέμπτων καλουμένων, καὶ ὁ ἔσχατος αὐτῶν ἐστι χίλιαι μυριάδες τῶν πέμπτων ἀριθμῶν. Φανερὸν οὖν ὅτι τοῦ ψάμμου τὸ πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδίων ρ μυριάδων ἔλασσόν ἐστιν ἢ χίλιαι μυριάδες τῶν πέμπτων ἀριθμῶν. Ἁ δὲ τὰν διάμετρον ἔχουσα σφαῖρα σταδίων μυριᾶν μυριάδων πολλαπλασίων ἐστὶ τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον σταδίων ρ μυριάδων ταῖς ρ μυριάδεσσιν. Εἰ δὴ γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον σταδίων μυριᾶν μυριάδων, φανερὸν ὅτι ἔλασσον ἐσσεῖται τὸ τοῦ [154] ψάμμου πλῆθος τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν χιλιᾶν μυριάδων τῶν πέμπτων ἀριθμῶν ταῖς ρ μυριάδεσσιν. Ἐπεὶ δ᾿ αἱ μὲν τῶν πέμπτων ἀριθμῶν χίλιαι μυριάδες τετρωκοστός ἐστιν ἀπὸ μονάδος ἀνάλογον, αἱ δὲ ρ μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὡς ὁ γενόμενος ἐσσεῖται ἕκτος καὶ τετρωκοστὸς ἀπὸ μονάδος. Τῶν δὲ τεσσαράκοντα καὶ ἓξ τούτων ὀκτὼ μὲν οἱ πρῶτοι σὺν τᾷ μονάδι τῶν πρώτων καλουμένων ἐντί, ὀκτὼ δὲ οἱ μετὰ τούτους τῶν δευτέρων, καὶ οἱ μετὰ τούτους ἄλλοι ὀκτὼ τῶν τρίτων, οἱ δὲ μετὰ τοὺς τρίτους ἄλλοι ὀκτὼ τῶν τετάρτων, καὶ οἱ μετὰ τοὺς τετάρτους ὀκτὼ τῶν πέμπτων, οἱ δὲ λοιποὶ ἓξ τῶν ἕκτων καλουμένων ἐντί, καὶ ὁ ἔσχατος αὐτῶν ἐστι ι μυριάδες τῶν ἕκτων ἀριθμῶν. Φανερὸν οὖν ὅτι τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδίων μυριάδων μυριᾶν ἔλασσόν ἐστιν ἢ ι μυριάδες τῶν ἕκτων ἀριθμῶν. Ἁ δὲ τὰν διάμετρον ἔχουσα σφαῖρα σταδίων μυριάκις μυριάδων ρ πολλαπλασία ἐστὶ τᾶς σφαίρας τᾶς ἐχούσας τὰν διάμετρον σταδίων μυριάδων μυριᾶν ταῖς ρ μυριάδεσσιν. Εἰ οὖν γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκα ἐστὶν ἁ σφαῖρα ἁ ἔχουσα τὰν διάμετρον σταδίων μυριάκις μυριάδων ρ, φανερὸν ὅτι τὸ τοῦ ψάμμου πλῆθος ἔλασσον ἐσσεῖται τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν ι μυριάδων τῶν ἕκτων ἀριθμῶν ταῖς ρ μυριάδεσσιν. Ἐπεὶ δ᾿ αἱ μὲν τῶν ἕκτων ἀριθμῶν δέκα [155] μυριάδες ἕκτος καὶ τετρωκοστός ἐστιν ἀπὸ μονάδος ἀνάλογον, αἱ δὲ ρ μυριάδες ἕβδομος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὅτι ὁ γενόμενος ἐσσεῖται δυοκαιπεντακοστὸς ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας. Τῶν δὲ δύο καὶ πεντήκοντα τούτων οἱ μὲν ὀκτὼ καὶ τεσσαράκοντα σὺν τᾷ μονάδι οἵ τε πρῶτοι καλούμενοι ἐντὶ καὶ οἱ δεύτεροι καὶ τρίτοι καὶ τέταρτοι καὶ πέμπτοι καὶ ἕκτοι, οἱ δὲ λοιποὶ τέσσαρες τῶν ἑβδόμων καλουμένων ἐντί, καὶ ὁ ἔσχατος αὐτῶν ἐστι χίλιαι μονάδες τῶν ἑβδόμων ἀριθμῶν. Φανερὸν οὖν ὅτι τοῦ ψάμμου τὸ πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ τᾷ τὰν διάμετρον ἐχούσᾳ σταδίων μυριάκις μυριάδων ρ ἔλασσόν ἐστιν ἢ Ϛα μονάδες τῶν ἑβδόμων ἀριθμῶν. Ἐπεὶ οὖν ἐδείχθη ἁ τοῦ κόσμου διάμετρος ἐλάσσων ἐοῦσα σταδίων μυριάκις μυριάδων ρ, δῆλον ὅτι καὶ τοῦ ψάμμου τὸ πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τῷ κόσμῳ ἔλασσόν ἐστιν ἢ Ϛα μονάδες τῶν ἑβδόμων ἀριθμῶν. Ὅτι μὲν οὖν τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τῷ ὑπὸ τῶν πλείστων ἀστρολόγων καλουμένῳ κόσμῳ ἔλασσόν ἐστιν ἢ Ϛα μονάδες τῶν ἑβδόμων ἀριθμῶν δέδεικται· ὅτι δὲ καὶ τὸ πλῆθος τοῦ ψάμμου τοῦ μέγεθος ἔχοντος ἴσον τᾷ σφαίρᾳ ταλικαύτᾳ, ἁλίκαν Ἀρίσταρχος ὑποτίθεται τὰν τῶν ἀπλανέων ἄστρων σφαῖραν εἶμεν, ἔλασσόν ἐστιν ἢ Ϛα μυριάδες τῶν ὀγδόων ἀριθμῶν δειχθήσεται. Ἐπεὶ γὰρ ὑπόκειται τὰν γᾶν τὸν αὐτὸν ἔχειν λόγον ποτὶ τὸν ὑφ᾿ ἁμῶν εἰρημένον κόσμον, ὃν ἔχει λόγον ὁ εἰρημένος κόσμος ποτὶ τὰν τῶν ἀπλανέων ἄστρων σφαῖραν, ἃν Ἀρίσταρχος ὑποτίθεται, καὶ αἱ διάμετροι τᾶν σφαιρᾶν τὸν αὐτὸν ἔχοντι λόγον ποτ᾿ ἀλλάλας. Ἁ δὲ τοῦ κόσμου διάμετρος τᾶς διαμέτρου τᾶς γᾶς δέδεικται ἐλάσσων [156] ἐοῦσα ἢ μυριοπλασίων· δῆλον οὖν ὅτι καὶ ἁ διάμετρος τᾶς τῶν ἀπλανέων ἄστρων σφαίρας ἐλάσσων ἐστὶν ἢ μυριοπλασίων τᾶς διαμέτρου τοῦ κόσμου. Ἐπεὶ δὲ αἱ σφαῖραι τριπλάσιον λόγον ἔχοντι ποτ᾿ ἀλλάλας τᾶν διαμέτρων, φανερὸν ὅτι ἁ τῶν ἀπλανέων ἄστρων σφαῖρα, ἃν Ἀρίσταρχος ὑποτίθεται, ἐλάττων ἐστὶν ἢ μυριάκις μυρίαις μυριάδεσσι πολλαπλασίων τοῦ κόσμου. Δέδεικται δὲ ὅτι τὸ τοῦ ψάμμου πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τῷ κόσμῳ ἔλασσόν ἐστιν ἢ Ϛα μονάδες τῶν ἑβδόμων ἀριθμῶν· δῆλον οὖν ὅτι, εἰ γένοιτο ἐκ τοῦ ψάμμου σφαῖρα ταλικαύτα τὸ μέγεθος, ἁλίκαν ὁ Ἀρίσταρχος ὑποτίθεται τὰν τῶν ἀπλανέων ἄστρων σφαῖραν εἶμεν, ἐλάσσων ἐσσεῖται ὁ τοῦ ψάμμου ἀριθμὸς τοῦ γενομένου ἀριθμοῦ πολλαπλασιασθεισᾶν τᾶν χιλιᾶν μονάδων ταῖς μυριάκις μυρίαις μυριάδεσσιν. Καὶ ἐπεὶ αἱ μὲν τῶν ἑβδόμων Ϛα μονάδες δυοκαιπεντακοστός ἐστιν ἀπὸ μονάδος ἀνάλογον, αἱ δὲ μυριάκις μύριαι μυριάδες τρισκαιδέκατος ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας, δῆλον ὅτι ὁ γενόμενος ἐσσεῖται τέταρτος καὶ ἑξηκοστὸς ἀπὸ μονάδος ἐκ τᾶς αὐτᾶς ἀναλογίας· οὗτος δέ ἐστι τῶν ὀγδόων ὄγδοος, ὅς κα εἴη χίλιαι μυριάδες τῶν ὀγδόων ἀριθμῶν. Φανερὸν τοίνυν ὅτι τοῦ ψάμμου τὸ πλῆθος τοῦ μέγεθος ἔχοντος ἴσον τᾷ τῶν ἀπλανέων ἄστρων σφαίρᾳ, ἃν Ἀρίσταρχος ὑποτίθεται, ἔλασσόν ἐστιν ἢ Ϛα μυριάδες τῶν ὀγδόων ἀριθμῶν. Ταῦτα δέ, βασιλεῦ Γέλων, τοῖς μὲν πολλοῖς καὶ μὴ κεκοινωνηκότεσσι τῶν μαθημάτων οὐκ εὔπιστα [157] φανήσειν ὑπολαμβάνω, τοῖς δὲ μεταλελαβηκότεσσιν καὶ περὶ τῶν ἀποστημάτων καὶ τῶν μεγεθέων τᾶς τε γᾶς καὶ τοῦ ἁλίου καὶ τᾶς σελήνας καὶ τοῦ ὅλου κόσμου πεφροντικότεσσιν πιστὰ διὰ τὰν ἀπόδειξιν ἐσσεῖσθαι· διόπερ ᾠήθην καὶ τὶν οὐκ ἀνάρμοστον εἶμεν [ἔτι] ἐπιθεωρῆσαι ταῦτα.

---

ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΟΡΘΟΓΩΝΙΟΥ ΚΩΝΟΥ ΤΟΜΗΣ (ΤΕΤΡΑΓΩΝΙΣΜΟΣ ΠΑΡΑΒΟΛΗΣ)

  

[164]

Ἀρχιμήδης Δοσιθέῳ εὖ πράττειν.

   Ἀκούσας Κόνωνα μὲν τετελευτηκέναι, ὃς ἦν οὐδὲν ἐπιλείπων ἁμῖν ἐν φιλίᾳ, τὶν δὲ Κόνωνος γνώριμον γεγενῆσθαι καὶ γεωμετρίας οἰκεῖον εἶμεν τοῦ μὲν τετελευτηκότος εἵνεκεν ἐλυπήθημες ὡς καὶ φίλου τοῦ ἀνδρὸς γεναμένου καὶ ἐν τοῖς μαθημάτεσσι θαυμαστοῦ τινος, ἐπροχειριξάμεθα δὲ ἀποστεῖλαί τοι γράψαντες, ὡς Κόνωνι γράφειν ἐγνωκότες ἦμες, γεωμετρικῶν θεωρημάτων, ὃ πρότερον μὲν οὐκ ἦν τεθεωρημένον, νῦν δὲ ὑφ᾿ ἁμῶν τεθεώρηται, πρότερον μὲν διὰ μηχανικῶν εὑρεθέν, ἔπειτα δὲ καὶ διὰ τῶν γεωμετρικῶν ἐπιδειχθέν. Τῶν μὲν οὖν πρότερον περὶ γεωμετρίαν πραγματευθέντων ἐπεχείρησάν τινες γράφειν ὡς δυνατὸν ἐὸν κύκλῳ τῷ δοθέντι καὶ κύκλου τμάματι τῷ δοθέντι χωρίον εὑρεῖν εὐθύγραμμον ἴσον, καὶ μετὰ ταῦτα τὸ περιεχόμενον χωρίον ὑπό τε τᾶς ὅλου τοῦ κώνου τομᾶς καὶ εὐθείας τετραγωνίζειν ἐπειρῶντο λαμβάνοντες οὐκ εὐπαραχώρητα λήμματα, διόπερ αὐτοῖς ὑπὸ τῶν πλείστων οὐχ εὑρισκόμενα ταῦτα κατεγνωσθέν. Τὸ δὲ ὑπ᾿ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς τμᾶμα [165] περιεχόμενον οὐδένα τῶν προτέρων ἐγχειρήσαντα τετραγωνίζειν ἐπιστάμεθα, ὃ δὴ νῦν ὑφ᾿ ἁμῶν εὕρηται· δείκνυται γὰρ ὅτι πᾶν τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς ἐπίτριτόν ἐστι τοῦ τριγώνου τοῦ βάσιν ἔχοντος τὰν αὐτὰν καὶ ὕψος ἴσον τῷ τμάματι λαμβανομένου τοῦδε τοῦ λήμματος ἐς τὰν ἀπόδειξιν αὐτοῦ· τῶν ἀνίσων χωρίων τὰν ὑπεροχάν, ᾇ ὑπερέχει τὸ μεῖζον τοῦ ἐλάσσονος, δυνατὸν εἶμεν αὐτὰν ἑαυτᾷ συντιθεμέναν παντὸς ὑπερέχειν τοῦ προτεθέντος πεπερασμένου χωρίου. Κέχρηνται δὲ καὶ οἱ πρότερον γεωμέτραι τῷδε τῷ λήμματι· τούς τε γὰρ κύκλους διπλασίονα λόγον ἔχειν ποτ᾿ ἀλλάλους τᾶν διαμέτρων ἀποδεδείχασιν αὐτῷ τούτῳ τῷ λήμματι χρώμενοι, καὶ τὰς σφαίρας ὅτι τριπλασίονα λόγον ἔχοντι ποτ᾿ ἀλλάλας τᾶν διαμέτρων, ἔτι δὲ καὶ ὅτι πᾶσα πυραμὶς τρίτον μέρος ἐστὶ τοῦ πρίσματος τοῦ τὰν αὐτὰν βάσιν ἔχοντος τᾷ πυραμίδι καὶ ὕψος ἴσον· καὶ διότι πᾶς κῶνος τρίτον μέρος ἐστὶ τοῦ κυλίνδρου τοῦ τὰν αὐτὰν βάσιν ἔχοντος τῷ κώνῳ καὶ ὕψος ἴσον, ὁμοῖον τῷ προειρημένῳ λῆμμά τι λαμβάνοντες ἔγραφον. Συμβαίνει δὲ τῶν προειρημένων θεωρημάτων ἕκαστον μηδενὸς ἧσσον τῶν ἄνευ τούτου τοῦ λήμματος ἀποδεδειγμένων πεπιστευκέναι· ἀρκεῖ δὲ ἐς τὰν ὁμοίαν πίστιν τούτοις ἀναγμένων τῶν ὑφ᾿ ἁμῶν ἐκδιδομένων. Ἀναγράψαντες οὖν αὐτοῦ τὰς ἀποδείξιας ἀποστέλλομες πρῶτον μὲν ὡς διὰ τῶν μηχανικῶν ἐθεωρήθη, μετὰ ταῦτα δὲ καὶ ὡς διὰ τῶν γεωμετρουμένων ἀποδείκνυται. Προγράφεται δὲ καὶ στοιχεῖα κωνικὰ χρεῖαν ἔχοντα ἐς τὰν ἀπόδειξιν. Ἔρρωσο.

[166]    α΄.

   Εἴ κα ᾖ ὀρθογωνίου κώνου τομά, ἐφ᾿ ἇς ἁ ΑΒΓ, ἁ δὲ ΒΔ παρὰ τὰν διάμετρον ἢ αὐτὰ διάμετρος, ἁ δὲ ΑΓ παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσαν τᾶς τοῦ κώνου τομᾶς, ἴσα ἐσσεῖται ἁ ΑΔ τᾷ ΔΓ· κἂν ἴσα ᾖ ἁ ΑΔ τᾷ ΔΓ, παράλληλοι ἐσσοῦνται ἅ τε ΑΓ καὶ ἁ κατὰ τὸ Β ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς.

   β΄.

   Εἴ κα ᾖ ὀρθογωνίου κώνου τομὰ ἁ ΑΒΓ, ᾖ δὲ ἁ μὲν ΒΔ παρὰ τὰν διάμετρον ἢ αὐτὰ διάμετρος, ἁ δὲ ΑΔΓ [167] παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσαν τᾶς τοῦ κώνου τομᾶς, ἁ δὲ ΕΓ τᾶς τοῦ κώνου τομᾶς ἐπιψαύουσα κατὰ τὸ Γ, ἐσσοῦνται αἱ ΒΔ, ΒΕ ἴσαι.

   γ΄.

   Εἴ κα ᾖ ὀρθογωνίου κώνου τομὰ ἁ ΑΒΓ, ἁ δὲ ΒΔ παρὰ τὰν διάμετρον ἢ αὐτὰ διάμετρος, καὶ ἀχθέωντί τινες αἱ ΑΔ, ΕΖ παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσαν τᾶς τοῦ κώνου τομᾶς, ἐσσεῖται, ὡς ἁ ΒΔ ποτὶ τὰν ΒΖ, δυνάμει ἁ ΑΔ ποτὶ τὰν ΕΖ.

   Ἀποδέδεικται δὲ ταῦτα ἐν τοῖς κωνικοῖς στοιχείοις.

   δ΄.

   Ἔστω τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τὸ ΑΒΓ, ἁ δὲ ΒΔ ἀπὸ μέσας τᾶς ΑΓ παρὰ τὰν διάμετρον ἄχθω ἢ αὐτὰ διάμετρος ἔστω, καὶ ἁ ΒΓ εὐθεῖα ἐπιζευχθεῖσα ἐκβεβλήσθω. Εἰ δή κα ἀχθῇ τις ἄλλα ἁ ΖΘ παρὰ τὰν ΒΔ τέμνουσα τὰν διὰ τῶν Β, Γ εὐθεῖαν, τὸν αὐτὸν ἕξει λόγον ἁ ΖΘ ποτὶ τὰν ΘΗ, ὃν ἁ ΔΑ ποτὶ τὰν ΔΖ.

   Ἄχθω γὰρ διὰ τοῦ Η παρὰ τὰν ΑΓ ἁ ΚΗ· ἔστιν ἄρα ὡς ἁ ΒΔ ποτὶ τὰν ΒΚ μάκει, οὕτως ἁ ΔΓ ποτὶ τὰν ΚΗ δυνάμει· ἀποδέδεικται γὰρ τοῦτο. Ἐσσεῖται ἄρα ὡς ἁ ΒΓ ποτὶ τὰν ΒΙ μάκει, οὕτως ἁ ΒΓ ποτὶ τὰν ΒΘ δυνάμει· ἴσαι γὰρ αἱ ΔΖ, ΚΗ· ἀνάλογον ἄρα ἐντὶ αἱ ΒΓ, ΒΘ, ΒΙ γραμμαί. Ὥστε τὸν αὐτὸν ἔχει λόγον ἁ ΒΓ ποτὶ τὰν ΒΘ, ὃν ἁ ΓΘ ποτὶ τὰν ΘΙ· ἔστιν ἄρα ὡς ἁ ΓΔ ποτὶ τὰν ΔΖ, οὕτως ἁ ΘΖ ποτὶ τὰν ΘΗ. Τᾷ δὲ ΔΓ ἴσα ἐστὶν ἁ ΔΑ· δῆλον οὖν ὅτι τὸν αὐτὸν ἔχει λόγον ἁ ΔΑ ποτὶ τὰν ΔΖ, ὃν ἁ ΖΘ ποτὶ τὰν ΘΗ.

   ε΄.

   Ἔστω τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τὸ ΑΒΓ, καὶ ἄχθω ἀπὸ τοῦ Α παρὰ τὰν διάμετρον ἁ ΖΑ, ἀπὸ δὲ τοῦ Γ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ ἁ ΓΖ. Εἰ δή τις ἀχθείη ἐν τῷ ΖΑΓ τριγώνῳ [169] παρὰ τὰν ΑΖ, τὸν αὐτὸν λόγον ἁ ἀχθεῖσα τετμήσεται ὑπὸ τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς καὶ ἁ ΑΓ ὑπὸ τᾶς ἀχθείσας [ἀνάλογον], ὁμόλογον δὲ ἐσσεῖται τὸ τμᾶμα τᾶς ΑΓ τὸ ποτὶ τῷ Α τῷ τμάματι τᾶς ἀχθείσας τῷ ποτὶ τῷ Α.

   Ἄχθω γάρ τις ἁ ΔΕ παρὰ τὰν ΑΖ, καὶ τεμνέτω πρῶτον ἁ ΔΕ τὰν ΑΓ δίχα. Ἐπεὶ οὖν ἐστιν ὀρθογωνίου κώνου τομὰ ἁ ΑΒΓ καὶ ἀγμένα ἁ ΒΔ παρὰ τὰν διάμετρον, αἱ δὲ ΑΔ, ΔΓ ἴσαι, ἐσσεῖται τᾷ ΑΓ παράλληλος ἁ κατὰ τὸ Β ἐπιψαύουσα τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς. Πάλιν, ἐπεὶ παρὰ τὰν διάμετρόν ἐστιν ἁ ΔΕ, καὶ ἀπὸ τοῦ Γ ἁ ΓΕ ἆκται ἐπιψαύουσα τᾶς τοῦ ὀρθογωνίου κώνου τομᾶς κατὰ τὸ Γ, ἁ δὲ ΔΓ παράλληλος τᾷ κατὰ τὸ Β ἐπιψαυούσᾳ, ἴσα ἐστὶν ἁ ΕΒ τᾷ ΒΔ· ὥστε τὸν αὐτὸν ἔχει λόγον ἁ ΑΔ ποτὶ τὰν ΔΓ, ὃν ἁ ΔΒ ποτὶ τὰν ΒΕ. Εἰ μὲν οὖν δίχα τέμνει ἁ ἀχθεῖσα τὰν ΑΓ, δέδεικται· εἰ δὲ μή, ἄχθω τις ἄλλα ἁ ΚΛ παρὰ τὰν ΑΖ· δεικτέον οὖν ὅτι τὸν αὐτὸν ἔχει λόγον ἁ ΑΚ ποτὶ τὰν ΚΓ, ὃν ἁ ΚΘ ποτὶ τὰν ΘΛ. Ἐπεὶ γὰρ [170] ἴσα ἐστὶν ἁ ΒΕ τᾷ ΒΔ, ἴσα ἐστὶ καὶ ἁ ΙΛ τᾷ ΚΙ· τὸν αὐτὸν ἄρα λόγον ἔχει ἁ ΛΚ ποτὶ τὰν ΚΙ, ὃν ἁ ΑΓ ποτὶ τὰν ΔΑ. Ἔχει δὲ καὶ ἁ ΚΙ ποτὶ τὰν ΚΘ τὸν αὐτὸν λόγον, ὃν ἁ ΔΑ ποτὶ τὰν ΑΚ· δέδεικται γὰρ ἐν τῷ πρότερον· ὥστε τὸν αὐτὸν λόγον ἔχει ἁ ΚΘ ποτὶ τὰν ΘΛ, ὃν ἁ ΑΚ ποτὶ τὰν ΚΓ. Δέδεικται οὖν τὸ προτεθέν.

   Ϛ΄.

   Νοείσθω δὲ τὸ [ὅτε ἐστὶν τὸ ἐν τᾷ θεωρίᾳ] προκείμενον [ὁρώμενον] ἐπίπεδον ὀρθὸν ποτὶ τὸν ὁρίζοντα, καὶ τᾶς ΑΒ γραμμᾶς [ἔπειτα] τὰ μὲν ἐπὶ τὰ αὐτὰ τῷ Δ κάτω νοείσθω, τὰ δὲ ἐπὶ θάτερα ἄνω, τὸ δὲ ΒΔΓ τρίγωνον ἔστω ὀρθογώνιον ὀρθὰν ἔχον τὰν ποτὶ τῷ Β γωνίαν καὶ τὰν ΒΓ πλευρὰν ἴσαν τᾷ ἡμισείᾳ τοῦ ζυγοῦ [δηλονότι ἴσης οὔσης τᾶς ΑΒ τῇ ΒΓ], κρεμάσθω δὲ τὸ τρίγωνον ἐκ τῶν Β, Γ σαμείων, κρεμάσθω δὲ καὶ ἄλλο χωρίον τὸ Ζ ἐκ τοῦ ἑτέρου μέρεος τοῦ ζυγοῦ κατὰ τὸ Α, καὶ ἰσορροπείτω τὸ Ζ χωρίον κατὰ τὸ Α κρεμάμενον τῷ ΒΔΓ τριγώνῳ οὕτως ἔχοντι, ὡς νῦν κεῖται. Φαμὶ δὴ τὸ Ζ χωρίον τοῦ ΒΔΓ τριγώνου μέρος τρίτον εἶμεν.

[171]    Ἐπεὶ γὰρ ὑπόκειται ἰσορροπέων ὁ ζυγός, εἴη κα ἁ ΑΓ γραμμὰ παρὰ τὸν ὁρίζοντα, αἱ δὲ ποτ᾿ ὀρθὰς ἀγόμεναι τᾷ ΑΓ ἐν τῷ ὀρθῷ ἐπιπέδῳ ποτὶ τὸν ὁρίζοντα κάθετοι ἐσσοῦνται ἐπὶ τὸν ὁρίζοντα. Τετμάσθω ἁ ΒΓ γραμμὰ κατὰ τὸ Ε οὕτως, ὥστε διπλασίονα εἶμεν τὰν ΓΕ τᾶς ΕΒ, καὶ ἄχθω παρὰ τὰν ΔΒ ἁ ΚΕ καὶ τετμάσθω δίχα κατὰ τὸ Θ· τοῦ δὴ ΒΔΓ τριγώνου κέντρον βάρεός ἐστι τὸ Θ σαμεῖον· δέδεικται γὰρ τοῦτο ἐν τοῖς Μηχανικοῖς· Εἴ κα οὖν τοῦ ΒΔΓ τριγώνου ἁ μὲν κατὰ τὰ Β, Γ κρέμασις λυθῇ, κατὰ δὲ τὸ Ε κρεμασθῇ, μενεῖ τὸ τρίγωνον ὡς νῦν ἔχει· ἕκαστον γὰρ τῶν κρεμαμένων, ἐξ οὗ σαμείου κα κατασταθῇ, μένει, ὥστε κατὰ κάθετον εἶμεν τό τε σαμεῖον τοῦ κρεμαστοῦ καὶ τὸ κέντρον τοῦ βάρεος τοῦ κρεμαμένου· δέδεικται γὰρ καὶ τοῦτο. Ἐπεὶ οὖν τὰν αὐτὰν ἕξει κατάστασιν τὸ ΒΔΓ τρίγωνον ποτὶ τὸν ζυγόν, ἰσορροπήσει ὁμοίως τὸ Ζ χωρίον. Ἐπεὶ δὲ ἰσορροπέοντι τὸ μὲν Ζ κρεμάμενον κατὰ τὸ Α, τὸ δὲ ΒΔΓ κατὰ τὸ Ε, δῆλον ὡς ἀντιπέπονθε τοῖς μάκεσιν, καί ἐστιν ὡς ἁ ΑΒ ποτὶ τὰν ΒΕ, οὕτως τὸ ΒΔΓ τρίγωνον ποτὶ τὸ Ζ χωρίον. Τριπλασία δὲ ἁ ΑΒ τᾶς ΒΕ· καὶ τὸ ΒΔΓ ἄρα τρίγωνον τριπλάσιόν ἐστι τοῦ Ζ χωρίου.

   Φανερὸν δὲ [ὅτι] καί, εἴ κα τριπλάσιον ᾖ τὸ ΒΔΓ τρίγωνον τοῦ Ζ χωρίου, ὅτι ἰσορροπήσει.

   ζ΄.

   Ἔστω πάλιν ζυγὸς ἁ ΑΓ γραμμά, μέσον δὲ αὐτᾶς ἔστω τὸ Β, καὶ κρεμάσθω κατὰ τὸ Β [τὸ ΓΔΗ τρίγωνον], [172] τὸ δὲ ΓΔΗ ἔστω τρίγωνον ἀμβλυγώνιον βάσιν μὲν ἔχον τὰν ΔΗ, ὕψος δὲ τὰν ἴσαν ἐοῦσαν τᾷ ἡμισείᾳ τοῦ ζυγοῦ, καὶ κρεμάσθω τὸ ΔΓΗ τρίγωνον ἐκ τῶν Β, Γ σαμείων, τὸ δὲ Ζ χωρίον κρεμάμενον κατὰ τὸ Α ἰσσορροπὲς ἔστω τῷ ΓΔΗ τριγώνῳ οὕτως ἔχοντι ὡς νῦν κεῖται. Ὁμοίως δὴ δειχθήσεται τὸ Ζ χωρίον τρίτον μέρος τοῦ ΓΔΗ τριγώνου.

   Κρεμάσθω γάρ τι καὶ ἄλλο χωρίον ἐκ τοῦ Α τρίτον μέρος ἐὸν τοῦ ΒΓΗ τριγώνου· ἰσορροπήσει δὴ τὸ ΒΔΓ τρίγωνον τῷ ΖΛ. Ἐπεὶ οὖν τὸ μὲν ΒΓΗ τρίγωνον ἰσορροπεῖ τῷ Λ, τὸ δὲ ΒΓΔ τῷ ΖΛ, καὶ τρίτον ἐστὶ τοῦ ΒΓΔ τὸ ΖΛ, φανερὸν ὅτι καὶ τὸ ΓΔΗ τρίγωνον τριπλάσιον τοῦ Ζ.

   η΄.

   Ἔστω ζυγὸς ὁ ΑΒΓ, μέσον δὲ αὐτοῦ τὸ Β, καὶ κρεμάσθω κατὰ τὸ Β, τὸ δὲ ΓΔΕ τρίγωνον ὀρθογώνιον ὀρθὰν ἔχον τὰν ποτὶ τῷ Ε γωνίαν, καὶ κρεμάσθω ἐκ τοῦ ζυγοῦ κατὰ τὰ Γ, Ε, τὸ δὲ Ζ χωρίον κρεμάσθω κατὰ τὸ Α καὶ ἰσορροπείτω τῷ ΓΔΕ οὕτως ἔχοντι, ὡς νῦν κεῖται, ὃν δὲ λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΕ, τοῦτον ἐχέτω τὸ ΓΔΕ τρίγωνον [173] ποτὶ τὸ Κ χωρίον. Φαμὶ δὴ τὸ Ζ χωρίον τοῦ μὲν ΓΔΕ τριγώνου ἔλασσον εἶμεν, τοῦ δὲ Κ μεῖζον.

   Λελάφθω γὰρ τοῦ ΔΕΓ τριγώνου τὸ κέντρον τοῦ βάρεος καὶ ἔστω τὸ Θ, καὶ ἁ ΘΗ ἄχθω παρὰ τὰν ΔΕ. Ἐπεὶ οὖν ἰσορροπεῖ τὸ ΓΔΕ τρίγωνον τῷ Ζ χωρίῳ, τὸν αὐτὸν ἔχει λόγον τὸ ΓΔΕ χωρίον ποτὶ τὸ Ζ, ὃν ἁ ΑΒ ποτὶ τὰν ΒΗ· ὥστε ἔλασσόν ἐστι τὸ Ζ τοῦ ΓΔΕ. Καὶ ἐπεὶ τὸ ΓΔΕ τρίγωνον ποτὶ μὲν τὸ Ζ τοῦτον ἔχει τὸν λόγον, ὃν ἁ ΒΑ ποτὶ τὰν ΒΗ, ποτὶ δὲ τὸ Κ ὃν ἁ ΒΑ ποτὶ τὰν ΒΕ, δῆλον ὡς μείζονα λόγον ἔχει τὸ ΓΔΕ τρίγωνον ποτὶ τὸ Κ ἢ ποτὶ τὸ Ζ· ὥστε μεῖζόν ἐστι τὸ Ζ τοῦ Κ.

   θ΄.

   Ἔστω πάλιν τὸ μὲν ΑΓ ζύγιον, μέσον δὲ αὐτοῦ τὸ Β, τὸ δὲ ΓΔΚ τρίγωνον ἀμβλυγώνιον βάσιν μὲν ἔχον τὰν ΔΚ, ὕψος δὲ τὰν ΕΓ, καὶ κρεμάσθω ἐκ τοῦ ζυγοῦ κατὰ [174] τὰ Γ, Ε, τὸ δὲ Ζ χωρίον κρεμάσθω κατὰ τὸ Α καὶ ἰσορροπείτω τῷ ΔΓΚ τριγώνῳ οὕτως ἔχοντι ὡς νῦν κεῖται, ὃν δὲ λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΕ, τοῦτον ἐχέτω τὸ ΓΔΚ τρίγωνον ποτὶ τὸ Λ. Φαμὶ δὴ τὸ Ζ τοῦ μὲν Λ μεῖζον εἶμεν, τοῦ δὲ ΔΓΚ ἔλασσον.

   Δειχθήσεται ὁμοίως τῷ πρότερον.

   ι΄.

   Ἔστω πάλιν τὸ μὲν ΑΒΓ ζύγιον καὶ μέσον αὐτοῦ τὸ Β, τὸ δὲ ΒΔΗΚ τραπέζιον τὰς μὲν ποτὶ τοῖς Β, Η σαμείοις γωνίας ὀρθὰς ἔχον, τὰν δὲ ΚΔ πλευρὰν ἐπὶ τὸ Γ νεύουσαν, καὶ ὃν ἔχει λόγον ἁ ΑΒ ποτὶ τὰν ΒΗ, τοῦτον ἐχέτω τὸ ΒΔΚΗ τραπέζιον ποτὶ τὸ Λ, κρεμάσθω δὲ τὸ ΒΔΗΚ τραπέζιον ἐκ τοῦ ζυγοῦ κατὰ τὰ Β, Η σαμεῖα, κρεμάσθω δὲ καὶ τὸ Ζ χωρίον κατὰ τὸ Α καὶ ἰσορροπείτω τῷ ΒΔΚΗ τραπεζίῳ οὕτως ἔχοντι ὡς νῦν ὑπόκειται. Φαμὶ τὸ Ζ χωρίον ἔλασσον εἶμεν τοῦ Λ.

   Τετμάσθω γὰρ ἁ ΑΓ κατὰ τὸ Ε οὕτως ὥστε, ὃν ἔχει λόγον ἁ διπλασία τᾶς ΔΒ καὶ ἁ ΚΗ ποτὶ τὰν διπλασίαν τᾶς ΚΗ καὶ τὰν ΒΔ, τοῦτον ἔχειν τὰν ΕΗ ποτὶ τὰν ΒΕ, [175] καὶ διὰ τοῦ Ε παρὰ τὰν ΒΔ ἀχθεῖσα ἁ ΕΝ τετμάσθω δίχα κατὰ τὸ Θ· τοῦ δὴ ΒΔΗΚ τραπεζίου κέντρον ἐστὶ τοῦ βάρεος τὸ Θ· δέδεικται γὰρ τοῦτο ἐν τοῖς Μηχανικοῖς. Ἢν οὖν τὸ ΒΔΗΚ τραπέζιον κατὰ μὲν τὸ Ε κρεμασθῇ, ἀπὸ δὲ τῶν Β, Η σαμείων λυθῇ, μένει τὰν αὐτὰν ἔχον κατάστασιν διὰ τὰ αὐτὰ τοῖς πρότερον καὶ ἰσορροπεῖ τῷ Ζ χωρίῳ. Ἐπεὶ οὖν ἰσορροπεῖ τὸ ΒΔΗΚ τραπέζιον κατὰ τὸ Ε κρεμάμενον τῷ Ζ χωρίῳ κατὰ τὸ Α κρεμαμένῳ, ἐσσεῖται ὡς ἁ ΑΒ ποτὶ τὰν ΒΕ, τὸ ΒΔΗΚ τραπέζιον ποτὶ τὸ Ζ χωρίον· μείζονα ἄρα λόγον ἔχει τὸ ΒΔΗΚ τραπέζιον ποτὶ τὸ Ζ ἤπερ ποτὶ τὸ Λ, ἐπεὶ καὶ ἁ ΑΒ ποτὶ τὰν ΒΕ μείζονα λόγον ἔχει ἤπερ ποτὶ τὰν ΒΗ· ὥστε ἔλασσον ἐσσεῖται τὸ Ζ τοῦ Λ.

   ια΄.

   Ἔστω πάλιν τὸ μὲν ΑΓ ζύγιον καὶ μέσον αὐτοῦ τὸ Β, τὸ δὲ ΚΔΤΡ τραπέζιον ἔστω τὰς μὲν ΚΔ, ΤΡ πλευρὰς ἔχον ἐπὶ τὸ Γ νευούσας, τὰς δὲ ΔΡ, ΚΤ καθέτους ἐπὶ τὰν ΒΓ, καὶ ἁ ΔΡ ἐπὶ τὸ Β πιπτέτω, ὃν δὲ λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΗ, τοῦτον ἐχέτω τὸ ΔΚΤΡ τραπέζιον ποτὶ τὸ Λ, τὸ δὲ ΔΚΤΡ τραπέζιον κρεμάσθω ἐκ τοῦ ζυγοῦ κατὰ τὰ [176] Β, Η καὶ τὸ Ζ κατὰ τὸ Α, καὶ ἰσορροπείτω τὸ Ζ τῷ ΔΚΡΤ τραπεζίῳ οὕτως ἔχοντι ὡς νῦν κεῖται. Ὁμοίως δὴ τοῖς πρότερον δειχθήσεται ἔλασσον τὸ Ζ χωρίον τοῦ Λ.

   ιβ΄.

   Ἔστω πάλιν τὸ μὲν ΑΓ ζύγιον, μέσον δὲ αὐτοῦ τὸ Β, τὸ δὲ ΔΕΚΗ τραπέζιον ἔστω τὰς μὲν ποτὶ τοῖς Ε, Η σαμείοις γωνίας ὀρθὰς ἔχον, τὰς δὲ ΚΔ, ΕΗ γραμμὰς ποτὶ τὸ Γ νευούσας, καὶ ὃν μὲν λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΗ, τοῦτον ἐχέτω τὸ ΔΚΕΗ τραπέζιον ποτὶ τὸ Μ, ὃν δὲ λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΕ, τοῦτον τὸν λόγον ἐχέτω τὸ ΔΚΕΗ τραπέζιον ποτὶ τὸ Λ, κρεμάσθω δὲ τὸ ΔΚΕΗ τραπέζιον ἐκ τοῦ ζυγοῦ κατὰ τὰ Ε, Η, τὸ δὲ Ζ χωρίον κρεμάσθω κατὰ τὸ Α, καὶ ἰσορροπείτω τῷ τραπεζίῳ οὕτως ἔχοντι ὡς νῦν ὑπόκειται. Φαμὶ δὴ τὸ Ζ τοῦ μὲν Λ μεῖζον εἶμεν, τοῦ δὲ Μ ἔλασσον.

   Ἔλαβον γὰρ τοῦ ΔΚΕΗ τραπεζίου τὸ κέντρον τοῦ βάρεος, ἔστω δὲ τὸ Θ· λαφθήσεται δὲ ὁμοίως τῷ πρότερον· καὶ ἄγω τὰν ΘΙ παρὰ τὰν ΔΕ. Ἂν οὖν τὸ τραπέζιον ἐκ τοῦ ζυγοῦ κρεμασθῇ κατὰ τὸ Ι, ἀπὸ δὲ τῶν Ε, Η λυθῇ, [177] μενεῖ τὰν αὐτὰν ἔχον κατάστασιν καὶ ἰσορροπήσει τῷ Ζ διὰ τὰ αὐτὰ τοῖς πρότερον. Ἐπεὶ δὲ ἰσορροπεῖ τὸ τραπέζιον κρεμάμενον κατὰ τὸ Ι τῷ Ζ κρεμαμένῳ κατὰ τὸ Α, τὸν αὐτὸν ἕξει λόγον τὸ τραπέζιον ποτὶ τὸ Ζ, ὃν ἁ ΑΒ ποτὶ τὰν ΒΙ· δῆλον οὖν ὅτι τὸ ΔΚΕΗ ποτὶ μὲν τὸ Λ μείζονα λόγον ἔχει ἢ ποτὶ τὸ Ζ, ποτὶ δὲ τὸ Μ ἐλάσσονα ἢ ποτὶ τὸ Ζ· ὥστε τὸ Ζ τοῦ μὲν Λ μεῖζόν ἐστι, τοῦ δὲ Μ ἔλασσον.

   ιγ΄.

   Ἔστω πάλιν τὸ μὲν ΑΓ ζύγιον, κατὰ μέσον δὲ αὐτοῦ τὸ Β, τὸ δὲ ΚΔΤΡ τραπέζιον, ὥστε τὰς μὲν ΚΔ, ΤΡ πλευρὰς νευούσας εἶμεν ἐπὶ τὸ Γ, τὰς δὲ ΔΤ, ΚΡ καθέτους ἐπὶ τὰν ΒΓ, κρεμάσθω δὲ ἐκ τοῦ ζυγοῦ κατὰ τὰ Ε, Η, τὸ δὲ Ζ χωρίον κρεμάσθω κατὰ τὸ Α καὶ ἰσορροπείτω τῷ ΔΚΤΡ τραπεζίῳ οὕτως ἔχοντι ὡς νῦν κεῖται, καὶ ὃν μὲν λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΕ, τοῦτον ἐχέτω τὸ ΔΚΤΡ τραπέζιον ποτὶ τὸ Λ χωρίον, ὃν δὲ λόγον ἔχει ἁ ΑΒ ποτὶ τὰν ΒΗ, τοῦτον ἐχέτω τὸ αὐτὸ τραπέζιον ποτὶ τὸ Μ. Ὁμοίως δὴ τῷ πρότερον δειχθήσεται τὸ Ζ τοῦ μὲν Λ μεῖζον, τοῦ δὲ Μ ἔλασσον.

[178]    ιδ΄.

   Ἔστω τμᾶμα τὸ ΒΘΓ περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς. Ἔστω δὴ πρῶτον ἁ ΒΓ ποτ᾿ ὀρθὰς τᾷ διαμέτρῳ, καὶ ἄχθω ἀπὸ μὲν τοῦ Β σαμείου ἁ ΒΔ παρὰ τὰν διάμετρον, ἀπὸ δὲ τοῦ Γ ἁ ΓΔ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ· ἐσσεῖται δὴ τὸ ΒΓΔ τρίγωνον ὀρθογώνιον. Διῃρήσθω δὴ ἁ ΒΓ ἐς ἴσα τμάματα ὁποσαοῦν τὰ ΒΕ, ΕΖ, ΖΗ, ΗΙ, ΙΓ, καὶ ἀπὸ τᾶν τομᾶν ἄχθωσαν παρὰ τὰν διάμετρον αἱ ΕΣ, ΖΤ, ΗΥ, ΙΞ, ἀπὸ δὲ τῶν σαμείων, καθ᾿ ἃ τέμνοντι αὗται τὰν τοῦ κώνου τομάν, ἐπεζεύχθωσαν ἐπὶ τὸ Γ καὶ ἐκβεβλήσθωσαν. Φαμὶ δὴ τὸ τρίγωνον τὸ ΒΔΓ τῶν μὲν τραπεζίων τῶν ΚΕ, ΛΖ, ΜΗ, ΝΙ καὶ τοῦ ΞΙΓ τριγώνου ἔλασσον εἶμεν ἢ τριπλάσιον, τῶν δὲ τραπεζίων τῶν ΖΦ, ΗΘ, ΙΠ καὶ τοῦ ΙΟΓ τριγώνου μεῖζον [ἐστιν] ἢ τριπλάσιον.

[179]    Διάχθω γὰρ εὐθεῖα ἁ ΑΒΓ, καὶ ἀπολελάφθω ἁ ΑΒ ἴσα τᾷ ΒΓ, καὶ νοείσθω ζύγιον τὸ ΑΓ· μέσον δὲ αὐτοῦ ἐσσεῖται τὸ Β· καὶ κρεμάσθω ἐκ τοῦ Β, κρεμάσθω δὲ καὶ τὸ ΒΔΓ ἐκ τοῦ ζυγοῦ κατὰ τὰ Β, Γ, ἐκ δὲ τοῦ θατέρου μέρεος τοῦ ζυγοῦ κρεμάσθω τὰ Ρ, Χ, Ψ, Ω, Δς χωρία κατὰ τὸ Α, καὶ ἰσορροπείτω τὸ μὲν Ρ χωρίον τῷ ΔΕ τραπεζίῳ οὕτως ἔχοντι, τὸ δὲ Χ τῷ ΖΣ τραπεζίῳ, τὸ δὲ Ψ τῷ ΤΗ, τὸ δὲ Ω τῷ ΥΙ, τὸ δὲ Δς τῷ ΞΙΓ τριγώνῳ· ἰσορροπήσει δὴ καὶ τὸ ὅλον τῷ ὅλῳ· ὥστε τριπλάσιον ἂν εἴη τὸ ΒΔΓ τρίγωνον τοῦ ΡΧΨΩΔς χωρίου. Καὶ ἐπεί ἐστιν τμᾶμα τὸ ΒΓΘ, ὃ περιέχεται ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, καὶ ἀπὸ μὲν τοῦ Β παρὰ τὰν διάμετρον ἆκται ἁ ΒΔ, ἀπὸ δὲ τοῦ Γ ἁ ΓΔ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ, ἆκται δέ τις καὶ ἄλλα παρὰ τὰν διάμετρον ἁ ΣΕ, τὸν αὐτὸν ἔχει λόγον ἁ ΒΓ ποτὶ τὰν ΒΕ, ὃν ἁ ΣΕ ποτὶ τὰν ΕΦ· ὥστε καὶ ἁ ΒΑ ποτὶ τὰν ΒΕ τὸν αὐτὸν ἔχει λόγον, ὃν τὸ ΔΕ τραπέζιον ποτὶ τὸ ΚΕ. Ὁμοίως δὲ δειχθήσεται ἁ ΑΒ ποτὶ τὰν ΒΖ τὸν αὐτὸν ἔχουσα λόγον, ὃν τὸ ΣΖ τραπέζιον ποτὶ τὸ ΛΖ, ποτὶ δὲ τὰν ΒΗ, ὃν τὸ ΤΗ ποτὶ τὸ ΜΗ, ποτὶ δὲ τὰν ΒΙ, ὃν τὸ ΥΙ ποτὶ τὸ ΝΙ. Ἐπεὶ οὖν ἐστι τραπέζιον τὸ ΔΕ τὰς μὲν ποτὶ τοῖς Β, Ε σαμείοις γωνίας ὀρθὰς ἔχον, τὰς δὲ πλευρὰς ἐπὶ τὸ Γ νευούσας, ἰσορροπεῖ δέ τι χωρίον αὐτῷ τὸ Ρ κρεμάμενον ἐκ τοῦ ζυγοῦ κατὰ τὸ Α οὕτως ἔχοντος τοῦ τραπεζίου ὡς νῦν κεῖται, καὶ ἔστιν ὡς ἁ ΒΑ ποτὶ τὰν ΒΕ, οὕτως τὸ ΔΕ τραπέζιον ποτὶ τὸ ΚΕ, μεῖζον ἄρα [180] ἐστὶν τὸ ΚΕ χωρίον τοῦ Ρ χωρίου : δέδεικται γὰρ τοῦτο. Πάλιν δὲ καὶ τὸ ΖΣ τραπέζιον τὰς μὲν ποτὶ τοῖς Ζ, Ε γωνίας ὀρθὰς ἔχον, τὰν δὲ ΣΤ νεύουσαν ἐπὶ τὸ Γ, ἰσορροπεῖ δὲ αὐτῷ χωρίον τὸ Χ ἐκ τοῦ ζυγοῦ κρεμάμενον κατὰ τὸ Α οὕτως ἔχοντος τοῦ τραπεζίου ὡς νῦν κεῖται, καὶ ἔστιν ὡς μὲν ἁ ΑΒ ποτὶ τὰν ΒΕ, οὕτως τὸ ΖΣ τραπέζιον ποτὶ τὸ ΖΦ, ὡς δὲ ἁ ΑΒ ποτὶ τὰν ΒΖ, οὕτως τὸ ΖΣ τραπέζιον ποτὶ τὸ ΛΖ· εἴη οὖν κα τὸ Χ χωρίον τοῦ μὲν ΛΖ τραπεζίου ἔλασσον, τοῦ δὲ ΖΦ μεῖζον· δέδεικται γὰρ καὶ τοῦτο. Διὰ τὰ αὐτὰ δὴ καὶ τὸ Ψ χωρίον τοῦ μὲν ΜΗ τραπεζίου ἔλασσον, τοῦ δὲ ΘΗ μεῖζον, καὶ τὸ Ω χωρίον τοῦ μὲν ΝΟΙΗ τραπεζίου ἔλασσον, τοῦ δὲ ΠΙ μεῖζον, ὁμοίως δὲ καὶ τὸ Δς χωρίον τοῦ μὲν ΞΙΓ τριγώνου ἔλασσον, τοῦ δὲ ΓΙΟ μεῖζον. Ἐπεὶ οὖν τὸ μὲν ΚΕ τραπέζιον μεῖζόν ἐστι τοῦ Ρ χωρίου, τὸ δὲ ΛΖ τοῦ Χ, τὸ δὲ ΜΗ τοῦ Ψ, τὸ δὲ ΝΙ τοῦ Ω, τὸ δὲ ΞΙΓ τρίγωνον τοῦ Δς, φανερὸν ὅτι καὶ πάντα τὰ εἰρημένα χωρία μείζονά ἐστι τοῦ ΡΧΨΩΔς χωρίου. Ἔστιν δὲ τὸ ΡΧΨΩΔς τρίτον μέρος τοῦ ΒΓΔ τριγώνου· δῆλον ἄρα ὅτι τὸ ΒΓΔ τρίγωνον ἔλασσόν ἐστιν ἢ τριπλάσιον τῶν ΚΕ, ΛΖ, ΜΗ, ΝΙ τραπεζίων καὶ τοῦ ΞΙΓ τριγώνου. Πάλιν, ἐπεὶ τὸ μὲν ΖΦ τραπέζιον ἔλασσόν ἐστι τοῦ Χ χωρίου, τὸ δὲ ΘΗ τοῦ Ψ, τὸ δὲ ΙΠ τοῦ Ω, τὸ δὲ ΙΟΓ τρίγωνον τοῦ Δς, φανερὸν ὅτι καὶ πάντα τὰ εἰρημένα ἐλάσσονά ἐστι τοῦ ΔσΩΨΧ χωρίου· φανερὸν οὖν ὅτι καὶ τὸ ΒΔΓ τρίγωνον μεῖζόν ἐστιν ἢ τριπλάσιον [181] τῶν ΦΖ, ΘΗ, ΙΠ τραπεζίων καὶ τοῦ ΙΓΟ τριγώνου, ἔλασσον δὲ ἢ τριπλάσιον τῶν προγεγραμμένων.

   ιε΄.

   Ἔστω πάλιν τὸ ΒΘΓ τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, ἁ δὲ ΒΓ μὴ ἔστω ποτ᾿ ὀρθὰς τᾷ διαμέτρῳ· ἀναγκαῖον δὴ ἤτοι τὰν ἀπὸ τοῦ Β σαμείου παρὰ τὰν διάμετρον ἀγμέναν ἐπὶ τὰ αὐτὰ τῷ τμάματι ἢ τὰν ἀπὸ τοῦ Γ ἀμβλεῖαν ποιεῖν γωνίαν ποτὶ τὰν ΒΓ. Ἔστω ἁ τὰν ἀμβλεῖαν ποιοῦσα ἁ ποτὶ τῷ Β, καὶ ἄχθω παρὰ τὰν διάμετρον ἀπὸ τοῦ Β ἁ ΒΔ, καὶ ἀπὸ τοῦ Γ ἁ ΓΔ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ, καὶ διῃρήσθω ἁ ΒΓ εἰς τμάματα ἴσα ὁποσαοῦν τὰ ΒΕ, ΕΖ, ΖΗ, ΗΙ, ΙΓ, ἀπὸ δὲ τῶν Ε, Ζ, Η, Ι παρὰ τὰν διάμετρον ἄχθωσαν αἱ ΕΣ, ΖΤ, ΗΨ, ΙΞ, καὶ ἀπὸ τῶν σαμείων, καθ᾿ ἃ τέμνοντι αὗται τὰν τοῦ κώνου τομάν, ἐπεζεύχθωσαν ἐπὶ τὸ Γ καὶ ἐκβεβλήσθωσαν. Φαμὶ δὴ καὶ νῦν τὸ ΒΔΓ τρίγωνον τῶν μὲν τραπεζίων τῶν ΒΦ, ΛΖ, ΜΗ, ΝΙ καὶ τοῦ ΓΙΞ τριγώνου ἔλασσον εἶμεν ἢ τριπλάσιον, τῶν δὲ ΖΦ, ΗΘ, ΙΠ καὶ τοῦ ΓΟΙ τριγώνου μεῖζον ἢ τριπλάσιον.

   Ἐκβεβλήσθω ἁ ΔΒ ἐπὶ θάτερα. Ἀγαγὼν οὖν κάθετον τὰν ΓΚ τᾷ ΓΚ ἴσαν ἀπέλαβον τὰν ΑΚ. Νοείσθω δὴ πάλιν ζύγιον τὸ ΑΓ, μέσον δὲ αὐτοῦ τὸ Κ, καὶ κρεμάσθω ἐκ τοῦ Κ, κρεμάσθω δὲ καὶ τὸ ΓΚΔ τρίγωνον ἐκ τοῦ ἡμίσεος τοῦ ζυγοῦ κατὰ τὰ Γ, Κ ἔχον ὡς νῦν κεῖται, καὶ ἐκ τοῦ θατέρου μέρεος τοῦ ζυγοῦ κρεμάσθωσαν κατὰ τὸ Α τὰ Ρ,

[182] Χ, Ψ, Ω, Δς χωρία, καὶ τὸ μὲν Ρ τῷ ΔΕ τραπεζίῳ ἰσορροπείτω οὕτως ἔχοντι ὡς νῦν κεῖται, τὸ δὲ Χ τῷ ΖΣ τραπεζίῳ, τὸ δὲ Ψ τῷ ΤΗ, τὸ δὲ Ω τῷ ΥΙ, τὸ δὲ Δς τῷ ΓΙΞ τριγώνῳ· ἰσορροπήσει δὴ καὶ τὸ ὅλον τῷ ὅλῳ· ὥστε εἴη ἂν καὶ τὸ ΔΒΓ τρίγωνον τριπλάσιον τοῦ ΡΧΨΩΔς χωρίου. Ὁμοίως δὴ τῷ πρότερον δειχθήσεται τό τε ΒΦ τραπέζιον τοῦ Ρ χωρίου μεῖζον, καὶ τὸ μὲν ΘΕ τραπέζιον μεῖζον ἐὸν τοῦ Χ χωρίου, τὸ δὲ ΖΦ ἔλαττον, καὶ τὸ μὲν ΜΗ τραπέζιον μεῖζον ἐὸν τοῦ Ψ χωρίου, τὸ δὲ ΗΘ ἔλασσον, καὶ ἔτι τὸ μὲν ΝΙ τραπέζιον μεῖζον ἐὸν τοῦ Ω χωρίου, τὸ δὲ ΠΙ ἔλασσον, καὶ τὸ μὲν ΞΙΓ τρίγωνον μεῖζον τοῦ Δς χωρίου, τὸ δὲ ΓΙΟ ἔλασσον· δῆλον οὖν ἐστιν.

   ιϚ΄.

   Ἔστω πάλιν τμᾶμα τὸ ΒΘΓ περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, καὶ ἄχθω διὰ μὲν τοῦ Β [183] ἁ ΒΔ παρὰ τὰν διάμετρον, ἀπὸ δὲ τοῦ Γ ἁ ΓΔ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ, ἔστω δὲ τοῦ ΒΔΓ τριγώνου τρίτον μέρος τῷ Ζ χωρίον. Φαμὶ δὴ τὸ ΒΘΓ τμᾶμα ἴσον εἶμεν τῷ Ζ χωρίῳ.

   Εἰ γὰρ μή ἐστιν ἴσον, ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. Ἔστω δὴ πρότερον, εἰ δυνατόν, μεῖζον· ἁ δὴ ὑπεροχά, ᾇ ὑπερέχει τὸ ΒΘΓ τμᾶμα τοῦ Ζ χωρίου, συντιθεμένα αὐτὰ ἑαυτᾷ ἐσσεῖται μείζων τοῦ ΒΓΔ τριγώνου. Δυνατὸν δέ ἐστι λαβεῖν τι χωρίον ἔλασσον τᾶς ὑπεροχᾶς, ὃ ἐσσεῖται μέρος τοῦ ΒΔΓ τριγώνου. Ἔστω δὴ τὸ ΒΓΕ τρίγωνον ἔλασσόν τε τᾶς εἰρημένας ὑπεροχᾶς καὶ μέρος τοῦ ΒΔΓ τριγώνου· ἐσσεῖται δὲ τὸ αὐτὸ ἁ ΒΕ μέρος τᾶς ΒΔ. Διῃρήσθω οὖν ἁ ΒΔ ἐς τὰ μέρεα, καὶ ἔστω τὰ τῶν διαιρέσιων σαμεῖα τὰ Η, Ι, Κ, καὶ ἀπὸ τῶν Η, Ι, Κ σαμείων [184] ἐπὶ τὸ Γ εὐθεῖαι ἐπεζεύχθωσαν· τέμνοντι δὴ αὗται τὰν τοῦ κώνου τομάν, ἐπεὶ ἁ ΓΔ ἐπιψαύουσά ἐντι αὐτᾶς κατὰ τὸ Γ· καὶ διὰ τῶν σαμείων, καθ᾿ ἃ τέμνοντι τὰν τομὰν αἱ εὐθεῖαι, ἄχθωσαν παρὰ τὰν διάμετρον αἱ ΜΦ, ΝΡ, ΞΘ, ΠΟ· ἐσσοῦνται δὲ αὗται καὶ παρὰ τὰν ΒΔ. Ἐπεὶ οὖν ἔλασσόν ἐστι τὸ ΒΓΕ τρίγωνον τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει τὸ ΒΘΓ τμᾶμα τοῦ Ζ χωρίου, δῆλον ὡς τὰ συναμφότερα τό τε Ζ χωρίον καὶ τὸ ΒΓΕ τρίγωνον ἐλάσσονά ἐντι τοῦ τμάματος. Καὶ τῷ ΒΓΕ τριγώνῳ ἴσα τὰ τραπέζιά ἐντι, δι᾿ ὧν ἁ τοῦ κώνου τομὰ πορεύεται, τὰ ΜΕ, ΦΛ, ΘΡ, ΘΟ, καὶ τὸ ΓΟΣ τρίγωνον· τὸ μὲν γὰρ ΜΕ τραπέζιον κοινόν, τὸ δὲ ΜΛ ἴσον τῷ ΦΛ καὶ τὸ ΛΞ ἴσον τῷ ΘΡ καὶ τὸ ΧΞ ἴσον τῷ ΟΘ καὶ τὸ ΓΧΠ τρίγωνον τῷ ΓΟΣ τριγώνῳ· τὸ δὴ Ζ χωρίον ἔλασσόν ἐστι τῶν τραπεζίων τῶν ΜΛ, ΞΡ, ΠΘ καὶ τοῦ ΠΟΓ τριγώνου. Καί ἐστι τὸ ΒΔΓ τρίγωνον τριπλάσιον τοῦ Ζ χωρίου· τὸ δὲ ΒΔΓ ἔλασσόν ἐστιν ἢ τριπλάσιον τῶν ΜΛ, ΡΞ, ΘΠ τραπεζίων καὶ τοῦ ΠΟΓ τριγώνου· ὅπερ ἀδύνατον· ἐδείχθη γὰρ μεῖζον ἐὸν ἢ τριπλάσιον. Οὐκοῦν οὐ μεῖζόν ἐστι τὸ ΒΘΓ τμᾶμα τοῦ Ζ χωρίου.

   Λέγω δὴ ὅτι οὐδὲ ἔλασσον. Ἔστω γάρ, εἰ δυνατόν, ἔλασσον. Πάλιν ἄρα ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ Ζ χωρίον τοῦ ΒΘΓ τμάματος, αὐτὰ ἑαυτᾷ συντιθεμένα ὑπερέχει καὶ τοῦ ΒΔΓ τριγώνου. Δυνατὸν δέ ἐστι λαβεῖν χωρίον ἔλασσον τᾶς ὑπεροχᾶς, ὃ ἐσσεῖται μέρος τοῦ ΒΔΓ τριγώνου. Ἔστω οὖν τὸ ΒΓΕ τρίγωνον ἔλασσον τᾶς ὑπεροχᾶς καὶ μέρος τοῦ ΒΔΓ τριγώνου, καὶ τὰ ἄλλα τὰ αὐτὰ κατεσκευάσθω. Ἐπεὶ οὖν ἐστι τὸ ΒΓΕ τρίγωνον ἔλασσον τᾶς [185] ὑπεροχᾶς, ᾇ ὑπερέχει τὸ Ζ χωρίον τοῦ ΒΘΓ τμάματος, τὸ ΒΕΓ τρίγωνον καὶ τὸ ΒΘΓ τμᾶμα ἀμφότερα ἐλάσσονά ἐστι τοῦ Ζ. Ἔστιν δὲ καὶ τὸ Ζ χωρίον ἔλασσον τῶν τετραπλεύρων τῶν ΕΜ, ΦΝ, ΨΞ, ΠΤ καὶ τοῦ ΓΠΣ τριγώνου· ἔστιν γὰρ τὸ ΒΔΓ τοῦ μὲν Ζ τριπλάσιον, τῶν δὲ εἰρημένων χωρίων ἔλασσον ἢ τριπλάσιον, ὡς ἐν τῷ πρὸ τούτου ἐδείχθη· ἔλασσον ἄρα τὸ ΒΓΕ τρίγωνον καὶ τὸ ΒΘΓ τμᾶμα τῶν τετραπλεύρων τῶν ΕΜ, ΦΝ, ΞΨ, ΠΤ καὶ τοῦ ΓΠΣ τριγώνου. Ὥστε κοινοῦ ἀφαιρεθέντος τοῦ τμάματος ἔλασσον εἴη κα καὶ τὸ ΓΒΕ τρίγωνον τῶν περιλειπομένων χωρίων· ὅπερ ἐστὶν ἀδύνατον· ἐδείχθη γὰρ ἴσον ἐὸν τὸ ΒΕΓ τρίγωνον τοῖς τραπεζίοις τοῖς ΕΜ, ΦΛ, ΘΡ, ΘΟ καὶ τῷ ΓΟΣ τριγώνῳ, ἅ ἐντι μείζονα τῶν περιλειπομένων χωρίων. Οὐκ ἄρα ἔλασσον τὸ ΒΘΓ τμᾶμα τοῦ Ζ χωρίου. Ἐδείχθη δὲ ὅτι οὐδὲ μεῖζον· ἴσον ἄρα τὸ τμᾶμα τῷ Ζ χωρίῳ.

   ιζ΄.

   Τούτου δεδειγμένου φανερὸν ὅτι πᾶν τμᾶμα περιεχόμενον ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς ἐπίτριτόν ἐστι τοῦ τριγώνου τοῦ ἔχοντος βάσιν τὰν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον.

   Ἔστω γὰρ τμᾶμα περιεχόμενον ὑπὸ εὐθείας τε καὶ ὀρθογωνίου κώνου τομᾶς, κορυφὰ δὲ αὐτοῦ ἔστω τὸ Θ σαμεῖον, καὶ ἐγγεγράφθω εἰς αὐτὸ τρίγωνον τὸ ΒΘΓ τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ὕψος ἴσον. Ἐπεὶ οὖν τὸ Θ σαμεῖον κορυφά ἐστι τοῦ τμάματος, ἁ ἀπὸ τοῦ Θ εὐθεῖα παρὰ τὰν διάμετρον ἀχθεῖσα δίχα τέμνει τὰν ΒΓ, καὶ ἁ ΒΓ ἐστὶ παρὰ τὰν ἐπιψαύουσαν τᾶς τομᾶς κατὰ τὸ Θ. Ἄχθω δὲ ἁ ΕΘ παρὰ τὰν διάμετρον, ἄχθω

[186] δὲ καὶ ἀπὸ τοῦ Β παρὰ τὰν διάμετρον ἁ ΒΔ, ἀπὸ δὲ τοῦ Γ ἁ ΓΔ ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Γ. Ἐπεὶ οὖν ἁ μὲν ΚΘ παρὰ τὰν διάμετρόν ἐστιν, ἁ δὲ ΓΔ ἐπιψαύουσα τᾶς τομᾶς κατὰ τὸ Γ, ἁ δὲ ΕΓ παράλληλός ἐστι τᾷ ἐπιψαυούσᾳ τᾶς τομᾶς κατὰ τὸ Θ, τὸ ΒΔΓ τρίγωνον τετραπλάσιόν ἐστι τοῦ ΒΘΓ τριγώνου. Ἐπεὶ δὲ τὸ ΒΔΓ τρίγωνον τοῦ μὲν ΒΘΓ τμάματος τριπλάσιόν ἐστι, τοῦ δὲ ΒΘΓ τριγώνου τετραπλάσιον, δῆλον ὡς ἐπίτριτόν ἐστι τὸ ΒΘΓ τμᾶμα τοῦ ΒΘΓ τριγώνου.

   Τῶν τμαμάτων τῶν περιεχομένων ὑπό τε εὐθείας καὶ καμπύλας γραμμᾶς βάσιν μὲν καλέω τὰν εὐθεῖαν, ὕψος δὲ τὰν μεγίσταν κάθετον ἀπὸ τᾶς καμπύλας γραμμᾶς ἀγομέναν ἐπὶ τὰν βάσιν τοῦ τμάματος, κορυφὰν δὲ τὸ σαμεῖον, ἀφ᾿ οὗ ἁ μεγίστα κάθετος ἄγεται.

   ιη΄.

   Εἴ κα ἐν τμάματι, ὃ περιέχεται ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, ἀπὸ μέσας τᾶς βάσιος ἀχθῇ εὐθεῖα [187] παρὰ τὰν διάμετρον, κορυφὰ ἐσσεῖται τοῦ τμάματος τὸ σαμεῖον, καθ᾿ ὃ ἁ παρὰ τὰν διάμετρον ἀχθεῖσα τέμνει τὰν τοῦ κώνου τομάν.

   Ἔστω γὰρ τμᾶμα τὸ ΑΒΓ περιεχόμενον ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, καὶ ἀπὸ μέσας τᾶς ΑΓ ἄχθω ἁ ΔΒ παρὰ τὰν διάμετρον. Ἐπεὶ οὖν ἐν ὀρθογωνίου κώνου τομᾷ ἁ ΒΔ ἆκται παρὰ τὰν διάμετρον, καὶ ἴσαι ἐντὶ αἱ ΑΔ, ΔΓ, δῆλον ὡς παράλληλοί ἐντι ἅ τε ΑΓ καὶ ἁ κατὰ τὸ Β ἐπιψαύουσα τᾶς τοῦ κώνου τομᾶς. Φανερὸν οὖν ὅτι τᾶν ἀπὸ τᾶς τομᾶς ἐπὶ τὰν ΑΓ ἀγομενᾶν καθέτων μεγίστα ἐσσεῖται ἁ ἀπὸ τοῦ Β ἀγομένα· κορυφὰ οὖν ἐστιν τοῦ τμάματος τὸ Β σαμεῖον.

   ιθ΄.

   Ἐν τμάματι περιεχομένῳ ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς ἁ ἀπὸ μέσας τᾶς βάσιος ἀχθεῖσα τᾶς ἀπὸ μέσας τᾶς ἡμισείας ἀγομένας ἐπίτριτος ἐσσεῖται μάκει.

[188]    Ἔστω γὰρ τὸ ΑΒΓ τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, καὶ ἄχθω παρὰ τὰν διάμετρον ἁ μὲν ΒΔ ἀπὸ μέσας τᾶς ΑΓ, ἁ δὲ ΕΖ ἀπὸ μέσας τᾶς ΑΔ, ἄχθω δὲ καὶ ἁ ΖΘ παρὰ ΑΓ. Ἐπεὶ οὖν ἐν ὀρθογωνίου κώνου τομᾷ ἁ ΒΔ παρὰ τὰν διάμετρον ἆκται, καὶ αἱ ΑΔ, ΖΘ παρὰ τὰν κατὰ τὸ Β ἐπιψαύουσάν ἐντι, δῆλον ὡς τὸν αὐτὸν ἔχει λόγον ἁ ΒΔ ποτὶ τὰν ΒΘ μάκει, ὃν ἁ ΑΔ ποτὶ τὰν ΖΘ δυνάμει· τετραπλασία ἄρα ἐστὶν καὶ ἁ ΒΔ τᾶς ΒΘ μάκει. Φανερὸν οὖν ὅτι ἐπίτριτός ἐστιν ἁ ΒΔ τᾶς ΕΖ μάκει.

   κ΄.

   Εἴ κα εἰς τμᾶμα περιεχόμενον ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τρίγωνον ἐγγραφῇ τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ὕψος τὸ αὐτό, μεῖζον ἐσσεῖται τὸ ἐγγραφὲν τρίγωνον ἢ ἥμισυ τοῦ τμάματος.

   Ἔστω γὰρ τὸ ΑΒΓ τμᾶμα οἷον εἴρηται, καὶ ἐγγεγράφθω εἰς αὐτὸ τρίγωνον τὸ ΑΒΓ τὰν αὐτὰν ἔχον βάσιν τῷ ὅλῳ καὶ ὕψος ἴσον. Ἐπεὶ οὖν τὸ τρίγωνον τῷ τμάματι τὰν αὐτὰν ἔχει βάσιν καὶ ὕψος τὸ αὐτό, ἀναγκαῖον τὸ Β σαμεῖον κορυφὰν εἶμεν τοῦ τμάματος· παράλληλος ἄρα ἐστὶν ἁ ΑΓ τᾷ κατὰ τὸ Β ἐπιψαυούσᾳ τᾶς τομᾶς. [189] Ἄχθω ἁ ΔΕ διὰ τοῦ Β παρὰ τὰν ΑΓ καὶ ἀπὸ τῶν Α, Γ αἱ ΑΔ, ΓΕ παρὰ τὰν διάμετρον· πεσοῦνται δὴ αὗται ἐκτὸς τοῦ τμάματος. Ἐπεὶ οὖν ἥμισύ ἐστι τὸ ΑΒΓ τρίγωνον τοῦ ΑΔΕΓ παραλληλογράμμου, φανερὸν ὅτι μεῖζόν ἐστιν ἢ τὸ ἥμισυ τοῦ τμάματος.

ΠΟΡΙΣΜΑ

   Δεδειγμένου δὲ τούτου δῆλον ὅτι ὡς ἐς τοῦτο τὸ τμᾶμα δυνατόν ἐστι πολύγωνον ἐγγράψαι, ὥστε εἶμεν τὰ περιλειπόμενα τμάματα παντὸς ἐλάσσονα τοῦ προτεθέντος χωρίου· ἀφαιρουμένου γὰρ ἀεὶ μείζονος τοῦ ἡμίσεος διὰ τοῦτο φανερὸν ὅτι ἐλασσοῦντες ἀεὶ τὰ λειπόμενα τμάματα ποιήσομες ταῦτα ἐλάσσονα παντὸς τοῦ προτεθέντος χωρίου.

   κα΄.

   Εἴ κα εἰς τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς τρίγωνον ἐγγραφῇ τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ὕψος τὸ αὐτό, ἐγγραφέωντι δὲ καὶ ἄλλα τρίγωνα εἰς τὰ λειπόμενα τμάματα τὰν αὐτὰν βάσιν ἔχοντα τοῖς τμαμάτεσσιν καὶ ὕψος τὸ αὐτό, ἑκατέρου τῶν τριγώνων τῶν εἰς τὰ περιλειπόμενα τμάματα ἐγγραφέντων ὀκταπλάσιον ἐσσεῖται τὸ τρίγωνον τὸ εἰς τὸ ὅλον τμᾶμα ἐγγραφέν.

   Ἔστω τὸ ΑΒΓ τμᾶμα οἷον εἴρηται, καὶ τετμάσθω ἁ ΑΓ δίχα τῷ Δ, ἁ δὲ ΒΔ ἄχθω παρὰ τὰν διάμετρον· τὸ Β ἄρα σαμεῖον κορυφά ἐστιν τοῦ τμάματος. Τὸ ἄρα ΑΒΓ

[190] τρίγωνον τὰν αὐτὰν βάσιν ἔχει τῷ τμάματι καὶ ὕψος τὸ αὐτό. Πάλιν τετμάσθω δίχα ἁ ΑΔ τῷ Ε, καὶ ἄχθω ἁ ΕΖ παρὰ τὰν διάμετρον, τετμάσθω δὲ ἁ ΑΒ κατὰ τὸ Θ· τὸ ἄρα Ζ σαμεῖον κορυφά ἐστι τοῦ τμάματος τοῦ ΑΖΒ. Τὸ δὴ ΑΖΒ τρίγωνον τὰν αὐτὰν βάσιν ἔχει τῷ [ΑΖΒ] τμάματι καὶ ὕψος τὸ αὐτό. Δεικτέον ὅτι ὀκταπλάσιόν ἐστι τὸ ΑΒΓ τρίγωνον τοῦ ΑΖΒ τριγώνου.

   Ἔστιν οὖν ἁ ΒΔ τᾶς μὲν ΕΖ ἐπίτριτος, τᾶς δὲ ΕΘ διπλασία· διπλασία ἄρα ἐστὶν ἁ ΕΘ τᾶς ΘΖ. Ὥστε καὶ τὸ ΑΕΒ τρίγωνον διπλάσιόν ἐστι τοῦ ΖΒΑ· τὸ μὲν γὰρ ΑΕΘ διπλάσιόν ἐστι τοῦ ΑΘΖ, τὸ δὲ ΘΒΕ τοῦ ΖΘΒ. Ὥστε τὸ ΑΒΓ τοῦ ΑΖΒ ἐστὶν ὀκταπλάσιον. Ὁμοίως δὲ δειχθήσεται καὶ τοῦ εἰς τὸ ΒΗΓ τμᾶμα ἐγγραφέντος.

   κβ΄.

   Εἴ κα ᾖ τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, καὶ χωρία τεθέωντι ἑξῆς ὁποσαοῦν ἐν τῷ τετραπλασίονι λόγῳ, ᾖ δὲ τὸ μέγιστον τῶν χωρίων ἴσον τῷ τριγώνῳ τῷ βάσιν ἔχοντι τὰν αὐτὰν τῷ τμάματι καὶ ὕψος τὸ αὐτό, σύμπαντα τὰ χωρία ἐλάσσονα ἐσσεῖται τοῦ τμάματος.

[191]    Ἔστω γὰρ τμᾶμα τὸ ΑΔΒΕΓ περιεχόμενον ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, χωρία δὲ ἔστω ὁποσαοῦν ἑξῆς κείμενα τὰ Ζ, Η, Θ, Ι, τετραπλάσιον δὲ ἔστω τὸ ἁγούμενον τοῦ ἑπομένου, μέγιστον δὲ ἔστω τὸ Ζ, καὶ ἔστω τὸ Ζ ἴσον τῷ τριγώνῳ τῷ βάσιν ἔχοντι τὰν αὐτὰν τῷ τμάματι καὶ ὕψος ἴσον. Λέγω ὅτι τὸ τμᾶμα τῶν Ζ, Η, Θ, Ι χωρίων μεῖζόν ἐστιν.

   Ἔστω τοῦ μὲν ὅλου τμάματος κορυφὰ τὸ Β, τῶν δὲ περιλειπομένων τμαμάτων τὰ Δ, Ε. Ἐπεὶ οὖν τὸ ΑΒΓ τρίγωνον ὀκταπλάσιόν ἐστιν ἑκατέρου τῶν ΑΔΒ, ΒΕΓ τριγώνων, δῆλον ὅτι ὡς ἀμφοτέρων αὐτῶν ἐστι τετραπλάσιον. Καὶ ἐπεὶ τὸ ΑΒΓ τρίγωνον ἴσον ἐστὶ τῷ Ζ χωρίῳ, κατὰ ταῦτα δὴ καὶ τὰ ΑΔΒ, ΒΕΓ τρίγωνα ἴσα ἐστὶ τῷ Η χωρίῳ. Ὁμοίως δὲ δειχθήσεται ὅτι καὶ τὰ εἰς τὰ περιλειπόμενα τμάματα ἐγγραφόμενα τρίγωνα τὰν αὐτὰν βάσιν ἔχοντα τοῖς τμαμάτεσσιν καὶ ὕψος τὸ αὐτὸ ἴσα ἐντὶ [192] τῷ Θ καὶ τὰ ἐς τὰ ὕστερον γενόμενα τμάματα ἐγγραφόμενα τρίγωνα ἴσα τῷ Ι χωρίῳ· σύμπαντα ἄρα τὰ προτεθέντα χωρία ἴσα ἐσσοῦνται πολυγώνῳ τινὶ ἐγγραφέντι εἰς τὸ τμᾶμα. Φανερὸν οὖν ὅτι ἐλάσσονά ἐστι τοῦ τμάματος.

   κγ΄.

   Εἴ κα μεγέθεα τεθέωντι ἑξῆς ἐν τῷ τετραπλασίονι λόγῳ, τὰ πάντα μεγέθεα καὶ ἔτι τοῦ ἐλαχίστου τὸ τρίτον μέρος ἐς τὸ αὐτὸ συντεθέντα ἐπίτριτα ἐσσοῦνται τοῦ μεγίστου.

   Ἔστω οὖν ὁποσαοῦν μεγέθεα ἑξῆς κείμενα τὰ Α, Β, Γ, Δ, Ε τετραπλασίονα ἕκαστον τοῦ ἑπομένου, μέγιστον δὲ ἔστω τὸ Α, ἔστω δὲ τὸ μὲν Ζ τρίτον τοῦ Β, τὸ δὲ Η τοῦ Γ, τὸ δὲ Θ τοῦ Δ, τὸ δὲ Ι τοῦ Ε. Ἐπεὶ οὖν τὸ μὲν Ζ τοῦ Β τρίτον μέρος ἐστίν, τὸ δὲ Β τοῦ Α τέταρτον μέρος ἐστίν, ἀμφότερα τὰ Β, Ζ μέρος τρίτον ἐστὶ τοῦ Α. Διὰ τὰ αὐτὰ δὴ καὶ τὰ Η, Γ τοῦ Β καὶ τὰ Θ, Δ τοῦ Γ καὶ τὰ Ι, Ε τοῦ Δ· καὶ τὰ σύμπαντα δὴ τὰ Β, Γ, Δ, Ε, Ζ, Η, Θ, Ι τρίτον μέρος ἐστὶ τῶν συμπάντων τῶν Α, Β, Γ, Δ. Ἐντὶ δὲ καὶ [193] αὐτὰ τὰ Ζ, Η, Θ τρίτον μέρος αὐτῶν τῶν Β, Γ, Δ· καὶ τὰ λοιπὰ ἄρα τὰ Β, Γ, Δ, Ε, Ι τοῦ λοιποῦ τρίτον μέρος ἐστὶ τοῦ Α. Δῆλον οὖν ὅτι τὰ σύμπαντα τὰ Α, Β, Γ, Δ, Ε καὶ τὸ Ι, τουτέστι τὸ τρίτον τοῦ Ε, τοῦ Α ἐστὶν ἐπίτριτα.

   κδ΄.

   Πᾶν τμᾶμα τὸ περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς ἐπίτριτόν ἐστι τριγώνου τοῦ τὰν αὐτὰν βάσιν ἔχοντος αὐτῷ καὶ ὕψος ἴσον.

   Ἔστω γὰρ τὸ ΑΔΒΕΓ τμᾶμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομᾶς, τὸ δὲ ΑΒΓ τρίγωνον ἔστω τὰν αὐτὰν βάσιν ἔχον τῷ τμάματι καὶ ὕψος ἴσον, τοῦ δὲ ΑΒΓ τριγώνου ἔστω ἐπίτριτον τὸ Κ χωρίον. Δεικτέον ὅτι ἴσον ἐστὶ τῷ ΑΔΒΕΓ τμάματι.

   Εἰ γὰρ μή ἐστιν ἴσον, ἤτοι μεῖζόν ἐστιν ἢ ἔλασσον. Ἔστω πρότερον, εἰ δυνατόν, μεῖζον τὸ ΑΔΒΕΓ τμᾶμα τοῦ Κ χωρίου. Ἐνέγραψα δὴ τὰ ΑΔΒ, ΒΕΓ τρίγωνα, ὡς εἴρηται, ἐνέγραψα δὲ καὶ εἰς τὰ περιλειπόμενα τμάματα ἄλλα τρίγωνα τὰν αὐτὰν βάσιν ἔχοντα τοῖς τμαμάτεσσιν καὶ ὕψος τὸ αὐτό, καὶ ἀεὶ εἰς τὰ ὕστερον γινόμενα τμάματα ἐγγράφω δύο τρίγωνα τὰν αὐτὰν βάσιν ἔχοντα τοῖς τμαμάτεσσιν καὶ ὕψος τὸ αὐτό· ἐσσοῦνται δὴ τὰ καταλειπόμενα [194] τμάματα ἐλάσσονα τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει τὸ ΑΔΒΕΓ τμᾶμα τοῦ Κ χωρίου. Ὥστε τὸ ἐγγραφόμενον πολύγωνον μεῖζον ἐσσεῖται τοῦ Κ· ὅπερ ἀδύνατον. Ἐπεὶ γάρ ἐστιν ἑξῆς κείμενα χωρία ἐν τῷ τετραπλασίονι λόγῳ, πρῶτον μὲν τὸ ΑΒΓ τρίγωνον τετραπλάσιον τῶν ΑΔΒ, ΒΕΓ τριγώνων, ἔπειτα δὲ αὐτὰ ταῦτα τετραπλάσια τῶν εἰς τὰ ἑπόμενα τμάματα ἐγγραφέντων καὶ ἀεὶ οὕτω, δῆλον ὡς σύμπαντα τὰ χωρία ἐλάσσονά ἐστιν ἢ ἐπίτριτα τοῦ μεγίστου, τὸ δὲ Κ ἐπίτριτόν ἐστι τοῦ μεγίστου χωρίου. Οὐκ ἄρα ἐστὶν μεῖζον τὸ ΑΔΒΕΓ τμᾶμα τοῦ Κ χωρίου.

   Ἔστω δέ, εἰ δυνατόν, ἔλασσον. Κείσθω δὴ τὸ μὲν ΑΒΓ τρίγωνον ἴσον τῷ Ζ, τοῦ δὲ Ζ τέταρτον τὸ Η, καὶ ὁμοίως τοῦ Η τὸ Θ, καὶ ἀεὶ ἑξῆς τιθέσθω, ἕως κα γένηται τὸ ἔσχατον ἔλασσον τᾶς ὑπεροχᾶς, ᾇ ὑπερέχει τὸ Κ χωρίον τοῦ τμάματος, καὶ ἔστω ἔλασσον τὸ Ι· ἔστιν δὴ τὰ Ζ, Η, Θ, Ι χωρία καὶ τὸ τρίτον τοῦ Ι ἐπίτριτα τοῦ Ζ. Ἔστιν δὲ καὶ τὸ Κ τοῦ Ζ ἐπίτριτον· ἴσον ἄρα τὸ Κ τοῖς Ζ, Η, Θ, Ι καὶ τῷ τρίτῳ μέρει τοῦ Ι. Ἐπεὶ οὖν τὸ Κ χωρίον [195] τῶν μὲν Ζ, Η, Θ, Ι χωρίων ὑπερέχει ἐλάσσονι τοῦ Ι, τοῦ δὲ τμάματος μείζονι τοῦ Ι, δῆλον ὡς μείζονά ἐντι τὰ Ζ, Η, Θ, Ι χωρία τοῦ τμάματος· ὅπερ ἀδύνατον· ἐδείχθη γὰρ ὅτι, ἐὰν ᾖ ὁποσαοῦν χωρία ἑξῆς κείμενα ἐν τετραπλασίονι λόγῳ, τὸ δὲ μέγιστον ἴσον ᾖ τῷ εἰς τὸ τμᾶμα ἐγγραφομένῳ τριγώνῳ, τὰ σύμπαντα χωρία ἐλάσσονα ἐσσεῖται τοῦ τμάματος. Οὐκ ἄρα τὸ ΑΔΒΕΓ τμᾶμα ἔλασσόν ἐστι τοῦ Κ χωρίου. Ἐδείχθη δὲ ὅτι οὐδὲ μεῖζον· ἴσον ἄρα ἐστὶν τῷ Κ. Τὸ δὲ Κ χωρίον ἐπίτριτόν ἐστι τοῦ τριγώνου τοῦ ΑΒΓ· καὶ τὸ ΑΔΒΕΓ ἄρα τμᾶμα ἐπίτριτόν ἐστι τοῦ ΑΒΓ τριγώνου.

 

---

ΠΕΡΙ ΟΧΟΥΜΕΝΩΝ Α΄

Ἀρχιμήδους Ὀχουμένων α΄

   Ὑποκείσθω τὸ ὑγρὸν φύσιν ἔχον τοιαύταν, ὥστε τῶν μερέων αὐτοῦ τῶν ἐξ ἴσου κειμένων καὶ συνεχέων ἐόντων ἐξωθεῖσθαι τὸ ἧσσον θλιβόμενον ὑπὸ τοῦ μᾶλλον θλιβομένου, καὶ ἕκαστον δὲ τῶν μερέων αὐτοῦ θλίβεσθαι τῷ ὑπεράνω αὐτοῦ ὑγρῷ κατὰ κάθετον ἐόντι, εἴ κα μὴ τὸ ὑγρὸν ᾖ καθειργμένον ἔν τινι καὶ ὑπ᾿ ἄλλου τινὸς θλιβόμενον.

   α΄.

   Εἴ κα ᾖ ἐπιφάνειά τις ἐπιπέδῳ τεμνομένα διά τινος ἀεὶ τοῦ σαμείου τὰν τομὰν ποιέοντι [8] [ἢ] κατὰ τὰν ΟΠ· ὥστε ἐξωθήσονται τὰ ἧσσον θλιβόμενα ὑπὸ τῶν μᾶλλον θλιβομένων· οὐ μένει ἄρα τὸ ὑγρόν. Ὑπέκειτο δὲ καθεστακὸς εἶμεν ὥστε μένειν ἀκίνητον· ἀναγκαῖον ἄρα τὰν ΑΒΓΔ γραμμὰν κύκλου περιφέρειαν εἶμεν καὶ κέντρον αὐτᾶς τὸ Κ. Ὁμοίως δὴ δειχθήσεται καί, ὅπως κα ἄλλως ἁ ἐπιφάνεια τοῦ ὑγροῦ ἐπιπέδῳ τμαθῇ διὰ τοῦ κέντρου τᾶς γᾶς, ὅτι ἁ τομὰ ἐσσεῖται κύκλου περιφέρεια, καὶ κέντρον αὐτᾶς ἐσσεῖται ὃ καὶ τᾶς γᾶς ἐστι κέντρον. Δῆλον οὖν ὅτι ἁ ἐπιφάνεια τοῦ ὑγροῦ καθεστακότος ἀκινήτου σφαίρας ἔχει τὸ σχῆμα τὸ αὐτὸ κέντρον ἐχούσας τᾷ γᾷ, ἐπειδὴ τοιαύτα ἐστίν, ὥστε [9] ‹διὰ τοῦ αὐτοῦ σαμείου τμαθεῖς›αν τὰν τομὰν ποιεῖν περιφέρειαν κύκλου κέντρον ἔχοντος τὸ σαμεῖον, δι᾿ οὗ τέμνεται τῷ ἐπιπέδῳ.

   γ΄. Τῶν στερεῶν μεγεθέων τὰ ἰσοβαρέοντα τῷ ὑγρῷ ἀφεθέντα εἰς τὸ ὑγρὸν καταβασοῦνται, ὥστε τᾶς ἐπιφανείας τᾶς τοῦ ὑγροῦ μὴ ὑπερέχειν μηδέν, καὶ οὐκέτι οἰσθήσονται ἐπὶ τὸ κάτω.

   Ἀφείσθω γάρ τι στερεὸν μέγεθος εἰς τὸ ὑγρὸν τῶν ἰσοβαρέων τῷ ὑγρῷ καί, εἰ δυνατόν, ὑπερεχέτω τι αὐτοῦ τᾶς τοῦ ὑγροῦ ἐπιφανείας, καθεστάτω δὲ τὸ ὑγρόν, ὥστε μένειν ἀκίνητον. Νοείσθω δή τι ἐπίπεδον ἐκβεβλημένον διά τε τοῦ κέντρου τᾶς γᾶς καὶ τοῦ ὑγροῦ καὶ διὰ τοῦ στερεοῦ μεγέθεος, τομὰ δὲ ἔστω τᾶς μὲν ἐπιφανείας τοῦ ὑγροῦ ἁ ΑΒΓΔ περιφέρεια, τοῦ δὲ στερεοῦ μεγέθεος τὸ ΕΖΗΘ σχῆμα, κέντρον δὲ τᾶς γᾶς τὸ Κ. Ἔστω δὴ τοῦ μὲν στερεοῦ τὸ μὲν ΒΓΗΘ ἐν τῷ ὑγρῷ, τὸ δὲ ΒΕΖΓ ἐκτός. [10] Νοείσθω δὴ τὸ στερεὸν σχῆμα περιλαμβανόμενον πυραμοειδεῖ βάσιν μὲν ἔχοντι τὸ παραλληλόγραμμον τὸ ἐν τᾷ ἐπιφανείᾳ τοῦ ὑγροῦ, κορυφὰν δὲ τὸ κέντρον τᾶς γᾶς, ‹τομὰ δὲ ἔστω τοῦ τε ἐπιπ›έδου, ἐν ᾧ ἐστιν ἁ ΑΒΓΔ περιφέρεια, καὶ τῶν τᾶς πυραμίδος ἐπιπέδων αἱ ΚΛ, ΚΜ. Γεγράφθω τις ἄλλας σφαίρας ἐπιφάνεια περὶ κέντρον τὸ Κ ἐν τῷ ὑγρῷ τῷ ὑπὸ τοῦ ΕΖΗΘ καὶ τεμνέσθω ἐπιπέδῳ, λελάφθω δέ τις καὶ ἄλλα πυραμὶς ἴσα καὶ ὁμοία τᾷ περιλαμβανούσᾳ τὸ στερεὸν συνεχὴς αὐτᾷ, τομὰ δὲ ἔστω τῶν ἐπιπέδων αὐτᾶς αἱ ΚΜ, ΚΝ, καὶ ἐν τῷ ὑγρῷ νοείσθω τι μέγεθος τοῦ ὑγροῦ ἀπολαμβανόμενον τὸ ΡΣΤΥ ἴσον καὶ ὅμοιον τῷ στερεῷ τῷ κατὰ τὰ Β, Η, Θ, Γ, ὅ ἐστιν αὐτοῦ ἐν τῷ ὑγρῷ· τὰ δὴ μέρεα τοῦ ὑγροῦ τά τε ἐν τᾷ πρώτᾳ πυραμίδι τὰ ὑπὸ τὰν ἐπιφάνειαν, ἐν ᾇ ἐστιν ἁ ΞΟ περιφέρεια, καὶ τὰ ἐν τᾷ ἑτέρᾳ, ἐν ᾇ ἐστιν ἁ ΠΟ, ἐξ ἴσου τέ ἐντι κείμενα καὶ συνεχέα. Οὐχ ὁμοίως δὲ θλίβονται· τὸ μὲν γὰρ κατὰ τὰν ΞΟ θλίβεται τῷ στερεῷ τῷ ΘΗΕΖ καὶ τῷ ὑγρῷ τῷ μεταξὺ τᾶν ἐπιφανειᾶν τᾶν κατὰ τὰς ΞΟ, ΛΜ καὶ τῶν τᾶς πυραμίδος ἐπιπέδων, τὸ δὲ κατὰ τὰν ΠΟ τῷ ὑγρῷ τῷ μεταξὺ τᾶν ἐπιφανειᾶν τᾶν κατὰ τὰς ΠΟ, ΜΝ καὶ τῶν τᾶς πυραμίδος ἐπιπέδων. Ἔλασσον δὲ ἐσσεῖται τὸ βάρος τοῦ ὑγροῦ τοῦ κατὰ τὰς ΜΝ, ΟΠ· τὸ μὲν γὰρ κατὰ τὸ ΡΣΤΥ ἔλασσόν ἐστι τοῦ ΕΖΗΘ στερεοῦ· αὐτῷ γὰρ τῷ κατὰ τὸ ΗΒΓΘ ἴσον ἐστὶν διὰ τὸ τῷ μεγέθει [11] ἴσον εἶμεν καὶ ἰσοβαρὲς ὑποκεῖσθαι τὸ στερεὸν ‹τῷ ὑγρῷ· τὸ δὲ λοιπὸν τῷ λοιπῷ› ἴσον ἐστί. Δῆλον οὖν ὅτι ἐξωθήσεται τὸ μέρος τὸ κατὰ τὰν ΟΠ περιφέρειαν ὑπὸ τοῦ κατὰ τὰν ΟΞ περιφέρειαν, καὶ οὐκ ἐσσεῖται τὸ ὑγρὸν ἀκίνητον. Ὑπόκειται δὲ ἀκίνητον ἐόν· οὐκ ἄρα ὑπερέξει τᾶς τοῦ ὑγροῦ ἐπιφανείας οὐδὲν τοῦ στερεοῦ μεγέθεος. Καταδὺν δὲ τὸ στερεὸν οὐκ οἰσθήσεται ἐς τὰ κάτω· ὁμοίως γὰρ πάντα θλιβησοῦντι τὰ μέρεα τοῦ ὑγροῦ τὰ ἐξ ἴσου κείμενα διὰ τὸ ἰσοβαρέα εἶμεν τὸ στερεὸν καὶ τὸ ὑγρόν.

   δ΄.

   Τῶν στερῶν μεγεθέων ὅ κα κουφότερον ᾖ τοῦ ὑγροῦ, ἀφεθὲν ἐς τὸ ὑγρὸν οὐ καταδύσεται ὅλον, ἀλλὰ ἐσσεῖταί τι αὐτοῦ ἐκτὸς τᾶς τοῦ ὑγροῦ ἐπιφανείας.

   Ἔστω γὰρ στερεὸν μέγεθος κουφότερον τοῦ ὑγροῦ καὶ ἀφεθὲν ἐς τὸ ὑγρὸν δεδυκέτω ὅλον, εἰ δυνατόν, καὶ μηδὲν αὐτοῦ ἔστω ἐκτὸς τᾶς τοῦ ὑγροῦ ἐπιφανείας, καθεστακέτω δὲ τὸ ὑγρόν, ὥστε μένειν ἀκίνητον. Νοείσθω [12] δή τι ἐπίπεδον ἐκβεβλημένον διὰ τοῦ κέντρου τᾶς γᾶς καὶ διὰ τοῦ ὑγροῦ καὶ τοῦ στερεοῦ μεγέθεος, τεμνέσθω δὲ ὑπὸ τοῦ ἐπιπέδου τούτου ἡ μὲν τοῦ ὑγροῦ ἐπιφάνεια κατὰ τὰν ΑΒΓ περιφέρειαν, τὸ δὲ στερεὸν μέγεθος κατὰ τὸ σχῆμα, ἐν ᾧ Ζ, κέντρον δὲ ἔστω τᾶς γᾶς τὸ Κ, νοείσθω δέ τις πυραμὶς περιλαμβάνουσα τὸ Ζ σχῆμα, καθ᾿ ἃ καὶ πρότερον, κορυφὰν ἔχουσα τὸ Κ σαμεῖον, τεμνέσθω δὲ αὐτᾶς τὰ ἐπίπεδα ὑπὸ τοῦ ἐπιπέδου τοῦ ΑΒΓ κατὰ τὰς ΑΚ, ΚΒ, λελάφθω δέ τις καὶ ἄλλα ἴσα πυραμὶς καὶ ὁμοία ταύτᾳ, τεμνέσθω δὲ αὐτᾶς τὰ ἐπίπεδα ὑπὸ τοῦ ἐπιπέδου κατὰ τὰς ΚΒ, ΚΓ, γεγράφθω δέ τις καὶ ἄλλας σφαίρας ἐπιφάνεια ἐν τῷ ὑγρῷ περὶ κέντρον τὸ Κ, ὑποκάτω δὲ τοῦ στερεοῦ μεγέθεος, τεμνέσθω δ᾿ αὕτα ὑπὸ τοῦ αὐτοῦ ἐπιπέδου κατὰ τὰν ΞΟΠ περιφέρειαν, νοείσθω δὲ καὶ μέγεθος ἀπολαμβανόμενον τοῦ ὑγροῦ τὸ κατὰ τὸ Η ἐν τᾷ ὕστερον πυραμίδι ἴσον τῷ κατὰ τὸ Ζ στερεῷ· τὰ δὴ μέρεα τοῦ ὑγροῦ τοῦ ἐν τᾷ πρώτᾳ πυραμίδι τὰ ὑπὸ τὰν ἐπιφάνειαν τὰν κατὰ τὰν ΞΟ περιφέρειαν καὶ τοῦ ἐν τᾷ δευτέρᾳ τὰ ὑπὸ τὰν ἐπιφάνειαν τὰν κατὰ τὰν ΟΠ περιφέρειαν ἐξ ἴσου τέ ἐντι κείμενα καὶ συνεχέα ἀλλάλοις. Οὐχ ὁμοίως δὲ θλίβονται· τὸ μὲν γὰρ ἐν τᾷ πρώτᾳ πυραμίδι θλίβεται τῷ κατὰ τὸ Ζ στερεῷ μεγέθει καὶ τῷ περιέχοντι ὑγρῷ αὐτὸ καὶ ἐόντι ἐν τῷ τόπῳ τᾶς πυραμίδος τῷ κατὰ τὰ Α, Β, Ο, Ξ, τὸ δ᾿ ἐν τᾷ ἑτέρᾳ πυραμίδι θλίβεται τῷ ὑγρῷ τῷ περιέχοντι αὐτὸ καὶ ἐόντι τᾶς πυραμίδος ἐν [13] τῷ τόπῳ τῷ κατὰ τὰ Π, Ο, Β, Γ, ἔστι δὲ τὸ βάρος τὸ κατὰ ‹τὸ Ζ ἔλασσον τοῦ βάρεος τοῦ κατὰ τὸ› Η, ἐπειδὴ τῷ μὲν μεγέθει ἴσον ἐστίν, κουφότερον δὲ ὑπόκειται τὸ στερεὸν μέγεθος εἶμεν τοῦ ὑγροῦ, τὰ δὲ τοῦ περιέχοντος ὑγροῦ τὰ Ζ, Η μεγέθεα ἐν ἑκατέρᾳ τᾶν πυραμίδων ἴσα· μᾶλλον οὖν θλιβήσεται τὸ μέρος τοῦ ὑγροῦ τὸ ὑπὸ τὰν ἐπιφάνειαν τὰν κατὰ τὰν ΟΠ περιφέρειαν· ἐξωθήσει οὖν τὸ ἧσσον θλιβόμενον, καὶ οὐ μενεῖ τὸ ὑγρὸν ἀκίνητον. Ὑπέκειτο δέ· οὐκ ἄρα καταδύσεται ὅλον, ἀλλ᾿ ἐσσεῖταί τι αὐτοῦ ἐκτὸς τᾶς τοῦ ὑγροῦ ἐπιφανείας.

   ε΄.

   Τῶν στερεῶν μεγεθέων ὅ κα ᾖ κουφότερον τοῦ ὑγροῦ, ἀφεθὲν εἰς τὸ ὑγρὸν ἐς τοσοῦτο καταδύσεται, ὥστε ταλικοῦτον ὄγκον τοῦ ὑγροῦ, ἁλίκος ἐστὶν ὁ τοῦ καταδεδυκότος ὄγκος, ἴσον βάρος ἔχειν ὅλῳ τῷ μεγέθει.

   Κατεσκευάσθω ταὐτὰ τοῖς πρότερον, καὶ ἔστω τὸ ὑγρὸν ἀκίνητον, ἔστω δὲ κουφότερον τοῦ ὑγροῦ τὸ [14] ΕΖΗΘ μέγεθος. Ἐπεὶ οὖν ἀκίνητόν ἐστιν τὸ ὑγρόν, ὁμοίως θλιβήσεται τὰ μέρεα αὐτοῦ τὰ ἐξ ἴσου κείμενα· ὁμοίως ἄρα θλιβήσεται τὸ ὑγρὸν τὸ ὑπὸ τὰν ἐπιφάνειαν τὰν κατὰ τὰς ΞΟ καὶ ΠΟ περιφερείας· ὥστε ἴσον ἐστὶ τὸ βάρος, ᾧ θλίβονται. Ἔστι δὲ καὶ τοῦ ὑγροῦ τὸ βάρος τοῦ ἐν τᾷ πρώτᾳ πυραμίδι χωρὶς τοῦ ΒΗΘΓ στερεοῦ ἴσον τῷ βάρει τῷ ‹τοῦ ἐν τᾷ ἑτέρᾳ πυραμίδι› χωρὶς τοῦ ΡΣΤΥ ὑγροῦ· δῆλον οὖν ὅτι τὸ τοῦ ΕΖΗΘ μεγέθεος βάρος ἴσον ἐστὶ τῷ τοῦ ΡΣΤΥ ὑγροῦ βάρει. Φανερὸν οὖν ὅτι ταλικοῦτος ὄγκος τοῦ ὑγροῦ, ἁλίκον ἐστὶ τὸ δεδυκὸς τοῦ στερεοῦ μεγέθεος, ἴσον βάρος ἔχει ὅλῳ τῷ μεγέθει.

   Ϛ΄.

   Τὰ κουφότερα στερεὰ τοῦ ὑγροῦ βιασθέντα εἰς τὸ ὑγρὸν ἀναφέρεται τοσαύτᾳ βίᾳ ἐς τὸ ἄνω, ὅσον ἐστὶ τὸ βάρος, ᾧ βαρύτερόν ἐστι τοῦ μεγέθεος τὸ ὑγρὸν τὸ ἴσον ὄγκον ἔχον τῷ μεγέθει.

   Ἔστω τι μέγεθος τὸ Α κουφότερον τοῦ ὑγροῦ, ἔστω δὲ τοῦ μὲν μεγέθεος τοῦ ἐν ᾧ Α βάρος τὸ Β, τοῦ δὲ ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος τῷ Α τὸ ΒΓ. Δεικτέον ὅτι τὸ [15] Α μέγεθος βιασθὲν ἐς τὸ ὑγρὸν ἀνοισεῖται ἐς τὸ ἐπάνω τοσαύτᾳ βίᾳ, ὅσον ἐστὶ τὸ βάρος τὸ Γ.

   Λελάφθω γάρ τι μέγεθος τὸ ἐν ᾧ τὸ Δ βάρος ἴσον ἔχον τῷ Γ· τὸ δὴ μέγεθος τὸ ἐξ ἀμφοτέρων τῶν ἐν οἷς Α, Δ μεγεθέων ἐς τὰ αὐτὰ συντεθέντων κουφότερόν ἐστι τοῦ ὑγροῦ· ἔστι γὰρ τοῦ μὲν μεγέθεος τοῦ ἐξ ἀμφοτέρων βάρος τὸ ΒΓ, τοῦ δὲ ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος αὐτῷ μεῖζον τοῦ ΒΓ διὰ τὸ τοῦ ἴσον ἔχοντος ὄγκον τῷ τοῦ Α τὸ βάρος εἶμεν τὸ ΒΓ. Ἀφεθὲν οὖν ἐς τὸ ὑγρὸν τὸ μέγεθος τὸ ἐξ ἀμφοτέρων τῶν Α, Δ συγκείμενον ἐς τοσοῦτον δύσεται, ‹ἔστε κα ταλικοῦτος ὄγκος τοῦ› ὑγροῦ, ἁλίκον καὶ τὸ δεδυκὸς τοῦ μεγέθεος, ἴσον βάρος ἔχῃ τῷ ὅλῳ μεγέθει· δέδεικται γὰρ τοῦτο. Ἔστω δὴ ἐπιφάνειά τινος ὑγροῦ ἁ ΑΒΓΔ περιφέρεια. Ἐπεὶ οὖν ὁ ταλικοῦτος ὄγκος τοῦ ὑγροῦ, ἁλίκον ἐστὶ τὸ Α μέγεθος, ἴσον βάρος ἔχει τοῖς Α, Δ μεγέθεσιν, δῆλον ὅτι τὸ δεδυκὸς αὐτοῦ ἐσσεῖται τὸ Α μέγεθος, τὸ δὲ λοιπὸν αὐτοῦ, ἐν ᾧ Δ, ἐσσεῖται ὅλον ὑπὲρ τᾶς τοῦ ὑγροῦ ἐπιφανείας· εἰ γὰρ α... δέδυκεν τὸ στερεόν, ἕπεται ...... τούτου δεδειγμένου. Δῆλον οὖν ὅτι ..... ἐς τὸ ἄνω φέρεται τὸ Α μέγεθος .......... .......... ὑπὸ τοῦ ἄνω τοῦ Δ ἐς τὸ κάτω, ἐπεὶ οὐδέτερον ὑπ᾿ οὐδετέρου ἐξωθεῖτο. Ἀλλὰ τὸ Δ ἐς τὸ κάτω θλίβει τοσούτῳ βάρει, ἁλίκον ἐστὶ τὸ Γ· ὑπέκειτο γὰρ τὸ βάρος τοῦ ἐν ᾧ τὸ Δ εἶμεν ἴσον τῷ Γ· δῆλον οὖν ὃ ἔδει δεῖξαι.

[16]    ζ΄.

   Τὰ βαρύτερα τοῦ ὑγροῦ ἀφεθέντα εἰς τὸ ὑγρὸν οἰσεῖται κάτω, ἔστ᾿ ἂν καταβᾶντι, καὶ ἐσσοῦνται κουφότερα ἐν τῷ ὑγρῷ τοσοῦτον, ὅσον ἔχει τὸ βάρος τοῦ ὑγροῦ τοῦ ταλικοῦτον ὄγκον ἔχοντος, ἁλίκος ἐστὶν ὁ τοῦ στερεοῦ μεγέθεος ὄγκος.

   Ὅτι μὲν οὖν οἰσεῖται ἐς τὸ κάτω, ἔστ᾿ ἂν καταβᾶντι, δῆλον· τὰ γὰρ ὑποκάτω αὐτοῦ μέρεα τοῦ ὑγροῦ θλιβησοῦνται μᾶλλον τῶν ἐξ ἴσου αὐτοῖς κειμένων μερέων, ἐπειδὴ βαρύτερον ὑπόκειται τὸ στερεὸν μέγεθος τοῦ ὑγροῦ· ὅτι δὲ κουφότερα ἐσσοῦνται, ὡς εἴρηται, δειχθήσεται.

   Ἔστω τι μέγεθος τὸ Α, ὅ ἐστι βαρύτερον τοῦ ὑγροῦ, βάρος δὲ ἔστω τοῦ μὲν ἐν ᾧ Α μεγέθεος τὸ ΒΓ, τοῦ δὲ ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος τῷ Α τὸ Β. Δεικτέον ὅτι τὸ Α μέγεθος ἐν τῷ ὑγρῷ ἐὸν βάρος ἕξει ἴσον τῷ Γ.

   Λελάφθω γάρ τι μέγεθος τὸ ἐν ᾧ τὸ Δ ‹κουφότερον τοῦ ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος αὐτῷ, ἔστω› δὲ τοῦ μὲν ἐν ᾧ τὸ Δ μεγέθεος βάρος ἴσον τῷ Β βάρει, τοῦ δὲ [17] ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος τῷ Δ μεγέθει τὸ βάρος ἔστω ἴσον τῷ ΒΓ βάρει. Συντεθέντων δὴ ἐς τὸ αὐτὸ τῶν μεγεθέων, ἐν οἷς τὰ Α, Δ, τὸ τῶν συναμφοτέρων μέγεθος ἰσοβαρὲς ἐσσεῖται τῷ ὑγρῷ· ἔστι γὰρ τῶν μεγεθέων συναμφοτέρων τὸ βάρος ἴσον συναμφοτέροις τοῖς βάρεσιν τῷ τε ΒΓ καὶ τῷ Β, τοῦ δὲ ὑγροῦ τοῦ ἴσον ὄγκον ἔχοντος ἀμφοτέροις τοῖς μεγέθεσι τὸ βάρος ἴσον ἐστὶ τοῖς αὐτοῖς βάρεσιν. Ἀφεθέντων οὖν τῶν μεγεθέων ἐς τὸ ὑγρὸν ἰσορροπησοῦνται τῷ ὑγρῷ καὶ οὔτε εἰς τὸ ἄνω οἰσοῦνται οὔτε εἰς τὸ κάτω· διὸ τὸ μὲν ἐν ᾧ Α μέγεθος οἰσεῖ‹ται ἐς τὸ κάτω καὶ τοσαύτᾳ βίᾳ ὑ›πὸ τοῦ ἐν ᾧ Δ μεγέθεος ἀνέλκεται ἐς τὸ ἄνω, τὸ δὲ ἐν ᾧ Δ μέγεθος, ἐπεὶ κουφότερόν ἐστι τοῦ ὑγροῦ, ἀνοισεῖται εἰς τὸ ἄνω τοσαύτᾳ βίᾳ, ὅσον ἐστὶ τὸ Γ βάρος· δέδεικται γὰρ ὅτι τὰ κουφότερα τοῦ ὑγροῦ μεγέθεα στερεὰ βιασθέντα ἐς τὸ ὑγρὸν ἀναφέρονται τοσαύτᾳ βίᾳ ἐς τὸ ἄνω, ὅσον ἐστὶ τὸ βάρος, ᾧ βαρύτερόν ἐστι τοῦ μεγέθεος τὸ ὑγρὸν τὸ ἴσογκον τῷ μεγέθει. Ἔστι δὲ τῷ Γ βάρει βαρύτερον τοῦ Δ μεγέθεος τὸ ὑγρὸν τὸ ἴσον ὄγκον ἔχον τῷ Δ· δῆλον οὖν ὅτι καὶ τὸ ἐν ᾧ Α μέγεθος ἐς τὸ κάτω οἰσεῖ‹ται τοσούτῳ βάρει, ὅσον ἐστὶ τὸ Γ›.

   Ὑποκεί‹σθω τῶν ἐν τῷ ὑγρῷ ἄνω› φερομένων ἕκαστον ἀναφέρεσθαι κατὰ τὰν κάθετον τὰν διὰ τοῦ κέντρου τοῦ βάρεος αὐτοῦ ἀγμέναν.

[18]    η΄.

   Εἴ κα στερεόν τι μέγεθος κουφότερον τοῦ ὑγροῦ σφαίρας τμάματος ἔχον σχῆμα εἰς τὸ ὑγρὸν ἀφεθῇ οὕτως, ὥστε τὰν βάσιν τοῦ τμάματος μὴ ἅπτεσθαι τοῦ ὑγροῦ, ὀρθὸν καταστασεῖται τὸ σχῆμα οὕτως, ὥστε τὸν ἄξονα τοῦ τμάματος κατὰ κάθετον εἶμεν· καὶ εἴ κα ὑπό τινος ἕλκηται τὸ σχῆμα οὕτως, ὥστε τὰν βάσιν τοῦ τμάματος ἅπτεσθαι τοῦ ὑγροῦ, οὐ μενεῖ κεκλιμένον, εἴ κα ἀφεθῇ, ἀλλ᾿ ὀρθὸν ἀποκαταστασεῖται.

   Νοείσθω γάρ τι μέγεθος, οἷον εἴρηται, ἐς τὸ ὑγρὸν ἀφε‹θέν, καὶ διά τε τοῦ ἄξονος τοῦ› τμάματος καὶ τοῦ κέντρου τᾶς γᾶς νοείσθω ἐπίπεδον ἐκβεβλημένον, τομὰ δ᾿ ἔστω τᾶς μὲν ἐπιφανείας τοῦ ὑγροῦ ἁ ΑΒΓΔ, τοῦ δὲ σχήματος τοῦ ἐς τὸ ὑγρὸν ἀφεθέντος ἁ ΕΖΗΘ περιφέρεια, ἄξων δὲ τοῦ τμάματος ἔστω ἁ ΘΖ· τὸ δὴ κέντρον τᾶς σφαίρας ἔστιν ἐπὶ τᾶς ΘΖ.

   Πρῶτον μὲν, εἰ μεῖζόν ἐστιν ἡμισφαιρίου τὸ τμᾶμα, ἔστω τὸ Κ, καὶ ἔστω, εἰ δυνατόν, κεκλιμένον τὸ σχῆμα [19] ἤτοι ὑπό τινος κλιθὲν ἢ καθ᾿ αὑτό. Δεικτέον οὖν ὅτι οὐ μενεῖ, ἀλλ᾿ εἰς ὀρθὸν ἀποκαταστασεῖται, ὥστε τὰ Ζ, Θ κατὰ κάθετον εἶμεν.

   Ἐπεὶ γὰρ ὑπόκειται κεκλίσθαι τὸ σχῆμα, οὐκ ἔστι τὰ Ζ, Θ κατὰ κάθετον. Ἄχθω δὴ διὰ τοῦ Κ καὶ τοῦ Λ ἁ ΚΛ, τὸ δὲ Λ κέντρον ὑποκείσθω τᾶς γᾶς· τὸ δὴ σχῆμα τὸ ἐν τῷ ὑγρῷ ἀπολελαμμένον ὑπὸ τᾶς τοῦ ὑγροῦ ἐπιφανείας τὸν ἄξονα ἔχει ἐπὶ τᾶς ΚΛ· εἰ γάρ κα δύο σφαιρᾶν ἐπιφάνειαι τέμνωντι ἀλλάλας, ἁ τομὰ κύκλος ἐστὶν ὀρθὸς ποτὶ τὰν εὐθεῖαν τὰν ἐπιζευγνύουσαν τὰ κέντρα τᾶν σφαιρᾶν. Ἔστιν οὖν τοῦ σχήματος τοῦ κατὰ τὰν ΒΝΓ περιφέρειαν ἀπολαμβανομένου ἐν τῷ ὑγρῷ τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΚΛ· ἔστω τὸ Ρ. Τοῦ δὲ τμάματος ὅλου τοῦ κατὰ τὰν ΘΗΖΕ περιφέρειαν τὸ κέντρον ἐστὶ τοῦ βάρεος ἐπὶ τᾶς ΖΘ· ἔστω τὸ Ξ. Τοῦ ἄρα ‹λοιποῦ σχήματος τοῦ ἐκτὸς› τᾶς τοῦ ὑγροῦ ἐπιφανείας τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΡΞ ἐστὶν ἐκβληθείσας καὶ ἀπολαφθείσας τινὸς τᾶς ΣΞ ποτὶ τὰν ΞΡ τὸν αὐτὸν λόγον ἐχούσας, ὃν ἔχει τὸ βάρος τοῦ κατὰ τὰν ΒΝΓ περιφέρειαν τοῦ τμάματος ποτὶ τὸ βάρος τοῦ ἐκτὸς τοῦ ὑγροῦ· δέδεικται γὰρ ταῦτα. Ἔστω δὴ τὸ Σ κέντρον τοῦ εἰρημένου σχήματος. Ἐπεὶ οὖν τοῦ μὲν σχήματος, ὅ ἐστιν ἐκτὸς τοῦ ὑγροῦ, τὸ βάρος ἐς τὸ κάτω φέρεται κατὰ τὰν εὐθεῖαν τὰν ΛΣ, τὸ δὲ ἐν τῷ ὑγρῷ ἐς τὸ ἄνω κατὰ τὰν εὐθεῖαν τὰν ΡΚ, δῆλον ὡς οὐ μενεῖ τὸ σχῆμα, ἀλλὰ τὰ ποτὶ τῷ Ε μέρεα αὐτοῦ [20] ἐς τὸ κάτω οἰσοῦνται, τὰ δὲ ποτὶ τῷ Η ἐς τὸ ἄνω, καὶ ἀεὶ ἐς τὸ αὐτὸ οἰσοῦνται, ἕως κα ἁ ΖΘ κατὰ κάθετον γένηται. Κατὰ κάθετον δὲ γενομένας τᾶς ΖΘ τὰ κέντρα τοῦ βάρεος ἐσσοῦνται τοῦ ἐν τῷ ὑγρῷ καὶ τοῦ ἔκτος ἐπὶ τᾶς αὐτᾶς καθέτου· ἐπὶ γὰρ τᾶς ΖΘ ἐσσοῦνται· ἀντιθλιψοῦνται οὖν ἀλλήλοις τὰ βάρεα κατὰ τὰν αὐτὰν κάθετον, τὸ μὲν ἐς τὸ κάτω φερόμενον, τὸ δὲ ἐς τὸ ἄνω. Ὥστε μένει τὸ σχῆμα· οὐδέτερον γὰρ ὑπ᾿ οὐδετέρου ἐξωθήσεται.

   Τὰ δ᾿ αὐτὰ ἐσσεῖται καὶ εἴ κα τὸ σχῆμα ἡμισφαίριον ᾖ ἢ ἔλασσον ἡμισφαιρίου.

   θ΄.

   Καὶ τοίνυν, εἴ κα τὸ σχῆμα κουφότερον ἐὸν τοῦ ὑγροῦ ἀφεθῇ ἐς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ ὅλαν εἶμεν ἐν τῷ ὑγρῷ, ὀρθὸν καταστασεῖται τὸ σχῆμα οὕτως, ὥστε τὸν ἄξονα αὐτοῦ κατὰ κάθετον εἶμεν.

[21]    Νοείσθω γάρ τι μέγεθος, οἷον εἴρηται, εἰς τὸ ὑγρὸν ἀφετώμενον, νοείσθω δὲ καὶ ἐπίπεδον ἀγόμενον διὰ τοῦ ἄξονος τοῦ τμάματος καὶ διὰ τοῦ κέντρου τᾶς γᾶς, τομὰ δὲ ἔστω τᾶς μὲν ἐπιφανείας τοῦ ὑγροῦ ἁ ΑΒΓΔ περιφέρεια, τοῦ δὲ σχήματος ἁ ΕΖΗ περιφέρεια καὶ ἁ ΕΗ εὐθεῖα, ἄξων δὲ ἔστω τοῦ τμάματος ἁ ΖΘ. Εἰ οὖν δυνατόν, μὴ κατὰ κάθετον ἔστω ἁ ΖΘ· δεικτέον οὖν ὅτι οὐ μενεῖ τὸ σχῆμα, ἀλλὰ ἐπ᾿ ὀρθὸν καταστασεῖται.

   Ἔστι δὴ τὸ κέντρον τᾶς σφαίρας ἐπὶ τᾶς ΖΘ· πάλιν γὰρ μεῖζον ἡμισφαιρίου ἔστω πρῶτον τὸ σχῆμα· καὶ ἔστω τὸ Κ· διὰ δὲ τοῦ Κ καὶ τοῦ κέντρου τᾶς γᾶς τοῦ Λ ἄχθω ἁ ΚΛ· τὸ δὴ σχῆμα τὸ ἐκτὸς τοῦ ὑγροῦ ἀπολαμβανόμενον ὑπὸ τᾶς τοῦ ὑγροῦ ἐπιφανείας τὸν ἄξονα ἔχει ἐπὶ τᾶς διὰ τοῦ Κ, καὶ διὰ ταὐτὰ τοῖς πρότερον ἔστιν αὐτοῦ τὸ κέντρον τοῦ βάρεος ἐπὶ τᾶς ΝΚ· ἔστω [γὰρ] τὸ Ρ. Τοῦ δὲ ὅλου τμάματος τὸ κέν‹τρον τοῦ βάρεός ἐστιν ἐπὶ τᾶς ΖΘ› μεταξὺ τῶν Κ, Ζ· ἔστω τὸ Τ. Τοῦ ἄρα λοιποῦ σχήματος τοῦ ἐν τῷ ὑγρῷ τὸ κέντρον ἐσσεῖται ἐπὶ τᾶς ΤΡ εὐθείας ἐκβληθείσας καὶ ἀπολαφθείσας τινός, ἃ ἕξει ποτὶ τὰν ΤΡ τὸν αὐτὸν λόγον, ὃν ἔχει τὸ βάρος τοῦ τμάματος τοῦ ἐκτὸς τοῦ ὑγροῦ ποτὶ τὸ βάρος τοῦ σχήματος τοῦ ἐν τῷ ὑγρῷ· καὶ ἔστω τὸ Ο κέντρον τοῦ εἰρημένου σχήματος, καὶ διὰ τοῦ Ο κάθετος ἔστω ἁ ΟΛ· οἰσεῖται οὖν τὸ βάρος τοῦ μὲν τμάματος ὅ ἐστιν [22] ἐκτὸς τοῦ ὑγροῦ, κατὰ τὰν εὐθεῖαν τὰν ΡΛ ἐς τὸ κάτω, τοῦ δ᾿ ἐν τῷ ὑγρῷ σχήματος κατὰ τὰν εὐθεῖαν τὰν ΟΛ ἐς τὸ ἄνω. Οὐκ ἄρα μενεῖ τὸ σχῆμα, ἀλλὰ τοῦ σχήματος τὰ μὲν ποτὶ τῷ Η μέρεα οἰσοῦνται ἐς τὸ κάτω, τὰ δὲ ποτὶ τῷ Ε ἐς τὸ ἄνω, καὶ ἀεὶ τοῦτο ἐσσεῖται, ἔστε κα ΘΖ κατὰ κάθετον γένηται.

---

ΠΕΡΙ ΟΧΟΥΜΕΝΩΝ Β΄

[23]    α΄.

   Εἴ κά τι μέγεθος κουφότερον ἐὸν τοῦ ὑγροῦ ἀφεθῇ ἐς τὸ ὑγρόν, τοῦτον ἕξει τὸν λόγον τῷ βάρει ποτὶ τὸ ὑγρόν, ὃν ἔχει τὸ δεδυκὸς μέγεθος ποτὶ τὸ ὅλον μέγεθος.

   Ἀφείσθω γάρ τι εἰς τὸ ὑγρὸν μέγεθος στερεὸν τὸ ΦΑ κουφότερον τοῦ ὑγροῦ ἐόν, ἔστω δὲ τὸ μὲν δεδυκὸς αὐτοῦ τὸ Α, τὸ δὲ ἐκτὸς τοῦ ὑγροῦ τὸ Φ. Δεικτέον ὅτι τὸ ΦΑ τῷ βάρει ποτὶ τὸ ὑγρὸν τὸ ἴσογκον τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὸ Α ποτὶ τὸ ΦΑ.

   Λελάφθω γάρ τι τοῦ ὑγροῦ μέγεθος τὸ ΝΙ ἴσον ὄγκον ἔχον τῷ ΦΑ, καὶ τῷ μὲν Φ ἴσον ἔστω τὸ Ν, τῷ δὲ Α τὸ Ι, καὶ ἔτι τὸ μὲν τοῦ ΦΑ μεγέθεος βάρος ἔστω τὸ Β, τοῦ δὲ ΝΙ τὸ ΡΟ, τοῦ δὲ Ι τὸ Ρ· τὸ ΦΑ ἄρα ποτὶ τὸ ΝΙ τοῦτον ἔχει τὸν λόγον, ὃν τὸ Β ποτὶ τὸ ΡΟ. Ἀλλ᾿ ἐπεὶ τὸ ΦΑ [24] μέγεθος ἐς τὸ ὑγρὸν ἀφείθη κουφότερον ὑπάρχον τοῦ ὑγροῦ, δῆλον ὡς ὁ τοῦ δεδυκότος μεγέθεος ὄγκος ἴσον βάρος ἔχει τῷ ΦΑ μεγέθει· δέδεικται γὰρ τοῦτο· ἴσον ἄρα τὸ Β βάρος τῷ Ρ, ἐπειδὴ τὸ μὲν Β τὸ βάρος ἐστὶ ὅλου τοῦ ΦΑ μεγέθεος, τὸ δὲ Ρ τοῦ Ι ὑγροῦ, ὃ τῷ μεγέθει ἐγένετο ἴσον τῷ ἴσον ὄγκον ἔχοντι τῷ δεδυκότι μεγέθει τῷ Α· ἔχει ἄρα τὸ ΦΑ μέγεθος τῷ βάρει ποτὶ τὸ ΝΙ ὡς τὸ Ρ ποτὶ τὸ ΡΟ. Ὃν δὲ λόγον ἔχει τὸ Ρ ποτὶ τὸ ΡΟ, τοῦτον ἔχει τὸν λόγον τὸ Ι ποτὶ τὸ ΙΝ καὶ τὸ Α ποτὶ τὸ ΦΑ· δέδεικται ἄρα τὸ προτεθέν.

   β΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὅταν τὸν ἄξονα ἔχῃ μὴ μείζονα ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, πάντα λόγον ἔχον ποτὶ τὸ ὑγρὸν τῷ βάρει, ἀφεθὲν εἰς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, τεθὲν κεκλιμένον οὐ μενεῖ κεκλιμένον, ἀλλὰ ἀποκαταστασεῖται ὀρθόν. Ὀρθὸν δὲ λέγω καθεστακέναι τὸ τοιοῦτο τμᾶμα, ὁπόταν τὸ ἀποτετμακὸς αὐτὸ ἐπίπεδον παρὰ τὰν ἐπιφάνειαν ᾖ τοῦ ὑγροῦ.

[25]    Ἔστω τμᾶμα ὀρθογωνίου κωνοειδέος, οἷον εἴρηται, καὶ κείσθω κεκλιμένον. Δεικτέον ὅτι οὐ μενεῖ, ἀλλ᾿ ἀποκαταστασεῖται ὀρθόν.

   Τμαθέντος δὴ αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὸ ‹ἐπίπεδον τὸ ἐπὶ τᾶς ἐπιφανείας› τοῦ ὑγροῦ τμάματος ἔστω τομὰ ἁ ΑΠΟΛ ὀρθογωνίου κώνου τομά, ἄξων δὲ τοῦ τμάματος καὶ διάμετρος τᾶς τομᾶς ἁ ΝΟ, τᾶς δὲ τοῦ ὑγροῦ ἐπιφανείας τομὰ ἁ ΙΣ. Ἐπεὶ οὖν τὸ τμᾶμα οὐκ ἐστὶν ὀρθόν, οὐκ ἂν εἴη παράλληλος ἁ ΑΛ τᾷ ΙΣ· ὥστε οὐ ποιήσει ὀρθὰν γωνίαν ἁ ΝΟ ποτὶ τὰν ΙΣ. Ἄχθω οὖν παράλληλος ἁ ἐφαπτομένα ἁ ΚΩ τᾶς τοῦ κώνου τομᾶς κατὰ τὸ Π, καὶ ἀπὸ τοῦ Π παρὰ τὰν ΝΟ ἄχθω ἁ ΠΦ· τέμνει δὴ ἁ ΠΦ δίχα τὰν ΙΣ· δέδεικται γὰρ ἐν τοῖς κωνικοῖς. Τετμάσθω ἁ ΠΦ, ὥστε εἶμεν διπλασίαν τὰν ΠΒ τᾶς ΒΦ, καὶ ἁ ΝΟ κατὰ τὸ Ρ τετμάσθω, ὥστε καὶ τὰν ΟΡ τᾶς ΡΝ διπλασίαν εἶμεν· ἐσσεῖται δὴ τοῦ μείζονος ἀποτμάματος τοῦ στερεοῦ κέντρον τοῦ βάρεος τὸ Ρ, τοῦ δὲ κατὰ τὰν ΙΠΟΣ τὸ Β· δέδεικται γὰρ ἐν ταῖς Ἰσορροπίαις, ὅτι παντὸς ὀρθογωνίου κωνοειδέος τμάματος τὸ κέντρον τοῦ βάρεός ἐστιν ἐπὶ τοῦ ἄξονος διῃρημένου οὕτως, ὥστε τὸ ποτὶ τᾷ κορυφᾷ τοῦ ἄξονος τμᾶμα διπλάσιον εἶμεν τοῦ λοιποῦ. Ἀφαιρεθέντος δὴ τοῦ κατὰ τὰν ΙΠΟΣ τμάματος στερεοῦ ἀπὸ τοῦ ὅλου τοῦ λοιποῦ ‹τὸ› κέντρον ἐσσεῖται τοῦ βάρεος ἐπὶ τᾶς ΒΓ εὐθείας· δέδεικται γὰρ τοῦτο ἐν τοῖς Στοιχείοις τῶν μηχα‹νικῶν ὅτι, εἴ κα μέγεθος ἀφαιρεθῇ μὴ› τὸ αὐτὸ κέντρον ἔχον τοῦ βάρεος τῷ ὅλῳ μεγέθει, τοῦ λοιποῦ τὸ κέντρον ἐσσεῖται τοῦ βάρεος ἐπὶ [26] τᾶς εὐθείας τᾶς ἐπιζευγνυούσας τὰ κέντρα τοῦ τε ὅλου μεγέθεος καὶ τοῦ ἀφῃρημένου ἐκβεβλημένας ἐπὶ τὰ αὐτά, ἐφ᾿ ἃ τὸ κέντρον τοῦ ὅλου μεγέθεός ἐστιν. Ἐκβεβλήσθω δὴ ἁ ΒΡ ἐπὶ τὸ Γ, καὶ ἔστω τὸ Γ κέντρον τοῦ βάρεος τοῦ λοιποῦ μεγέθεος. Ἐπεὶ οὖν ἁ ΝΟ τᾶς μὲν ΟΡ ἡμιολία, τᾶς δὲ μέχρι τοῦ ἄξονος οὐ μείζων ἢ ἡμιολία, δῆλον ὅτι ἁ ΡΟ τᾶς μέχρι τοῦ ἄξονος οὐκ ἐστὶ μείζων· ἁ ΠΡ ἄρα ποτὶ τὰν ΚΩ γωνίας ἀνίσους ποιεῖ, καὶ ἁ ὑπὸ τῶν ΡΠΩ γίνεται ὀξεῖα· ἁ ἀπὸ τοῦ Ρ ἄρα κάθετος ἐπὶ τὰν ΠΩ ἀγομένα μεταξὺ πεσεῖται τῶν Π, Ω. Πιπτέτω ὡς ἁ ΡΘ· ἁ ΡΘ ἄρα ὀρθά ἐστιν ποτὶ τὸ .......κ..ος ἐπίπεδον, ἐν ᾧ ἐστιν ἁ ΣΙ, ὅ ἐστιν ἐπὶ τᾶς ἐπιφανείας τοῦ ὑγροῦ. Ἄχθωσαν δή τινες ἀπὸ τῶν Β, Γ παρὰ τὰν ΡΘ· ἐνεχθήσεται δὴ τὸ μὲν ἐκτὸς τοῦ ὑγροῦ τοῦ μεγέθεος εἰς τὸ κάτω κατὰ τὰν διὰ τοῦ Γ ἀγομέναν κάθετον· ὑπόκειται γὰρ ἕκαστον τῶν βαρέων εἰς τὸ κάτω φέρεσθαι κατὰ τὰν κάθετον τὰν διὰ τοῦ κέντρου ἀγομέναν· τὸ δὲ ἐν τῷ ὑγρῷ μέγεθος, ἐπεὶ κουφότερον γίνεται τοῦ ὑγροῦ, ἐνεχθήσεται εἰς τὸ ἄνω κατὰ τὰν κάθετον τὰν διὰ τοῦ Β ἀγομέναν. Ἐπεὶ δὲ οὐ κατὰ τὰν αὐτὰν κάθετον ἀλλάλοις ἀντιθλίβονται, ‹οὐ μενεῖ τὸ σχῆμα, ἀλλὰ τὰ μὲν κατὰ› τὸ Α εἰς τὸ ἄνω ἐνεχθήσεται, τὰ δὲ κατὰ τὸ Λ εἰς τὸ κάτω, καὶ τοῦτο ἀεὶ ἐσσεῖται, ἕως ἂν ὀρθὸν ἀποκατασταθῇ.

   γ΄.

   Ὀρθὸν τμᾶμα ὀρθογωνίου κωνοειδέος, ὅταν τὸν ἄξονα ἔχῃ μὴ μείζονα ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, πάντα [27] λόγον ἔχον ποτὶ τὸ ὑγρὸν τῷ βάρει, ἀφεθὲν εἰς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ ὅλαν εἶμεν ἐν τῷ ὑγρῷ, τεθὲν κεκλιμένον οὐ μενεῖ κεκλιμένον, ἀλλ᾿ ἀποκαταστασεῖται οὕτως, ὥστε τὸν ἄξονα αὐτοῦ κατὰ κάθετον εἶμεν.

   Ἀφείσθω γάρ τι τμᾶμα εἰς τὸ ὑγρόν, οἷον εἴρηται, καὶ ἔστω αὐτοῦ ἁ βάσις ἐν τῷ ὑγρῷ, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ τομὰ ἔστω ἁ ΑΠΟΛ ὀρθογωνίου κώνου τομά, ἄξων δὲ τοῦ τμάματος καὶ διάμετρος τᾶς τομᾶς ἁ ΠΦ, τᾶς δὲ ἐπιφανείας τοῦ ὑγροῦ τομὰ ἁ ΙΣ. Ἐπειδὴ οὖν κεκλιμένον κεῖται τὸ τμᾶμα, οὐκ ἐσσεῖται κατὰ κάθετον ὁ ἄξων· οὐκ ἄρα ποιήσει ἁ ΠΦ ἴσας γωνίας ποτὶ τὰν ΙΣ. Ἄχθω δή τις ‹ἁ ΚΩ παρὰ τὰν ΙΣ ἐφαπτομένα κατὰ› τὸ Ο τᾶς ΑΠΟΛ τομᾶς, καὶ τοῦ μὲν ΑΠΟΛ στερεοῦ κέντρον ἔστω τοῦ βάρεος τὸ Ρ, τοῦ δὲ ΙΠΟΣ στερεοῦ τὸ Β, καὶ ἐπιζευχθεῖσα ἁ ΒΡ ἐκβεβλήσθω, καὶ ἔστω κέντρον τοῦ βάρεος τὸ Γ τοῦ ΙΣΛΑ. Ὁμοίως δὴ δειχθήσεται ἁ μὲν ὑπὸ τᾶν ΡΟ, ΟΚ γωνία ὀξεῖα, ἁ δὲ ἀπὸ τοῦ Ρ κάθετος [28] ἐπὶ τὰν ΚΩ ἀγομένα μεταξὺ πίπτουσα τῶν Κ, Ο· ἔστω ἁ ΡΘ. Ἐὰν δὴ ἀπὸ τῶν Γ, Β ἀχθέωντί τινες παρὰ τὰν ΡΘ, τὸ μὲν ἐν τῷ ὑγρῷ ἀπολαφθὲν ἐνεχθήσεται ἄνω κατὰ τὰν διὰ τοῦ Γ ἀγομέναν, τὸ δ᾿ ἐκτὸς τοῦ ὑγροῦ κατὰ τὰν διὰ τοῦ Β ἀγομέναν κάτω, καὶ οὐ μενεῖ τὸ ΑΠΟΛ στερεὸν οὕτως ἔχον ἐν τῷ ὑγρῷ, ἀλλὰ τὸ μὲν κατὰ τὸ Α ἄνω τὰν φορὰν ἕξει, τὸ δὲ κατὰ τὸ Λ κάτω, ἕως ἂν γένηται ἁ ΠΦ κατὰ κάθετον.

   δ΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὁπόταν κουφότερον ᾖ τοῦ ὑγροῦ καὶ τὸν ἄξονα ἔχῃ μείζονα ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, ὅταν τῷ βάρει ποτὶ τὸ ἴσογκον ὑγρὸν μὴ ἐλάσ‹σονα λόγον ἔχῃ τοῦ ὃν ἔχει› τὸ τετράγωνον τὸ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τοῦ ἄξονος, ἀφεθὲν εἰς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, τεθὲν κεκλιμένον οὐ μενεῖ κεκλιμένον, ἀλλὰ ἀποκαταστασεῖται εἰς ὀρθόν.

[29]    Ἔστω τμᾶμα ὀρθογωνίου κωνοειδέος, οἷον εἴρηται, καὶ ἀφεθὲν εἰς τὸ ὑγρόν, εἰ δυνατόν, ἔστω μὴ ὀρθόν, ἀλλὰ κεκλιμένον, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ τοῦ μὲν τμάματος τομὰ

[36]    ζ΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὅταν τοῦ ὑγροῦ κουφότερον ᾖ καὶ τὸν ἄξονα ἔχῃ μείζονα μὲν ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, ἐλάσσονα δὲ ἢ ὥστε λόγον ἔχειν ποτὶ τὰν μέχρι τοῦ ἄξονος, ὃν τὰ ιε ποτὶ δ, ἀφεθὲν εἰς τὸ ὑγρὸν οὕτως ὥστε τὰν βάσιν ὅλαν εἶμεν ἐν τῷ ὑγρῷ, οὐδέποτε καταστασεῖται οὕτως, ὥστε τὰν [37] βάσιν αὐτοῦ ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, ἀλλ᾿ ὥστε ὅλαν εἶμεν ἐν τῷ ὑγρῷ μηδὲ καθ᾿ ἓν σαμεῖον ἁπτομέναν τᾶς ἐπιφανείας.

   Ἔστω τμᾶμα οἷον εἴρηται, καὶ ἀφεθὲν ἐς τὸ ὑγρὸν καθάπερ ἐρρέθη καθεστακέτω οὕτως, ὥστε τὰν βάσιν αὐτοῦ ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας. Δεικτέον ὅτι οὐ μενεῖ, ἀλλὰ ἀνακλιθήσεται οὕτως, ὥστε τὰν βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας.

   Τμαθέντος γὰρ αὐτοῦ ἐπιπέδῳ ὀρθῷ ποτὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν τομὰ ἔστω ἁ ΑΠΟΛ ὀρθογωνίου κώνου τομά, ἔστω δὲ καὶ τᾶς τοῦ ὑγροῦ ἐπιφανείας τομὰ ἁ ΣΛ, ἄξων δὲ ἔστω τοῦ τμάματος καὶ διάμετρος ἁ ΠΦ, πάλιν δὲ τεμνέσθω ἁ ΠΦ κατὰ μὲν τὸ Ρ, ὥστε διπλασίαν εἶμεν τὰν ΡΠ τᾶς ΡΦ, κατὰ δὲ τὸ Ω, ὥστε τὰν ΠΦ ποτὶ τὰν ΡΩ λόγον ἔχειν ὃν τὰ ιε ποτὶ τὰ δ, καὶ ἁ ΩΚ ὀρθὰ ἄχθω τᾷ ΠΦ· ἐσσεῖται δὴ ἐλάσσων ἁ ΡΩ τᾶς μέχρι τοῦ ἄξονος. Ἀπολελάφθω οὖν τᾷ μέχρι τοῦ ἄξονος ἴσα ἁ ΡΗ, καὶ ἁ μὲν ΤΟ ἄχθω ἐφαπτομένα τᾶς τομᾶς κατὰ τὸ Ο παράλληλος ἐοῦσα τᾷ ΣΛ, ἁ δὲ ΝΟ τᾷ ΠΦ, τεμνέτω δὲ ἁ ΝΟ [38] τὰν ΚΩ πρότερον κατὰ τὸ Ι. Ὁμοίως δὴ τῷ πρὸ τούτου δειχθήσεται ὅτι ἁ ΝΟ ἤτοι ἡμιολία τᾶς ΟΙ ἢ μείζων ἢ ἡμιολία· γίνεται δὴ ἁ ΟΙ τᾶς ΙΝ ἐλάσσων ἢ διπλασία. Ἔστω δὴ ἁ ΟΒ διπλασία τᾶς ΒΝ, καὶ κατεσκευάσθω τὰ αὐτά· ὁμοίως δὴ δειχθήσεται ἁ ΡΘ ὀρθὰς γωνίας ποιοῦσα ποτὶ τὰν ΤΟ καὶ ποτὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν, καὶ ἀπὸ τῶν Β, Γ ἀχθεῖσαι παρὰ τὰν ΡΘ κάθετοι ἐσσοῦνται ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν. Κατενεχθήσεται οὖν τὸ μὲν ἐκτὸς τοῦ ὑγροῦ τμᾶμα εἰς τὸ ὑγρὸν κατὰ τὰν διὰ τοῦ Β κάθετον, τὸ δ᾿ ἐν τῷ ὑγρῷ ἀνενεχθήσεται κατὰ τὰν διὰ τοῦ Γ· φανερὸν οὖν ὅτι ἐπικλιθήσεται τὸ στερεόν, ὥστε τὰν βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, ἐπειδὴ νῦν καθ᾿ ἓν σαμεῖον ‹ἁπτόμενον ἐπὶ τὸ κάτω φέρε›ται ἐπὶ τὰ αὐτὰ τῷ Λ.

   Φανερὸν δὲ ὅτι, κἂν ἁ ΟΝ μὴ τέμνῃ τὰν ΩΚ, ταὐτὰ δειχθήσεται.

[39]    η΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὅταν τὸν ἄξονα ἔχῃ μείζονα ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, ἐλάσσονα δὲ ἢ ὥστε ποτὶ τὰν μέχρι τοῦ ἄξονος τοῦτον ἔχειν τὸν λόγον ὃν ἔχει τὰ ιε ποτὶ τὰ δ, ὅταν τὸ βάρος ποτὶ τὸ ὑγρὸν ἐλάσσονα λόγον ἔχῃ τοῦ ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τοῦ ἄξονος, ἀφεθὲν ἐς τὸ ὑγρόν, ὥστε τὰν βάσιν μὴ ἅπτεσθαι τοῦ ὑγροῦ, οὔτ᾿ ἐς ὀρθὸν ἀποκαταστασεῖται οὔτε μενεῖ κεκλιμένον, πλὴν ὁπόταν ὁ ἄξων αὐτοῦ ποτὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν ποιῇ γωνίαν ἴσαν τᾷ μελλούσᾳ λέγεσθαι.

   Ἔστω τμᾶμα οἷον εἴρηται, καὶ ἁ ΒΔ ἴσα τῷ ἄξονι, καὶ ἁ μὲν ΒΚ τᾶς ΚΔ διπλασία, ἁ δὲ ΚΡ ἴσα τᾷ μέχρι τοῦ ἄξονος, ἔστω δὲ καὶ ἁ μὲν ΤΒ ἡμιολία τᾶς ΒΡ, ἁ δὲ ΤΔ τᾶς ΚΡ, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ [40] ὑγρόν, τοῦτον ἐχέτω τὸ ἀπὸ τᾶς ΦΧ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΔΒ, ἔστω δὲ καὶ ἁ Φ ‹διπλασία τᾶς Χ. Δῆλον οὖν ὅτι› ἁ ΦΧ ποτὶ τὰν ΔΒ ἐλάσσονα λόγον ἔχει τοῦ ὃν ἔχει ἁ ΤΒ ποτὶ τὰν ΒΔ· ἔστι γὰρ ἁ ΤΒ ἁ ὑπεροχά, ᾇ μείζων ἢ ἡμιόλιος ὁ ἄξων τᾶς μέχρι τοῦ ἄξονος· ἐλάσσων ἄρα ἁ ΦΧ τᾶς ΒΤ· ὥστε καὶ ἁ Φ τᾶς ΒΡ. Ἔστω δὴ τᾷ Φ ἴσα ἁ ΡΨ, καὶ τᾷ ΒΔ ὀρθὰ ἄχθω ἁ ΨΕ δυναμένα τὸ ἥμισυ τοῦ ὑπὸ τῶν ΚΡ, ΒΨ, καὶ ἐπεζεύχθω ἁ ΒΕ. Δεικτέον ὅτι τὸ τμᾶμα ἀφεθὲν εἰς τὸ ὑγρὸν ὡς εἴρηται καταστασεῖται κεκλιμένον, ὥστε τὸν ἄξονα ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ποιεῖν γωνίαν ἴσαν τᾷ ΕΒΨ.

   Ἀφείσθω γάρ τι ἐς τὸ ὑγρὸν τμᾶμα, καὶ ἁ βάσις αὐτοῦ μὴ ἁπτέσθω τᾶς τοῦ ὑγροῦ ἐπιφανείας, καί, εἰ δυνατόν, μὴ ποιείσθω ὁ ἄξων αὐτοῦ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ἴσαν τᾷ Β, ἀλλὰ μείζω πρῶτον.

   Τμαθέντος δὴ τοῦ τμάματος ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ τομὰ ἔστω ἁ ΑΠΟΛ ὀρθογωνίου κώνου τομά, ἐν δὲ τᾷ τοῦ ὑγροῦ ἐπιφανείᾳ ἁ ΞΣ, ἄξων δὲ καὶ διάμετρος [τοῦ τμήματος] ἁ ΝΟ. Ἄχθω δὴ καὶ ἁ μὲν ΠΥ παρὰ τὰν ΞΣ ἐφαπτομένα τᾶς ΑΠΟΛ τομᾶς κατὰ τὸ Π, ἁ δὲ ΠΜ παρὰ τὰν ΝΟ, ἁ δὲ ΠΙ κάθετος ἐπὶ τὰν ΝΟ, καὶ τᾷ ΒΡ ἔστω ἴσα ἁ ΟΩ, τᾷ δὲ ΡΚ ἁ ΩΘ, καὶ ὀρθὰ ἁ ΩΗ τῷ ἄξονι. Ἐπεὶ οὖν ὑπόκειται ὁ ἄξων τοῦ τμάματος ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ποιεῖν μείζονα τᾶς Β, δῆλον ὅτι τοῦ ΠΙΥ τριγώνου ἁ ποτὶ τῷ [41] Υ γωνία μείζων τᾶς Β· μείζονα δὴ λόγον ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΙ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΙΥ ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΕΨ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΨΒ. Ἀλλ᾿ ὃν μὲν λόγον ἔχει τὸ ἀπὸ τᾶς ΠΙ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΙΥ, τοῦτον ἔχει ἁ ΚΡ ποτὶ ΥΙ, ὃν δὲ λόγον ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΕΨ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΨΒ, τοῦτον ἔχει ἁ ἡμίσεια τᾶς ΚΡ ποτὶ τὰν ΨΒ· μείζονα ἄρα λόγον ἔχει ἁ ΚΡ ποτὶ τὰν ΥΙ ἤπερ ἁ ἡμίσεια τᾶς ΚΡ ποτὶ τὰν ΨΒ· ἐλάσσων ἄρα ἢ διπλασία ἁ ΥΙ τᾶς ΨΒ. Τᾶς δὲ ΟΙ διπλασία ἁ ΙΥ· ἐλάσσων ἄρα ἁ ΟΙ τᾶς ΨΒ· ὥστε ἁ ΙΩ μείζων ἐστὶ τᾶς ΨΡ. Ἁ δὲ ΨΡ ἴσα ἐστὶ τᾷ Φ· μείζων ἄρα ἐστὶν ἁ ΙΩ τᾶς Φ. Καὶ ἐπεὶ ὑπόκειται τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν ἔχειν λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΦΧ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρόν, τοῦτον ἔχει τὸν λόγον τὸ δεδυκὸς αὐτοῦ ποτὶ τὸ ὅλον τμᾶμα, ὃν δὲ τὸ δεδυκὸς ποτὶ τὸ ὅλον, τοῦτον ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΜ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΟΝ, ὃν ἄρα λόγον ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΦΧ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, τοῦτον ἔχει τὸν λόγον τὸ τετράγωνον τὸ ἀπὸ τᾶς ΜΠ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΟΝ· ἴσα ἄρα ἐστὶν ἁ ΦΧ τᾷ ΠΜ. Ἁ δὲ ΠΗ ἐδείχθη μείζων ἐοῦσα τᾶς Φ· δῆλον οὖν ὅτι ἁ ΠΜ ἐλάσσων ἢ ἡμιολία ἐστὶν τᾶς ΠΗ, ἁ δὲ ΠΗ τᾶς ΗΜ μείζων ἢ διπλασίων. Ἔστω οὖν ἁ ΠΖ διπλασίων τᾶς ΖΜ· ἐσσεῖται δὴ τὸ μὲν Θ κέντρον τοῦ βάρεος τοῦ στερεοῦ, τοῦ δὲ ἐν τῷ ὑγρῷ τὸ Ζ· τοῦ δὴ λοιποῦ μεγέθεος τὸ κέντρον τοῦ βάρεος ἐσσεῖται ἐπὶ τᾶς ΖΘ εὐθείας [42] ἐπιζευχθείσας καὶ ἐκβληθείσας. Ἐκβεβλήσθω ἐπὶ τὸ Γ· δειχθήσεται δὴ ὁμοίως ἁ ΘΗ κάθετος ἐοῦσα ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν, καὶ τὸ μὲν ἐντὸς τοῦ ὑγροῦ τμᾶμα ἐνεχθήσεται εἰς τὸ ἐκτὸς τοῦ ὑγροῦ κατὰ τὰν διὰ τοῦ Ζ ἀγμέναν κάθετον ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν, τὸ δὲ ἐκτὸς τοῦ ὑγροῦ ἐνεχθήσεται εἰς τὸ ἐντὸς κατὰ τὰν διὰ τοῦ Γ· οὐ μενεῖ δὴ τὸ τμᾶμα κατὰ τὰν ὑποκειμέναν κλίσιν.

   Οὐδὲ μὴν εἰς τὸ ὀρθὸν ἀποκαταστασεῖται. Δῆλον δὲ διὰ τούτων· ἐπειδὴ τῶν ἀγμένων διὰ τῶν Ζ, Γ καθέτων ἁ μὲν διὰ τοῦ Ζ ἀγμένα τᾶς ΓΖ ἐπὶ τὰ αὐτὰ μέρεα πίπτει, ἐφ᾿ ἅ ἐστι τὸ Λ, ἁ δὲ διὰ τοῦ Γ ἐπὶ τὰ αὐτὰ τῷ Α, δῆλον ὅτι διὰ τὰ προειρημένα τὸ μὲν Ζ κέντρον ἄνω οἰσθήσεται, τὸ δὲ Γ κάτω· ὥστε τοῦ ὅλου μεγέθεος τὰ μέρεα τὰ ἀπὸ τοῦ Α κάτω οἰσθήσεται.

   Τοῦτο δ᾿ ἦν εὔχρηστον ποτὶ τὸ δεῖξαι.

   Ὑποκείσθω πάλιν τὰ μὲν ἄλλα τὰ αὐτά, ὁ δὲ ἄξων τοῦ τμάματος ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ποιεί‹τω γωνίαν ἐλάσσονα τᾶς ποτὶ τῷ Β· ἐλάσσονα δὴ λόγον› ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΙ ποτὶ τὸ ἀπὸ τᾶς ΙΥ ἢ τὸ ἀπὸ τᾶς ΕΨ ποτὶ τὸ ἀπὸ τᾶς ΨΒ· καὶ ἁ ΚΡ ἄρα ποτὶ τὰν ΥΙ ἐλάσσονα λόγον ἔχει ἤπερ ἁ ἡμίσεια τᾶς ΚΡ ποτὶ τὰν ΨΒ. Μείζων ἄρα ἐσσεῖται ἢ διπλασίων ἁ ΙΥ τᾶς ΨΒ· ἁ ἄρα ΩΙ ἐλάσσων τᾶς ΨΡ. Ἐσσεῖται οὖν καὶ ἁ ΠΗ ἐλάσσων τᾶς Φ. Ἁ δὲ ΜΠ τᾷ ΦΧ ἴσα· δῆλον οὖν ὅτι μείζων ἢ ἡμιολία ἁ ΠΜ τᾶς ΠΗ, ἁ δὲ ΠΗ ἐλάσσων ἢ διπλασίων [43] τᾶς ΗΜ. Ἔστω οὖν ἁ ΠΖ τᾶς ΖΜ διπλασία. Πάλιν οὖν τοῦ μὲν ὅλου κέντρον ἐσσεῖται τοῦ βάρεος τὸ Θ, τοῦ δ᾿ ἐν τῷ ὑγρῷ τὸ Ζ· ἐπιζευχθείσας δὴ τᾶς ΖΘ καὶ ἐκβληθείσας ἐσσεῖται τὸ ‹κέντρον τοῦ βάρεος τοῦ ἐκτὸς τοῦ ὑγροῦ ἐπὶ τᾶς ἐκβληθείσας. Ἔστω τὸ Γ, καὶ ἄχθωσαν κά›θετοι ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν διὰ τῶν Ζ, Γ παρὰ τὰν ΗΘ· δῆλον οὖν ὅτι οὐ μενεῖ τὸ ὅλον τμᾶμα, ἀλλὰ κλιθήσεται, ὥστε τὸν ἄξονα ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ποιεῖν γωνίαν μείζονα ἇς νῦν ποιεῖ.

   Ἐπεὶ οὖν οὔτε γωνίαν μείζονα τᾶς Β ποιοῦντος τοῦ ἄξονος ποτὶ τὸ ὑγρὸν σταθήσεται τὸ τμᾶμα οὔτ᾿ ἐλάσσονα, φανερὸν ὅτι ταλικαύταν ποιοῦντος γωνίαν σταθήσεται· οὕτως γὰρ ἁ ΙΟ ἐσσεῖται ἴσα τᾷ ΨΒ καὶ ἁ ΩΙ τᾷ ΨΡ καὶ τᾷ Φ ἁ ΠΗ· ἡμιολία ἄρα ἐσσεῖται ἁ ΜΠ τᾶς ΠΗ, ἁ δὲ ΠΗ τᾶς ΗΜ διπλασία. Τὸ Η ἄρα τοῦ ἐν τῷ ὑγρῷ βάρεος [44] κέντρον ἐστίν· ὥστε κατὰ τὰν αὐτὰν κάθετον ἀνενεχθήσεται, καὶ τὸ ἐκτὸς ἐς τὸ κάτω ἐνεχθήσεται. Μενεῖ ἄρα· ἀντωθοῦνται γὰρ ὑπ᾿ ἀλλάλων.

   θ΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὅταν τὸν ἄξονα ἔχη μείζονα μὲν ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, ἐλάσσονα δὲ ἢ ὥστε τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει τὰ ιε ποτὶ δ, καὶ τῷ βάρει ποτὶ τὸ ὑγρὸν μείζονα λόγον ἔχῃ τοῦ ὃν ἔχει ἁ ὑπεροχά, ᾇ μεῖζόν ἐστι τὸ ἀπὸ τοῦ ἄξονος τετράγωνον τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τοῦ ἄξονος, ἀφεθὲν εἰς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ ὅλαν εἶμεν ἐν τῷ ὑγρῷ, τεθὲν κεκλιμένον οὔτε κατασταθήσεται, ὥστε τὸν ἄξονα αὐτοῦ κατὰ κάθετον εἶμεν, οὔτε μενεῖ κεκλιμένον, πλὴν ὅταν ὁ ἄξων αὐτοῦ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ποιῇ γωνίαν ἴσαν τᾷ λαφθείσᾳ ὁμοίως ᾇ πρότερον.

[45]    Ἔστω τμᾶμα οἷον εἴρηται, καὶ κείσθω ἁ ΔΒ ἴσα τῷ ἄξονι τοῦ τμάματος, καὶ ἁ μὲν ΒΚ τᾶς ΚΔ διπλασία ἔστω, ἁ δὲ ΚΡ ἴσα τᾷ μέχρι τοῦ ἄξονος, ἁ δὲ ΤΒ ἡμιολία τᾶς ΒΡ, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρόν, τοῦτον ἐχέτω ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ΦΧ, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ἔστω δὲ ἁ Φ διπλασία τᾶς Χ. Δῆλον οὖν ὅτι ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ ἀπὸ τᾶς ΒΤ, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ ἐλάσσονα λόγον ἔχει ἢ ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ΦΧ, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ· ἔστι γὰρ ἁ ΒΤ ἁ ὑπεροχά, ᾇ μείζων ἐστὶν ἢ ἡμιόλιος ὁ ἄξων τοῦ τμάματος τᾶς μέχρι τοῦ ἄξονος. Μείζονι ἄρα ὑπερέχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ ἀπὸ τᾶς ΦΧ ἢ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ΒΤ· ὥστε ἁ ΦΧ ἐλάσσων ἐστὶ τᾶς ΒΤ· καὶ ἁ Φ ἄρα τᾶς ΒΡ.

   Ἔστω οὖν τᾷ Φ ἴσα ἁ ΡΨ, καὶ ἁ ΨΕ ὀρθὰ ἄχθω τᾷ ΒΔ δυναμένα τὸ ἥμισυ τοῦ περιεχομένου ὑπὸ τᾶν ΚΡ, ΨΒ. Φαμὶ ὅτι τὸ τμᾶμα ἀφεθὲν ἐς τὸ ὑγρόν, ὥστε τὰν βάσιν αὐτοῦ ὅλαν εἶμεν ἐν τῷ ὑγρῷ, καταστασεῖται οὕτως, ὥστε τὸν ἄξονα αὐτοῦ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ποιεῖν ἴσαν τᾷ Β.

   Ἀφείσθω [μὲν] γὰρ τὸ τμᾶμα, ὡς εἴρηται, ἐς τὸ ὑγρόν, καὶ μὴ ποιείτω ὁ ἄξων ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ἴσαν τᾷ Β, ἀλλὰ μείζονα πρότερον.

   Τμαθέντος δὴ αὐτοῦ ἐπιπέδῳ ὀρθῷ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ἔστω τοῦ τμάματος τομὰ ἁ ΑΠΟΛ ὀρθογωνίου [46] κώνου τομά, τᾶς δὲ τοῦ ὑγροῦ ἐπιφανείας ἁ ΤΙ, ἄξων δὲ [τῆς τομῆς] καὶ διάμετρος ἁ ΝΟ, καὶ τετμάσθω κατὰ τὰ Ω, Θ, ὡς καὶ πρότερον, ἄχθω δὲ καὶ ἁ μὲν ΥΠ παρὰ τὰν ΤΙ ἐφαπτομένα τᾶς τομᾶς κατὰ τὸ Π, ἁ δὲ ΠΜ μείζων ἄρα ἁ ΣΩ τᾶς ΡΨ καὶ ἁ ΠΗ τᾶς Φ. Καὶ ἐπεὶ τὸ τμᾶμα βάρει λόγον ἔχει ποτὶ τὸ ὑγρόν, ὃν ἁ ὑπεροχά, ᾇ μεῖζόν ἐστιν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ΦΧ, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρόν, τοῦτον ἔχει τὸν λόγον τὸ δεδυκὸς αὐτοῦ τμᾶμα ποτὶ τὸ ὅλον, δῆλον ὅτι τὸν αὐτὸν ἕξει λόγον τὸ δεδυκὸς αὐτοῦ μέρος ποτὶ τὸ ὅλον τμᾶμα, ὃν ἁ ὑπεροχά, ᾇ ὑπερέχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ τοῦ τετραγώνου τοῦ ἀπὸ τᾶς ΦΧ, ποτὶ τὸ τετράγωνον τὸ ἀπὸ ΒΔ· ἕξει οὖν καὶ τὸ ὅλον τμᾶμα ποτὶ τὸ ἐκτὸς τοῦ ὑγροῦ λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ ποτὶ τὸ ἀπὸ τᾶς ΦΧ. Ὃν δὲ λόγον ἔχει τὸ ὅλον τμᾶμα ποτὶ τὸ ἐκτὸς τοῦ ὑγροῦ, τοῦτον ἔχει τὸ ἀπὸ τᾶς ΝΟ ποτὶ τὸ ἀπὸ ΠΜ· ἴσα ἄρα ἁ ΜΠ τᾷ [47] ΦΧ. Ἁ δὲ ΠΗ δέδεικται μείζων τᾶς Φ· ἁ ἄρα ΜΗ ἐλάσσων ἐστὶν τᾶς Χ· μείζων ‹ἄρα ἐστὶν ἢ διπλασία ἁ ΠΗ› τᾶς ‹ΗΜ. Ἔστω δὴ ἁ ΠΖ διπλασία τᾶς ΖΜ, καὶ ἐπιζευχθεῖσα ἁ ΖΘ ἐκβεβλήσθω ἐπὶ τὸ Γ· ἔσται οὖν τοῦ μὲν ὅλου τμάματος κέντρον τοῦ βάρεος τὸ Θ, τοῦ δὲ ἐκτὸς› τοῦ ὑγροῦ τὸ ‹Ζ, τοῦ δὲ ἐντὸς ἐν τᾷ ΘΓ· ἔστω δὲ τὸ› Γ. ‹Δειχθήσεται δὴ ὁμοίως τοῖς πρότερον ἁ ΘΗ› κάθετος ἐπὶ ‹τὰν ἐπιφάνειαν τοῦ ὑγροῦ καὶ αἱ διὰ τῶν Ζ, Γ παρὰ τὰν ΘΗ› ἀγόμεναι κάθετοι καὶ αὐταὶ ἐπὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ. Κατενεχθήσεται ἄρα τὸ μὲν ἐκτὸς τοῦ ὑγροῦ τμᾶμα ἐς τὸ κάτω κατὰ τὰν διὰ τοῦ Ζ, τὸ δὲ ἐντὸς κατὰ τὰν διὰ τοῦ Γ ἀνενεχθήσεται· οὐ μενεῖ οὖν τὸ ὅλον τμᾶμα ἀκλινές. Οὐδὲ μὴν καταστραφήσεται, ὥστε κατὰ κάθετον εἶμεν τὸν ἄξονα ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν, ἐπειδὴ τὰ ἐπὶ ‹τὰ αὐτὰ τῷ Λ κάτω, τὰ δὲ ἐπὶ τὰ αὐτὰ τῷ Α ἐς τὰ ἄνω οἰσθήσεται,› διὰ τὰ ἀνάλογον τοῖς λεγομένοις ἐπὶ τοῦ πρὸ αὐτοῦ.

   Ἐὰν δὲ ὁ ἄξων ποτὶ τὸ ὑγρὸν ποιῇ γωνίαν ἐλάσσονα τᾶς Β, ὁμοίως τοῖς πρότερον δειχθήσεται ὅτι οὐ μενεῖ τὸ τμᾶμα, ἀλλὰ κλιθήσεται, ἕως ἂν ὁ ἄξων ποιῇ γωνίαν ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ἴσαν τᾷ Β.

[48]    ι΄.

   Τὸ ὀρθὸν τμᾶμα τοῦ ὀρθογωνίου κωνοειδέος, ὅταν κουφότερον ὂν τοῦ ὑγροῦ τὸν ἄξονα ἔχῃ μείζονα ἢ ὥστε λόγον ἔχειν ποτὶ τὰν μέχρι τοῦ ἄξονος [τοῦ] ὃν ἔχει τὰ ιε ποτὶ τὰ δ, ἀφεθὲν εἰς τὸ ὑγρὸν ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, ὁτὲ μὲν ὀρθὸν καταστασεῖται, ὁτὲ δὲ κεκλιμένον, καὶ ποτὲ μὲν οὕτω κεκλιμένον, ὥστε τὰν βάσιν αὐτοῦ καθ᾿ ἓν σαμεῖον ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, καὶ τοῦτο ἐν δισσοῖς κλιμάτεσσι ποιήσει, ποτὲ δὲ οὕτως κεκλιμένον καταστασεῖται, ὥστε τὰν βάσιν αὐτοῦ κατὰ πλείονα τόπον βρέχεσθαι, ποτὲ δὲ οὕτως, ὥστε τὰν βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφα‹νείας· ὃν δὲ λόγον ἔχοντος τῷ› βάρει ποτὶ τὸ ὑγρὸν ἕκαστα αὐτῶν ἐσσεῖται, νῦν δηλωθήσεται.

[49]    Ἔστω τμᾶμα οἷον εἴρηται, καὶ τμαθέντος αὐτοῦ ἐπιπέδῳ ὀρθῷ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ τομὰ ἔστω ἐν τᾷ ἐπιφανείᾳ ἁ ΑΠΟΛ ὀρθογωνίου κώνου τομά, ἄξων δὲ ἔστω καὶ διάμετρος τᾶς τομᾶς ὁ ΒΔ, τετμάσθω δὲ ὁ ΒΔ κατὰ τὸ Κ, ὥστε διπλασίαν εἶμεν τὰν ΒΚ τᾶς ΚΔ, κατὰ δὲ τὸ Τ, ὥστε τὰν ΔΒ ποτὶ τὰν ΚΤ λόγον ἔχειν ὡς τὰ ιε ποτὶ δ· δῆλον οὖν ὅτι ἁ ΚΤ μείζων ἐστὶ τᾶς μέχρι τοῦ ἄξονος. Ἔστω οὖν ἁ ΚΡ ἴσα τᾷ μέχρι τοῦ ἄξονος, τᾶς δὲ ΒΡ ἡμίσεια ἔστω ἁ ΡΣ· ἔστι δὴ καὶ ἁ ΣΒ ἡμιολία τᾶς ΒΡ. Ἐπιζευχθείσας δὲ τᾶς ΑΒ καὶ τᾶς ΤΕ ὀρθᾶς ἀχθείσας ἄχθω ἁ ΕΖ παρὰ τὰν ΒΔ, καὶ πάλιν τᾶς ΑΒ δίχα τμαθείσας κατὰ τὸ Θ ἄχθω παρὰ τὰν ΒΔ ἁ ΘΗ, καὶ λελάφθω ὀρθογωνίου κώνου τομὰ ἁ ΑΕΙ περὶ διάμετρον τὰν ΕΖ καὶ ἁ ΑΘΔ περὶ διάμετρον τὰν ΘΗ, ὥστε ὅμοια εἶμεν τὰ ΑΕΙ, ΑΘΔ τμάματα τῷ ΑΒΛ τμάματι· γραφήσεται δὴ ἁ ΑΕΙ κώνου τομὰ διὰ τοῦ Κ, ἁ δὲ ἀπὸ τοῦ Ρ ὀρθὰ ἀχθεῖσα τᾷ ΒΔ τεμεῖ τὰν ΑΕΙ. Τεμνέτω κατὰ τὰ Υ, Γ, καὶ διὰ τῶν Υ, Γ ἄχθωσαν παρὰ τὰν ΒΔ αἱ ΥΧ, ΓΝ, τεμνέτωσαν δὲ αὗται τὰν ΑΘΔ τομὰν κατὰ τὰ Ξ, Φ, ἄχθωσαν δὲ καὶ αἱ ΠΨ, ΟϞ ἐφαπτόμεναι τᾶς ΑΠΟΛ τομᾶς κατὰ τὰ Ο, Π. Δεδομένα δὴ τρία τινὰ τμάματα τὰ ΑΠΟΛ, ΑΕΙ, ΑΘΔ περιεχόμενα ὑπὸ τᾶν εὐθειᾶν καὶ τᾶν ὀρθογωνίων κώνων τομᾶν ὀρθὰ καὶ ὅμοια, ἄνισα δέ, καὶ ἀπολέλαπται ἀφ᾿ ἑκάστας βάσιος, ἀπὸ δὲ τοῦ Ν ἀναγμέναι αἱ ΝΞ, ΝΓ, ΝΟ· ἁ ΟΓ ἄρα ποτὶ τὰν ΓΞ τὸν συγκείμενον λόγον ἕξει ἔκ τε τοῦ, ὃν ἔχει ἁ [50] ΙΛ ποτὶ ΛΑ, καὶ ὃν ἔχει ἁ ΑΔ ποτὶ ΔΙ. Ἔχει δὲ καὶ ἁ ΛΙ ποτὶ ΛΑ ὃν δύο ποτὶ ε· ἅ τε γὰρ ΤΒ ποτὶ ΒΔ ἐστὶν ὡς δύο ποτὶ ε, καὶ ἁ ΕΒ ποτὶ ΒΑ καὶ ἁ ΔΖ ποτὶ ΔΑ, τούτων δὲ διπλάσιαι αἱ ΛΙ, ΛΑ· ἁ δὲ ΑΔ ποτὶ ΔΙ ἔχει ὅσον πέντε πρὸς α, ὁ δὲ συγκείμενος λόγος ἐξ οὗ ὃν ἔχει τὰ δύο ποτὶ τὰ ε καὶ ἐξ οὗ ὃν ἔχει τὰ πέντε ποτὶ τὸ ἓν ὁ αὐτός ἐστι τῷ ὃν ἔχει τὰ δύο ποτὶ τὸ α· διπλασία ἄρα ἐστὶν ἁ ΟΓ τᾶς ΓΞ. Διὰ τὰ αὐτὰ δὴ καὶ ἁ ΠΥ τᾶς ΥΦ. Ἐπεὶ δέ ἐστιν ἁ ΔΣ ἡμιολία τᾶς ΚΡ, δῆλον ὅτι ἁ ΒΣ ἁ ὑπεροχά ἐστιν, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος.

   Εἰ μὲν οὖν τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν τοῦτον ἔχει τὸν λόγον, ὃν τὸ ἀπὸ τᾶς ΒΣ ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ἢ μείζονα τούτου τοῦ λόγου, ἀφεθὲν τὸ τμᾶμα εἰς τὸ ὑγρὸν οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, ὀρθὸν καταστασεῖται· δέδεικται γὰρ πρότερον ὅτι [ἐὰν] τμᾶμα μείζονα ἔχον τὸν ἄξονα ἢ ἡμιόλιον τᾶς μέχρι τοῦ ἄξονος, ἐὰν τῷ βάρει ποτὶ τὸ ὑγρὸν μὴ ἐλάσσονα λόγον ἔχῃ τοῦ ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ὑπεροχᾶς, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος, ποτὶ τὸ τετράγωνον τὸ ἀπὸ τοῦ ἄξονος, ἀφεθὲν ἐς τὸ ὑγρὸν οὕτως ὡς εἴρηται, ὀρθὸν καταστασεῖται.

   Ἐπὴν δὲ τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν ἐλάσσονα μὲν λόγον ἔχῃ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΣΒ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, μείζονα δὲ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΟΞ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ἀφεθὲν ἐς τὸ ὑγρὸν [51] κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, καταστασεῖται κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, καὶ τὸν ἄξονα αὐτοῦ γωνίαν ποιεῖν ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ μείζονα τᾶς Ϟ.

   Ἐὰν δὲ τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν τοῦτον ἔχῃ τὸν λόγον, ὃν τὸ τετράγωνον τὸ ἀπὸ τᾶς ΞΟ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ἀφεθὲν ἐς τὸ ὑγρὸν κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, καταστασεῖται κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ ἅπτεσθαι καθ᾿ ἓν τᾶς τοῦ ὑγροῦ ἐπιφανείας, καὶ τὸν ἄξονα αὐτοῦ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ποιεῖν ἴσαν τᾷ Ϟ.

   Ἐὰν δὲ τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν ἐλάσσονα μὲν λόγον ἔχῃ τοῦ ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΞΟ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, μείζονα δὲ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΠΦ ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ἀφεθὲν ἐς τὸ ὑγρὸν καὶ τεθὲν κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, καταστασεῖται κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ κατὰ πλείονα τόπον τέμνεσθαι ὑπὸ τοῦ ὑγροῦ.

   Εἰ δὲ τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν τοῦτον ἔχει τὸν λόγον, ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΦ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ἀφεθὲν ἐς τὸ ὑγρὸν καὶ τεθὲν κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, καταστασεῖται κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ καθ᾿ ἓν σαμεῖον ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, καὶ τὸν ἄξονα αὐτοῦ ποιεῖν γωνίαν ἴσαν τᾷ Ψ.

[52]    Ἐὰν δὲ τὸ τμᾶμα τῷ βάρει πρὸς τὸ ὑγρὸν ἐλάσσονα λόγον ἔχῃ τοῦ ὃν ἔχει τὸ τετράγωνον τὸ ἀπὸ τᾶς ΠΦ ποτὶ τὸ τετράγωνον τὸ ἀπὸ τᾶς ΒΔ, ἀφεθὲν ἐς τὸ ὑγρὸν καὶ τεθὲν κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, καταστασεῖται κεκλιμένον οὕτως, ὥστε τὸν μὲν ἄξονα αὐτοῦ ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ποιεῖν ἐλάσσονα τᾶς Ψ, τὰν δὲ βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας.

   Δειχθήσεται δὲ ταῦτα ἑξῆς.

   Ἐχέτω δὴ πρῶτον τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρὸν μείζονα μὲν λόγον τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΞΟ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ἐλάσσονα δὲ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ὑπεροχᾶς τετράγωνον, ᾇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος, ποτὶ τὸ ἀπὸ τᾶς ΒΔ τετράγωνον, καὶ ὑποκείσθω τὸ πρότερον κατεσκευασμένον σχῆμα, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρόν, τοῦτον ἐχέτω τὸ ἀπὸ τᾶς Ψ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ· ἔστι δὴ ἁ Ψ τᾶς μὲν ΞΟ μείζων, ἐλάσσων δὲ τᾶς ὑπεροχᾶς, [53] ἇ μείζων ἐστὶν ὁ ἄξων ἢ ἡμιόλιος τᾶς μέχρι τοῦ ἄξονος. Ἐναρμόσθω δέ τις μεταξὺ τῶν ΑΠΟΛ, ΑΞΔ κώνων ‹τομᾶν›,

[57]    Καὶ ἐπεζεύχθω ἁ ΗΚ καὶ ἐκβεβλήσθω ἐπὶ τὸ Ω. Ἐσσεῖται δὴ τοῦ μὲν ὅλου τμάματος κέντρον τοῦ βάρεος τὸ Κ, τοῦ δὲ ἐν τῷ ὑγρῷ τὸ Η, τοῦ δ᾿ ἐκτὸς ἐπὶ τᾶς ΚΩ· ἔστω τὸ Ω. Δειχθήσεται δὴ ὁμοίως ἅ τε ΚϠ κάθετος ἐπὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν καὶ αἱ διὰ τῶν Η, Ω σαμείων παρὰ τὰν ΚϠ. Δῆλον οὖν ὅτι οὐ μενεῖ τὸ τμᾶμα, ἀλλ᾿ ἐπικλιθήσεται, ἕως ἂν ἁ βάσις αὐτοῦ ἅπτηται καθ᾿ ἓν σαμεῖον τᾶς τοῦ ὑγροῦ ἐπιφανείας, καθάπερ [58] ‹κάθετός ἐστιν ἐπὶ τὰν τοῦ ὑγροῦ› ἐπιφάνειαν. Κατὰ τὰς αὐτὰς οὖν εὐθείας τό τε ἐν τῷ ὑγρῷ ἀνενεχθήσεται καὶ τὸ ‹ἐκτὸς τοῦ ὑγροῦ› κατενεχθήσεται· μενεῖ ‹δὴ τὸ τμᾶμα, καὶ› ἅ τε ‹βάσις καθ᾿ ἓν σαμεῖον ἅψεται τᾶς τοῦ› ὑγροῦ [59] ἐπιφανείας, καὶ ὁ ἄξων ‹τοῦ τμάματος› ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ ποιήσει γωνίαν ἴσαν τᾷ προγεγραμμένᾳ. εὐθεῖαν κατὰ τὸ Η. Δειχθήσεται δὴ ἁ ΠΥ διπλασία τᾶς ΥΙ, καθάπερ ἐδείχθη καὶ ἁ ΓΟ τᾶς ΓΧ. Ἄχθω δὲ καὶ ἁ μὲν ΠΩ ἐφαπτομένα τᾶς ΑΠΟΛ κατὰ τὸ Π, ἁ δὲ ΠΕ κάθετος ἐπὶ τὰν ΒΔ, καὶ ἁ ΙΑ ἐπιζευχθεῖσα ‹ἐκβεβλήσθω› ἐπὶ τὸ Χ· ἐσσεῖται δὲ ἁ ΑΙ τᾷ ΙΧ ἴσα καὶ ἁ ΑΧ τᾷ ΠΩ παράλληλος. Δεικτέον δὴ ὅτι τὸ τμᾶμα ἀφεθὲν εἰς τὸ ὑγρὸν καὶ κεκλιμένον οὕτως, ὥστε τὰν βάσιν αὐτοῦ μὴ ἅπτεσθαι τοῦ ὑγροῦ, οὕτως καταστασεῖται κεκλιμένον, ὥστε τὸν ἄξονα ποτὶ τὰν ἐπιφάνειαν τοῦ ὑγροῦ γωνίαν ποιεῖν ‹ἐλάσσονα τᾶς Φ, τὰν δὲ βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας.

[60]    Ἀφείσθω γὰρ εἰς τὸ ὑγρὸν καὶ καθεστακέτω οὕτως, ὥστε τὰν βάσιν› αὐτοῦ καθ᾿ ἓν σαμεῖον ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, τμαθέντος δὲ τοῦ τμάματος ἐπιπέδῳ ὀρθῷ ποτὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν διὰ τοῦ ἄξονος τομὰ ἔστω τᾶς μὲν τοῦ τμάματος ἐπιφανείας ἁ ΑΗΒΛ ὀρθογωνίου κώνου τομά, τᾶς δὲ τοῦ ὑγροῦ ἐπιφανείας ἁ ΑΖ, ἄξων δὲ καὶ διάμετρος τᾶς τομᾶς ἁ ΒΔ, καὶ τετμάσθω ἁ ΒΔ κατὰ τὰ Κ, Ρ ὁμοίως

[62]    ‹κατε]σκευάσθω τὰ αὐτὰ τοῖς ἐν τῷ τρίτῳ σχήματι. Ὁμοίως δὴ δειχθήσεται ἁ ΘΗ ἴσα τᾷ Ψ· ὥστε καὶ τᾷ ΙΠ ἴσα. Ἐπεὶ οὖν ἁ Λ γωνία οὐκ ἐλάσσων ἐστὶ τᾶς Φ, οὐκ ἄρα μείζων ἐστὶν ἁ ΓΒ τᾶς ΣΒ, οὐδὲ ἁ ΓΡ ἐλάσσων τᾶς ΣΡ οὐδὲ ἁ ΗϠ τᾶς ΘϞ. Καὶ ἐπειδὴ ἁ ΙΠ ἡμιολία ἐστὶ τᾶς ΠΥ, ἐλάσσων δὲ ἁ ΠΥ τᾶς ΘϞ, καὶ ἁ μὲν ΗΘ ἴσα τᾷ ΠΙ, ἁ δὲ ΗϠ οὐκ ἐλάσσων τᾶς ΘϞ, μείζων ἔσται ἁ ϠΗ τᾶς ΠΥ· ἁ ἄρα ΗϠ μείζων ἐστὶν ἢ διπλασία τᾶς ϠΘ. Ἔστω δὴ ἁ ΗΥ διπλασία τᾶς ΥΘ, καὶ ἐπιζευχθεῖσα ἁ ΥΚ ἐκβεβλήσθω· δῆλον δὴ ὁμοίως τοῖς πρότερον ὅτι οὐ μενεῖ τὸ τμᾶμα, ἀλλὰ κλιθήσεται, ὥστε τὸν ἄξονα αὐτοῦ ποτὶ τὰν ἐπιφάνειαν ‹τοῦ ὑγροῦ γωνίαν ποιεῖν ἐλάσσονα τᾶς Φ›.

[63]    Ἔστω δὴ πάλιν τὸ τμᾶμα ποτὶ τὸ ὑγρὸν τῷ βάρει μείζονα μὲν λόγον ἔχον τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΖΠ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ἐλάσσονα δὲ τοῦ ὃν ἔχει τὸ ἀπὸ τᾶς ΞΟ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ, ὃν δὲ λόγον ἔχει τὸ τμᾶμα τῷ βάρει ποτὶ τὸ ὑγρόν, τοῦτον ἐχέτω τὸ ἀπὸ τᾶς Ψ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ· δῆλον οὖν ὅτι ἁ Ψ τᾶς μὲν ΖΠ μείζων ἐστίν, τᾶς δὲ ΞΟ ἐλάσσων. Ἐναρμόσθω δὴ εἰς τὸ μεταξὺ τᾶν ΑΞΔ, ΑΠΟΛ [τμημάτων] ἴσα τᾷ Ψ, παράλληλος δὲ τᾷ ΒΔ ἁ ΦΙ τέμνουσα τὰν μεταξὺ [τοῦ] κώνου τομὰν κατὰ τὸ Υ· πάλιν δὴ ἁ ΦΥ διπλασία τᾶς ΥΙ δειχθήσεται, καθάπερ ἁ ΟΓ τᾶς ΞΓ. Ἄχθω δὲ ἀπὸ τοῦ Φ τοῦ ΑΠΟΛ ἐφαπτομένα κατὰ τὸ Φ ἁ ΦΩ· ὁμοίως δὴ τοῖς πρότερον δειχθήσεται ἁ μὲν ΑΙ τᾷ ΧΙ ἴσα, ἁ δὲ ΑΧ τᾷ ΦΩ παράλληλος. Δεικτέον δὲ ὅτι τὸ τμᾶμα ἀφεθὲν ἐς τὸ ὑγρόν, ὥστε τὰν βάσιν μὴ ἅπτεσθαι τᾶς ἐπιφανείας τοῦ ὑγροῦ, καὶ τεθὲν κεκλιμένον οὕτως κλιθήσεται, ὥστε τὰν βάσιν αὐτοῦ κατὰ πλείονα τόπον τέμνεσθαι ὑπὸ τοῦ ὑγροῦ.

[64]    Ἀφείσθω γὰρ εἰς τὸ ὕγρον ὡς εἴρηται, καὶ κείσθω τὸ πρῶτον [καὶ] οὕτως κεκλιμένον, ‹ὥστε τὰν βάσιν αὐτοῦ μηδὲ καθ᾿ ἓν› ἅπτεσθαι τᾶς τοῦ ὑγροῦ ἐπιφανείας, τμαθέντος δὲ αὐτοῦ ἐπιπέδῳ διὰ τοῦ ἄξονος ὀρθῷ ποτὶ τὰν τοῦ ὑγροῦ ἐπιφάνειαν ἐν μὲν τᾷ τοῦ τμάματος ἐπιφανείᾳ γίνεται τομὰ ἁ ΑΒΓ, ἐν δὲ τᾷ τοῦ ὑγροῦ ἁ ΕΖ, ἄξων δὲ ἔστω [τῆς τομῆς] καὶ διάμετρος [τοῦ τμήματος] ἁ ΒΔ, καὶ τετμάσθω ἁ ΒΔ κατὰ τὰ Κ, Ρ ὁμοίως τοῖς πρότερον, ἄχθω δὲ καὶ ἁ μὲν ΗΛ παρὰ τὰν ΕΖ ἐφαπτομένα τᾶς [ἀπὸ τῆς] ΑΒΓ τομᾶς κατὰ τὸ Η, ἁ δὲ ΗΘ παρὰ τὰν ΒΔ, ἁ δὲ ΗΣ κάθετος ἐπὶ τὰν ΒΔ. Ἐπεὶ δὲ τὸ τμᾶμα τῷ βάρει λόγον ἔχει ποτὶ τὸ ὑγρόν, ὃν τὸ ἀπὸ τᾶς Ψ τετράγωνον ποτὶ τὸ ἀπὸ τᾶς ΒΔ, δῆλον ὅτι ἁ Ψ ἴσα ἐστὶν τᾷ ΗΘ· δειχθήσεται γὰρ ὁμοίως τοῖς πρότερον· ὥστε καὶ ἁ ΗΘ ἴσα ἐστὶν τᾷ ΦΙ· καὶ τὰ τμάματα ἄρα τὰ ΑΦΧ, ΕΒΖ ἴσα ἐστὶν ἀλλάλοις. Ἐπεὶ δ᾿ ἐν ἴσοις καὶ ὁμοίοις τμαμάτεσσι τοῖς ΑΠΟΛ, ΑΒΓ ἀγμέναι ἐντὶ αἱ ΑΧ, ΕΖ [65] ἴσα τμάματα ἀφαιροῦσαι, καὶ ἁ μὲν ἀπ᾿ ἄκρας τᾶς βάσιος, ἁ δὲ οὐκ ἀπ᾿ ἄκρας, ἐλάσσονα ποιήσει τὰν ὀξεῖαν ποτὶ τὰν διάμετρον τοῦ τμάματος ἁ ἀπ᾿ ἄκρας τᾶς βάσιος ἀχθεῖσα. Καὶ ἐπειδὴ τοῦ ΗΛΣ τριγώνου ἁ Λ μείζων τᾶς Ω γωνίας τοῦ ΦΤΩ τριγώνου, δῆλον ὅτι ἐλάσσων ἐστὶν ἁ ΒϚ τᾶς ΒΤ, ἁ δὲ ϚΡ τᾶς ΡΤ μείζων, καὶ ἁ ΗϠ μείζων τᾶς ΦΗ· ἁ ϠΘ ἄρα ἐλάσσων τᾶς ΗΙ. Καὶ ἐπεὶ διπλασία ἐστὶν ἁ ΦΥ τᾶς ΥΙ, δῆλον ὅτι ἁ ΗϠ μείζων ἐστὶν ἢ διπλασία τᾶς ‹ϠΘ. Ἔστω δὴ ἁ ΗΑ΄ διπλασία› τᾶς Α΄Θ· δῆλον δὴ ἐκ τούτων ὅτι οὐ μενεῖ τὸ τμᾶμα, ἀλλὰ ἐπικλιθήσεται, ἕως ἂν ἁ βάσις αὐτοῦ θίγῃ καθ᾿ ἓν σαμεῖον τᾶς τοῦ ὑγροῦ ἐπιφανείας.

   Ἁπτέσθω δὴ καθ᾿ ἓν σαμεῖον, ὡς ἐν τῷ τρίτῳ σχήματι ἐγράφθη, καὶ τὰ ἄλλα τὰ αὐτὰ κατεσκευάσθω· δειχθήσεται δὴ πάλιν ἅ τε ΘΗ ἴσα ἐοῦσα τᾷ ΦΙ καὶ τὰ ΑΦΧ, ΑΒΖ τμάματα ἴσα ἀλλάλοις. Καὶ ἐπεὶ ἐν ἴσοις καὶ ὁμοίοις τμαμάτεσσι τοῖς ΑΠΟΛ, ΑΒΓ ἀγμέναι ἐντὶ αἱ ΑΧ, ΑΖ ἴσα τμάματα ἀφαιροῦσαι, ἴσας ποιοῦσι γωνίας ποτὶ [66] ταῖς διαμέτροις τῶν τμαμάτων· τῶν ἄρα ΛΗΣ, ΦΤΩ αἱ ποτὶ τοῖς Λ, Ω γωνίαι ἴσαι ἐντί, καὶ ἁ ΒΣ εὐθεῖα τᾷ ΒΤ ἴσα καὶ ἁ ΣΡ τᾷ ΡΤ καὶ ἁ ΗϠ τᾷ ΦΗ καὶ ἁ ϠΘ τᾷ ΗΙ. Ἐπεὶ δὲ διπλασία ἐστὶν ἁ ΦΥ τᾶς ΥΙ, φανερὸν ὅτι ἁ ΗϠ μείζων ἐστὶν ἢ διπλασία τᾶς ϠΘ. Ἔστω οὖν ἁ ΗϞ τᾶς ϞΘ διπλασίων· πάλιν δὴ ἐκ τούτων δῆλον ὡς οὐ μενεῖ τὸ τμᾶμα, ἀλλ᾿ ἐπικλιθήσεται ἐπὶ τὰ αὐτὰ τῷ Α. Ἐπεὶ δὴ καθ᾿ ἓν σαμεῖον ὑπετέθη τὸ τμᾶμα ἅπτεσθαι τοῦ ὑγροῦ, δῆλον ὅτι κατὰ πλείονα τόπον ἁ βάσις ὑπὸ τοῦ ὑγροῦ καταλαφθήσεται.

---

ΣΤΟΜΑΧΙΟΝ

[70]    Τοῦ λεγομένου Στομαχίου ποικίλαν ἔχοντος τᾶς ἐξ ὧν συνέστακε σχημάτων μεταθέσεως θεωρίαν ἀναγκαῖον ἡγησάμην πράττον του ‹......› ρῶν ἐκθέσθαι, εἴς τε ἃ διαιρεῖται, ἕκαστόν τε αὐτῶν τίνι ἐστὶν ὁμοιούμενον, ἔτι δὲ καὶ ποῖαι γωνίαι σύνδυο λαμβανόμεναι ‹....› καὶ ‹...› θάς, εἴρηται πρὸς τὸ τὰς ἐναρμόσεις τῶν ἐξ αὐτῶν γεννωμένων σχαμάτων γιγνώσκεσθαι, εἴτε ἐπ᾿ εὐθείας εἰσὶν αἱ γεννώμεναι ἐν τοῖς σχάμασι πλευραί, εἴτε καὶ μικρῶς λείπουσαι τᾷ θεωρίᾳ λανθάνουσιν· τὰ γὰρ τοιαῦτα φιλότεχνα· καὶ ἐὰν ἐλάχιστον μὲν λείπηται, τᾷ δὲ θεωρίᾳ λανθάνῃ, οὐ παρὰ τοῦτ᾿ ἐστὶν ἔκβλητα ἃ συνίσταται.

   Ἔστι μὲν οὖν ἐξ αὐτῶν οὐκ ὀλίγων σχημάτων .......ο.. διὰ τὸ .....ν..τον εἶναι εἰς ἕτερον τόπον τοῦ ἴσου καὶ ἰσογωνίου σχάματος μετατιθεμε... καὶ ἑτέ..... λαμβάνοντας. ‹Ἐνιό›τε δὲ καὶ δύο σχημάτων συνάμφω ἑνὶ σχήματι ἴσων ὄντων καὶ ὁμοίων τῷ ἑνὶ σχήματι ἢ καὶ δύο σχημάτων συνάμφω ἴσων τε καὶ ὁμοίων ὄντων δυσὶ σχήμασι συνάμφω πλείονα σχήματα συνίσταται ἐκ τῆς μεταθέσεως. Προγράφομεν οὖν τι θεώρημα εἰς αὐτὸ συντεῖνον.

[71]    Ἔστω γὰρ παραλληλόγραμμον ὀρθογώνιον τὸ ΖΓ, καὶ δε. ι.....ω ἡ ΕΖ τῷ Κ, καὶ .. διήχθωσαν ἀπὸ τῶν Γ, Β αἱ ΓΚ, ΒΕ. ει..ων... τῶν ... Γ ....... ἐκ‹βεβλή›σθωσαν αἱ ΓΚ, ΒΖ καὶ συμπιπτέ‹τωσαν κατὰ τὸ Δ.....› ἡ ΓΗ. Ἐπεὶ ἴση ἐστὶν ἡ ΕΚ τῇ ΚΖ, ‹ἴση› καὶ ἡ ΓΕ, τουτέστιν ἡ ΒΖ, τῇ ΖΔ· ὥ‹στε› μείζων ἡ ΓΖ τῆς ΖΔ· καὶ γωνία ‹ἄρα› ἡ ὑπὸ τῶν ΖΔΓ τῆς ὑπὸ τῶν ΖΓΔ μείζων. Ἴσαι δέ εἰσιν αἱ ὑπὸ ΗΒΔ, ΖΓΒ· ἡμίσεια γὰρ ὀρθῆς ἑκατέρα· μείζων ἄρα καὶ ἡ ὑπὸ τῶν ΓΗΒ, ἐπεὶ ἡ ὑπὸ ΓΗΒ ἴση δυσὶ ταῖς ἐντὸς καὶ ἀπεναντίον ταῖς ὑπὸ ΗΒΔ, ΗΔΒ, τῆς ὑπὸ τῶν ΗΓΒ· ὥστε μείζων ἐστὶν ἡ ΓΒ τῆς ΒΗ. Ἐὰν ἄρα δίχα τμηθῇ ἡ ΓΗ κατὰ Χ, ἔσται ἀμβλεῖα μὲν ἡ ὑπὸ ΓΧΒ· ἐπεὶ γὰρ ἴση ἡ ΓΧ τῇ ΧΗ, καὶ κοινὴ ἡ ΧΒ, δύο δυσὶν ἴσαι· καὶ βάσις ἡ ΓΒ τῆς ΒΗ μείζων· καὶ ἡ γωνία ἄρα τῆς γωνίας μείζων. Ἀμβλεῖα μὲν ἄρα ἡ ὑπὸ ΓΧΒ, ὀξεῖα δὲ ἡ ἐφεξῆς. Ἡμίσεια δὲ ὀρθῆς ἡ ὑπὸ ΓΒΗ· τοῦτο γάρ ἐστιν ὑποκείμενον τοῦ παραλληλογράμμου· ὀξεῖα δὲ ἡ ὑπὸ ΒΧΗ. Καὶ. τι δὴ ἴση ἡ λοιπαὶ ΓΒΗ καὶ συνίσταται καὶ διαιρεῖται τοῦτο ἐπ. ον τον.... ....... βάσιος..τι....... αστ..α.. ἄρα ο... ΑΒ....αν..ο...τὴν ΓΑ.....νῶν.......έχον...τὸ [72] ἐπίλοιπ.................. δύνασθαι ἀρ....ξειν ἐκ....τῶν τομῶν ....τῶν τάξιν ἐχοντ..

   Τετμήσθω ἡ ΓΑ δίχα κατὰ τὸ Ε, καὶ διὰ τοῦ Ε τῇ ΒΓ παράλληλος ἤχθω ἡ ΕΖ· ἔστιν οὖν τετράγωνα τὰ ΓΖ, ΖΑ. Ἤχθωσαν διάμετροι αἱ ΓΔ, ΒΕ, ΕΔ, καὶ τετμήσθωσαν δίχα αἱ ΓΗ, ΕΔ κατὰ τὰ Θ, Χ, καὶ ἐπεζεύχθωσαν αἱ ΒΘ, ΧΖ, καὶ διὰ τῶν..., Κ τῇ ΒΔ παράλληλοι ἤχθωσαν αἱ Κ.., ..Ξ. Διὰ τὸ προκείμενον ἄρα θεώρημα τοῦ ΒΓΘ τριγώνου ἡ πρὸς τῷ Θ γωνία ἀμβλεῖα, ἡ δὲ λοιπὴ ὀξεῖα .... νερὸν φανερὸν δὲ ...ει...

  

---

ΠΕΡΙ ΜΗΧΑΝΙΚΩΝ ΘΕΩΡΗΜΑΤΩΝ
ΠΡΟΣ ΕΡΑΤΟΣΘΕΝΗ ΕΦΟΔΟΣ (=ΜΕΘΟΔΟΣ)

Ἀρχιμήδους Περὶ τῶν μηχανικῶν θεωρημάτων πρὸς Ἐρατοσθένην ἔφοδος

   Ἀρχιμήδης Ἐρατοσθένει εὖ πράττειν.

   Ἀπέστειλά σοι πρότερον τῶν εὑρημένων θεωρημάτων ἀναγράψας αὐτῶν τὰς προτάσεις φάμενος εὑρίσκειν ταύτας τὰς ἀποδείξεις, ἃς οὐκ εἶπον ἐπὶ τοῦ παρόντος· ἦσαν δὲ τῶν ἀπεσταλμένων θεωρημάτων αἱ προτάσεις αἵδε· τοῦ μὲν πρώτου· ἐὰν εἰς πρίσμα ὀρθὸν παραλληλόγραμμον ἔχον βάσιν κύλινδρος ἐγγραφῇ τὰς μὲν βάσεις ἔχων ἐν τοῖς ἀπεναντίον παραλληλογράμμοις, τὰς δὲ πλευρὰς ἐπὶ τῶν λοιπῶν τοῦ πρίσματος ἐπιπέδων, καὶ διά τε ‹τοῦ κέντρου τοῦ κύκλου,› ὅς ἐστι βάσις τοῦ κυλίνδρου, καὶ μιᾶς πλευρᾶς τοῦ τετραγώνου τοῦ ἐν τῷ κατεναντίον ἐπιπέδῳ ἀχθῇ ἐπίπεδον, τὸ ἀχθὲν ἐπιπίπεδον ἀποτεμεῖ τμῆμα ἀπὸ τοῦ κυλίνδρου, ὅ ἐστι περιεχόμενον ὑπὸ δύο ἐπιπέδων καὶ ἐπιφανείας κυλίνδρου, ἑνὸς μὲν τοῦ ἀχθέντος, ἑτέρου δὲ ἐν ᾧ ἡ βάσις ἐστὶν τοῦ κυλίνδρου, τῆς δὲ ἐπιφανείας τῆς μεταξὺ τῶν εἰρημένων ἐπιπέδων, τὸ δὲ ἀποτμηθὲν ἀπὸ τοῦ κυλίνδρου τμῆμα ἕκτον μέρος ἐστὶ τοῦ ὅλου πρίσματος. Τοῦ δὲ ἑτέρου θεωρήματος ἡ πρότασις ἥδε· ἐὰν εἰς κύβον κύλινδρος ἐγγραφῇ τὰς μὲν βάσεις ἔχων πρὸς τοῖς κατεναντίον παραλληλογράμμοις, [83] τὴν δὲ ἐπιφάνειαν τῶν λοιπῶν τεσσάρων ἐπιπέδων ἐφαπτομένην, ἐγγραφῇ δὲ καὶ ἄλλος κύλινδρος εἰς τὸν αὐτὸν κύβον τὰς μὲν βάσεις ἔχων ἐν ἄλλοις παραλληλογράμμοις, τὴν δὲ ἐπιφάνειαν τῶν λοιπῶν τεσσάρων ἐπιπέδων ἐφαπτομένην, τὸ περιληφθὲν σχῆμα ὑπὸ τῶν ἐπιφανειῶν τῶν κυλίνδρων, ὅ ἐστιν ἐν ἀμφοτέροις τοῖς κυλίνδροις, δίμοιρόν ἐστι τοῦ ὅλου κύβου. Συμβαίνει δὲ ταῦτα τὰ θεωρήματα διαφέρειν τῶν πρότερον εὑρημένων· ἐκεῖνα μὲν γὰρ τὰ σχήματα, τά τε κωνοειδῆ καὶ σφαιροειδῆ καὶ τὰ τμήματα ‹αὐτῶν, τῷ μεγέθει σχήμασι› κώνων καὶ κυλίνδρων συνεκρίναμεν, ἐπιπέδοις δὲ περιεχομένῳ στερεῷ σχήματι οὐδὲν αὐτῶν ἴσον ἐὸν εὕρηται, τούτων δὲ τῶν σχημάτων τῶν δυσὶν ἐπιπέδοις καὶ ἐπιφανείαις κυλίνδρων ἕκαστον ἑνὶ τῶν ἐπιπέδοις περιεχομένων στερεῶν σχημάτων ἴσον εὑρίσκεται.

   Τούτων δὴ τῶν θεωρημάτων τὰς ἀποδείξεις ἐν τῷδε τῷ βιβλίῳ γράψας ἀποστελῶ σοι.

   Ὁρῶν δέ σε, καθάπερ λέγω, σπουδαῖον καὶ φιλοσοφίας προεστῶτα ἀξιολόγως καὶ τὴν ἐν τοῖς μαθήμασιν κατὰ τὸ ὑποπίπτον θεωρίαν τετιμηκότα ἐδοκίμασα γράψαι σοι καὶ εἰς τὸ αὐτὸ βιβλίον ἐξορίσαι τρόπου τινὸς ἰδιότητα, καθ᾿ ὅν σοι παρεχόμενον ἔσται λαμβάνειν ἀφορμὰς εἰς τὸ δύνασθαί τινα τῶν ἐν τοῖς μαθήμασι θεωρεῖν διὰ τῶν μηχανικῶν. Τοῦτο δὲ πέπεισμαι χρήσιμον εἶναι οὐδὲν ἧσσον καὶ εἰς τὴν ἀπόδειξιν αὐτῶν τῶν θεωρημάτων. Καὶ γάρ τινα τῶν πρότερόν μοι φανέντων μηχανικῶς ὕστερον γεωμετρικῶς ἀπεδείχθη διὰ τὸ χωρὶς ἀποδείξεως εἶναι τὴν διὰ τούτου τοῦ τρόπου θεωρίαν· ἑτοιμότερον [84] γάρ ἐστι προλαβόντα διὰ τοῦ τρόπου γνῶσίν τινα τῶν ζητημάτων πορίσασθαι τὴν ἀπόδειξιν μᾶλλον ἢ μηδενὸς ἐγνωσμένου ζητεῖν. ‹... Διόπερ καὶ τῶν θεωρη›μάτων τούτων, ὧν Εὔδοξος ἐξηύρηκεν πρῶτος τὴν ἀπόδειξιν, περὶ τοῦ κώνου καὶ τῆς πυραμίδος, ὅτι τρίτον μέρος ὁ μὲν κῶνος τοῦ κυλίνδρου, ἡ δὲ πυραμὶς τοῦ πρίσματος, τῶν βάσιν ἐχόντων τὴν αὐτὴν καὶ ὕψος ἴσον, οὐ μικρὰν ἀπονείμαι ἄν τις Δημοκρίτῳ μερίδα πρώτῳ τὴν ἀπόφασιν τὴν περὶ τοῦ εἰρημένου σχήματος χωρὶς ἀποδείξεως ἀποφηναμένῳ. Ἡμῖν δὲ συμβαίνει καὶ τοῦ νῦν ἐκδιδομένου θεωρήματος τὴν εὕρεσιν ὁμοίαν ταῖς πρότερον γεγενῆσθαι· ἠβουλήθην δὲ τὸν τρόπον ἀναγράψας ἐξενεγκεῖν ἅμα μὲν καὶ διὰ τὸ προειρηκέναι ὑπὲρ αὐτοῦ, μή τισιν δοκῶμεν κενὴν φωνὴν καταβεβλῆσθαι, ἅμα δὲ καὶ πεπεισμένος εἰς τὸ μάθημα οὐ μικρὰν ἂν συμβαλέσθαι χρείαν· ὑπολαμβάνω γάρ τινας ἢ τῶν ὄντων ἢ ἐπιγινομένων διὰ τοῦ ἀποδειχθέντος τρόπου καὶ ἄλλα θεωρήματα οὔπω ἡμῖν συνπαραπεπτωκότα εὑρήσειν.

   Γράφομεν οὖν πρῶτον τὸ καὶ πρῶτον φανὲν διὰ τῶν μηχανικῶν, ὅτι πᾶν τμῆμα ὀρθογωνίου κώνου τομῆς ἐπίτριτόν ἐστιν τριγώνου τοῦ βάσιν ἔχοντος τὴν αὐτὴν καὶ ὕψος ἴσον, μετὰ δὲ τοῦτο ἕκαστον τῶν διὰ τοῦ αὐτοῦ τρόπου θεωρηθέντων· ἐπὶ τέλει δὲ τοῦ βιβλίου γράφομεν τὰς γεωμετρι‹κὰς ἀποδείξεις ἐκείνων τῶν θεωρημάτων, ὧν τὰς προ›τάσεις ἀπεστείλαμέν ‹σοι πρότερον›.

ΠΡΟΛΑΜΒΑΝΟΜΕΝΑ

   Ἐὰν ἀπὸ μεγέθους μέγεθος ἀφαιρεθῇ, ‹τὸ δὲ αὐτὸ σημεῖον κέν›τρον τοῦ βάρους ‹ᾖ τοῦ τε ὅλου› καὶ [85] τοῦ ἀφαιρουμένου, ‹τοῦ› λοιποῦ τὸ αὐτὸ σημεῖον ‹κέντρον› ἐστὶ τοῦ βάρους.

   ‹Ἐὰν ἀπὸ μεγέ›θους μέγεθο‹ς ἀφαιρεθῇ, ᾖ δὲ› μὴ τὸ αὐτὸ σημεῖον κέντρον τοῦ βάρους τοῦ τε ὅλου μεγέθους καὶ τοῦ ἀφαιρουμένου μεγέθους, τὸ κέντρον ἐστὶ τοῦ βάρους τοῦ λοιποῦ μεγέθους ἐπὶ τῆς ‹εὐθείας› τῆς ἐπιζευγνυούσης τὰ κέντρα τοῦ βάρους τοῦ τε ὅλου ‹καὶ τοῦ ἀφαιρουμέ›νου ἐκβεβλημένης καὶ ἀφαιρεθείσης ἀπ᾿ αὐτῆς πρὸς τὴν μεταξὺ τῶν εἰρημένων κέντρων τοῦ βάρους τοῦτον ἐχούσης τὸν λόγον, ὃν ἔχει τὸ βάρος τοῦ ἀφαιρουμένου μεγέθους πρὸς τὸ [λοιπὸν] βάρος τοῦ λοιποῦ μεγέθους.

   Ἐὰν ὁποσωνοῦν μεγεθέων τὸ κέντρον τοῦ βάρους ἐπὶ τῆς αὐτῆς εὐθείας ᾖ, καὶ τοῦ ἐκ πάντων συγκειμένου μεγέθους τὸ κέντρον ἔσται ἐπὶ τῆς αὐτῆς εὐθείας.

   Πάσης εὐθείας τὸ κέντρον ἐστὶ τοῦ βάρους ἡ διχοτομία τῆς εὐθείας.

   Παντὸς τριγώνου τὸ κέντρον ἐστὶν τοῦ βάρους τὸ σημεῖον, καθ᾿ ὃ αἱ ἐκ τῶν γωνιῶν τοῦ τριγώνου ἐπὶ μέσας τὰς πλευρὰς ἀγόμεναι εὐθεῖαι τέμνουσιν ἀλλήλας.

   Παντὸς παραλληλογράμμου τὸ κέντρον ἐστὶν ‹τοῦ βάρους τὸ σημεῖον, καθ᾿ ὃ αἱ διάμετροι συμπίπτουσιν.

   Κύκλου› τὸ κέντρον τοῦ βάρους ἐστὶν ὃ καὶ ‹τοῦ κύκλου› ἐστὶ κέντρον.

   Παντὸς κυλίνδρου τὸ κέντρον τοῦ βάρους ἐστὶν ἡ διχοτομία τοῦ ἄξονος.

   Παντὸς πρίσματος τὸ κέντρον ἐστὶ τοῦ βάρους ἡ διχοτομία τοῦ ἄξονος.

   Παντὸς κώνου τὸ κέντρον ἐστὶν τοῦ βάρους ἐπὶ τοῦ ἄξονος διαιρεθέντος οὕτως, ὥστε τὸ πρὸς τῇ κορυφῇ τμῆμα τριπλάσιον εἶναι τοῦ λοιποῦ.

[86]    Χρησόμεθα δὲ καὶ [ἐν τῷ προγεγραμμένῳ Κωνοειδῶν] τῷδε τῷ θεωρήματι· Ἐὰν ὁποσαοῦν μεγέθη ἄλλοις μεγέθεσιν ἴσοις τὸ πλῆθος κατὰ δύο τὸν αὐτὸν ἔχῃ λόγον τὰ ὁμοίως τεταγμένα, ᾖ δὲ τὰ πρῶτα μεγέθη πρὸς ἄλλα μεγέθη ἐν λόγοις ὁποιοισοῦν, ἢ τὰ πάντα ἤ τινα αὐτῶν, καὶ τὰ ὕστερον μεγέθη πρὸς ἄλλα μεγέθη τὰ ὁμόλογα ἐν τοῖς αὐτοῖς λόγοις ᾖ, πάντα τὰ πρῶτα μεγέθη πρὸς πάντα τὰ λεγόμενα τὸν αὐτὸν ἔχει λόγον, ὃν ἔχει πάντα τὰ ὕστερον πρὸς πάντα τὰ λεγόμενα.

   α΄.

   Ἔστω τμῆμα τὸ ΑΒΓ περιεχόμενον ὑπὸ εὐθείας τῆς ΑΓ καὶ ὀρθογωνίου κώνου τομῆς τῆς ΑΒΓ, καὶ τετμήσθω δίχα ἡ ΑΓ τῷ Δ, καὶ παρὰ τὴν διάμετρον ἤχθω ἡ ΔΒΕ, καὶ ἐπεζεύχθωσαν αἱ ΑΒ, ΒΓ.

   Λέγω ὅτι ἐπίτριτόν ἐστιν τὸ ΑΒΓ τμῆμα τοῦ ΑΒΓ τριγώνου.

[87]    Ἤχθωσαν ἀπὸ τῶν Α, Γ σημείων ἡ μὲν ΑΖ παρὰ τὴν ΔΒΕ, ἡ δὲ ΓΖ ἐπιψαύουσα τῆς τομῆς, καὶ ἐκβεβλήσ‹θω ἡ ΓΒ ἐπὶ τὸ Κ, καὶ κείσθω τῇ ΓΚ ἴση ἡ ΚΘ›. Νοείσθω ζυγὸς ὁ ΓΘ καὶ μέσον αὐτοῦ τὸ Κ καὶ τῇ ΕΔ παράλληλος τυχοῦσα ἡ ΜΞ.



   Ἐπεὶ οὖν παραβολή ἐστιν ἡ ΓΒΑ, καὶ ἐφάπτεται ἡ ΓΖ, καὶ τεταγμένως ἡ ΓΔ, ἴση ἐστὶν ἡ ΕΒ τῇ ΒΔ· τοῦτο γὰρ ἐν τοῖς στοιχείοις δείκνυται· διὰ δὴ τοῦτο, καὶ διότι παράλληλοί εἰσιν αἱ ΖΑ, ΜΞ τῇ ΕΔ, ἴση ἐστὶν καὶ ἡ μὲν ΜΝ τῇ ΝΞ, ἡ δὲ ΖΚ τῇ ΚΑ. Καὶ ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς ΑΞ, οὕτως ἡ ΜΞ πρὸς ΞΟ [τοῦτο γὰρ ἐν λήμματι δείκνυται], ὡς δὲ ἡ ΓΑ πρὸς ΑΞ, οὕτως ἡ ΓΚ πρὸς ΚΝ, καὶ ἴση ἐστὶν ἡ ΓΚ τῇ ΚΘ, ὡς ἄρα ἡ ΘΚ πρὸς ΚΝ, οὕτως ἡ ΜΞ πρὸς ΞΟ. Καὶ ἐπεὶ τὸ Ν σημεῖον κέντρον τοῦ βάρους τῆς ΜΞ εὐθείας ἐστίν, ἐπείπερ ἴση ἐστὶν ἡ ΜΝ τῇ ΝΞ, ἐὰν ἄρα τῇ ΞΟ ἴσην θῶμεν τὴν ΤΗ καὶ κέντρον τοῦ βάρους αὐτῆς τὸ Θ, ὅπως ἴση ᾖ ἡ ΤΘ τῇ ΘΗ, ἰσορροπήσει ἡ ΤΘΗ τῇ ΜΞ αὐτοῦ μενούσῃ διὰ τὸ ἀντιπεπονθότως τετμῆσθαι τὴν ΘΝ τοῖς ΤΗ, ΜΞ βάρεσιν, καὶ ὡς τὴν ΘΚ πρὸς ΚΝ, οὕτως τὴν ΜΞ πρὸς τὴν ΗΤ· ὥστε τοῦ ἐξ ἀμφοτέρων βάρους κέντρον ἐστὶν τοῦ βάρους τὸ Κ. Ὁμοίως δὲ καὶ ὅσαι ἂν ἀχθῶσιν ἐν τῷ ΖΑΓ τριγώνῳ παράλληλοι τῇ ΕΔ ἰσορροπήσουσιν αὐτοῦ μένουσαι ταῖς ἀπολαμβανομέναις ἀπ᾿ αὐτῶν ὑπὸ τῆς τομῆς μετενεχθείσαις ἐπὶ τὸ ‹Θ, ὥστε εἶναι τοῦ ἐξ ἀμφοτέ›ρων κέντρον τοῦ βάρους τὸ Κ. Καὶ ἐπεὶ ἐκ μὲν τῶν ἐν τῷ ΓΖΑ τριγώνῳ τὸ ΓΖΑ τρίγωνον συνέστηκεν, ἐκ δὲ τῶν ἐν τῇ τομῇ ὁμοίως τῇ ΞΟ λαμβανομένων συνέστηκε τὸ ΑΒΓ τμῆμα, ἰσορροπήσει ἄρα τὸ ΖΑΓ τρίγωνον αὐτοῦ μένον τῷ τμήματι τῆς τομῆς τεθέντι περὶ κέντρον τοῦ βάρους [88] τὸ Θ κατὰ τὸ Κ σημεῖον, ὥστε τοῦ ἐξ ἀμφοτέρων κέντρον εἶναι τοῦ βάρους τὸ Κ. Τετμήσθω δὴ ἡ ΓΚ τῷ Χ, ὥστε τριπλασίαν εἶναι τὴν ΓΚ τῆς ΚΧ· ἔσται ἄρα τὸ Χ σημεῖον κέντρον βάρους τοῦ ΑΖΓ τριγώνου· δέδεικται γὰρ ἐν τοῖς Ἰσορροπικοῖς. Ἐπεὶ οὖν ἰσόρροπον τὸ ΖΑΓ τρίγωνον αὐτοῦ μένον τῷ ΒΑΓ τμήματι κατὰ τὸ Κ τεθέντι περὶ τὸ Θ κέντρον τοῦ βάρους, καί ἐστιν τοῦ ΖΑΓ τριγώνου κέντρον βάρους τὸ Χ, ἔστιν ἄρα ὡς τὸ ΑΖΓ τρίγωνον πρὸς τὸ ΑΒΓ τμῆμα κείμενον περὶ τὸ Θ κέντρον, οὕτως ἡ ΘΚ πρὸς ΧΚ. Τριπλασία δέ ἐστιν ἡ ΘΚ τῆς ΚΧ· τριπλάσιον ἄρα καὶ τὸ ΑΖΓ τρίγωνον τοῦ ΑΒΓ τμήματος· Ἔστι δὲ καὶ τὸ ΖΑΓ τρίγωνον τετραπλάσιον τοῦ ΑΒΓ τριγώνου διὰ τὸ ἴσην εἶναι τὴν μὲν ΖΚ τῇ ΚΑ, τὴν δὲ ΑΔ τῇ ΔΓ· ἐπίτριτον ἄρα ἐστὶν τὸ ΑΒΓ τμῆμα τοῦ ΑΒΓ τριγώνου. [Τοῦτο οὖν φανερόν ἐστιν].

   β΄.

   Τοῦτο δὴ διὰ μὲν τῶν νῦν εἰρημένων οὐκ ἀποδέδεικται, ἔμφασιν δέ τινα πεποίηκε τὸ συμπέρασμα ἀληθὲς εἶναι· διόπερ ἡμεῖς ὁρῶντες μὲν οὐκ ἀποδεδειγμένον, ὑπονοοῦντες δὲ τὸ συμπέρασμα ἀληθὲς εἶναι, τάξομεν τὴν γεωμετρουμένην ἀπόδειξιν ἐξευρόντες αὐτοὶ τὴν ἐκδοθεῖσαν πρότερον.

   Ὅτι δὲ πᾶσα σφαῖρα τετραπλασία ἐστὶν τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας, καὶ ὁ κύλινδρος ὁ βάσιν μὲν ἔχων ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας, ἡμιόλιος τῆς σφαίρας ἐστίν, ὧδε θεωρεῖται κατὰ τρόπον τόνδε·

[89]    Ἔστω γάρ τις σφαῖρα, ἐν ᾗ μέγιστος κύκλος ὁ ΑΒΓΔ, διάμετροι δὲ αἱ ΑΓ, ΒΔ πρὸς ὀρθὰς ἀλλήλαις οὖσαι, ἔστω δὲ κύκλος ἐν τῇ σφαίρᾳ περὶ διάμετρον τὴν ΒΔ ὀρθὸς πρὸς τὸν ΑΒΓΔ κύκλον, καὶ ἀπὸ τοῦ ὀρθοῦ κύκλου τούτου κῶνος ἀναγεγράφθω κορυφὴν ἔχων τὸ Α σημεῖον, καὶ ἐκβληθείσης τῆς ἐπιφανείας αὐτοῦ τετμήσθω ὁ κῶνος ἐπιπέδῳ διὰ τοῦ Γ παρὰ τὴν βάσιν· ‹ποιήσει δὴ κύκλον ὀρθὸν πρὸς› τὴν ΑΓ, καὶ διάμετρος αὐτοῦ ἡ ΕΖ. Ἀπὸ δὲ τοῦ κύκλου τούτου κύλινδρος ἀναγεγράφθω ἄξονα ἔχων τῇ ΑΓ ἴσον, πλευραὶ δὲ ἔστωσαν τοῦ κυλίνδρου αἱ ΕΛ, ΖΗ· καὶ ἐκβεβλήσθω ἡ ΓΑ, καὶ κείσθω αὐτῇ ἴση ἡ ΑΘ, καὶ νοείσθω ζυγὸς ὁ ΓΘ, μέσον δὲ αὐτοῦ τὸ Α, καὶ ἤχθω τις παράλληλος ὑπάρχουσα τῇ ΒΔ ἡ ΜΝ, τεμνέτω δὲ αὕτη τὸν μὲν ΑΒΓΔ κύκλον κατὰ τὰ Ξ, Ο, τὴν δὲ ΑΓ διάμετρον κατὰ τὸ Σ, τὴν δὲ ΑΕ εὐθεῖαν κατὰ τὸ Π, τὴν δὲ ΑΖ κατὰ τὸ Ρ, καὶ ἀπὸ τῆς ΜΝ εὐθείας ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΑΓ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ κυλίνδρῳ τομὴν ‹κύκλον, οὗ ἔσται διάμετρος ἡ ΜΝ, [90] ἐν δὲ τῇ ΑΒΓΔ σφαίρᾳ› κύκλον, οὗ ἔσται διάμετρος ἡ ΞΟ, ἐν δὲ τῷ ΑΕΖ κώνῳ κύκλον, οὗ ἔσται διάμετρος ἡ ΠΡ.



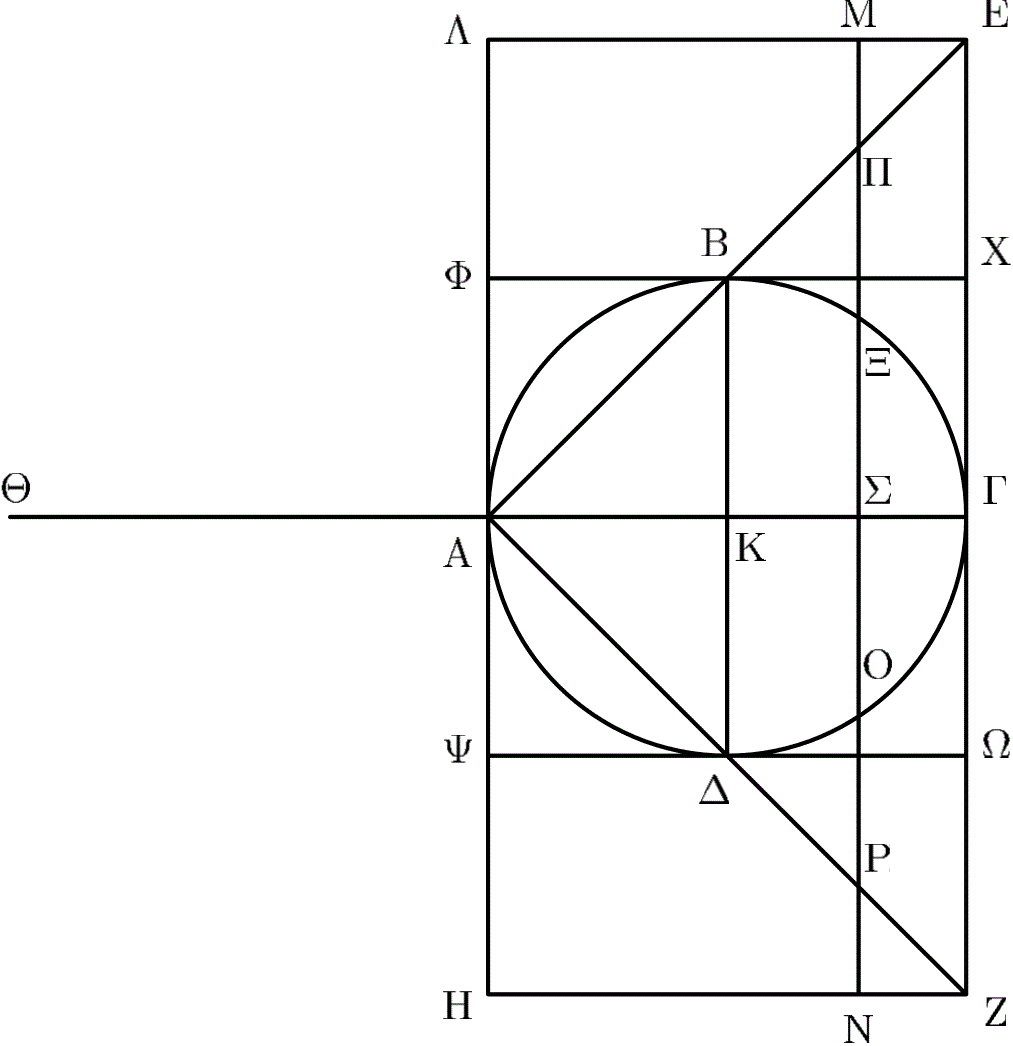
   Καὶ ἐπεὶ ἴσον ἐστὶν τὸ ὑπὸ ΓΑ, ΑΣ τῷ ὑπὸ ΜΣ, ΣΠ, ἴση γὰρ ἡ μὲν ΑΓ τῇ ΣΜ, ἡ δὲ ΑΣ τῇ ΠΣ, τῷ δὲ ὑπὸ ΓΑ, ΑΣ ἴσον ἐστὶν τὸ ἀπὸ ΑΞ, τουτέστιν τὰ ἀπὸ ΞΣ, ΣΠ, ἴσον ἄρα τὸ ὑπὸ τῶν ΜΣ, ΣΠ τοῖς ἀπὸ τῶν ΞΣ, ΣΠ. Καὶ ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς ΑΣ, οὕτως ἡ ΜΣ πρὸς ΣΠ, ἴση δὲ ἡ ΓΑ τῇ ΑΘ, ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, ἡ ΜΣ πρὸς ΣΠ, τουτέστι τὸ ἀπὸ ΜΣ πρὸς τὸ ὑπὸ ΜΣ, ΣΠ. Τῷ δὲ ὑπὸ ΜΣ, ΣΠ ἴσα ἐδείχθη τὰ ἀπὸ ΞΣ, ΣΠ· ὡς ἄρα ἡ ΑΘ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΜΣ πρὸς τὰ ἀπὸ ΞΣ, ΣΠ. Ὡς δὲ τὸ ἀπὸ ΜΣ πρὸς τὰ ἀπὸ ΞΣ, ΣΠ, οὕτως τὸ ἀπὸ ΜΝ πρὸς τὰ ἀπὸ ΞΟ, ΠΡ, ὡς δὲ τὸ ἀπὸ ΜΝ πρὸς τὰ ἀπὸ ΞΟ, ΠΡ, οὕτως ὁ κύκλος ὁ ἐν τῷ κυλίνδρῳ, οὗ διάμετρος ἡ ΜΝ, πρὸς ‹ἀμφοτέρους τοὺς κύκλους τόν τε ἐν τῷ κώνῳ, οὗ διάμετρος ἡ ΠΡ,› καὶ τὸν ἐν τῇ σφαίρᾳ, οὗ ἐστιν διάμετρος ἡ ΞΟ· ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως ὁ κύκλος ὁ ἐν τῷ κυλίνδρῳ πρὸς τοὺς κύκλους τόν τε ἐν τῇ σφαίρᾳ καὶ τὸν ἐν τῷ κώνῳ. Ἐπεὶ οὖν ὡς ἡ ΘΑ πρὸς ΑΣ, οὕτως αὐτὸς ὁ κύκλος ὁ ἐν τῷ κυλίνδρῳ αὐτοῦ μένων ἀμφοτέροις τοῖς κύκλοις, ὧν εἰσιν διάμετροι αἱ ΞΟ, ΠΡ, μετενεχθεῖσιν καὶ τεθεῖσιν οὕτως ἐπὶ τὸ Θ, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ, ἰσορροπήσουσι κατὰ τὸ Α σημεῖον. Ὁμοίως δὲ δειχθήσεται, καὶ ἐὰν ἄλλη ἀχθῇ ἐν τῷ ΛΖ παραλληλογράμμῳ παρὰ τὴν ΕΖ, καὶ ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀνασταθῇ ὀρθὸν πρὸς τὴν ΑΓ, ὅτι ὁ γενόμενος κύκλος ἐν τῷ κυλίνδρῳ ἰσορροπήσει περὶ τὸ Α σημεῖον [91] αὐτοῦ μένων ἀμφοτέροις τοῖς κύκλοις τῷ τε ἐν τῇ σφαίρᾳ γινομένῳ καὶ τῷ ἐν τῷ κώνῳ μετενεχθεῖσι καὶ τεθεῖσιν ἐπὶ τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ. Συμπληρωθέντος οὖν τοῦ κυλίνδρου ὑπὸ τῶν ληφθέντων κύκλων καὶ τῆς σφαίρας καὶ τοῦ κώνου ἰσορροπήσει ὁ κύλινδρος περὶ τὸ Α σημεῖον αὐτοῦ μένων συναμφοτέροις τῇ τε σφαίρᾳ καὶ τῷ κώνῳ μετενεχθεῖσι καὶ τεθεῖσιν ἐπὶ τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ. Ἐπεὶ οὖν ἰσορροπεῖ τὰ εἰρημένα στερεὰ κατὰ τὸ Α σημεῖον τοῦ μὲν κυλίνδρου μένοντος περὶ κέντρον τοῦ βάρους τὸ Κ, τῆς δὲ σφαίρας καὶ τοῦ κώνου μετενηνεγμένων, ὡς εἴρηται, περὶ κέντρον βάρους τὸ Θ, ἔσται ὡς ἡ ΘΑ πρὸς ΑΚ, οὕτως ὁ κύλινδρος πρὸς τὴν σφαῖραν καὶ τὸν κῶνον. Διπλασία δὲ ἡ ΘΑ τῆς ΑΚ· διπλασίων ἄρα καὶ ὁ κύλινδρος συναμφοτέρου τῆς τε σφαίρας καὶ τοῦ κώνου. Αὐτοῦ δὲ τοῦ κώνου τριπλασίων ἐστί· τρεῖς ἄρα κῶνοι ἴσοι εἰσὶ δυσὶ κώνοις τοῖς αὐτοῖς καὶ δυσὶ σφαίραις. Κοινοὶ ἀφῃρήσθωσαν δύο κῶνοι· εἷς ἄρα κῶνος ὁ ἔχων τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΕΖ ἴσος ἐστὶ ταῖς εἰρημέναις δυσὶ σφαίραις. Ὁ δὲ κῶνος, οὗ τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΕΖ, ἴσος ἐστὶν ὀκτὼ κώνοις, ὧν ἐστι τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΒΔ, διὰ τὸ διπλῆν εἶναι τὴν ΕΖ τῆς ΒΔ. Οἱ ἄρα ὀκτὼ κῶνοι οἱ εἰρημένοι ἴσοι εἰσὶ δυσὶ σφαίραις. Τετραπλασίων ἄρα ἐστὶν ἡ σφαῖρα, ἧς μέγιστος κύκλος ὁ ΑΒΓΔ, τοῦ κώνου, οὗ κορυφὴ μέν ἐστι τὸ Α σημεῖον, βάσις δὲ ὁ περὶ διάμετρον τὴν ΒΔ κύκλος ὀρθὸς ὢν πρὸς τὴν ΑΓ.

   Ἤχθωσαν δὴ διὰ τῶν Β, Δ σημείων ἐν τῷ ΛΖ παραλληλογράμμῳ [92] τῇ ΑΓ παράλληλοι αἱ ΦΒΧ, ΨΔΩ, καὶ νοείσθω κύλινδρος, οὗ βάσεις μὲν οἱ περὶ διαμέτρους τὰς ΦΨ, ΧΩ κύκλοι, ἄξων δὲ ὁ ΑΓ. Ἐπεὶ οὖν διπλάσιός ἐστιν ὁ κύλινδρος, οὗ ἐστι τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΩ, τοῦ κυλίνδρου, ‹οὗ ἐστι τὸ διὰ τοῦ ἄξονος παραλ›ληλόγραμμον τὸ ΦΔ, αὐτὸς δὲ οὗτος τριπλασίων ἐστὶν τοῦ κώνου, οὗ ἐστι τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΒΔ, ὡς ἐν τοῖς Στοιχείοις, ἑξαπλασίων ἄρα ὁ κύλινδρος, οὗ ἐστι τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΩ, τοῦ κώνου, οὗ τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΒΔ. Ἐδείχθη δὲ τοῦ αὐτοῦ κώνου τετραπλασία οὖσα ἡ σφαῖρα, ἧς μέγιστός ἐστιν κύκλος ὁ ΑΒΓΔ· ἡμιόλιος ἄρα ὁ κύλινδρος τῆς σφαίρας· ὅπερ ἔδει δειχθῆναι.

   Τούτου τεθεωρημένου, διότι πᾶσα σφαῖρα τετραπλασία ἐστὶ τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος τὸν μέγιστον κύκλον, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας, ἡ ἔννοια ἐγένετο ὅτι πάσης σφαίρας ἡ ἐπιφάνεια τετραπλασία ἐστὶ τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ· ὑπόληψις γὰρ ἦν καὶ διότι πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ τῷ βάσιν μὲν ἔχοντι τὴν τοῦ κύκλου περιφέρειαν, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τοῦ κύκλου, καὶ διότι πᾶσα σφαῖρα ἴση ἐστὶ κώνῳ τῷ βάσιν μὲν ἔχοντι τὴν ἐπιφάνειαν τῆς σφαίρας, ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου τῆς σφαίρας.

   γ΄.

   Θεωρεῖται δὲ διὰ τοῦ τρόπου τούτου ‹καὶ ὅτι ὁ κύλινδρος ὁ τὴν μὲν βάσιν› ἔχων ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῷ σφαιροειδεῖ, ὕψος δὲ ἴσον τῷ ἄξονι τοῦ σφαιροειδοῦς, [93] ἡμιόλιός ἐστι τοῦ σφαιροειδοῦς· τούτου δὲ θεωρηθέντος φανερὸν ὅτι παντὸς σφαιροειδοῦς ἐπιπέδῳ τμηθέντος διὰ τοῦ κέντρου ὀρθῷ πρὸς τὸν ἄξονα τὸ ἥμισυ τοῦ σφαιροειδοῦς διπλάσιόν ἐστι τοῦ κώνου τοῦ βάσιν μὲν ἔχοντος τὴν αὐτὴν τῷ τμήματι καὶ ἄξονα τὸν αὐτόν.

   Ἔστω γάρ τι σφαιροειδὲς καὶ τετμήσθω ἐπιπέδῳ διὰ τοῦ ἄξονος, καὶ γινέσθω ἐν τῇ ἐπιφανείᾳ αὐτοῦ ὀξυγωνίου κώνου τομὴ ἡ ΑΒΓΔ, διάμετροι δὲ αὐτῆς ἔστωσαν αἱ ΑΓ, ΒΔ, κέντρον δὲ τὸ Κ, ἔστω δὲ κύκλος ἐν τῷ σφαιροειδεῖ περὶ διάμετρον τὴν ΒΔ ὀρθὸς πρὸς τὴν ΑΓ, νοείσθω δὲ κῶνος βάσιν ἔχων τὸν εἰρημένον κύκλον, κορυφὴν δὲ τὸ Α σημεῖον, καὶ ἐκβληθείσης τῆς ἐπιφανείας αὐτοῦ τετμήσθω ὁ κῶνος ἐπιπέδῳ διὰ τοῦ Γ παρὰ τὴν βάσιν· ἔσται δὴ ἡ τομὴ αὐτοῦ κύκλος ὀρθὸς πρὸς τὴν ΑΓ, διάμετρος δὲ αὐτοῦ ἡ ΕΖ. Ἔστω δὲ καὶ κύλινδρος βάσιν μὲν ἔχων τὸν αὐτὸν κύκλον, οὗ διάμετρος ἡ ΕΖ, ἄξονα δὲ τὴν ΑΓ εὐθεῖαν, καὶ ἐκβληθείσης τῆς ΓΑ κείσθω αὐτῇ ἴση ἡ ΑΘ, καὶ νοείσθω ζυγὸς ὁ ΘΓ, μέσον δὲ αὐτοῦ τὸ Α, [94] ἤχθω δέ τις ἐν τῷ ΛΖ παραλληλογράμμῳ παρὰ τὴν ΕΖ ἡ ΜΝ, καὶ ἀπὸ τῆς ΜΝ ἐπίπεδον ἀνεστάτω ὀρ‹θὸν πρὸς τὴν ΑΓ· ποιήσει δὴ τοῦτο ἐν› μὲν τῷ κυλίνδρῳ τομὴν κύκλον, οὗ διάμετρος ἡ ΜΝ, ἐν δὲ τῷ σφαιροειδεῖ τομὴν κύκλον, οὗ διάμετρος ἡ ΞΟ, ἐν δὲ τῷ κώνῳ τομὴν κύκλον, οὗ διάμετρος ἡ ΠΡ.



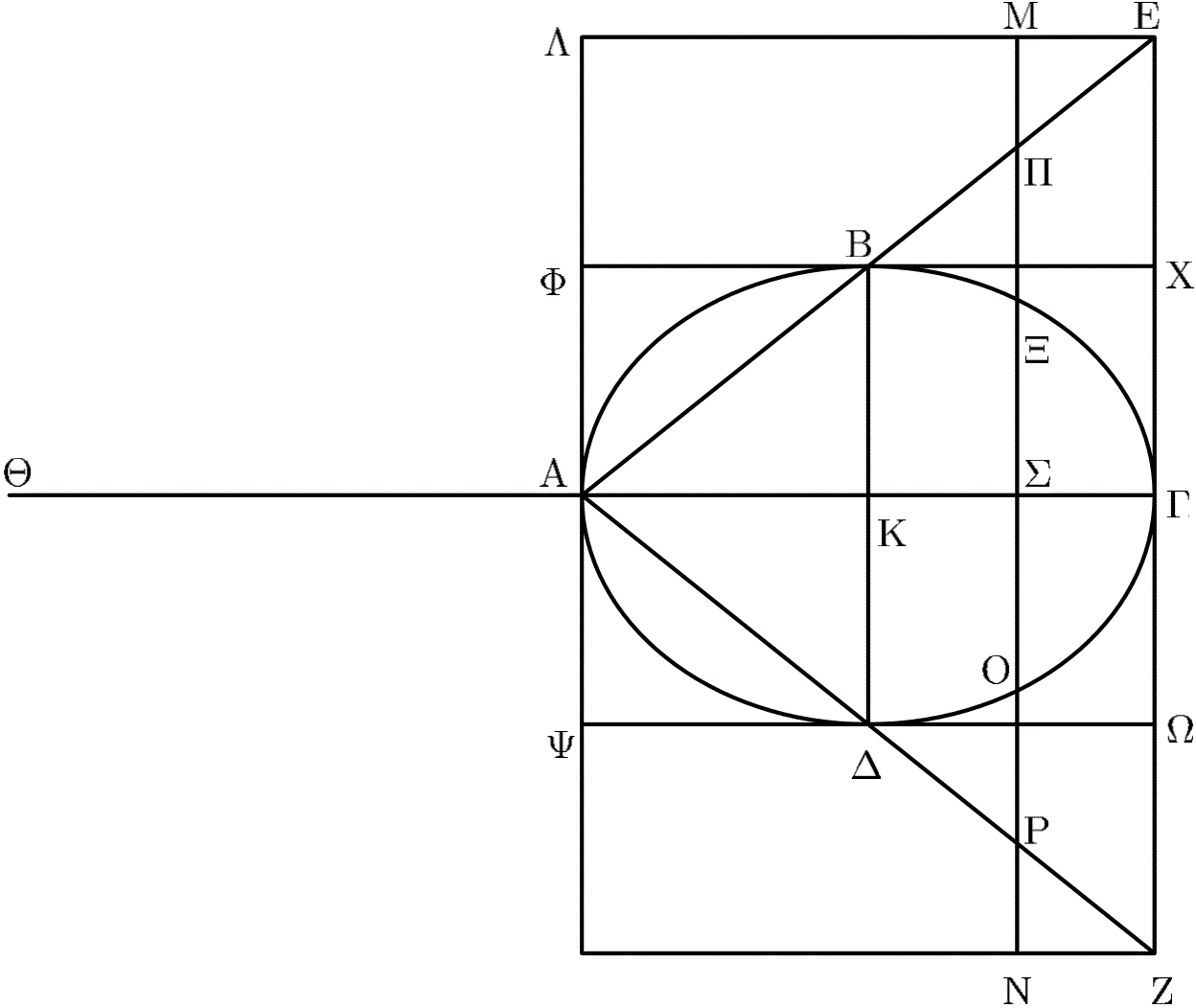
   Καὶ ἐπεί ἐστιν ὡς ἡ ΓΑ πρὸς τὴν ΑΣ, οὕτως ἡ ΕΑ πρὸς ΑΠ, τουτέστιν ἡ ΜΣ πρὸς τὴν ΣΠ, ἴση δὲ ἡ ΓΑ τῇ ΑΘ, ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως ἡ ΜΣ πρὸς ΣΠ. Ὡς δὲ ἡ ΜΣ πρὸς ΣΠ, οὕτως τὸ ἀπὸ ΜΣ πρὸς τὸ ὑπὸ ΜΣ, ΣΠ· τῷ δὲ ὑπὸ ΜΣ, ΣΠ ἴσα τὰ ἀπὸ τῶν ΠΣ, ΣΞ. Ἐπεὶ γάρ ἐστιν ὡς τὸ ὑπὸ ΑΣ, ΣΓ πρὸς τὸ ἀπὸ ΣΞ, οὕτως τὸ ὑπὸ ΑΚ, ΚΓ, τουτέστιν τὸ ἀπὸ ΑΚ, πρὸς τὸ ἀπὸ ΚΒ [ἀμφότεροι γὰρ οἱ λόγοι ἐν τῷ τῆς πλαγίας πρὸς τὴν ὀρθίαν εἰσίν], ὡς δὲ τὸ ἀπὸ ΑΚ πρὸς τὸ ἀπὸ ΚΒ, οὕτως τὸ ἀπὸ ΑΣ πρὸς τὸ ἀπὸ ΣΠ, ἐναλλὰξ ἄρα ἔσται ὡς τὸ ἀπὸ ΑΣ πρὸς τὸ ὑπὸ ΑΣΓ, τὸ ἀπὸ ΠΣ πρὸς τὸ ἀπὸ ΣΞ. Ὡς δὲ τὸ ἀπὸ ΑΣ πρὸς τὸ ὑπὸ ΑΣΓ, τὸ ἀπὸ ΣΠ πρὸς τὸ ὑπὸ ΣΠ, ΠΜ· ἴσον ἄρα τὸ ὑπὸ ΜΠ, ΠΣ τῷ ἀπὸ ΞΣ. Κοινὸν προσκείσθω τὸ ἀπὸ ΠΣ· τὸ ἄρα ὑπὸ ΜΣ, ΣΠ τοῖς ἀπὸ ΠΣ, ΣΞ ἴσον. Ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, τὸ ἀπὸ ΜΣ πρὸς τὰ ἀπὸ ΠΣ, ΣΞ. Ὡς δὲ τὸ ἀπὸ ΜΣ πρὸς τὰ ἀπὸ ΣΞ, ΣΠ, οὕτως ὁ ἐν τῷ κυλίνδρῳ κύκλος, οὗ διάμετρος ἡ ΜΝ, πρὸς ἀμφοτέρους τοὺς κύκλους, ὧν διάμετροι αἱ ΞΟ, ΠΡ· ὥστε ἰσορροπήσει περὶ τὸ Α σημεῖον ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, αὐτοῦ μένων ἀμφοτέροις τοῖς κύκλοις, ὧν διάμετροι αἱ ΞΟ, ΠΡ, μετενεχθεῖσι καὶ τεθεῖσιν τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ. [95] Συναμφοτέρων δὲ τῶν κύκλων, ὧν εἰσι διάμετροι αἱ ΞΟ, ΠΡ, μετενηνεγμένων κέντρον τοῦ βάρους τὸ Θ· καὶ ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, πρὸς ἀμφοτέρους τοὺς κύκλους, ὧν διάμετροι αἱ ΞΟ, ΠΡ. Ὁμοίως δὲ δειχθήσεται, καὶ ἐὰν ἄλλη τις ἀχθῇ ἐν τῷ ΛΖ παραλληλογράμμῳ παρὰ τὴν ΕΖ, καὶ ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀνασταθῇ ὀρθὸν πρὸς τὴν ΑΓ, ὅτι ὁ γενόμενος κύκλος ἐν τῷ κυλίνδρῳ ἰσορροπήσει περὶ τὸ Α σημεῖον αὐτοῦ μένων συναμφοτέροις τοῖς κύκλοις τῷ τε ἐν τῷ σφαιροειδεῖ γινομένῳ καὶ τῷ ἐν τῷ κώνῳ μετενεχθεῖσιν τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ. Συμπληρωθέντος οὖν τοῦ κυλίνδρου ὑπὸ τῶν ληφθέντων κύκλων καὶ τοῦ σφαιροειδοῦς καὶ τοῦ κώνου ἰσόρροπος ὁ κύλινδρος ἔσται περὶ τὸ Α σημεῖον αὐτοῦ μένων τῷ τε σφαιροειδεῖ καὶ τῷ κώνῳ μετενεχθεῖσι καὶ τεθεῖσιν ἐπὶ τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε ἑκατέρου αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ. Καί ἐστι τοῦ μὲν κυλίνδρου κέντρον τοῦ βάρους τὸ Κ, τοῦ δὲ σφαιροειδοῦς καὶ τοῦ κώνου συναμφοτέρων, ὡς ἐρρέθη, κέντρον τοῦ βάρους τὸ Θ· ἔστιν οὖν ὡς ἡ ΘΑ πρὸς ΑΚ, ὁ κύλινδρος πρὸς ἀμφότερα τό τε σφαιρο‹ειδὲς καὶ τὸν κῶνον›. Δ‹ιπλα›σία δὲ ἡ ΑΘ τῆς ΑΚ· διπλάσιος ἄρα καὶ ὁ κύλινδρος ἀμφοτέρων τοῦ τε σφαιροειδοῦς καὶ τοῦ κώνου· εἷς ἄρα κύλινδρος ἴσος δυσὶν κώνοις καὶ δυσὶ σφαιροειδέσιν. Εἷς δὲ κύλινδρος ἴσος ἐστὶ τρισὶ κώνοις τοῖς αὐτοῖς· τρεῖς ἄρα κῶνοι ἴσοι εἰσὶ δυσὶ κώνοις καὶ δυσὶ σφαιροειδέσι. Κοινοὶ ἀφῃρήσθωσαν δύο κῶνοι· λοιπὸς ἄρα εἷς κῶνος, οὗ ἐστι τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΕΖ, ἴσος ἐστὶ δυσὶ σφαιροειδέσιν. Εἷς δὲ κῶνος ὁ αὐτὸς ἴσος ἐστὶν ὀκτὼ κώνοις, ὧν ἐστι [96] τὸ διὰ τοῦ ἄξονος τρίγωνον τὸ ΑΒΔ· ὀκτὼ ἄρα κῶνοι οἱ εἰρημένοι ἴσοι εἰσὶ δυσὶ σφαιροειδέσιν· καὶ τέσσαρες ἄρα κῶνοι ἴσοι ἑνὶ σφαιροειδεῖ· τετραπλάσιον ἄρα ἐστὶ τὸ σφαιροειδὲς τοῦ κώνου, οὗ κορυφὴ μέν ἐστι τὸ Α σημεῖον, βάσις δὲ ὁ περὶ διάμετρον τὴν ΒΔ κύκλος ὀρθὸς ὢν πρὸς τὴν ΑΓ, καὶ τὸ ἥμισυ τοῦ σφαιροειδοῦς διπλάσιόν ἐστι τοῦ εἰρημένου κώνου.

   Ἤχθωσαν δὲ διὰ τῶν Β, Δ σημείων ἐν τῷ ΛΖ παραλληλογράμμῳ τῇ ΑΓ παράλληλοι αἱ ΦΧ, ΨΩ, καὶ νοείσθω κύλινδρος, οὗ βάσεις μὲν οἱ περὶ διαμέτρους τὰς ΦΨ, ΧΩ κύκλοι, ἄξων δὲ ἡ ΑΓ εὐθεῖα.

   Ἐπεὶ οὖν διπλάσιός ἐστιν ὁ κύλινδρος, οὗ ἐστι τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΩ, τοῦ κυλίνδρου, οὗ τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΔ, διὰ τὸ ἴσας αὐτῶν εἶναι τὰς βάσεις, τὸν δὲ ἄξονα τοῦ ἄξονος διπλάσιον, αὐτὸς δὲ ὁ κύλινδρος, οὗ τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΔ, τριπλασίων ἐστὶ τοῦ κώνου, οὗ κορυφὴ μὲν τὸ Α σημεῖον, βάσις δὲ ὁ περὶ διάμετρον τὴν ΒΔ κύκλος ὀρθὸς ὢν πρὸς τὴν ΑΓ, ἑξαπλάσιος ἄρα ὁ κύλινδρος, οὗ ἐστι τὸ διὰ τοῦ ἄξονος παραλληλόγραμμον τὸ ΦΩ, τοῦ εἰρημένου κώνου. Ἐδείχθη δὲ τοῦ αὐτοῦ κώνου τετραπλάσιον τὸ σφαιροειδές· ἡμιόλιος ἄρα ἐστὶν ὁ κύλινδρος τοῦ σφαιροειδοῦς· οι.

   δ΄.

   Ὅτι δὲ πᾶν τμῆμα ὀρθογωνίου κωνοειδοῦς ἐπιπέδῳ ἀποτεμνόμενον ὀρθῷ πρὸς τὸν ἄξονα ἡμιόλιόν ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὴν αὐτὴν τῷ τμήματι καὶ τὸν ἄξονα τὸν αὐτόν, ὧδε διὰ τοῦ τρόπου τούτου θεωρεῖται.

[97]    Ἔστω γὰρ ὀρθογώνιον κωνοειδὲς καὶ τετμήσθω ἐπιπέδῳ διὰ τοῦ ἄξονος, καὶ ποιείτω τομὴν ἐν τῇ ἐπιφανείᾳ ὀρθογωνίου κώνου τομὴν τὴν ΑΒΓ, τετμήσθω δὲ καὶ ἑτέρῳ ἐπιπέδῳ ὀρθῷ πρὸς τὸν ἄξονα, καὶ ἔστω αὐτῶν κοινὴ τομὴ ἡ ΒΓ, ἄξων δὲ ἔστω τοῦ τμήματος ἡ ΔΑ, καὶ ἐκβεβλήσθω ἡ ΔΑ ἐπὶ τὸ Θ, καὶ κείσθω αὐτῇ ἴση ἡ ΑΘ, καὶ νοείσθω ζυγὸς ὁ ΔΘ, μέσον δὲ αὐτοῦ τὸ Α, ἔστω δὲ ἡ τοῦ τμήματος βάσις ὁ περὶ διάμετρον τὴν ΒΓ κύκλος ὀρθὸς ὢν πρὸς ‹τὴν ΑΔ, νοείσθω δὲ κῶνος βάσιν› μὲν ἔχων τὸν κύκλον, οὗ ἐστι διάμετρος ἡ ΒΓ, κορυφὴν δὲ τὸ Α σημεῖον, ἔστω δὲ καὶ κύλινδρος βάσιν μὲν ἔχων τὸν κύκλον, οὗ διάμετρος ἡ ΒΓ, ἄξονα δὲ τὸν ΑΔ, καὶ ἤχθω τις ἐν τῷ παραλληλογράμμῳ ἡ ΜΝ παράλληλος οὖσα τῇ ΒΓ, καὶ ἀπὸ τῆς ΜΝ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΑΔ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ κυλίνδρῳ τομὴν κύκλον, οὗ διάμετρος ἡ ΜΝ, ἐν δὲ τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδοῦς τομὴν κύκλον, οὗ διάμετρος ἡ ΞΟ.



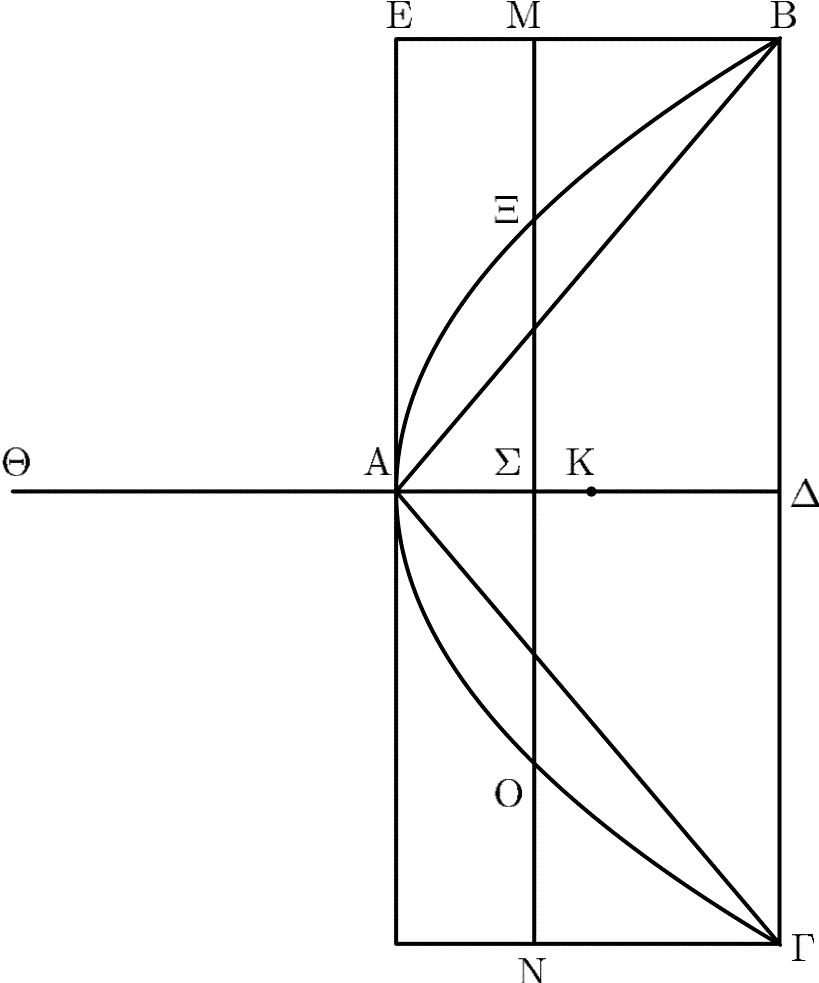
   Καὶ ἐπεὶ ὀρθογωνίου κώνου τομή ἐστιν ἡ ΒΑΓ, διάμετρος δὲ αὐτῆς ἡ ΑΔ, καὶ τεταγμένως κατηγμέναι [98] εἰσὶν αἱ ΞΣ, ΒΔ, ἔστιν ὡς ἡ ΔΑ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΞΣ. Ἴση δὲ ἡ ΔΑ τῇ ΑΘ· ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΜΣ πρὸς τὸ ἀπὸ ΣΞ. Ὡς δὲ τὸ ἀπὸ ΜΣ πρὸς τὸ ἀπὸ ΣΞ, οὕτως ὁ κύκλος ὁ ἐν τῷ κυλίνδρῳ, οὗ διάμετρος ἡ ΜΝ, πρὸς τὸν κύκλον τὸν ἐν τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδοῦς, οὗ διάμετρος ἡ ΞΟ· ἔστιν ἄρα ὡς ἡ ΘΑ πρὸς ΑΣ, οὕτως ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, πρὸς τὸν κύκλον, οὗ διάμετρος ἡ ΞΟ. Ἰσόρροπος ἄρα ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, ὁ ἐν τῷ κυλίνδρῳ περὶ τὸ Α σημεῖον αὐτοῦ μένων τῷ κύκλῳ, οὗ διάμετρος ἡ ΞΟ, μετενεχθέντι καὶ τεθέντι ἐπὶ τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον αὐτοῦ ‹εἶναι τοῦ βάρους τὸ› Θ· ‹καί ἐστι τοῦ› μὲν ‹κύκλου, οὗ διάμετρός ἐστιν ἡ› ΜΝ, κέντρον τοῦ βάρους τὸ Σ, τοῦ δὲ κύκλου, οὗ ἐστι διάμετρος ἡ ΞΟ, μετενηνεγμένου κέντρον τοῦ βάρους τὸ Θ, καὶ ἀντιπεπονθότως τὸν αὐτὸν ἔχει λόγον ἡ ΘΑ πρὸς ΑΣ ὃν ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, πρὸς τὸν κύκλον, οὗ διάμετρος ἡ ΞΟ. Ὁμοίως δὲ δειχθήσεται, καὶ ἐὰν ἄλλη τις ἀχθῇ ἐν τῷ ΕΓ παραλληλογράμμῳ παρὰ τὴν ΒΓ, καὶ ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀνασταθῇ ὀρθὸν πρὸς τὴν ΑΘ, ὅτι ἰσορροπήσει πρὸς τῷ Α σημείῳ ὁ γενόμενος κύκλος ἐν τῷ κυλίνδρῳ αὐτοῦ μένων τῷ γενομένῳ ἐν τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδέος μετενεχθέντι ἐπὶ τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ. Συμπληρωθέντος οὖν τοῦ κυλίνδρου καὶ τοῦ τμήματος τοῦ ὀρθογωνίου κωνοειδοῦς ἰσορροπήσει περὶ τὸ Α σημεῖον ὁ κύλινδρος αὐτοῦ μένων τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδέος μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε τὸ κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ. Ἐπεὶ δὲ ἰσορροπεῖ περὶ τὸ Α σημεῖον τὰ εἰρημένα μεγέθη, καί ἐστι τοῦ μὲν κυλίνδρου κέντρον βάρους τὸ Κ σημεῖον [99] δίχα τεμνομένης τῆς ΑΔ κατὰ τὸ Κ σημεῖον, τοῦ δὲ τμήματος μετενηνεγμένου κέντρον ἐστὶ τοῦ βάρεος τὸ Θ, ἀντιπεπονθότως τὸν αὐτὸν ἕξει λόγον ‹ἡ ΘΑ πρὸς τὴν ΑΚ, ὃν ὁ› κύλινδρος πρὸς τὸ τμῆμα. Διπλασία δὲ ἡ ΘΑ τῆς ΑΚ· διπλάσιος ἄρα καὶ ὁ κύλινδρος τοῦ τμήματος. Ὁ δὲ αὐτὸς κύλινδρος τριπλάσιός ἐστι τοῦ κώνου τοῦ βάσιν ἔχοντος τὸν κύκλον, οὗ διάμετρος ἡ ΒΓ, κορυφὴν δὲ τὸ Α σημεῖον· δῆλον οὖν ὅτι τὸ τμῆμα ἡμιόλιόν ἐστιν τοῦ αὐτοῦ κώνου.

   ε΄.

   Ὅτι δὲ τοῦ τμήματος τοῦ ὀρθογωνίου κωνοειδέος τοῦ ἀποτεμνομένου ἐπιπέδῳ ὀρθῷ πρὸς τὸν ἄξονα τὸ κέντρον τοῦ βάρους ἐστὶν ἐπὶ τῆς εὐθείας, ἥ ἐστιν ἄξων τοῦ τμήματος, τμηθείσης οὕτως τῆς εἰρημένης εὐθείας, ὥστε διπλάσιον εἶναι τὸ μέρος αὐτοῦ τὸ πρὸς τῇ κορυφῇ τοῦ λοιποῦ τμήματος, ὧδε διὰ τοῦ τρόπου θεωρεῖται·

[100]    Ἔστω τμῆμα ὀρθογωνίου κωνοειδοῦς ἀποτεμνόμενον ἐπιπέδῳ ὀρθῷ πρὸς τὸν ἄξονα καὶ τετμήσθω ἐπιπέδῳ ἑτέρῳ διὰ τοῦ ἄξονος, καὶ ποιείτω τομὴν ἐν τῇ ἐπιφανείᾳ τὴν ΑΒΓ ὀρθογωνίου κώνου τομήν, τοῦ δὲ ἀποτετμηκότος τὸ τμῆμα ἐπιπέδου καὶ τοῦ τέμνοντος κοινὴ τομὴ ἔστω ἡ ΒΓ, ἄξων δὲ ἔστω τοῦ τμήματος καὶ διάμετρος τῆς ΑΒΓ τομῆς ἡ ΑΔ εὐθεῖα, καὶ τῆς ‹ΔΑ ἐκβληθείσης ἴση αὐτῇ κείσθω ἡ ΑΘ, καὶ› νοείσθω ζυγὸς ὁ ΔΘ, μέσον δὲ αὐτοῦ τὸ Α, ἔστω δὲ καὶ κῶνος ἐγγεγραμμένος ἐν τῷ τμήματι, πλευραὶ δὲ αὐτοῦ αἱ ΒΑ, ΑΓ, ἤχθω δέ τις ἐν τῇ τοῦ ὀρθογωνίου κώνου τομῇ ἡ ΞΟ παράλληλος οὖσα τῇ ΒΓ, τεμνέτω δὲ αὕτη τὴν μὲν τοῦ ὀρθογωνίου κώνου τομὴν κατὰ τὰ Ξ, Ο, τὰς δὲ τοῦ κώνου πλευρὰς κατὰ τὰ Π, Ρ σημεῖα.



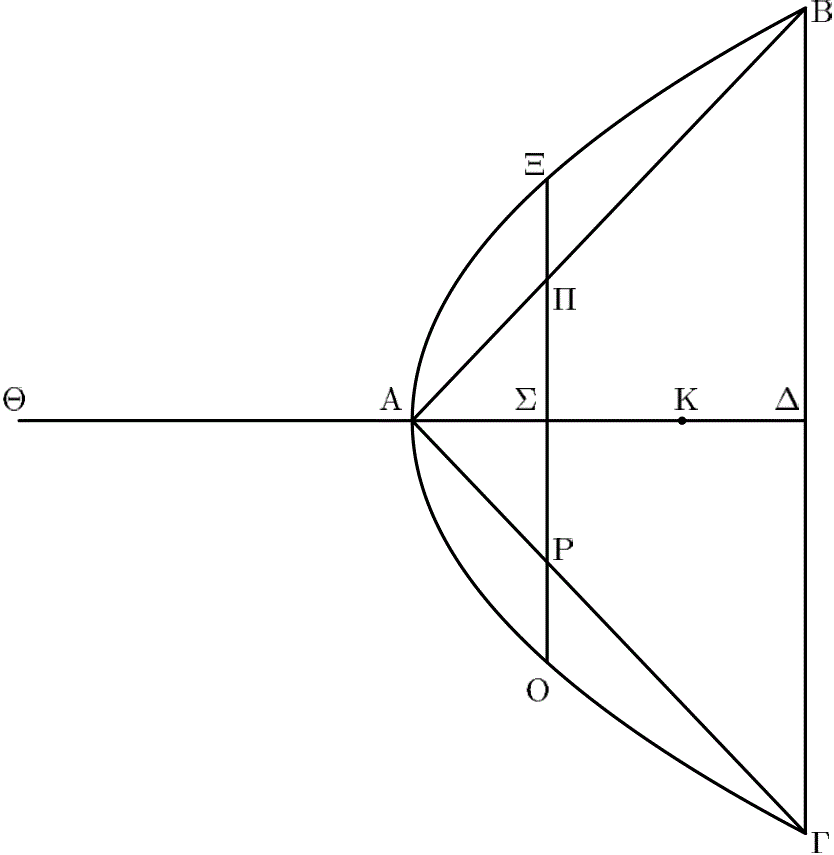
   Ἐπεὶ οὖν ἐν ὀρθογωνίου κώνου τομῇ κάθετοι ἠγμέναι εἰσὶν ἐπὶ τὴν διάμετρον αἱ ΞΣ, ΒΔ, ἔστιν ὡς ἡ ΔΑ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΞΣ. Ὡς δὲ ἡ ΔΑ πρὸς ΑΣ, οὕτως ἡ ΒΔ πρὸς ΠΣ, ὡς δὲ ἡ ΒΔ πρὸς ΠΣ, οὕτως τὸ ἀπὸ ΒΔ πρὸς τὸ ὑπὸ τῶν ΒΔ, ΠΣ· ἔσται ἄρα καὶ ὡς τὸ ἀπὸ ΒΔ πρὸς τὸ ἀπὸ ΞΣ, οὕτως τὸ ἀπὸ ΒΔ πρὸς τὸ ὑπὸ ΒΔ, ΠΣ. Ἴσον ἄρα τὸ ἀπὸ ΞΣ τῷ ὑπὸ ΒΔ, ΠΣ· ἀνάλογον ἄρα εἰσὶν αἱ ΒΔ, ΣΞ, ΣΠ, καὶ διὰ τοῦτό ἐστιν ὡς ἡ ΒΔ πρὸς ΠΣ, οὕτως τὸ ἀπὸ ΞΣ πρὸς τὸ ἀπὸ ΣΠ. Ὡς δὲ ἡ ΒΔ πρὸς ΠΣ, οὕτως ἡ ΔΑ πρὸς ΑΣ, τουτέστιν ἡ ΘΑ πρὸς ΑΣ· καὶ ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΞΣ πρὸς τὸ ἀπὸ ΣΠ. Ἀνεστάτω δὴ ἀπὸ τῆς ΞΟ ἐπίπεδον ὀρθὸν πρὸς τὴν ΑΔ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδέος κύκλον, οὗ διάμετρος ἡ ΞΟ, ἐν δὲ τῷ κώνῳ κύκλον, οὗ διάμετρος ἡ ΠΡ. Καὶ ἐπεί ἐστιν [101] ὡς ἡ ΘΑ πρὸς ΑΣ, οὕτως τὸ ἀπὸ ΞΣ πρὸς τὸ ἀπὸ ΣΠ, ὡς δὲ τὸ ἀπὸ ΞΣ πρὸς τὸ ἀπὸ ΣΠ, οὕτως ὁ κύκλος, οὗ διάμετρος ἡ ΞΟ, πρὸς τὸν κύκλον, οὗ διάμετρος ἡ ΠΡ, ὡς ἄρα ἡ ΘΑ πρὸς ΑΣ, οὕτως ὁ κύκλος, οὗ διάμετρος ἡ ΞΟ, πρὸς τὸν κύκλον, οὗ διάμε‹τρος ἡ ΠΡ. Ἰσορροπήσει ἄρα πε›ρὶ τὸ Α σημεῖον ὁ κύκλος, οὗ διάμετρος ἡ ΞΟ, αὐτοῦ μένων τῷ κύκλῳ, οὗ διάμετρος ἡ ΠΡ, μετενεχθέντι τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε κέντρον εἶναι τοῦ βάρους τὸ Θ. Ἐπεὶ οὖν τοῦ μὲν κύκλου, οὗ διάμετρος ἡ ΞΟ, αὐτοῦ μένοντος κέντρον ἐστὶν τοῦ βάρους τὸ Σ, τοῦ δὲ κύκλου, οὗ διάμετρος ἡ ΠΡ, μετενεχθέντος ὡς ἐρρέθη κέντρον τοῦ βάρους τὸ Θ, καὶ ἀντιπεπονθότως τὸν αὐτὸν ἔχει λόγον ἡ ΘΑ πρὸς ΑΣ, ὃν ὁ κύκλος, οὗ διάμετρος ἡ ΞΟ, πρὸς τὸν κύκλον, οὗ διάμετρος ἡ ΠΡ, ἰσορροπήσουσιν ἄρα πρὸς τῷ Α σημείῳ. Ὁμοίως δὲ δειχθήσεται, καὶ ἐὰν ἄλλη τις ἀχθῇ ἐν τῇ τοῦ ὀρθογωνίου κώνου τομῇ παράλληλος τῇ ΒΓ, καὶ ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀνασταθῇ ὀρθὸν πρὸς τὴν ΑΔ, ὅτι ὁ γενόμενος κύκλος ἐν τῷ τμήματι τοῦ ὀρθογωνίου κωνοειδέος αὐτοῦ μένων ἰσορροπήσει περὶ τὸ Α σημεῖον τῷ γενομένῳ κύκλῳ ἐν τῷ κώνῳ μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ. Συμπληρωθέντων οὖν ὑπὸ τῶν κύκλων τοῦ τε τμήματος καὶ τοῦ κώνου ἰσορροπήσουσι περὶ τὸ Α σημεῖον τεθέντες πάντες οἱ κύκλοι οἱ ἐν τῷ τμήματι αὐτοῦ μένοντες πᾶσι τοῖς κύκλοις τοῖς ἐν τῷ κώνῳ μετενεχθεῖσι καὶ τεθεῖσι τοῦ ζυγοῦ ‹κατὰ τὸ Θ σημεῖον οὕτως, ὥστε› αὐτῶν κέντρον εἶναι τοῦ βάρους τὸ Θ· ἰσόρροπον οὖν καὶ τὸ τμῆμα τοῦ ὀρθογωνίου κωνοειδέος περὶ τὸ Α σημεῖον αὐτοῦ μένον τῷ κώνῳ μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Θ [102] οὕτως, ὥστε κέντρον εἶναι τοῦ βάρους αὐτοῦ τὸ Θ. Ἐπεὶ οὖν συναμφοτέρων τῶν μεγεθῶν ὡς ἑνὸς λεγομένων κέντρον ἐστὶν τοῦ βάρους τὸ Α, αὐτοῦ δὲ τοῦ κώνου τοῦ μετενηνεγμένου κέντρον τοῦ βάρους τὸ Θ, τοῦ λοιποῦ ἄρα μεγέθους τὸ κέντρον ἐστὶ τοῦ βάρους ἐπὶ τῆς ΑΘ εὐθείας ἐκβεβλημένης ἐπὶ τὸ Α καὶ ἀποληφθείσης ἀπ᾿ αὐτῆς τῆς ΑΚ τηλικαύτης, ‹ὥστε τὴν ΑΘ› πρὸς αὐτὴν τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει τὸ τμῆμα πρὸς τὸν κῶνον. Ἡμιόλιον δέ ἐστιν τὸ τμῆμα τοῦ κώνου· ἡμιόλιος ἄρα ἐστὶ καὶ ἡ ΘΑ τῆς ΑΚ, καί ἐστιν τὸ Κ κέντρον τοῦ βάρους τοῦ ὀρθογωνίου κωνοειδέος τῆς ΑΔ τετμημένης οὕτως, ὥστε διπλάσιον εἶναι τὸ μέρος αὐτῆς τὸ πρὸς τῇ κορυφῇ τοῦ τμήματος τοῦ λοιποῦ τμήματος.

   Ϛ΄.

   Παντὸς ἡμισφαιρίου τὸ κέντρον ‹τοῦ βάρους ἐπὶ τῆς εὐθείας ἐστίν, ἥ› ἐστιν ἄξων αὐτοῦ, τμηθείσης οὕτως, ὥστε τὸ τμῆμα αὐτῆς τὸ πρὸς τῇ ἐπιφανείᾳ τοῦ ἡμισφαιρίου πρὸς τὸ λοιπὸν τμῆμα τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει τὰ πέντε πρὸς τὰ τρία.

[103]    Ἔστω σφαῖρα καὶ τετμήσθω ἐπιπέδῳ διὰ τοῦ κέντρου, καὶ γενέσθω ἐν τῇ ἐπιφανείᾳ τομὴ ὁ ΑΒΓΔ κύκλος, διάμετροι δὲ ἔστωσαν τοῦ κύκλου πρὸς ὀρθὰς ἀλλήλαις αἱ ΑΓ, ΒΔ, ἀπὸ δὲ τῆς ΒΔ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΑΓ, καὶ ἔστω κῶνος βάσιν μὲν ἔχων τὸν περὶ διάμετρον τὴν ΒΔ κύκλον, κορυφὴν δὲ τὸ Α σημεῖον, πλευραὶ δὲ ἔστωσαν τοῦ κώνου αἱ ΒΑ, ΑΔ, καὶ ἐκβεβλήσθω ἡ ΓΑ, καὶ κείσθω τῇ ΓΑ ἴση ἡ ΑΘ, καὶ νοείσθω ζυγὸς ἡ ΘΓ εὐθεῖα, μέσον δὲ αὐτοῦ τὸ Α, καὶ ἤχθω τις ἐν τῷ ΒΑΔ ἡμικυκλίῳ ἡ ΞΟ παράλληλος οὖσα τῇ ΒΔ, τεμνέτω δὲ αὕτη τὴν μὲν τοῦ ἡμικυκλίου περιφέρειαν κατὰ τὰ Ξ, Ο, τὰς δὲ τοῦ κώνου πλευρὰς κατὰ τὰ Π, Ρ σημεῖα, τὴν δὲ ΑΓ κατὰ τὸ Ε, καὶ ἀπὸ τῆς ΞΟ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΑΕ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ ἡμισφαιρίῳ τομὴν κύκλον, οὗ διάμετρος ἡ ΞΟ, ἐν δὲ τῷ κώνῳ τομὴν κύκλον, οὗ διάμετρος ἡ ΠΡ.



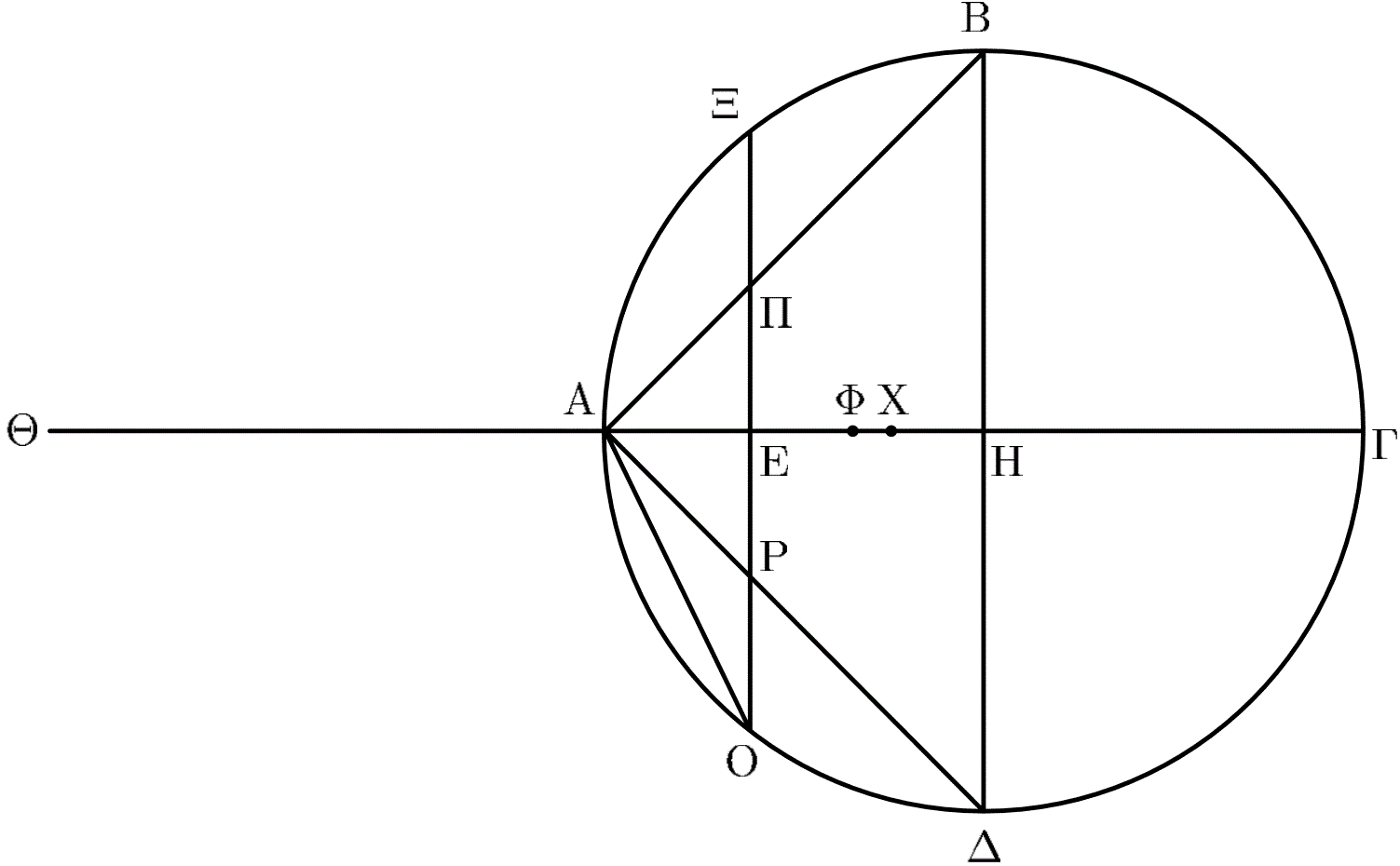
   Καὶ ἐπεί ἐστιν ὡς ἡ ΑΓ πρὸς ΑΕ, τὸ ἀπὸ ΞΑ πρὸς τὸ ἀπὸ ΑΕ, τῷ δὲ ἀπὸ ΞΑ ἴσα τὰ ἀπὸ ‹ΑΕ, ΕΞ, τῇ δὲ ΑΕ ἴση ἡ ΕΠ, ὡς ἄρα ἡ ΑΓ› πρὸς ΑΕ, οὕτως τὰ ἀπὸ ΞΕ, ΕΠ πρὸς τὸ ἀπὸ ΕΠ. Ὡς δὲ τὰ ἀπὸ ΞΕ, ΕΠ πρὸς τὸ ἀπὸ ΕΠ, οὕτως ὁ κύκλος ὁ περὶ διάμετρον τὴν ΞΟ καὶ ὁ κύκλος ὁ περὶ διάμετρον τὴν ΠΡ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΠΡ, καί ἐστιν ἡ ΓΑ τῇ ΑΘ ἴση· ὡς ἄρα ἡ ΘΑ πρὸς ΑΕ, οὕτως ὁ κύκλος ὁ περὶ διάμετρον τὴν ΞΟ καὶ ὁ κύκλος ὁ περὶ διάμετρον τὴν ΠΡ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΠΡ. Ἰσορροπήσουσιν ἄρα περὶ τὸ Α σημεῖον ἀμφότεροι οἱ κύκλοι, ὧν εἰσι διάμετροι αἱ ΞΟ, ΠΡ, αὐτοῦ μένοντες τῷ κύκλῳ, οὗ διάμετρος ἡ ΠΡ, μετενεχθέντι καὶ τεθέντι κατὰ τὸ Θ οὕτως, ὥστε κέντρον [104] εἶναι αὐτοῦ τοῦ βάρους τὸ Θ. Ἐπεὶ οὖν ἀμφοτέρων μὲν τῶν κύκλων, ὧν εἰσι διάμετροι αἱ ΞΟ, ΠΡ, αὐτοῦ μενόντων κέντρον τοῦ βάρους ἐστὶν ‹τὸ Ε, τοῦ δὲ κύκλου, οὗ ἐστι διάμετρος ἡ ΠΡ, μετενεχθέντος τὸ Θ, ἔστιν ὡς ἡ ΕΑ πρὸς ΑΘ, οὕτως ὁ κύκλος, οὗ διάμετρος ἡ ΠΡ, πρὸς τοὺς κύκλους, ὧν διάμετροι αἱ› ΞΟ, ‹ΠΡ. Ὁμοίως δὲ καὶ ἐὰν ἄλλη τις ἀχθῇ ἐν τῇ τοῦ ὀρθογωνίου κώνου τομῇ παράλληλος τῇ› Β‹Η›Δ, καὶ ‹ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀναστα›θῇ ὀρθὸν πρὸς ‹τὴν ΑΓ›, ἰσορροπ‹ήσουσιν› περὶ τὸ Α ‹σημεῖον› ἀμφότερ‹οι οἱ κύκλοι ὅ τε ἐν τῷ ἡμισφαιρίῳ γενό›μεν‹ος› κ‹αὶ ὁ ἐν τῷ κών›ῳ αὐ‹τοῦ μένοντες τῷ γ›ενομένῳ ‹κύκλῳ ἐν τῷ κώνῳ› μετενεχθέντι ‹καὶ› τε‹θέντι τοῦ› ζυγοῦ κατὰ τὸ Θ. ‹Συμπληρωθέντων οὖν ὑπὸ τῶν κύκλων τοῦ τε› ἡμισφαιρίου καὶ τοῦ κώ‹νου› ἰσορ‹ροπήσουσι περὶ τὸ Α σημεῖον πάντες οἱ κύκλοι οἱ ἐν τῷ ἡμισφαι›ρίῳ καὶ οἱ ‹ἐν τῷ κώνῳ αὐτοῦ› μένοντες ‹πᾶσι τοῖς κύκλοις τοῖς ἐν› τῷ κώνῳ μετενεχθεῖσι καὶ τεθεῖσι τοῦ ζυγοῦ κατὰ τὸ Θ οὕτως, ὥστε κέντρον ‹εἶναι αὐτῶν› τοῦ βάρους τὸ Θ· ‹ὥστε ἰσορροπήσουσι περὶ τὸ Α σημεῖον τό τε ἡμισφαίριον καὶ ὁ κῶνος αὐτοῦ› μένοντα τῷ κώνῳ μετενεχθέντι καὶ τεθέντι ‹τοῦ ζυγοῦ κατὰ τὸ Θ› οὕτως, ὥστε κέν‹τρον› αὐτοῦ ‹εἶναι τοῦ βάρους› τὸ Θ σημεῖον ..........δ........ ἔλασσον ............................................. ............................................. ...........τῶν δὲ ..... ‹ἰσορροπ›ού‹ντ›ων κατὰ τὸ ‹Α›........τρ......τὸ ..... ‹καὶ ἐπεί› ἐστιν, [105] ὡς ἡ Θ‹Α πρὸσ›ΑΧ, ............. ἄξων ὁ ΑΗ.. τὰ ....... μον ................................. ‹ση›μεῖ‹ον›........ κῶνον τοῖ‹ς›...... τοῦ κώνου ........ καὶ ἐπεὶ τετρα‹πλασία ἐστὶν› ἡ σφαῖρα τοῦ ‹κώνου, οὗ βάσις ὁ› περὶ ‹διάμετρον τὴν ΒΔ κύκλος, ἄξων δὲ ἡ ΑΗ› ................................. ............................................. .............................................

   ζ΄.

   Θεωρεῖται ‹δὲ› διὰ τοῦ ‹τρόπου τού›του καὶ ὅτι π‹ᾶν τμῆμα› σφαίρας πρὸς τὸν κῶνον ‹τὸν βάσιν› ἔχοντα τὴν αὐ‹τὴν τῷ τμήματι› καὶ ἄξονα ‹τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερος ἥ τε ἐκ τοῦ κέντρου τῆς σφαίρας καὶ τὸ ὕψος τοῦ λοιποῦ τμήματος [106] πρὸς τὸ ὕψος τοῦ λοιποῦ τμήματος›................. ............. τω ............................ ........ὀρθὴ ....... τὸ αὐτὸ ................. ............................................. ...............παρὰ ......................... .... ‹καὶ ἀπὸ τῆς› ΜΝ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΑΓ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ κυλίνδρῳ τομὴν κύκλον, οὗ ἐστι διάμετρος ἡ ΜΝ, ἐν δὲ τῷ τμήματι τῆς σφαίρας τομὴν κύκλον, οὗ διάμετρος ἡ ΞΟ, ἐν δὲ τῷ κώνῳ, οὗ βάσις ὁ περὶ διάμετρον τὴν ΕΖ κύκλος, κορυφὴ δὲ τὸ Α σημεῖον, κύκλον, οὗ διάμετρός ἐστιν ἡ ΠΡ. Ὁμοίως δὴ τοῖς πρότερον δειχθήσεται ἰσόρροπος περὶ τὸ Α σημεῖον ὁ κύκλος, οὗ διάμετρος ἡ ΜΝ, αὐτοῦ μένων ἀμφοτέροις τοῖς κύ‹κλοις, ὧν διάμετροι αἱ ΞΟ, ΠΡ, μετεν›εχθεῖσι τοῦ ζυγοῦ ‹κατὰ τὸ Θ,› ὥστε ἑκατέρου αὐτῶν κέντρον ‹τοῦ βάρους εἶναι τὸ Θ· ὁμοίως› δὲ ‹ἐπὶ πάντων›. Συμπληρωθέντων οὖν καὶ τοῦ κυλίνδρου καὶ τοῦ ‹κώνου καὶ τοῦ› τμήματος ‹τῆς σφαίρας ὑπὸ τῶν κύκλων ἰσορροπήσει καὶ› ὁ κύλινδρος αὐτοῦ μένων [107] συναμφοτέροις τῷ τε κώνῳ καὶ τῷ τμήματι τῆς σφαίρας μετενηνεγμένοις καὶ κειμένοις τοῦ ζυγοῦ κατὰ τὸ Θ. Τεμνέσθω δὲ ἡ ΑΗ κατὰ τὰ Φ, Χ σημεῖα οὕτως ὥστε τὴν μὲν ΑΧ εἶναι ἴσην τῇ ΧΗ, τὴν δὲ ΗΦ τρίτον μέρος τῆς ΑΗ· ἔσται δὴ τοῦ μὲν κυλίνδρου κέντρον τοῦ βάρους τὸ Χ διὰ τὸ διχοτομίαν εἶναι τοῦ ΑΗ ἄξονος. Ἐπεὶ οὖν ἰσορροπεῖ περὶ τὸ Α σημεῖον τὰ εἰρημένα μεγέθη, ἔσται ὡς ὁ κύλινδρος πρὸς ἀμφότερον τόν τε κῶνον, οὗ διάμετρος τῆς βάσεως ἡ ΕΖ, καὶ τὸ τμῆμα τῆς σφαίρας τὸ ΒΑΔ, οὕτως ἡ ΘΑ πρὸς ΑΧ. Καὶ ἐπεὶ ‹τριπλ›ασία ἐστὶν ἡ ΗΑ τῆς ΗΦ, τρίτον μέρος ἐστὶν ‹τὸ ὑπὸ ΓΗ, ΗΦ τοῦ ὑπὸ ΑΗ, ΗΓ. Ἴσον δὲ› τῷ ὑπὸ ΑΗ, ΗΓ τὸ ἀπὸ ΗΒ· ἔσται δὴ καὶ τοῦ ἀπὸ τῆς ΒΗ τρίτον μέρος τὸ ὑπὸ ΓΗ, ‹ΗΦ›... ............. ὑπὸ ΗΓ ... τὸ δὲ ἀπὸ ΑΗ............. ὑπὸ ΗΓ ...................................... ..........τῆς.........................ΚΛ.... ........τρον............. οὕτως ‹ὁ κύλινδρος, οὗ βάσις ὁ περὶ› διάμετρον ‹τὴν .. κύκλος› πρὸς τὸν ..... ..... ‹ὁ κύλινδρος, οὗ› βάσις ‹.... ὁ περὶ› διάμετρον τὴν ΚΛ κύκλος πρὸς τὸν ΑΕΖ κῶνον. Ὡς δὲ τὸ ἀπὸ ΘΑ πρὸς ............ ἄρα ἡ ........... πρὸς τὸν κῶνον. Ἐδείχθη δὲ καὶ ‹ὡς ἡ ΘΑ› πρὸς ΑΧ, οὕτως ὁ κύλινδρος, οὗ βάσις ὁ περὶ διάμετρ‹ον› τὴν ΚΛ κύκλος ‹πρὸς τὸ› τμῆμα ‹τῆς σφαίρας τὸ ΑΒΔ καὶ τὸν› κῶνον· καὶ ὡς ἄρα ἡ ΘΑ πρὸς συναμφοτέρας τὰς ....... Φ. ........... τὸ ΑΒΔ ‹τμῆμα τῆς ς›φαίρ‹ας›... τα.......... καὶ ................. ὅ τε...... ......................................... ὡς τὸ ΑΒΔ τμῆμα πρὸς τὸν κύλινδρον, οὗ ἐστι βάσις ὁ περὶ διάμετρον τὴν .. κύκ‹λος›, ἄξων ‹δὲ ὁ› α‹ὐτός, οὕτως› [108] .......Χ πρὸς....ὡ‹ς δὲ ὁ› κύλινδρος, οὗ βάσις ‹ὁ περὶ διάμετρον› τὴν Κ‹Λ κύκλος, πρὸς τὸν› ΑΒΔ κῶνον, ‹οὕτως› ......... τω..........τρὸς .. Β.. .......η.Φ.........ὡς ἡ..................... ἡ Α. Τῇ..................................... ......καὶ ἡ ΗΓ καὶ......



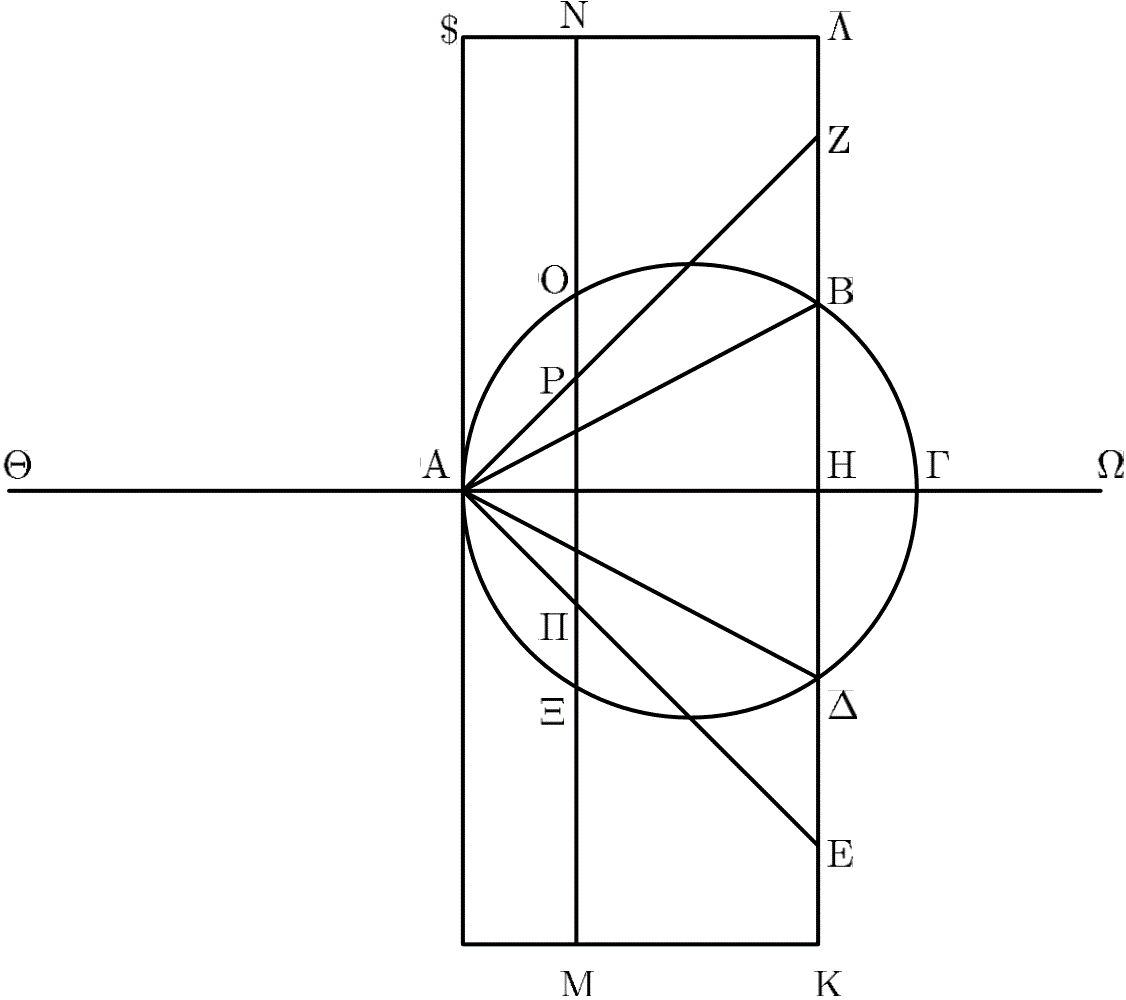
   η΄.

   ‹Ὁμοίως δὲ θεωρεῖτ›αι διὰ τοῦ ‹αὐτοῦ τρόπου καὶ ὅτι› πᾶν τμῆμα ‹σφαιροειδέος› ἀποτετμημένον ἐπιπέδῳ ὀρθῷ πρὸς τὸν κῶνον τὸν βάσιν ἔχοντα τὴν αὐτὴν τῷ τμήματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερος ἥ τε ἡμίσεια τοῦ ἄξονος τοῦ ‹ς›φαιρο‹ειδέος› καὶ ‹τοῦ ἄξονος› τοῦ ‹ἀντι›κειμένου ‹τμήματος› πρὸ‹ς τὸν ἄξονα τοῦ ἀντικειμένου τμήματος›.

   θ΄.

   ‹Παντὸς τμήματος σφαίρας τὸ κέντρον τοῦ βάρους ἐστὶν ἐπὶ τῆς εὐθείας, ἥ ἐστιν ἄξων τοῦ τμήματος, διῃρημένης [109] οὕτως ὥστε τὸ μέρος αὐτῆς τὸ πρὸς τῇ κορυφῇ τοῦ τμήματος πρὸς τὸ λοιπὸν τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει συναμφότερον ὅ τε ἄξων τοῦ τμήματος καὶ ἡ τετραπλασία τοῦ ἄξονος τοῦ ἐν τῷ ἀντικειμένῳ τμήματι πρὸς συναμφότερον τόν τε ἄξονα τοῦ τμήματος καὶ τὴν διπλασίαν τοῦ ἄξονος τοῦ ἐν τῷ ἀντικειμένῳ τμήματι ἐμπεριεχομένου.›............................... ..................................... ‹τοῦ δὲ ἀποτε›τμηκότος ‹τὸ τμῆμα ἐπιπέδου ἡ ΒΔ, ἡ δὲ› ΓΑ εὐθεῖα διά‹με›τρ‹ος ἔστω ὀρθὴ πρὸς τὴν› ΒΔ καὶ τετμή‹σθω κ›ατ‹ὰ τὸ Η σημεῖον· ὥ›στε τοῦ τμήμ‹ατος, οὗ κορυ›φὴ τὸ Α σημεῖον, ἄξων ‹ἔσται ἡ ΑΗ,› τ‹οῦ δ›ὲ ἀντικειμέν‹ου ἄξων ἡ Η›Γ.



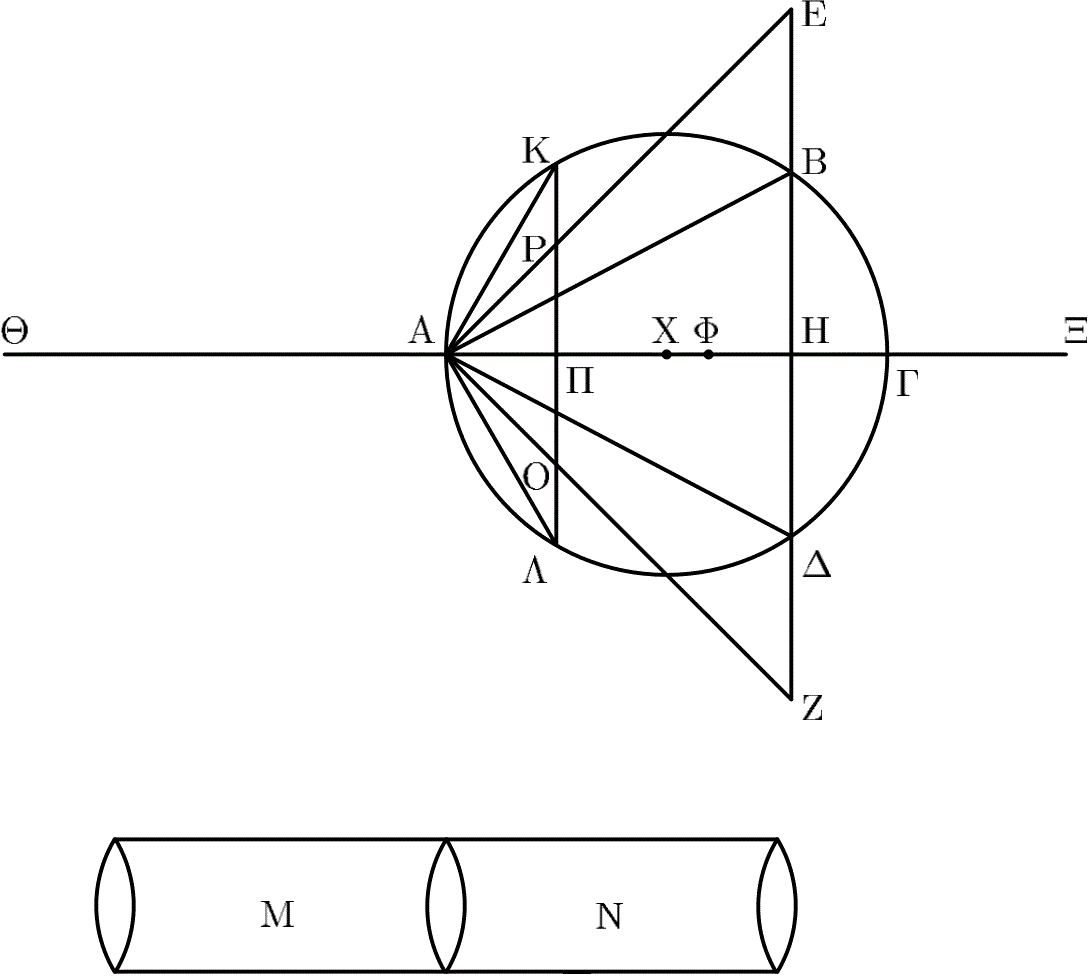
Τετμήσθω δὲ ἡ ΑΗ κατὰ ‹τὸ Χ, ὥστε› εἶναι ὡς τὴν ‹Α›Χ πρὸς ΧΗ, ‹οὕτως τήν τε ΑΗ καὶ τὴν› τετρα‹πλασί›αν τῆς ΗΓ πρὸς τὴν ΑΗ καὶ τὴν διπλασίαν ‹τῆς ΗΓ. Λ›έγω ὅτι ‹τοῦ τ›μ‹ήματος, οὗ› κορυφὴ τὸ Α σημεῖον, ‹κ›έντρ‹ον τοῦ βάρους ἐστὶ τὸ› Χ.............. φοτέροις .... τμημ..., οὗ κορυ‹φὴ› ... σημεῖον ...... ΗΑ.. ἐχ............ ..... τὴν Η. Λόγον ........ κέντρον ............ ...... Χ. εἰ.. τμήθη... ρ.............. χηματ.. μει....ω... ἐν δὴ ... τερ....... καὶ ἐκβεβλήσθω [110] ἡ ΑΓ, καὶ κείσθω αὐτῇ ἴση ἡ ΑΘ καὶ τῇ ἐκ τοῦ κέντρου τῆς σφαίρας ἴση ἡ ΓΞ, καὶ νοείσθω ζυγὸς ἡ ΓΘ, μέσον δὲ αὐτοῦ τὸ Α, γεγράφθω δὲ καὶ κύκλος ἐν τῷ ἐπιπέδῳ τῷ ἀποτέμνοντι τὸ τμῆμα κέντρῳ μὲν τῷ Η, διαστήματι δὲ τῷ ἴσῳ τῇ ΑΗ, καὶ ἀπὸ τοῦ κύκλου τούτου ‹γεγράφθω κῶνος κορυφὴν ἔχων τὸ Α σημεῖον,› πλευραὶ δὲ ἔστωσαν τοῦ κώνου αἱ ΑΕ, ΑΖ, καὶ ἤχθω τις τῇ ΕΖ παράλληλος ἡ ΚΛ καὶ συμβαλλέτω τῇ μὲν περιφερείᾳ τοῦ τμήματος κατὰ τὰ Κ, Λ, ταῖς δὲ τοῦ ΑΕΖ κώνου πλευραῖς κατὰ τὰ Ρ, Ο, τῇ δὲ ΑΓ κατὰ τὸ Π. Ἐπεὶ δή ἐστιν ὡς ἡ ΑΓ πρὸς ΑΠ, οὕτως τὸ ἀπὸ ΚΑ πρὸς τὸ ἀπὸ ΑΠ, καί ἐστι τῷ μὲν ἀπὸ ΚΑ ἴσα τὰ ἀπὸ τῶν ΑΠ, ΠΚ, τῷ δὲ ἀπὸ τῆς ΑΠ τὸ ἀπὸ ΠΟ, ἐπεὶ καὶ τῷ ἀπὸ ΑΗ τὸ ἀπὸ τῆς ΕΗ ἐστὶν ἴσον, ὡς ἄρα ἡ ΓΑ πρὸς ΑΠ, οὕτως τὰ ἀπὸ ΚΠ, ΠΟ πρὸς τὸ ἀπὸ ΟΠ. Ὡς δὲ τὰ ἀπὸ ΚΠ, ΠΟ πρὸς τὸ ἀπὸ ΠΟ, οὕτως ὁ κύκλος ὁ περὶ διάμετρον τὴν ΚΛ καὶ ὁ περὶ διάμετρον τὴν ΟΡ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΟΡ, καὶ ἴση ἐστὶν ἡ ΓΑ τῇ ΑΘ· ὡς ἄρα ἡ ΘΑ πρὸς ΑΠ, οὕτως ὁ περὶ διάμετρον τὴν ΚΛ καὶ ὁ περὶ διάμετρον τὴν ΟΡ κύκλος πρὸς τὸν περὶ τὴν ΟΡ. Ἐπεὶ οὖν ὡς οἱ περὶ διαμέτρους τὰς ΚΛ, ΟΡ κύκλοι πρὸς τὸν περὶ διάμετρον τὴν ΟΡ, οὕτως ἡ ΑΘ πρὸς ΠΑ, μετακείσθω ὁ περὶ διάμετρον τὴν ΟΡ κύκλος καὶ κείσθω τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ· ὡς ἄρα ἡ ΘΑ πρὸς ΑΠ, οὕτως ὁ κύκλος ὁ περὶ διάμετρον τὴν ΚΛ καὶ ὁ περὶ διάμετρον τὴν ΟΡ αὐτοῦ μένοντες πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΟΡ μετενεχθέντα καὶ τεθέντα τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ· ἰσόρροποι ἄρα οἱ κύκλοι ὅ τε ἐν τῷ τμήματι τῷ ΒΑΔ καὶ ὁ ἐν τῷ ΑΕΖ ‹κώνῳ τῷ ἐν τῷ ΑΕΖ κώνῳ περὶ› [111] τὸ Α. Ὁμοίως δὲ καὶ πάντες οἱ κύκλοι οἱ ἐν τῷ ΒΑΔ τμήματι καὶ ἐν τῷ ΑΕΖ κώνῳ αὐτοῦ μένοντες κατὰ τὸ Α σημεῖον ἰσόρροποι πᾶσι τοῖς κύκλοις τοῖς ἐν τῷ ΑΕΖ κώνῳ μετενεχθεῖσι καὶ τεθεῖσι τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτῶν τοῦ βάρους τὸ Θ· ὥστε καὶ τὸ ΑΒΔ τμῆμα τῆς σφαίρας καὶ ὁ ΑΕΖ κῶνος ἰσορροπεῖ περὶ τὸ Α σημεῖον αὐτοῦ μένοντα τῷ ΕΑΖ κώνῳ μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ. Ἔστω δὲ τῷ κώνῳ τῷ βάσιν μὲν ἔχοντι τὸν περὶ διάμετρον τὴν ΕΖ κύκλον, κορυφὴν δὲ τὸ Α σημεῖον, ἴσος κύλινδρος ὁ ΜΝ, καὶ τετμήσθω ἡ ΑΗ κατὰ τὸ Φ, ὥστε τετραπλασίαν εἶναι τὴν ΑΗ τῆς ΦΗ· τὸ Φ ἄρα σημεῖον κέντρον ἐστὶ τοῦ βάρους τοῦ ΕΑΖ κώνου· τοῦτο γὰρ προγράφεται. Καὶ τετμήσθω ἔτι ὁ ΜΝ κύλινδρος ἐπιπέδῳ τέμνοντι πρὸς ὀρθάς, ‹ὥστε τὸν Μ κύλιν›δρον ἰσορροπεῖν τῷ ΕΑΖ κώνῳ. Ἐπεὶ οὖν ἰσόρροπος ὁ ΕΑΖ κῶνος καὶ τὸ ΑΒΔ τμῆμα αὐτοῦ μένοντα τῷ ΕΑΖ κώνῳ μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Θ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Θ, καί ἐστιν τῷ ΕΑΖ κώνῳ ἴσος ὁ ΜΝ κύλινδρος, καὶ κεῖται ἑκάτερος τῶν Μ, Ν κυλίνδρων κατὰ τὸ Θ, καὶ ἰσόρροπος ὁ ΜΝ κύλινδρος ἑκατέροις, ἰσόρροπος καὶ ὁ Ν τῷ τμήματι τῆς σφαίρας κατὰ τὸ Α σημεῖον. Καὶ [ἐπεί] ἐστιν ὡς τὸ ΒΑΔ τμῆμα τῆς σφαίρας πρὸς τὸν κῶνον, οὗ βάσις ὁ περὶ διάμετρον τὴν ΒΔ κύκλος, κορυφὴ δὲ τὸ Α σημεῖον, οὕτως ἡ ΞΗ πρὸς ΗΓ· τοῦτο γὰρ προγράφεται. Ὡς δὲ ὁ ΒΑΔ κῶνος πρὸς τὸν ΕΑΖ κῶνον, οὕτως ὁ κύκλος ὁ περὶ διάμετρον τὴν ΒΔ πρὸς τὸν κύκλον τὸν περὶ διάμετρον τὴν ΕΖ, ὡς δὲ ὁ κύκλος πρὸς τὸν κύκλον, οὕτως τὸ ἀπὸ ΒΗ πρὸς τὸ ἀπὸ ΗΕ, [112] καί ἐστι τῷ μὲν ἀπὸ ΒΗ ἴσον τὸ ὑπὸ ΓΗ, ΗΑ, τῷ δὲ ἀπὸ ΗΕ ἴσον τὸ ἀπὸ ΗΑ, ὡς δὲ τὸ ὑπὸ ΓΗ, ΗΑ πρὸς τὸ ἀπὸ ΗΑ, οὕτως ἡ ΓΗ πρὸς ΗΑ· ὡς ἄρα ὁ ΒΑΔ κῶνος πρὸς τὸν ΕΑΖ κῶνον, οὕτως ἡ ΓΗ πρὸς ΗΑ. Ἐδείχθη δὲ καὶ ὡς ὁ ΒΑΔ κῶνος πρὸς τὸ ΒΑΔ τμῆμα, οὕτως ἡ ΓΗ πρὸς ΗΞ· δι᾿ ἴσου ἄρα ὡς τὸ ΒΑΔ τμῆμα πρὸς τὸν ΕΑΖ κῶνον, οὕτως ἡ ΞΗ πρὸς ΗΑ. Καὶ ἐπεί ἐστιν ὡς ἡ ΑΧ πρὸς ΧΗ, οὕτως ἡ ΗΑ καὶ ἡ τετραπλασία τῆς ΗΓ πρὸς τὴν ΑΗ καὶ τὴν διπλασίαν τῆς ΗΓ, ἀνάπαλιν ἔσται ὡς ἡ ΗΧ πρὸς ΧΑ, οὕτως ἡ διπλασία τῆς ΓΗ καὶ ἡ ΗΑ πρὸς τὴν τετραπλῆν τῆς ΓΗ καὶ τὴν ΗΑ. Συνθέντι ὡς ἡ ΗΑ πρὸς ΑΧ, οὕτως ἡ ἑξαπλασία τῆς ΓΗ καὶ διπλασία τῆς ΗΑ πρὸς τὴν ΗΑ καὶ τετραπλῆν τῆς ΗΓ. Καὶ τῆς μὲν ἑξαπλασίας τῆς ΗΓ καὶ διπλασίας τῆς ΗΑ ἡ ΗΞ, τῆς δὲ τετραπλασίας τῆς ΗΓ καὶ τῆς ΗΑ τέταρτον μέρος ἡ ΓΦ· τοῦτο γὰρ φανερόν· ὡς ἄρα ἡ ΗΑ πρὸς ΑΧ, οὕτως ἡ ΞΗ πρὸς ΓΦ· ὥστε καὶ ὡς ἡ ΞΗ πρὸς ΗΑ, οὕτως ἡ ΓΦ πρὸς ΧΑ. Ἐδείχθη δὲ καὶ ὡς ἡ ΞΗ πρὸς ΗΑ, οὕτως τὸ τμῆμα, οὗ ἐστι κορυφὴ τὸ Α σημεῖον, βάσις δὲ ὁ περὶ διάμετρον τὴν ΒΔ κύκλος, πρὸς τὸν κῶνον, οὗ ἐστι κορυφὴ τὸ Α σημεῖον, βάσις δὲ ὁ περὶ διάμετρον τὴν ΕΖ κύκλος· ὡς ἄρα τὸ ΒΑΔ τμῆμα πρὸς τὸν ΕΑΖ κῶνον, οὕτως ἡ ΓΦ πρὸς ΧΑ. Καὶ ἐπεὶ ἰσόρροπος ὁ Μ κύλινδρος τῷ ΕΑΖ κώνῳ κατὰ τὸ Α, καί ἐστι τοῦ μὲν κυλίνδρου κέντρον βάρους τὸ Θ, τοῦ δὲ ΕΑΖ κώνου τὸ Φ, ἔσται ἄρα ὡς ὁ ΕΑΖ κῶνος πρὸς τὸν Μ κύλινδρον, οὕτως ἡ ΘΑ πρὸς ΑΦ, τουτέστιν ἡ ΓΑ πρὸς ΑΦ. Καί ἐστι τῷ ΕΑΖ κώνῳ ἴσος ὁ ΜΝ κύλινδρος· διελόντι ἄρα ὡς ὁ ΜΝ κύλινδρος πρὸς τὸν Ν κύλινδρον, οὕτως ἡ ΑΓ πρὸς ΓΦ. Καί ἐστιν ἴσος ὁ ΜΝ κύλινδρος τῷ ΕΑΖ [113] κώνῳ· ὡς ἄρα ὁ ΕΑΖ κῶνος πρὸς τὸν Ν κύλινδρον, οὕτως ἡ ΓΑ πρὸς ΓΦ, τουτέστιν ἡ ΘΑ πρὸς ΓΦ. Ἐδείχθη δὲ καὶ ὡς τὸ ΒΑΔ τμῆμα πρὸς τὸν ΕΑΖ κῶνον, οὕτως ἡ ΓΦ πρὸς ΧΑ· δι᾿ ἴσου ἄρα ἔσται ὡς τὸ ΑΒΔ τμῆμα πρὸς τὸν Ν κύλινδρον, οὕτως ἡ ΘΑ πρὸς ΑΧ. Καὶ ἐδείχθη ἰσόρροπον τὸ ΒΑΔ τμῆμα τῷ Ν κυλίνδρῳ κατὰ τὸ Α, καί ἐστι τοῦ Ν κυλίνδρου κέντρον βάρους τὸ Θ· καὶ τοῦ ΒΑΔ ἄρα τμήματος κέντρον τὸ Χ σημεῖον. [τὸ σχῆμα].

   ι΄.

   Ὁμοίως δὲ τούτοις θεωρεῖται καὶ ὅτι παντὸς τμήματος σφαιροειδέος τὸ κέντρον ἐστὶν τοῦ βάρους ἐπὶ τῆς εὐθείας, ἥ ἐστιν ἄξων τοῦ τμήματος, διῃρημένης τῆς εὐθείας, ὥστε τὸ μέρος αὐτῆς τὸ πρὸς τῇ κορυφῇ τοῦ τμήματος πρὸς τὸ λοιπὸν τοῦτον ἔχειν τὸν λόγον, ὃν ἔχει συναμφότερον ὅ τε ἄξων τοῦ τμήματος καὶ ἡ τετραπλασία τοῦ ἄξονος τοῦ ἐν τῷ ἀντικειμένῳ τμήματι πρὸς συναμφότερον τόν τε ἄξονα τοῦ τμήματος καὶ τὴν διπλασίαν τοῦ ἄξονος τοῦ ἐν τῷ ἀντικειμένῳ τμήματι ἐμπεριεχομένου.

   ια΄.

   Θεωρεῖται δὲ διὰ τοῦ τρόπου ‹καὶ ὅτι πᾶν τμῆμα ἀμβλυγωνίου κωνοειδέος› πρὸς τὸν κῶνον τὸν βάσιν ἔχοντα τὴν αὐτὴν τῷ τμήματι καὶ ἄξονα τὸν αὐτὸν τοῦτον ἔχει τὸν λόγον, ὃν ἔχει συναμφότερος ὅ τε ἄξων τοῦ τμήματος καὶ ἡ τριπλασία τῆς προσούσης τῷ ἄξονι πρὸς συναμφότερον τόν τε ἄξονα τοῦ τμήματος τοῦ κωνοειδέος καὶ τὴν διπλασίαν τῆς προσούσης τῷ ἄξονι, κέντρον δὲ τοῦ βάρους τοῦ ἀμβλυγωνίου κωνοειδέος [114] τμηθέντος τοῦ ἄξονος, ‹ὥστε› τὸ πρὸς τῇ κορυφῇ τμῆμα πρὸς τὸ λοιπὸν λόγον ἔχειν, ὃν ἔχει ὅ τε τριπλάσιος τοῦ ἄξονος ‹καὶ ἡ ὀκταπλασία› τῆς προσκειμένης πρὸς τὸν ἄξονα αὐτοῦ τοῦ κωνοειδέος καὶ τὴν τετραπλασίαν αὐτῆς τῆς προσκειμένης πρὸς αὐτόν· καὶ ἄλλων πλειόνων ἁ .........θεωρουμένων τὰ ..... περιλήψομεν ῥη.... τως, ἐπεὶ ὁ τρόπος ὑποδέδεικται διὰ τῶν προειρημένων.

   ιβ΄.

   Ἐὰν εἰς πρίσμα ὀρθὸν τετραγώνους ἔχον βάσεις κύλινδρος ἐγγραφῇ τὰς μὲν βάσεις ἔχων ἐν τοῖς ἀπεναντίον τετραγώνοις, τὴν δὲ ἐπιφάνειαν τῶν λοιπῶν [παραλληλογράμμων] τεσσάρων ἐπιπέδων ἐφαπτομένην, διὰ δὲ τοῦ κέντρου τοῦ κύκλου, ὅς ἐστι βάσις τοῦ κυλίνδρου, καὶ μιᾶς πλευ‹ρᾶς τοῦ ἀπεναντίον τετραγώνου ἐπίπε›δον ἀχθῇ, ὅτι τὸ ἀποτμηθὲν σχῆμα ὑπὸ τοῦ ἀχθέντος ἐπιπέδου ‹ἕκτον› ἐστὶ μέρος τοῦ ὅλου πρίσματος, διὰ τοῦ τρόπου τούτου θεωρεῖται. Δείξαντες δὲ ἀναχωρήσομεν ἐπὶ τὴν διὰ τῶν γεωμετρουμένων ἀπόδειξιν αὐτοῦ.

[115]    Νοείσθω πρίσμα ὀρθὸν τετραγώνους ἔχον βάσεις καὶ ἐν τῷ πρίσματι κύλινδρος ἐγγεγραμμένος ὡς εἴρηται, τμηθέντος δὲ τοῦ πρίσματος διὰ τοῦ ἄξονος ἐπιπέδῳ ὀρθῷ πρὸς τὸ ἐπίπεδον τὸ ἀποτετμηκὸς τὸ τμῆμα τοῦ κυλίνδρου τοῦ μὲν πρίσματος τοῦ τὸν κύλινδρον ἔχοντος τομὴ ἔστω τὸ ΑΒ παραλληλόγραμμον, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμηκότος τὸ τμῆμα ἀπὸ τοῦ κυλίνδρου καὶ τοῦ διὰ τοῦ ἄξονος ἠγμένου ἐπιπέδου ὀρθοῦ πρὸς τὸ ἐπίπεδον τὸ ἀποτετμηκὸς τὸ ἀπὸ τοῦ κυλίνδρου τμῆμα κοινὴ τομὴ ἔστω ἡ ΒΓ εὐθεῖα, ἄξων δὲ ἔστω τοῦ πρίσματος καὶ τοῦ κυλίνδρου ἡ ΓΔ εὐθεῖα, καὶ τεμνέτω αὐτὴν ἡ ΕΖ δίχα καὶ πρὸς ὀρθάς, καὶ διὰ τῆς ΕΖ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΓΔ· ποιήσει δὴ τοῦτο ἐν μὲν τῷ πρίσματι τομὴν τετράγωνον, ἐν δὲ τῷ κυλίνδρῳ τομὴν κύκλον. Ἔστω οὖν τοῦ μὲν πρίσματος τομὴ τὸ ΜΝ τετράγωνον, τοῦ δὲ κυλίνδρου ὁ ΞΟΠΡ ‹κύκλος, καὶ ἐφαπτέσθω ὁ κύκλος› τῶν τοῦ τετραγώνου πλευρῶν κατὰ τὰ Ξ, Ο, Π, Ρ σημεῖα, τοῦ δὲ ἐπιπέδου τοῦ ἀποτετμηκότος τὸ τμῆμα ἀπὸ τοῦ κυλίνδρου καὶ τοῦ διὰ τῆς ΕΖ ἀχθέντος ἐπιπέδου ὀρθοῦ πρὸς τὸν ἄξονα τοῦ κυλίνδρου κοινὴ τομὴ ἔστω ἡ ΚΛ εὐθεῖα· τέμνει δὲ αὐτὴν δίχα ἡ ΠΘΞ. Ἤχθω δέ τις εὐθεῖα ἐν τῷ ΟΠΡ ἡμικυκλίῳ ἡ ΣΤ πρὸς ὀρθὰς οὖσα τῇ ΠΧ, καὶ ἀπὸ τῆς ΣΤ ἐπίπεδον ἀνασταθὲν ὀρθὸν πρὸς τὴν ΞΠ ἐκβεβλήσθω ἐφ᾿ ἑκάτερα τοῦ ἐπιπέδου, ἐν ᾧ ἐστιν ὁ ΞΟΠΡ κύκλος· ποιήσει δὴ τοῦτο ἐν τῷ ἡμικυλίνδρῳ, οὗ ἐστι βάσις τὸ ΟΠΡ ἡμικύκλιον, ὕψος δὲ ὁ ἄξων τοῦ πρίσματος, τομὴν παραλληλόγραμμον, οὗ ἔσται μία μὲν πλευρὰ ἡ ἴση τῇ ΣΤ, ἡ δὲ ἑτέρα τῇ τοῦ κυλίνδρου πλευρᾷ, ποιήσει δὲ καὶ ἐν τῷ τμήματι τῷ ἀποτετμημένῳ ἀπὸ τοῦ κυλίνδρου τομὴν παραλληλόγραμμον, οὗ ἐστιν [116] ἡ μὲν ἑτέρα πλευρὰ ἴση τῇ ΣΤ, ἡ δὲ ἑτέρα τῇ ΝΥ· ἔστω δὲ οὕτως ἡ ΝΥ ἠγμένη ἐν τῷ ΔΕ παραλληλογράμμῳ παράλληλος οὖσα τῇ ΒΩ ἴσην ἀπολαμβάνουσα τὴν ΕΙ τῇ ΠΧ.




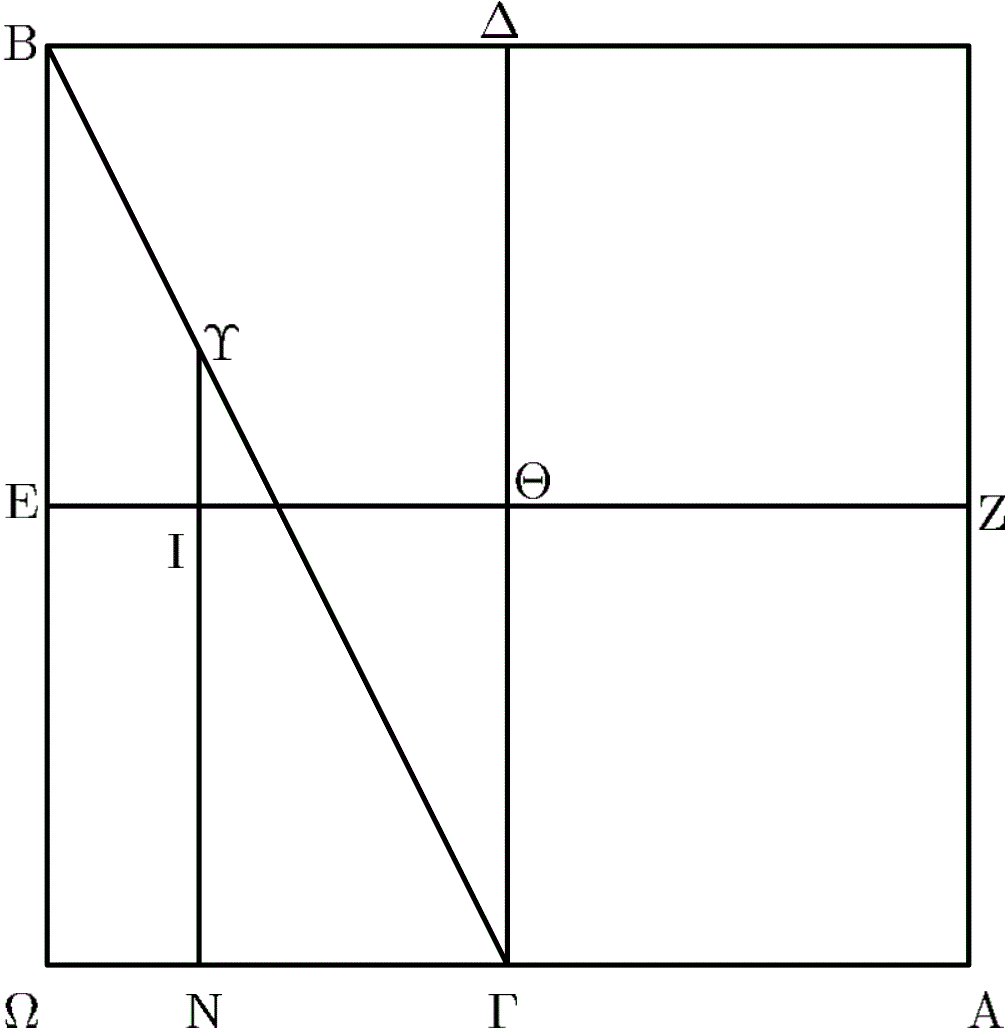
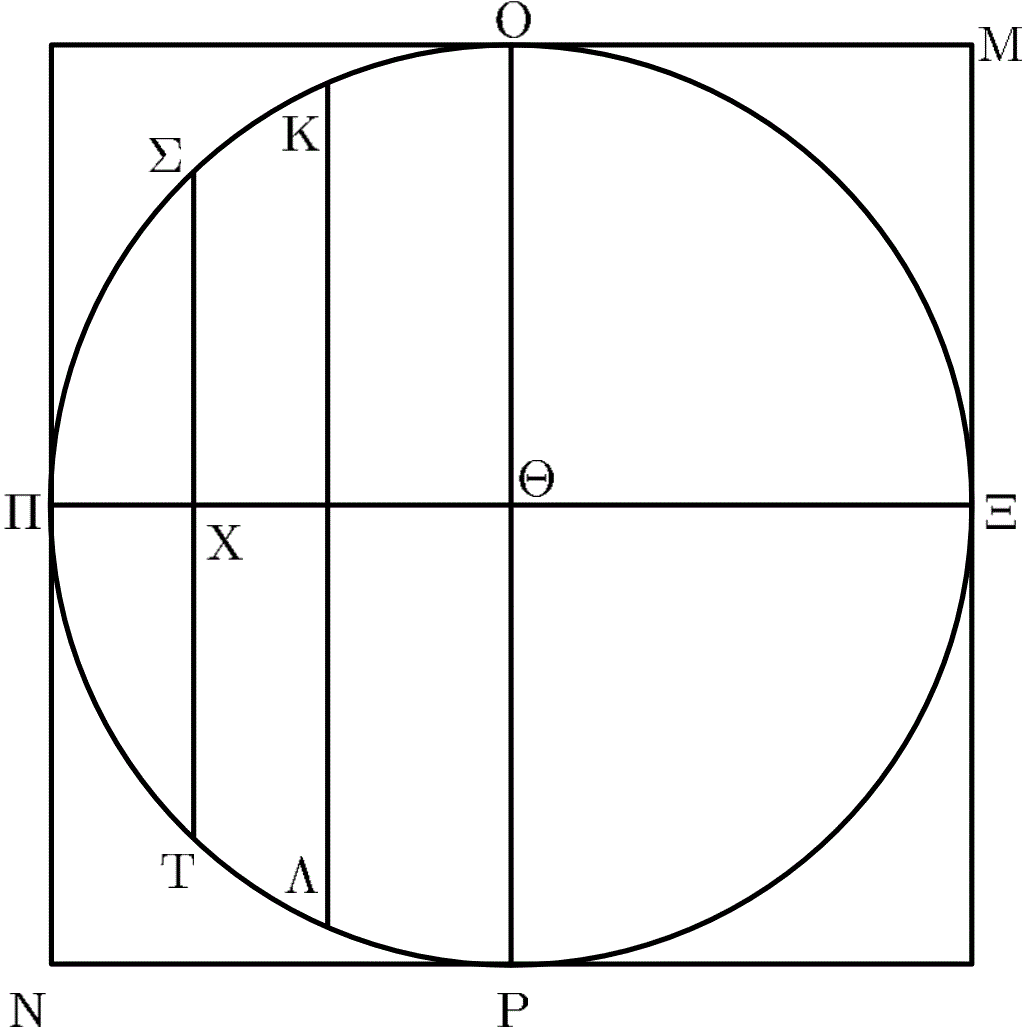
Καὶ ἐπεὶ παραλληλόγραμμόν ἐστι τὸ ΕΓ, καὶ παράλληλος ἡ ΝΙ τῇ ΘΓ, καὶ διηγμέναι εἰσὶν αἱ ΕΘ, ΓΒ, ἔστιν ὡς ἡ ΕΘ πρὸς ΘΙ, οὕτως ἡ ΩΓ πρὸς ΓΝ, τουτέστιν ἡ ΒΩ πρὸς ΥΝ. Ὡς δὲ ἡ ΒΩ πρὸς ΥΝ, οὕτως τὸ παραλληλόγραμμον τὸ γενόμενον ‹ἐν τῷ ἡμικυλινδρίῳ πρὸς τὸ γε›νόμενον ἐν τῷ ἀποτμήματι τῷ ἀποτμηθέντι ἀπὸ τοῦ κυλίνδρου· ἀμφοτέρων γὰρ τῶν παραλληλογράμμων ἡ αὐτὴ πλευρά ἐστιν ἡ ΣΤ· καὶ ἴση ἐστὶν ἡ ΕΘ τῇ ΘΠ, ἡ δὲ ΙΘ τῇ ΧΘ· καὶ ἐπεὶ ἴση ἐστὶν ἡ ΠΘ τῇ ΘΞ, ὡς ἄρα ἡ ΘΞ πρὸς ΘΧ, οὕτως τὸ γενόμενον παραλληλόγραμμον ἐν τῷ ἡμικυλινδρίῳ πρὸς τὸ γενόμενον ἐν τῷ ἀποτμήματι τῷ ἀπὸ τοῦ κυλίνδρου.

   Νοείσθω μετακείμενον τὸ ἐν τῷ τμήματι παραλληλόγραμμον καὶ κείμενον κατὰ τὸ Ξ, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Ξ, καὶ ἔτι νοείσθω ζυγὸς ἡ ΠΞ, μέσον δὲ αὐτοῦ τὸ Θ· ἰσορροπεῖ δὴ περὶ τὸ Θ σημεῖον τὸ παραλληλόγραμμον τὸ ἐν τῷ ἡμικυλινδρίῳ αὐτοῦ μένον τῷ παραλληλογράμμῳ τῷ γενομένῳ ἐν τῷ ἀποτμήματι [117] τῷ ἀπὸ τοῦ κυλίνδρου μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Ξ οὕτως, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Ξ σημεῖον. Καὶ ἐπεί ἐστι τοῦ μὲν παραλληλογράμμου τοῦ γενομένου ἐν τῷ ἡμικυλινδρίῳ κέντρον τοῦ βάρους τὸ Χ, τοῦ δὲ παραλληλογράμμου τοῦ γενομένου ἐν τῷ τμήματι τῷ ἀποτμηθέντι μετενηνεγμένου κέντρον τοῦ βάρους τὸ Ξ, καὶ τὸν αὐτὸν ἔχει λόγον ἡ ΞΘ πρὸς ΘΧ, ὃν τὸ παραλληλόγραμμον, οὗ εἴπομεν κέντρον εἶναι τοῦ βάρους τὸ Χ, πρὸς τὸ παραλληλόγραμμον, οὗ εἴπομεν κέντρον εἶναι τοῦ βάρους τὸ Ξ, ἰσορροπήσει ἄρα περὶ τὸ Θ τὸ παραλληλόγραμμον, οὗ κέντρον τοῦ βάρους τὸ Χ, τῷ παραλληλογράμμῳ, οὗ κέντρον τοῦ βάρους τὸ Ξ. Ὁμοίως δὲ δειχθήσεται ὅτι καὶ ὅταν ἄλλη τις ἀχθῇ ἐν τῷ ΟΠΡ ἡμικυκλίῳ πρὸς ὀρθὰς τῇ ΠΘ, καὶ ἀπὸ τῆς ἀχθείσης ἐπίπεδον ἀνασταθῇ ὀρθὸν πρὸς τὴν ΠΘ καὶ ἐκβληθῇ ἐφ᾿ ἑκάτερα τοῦ ἐπιπέδου τοῦ ἐν ᾧ ἐστιν ὁ ΞΟΠΡ κύκλος, [ὅτι] τὸ γινόμενον παραλληλόγραμμον ἐν τῷ ἡμικυλινδρίῳ ἰσόρροπον περὶ τὸ Θ σημεῖον αὐτοῦ μένον τῷ παραλληλογράμμῳ τῷ γενομένῳ ἐν τῷ τμήματι τῷ ἀποτμηθέντι ἀπὸ τοῦ κυλίνδρου μενενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Ξ οὕτως, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Ξ σημεῖον. Καὶ πάντα ἄρα τὰ παραλληλόγραμμα τὰ γενόμενα ἐν τῷ ἡμικυλινδρίῳ αὐτοῦ μένοντα ἰσορροπήσει περὶ τὸ Θ σημεῖον πᾶσι τοῖς παραλληλογράμμοις τοῖς γενομένοις ἐν τῷ τμήματι τῷ ἀποτμηθέντι ἀπὸ τοῦ κυλίνδρου μετενηνεγμένοις καὶ κειμένοις τοῦ ζυγοῦ κατὰ τὸ Ξ σημεῖον· ὥστε ἰσορροπεῖν καὶ τὸ ἡμικυλίνδριον αὐτοῦ μένον περὶ τὸ Θ σημεῖον τῷ τμήματι τῷ ἀποτμηθέντι [118] μετενεχθέντι καὶ τεθέντι τοῦ ζυγοῦ κατὰ τὸ Ξ οὕτως, ὥστε κέντρον εἶναι αὐτοῦ τοῦ βάρους τὸ Ξ σημεῖον.

   ιγ΄.

   Ἔστω δὴ πάλιν τὸ ‹ὀρθὸν πρὸς› τὸν ἄξονα παραλληλόγραμμον τὸ ΜΝ καὶ ὁ κύκλος ‹ὁ› ΞΟ‹ΠΡ›, καὶ ἐπεζ‹εύχθω›σαν αἱ ΘΜ, ΘΗ, καὶ ἀνεστάτω ἀπ᾿ αὐτῶν ἐπίπεδα ὀρθὰ πρὸς τὸ ἐπίπεδον, ἐν ᾧ ἐστι τὸ ΟΠΡ ἡμικύκλιον, καὶ ἐκβεβλήσθω ἐφ᾿ ἑκάτερα τὰ εἰρημένα ἐπίπεδα· ἔσται δή τι πρίσμα βάσιν μὲν ἔχον τηλικαύτην, ἡλίκη ἐστὶ τὸ ΘΜΗ τρίγωνον, ὕψος δὲ ἴσον τῷ ἄξονι τοῦ κυλίνδρου, καί ἐστι τὸ πρίσμα τοῦτο τέταρτον μέρος τοῦ ὅλου πρίσματος τοῦ περιέχοντος τὸν κύλινδρον. Ἤχθωσαν δέ τινες εὐθεῖαι ἐν τῷ ΟΠΡ ἡμικυκλίῳ καὶ ἐν τῷ ΜΝ τετραγώνῳ αἱ ΚΛ, ΤΥ ἴσον ἀπέχουσαι τῆς ΠΞ· τέμνουσιν δὴ αὗται τὴν μὲν τοῦ ΟΠΡ ἡμικυκλίου περιφέρειαν κατὰ τὰ Κ, Τ σημεῖα, τὴν δὲ ΟΡ διάμετρον κατὰ τὰ Σ, Ζ, τὰς δὲ ΘΗ, ΘΜ κατὰ τὰ Φ, Χ, καὶ ἀνεστάτω ἀπὸ τῶν ΚΛ, ΤΥ ἐπίπεδα ὀρθὰ πρὸς τὴν ΟΡ καὶ ἐκβεβλήσθω ἐφ᾿ ἑκάτερα τοῦ ἐπιπέδου, ἐν ᾧ ἐστιν ὁ ‹ΞΟΠΡ κύκλος· ποιήσει δὴ [119] τὸ ἕτερον ἐν› μὲν τῷ ἡμικυλινδρίῳ, οὗ βάσις μέν ἐστιν τὸ ΟΠΡ ἡμικύκλιον, ὕψος δὲ τὸ αὐτὸ τῷ κυλίνδρῳ, τομὴν παραλληλόγραμμον, οὗ ἐστιν μία μὲν πλευρὰ ἴση τῇ ΚΣ, ἡ δὲ ἑτέρα ἴση τῷ ἄξονι τοῦ κυλίνδρου, ἐν δὲ τῷ πρίσματι τῷ ΘΗΜ ὁμοίως παραλληλόγραμμον, οὗ ἔσται μία μὲν ἴση τῇ ΛΧ, ἡ δὲ ἑτέρα ἴση τῷ ἄξονι· διὰ δὲ τὰ αὐτὰ ἐν τῷ αὐτῷ ἡμικυλινδρίῳ ἔσται τι παραλληλόγραμμον, οὗ ἐστι μία μὲν πλευρὰ ἴση τῇ ΤΖ, ἡ δὲ ἑτέρα ἴση τῷ ἄξονι ‹τοῦ κυλίνδρου, ἐν δὲ τῷ πρίσματι παραλληλόγραμμον, οὗ ἐστιν ἡ μὲν μία› πλευρὰ ἴση τῇ ΥΦ, ἡ δὲ ἑτέρα ἴση τῷ ἄξονι τοῦ κυλίνδρου ......



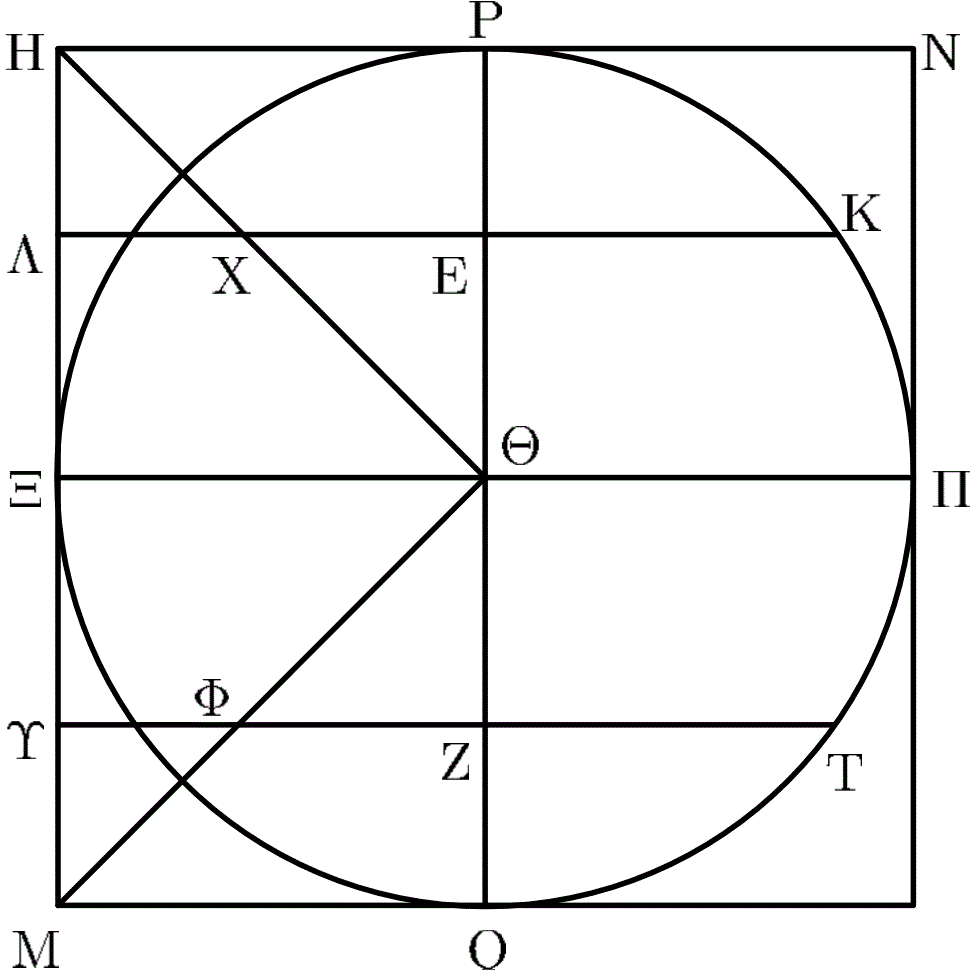
   ιδ΄.

   Ἔστω πρίσμα ὀρθὸν τετραγώνους ἔχον βάσεις, καὶ ἔστω αὐτοῦ μία τῶν βάσεων τὸ ΑΒΓΔ τετράγωνον, καὶ ἐγγεγράφθω εἰς τὸ πρίσμα κύλινδρος, καὶ ἔστω τοῦ κυλίνδρου βάσις ὁ ΕΖΗΘ κύκλος ἐφαπτόμενος τῶν τοῦ ΑΒΓΔ πλευρῶν κατὰ τὰ Ε, Ζ, Η, Θ, διὰ δὲ τοῦ κέντρου αὐτοῦ καὶ τῆς τοῦ τετραγώνου πλευρᾶς τῆς ἐν τῷ κατεναντίον [120] ἐπιπέδῳ τοῦ ΑΒΓΔ τῆς κατὰ τὴν ΓΔ ἐπίπεδον ἤχθω· ἀποτεμεῖ δὴ τοῦτο ἀπὸ τοῦ ὅλου πρίσματος ἄλλο πρίσμα, ὃ ἔσται τέταρτον μέρος τοῦ ὅλου πρίσματος, αὐτὸ δὲ τοῦτο ἔσται περιεχόμενον ὑπὸ τριῶν παραλληλογράμμων καὶ δύο τριγώνων κατεναντίον ἀλλήλοις. Γεγράφθω δὴ ἐν τῷ ΕΖΗ ἡμικυκλίῳ ὀρθογωνίου κώνου τομή, ἔστω ‹δὲ› .............. ἐν τῇ τομῇ.. τῆς ἡ ΖΚ, καὶ ἤχθω τις ἐν τῷ ΔΗ παραλληλογράμμῳ ἡ ΜΝ παράλληλος οὖσα τῇ ΚΖ·



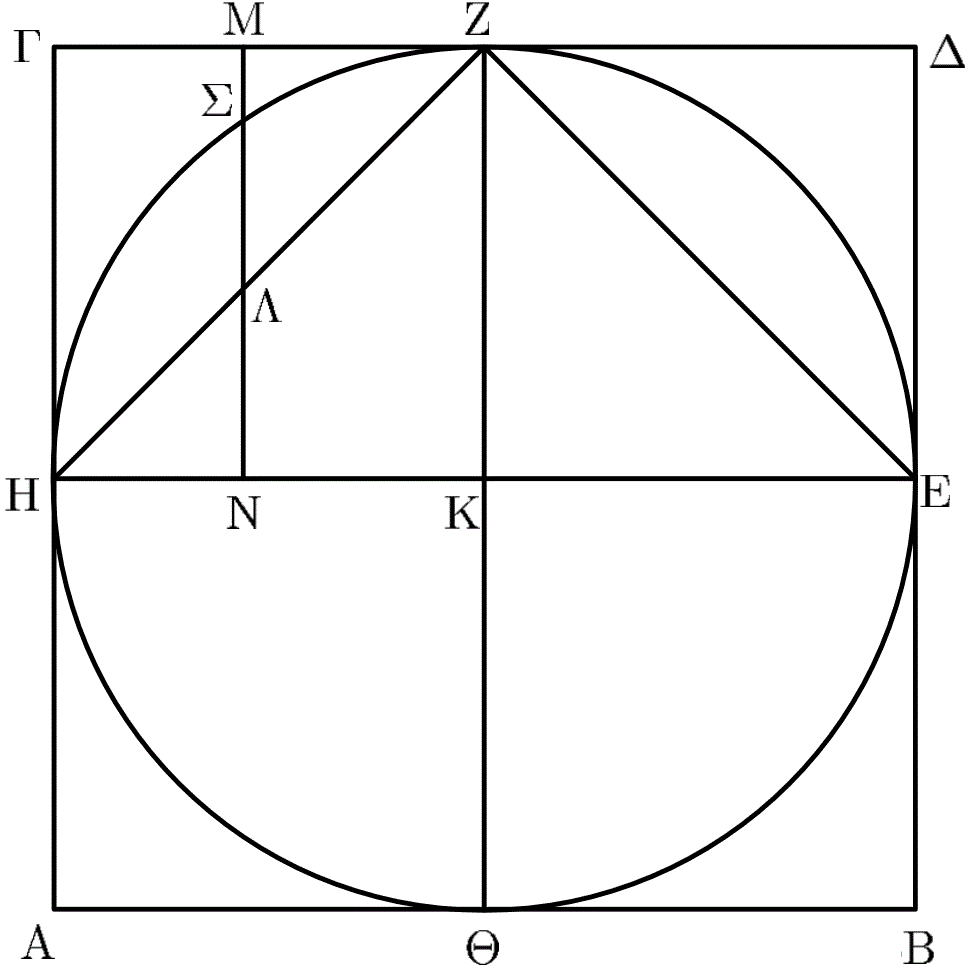
τεμεῖ δὴ αὕτη τὴν μὲν τοῦ ἡμικυκλίου περιφέρειαν κατὰ τὸ Ξ, τὴν δὲ τοῦ κώνου τομὴν κατὰ τὸ Λ. Καί ἐστιν ἴσον τὸ ὑπὸ ΜΝΛ τῷ ἀπὸ τῆς ΝΖ· τοῦτο γάρ ἐστι σαφές· διὰ τοῦτο δὴ ἔσται ὡς ἡ ΜΝ πρὸς ΝΛ, οὕτως τὸ ἀπὸ ΚΗ πρὸς τὸ ἀπὸ ΛΣ. Καὶ ἀπὸ τῆς ΜΝ ἐπίπεδον ἀνεστάτω ὀρθὸν πρὸς τὴν ΕΗ· ποιήσει δὴ τὸ ἐπίπεδον ἐν τῷ πρίσματι τῷ ἀποτμηθέντι ἀπὸ τοῦ ὅλου πρίσματος τομὴν τρίγωνον ὀρθογώνιον, οὗ ἔσται μία τῶν περὶ τὴν ὀρθὴν γωνίαν ἡ ΜΝ, ἡ δὲ ἑτέρα ἐν τῷ ἐπιπέδῳ τῷ ἀπὸ τῆς ΓΔ ὀρθὴ πρὸς τὴν ΓΔ ἀναγομένη ἀπὸ τοῦ Ν ἴση τῷ ἄξονι τοῦ κυλίνδρου, ἡ δὲ ὑποτείνουσα ἐν αὐτῷ τῷ τέμνοντι ἐπιπέδῳ· ποιήσει δὲ καὶ ἐν τῷ τμήματι τῷ ἀποτμηθέντι ἀπὸ τοῦ κυλίνδρου ὑπὸ τοῦ ἐπιπέδου τοῦ ἀχθέντος διὰ τῆς ΕΗ καὶ τῆς τοῦ τετραγώνου πλευρᾶς τῆς κατεναντίον τῇ ΓΔ τομὴν τρίγωνον ὀρθογώνιον, οὗ ἔσται μία τῶν περὶ τὴν ὀρθὴν γωνίαν ἡ ΜΞ, ἡ δὲ ἕτερα ἐν τῇ ἐπιφανείᾳ τοῦ κυλίνδρου ‹ἀν›ηγμένη ‹ἀπὸ τοῦ Ξ› ὀρθὴ πρὸς τὸ ΚΝ ἐπίπεδον, ‹ἡ δὲ› ὑποτείνουσα ἐν ‹τῷ τέμνοντι ἐπιπέδῳ›. Ὁμοίως οὖν, ἐπεὶ ἴσον ἐστὶν τὸ ὑπὸ ΜΝ, ΜΛ τῷ ἀπὸ ΜΞ· ‹τοῦτο γὰρ φανε›ρόν ‹ἐστιν›· ἔσται ὡς ἡ ‹ΜΝ› πρὸς τὴν ‹ΜΛ, οὕτως τὸ ἀπὸ ΜΝ› πρὸς τὸ ‹ἀπὸ ΜΞ. Ὡς δὲ τὸ ἀπὸ› ΜΝ πρὸς τὸ ἀπὸ ‹ΜΞ, [121] οὕτως τὸ ἀπὸ τῆς› ΜΝ τρίγω‹νον τὸ ἐν τῷ πρίσμα›τι γε‹νόμενον πρὸς τὸ ἀπὸ ΜΞ τρίγω›νον τὸ ἐν τῷ ‹τμήματι ἀφῃρημένον› ὑπὸ τῆς τοῦ κυλίνδρου ἐπιφανείας· ὡς ἄρα ἡ ΜΝ πρὸς ΜΛ, ‹οὕτως τὸ τρίγωνον› πρὸς τὸ τρίγωνον. Ὁμοίως δὲ ‹δ›εί‹ξομεν καί›, ἐὰν ‹ἄλλ›η τ‹ις ἀχθῇ ἐν τῷ περὶ τὴν τομὴν πε›ριγραφ‹έντι› παραλληλογράμμῳ ‹παρὰ› τὴν ΚΖ, καὶ ἀπὸ τῆς ἀχθείσης ἐπί‹πεδον ἀνασταθῇ ὀρθὸν› πρὸς τὴν ΕΗ, ὅτι ἔσται ὡς τὸ τρίγωνον τὸ γενόμενον ἐν τῷ πρίσματι πρὸς τὸ .............τμήματι..... ἀπὸ τοῦ κυλίνδρου, οὕτως ἡ ἀχθεῖσα ‹ἐν› τῷ ΔΗ παραλληλογράμμῳ παράλληλος τῇ ΚΖ ‹πρὸς τὴν› ἀποληφθεῖσαν ὑπὸ τῆς ΕΗΖ τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ διαμέτρου. Συμπληρωθέντος οὖν τοῦ ΔΗ παραλληλογράμμου ὑπὸ τῶν ἡγμένων παρὰ τὴν ΚΖ καὶ τοῦ τμήματος τοῦ περιεχομένου ὑπό τε τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς διαμέτρου ὑπὸ τῶν ἀπολαμβανομένων ἐν τῷ τμήματι συμπληρω .........τοῦ τμήματος τοῦ..... ἐν τῷ ἀπὸ τοῦ .....γινομ.....πων.... τὰ γ..........α καὶ ..... τῷ ΔΗ............................... δὲ ετι................ μα...................... η ετι.............. ἀπ.......................... ................. ἀγομένων παρὰ τὴν ΚΖ...... ...................τομῆς καὶ ........ ει ταῖς ἐν τῷ ΔΗ παραλληλογράμμῳ ἠγμέναις παρὰ τὴν ΚΖ, καὶ ἔσται ὡς πάντα τὰ τρίγωνα τὰ ἐν τῷ πρίσματι πρὸς πάντα τὰ τρίγωνα τὰ ἐν τῷ ἀποτμηθέντι τμήματι τοῦ κυλίνδρου ἀφῃρημένα, οὕτως πᾶσαι αἱ εὐθεῖαι αἱ ἐν τῷ ΔΗ παραλληλογράμμῳ πρὸς πάσας τὰς εὐθείας τὰς μεταξὺ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ [122] εὐθείας. Καὶ ἐκ μὲν τῶν ἐν τῷ πρίσματι τριγώνων σύγκειται τὸ πρίσμα, ἐκ δὲ τῶν ἐν τῷ ἀποτμήματι τῷ ‹ἀποτμηθέντι ἀπὸ τοῦ κυλίνδρου τὸ ἀπότμημα, ἐκ δὲ τῶν ἐν τῷ ΔΗ παραλληλογράμμῳ παραλλήλων τῇ ΚΖ τὸ ΔΗ παραλληλόγραμμον, ἐκ δὲ τῶν ..... μεταξὺ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ ‹τὸ τμῆμα› [τῆς παραβολῆς]· ὡς ἄρα τὸ πρίσμα πρὸς τὸ ἀπότμημα τὸ ἀπὸ τοῦ κυλίνδρου, οὕτω τὸ ΔΗ παραλληλόγραμμον πρὸς τὸ ΕΖΗ τμῆμα τὸ περιεχόμενον ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας. Ἡμιόλιον δὲ τὸ ΔΗ παραλληλόγραμμον τοῦ τμήματος τοῦ περιεχομένου ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας· δέδεικται γὰρ τοῦτο ἐν τοῖς πρότερον ἐκδεδομένοις· ἡμιόλιον ἄρα ἐστὶ καὶ τὸ πρίσμα τοῦ ἀποτμήματος τοῦ ἀφῃρημένου ἀπὸ τοῦ κυλίνδρου· οἵων ἄρα ἐστὶ τὸ ἀπότμημα τοῦ κυλίνδρου δύο, τοιούτων ἐστὶ τὸ πρίσμα τριῶν. Οἵων δὲ τὸ πρίσμα τριῶν, τοιούτων ἐστὶν τὸ ὅλον πρίσμα τὸ περιέχον τὸν κύλινδρον ιβ διὰ τὸ δ΄ εἶναι τὸ ἕτερον τοῦ ἑτέρου· οἵων ἄρα τὸ ἀπότμημα τοῦ κυλίνδρου δύο, τοιούτων ἐστὶν τὸ ὅλον πρίσμα ιβ· ὥστε τὸ τμῆμα τὸ ἀποτμηθὲν ἀπὸ τοῦ κυλίνδρου ἕκτον μέρος ἐστὶ τοῦ πρίσματος.

   ιε΄.

   Ἔστω πρίσμα ὀρθὸν τετραγώνους ἔχον βάσεις, ὧν μία ἔστω τὸ ΑΒΓΔ τετράγωνον, καὶ ἐγγεγράφθω εἰς τὸ πρίσμα κύλινδρος, οὗ βάσις ἔστω ὁ ΕΖΗ κύκλος· ‹ἐφάπτεται› δὴ οὗτος τῶν τοῦ τετραγώνου πλευρῶν κατὰ τὰ Ε, Ζ, Η, Θ σημεῖα· κέντρον δὲ ‹ἔστω τὸ Κ, καὶ [123] διὰ τῆς› ΕΗ διαμέτρου ‹καὶ μιᾶς πλευρᾶς› ....... ‹ἐπίπεδον ἤχθω›· τοῦτο δὴ τὸ ἐπίπεδον ἀποτέμνει πρίσμα ἀπὸ τοῦ ὅλου πρίσματος καὶ ἀπὸ τοῦ κυλίνδρου ἀπότμημα κυλίνδρου. ‹Λέγω δὴ ὅτι τοῦ›το ‹τὸ› τμῆμα τὸ ἀποτετμημένον ἀπὸ τοῦ κυλίνδρου ὑπὸ τοῦ ἀχθέντος ἐπιπέδου ἕκτον μέρος ὂν δειχθήσεται τοῦ ὅλου πρίσματος.

   Πρῶτον δὲ δείξομεν ὅτι δυνατὸν ἔσται εἰς τὸ τμῆμα τὸ ἀποτμηθὲν ἀπὸ τοῦ κυλίνδρου σχῆμα στερεὸν ἐγγράψαι καὶ ἄλλο περιγράψαι ἐκ πρισμάτων συγκείμενον ἴσον ὕψος ἐχόντων καὶ βάσεις τριγώνους ἐχόντων ὁμοίας, ὥστε τὸ περιγραφὲν σχῆμα τοῦ ἐγγραφέντος ὑπερέχειν ἐλάσσονι παντὸς τοῦ προτεθέντος μεγέθους ..... γὰρ τοῦ πρίσματος τοῦ κατὰ τὸ ΒΔ παραλληλογράμμου ............ καὶ ... ω........ γραμμένου. ω.. το..Ξ. ἐπιπέδῳ.. ‹ς›ημεῖα τοῦ ..... ατος... η... ρετό.πω.........νομεν.....εστ..σων.......ἔστω ....το..λειπόμενον..νι.μια ἐλας....ν..τοῦ λείμματος. στ..........ε ..ει...καὶ...ει... α τω. ει........ το .. ατα.......................... τω ἐν....................... τμῆμα τὸν το...... ἀπο‹τ›μ‹η›θ.... ἀπὸ.... δι ........ ε... μάτων ....μεν....ων.... ται καὶ τῶν..... ἐγγεγραμμένω ...δι....... των κει..... τα... ΚΩ παραλληλόγραμμον............. αμμον............ σχήματι πρίσμα......ης.........................τὸ ἀπὸ ........ δρου. ἐγγεγράφθω......μια............ ................... σχῆμα, τὸ εἰρ‹ημένον› σχῆμα τοῦ ἐγγεγραμμένου......... ἔχει... τοῦ δοθέντος ......ἐχέτω......ος.....τῶν πρισμάτων........ ......................... ἴσον αὐ... ‹ση ‑ ›μεῖα .......... ἐγγεγρά‹φθω›............ν ἐσ......

[124] δευτέρῳ........ γεγρ.... γει..... η ...... ‹τέ›τμηται κατὰ τὸ αὐτὸ........ ‹ἐγγεγρ›αμμένον ἐν ...... κύκλ... το‹ῦ› τμήματος τη συνθε.τ.... ἀπο....μείζων ἐστὶν τοῦ ἐγγεγραμμένου...... ‹τμ›ήματος ἐν τῷ πρίσματι τῷ κατὰ τὸ..............ω [125] ‹...... ἔλασσον ἄρα ἢ ἡμιό›λιον τὸ πρίσμα τὸ ἀποτετμημένον ὑπὸ τοῦ λοξοῦ ἐπιπέδου τοῦ ἐγγεγραμμένου εἰς τὸ ἀπότμημα τὸ ἀπὸ τοῦ κυλίνδρου στερεοῦ. Ἐδείχθη δὲ ὡς τὸ ὑπὸ τοῦ λοξοῦ ἐπιπέδου ἀφῃρημένον πρίσμα πρὸς τὸ ἐγγεγραμμένον στερεὸν εἰς τὸ ἀπότμημα τὸ ἀπὸ τοῦ κυλίνδρου, οὕτως τὸ ΔΗ παραλληλόγραμμον πρὸς τὰ ἐγγεγραμμένα παραλληλόγραμμα εἰς τὸ τμῆμα τὸ περιεχόμενον ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας· ἔλασσον ἄρα ἢ ἡμιόλιον τὸ ΔΗ παραλληλόγραμμον τῶν παραλληλογράμμων τῶν ἐν τῷ τμήματι τῷ περιεχομένῳ ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας· ὅπερ ἀδύνατον, ἐπεὶ τοῦ τμήματος τοῦ περιεχομένου ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας ἡμιόλιον δέδεικται τὸ ΔΗ παραλληλόγραμμον ἐν ἑτέροις.



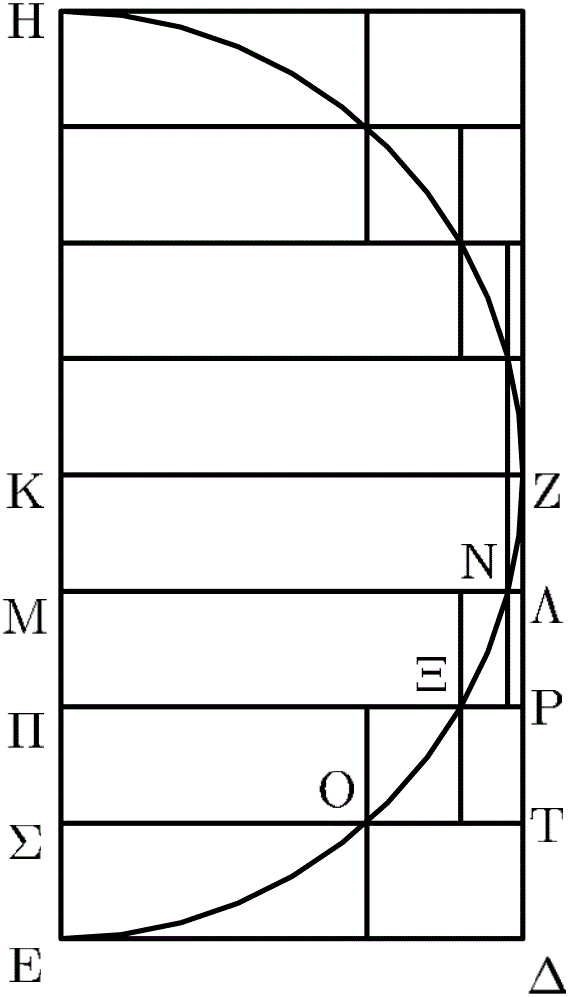
Οὐκ ἄρα μεῖ‹ζον› [126] ..................................... ‹στε›ρεὸν ἐτ..... ‹ἀ›ποτεμν.........σχῆμ‹α›....... τα ὀρθο.......... περιγραφ....... ‹τοῦ ἐγγρα]φέντος ἐν......... ἐπεὶ......... τμήματ...... .... ἐγγεγράφ‹θω..... ἐν τῷ τμή›ματι τῷ ‹περιεχομένῳ ὑπό τε› τῆς τοῦ ὀρθ‹ογωνίου κώνου τομῆς› καὶ τῆς ‹ΕΗ εὐθείας› .......γεγράφθ‹ω›.......τοῦ ὀρθ‹ογωνίου κώνου›.... φὲν περι....... ‹ἐγγεγραμ›μένον ἐν τ‹ῷ›...... τοῦ κυλίνδρ‹ου› ...... τοῦ στερε‹οῦ› .......τοῦ κυλίν‹δρου› ..... τμήματ........ ἐστὶν καὶ........γραμμέν........................... ............................................. ............................................. ............... εχομεν ..................... νη .................... Η .......... τιν ...... ......... πρὸς τὸ ........ τὸ ἐν τ‹ῷ› ........ ........... ‹πε›ριεχομε........ γο ... τῆς ΕΗ καὶ ......... τοῖς λόγ‹οις› ...... αμμέν....... .... τμήματος........ δρ ............ νον ἀπὸ τῆς .......... ‹τ›ῆς πλευρ‹ᾶς›................ ....... ἐν τῷ........ τετμή‹σθω›.............. ....... ἐχθήσ........ τὸ μεῖ‹ζον›............. ..................................... ‹εὐθ›είας καὶ πάντα τὰ πρίσματα τὰ ἐν τῷ πρίσματι τῷ ἀποτετμημένῳ ὑπὸ τοῦ λοξοῦ ἐπιπέδου πρὸς πάντα τὰ πρίσματα τὰ ἐν τῷ σχήματι τῷ περιγεγραμμένῳ περὶ τὸ ἀπότμημα τοῦ κυλίνδρου τὸν αὐτὸν ἕξει λόγον, ὃν πάντα τὰ παραλληλόγραμμα τὰ ἐν τῷ ΔΗ παραλληλογράμμῳ πρὸς πάντα τὰ παραλληλόγραμμα τὰ ἐν τῷ σχήματι τῷ περιγεγραμμένῳ περὶ τὸ τμῆμα τὸ περιεχόμενον ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας, [127] τουτέστιν τὸ πρίσμα τὸ ἀποτετμημένον ὑπὸ τοῦ λοξοῦ ἐπιπέδου πρὸς τὸ σχῆμα τὸ περιγεγραμμένον περὶ τὸ τμῆμα τοῦ κυλίνδρου τὸν αὐτὸν ἕξει λόγον, ὃν τὸ ΔΗ παραλληλόγραμμον πρὸς τὸ σχῆμα τὸ περιγεγραμμένον περὶ τὸ τμῆμα τὸ περιεχόμενον ὑπὸ τῆς τοῦ ὀρθογωνίου κώνου τομῆς καὶ τῆς ΕΗ εὐθείας. Μεῖζον δέ ἐστι τὸ πρίσμα τὸ ἀποτετμημένον ὑπὸ τοῦ λοξοῦ ἐπιπέδου ἢ ἡμιόλιον τοῦ στερεοῦ σχήματος τοῦ περιγε‹γραμμένου περὶ τὸ τμῆμα τοῦ κυλίνδρου›........

 

---

 

[170]

Πρόβλημα βοεικόν

ὅπερ Ἀρχιμήδης ἐν ἐπιγράμμασιν εὑρὼν τοῖς ἐν Ἀλεξανδρείᾳ περὶ ταῦτα πραγματευομένοις ζητεῖν ἀπέστειλεν ἐν τῇ πρὸς Ἐρατοσθένην τὸν Κυρηναῖον ἐπιστολῇ.

   Πληθὺν Ἠελίοιο βοῶν, ὦ ξεῖνε, μέτρησον

     φροντίδ᾿ ἐπιστήσας, εἰ μετέχεις σοφίης,

   πόσση ἄρ᾿ ἐν πεδίοις Σικελῆς ποτ᾿ ἐβόσκετο νήσου

     Θρινακίης τετραχῇ στίφεα δασσαμένη

 5 χροιὴν ἀλάσσοντα· τὸ μὲν λευκοῖο γάλακτος,

     κυανέῳ δ᾿ ἕτερον χρώματι λαμπόμενον,

   ἄλλο γε μὲν ξανθόν, τὸ δὲ ποικίλον. Ἐν δὲ ἑκάστῳ

     στίφει ἔσαν ταῦροι πλήθεσι βριθόμενοι

   συμμετρίης τοιῆσδε τετευχότες· ἀργότριχας μὲν

10   κυανέων ταύρων ἡμίσει ἠδὲ τρίτῳ

   καὶ ξανθοῖς σύμπασιν ἴσους, ὦ ξεῖνε, νόησον,

     αὐτὰρ κυανέους τῷ τετράτῳ τε μέρει

   μικτοχρόων καὶ πέμπτῳ, ἔτι ξανθοῖσί τε πᾶσιν.

     Τοὺς δ᾿ ὑπολειπομένους ποικιλόχρωτας ἄθρει

15 ἀργεννῶν ταύρων ἕκτῳ μέρει ἑβδομάτῳ τε

     καὶ ξανθοῖς αὐτοὺς πᾶσιν ἰσαζομένους.

   Θηλείαισι δὲ βουσὶ τάδ᾿ ἔπλετο· λευκότριχες μὲν

     ἦσαν συμπάσης κυανέης ἀγέλης

   τῷ τριτάτῳ τε μέρει καὶ τετράτῳ ἀτρεκὲς ἶσαι·

[171] 20 αὐτὰρ κυάνεαι τῷ τετράτῳ τε πάλιν

   μικτοχρόων καὶ πέμπτῳ ὁμοῦ μέρει ἰσάζοντο

     σὺν ταύροις πάσαις εἰς νομὸν ἐρχομέναις.

   Ξανθοτρίχων δ᾿ ἀγέλης πέμπτῳ μέρει ἠδὲ καὶ ἕκτῳ

     ποικίλαι ἰσάριθμον πλῆθος ἔχον τετραχῇ.

25 Ξανθαὶ δ᾿ ἠριθμεῦντο μέρους τρίτου ἡμίσει ἶσαι

     ἀργεννῆς ἀγέλης ἑβδομάτῳ τε μέρει.

   Ξεῖνε, σὺ δ᾿ Ἠελίοιο βόες πόσαι ἀτρεκὲς εἰπών,

     χωρὶς μὲν ταύρων ζατρεφέων ἀριθμόν,

   χωρὶς δ᾿ αὖ θήλειαι ὅσαι κατὰ χροιὰν ἕκασται,

30   οὐκ ἄιδρίς κα λέγοι᾿ οὐδ᾿ ἀριθμῶν ἀδαής,

   οὐ μὴν πώ γε σοφοῖς ἐναρίθμιος. Ἀλλ᾿ ἴθι φράζευ

     καὶ τάδε πάντα βοῶν Ἠελίοιο πάθη.

   Ἀργότριχες ταῦροι μὲν ἐπεὶ μιξαίατο πληθὺν

     κυανέοις, ἵσταντ᾿ ἔμπεδον ἰσόμετροι

35 εἰς βάθος εἰς εὖρός τε, τὰ δ᾿ αὖ περιμήκεα πάντη

     πίμπλαντο πλίνθου Θρινακίης πεδία.

   Ξανθοὶ δ᾿ αὖτ᾿ εἰς ἓν καὶ ποικίλοι ἀθροισθέντες

     ἵσταντ᾿ ἀμβολάδην ἐξ ἑνὸς ἀρχόμενοι

   σχῆμα τελειοῦντες τὸ τρικράσπεδον οὔτε προσόντων

40   ἀλλοχρόων ταύρων οὔτ᾿ ἐπιλειπομένων.

   Ταῦτα συνεξευρὼν καὶ ἐνὶ πραπίδεσσιν ἀθροίσας

     καὶ πληθέων ἀποδούς, ξεῖνε, τὰ πάντα μέτρα

   ἔρχεο κυδιόων νικηφόρος ἴσθι τε πάντως

     κεκριμένος ταύτῃ γ᾿ ὄμπνιος ἐν σοφίῃ.

Σχόλιον

   Τὸ μὲν οὖν πρόβλημα διὰ τοῦ ποιήματος ὁ Ἀρχιμήδης ἐδήλωσε σαφῶς· ἰστέον δὲ λεγόμενον, ὅτι τέσσαρας [172] ἀγέλας εἶναι δεῖ βοῶν, λευκοτρίχων μὲν μίαν ταύρων καὶ θηλειῶν, ὧν τὸ πλῆθος ὁμοῦ συνάγει μυριάδας διπλᾶς ιδ΄ καὶ ἁπλᾶς φπβ΄ καὶ μονάδας Ϛζτξ΄, κυανοχρόων δ᾿ ἄλλην ὁμοῦ ταύρων καὶ θηλειῶν, ὧν τὸ πλῆθός ἐστι μυριάδων διπλῶν ἐννέα καὶ ἁπλῶν Ϛηωλ΄ καὶ μονάδων ω΄, μιξοτρίχων δ᾿ ἄλλην ταύρων καὶ θηλειῶν, ὧν τὸ πλῆθός ἐστι μυριάδων διπλῶν η΄ καὶ ἁπλῶν ϚϠϠϞα΄ καὶ μονάδων υ΄· τῆς δὲ λοιπῆς ἀγέλης ξανθοχρόων συνάγει τὸ πλῆθος διπλᾶς μυριάδας ζ΄ καὶ ἁπλᾶς ϚϚψη΄, μονάδας δὲ Ϛη· ὥστε συνάγεσθαι ὁμοῦ τὸ πλῆθος τῶν δ᾿ ἀγελῶν μυριάδας διπλᾶς μ΄ καὶ ἁπλᾶς Ϛγριβ΄ καὶ μονάδας ϚϚφξ΄. Καὶ ἡ μὲν ἀγέλη τῶν λευκοτρίχων ταύρων ἔχει μυριάδας διπλᾶς η΄ καὶ ἁπλᾶς ϚβϠλα΄ καὶ μονάδας Ϛηφξ΄, θηλειῶν δὲ μυριάδας διπλᾶς ε΄ καὶ ἁπλᾶς Ϛζχν΄ καὶ μονάδας Ϛηω΄, ἡ δὲ ἀγέλη τῶν κυανοχρόων ταύρων ἔχει μὲν μυριάδας διπλᾶς ε΄ καὶ ἁπλᾶς Ϛθχπδ΄ καὶ μονάδας Ϛαρκ΄, θηλειῶν δὲ μυριάδας διπλᾶς γ΄ καὶ ἁπλᾶς Ϛθρμε΄ καὶ μονάδας Ϛθχπ΄, ἡ δ᾿ ἀγέλη τῶν ποικιλοτρίχων ταύρων ἔχει μὲν μυριάδας διπλᾶς ε΄ καὶ ἁπλᾶς Ϛηωξδ΄ καὶ μονάδας Ϛδω΄, θηλειῶν δὲ μυριάδας διπλᾶς β΄ καὶ ἁπλᾶς ϚηρκϚ΄ καὶ μονάδας Ϛεχ΄, ἡ δ᾿ ἀγέλη τῶν ξανθοχρωμάτων ταύρων ἔχει μὲν μυριάδας διπλᾶς γ΄ καὶ ἁπλᾶς ϚγρϞε΄ καὶ μονάδας Ϡξ΄, θηλειῶν δὲ μυριάδας διπλᾶς δ΄ καὶ ἁπλᾶς Ϛγφιγ΄ [173] καὶ μονάδας Ϛζμ΄. Καί ἐστι τὸ πλῆθος τῶν λευκοτρίχων ταύρων ἴσον τῷ ἡμίσει καὶ τρίτῳ μέρει τοῦ πλήθους τῶν κυανοχρόων ταύρων καὶ ἔτι ὅλῃ τῇ τῶν ξανθοχρωμάτων ἀγέλῃ, τὸ δὲ πλῆθος τῶν κυανοχρωμάτων ἴσον τῷ τετάρτῳ καὶ πέμπτῳ μέρει τῶν ποικιλοτρίχων ταύρων καὶ ὅλῳ τῷ πλήθει τῶν ξανθοχρωμάτων, τὸ δὲ πλῆθος τῶν ποικιλοτρίχων ταύρων ἴσον τῷ ἕκτῳ καὶ ἑβδόμῳ μέρει τῶν λευκοτρίχων ταύρων καὶ ἔτι τῷ πλήθει ὅλῳ τῶν ξανθοχρωμάτων ταύρων, καὶ πάλιν τὸ πλῆθος τῶν λευκῶν θηλειῶν ἴσον τῷ τρίτῳ καὶ τετάρτῳ μέρει ὅλης τῆς ἀγέλης τῶν κυανοχρόων, τὸ δὲ τῶν κυανοχρόων ἴσον τῷ τετάρτῳ καὶ πέμπτῳ μέρει τῆς ὅλης ἀγέλης τῶν ποικιλοτρίχων, τὸ δὲ τῶν ποικιλοτρίχων ἴσον τῷ πέμπτῳ καὶ ἕκτῳ μέρει τῆς ὅλης τῶν ξανθῶν βοῶν. Πάλιν δὲ τὸ τῶν ξανθῶν θηλειῶν πλῆθος ἦν ἴσον τῷ ἕκτῳ τε καὶ ἑβδόμῳ μέρει τῆς ὅλης ἀγέλης τῶν λευκῶν βοῶν. Καὶ ἡ μὲν ἀγέλη τῶν λευκοτρίχων ταύρων καὶ ἡ τῶν κυανοχρόων ταύρων συντεθεῖσα ποιεῖ τετράγωνον ἀριθμόν, ἡ δ᾿ ἀγέλη τῶν ξανθοτρίχων ταύρων μετὰ τῆς ἀγέλης τῶν ποικιλοχρόων συντεθεῖσα ποιεῖ τρίγωνον, ὡς ἔχει τὰ τῶν ὑποκειμένων κανόνων καθ᾿ ἕκαστον χρῶμα.

---

 

ΟΙ ΑΝΑΦΟΡΕΣ ΣΤΟΝ ΑΡΧΙΜΗΔΗ

1. Plutarchus Biogr., Phil., Marcellus (0007: 022) “Plutarchi vitae parallelae, vol. 2.2, 2nd edn.”, Ed. Ziegler, K. Leipzig: Teubner, 1968. Chapter 14, section 8, line 4
   
   ὧν ὡς μὲν ἔργον ἄξιον σπουδῆς οὐδὲν ὁ ἀνὴρ προὔθετο, γεωμετρίας δὲ παιζούσης ἐγεγόνει πάρεργα τὰ πλεῖστα, πρότερον φιλοτιμηθέντος Ἱέρωνος τοῦ βασιλέως καὶ πείσαντος Ἀρχιμήδη τρέψαι τι τῆς τέχνης ἀπὸ τῶν νοητῶν ἐπὶ τὰ σωματικά, καὶ τὸν λόγον ἁμῶς γέ πως δι' αἰσθήσεως μείξαντα ταῖς χρείαις ἐμφανέστερον καταστῆσαι τοῖς πολλοῖς.
   
   
2. Plutarchus Biogr., Phil., Marcellus Chapter 17, section 4, line 5
   
   τέλος δὲ τοὺς Ῥωμαίους [ὁρῶν] οὕτω περιφόβους γεγονότας ὁ Μάρκελλος, ὥστ' εἰ καλῴδιον ἢ ξύλον ὑπὲρ τοῦ τείχους μικρὸν ὀφθείη προτεινόμενον, τοῦτ' ἐκεῖνο, μηχανήν τινα κινεῖν ἐπ᾿ αὐτοὺς Ἀρχιμήδη βοῶντας ἀποτρέπεσθαι καὶ φεύγειν, ἀπέσχετο μάχης ἁπάσης καὶ προσβολῆς, τὸ λοιπὸν ἐπὶ τῷ χρόνῳ τὴν πολιορκίαν θέμενος.
   
   
3. Plutarchus Biogr., Phil., Marcellus Chapter 14, section 14, line 2
   
   ἐκπλαγεὶς οὖν ὁ βασιλεὺς καὶ συννοήσας τῆς τέχνης τὴν δύναμιν, ἔπεισε τὸν Ἀρχιμήδην ὅπως αὐτῷ τὰ μὲν ἀμυνομένῳ τὰ δ' ἐπιχειροῦντι μηχανήματα κατασκευάσῃ πρὸς πᾶσαν ἰδέαν πολιορκίας.
   
   
4. Plutarchus Biogr., Phil., Marcellus Chapter 15, section 8, line 3
   
   Βουλευομένοις δ' ἔδοξεν αὐτοῖς ἔτι νυκτὸς ἂν δύνωνται προσμεῖξαι τοῖς τείχεσι· τοὺς γὰρ τόνους, οἷς χρῆσθαι τὸν Ἀρχιμήδην, ῥύμην ἔχοντας ὑπερπετεῖς ποιήσεσθαι τὰς τῶν βελῶν ἀφέσεις, ἐγγύθεν δὲ καὶ τελέως ἀπράκτους εἶναι, διάστημα τῆς πληγῆς οὐκ ἐχούσης.
   
   
5. Plutarchus Biogr., Phil., Marcellus Chapter 14, section 12, line 1
   
   καὶ μέντοι καὶ Ἀρχιμήδης, Ἱέρωνι τῷ βασιλεῖ συγγενὴς ὢν καὶ φίλος, ἔγραψεν ὡς τῇ δοθείσῃ δυνάμει τὸ δοθὲν βάρος κινῆσαι δυνατόν ἐστι, καὶ νεανιευσάμενος ὥς φασι ῥώμῃ τῆς ἀποδείξεως εἶπεν ὡς εἰ γῆν εἶχεν ἑτέραν, ἐκίνησεν ἂν ταύτην μεταβὰς εἰς ἐκείνην.
   
   
6. Plutarchus Biogr., Phil., Marcellus Chapter 17, section 5, line 2
   
   Τηλικοῦτον μέντοι φρόνημα καὶ βάθος ψυχῆς καὶ τοσοῦτον ἐκέκτητο θεωρημάτων πλοῦτον Ἀρχιμήδης, ὥστ' ἐφ' οἷς ὄνομα καὶ δόξαν οὐκ ἀνθρωπίνης, ἀλλὰ δαιμονίου τινὸς ἔσχε συνέσεως, μηθὲν ἐθελῆσαι σύγγραμμα περὶ τούτων ἀπολιπεῖν, ἀλλὰ τὴν περὶ τὰ μηχανικὰ πραγματείαν καὶ πᾶσαν ὅλως τέχνην χρείας ἐφαπτομένην ἀγεννῆ καὶ βάναυσον ἡγησάμενος, [εἰς] ἐκεῖνα καταθέσθαι μόνα τὴν αὑτοῦ φιλοτιμίαν, οἷς τὸ καλὸν καὶ περιττὸν ἀμιγὲς τοῦ ἀναγκαίου πρόσεστιν, ἀσύγκριτα μὲν ὄντα τοῖς ἄλλοις, ἔριν δὲ παρέχοντα πρὸς τὴν ὕλην τῇ ἀποδείξει, τῆς μὲν τὸ μέγεθος καὶ τὸ κάλλος, τῆς δὲ τὴν ἀκρίβειαν καὶ
   
   
7. Plutarchus Biogr., Phil., Marcellus Chapter 18, section 1, line 1
   
   πολλῶν δὲ καὶ καλῶν εὑρετὴς γεγονώς, λέγεται τῶν φίλων δεηθῆναι καὶ τῶν συγγενῶν, ὅπως αὐτοῦ μετὰ τὴν τελευτὴν ἐπιστήσωσι τῷ τάφῳ τὸν περιλαμβάνοντα τὴν σφαῖραν ἐντὸς κύλινδρον, ἐπιγράψαντες τὸν λόγον τῆς ὑπεροχῆς τοῦ περιέχοντος στερεοῦ πρὸς τὸ περιεχόμενον. Ἀρχιμήδης μὲν οὖν τοιοῦτος γενόμενος, ἀήττητον ἑαυτόν τε καὶ τὴν πόλιν ὅσον ἐφ' ἑαυτῷ διεφύλαξε.
   
   
8. Plutarchus Biogr., Phil., Marcellus Chapter 14, section 7, line 2
   
   ὑπὲρ δὲ μεγάλου ζεύγματος νεῶν ὀκτὼ πρὸς ἀλλήλας συνδεδεμένων μηχανὴν ἄρας, ἐπέπλει πρὸς τὸ τεῖχος, τῷ πλήθει καὶ τῇ λαμπρότητι τῆς παρασκευῆς καὶ τῇ δόξῃ τῇ περὶ αὑτὸν πεποιθώς· ἧς ἄρα λόγος οὐδεὶς ἦν Ἀρχιμήδει καὶ τοῖς Ἀρχιμήδους μηχανήμασιν.
   
   
9. Plutarchus Biogr., Phil., Marcellus Chapter 15, section 2, line 2
   
   σχάσαντος δὲ τὰς μηχανὰς τοῦ Ἀρχιμήδους, ἅμα τοῖς μὲν πεζοῖς ἀπήντα τοξεύματά τε παντοδαπὰ καὶ λίθων ὑπέρογκα μεγέθη, ῥοίζῳ καὶ τάχει καταφερομένων ἀπίστῳ καὶ μηδενὸς ὅλως τὸ βρῖθος στέγοντος ἀθρόους ἀνατρεπόντων τοὺς ὑποπίπτοντας καὶ τὰς τάξεις συγχεόντων· ταῖς δὲ ναυσὶν ἄφνω τῶν τειχῶν ὑπεραιωρούμεναι κεραῖαι, τὰς μὲν ὑπὸ βρίθους στηρίζοντος ἄνωθεν ὠθοῦσαι κατέδυον εἰς βυθόν, τὰς δὲ χερσὶ σιδηραῖς [ἢ] στόμασιν εἰκασμέναις γεράνων ἀνασπῶσαι πρῴραθεν ὀρθὰς ἐπὶ πρύμναν [ἀν]ἐβάπτιζον, ἢ δι' ἀντιτόνων ἔνδον
   
   
10. Plutarchus Biogr., Phil., Marcellus Chapter 17, section 3, line 2
    
    τῷ γὰρ ὄντι πάντες οἱ λοιποὶ Συρακόσιοι σῶμα τῆς Ἀρχιμήδους παρασκευῆς ἦσαν, ἡ δὲ κινοῦσα πάντα καὶ στρέφουσα ψυχὴ μία, τῶν μὲν ἄλλων ὅπλων ἀτρέμα κειμένων, μόνοις δὲ τοῖς ἐκείνου τότε τῆς πόλεως χρωμένης καὶ πρὸς ἄμυναν καὶ πρὸς ἀσφάλειαν.
    
    
11. Plutarchus Biogr., Phil., Marcellus Chapter 19, section 8, line 1
    
    μάλιστα δὲ τὸ Ἀρχιμήδους πάθος ἠνίασε Μάρκελλον.
    
    
12. Plutarchus Biogr., Phil., Marcellus Chapter 16, section 3, line 2
    
    τὰ γὰρ πλεῖστα τῶν ὀργάνων ὑπὸ τὸ τεῖχος ἐσκευοποίητο τῷ Ἀρχιμήδει, καὶ θεομαχοῦσιν ἐῴκεσαν οἱ Ῥωμαῖοι, μυρίων αὐτοῖς κακῶν ἐξ ἀφανοῦς ἐπιχεομένων.
    
    
13. Plutarchus Biogr., Phil., An seni respublica gerenda sit (783b–797f) (0007: 117) “Plutarch's moralia, vol. 10”, Ed. Fowler, H.N. Cambridge, Mass.: Harvard University Press, 1936, Repr. 1969. Stephanus page 786, section C, line 2
    
    εἰ γὰρ Νικίας ὁ ζῳγράφος οὕτως ἔχαιρε τοῖς τῆς τέχνης ἔργοις, ὥστε τοὺς οἰκέτας ἐρωτᾶν πολλάκις, εἰ λέλουται καὶ ἠρίστηκεν· Ἀρχιμήδην δὲ τῇ σανίδι προσκείμενον ἀποσπῶντες βίᾳ καὶ ἀποδύοντες ἤλειφον οἱ θεράποντες, ὁ δ' ἐπὶ τοῦ σώματος ἀληλιμμένου διέγραφε τὰ σχήματα· Κάνος δ' ὁ αὐλητής, ὃν καὶ σὺ γιγνώσκεις, ἔλεγεν ἀγνοεῖν τοὺς ἀνθρώπους, ὅσῳ μᾶλλον αὑτὸν αὐλῶν ἢ ἑτέρους εὐφραίνει· λαμβάνειν γὰρ ἂν μισθὸν οὐ διδόναι τοὺς ἀκούειν ἐθέλοντας· ἆρ' οὐκ ἐπινοοῦμεν, ἡλίκας ἡδονὰς αἱ ἀρεταὶ τοῖς χρωμένοις ἀπὸ τῶν καλῶν πράξεων καὶ τῶν κοινωνικῶν ἔργων καὶ
    
    
14. Plutarchus Biogr., Phil., Non posse suaviter vivi secundum Epicurum (1086c–1107c) (0007: 139) “Plutarchi moralia, vol. 6.2, 2nd edn.”, Ed. Westman, R. (post M. Pohlenz) Leipzig: Teubner, 1959. Stephanus page 1093, section E, line 8
    
    ὅπου γὰρ οἱ φιλογραφοῦντες οὕτως ἄγονται τῇ πιθανότητι τῶν ἔργων, ὥστε Νικίαν γράφοντα τὴν Νεκυίαν ἐρωτᾶν πολλάκις τοὺς οἰκέτας εἰ ἠρίστηκε, Πτολεμαίου δὲ τοῦ βασιλέως ἑξήκοντα τάλαντα τῆς γραφῆς συντελεσθείσης πέμψαντος αὐτῷ, μὴ λαβεῖν μηδ' ἀποδόσθαι τὸ ἔργον, τίνας οἰόμεθα καὶ πηλίκας ἡδονὰς ἀπὸ γεωμετρίας δρέπεσθαι καὶ ἀστρολογίας Εὐκλείδην γράφοντα τὰ διοπτικὰ καὶ Φίλιππον ἀποδεικνύντα περὶ τοῦ σχήματος τῆς σελήνης καὶ Ἀρχιμήδην ἀνευρόντα τῇ γωνίᾳ τὴν διάμετρον τοῦ ἡλίου τηλικοῦτον τοῦ μεγίστου κύκλου μέρος οὖσαν, ἡλίκον ἡ γωνία τῶν τεσσάρων ὀρθῶν, καὶ Ἀπολλώνιον καὶ Ἀρίσταρχον ἑτέρων τοιούτων εὑρετὰς γενομένους, ὧν νῦν ἡ θέα καὶ κατανόησις ἡδονάς τε μεγάλας καὶ φρόνημα θαυμάσιον ἐμποιεῖ τοῖς μανθάνουσιν;
    
    
15. Plutarchus Biogr., Phil., Non posse suaviter vivi secundum Epicurum (1086c-1107c) Stephanus page 1094, section B, line 8
    
    σχῆμα τοῦ ἄστρου καὶ τὸ μέγεθος καὶ τὸ εἶδος ὡς ὁ Φαέθων καταφλεγῆναι, καὶ Πυθαγόρας ἐπὶ τῷ διαγράμματι βοῦν ἔθυσεν, ὥς φησιν Ἀπολλόδωρος· ’ἡνίκα Πυθαγόρης τὸ περικλεὲς εὕρετο γράμμα, κεῖνος ἐφ' ᾧ λαμπρὴν ἤγαγε βουθυσίην,’ εἴτε περὶ τῆς ὑποτεινούσης ὡς ἴσον δύναται ταῖς περιεχούσαις τὴν ὀρθήν, εἴτε [πρόβλημα] περὶ τοῦ χωρίου τῆς παραβολῆς. Ἀρχιμήδην δὲ βίᾳ τῶν διαγραμμάτων ἀποσπῶντες ὑπήλειφον οἱ θεράποντες· ὁ δ' ἐπὶ τῆς κοιλίας ἔγραφε τὰ σχήματα τῇ στλεγγίδι, καὶ λουόμενος ὥς φασιν ἐκ τῆς ὑπερχύσεως ἐννοήσας τὴν τοῦ στεφάνου μέτρησιν οἷον ἔκ τινος κατοχῆς ἢ ἐπιπνοίας ἐξήλατο βοῶν ’εὕρηκα’, καὶ τοῦτο πολλάκις φθεγγόμενος ἐβάδιζεν.
    
    
16. Plutarchus Biogr., Phil., Non posse suaviter vivi secundum Epicurum (1086c-1107c) Stephanus page 1093, section D, line 10
    
    καὶ ἁρμονικῆς δριμὺ καὶ ποικίλον ἔχουσαι τὸ δέλεαρ οὐθὲν τῶν ἀγωγίμων ἀποδέουσιν, ἕλκουσαι καθάπερ ἴυγξι τοῖς διαγράμμασιν· ὧν ὁ γευσάμενος, ἄνπερ ἔμπειρος ᾖ, τὰ Σοφοκλέους περίεισιν ᾄδων (fr. 224) ’μουσομανεῖ † δὲ λάφθην δαν καὶ τὸ ποτιδειραν, εὔχομαι δ' ἔκ τε λύρας ἔκ τε νόμων, οὓς Θαμύρας περίαλλα μουσοποιεῖ’ καὶ νὴ Δί' Εὔδοξος καὶ Ἀρίσταρχος καὶ Ἀρχιμήδης.
    
    
17. Plutarchus Biogr., Phil., Non posse suaviter vivi secundum Epicurum (1086c-1107c) Stephanus page 1094, section C, line 9
    
    Εὐδόξῳ δὲ καὶ Ἀρχιμήδει καὶ Ἱππάρχῳ συνενθουσιῶμεν, καὶ Πλάτωνι πειθόμεθα περὶ τῶν μαθημάτων, ὡς ἀμελούμενα δι' ἄγνοιαν καὶ ἀπειρίαν ‘ὅμως βίᾳ ὑπὸ χάριτος αὐξάνεται’ (Rep. 528c).
    
    
18. Athenaeus Soph., Deipnosophistae (0008: 001) “Athenaei Naucratitae deipnosophistarum libri xv, 3 vols.”, Ed. Kaibel, G. Leipzig: Teubner, 1–2:1887; 3:1890, Repr. 1–2:1965; 3:1966. Book 14, Kaibel paragraph 34, line 30
    
    Πολύβιος δ' ἐν τῇ ὀγδόῃ τῶν Ἱστοριῶν (c. 8, 6) ‘Μάρκελλος, φησί, δυσχρηστούμενος ἐν τῇ Συρακουσῶν πολιορκίᾳ ὑπὸ τῶν Ἀρχιμήδους κατασκευασμάτων ἔλεγεν ταῖς μὲν ναυσὶν αὑτοῦ κυαθίζειν ἐκ θαλάσσης Ἀρχιμήδην, τὰς δὲ σαμβύκας ῥαπιζομένας ὥσπερ ἐκ πότου μετ' αἰσχύνης ἐκπεπτωκέναι.
    
    
19. Athenaeus Soph., Deipnosophistae Book 5, Kaibel paragraph 40, line 2
    
    περὶ δὲ τῆς ὑπὸ Ἱέρωνος τοῦ Συρακοσίου κατασκευασθείσης νεώς, ἧς καὶ Ἀρχιμήδης ἦν ὁ γεωμέτρης ἐπόπτης, οὐκ ἄξιον εἶναι κρίνω σιωπῆσαι, σύγγραμμα ἐκδόντος Μοσχίωνός τινος, ᾧ οὐ παρέργως ἐνέτυχον ὑπογυίως.
    
    
20. Athenaeus Soph., Deipnosophistae Book 5, Kaibel paragraph 40, line 37
    
    ὡς δὲ περὶ τὸν καθελκυσμὸν αὐτοῦ τὸν εἰς τὴν θάλασσαν πολλὴ ζήτησις ἦν, Ἀρχιμήδης ὁ μηχανικὸς μόνος αὐτὸ κατήγαγε δι' ὀλίγων σωμάτων.
    
    
21. Athenaeus Soph., Deipnosophistae Book 5, Kaibel paragraph 40, line 40
    
    πρῶτος δ' Ἀρχιμήδης εὗρε τὴν τῆς ἕλικος κατασκευήν.
    
    
22. Athenaeus Soph., Deipnosophistae Book 5, Kaibel paragraph 43, line 14
    
    τοῦτο δὲ τὸ μηχάνημα κατεσκεύασεν Ἀρχιμήδης.
    
    
23. Athenaeus Soph., Deipnosophistae Book 5, Kaibel paragraph 43, line 38
    
    ἡ δὲ ἀντλία καίπερ βάθος ὑπερβάλλον ἔχουσα δι' ἑνὸς ἀνδρὸς ἐξηντλεῖτο διὰ κοχλίου, Ἀρχιμήδους ἐξευρόντος.
    
    
24. Athenaeus Soph., Deipnosophistae (epitome) (0008: 003) “Athenaei dipnosophistarum epitome, vols. 2.1–2.2”, Ed. Peppink, S.P. Leiden: Brill, 2.1:1937; 2.2:1939. Volume 2,1, page 75, line 35
    
    ὅτι Διοκλείδης μὲν ὁ Ἀβδηρίτης θαυμάζεται ἐπὶ τῇ πρὸς τὴν Ῥοδίων πόλιν ὑπὸ Δημητρίου προσαχθείσῃ τοῖς τείχεσιν ἑλεπόλει, Τίμαιος δὲ ἐπὶ τῇ πυρᾷ τῇ κατασκευασθείσῃ [Διονύσῳ τῷ] Σικελίας τυράννῳ, Ἱερώνυμος δὲ ἐπὶ τῇ κατασκευῇ τῆς ἁρμαμάξης ᾗ κατεκομίσθη τὸ Ἀλεξάνδρου σῶμα, Πολύκλειτος δὲ ἐπὶ τῷ λυχνίῳ τῷ κατασκευασθέντι τῷ Πέρσῃ, Ἱέρων δὲ ὁ Συρακούσιος βασιλεὺς ἐσπουδάκει μὲν καὶ περὶ ἱερῶν καὶ γυμνασίων κατασκευὰς, ἦν δὲ καὶ περὶ ναυπηγίας φιλότιμος, φησὶ Μοσχίων, πλοῖα σιτηγὰ κατασκευαζόμενος, ὧν ἑνός, φησί, τῆς κατασκευῆς μνησθήσομαι, οὗ καὶ Ἀρχιμήδης ἦν ὁ γεωμέτρης ἐπόπτης.
    
    
25. Athenaeus Soph., Deipnosophistae (epitome) Volume 2,1, page 76, line 11
    
    ὡς δὲ πολλὴ περὶ τούτου ζήτησις ἦν, Ἀρχιμήδης μόνος αὐτὸ κατήγαγε δι' ὀλίγων σωμάτων.
    
    
26. Athenaeus Soph., Deipnosophistae (epitome) Volume 2,1, page 77, line 12
    
    τοῦτο δὲ τὸ μηχάνημα κατεσκευάσεν Ἀρχιμήδης.
    
    
27. Athenaeus Soph., Deipnosophistae (epitome) Volume 2,1, page 77, line 27
    
    ἡ δὲ ἀντλία καίπερ βάθος ὑπερβάλλον ἔχουσα δι' ἑνὸς ἐξηντλεῖτο διὰ κοχλίου, Ἀρχιμήδους ἐξευρόντος.
    
    
28. Galenus Med., De temperamentis libri iii (0057: 009) “Galeni de temperamentis libri iii”, Ed. Helmreich, G. Leipzig: Teubner, 1904, Repr. 1969. Kühn volume 1, page 657, line 17
    
    οὕτω δέ πως, οἶμαι, καὶ τὸν Ἀρχιμήδην φασὶ διὰ τῶν πυρείων ἐμπρῆσαι τὰς τῶν πολεμίων τριήρεις.
    
    
29. Galenus Med., De usu partium (0057: 017) “Galeni de usu partium libri xvii”, Ed. Helmreich, G. Leipzig: Teubner, 1:1907; 2:1909, Repr. 1968. Kühn volume 4, page 359, line 13
    
    ἰδεῖν δ' ἔστι νοῦ φύσιν καὶ κατ' αὐτοὺς τοὺς ἀνθρώπους ἐννοήσαντα Πλάτωνα καὶ Ἀριστοτέλη καὶ Ἵππαρχον καὶ Ἀρχιμήδην καὶ πολλοὺς ἄλλους τοιούτους.
    
    
30. Galenus Med., De methodo medendi libri xiv (0057: 066) “Claudii Galeni opera omnia, vol. 10”, Ed. Kühn, C.G. Leipzig: Knobloch, 1825, Repr. 1965. Volume 10, page 12, line 10
    
    εἰ γὰρ δὴ γεωμετρῶν ἔτι καὶ γραμματικῶν καὶ μουσικῶν ὀνομαστὶ μνημονεύοιμι μετὰ τὰς τηλικαύτας νίκας, ὑβρίζειν δόξω τὸν ἄνθρωπον· ὅπου γὰρ Λυκοῦργος καὶ Σόλων καὶ Πλάτων καὶ Σωκράτης καὶ Πυθαγόρας ἐνικήθησαν, ἦπου ἄρα καλὸν ἔτι μνημονεύειν Ἱππάρχου καὶ Ἀρχιμήδους καὶ Ἀριστοξένου καὶ Ἀριστάρχου καί τινων ἑτέρων τοιούτων οὐδενὸς ἀξίων, ὡς ἂν εἴποι Θεσσαλός;
    
    
31. Galenus Med., In Hippocratis librum de articulis et Galeni in eum commentarii iv (0057: 095) “Claudii Galeni opera omnia, vol. 18.1”, Ed. Kühn, C.G. Leipzig: Knobloch, 1829, Repr. 1965. Volume 18a, page 747, line 9
    
    εἰ δ' ἄρα τις θέλει καὶ ἄλλοις χρῆσθαι, πρὸς μὲν τὰς ὁδοιπορίας τὸ πολύσπαστον καλούμενον ἐπιτήδειον, Ἀρχιμήδους δ' αὐτό φασιν εὕρημα εἶναι, πρὸς δὲ τὰς ἐν πόλει χρείας στάσιμον μὲν ἄξιον λόγου τὸ τοῦ τέκτονος καλούμενόν ἐστιν ἢ τὸ τοῦ Ἀνδρέου, ἐφεδράνον δὲ τουτὶ τὸ Ἱπποκράτους βάθρον, ὅ τινες τῶν νεωτέρων ἰατρῶν, ἐπειδὴ ἐσκευάκασι ποικιλώτερον, ὥσπερ καὶ τὴν μηχανικὴν ἄμβην.
    
    
32. Diodorus Siculus Hist., Bibliotheca historica (lib. 1–20) (0060: 001) “Diodori bibliotheca historica, 5 vols., 3rd edn.”, Ed. Vogel, F., Fischer, K.T. (post I. Bekker and L. Dindorf) Leipzig: Teubner, 1:1888; 2:1890; 3:1893; 4–5:1906, Repr. 1964. Book 1, chapter 34, section 2, line 8
    
    ποταμόχωστος γὰρ οὖσα καὶ κατάῤῥυτος πολλοὺς καὶ παντοδαποὺς ἐκφέρει καρπούς, τοῦ μὲν ποταμοῦ διὰ τὴν κατ' ἔτος ἀνάβασιν νεαρὰν ἰλὺν ἀεὶ καταχέοντος, τῶν δ' ἀνθρώπων ῥᾳδίως ἅπασαν ἀρδευόντων διά τινος μηχανῆς, ἣν ἐπενόησε μὲν Ἀρχιμήδης ὁ Συρακόσιος, ὀνομάζεται δὲ ἀπὸ τοῦ σχήματος κοχλίας.
    
    
33. Diodorus Siculus Hist., Bibliotheca historica (lib. 1-20) Book 5, chapter 37, section 3, line 9
    
    ταῖς γὰρ ἀδιαψεύστοις τοῦ κέρδους προσδοκίαις πιεζόμενοι πρὸς τὸ τέλος ἄγουσι τὰς ἰδίας ἐπιβολάς, καὶ τὸ πάντων παραδοξότατον, ἀπαρύτουσι τὰς ῥύσεις τῶν ὑδάτων τοῖς Αἰγυπτιακοῖς λεγομένοις κοχλίαις, οὓς Ἀρχιμήδης ὁ Συρακόσιος εὗρεν, ὅτε παρέβαλεν εἰς Αἴγυπτον· διὰ δὲ τούτων συνεχῶς ἐκ διαδοχῆς παραδιδόντες μέχρι τοῦ στομίου, τὸν τῶν μετάλλων τόπον ἀναξηραίνουσι καὶ κατασκευάζουσιν εὔθετον πρὸς τὴν τῆς ἐργασίας πραγματείαν.
    
    
34. Diodorus Siculus Hist., Bibliotheca historica (lib. 1-20) Book 5, chapter 37, section 4, line 9
    
    θαυμάσαι δ' ἄν τις εἰκότως τοῦ τεχνίτου τὴν ἐπίνοιαν οὐ μόνον ἐν τούτοις, ἀλλὰ καὶ ἐν ἄλλοις πολλοῖς καὶ μείζοσι, διαβεβοημένοις κατὰ πᾶσαν τὴν οἰκουμένην, περὶ ὧν τὰ κατὰ μέρος ὅταν ἐπὶ τὴν Ἀρχιμήδους ἡλικίαν ἔλθωμεν ἀκριβῶς διέξιμεν.
    
    
35. Diodorus Siculus Hist., Bibliotheca historica (lib. 21–40) (0060: 003) “Diodorus of Sicily, vols. 11–12”, Ed. Walton, F.R. Cambridge, Mass.: Harvard University Press, 11:1957; 12:1967, Repr. 11:1968. Book 26, chapter 18, section 1, line 7
    
    (Diod. 5. 37. 4.) Ὁ Ἀρχιμήδης ὁ σοφὸς μηχανητὴς ἐκεῖνος τῷ γένει Συρακούσιος, ἦν γέρων γεωμέτρης, χρόνους τε ἑβδομήκοντα καὶ πέντε παρελαύνων.
    
    
36. Diodorus Siculus Hist., Bibliotheca historica (lib. 21-40) Book 26, chapter 18, section 1, line 5
    
    (Const. Exc. 4, p. 355.) [Θαυμάσαι δ' ἄν τις εἰκότως τοῦ τεχνίτου τὴν ἐπίνοιαν οὐ μόνον ἐν τούτοις, ἀλλὰ καὶ ἐν ἄλλοις πολλοῖς καὶ μείζοσι διαβεβοημένοις κατὰ πᾶσαν τὴν οἰκουμένην, περὶ ὧν τὰ κατὰ μέρος ὅταν ἐπὶ τὴν Ἀρχιμήδους ἡλικίαν ἔλθωμεν ἀκριβῶς διέξιμεν.
    
    
37. Lucianus Soph., Hippias (0062: 002) “Lucian, vol. 1”, Ed. Harmon, A.M. Cambridge, Mass.: Harvard University Press, 1913, Repr. 1961. Section 2, line 9
    
    τοιοῦτον ἀκούομεν τὸν Ἀρχιμήδη γενέσθαι καὶ τὸν Κνίδιον Σώστρατον, τὸν μὲν Πτολεμαίῳ χειρωσάμενον τὴν Μέμφιν ἄνευ πολιορκίας ἀποστροφῇ καὶ διαιρέσει τοῦ ποταμοῦ, τὸν δὲ τὰς τῶν πολεμίων τριήρεις καταφλέξαντα τῇ τέχνῃ.
    
    
38. Agatharchides Geogr., Fragmenta (0067: 004)“FGrH #86”.Volume-Jacoby
    
    ποταμόχωστος γὰρ οὖσα καὶ κατάῤῥυτος πολλοὺς καὶ παντοδαποὺς ἐκφέρει καρπούς, τοῦ μὲν ποταμοῦ διὰ τὴν κατ' ἔτος ἀνάβασιν νεαρὰν ἰλὺν ἀεὶ καταχέοντος, τῶν δ' ἀνθρώπων ῥαιδίως ἅπασαν ἀρδευόντων διά τινος μηχανῆς, ἣν ἐπενόησε μὲν Ἀρχιμήδης ὁ Συρακόσιος, ὀνομάζεται δὲ ἀπὸ τοῦ σχήματος κοχλίας.
    
    
39. Aelius Herodianus et Pseudo-Herodianus Gramm., Rhet., Partitiones (= Ἐπιμερισμοί) [Sp.?] (e codd. Paris. 2543 + 2570) (0087: 036) “Herodiani partitiones”, Ed. Boissonade, J.F. London, 1819, Repr. 1963. Page 183, line 1
    
    Πλὴν τῶν παρὰ τὸ μῆδος, ὃ δηλοῖ τὴν βουλήν· ταῦτα γὰρ διὰ τοῦ η γράφονται· οἷον· Ἀρχιμήδης· Παλαμήδης· Διομήδης· Γαννυμήδης· Νικομήδης· καὶ τὰ ὅμοια.
    
    
40. Aristoxenus Mus., Fragmenta (0088: 006) “Aristoxenos”, Ed. Wehrli, F. Basel: Schwabe, 1967; Die Schule des Aristoteles, vol. 2, 2nd edn.. Fragment 69e, line 3
    
    
41. Alexander Aphrod. Comment. in Aristot. Topica 105 a 34:
    
    θείη γὰρ ἄν τις ὡς ἔνδοξον τὸ ὑπὸ Ἱπποκράτους λεγόμενον ἐν ἰατρικῇ καὶ τὸ ὑπὸ Ἀρχιμήδους ἐν γεωμετρίᾳ καὶ τὸ ὑπὸ Ἀριστοξένου ἐν μουσικῇ.
    
    
42. Strabo Geogr., Geographica (0099: 001) “Strabonis geographica, 3 vols.”, Ed. Meineke, A. Leipzig: Teubner, 1877, Repr. 1969. Book 1, chapter 3, section 12, line 29
    
    καὶ μάλιστα κατὰ τὰς σφαιροποιούσας ὑποθέσεις τὰ τέτταρα σώματα, ἃ δὴ καὶ στοιχεῖα φαμέν· οὐ γὰρ ὥσπερ ἡ γῆ κατὰ ἕξιν ἐσχημάτισται στερεὰ οὖσα, ὥστε καὶ κοιλάδας ἔχειν συμμενούσας καὶ ἀναστήματα, οὕτω καὶ τὸ ὕδωρ, ἀλλ' αὐτῇ τῇ κατὰ τὸ βάρος ῥοπῇ τὴν ὄχησιν ἐπὶ τῆς γῆς ποιεῖται καὶ τοιαύτην λαμβάνει τὴν ἐπιφάνειαν οἵαν ὁ Ἀρχιμήδης φησιν.
    
    
43. Strabo Geogr., Geographica Book 1, chapter 3, section 11, line 2
    
    Ὁ δ' οὕτως ἡδύς ἐστιν ὥστε καὶ μαθηματικὸς ὢν οὐδὲ τὴν Ἀρχιμήδους βεβαιοῖ δόξαν, ὅτι φησὶν ἐκεῖνος ἐν τοῖς περὶ τῶν ὀχουμένων, παντὸς ὑγροῦ καθεστηκότος καὶ μένοντος τὴν ἐπιφάνειαν σφαιρικὴν εἶναι, σφαίρας ταὐτὸ κέντρον ἐχούσης τῇ γῇ· ταύτην γὰρ τὴν δόξαν ἀποδέχονται πάντες οἱ μαθημάτων πως ἁψάμενοι.
    
    
44. Claudius Ptolemaeus Math., Syntaxis mathematica (0363: 001) “Claudii Ptolemaei opera quae exstant omnia, vols. 1.1–1.2”, Ed. Heiberg, J.L. Leipzig: Teubner, 1.1:1898; 1.2:1903. Volume 1,1, page 195, line 2
    
    ἀλλ' ἐπὶ μὲν τῶν τροπῶν οὐκ ἀπελπίζω καὶ ἡμᾶς καὶ τὸν Ἀρχιμήδη καὶ ἐν τῇ τηρήσει καὶ ἐν τῷ συλλογισμῷ διαμαρτάνειν καὶ ἕως τετάρτου μέρους ἡμέρας.
    
    
45. Claudius Ptolemaeus Math., Syntaxis mathematica Volume 1,1, page 513, line 4
    
    ἐπελογισάμεθα δὲ καὶ τὰς τοιαύτας ἐπιβολὰς ἐπὶ μόνων τῶν γινομένων μεγεθῶν κατὰ τὸ μέσον ἀπόστημα τῆς σελήνης οὔσης· ὁ γὰρ αὐτὸς ἔγγιστα λόγος ἐπί γε τῆς τηλικαύτης τῶν διαμέτρων αὐξομειώσεως συνίσταται καὶ ὡς τοῦ λόγου τῶν περιμέτρων πρὸς τὰς διαμέτρους ὄντος, ὃν ἔχει τὰ [γ] [η] [λ] πρὸς τὸ ἕν· οὗτος γὰρ ὁ λόγος μεταξύ ἐστιν ἔγγιστα τοῦ τε τριπλασίου πρὸς τῷ ζ΄ μέρει καὶ τοῦ τριπλασίου πρὸς τοῖς δέκα ἑβδομηκοστομόνοις, οἷς ὁ Ἀρχιμήδης κατὰ τὸ ἁπλούστερον συνεχρήσατο.
    
    
46. Cassius Dio Hist., Historiae Romanae (versio 1 in volumine 1) (0385: 002) “Cassii Dionis Cocceiani historiarum Romanarum quae supersunt, vol. 1”, Ed. Boissevain, U.P. Berlin: Weidmann, 1895, Repr. 1955. Page 235, line 5
    
    ἐγκρατεῖς δὲ τούτων οἱ Ῥωμαῖοι γενόμενοι ἄλλους τε πολλοὺς καὶ τὸν Ἀρχιμήδην ἀπέκτειναν.
    
    
47. Cassius Dio Hist., Historiae Romanae (versio 1 in volumine 1) Page 233, line 1
    
    καὶ δι' ἐλαχίστου ἂν αὐτὰς ἐχειρώσατο καὶ κατὰ γῆν καὶ κατὰ θάλασσαν ἅμα προσβαλὼν τῷ [Zonaras 9, 4, 7 – 9 (2, 210, 1 sqq. B. = 2, 262, 27 sqq. D.)] τείχει, εἰ μὴ ὁ Ἀρχιμήδης μηχαναῖς ἐπὶ πλεῖστον αὐτοὺς ἐποίησεν ἀντισχεῖν.
    
    
48. Cassius Dio Hist., Historiae Romanae (versio 1 in volumine 1) Page 233, line 25
    
    ἀπογνοὺς οὖν ὁ Μάρκελλος τὴν πόλιν αἱρήσειν διὰ τὸ τοῦ Ἀρχιμήδους εὐμήχανον, λιμῷ αὐτοὺς κατασχεῖν ἐκ προσεδρείας διεμελέτησε.
    
    
49. Pausanias Perieg., Graeciae descriptio (0525: 001) “Pausaniae Graeciae descriptio, 3 vols.”, Ed. Spiro, F. Leipzig: Teubner, 1903, Repr. 1:1967. Book 4, chapter 24, section 5, line 5
    
    Μεσσηνίων δὲ τοὺς ἐγκαταληφθέντας ἐν τῇ γῇ, συντελοῦντας κατὰ ἀνάγκην ἐς τοὺς εἵλωτας, ἐπέλαβεν ἀπὸ Λακεδαιμονίων ὕστερον ἀποστῆναι κατὰ τὴν ἐνάτην ὀλυμπιάδα καὶ ἑβδομηκοστήν, ἣν Κορίνθιος ἐνίκα Ξενοφῶν, Ἀρχιμήδους Ἀθήνῃσιν ἄρχοντος· ἀπέστησαν δὲ καιρὸν τοιόνδε εὑρόντες.
    
    
50. Polybius Hist., Historiae (0543: 001) “Polybii historiae, vols. 1–4”, Ed. Büttner–Wobst, T. Leipzig: Teubner, 1:1905; 2:1889; 3:1893; 4:1904, Repr. 1:1962; 2–3:1965; 4:1967. Book 8, chapter 6, section 6, line 3
    
    Μάρκος δὲ δυσχρηστούμενος ἐπὶ τοῖς ἀπαντωμένοις ὑπ' Ἀρχιμήδους, καὶ θεωρῶν μετὰ βλάβης καὶ χλευασμοῦ τοὺς ἔνδον ἀποτριβομένους αὑτοῦ τὰς ἐπιβολάς, δυσχερῶς μὲν ἔφερε τὸ συμβαῖνον, ὅμως δ' ἐπισκώπτων τὰς αὑτοῦ πράξεις ἔφη ταῖς μὲν ναυσὶν αὐτοῦ κυαθίζειν ἐκ θαλάττης Ἀρχιμήδη, τὰς δὲ σαμβύκας ῥαπιζομένας ὥσπερ ἐκσπόνδους μετ' αἰσχύνης ἐκπεπτωκέναι.
    
    
51. Polybius Hist., Historiae Book 8, chapter 7, section 10, line 1
    
    ἐκεῖνοι γοῦν τηλικαύτας δυνάμεις ἔχοντες καὶ κατὰ γῆν καὶ κατὰ θάλατταν, εἰ μὲν ἀφέλοι τις πρεσβύτην ἕνα Συρακοσίων, παραχρῆμα τῆς πόλεως κυριεύσειν ἤλπιζον, τούτου δὲ συμπαρόντος οὐκ ἐθάῤῥουν οὐδ' ἐπιβαλέσθαι κατά γε τοῦτον τὸν τρόπον, καθ᾿ ὃν ἀμύνασθαι δυνατὸς ἦν Ἀρχιμήδης.
    
    
52. Polybius Hist., Historiae Book 8, chapter 3, section 3, line 5
    
    ἑτοιμασάμενοι δὲ γέῤῥα καὶ βέλη καὶ τἄλλα τὰ πρὸς τὴν πολιορκίαν, ἐν ἡμέραις πέντε διὰ τὴν πολυχειρίαν ἤλπισαν καταταχήσειν τῇ παρασκευῇ τοὺς ὑπεναντίους, οὐ λογισάμενοι τὴν Ἀρχιμήδους δύναμιν, οὐδὲ προϊδόμενοι διότι μία ψυχὴ τῆς ἁπάσης ἐστὶ πολυχειρίας ἐν ἐνίοις καιροῖς ἀνυστικωτέρα.
    
    
53. Polybius Hist., Historiae Book 8, chapter 7, section 3, line 1
    
    ἔτι μὲν γὰρ ὄντες ἐν ἀποστήματι τοῖς τε πετροβόλοις καὶ καταπέλταις τυπτόμενοι διεφθείροντο, διὰ τὸ θαυμάσιον εἶναι τὴν τῶν βελῶν κατασκευὴν καὶ κατὰ τὸ πλῆθος καὶ κατὰ τὴν ἐνέργειαν, ὡς ἂν Ἱέρωνος μὲν χορηγοῦ γεγονότος, ἀρχιτέκτονος δὲ καὶ δημιουργοῦ τῶν ἐπινοημάτων Ἀρχιμήδους.
    
    
54. Sextus Empiricus Phil., Adversus mathematicos (0544: 002) “Sexti Empirici opera, vols. 2 and 3 (2nd edn.)”, Ed. Mutschmann, H., Mau, J. Leipzig: Teubner, 2:1914; 3:1961. Book 1, section 301, line 9
    
    ποῦ γάρ τις δύναται τῶν ὠφρυωμένων γραμματικῶν Ἡράκλειτον συνεῖναι καὶ Πλάτωνι παρακολουθῆσαι λέγοντι ’τῆς ἀμερίστου καὶ ἀεὶ κατὰ ταὐτὰ ἐχούσης οὐσίας καὶ τῆς περὶ τὰ σώματα μεριστῆς τρίτον ἐξ ἀμφοῖν συνεκεράσατο οὐσίας εἶδος, τῆς τε ταὐτοῦ φύσεως καὶ τῆς θατέρου’ καὶ ἤδη τὰ ἑξῆς, – περὶ τὴν λέξιν πάντες οἱ Πλάτωνος ἐξηγηταὶ ἐσίγησαν – ἢ ποῦ τοῖς Χρυσίππου διαλεκτικοῖς θεωρήμασιν ἢ Ἀρχιμήδους τε καὶ Εὐδόξου μαθηματικοῖς ἐπιβάλλειν ἰσχύσει;
    
    
55. Sextus Empiricus Phil., Adversus mathematicos Book 9, section 115, line 3
    
    τὴν γοῦν Ἀρχιμήδειον σφαῖραν θεωροῦντες σφόδρα ἐκπληττόμεθα, ἐν ᾗ ἥλιός τε καὶ σελήνη κινεῖται καὶ τὰ λοιπὰ τῶν ἀστέρων, οὐ μὰ Δία ἐπὶ τοῖς ξύλοις οὐδ' ἐπὶ τῇ κινήσει τούτων τεθηπότες, ἀλλ' ἐπὶ τῷ τεχνίτῃ καὶ ταῖς κινούσαις αἰτίαις.
    
    
56. Heron Mech., Pneumatica (0559: 001) “Heronis Alexandrini opera quae supersunt omnia, vol. 1”, Ed. Schmidt, W. Leipzig: Teubner, 1899. Book 1, chapter proem, line 291
    
    ἀπεδείχθη γὰρ Ἀρχιμήδει ἐν τοῖς Ὀχουμένοις, ὅτι τὰ ἰσοβαρῆ τῷ ὑγρῷ σώματα ἀφεθέντα εἰς τὸ ὑγρὸν οὔτε ὑπερέξει τοῦ ὑγροῦ οὔτε καταδύσεται, οὐδ' ἄρα θλίψει τὰ ὑποκείμενα.
    
    
57. Heron Mech., Mechanicorum fragmenta (0559: 004) “Heronis Alexandrini opera quae supersunt omnia, vol. 2.1”, Ed. Nix, L., Schmidt, W. Leipzig: Teubner, 1900. Book 2, fragment 35, line 3
    
    Τὸ μὲν οὖν μάλιστα συνέχον τὴν κεντροβαρικὴν πραγματείαν τοῦτ' ἂν εἴη, μάθοις δ' ἂν τὰ μὲν στοιχειώδη ὄντα διὰ ταύτης δεικνύμενα τοῖς Ἀρχιμήδους Περὶ ἰσοῤῥοπιῶν ἐντυχὼν καὶ τοῖς Ἥρωνος Μηχανικοῖς, ὅσα δὲ μὴ γνώριμα τοῖς πολλοῖς γράψομεν ἐφεξῆς, οἷον τὰ τοιαῦτα.
    
    
58. Heron Mech., Metrica (0559: 006) “Heronis Alexandrini opera quae supersunt omnia, vol. 3”, Ed. Schöne, H. Leipzig: Teubner, 1903. Book 2, chapter 20, line 4
    
    Τῶν δὴ ἐν τάξει στερεῶν σωμάτων μετρηθέντων εὔλογον ὑπολαμβάνομεν καὶ τὰ ἄτακτα, οἷον ῥιζώδη ἢ πετρώδη, παριστορῆσαι τῇ μετρήσει, ὡς ἔνιοι ἱστοροῦσι τὸν Ἀρχιμήδη ἐπινενοηκέναι πρὸς τὰ τοιαῦτα μέθοδον.
    
    
59. Heron Mech., Metrica Book 2, chapter proem, line 7
    
    ΗΡΩΝΟΣ ΜΕΤΡΙΚΩΝ Β ΠΡΟΟΙΜΙΟΝ Μετὰ τὴν τῶν ἐπιφανειῶν μέτρησιν εὐθυγράμμων τε καὶ μὴ κατὰ τὸ ἀκόλουθον ἐπὶ τὰ στερεὰ σώματα χωρητέον, ὧν καὶ τὰς ἐπιφανείας ἐν τῷ πρὸ τούτου βιβλίῳ ἐμετρήσαμεν ἐπιπέδους τε καὶ σφαιρικάς, ἔτι τε κωνικὰς καὶ κυλινδρικάς, πρὸς δὲ τούτοις ἀτάκτους, ὧν τὰς ἐπινοίας ὥσπερ παραδόξους οὔσας τινὲς εἰς Ἀρχιμήδην ἀναφέρουσιν κατὰ διαδοχὴν ἱστοροῦντες.
    
    
60. Heron Mech., Metrica Book 1, chapter 26, line 1
    
    Ὅσα δὲ τῶν πολυγώνων σχημάτων οὔκ ἐστιν ἰσόπλευρα καὶ ἰσογώνια, ταῦτα εἰς τρίγωνα καταδιαιρούμενα μετρεῖται· τὰ δὲ περιφερῆ τῶν ἐπιπέδων σχημάτων καὶ καθόλου τῶν ἐπιφανειῶν ὅσαι δύνανται μετρεῖσθαι, ἑξῆς κατὰ τὸ ἀκόλουθον ἐκθησόμεθα. Ἀρχιμήδης μὲν οὖν ἐν τῇ τοῦ κύκλου μετρήσει δείκνυσιν, ὅτι ια τετράγωνα τὰ ἀπὸ τῆς διαμέτρου τοῦ κύκλου ἴσα γίγνεται ὡς ἔγγιστα ιδ κύκλοις· ὥστε ἐὰν δοθῇ ἡ διάμετρος τοῦ κύκλου εἰ τύχοι μονάδων ι, δεήσει τὰ ι ἐφ' ἑαυτὰ ποιῆσαι· γίγνονται ρ· ταῦτα ἐπὶ τὰ ια· γίγνεται ͵αρ· ὧν τὸ ιδ΄.
    
    
61. Heron Mech., Metrica Book 1, chapter 26, line 8
    
    ὁ δὲ αὐτὸς Ἀρχιμήδης δείκνυσιν ἐν τῷ περὶ πλινθίδων καὶ κυλίνδρων, ὅτι παντὸς κύκλου ἡ περίμετρος πρὸς τὴν διάμετρον μείζονα μὲν λόγον ἔχει [ἢ ὃν ἔχει] μ[κα] ͵αωοε πρὸς μ[ϛ] ͵ζυμα, ἐλάσσονα δὲ ἢ ὃν ἔχειν μ[ιθ] ͵ζωπη πρὸς μ[ϛ] ͵βτνα· ἀλλ' ἐπεὶ οὗτοι οἱ ἀριθμοὶ πρὸς τὰς μετρήσεις οὐκ εὐθετοῦσι, καταβιβάζονται εἰς ἐλαχίστους ἀριθμούς, ὡς τὸν κβ πρὸς τὰ ζ. ὥστε ἐὰν δοθῇ ἡ διάμετρος τοῦ κύκλου εἰ τύχοι μονάδων ιδ καὶ βούληταί τις τὴν περίμετρον εὑρεῖν, δεῖ ποιῆσαι τὰ ιδ ἐπὶ τὰ κβ καὶ τούτων λαβεῖν τὸ ἕβδομον
    
    
62. Heron Mech., Metrica Book 1, chapter 26, line 23
    
    δείκνυσι δὲ ὁ αὐτὸς Ἀρχιμήδης ἐν τῇ τοῦ κύκλου μετρήσει ὅτι τὸ ὑπὸ τῆς περιφερείας τοῦ κύκλου καὶ τῆς ἐκ τοῦ κέντρου διπλάσιόν ἐστι τοῦ κύκλου· ὥστε ἐὰν δοθῇ ἡ περίμετρος μονάδων μδ, λαβόντες τῆς διαμέτρου τὸ ἥμισυ· εἰσὶ δὲ μονάδες ζ· πολλαπλασιάσομεν ἐπὶ τὰ μδ· καὶ τῶν γενομένων τὸ ἥμισυ λαβόντες· εἰσὶ δὲ μονάδες ρνδ· τοσούτου ἀποφα[ι]νούμεθα τὸ ἐμβαδὸν τοῦ κύκλου.
    
    
63. Heron Mech., Metrica Book 1, chapter 32, line 58
    
    ἔδειξε γὰρ Ἀρχιμήδης ἐν τῷ ἐφοδικῷ, ὅτι πᾶν τμῆμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομῆς, τουτέστι παραβολῆς, ἐπίτριτόν ἐστι τριγώνου τοῦ βάσιν μὲν ἔχοντος αὐτῷ τὴν αὐτὴν καὶ ὕψος δὲ ἴσον.
    
    
64. Heron Mech., Metrica Book 1, chapter 35, line 10
    
    τῷ ἄρα ἐμβαδῷ τοῦ ΑΒΓ τριγώνου ἴσον ἐστὶ τὸ ἥμισυ τοῦ ὑπὸ ΑΓ ΒΔ, τουτέστι μονάδων λ. ἀπέδειξεν δὲ Ἀρχιμήδης ἐν τῷ ἐφοδικῷ, ὡς προείρηται, ὅτι πᾶν τμῆμα περιεχόμενον ὑπό τε εὐθείας καὶ ὀρθογωνίου κώνου τομῆς, τουτέστι παραβολῆς, ἐπίτριτόν ἐστι τριγώνου τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῷ καὶ ὕψος ἴσον, τουτέστι τοῦ ΑΒΓ τριγώνου.
    
    
65. Heron Mech., Metrica Book 1, chapter 38, line 2
    
    Τὴν δὲ ἐπιφάνειαν τῆς σφαίρας ὁ αὐτὸς ἐμέτρησεν Ἀρχιμήδης ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου ἀποδείξας τετραπλασίονα οὖσαν τοῦ μεγίστου κύκλου τῶν ἐν τῇ σφαίρᾳ· ὥστε ἐὰν δοθῇ ἡ διάμετρος τῆς σφαίρας μονάδων ιδ, δεῖ εὑρεῖν κύκλον τετραπλασίονα τοῦ κύκλου, οὗ ἡ διάμετρός ἐστι μονάδων ιδ.
    
    
66. Heron Mech., Metrica Book 1, chapter 38, line 15
    
    ἢ καὶ ἄλλως· ἀπέδειξεν Ἀρχιμήδης, ὅτι ἡ ἐπιφάνεια τῆς σφαίρας ἴση ἐστὶν ἐπιφανείᾳ κυλίνδρου χωρὶς τῶν βάσεων, οὗ ἡ μὲν διάμετρος τῆς βάσεως ἴση ἐστὶ τῇ διαμέτρῳ τῆς σφαίρας, τὸ δὲ ὕψος ἴσον· ὥστε δεήσει ἐπιφάνειαν κυλίνδρου μετρῆσαι, οὗ ἡ μὲν διάμετρος τῆς βάσεώς ἐστι μονάδων ιδ, τὸ δὲ ὕψος ὁμοίως ιδ.
    
    
67. Heron Mech., Metrica Book 1, chapter 39, line 8
    
    ἀπέδειξεν δὲ ὁ αὐτὸς Ἀρχιμήδης ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου ὅτι παντὸς τμήματος σφαίρας ἡ ἐπιφάνεια ἴση ἐστὶ κύκλῳ, [οὗ] ἡ ἐκ τοῦ κέντρου ἴση ἐστὶ τῇ ἐκ τοῦ πόλου τῆς βάσεως τοῦ τμήματος· ἡ δὲ ΑΕ ἐκ τοῦ πόλου ἐστὶ τοῦ ΑΒΓΔ κύκλου· καὶ ἔστι μονάδων ιγ.
    
    
68. Heron Mech., Metrica Book 2, chapter 11, line 2
    
    Σφαίρας δοθείσης τῆς διαμέτρου μονάδων ι εὑρεῖν τὸ στερεόν. Ἀρχιμήδης ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου δείκνυσιν, ὅτι ὁ κύλινδρος ὁ βάσιν μὲν ἔχων ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν τῇ σφαίρᾳ, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας ἡμιόλιός ἐστι τῆς σφαίρας.
    
    
69. Heron Mech., Metrica Book 2, chapter 12, line 3
    
    Ἔστω δὴ τμῆμα σφαίρας μετρῆσαι, οὗ ἡ μὲν διάμετρος τῆς βάσεως ἔστω μονάδων ιβ, ἡ δὲ κάθετος μονάδων β. πάλιν οὖν ὁ αὐτὸς Ἀρχιμήδης δείκνυσιν ὅτι πᾶν τμῆμα σφαίρας πρὸς τὸν κῶνον τὸν τὴν αὐτὴν βάσιν ἔχοντα αὐτῷ καὶ ὕψος ἴσον λόγον ἔχει, ὃν ἡ τοῦ λοιποῦ τμήματος κάθετος μετὰ τῆς ἐκ τοῦ κέντρου τῆς σφαίρας πρὸς τὴν αὐτὴν κάθετον.
    
    
70. Heron Mech., Metrica Book 2, chapter 14, line 4
    
    Ἔστω κυλίνδρου τμῆμα μετρῆσαι τετμημένου διὰ τοῦ κέντρου μιᾶς τῶν βάσεων· καὶ ἔστω ἡ μὲν διάμετρος τῆς βάσεως ἡ ΑΒ μονάδων ζ, τὸ δὲ ὕψος τοῦ τμήματος μονάδων κ· ἀποδέδειχεν Ἀρχιμήδης ἐν τῷ ἐφοδικῷ, ὅτι τὸ τοιοῦτον τμῆμα ἕκτον μέρος ἐστὶ τοῦ στερεοῦ παραλληλεπιπέδου τοῦ βάσιν μὲν ἔχοντος τὸ περιγραφόμενον περὶ τὴν βάσιν τοῦ κυλίνδρου τετράγωνον, ὕψος δὲ τὸ αὐτὸ τῷ τμήματι.
    
    
71. Heron Mech., Metrica Book 2, chapter 15, line 1 Ὁ δ' αὐτὸς Ἀρχιμήδης ἐν τῷ αὐτῷ βιβλίῳ δείκνυσιν, ὅτι ἐὰν εἰς κύβον δύο κύλινδροι διωσθῶσιν τὰς βάσεις ἔχοντες ἐφαπτομένας τῶν πλευρῶν τοῦ κύβου, τὸ κοινὸν τμῆμα τῶν κυλίνδρων δίμοιρον ἔσται τοῦ κύβου.
    
    
72. Heron Mech., Metrica Book 1, chapter proem, line 10
    
    Ἡ πρώτη γεωμετρία, ὡς ὁ παλαιὸς ἡμᾶς διδάσκει λόγος, περὶ τὰς ἐν τῇ γῇ μετρήσεις καὶ διανομὰς κατησχολεῖτο, ὅθεν καὶ γεωμετρία ἐκλήθη· χρειώδους δὲ τοῦ πράγματος τοῖς ἀνθρώποις ὑπάρχοντος ἐπὶ πλέον προήχθη τὸ γένος, ὥστε καὶ ἐπὶ τὰ στερεὰ σώματα χωρῆσαι τὴν διοίκησιν τῶν τε μετρήσεων καὶ διανομῶν· καὶ ἐπειδὴ οὐκ ἐξήρκει τὰ πρῶτα ἐπινοηθέντα θεωρήματα, προσεδεήθησαν ἔτι περισσοτέρας ἐπισκέψεως, ὥστε καὶ μέχρι νῦν τινὰ αὐτῶν ἀπορεῖσθαι, καίτοι Ἀρχιμήδους τε καὶ Εὐδόξου γενναίως ἐπιβεβληκότων τῇ πραγματείᾳ.
    
    
73. Heron Mech., Metrica Book 1, chapter proem, line 16
    
    καὶ πρὸ[ς] τῆς Ἀρχιμήδους συνέσεως ἄπιστον ἦν ἐπινοῆσαι, διότι ἡ τῆς σφαίρας ἐπιφάνεια τετραπλασία ἐστὶ τοῦ μεγίστου κύκλου τῶν ἐν αὐτῇ καὶ ὅτι τὸ στερεὸν αὐτῆς δύο τριτημόριά ἐστι τοῦ περιλαμβάνοντος αὐτὴν κυλίνδρου καὶ ὅσα τούτων ἀδελφὰ τυγχάνει.
    
    
74. Heron Mech., Metrica Book 1, chapter 34, line 3
    
    ἐπεὶ οὖν ἐν τοῖς κωνοειδέσιν Ἀρχιμήδους δείκνυται ὅτι τὸ ὑπὸ τῶν ἀξόνων δύναται κύκλον ἴσον τῇ ἐλλείψει, δεήσει τὰ ιϛ ἐπὶ τὰ ιβ πολλαπλασιάσαντα τούτων λαβεῖν τὰ ια ιδ΄· ἔστι δὲ ρμϛ𐅵· τοσούτου ἀποφαίνεσθαι τὸ ἐμβαδὸν τῆς ἐλλείψεως.
    
    
75. Heron Mech., Metrica Book 2, chapter proem, line 8
    
    εἴτε δὲ Ἀρχιμήδους εἴτε ἄλλου τινός, ἀναγκαῖον καὶ ταύτας προσυπογράψαι, ὅπως κατὰ μηδὲν ἐνδεὴς ἡ πραγματεία τυγχάνῃ τοῖς βουλομένοις αὐτὰ μεταχειρίζεσθαι.
    
    
76. Heron Mech., Metrica Book 1, chapter 37, line 20
    
    ἐὰν οὖν πάλιν δοθῇ ἡ μὲν διάμετρος τῆς βάσεως τοῦ κώνου μονάδων ιδ, ἡ δὲ πλευρὰ μονάδων ι, ἔσται ἡ μὲν ΒΓ περιφέρεια μονάδων μδ, ἡ δὲ ΑΒ μονάδων ι. δέδεικται δὲ Ἀρχιμήδει ἐν τῇ τοῦ κύκλου μετρήσει, ὅτι πᾶς τομεὺς ἥμισύς ἐστι τοῦ περιεχομένου ὑπό τε τῆς τοῦ τομέως περιφερείας καὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου, οὗ ἔστιν ὁ τομεύς· τὸ δὲ ὑπὸ τῶν ΑΒ ΒΓ ἐστὶ μονάδων υπ· τὸ ἄρα ἐμβαδὸν τοῦ τομέως ἔσται μονάδων σκ.
    
    
77. Heron Mech., Metrica Book 3, chapter 17, line 26
    
    αἱ ἄρα εἰρημέναι ἐπιφάνειαι λόγον ἔχουσι πρὸς ἀλλήλας τὸν τῆς Α πρὸς τὴν Β· ταῦτα γὰρ ἐν τῷ β΄ περὶ σφαίρας Ἀρχιμήδει δέδεικται Τὸν δοθέντα κύκλον διελεῖν εἰς τρία ἴσα δυσὶν εὐθείαις.
    
    
78. Heron Mech., Metrica Book 3, chapter 23, line 17
    
    τοῦτο γὰρ ὁμοίως Ἀρχιμήδει δέδεικται ἐν τῷ β΄ περὶ σφαίρας.
    
    
79. Heron Mech., Definitiones (0559: 008) “Heronis Alexandrini opera quae supersunt omnia, vol. 4”, Ed. Heiberg, J.L. Leipzig: Teubner, 1903. Chapter 104, section 1, line 7
    
    Εὐκλείδης μὲν οὖν ἐν τῷ ιγ΄ τῶν Στοιχείων ἀπέδειξε, πῶς τῇ σφαίρᾳ τὰ πέντε ταῦτα σχήματα περι- λαμβάνει· μόνα γὰρ τὰ Πλάτωνος οἴεται. Ἀρχιμήδης δὲ τριακαίδεκα ὅλα φησὶν εὑρίσκεσθαι σχήματα δυνάμενα ἐγγραφῆναι τῇ σφαίρᾳ προστιθεὶς ὀκτὼ μετὰ τὰ εἰρημένα πέντε· ὧν εἰδέναι καὶ Πλάτωνα τὸ τεσσαρεσκαιδεκάεδρον, εἶναί τε τοῦτο διπλοῦν, τὸ μὲν ἐξ ὀκτὼ τριγώνων καὶ τετραγώνων ἓξ σύνθετον, ἐκ γῆς καὶ ἀέρος, ὅπερ καὶ τῶν ἀρχαίων τινὲς ᾔδεσαν, τὸ δὲ ἕτερον πάλιν ἐκ τετραγώνων μὲν ὀκτώ, τριγώνων δὲ [ϛ], ὃ καὶ χαλεπώτερον εἶναι δοκεῖ.
    
    
80. Heron Mech., Definitiones Chapter 136, section 30, line 2
    
    ὁ Ἀρχιμήδης ἔδειξεν, ὅτι πᾶς κύκλος ἴσος ἐστὶν τριγώνῳ ὀρθογωνίῳ, οὗ ἡ μὲν ἐκ τοῦ κέντρου ἴση ἐστὶ μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῇ βάσει.
    
    
81. Heron Mech., Definitiones Chapter 137, section 4, line 6
    
    Ταύρου Σιδονίου ἔστιν ὑπόμνημα εἰς Πολιτείαν Πλάτωνος, ἐν ᾧ ἔστι ταῦτα· Ὡρίσατο ὁ Πλάτων τὴν γεωμετρίαν ἐν τῷ Μένωνι οὕτως· δόξαν ὀρθὴν δεθεῖσαν αἰτίας λογισμῷ· Ἀριστοτέλης δ' ὑπόληψιν μετὰ ἀποδείξεως, Ζήνων δὲ ἕξιν ἐν προσδέξει φαντασιῶν ἀμετάπτωτον ὑπὸ λόγου. Ἀρχιμήδης Συρακούσιος Δωρίδι φωνῇ, Εὐκλείδης, Ἀπολλωνίου, Εὔδοξος.
    
    
82. Heron Mech., Definitiones Chapter 135, section 5, line 8
    
    θεωρεῖ οὖν τὸ μὲν κληθὲν ὑπ' Ἀρχιμήδους βοϊκὸν πρόβλημα, τοῦτο δὲ μηλίτας καὶ φιαλίτας ἀριθμούς, τοὺς μὲν ἐπὶ φιάλης, τοὺς δὲ ἐπὶ ποίμνης, καὶ ἐπ᾿ ἄλλων δὲ γενῶν τὰ πλήθη τῶν αἰσθητῶν σωμάτων σκοποῦσα, ὡς περιττὸν ἀποφαίνεσθαι.
    
    
83. Heron Mech., Definitiones Chapter 136, section 1, line 16
    
    οὐ πολὺ δὲ τούτων νεώτερός ἐστιν ὁ Εὐκλείδης ὁ τὰ Στοιχεῖα συναγαγών, γέγονε δὲ οὗτος ἐπὶ τοῦ πρώτου Πτολεμαίου νεώτερος μὲν τοῦ Πλάτωνος, ἀρχαιότερος δὲ τοῦ Ἐρατοσθένους καὶ Ἀρχιμήδους· οὗτοι γὰρ σύγχρονοι ἀλλήλοις ἦσαν.
    
    
84. Heron Mech., Geometrica (0559: 009) “Heronis Alexandrini opera quae supersunt omnia, vol. 4”, Ed. Heiberg, J.L. Leipzig: Teubner, 1903. Chapter 21, section 25, line 1
    
    τὰ δὲ περιφερῆ τῶν ἐπιπέδων σχημάτων, ὅσα δύνανται μετρεῖσθαι, ἐν τοῖς προλαβοῦσι κατὰ τὸ ἀκόλουθον ἐξεθέμεθα. Ἀρχιμήδης μὲν οὖν ἐν τῇ τοῦ κύκλου μετρήσει δείκνυσιν, ὡς [ια] τετράγωνα τὰ ἀπὸ τῆς διαμέτρου τοῦ κύκλου ἴσα γίνεται ὡς ἔγγιστα δεκατέσσαρσι κύκλοις· ὥστε, ἐὰν δοθῇ ἡ διάμετρος τοῦ κύκλου ποδῶν [ι], δεήσει τὰ [ι] ἐφ' ἑαυτὰ ποιήσαντα καὶ τὰ γινόμενα ἐπὶ τὰ [ια], καὶ τούτων τὸ ιδ΄· γίνονται [οη] 𐅵΄ ιδ΄· τοσούτων ἀποφαίνεσθαι χρὴ τοῦ κύκλου τὸ ἐμβαδόν.
    
    
85. Heron Mech., Stereometrica (0559: 010) “Heronis Alexandrini opera quae supersunt omnia, vol. 5”, Ed. Heiberg, J.L. Leipzig: Teubner, 1914. Chapter 1, subchapter 1, section 1, line 2
    
    Σφαίρας δοθείσης τῆς διαμέτρου ποδῶν [ι] εὑρεῖν τὸ στερεόν. Ἀρχιμήδης ἐν τοῖς Περὶ σφαίρας καὶ κυλίνδρου δείκνυσιν, ὅτι ὁ κύλινδρος ὁ βάσιν μὲν ἔχων ἴσην τῷ μεγίστῳ τῶν ἐν τῇ σφαίρᾳ κύκλων, ὕψος δὲ ἴσον τῇ διαμέτρῳ τῆς σφαίρας, ἡμιόλιός ἐστι τῆς σφαίρας· ὥστε κατὰ τοῦτον τὸν λόγον δεῖ τὰ [ι] ἐφ' ἑαυτὰ λαβεῖν, καὶ τῶν γινομένων ἐπὶ τὰ [ια] [ὧν] τὸ ιδ΄, καὶ ταῦτα ἐπὶ τὸ ὕψος τοῦ κυλίνδρου πολυπλασιασθέντα, τουτέστιν ἐπὶ τὰ [ι], καὶ τῶν γινομένων λαβεῖν τὸ 𐅵΄ ϛ΄ καὶ ἀποφέρεσθαι ἐπὶ τὸ τῆς σφαίρας στερεόν· εἰσὶ δὲ πόδες [φκγ] καὶ [ιζ] εἰκοστομόνα.
    
    
86. Heron Mech., Stereometrica Chapter 1, subchapter 4, section 2, line 2
    
    ἐποίησα δὲ τὰ γενόμενα τετράκις παρὰ ταύτην τὴν αἰτίαν· δείκνυσι γὰρ Ἀρχιμήδης, ὅτι ἡ ἐπιφάνεια τῆς σφαίρας τετραπλάσιον ἑνὸς μεγίστου κύκλου.
    
    
87. Heron Mech., Stereometrica Chapter 1, subchapter 7, section 1, line 7
    
    ἐποιήσαμεν δὲ τὰ γενόμενα ἑνδεκάκις καὶ [ὧν] τὸ κα΄ ἐλάβομεν διὰ ταύτην τὴν αἰτίαν· δείκνυσιν Ἀρχιμήδης, ὅτι [ια] κύβοι ἴσοι γίνονται [κα] σφαίραις.
    
    
88. Heron Mech., Stereometrica Chapter 1, subchapter 92, section 1, line 3
    
    ἐπειδὴ οὖν ἐν τοῖς Κωνοειδέσιν ὁ Ἀρχιμήδης δείκνυσιν, ὅτι τὸ ὑπὸ τῶν ἀξόνων δύναται τὸ ἀπὸ κύκλου διαμέτρου ἴσου τῇ ἐλλείψει, ποίει οὕτως· πολυπλασίαζε τὰ [ιβ] ἐπὶ τὰ [ιϛ]· γίνονται πόδες [ρϞβ].
    
    
89. Heron Mech., Stereometrica Chapter 1, subchapter 93, section 1, line 5
    
    ἀπέδειξεν δὲ ὁ Ἀρχιμήδης ἐν τῷ Ἐφοδικῷ λόγῳ, ὡς προείρηται, ὅτι πᾶν τμῆμα περιεχόμενον ὑπὸ εὐθείας καὶ ὀρθογωνίου κώνου τομῆς, τουτέστι παραβολῆς, ἐπίτριτον τοῦ τριγώνου τοῦ τὴν βάσιν ἔχοντος αὐτοῦ καὶ ὕψος ἴσον, τουτέστιν τοῦ ΑΒΓ τριγώνου.
    
    
90. Heron Mech., Stereometrica Chapter 2, subchapter 36, section 1, line 5
    
    λέγει τοῦτο Ἀρχιμήδης ἐν τῷ περὶ σφαιρικῶν.
    
    
91. Marcus Aurelius Antoninus Imperator Phil., Τὰ εἰς ἑαυτόν (0562: 001) “The meditations of the emperor Marcus Aurelius, vol. 1”, Ed. Farquharson, A.S.L. Oxford: Clarendon Press, 1944, Repr. 1968. Book 6, chapter 47, section 1, line 8
    
    μέτιθι νῦν ἐπὶ τὰ ἄλλα φῦλα· ἐκεῖ δὴ μεταβαλεῖν ἡμᾶς δεῖ ὅπου τοσοῦτοι μὲν δεινοὶ ῥήτορες, τοσοῦτοι δὲ σεμνοὶ φιλόσοφοι, Ἡράκλειτος, Πυθαγόρας, Σωκράτης, τοσοῦτοι δὲ ἥρωες πρότερον, τοσοῦτοι δὲ ὕστερον στρατηγοί, τύραννοι· ἐπὶ τούτοις δὲ Εὔδοξος, Ἵππαρχος, Ἀρχιμήδης, ἄλλαι φύσεις ὀξεῖαι, μεγαλόφρονες, φιλόπονοι, πανοῦργοι, αὐθάδεις, αὐτῆς τῆς ἐπικήρου καὶ ἐφημέρου τῶν ἀνθρώπων ζωῆς χλευασταί, οἷον Μένιππος καὶ ὅσοι τοιοῦτοι.
    
    
92. Polyaenus Rhet., Strategemata (0616: 001) “Polyaeni strategematon libri viii”, Ed. Woelfflin, E., Melber, J. Leipzig: Teubner, 1887, Repr. 1970. Book 8, chapter 11, section 1, line 2
    
    Μάρκελλος Συρακούσας πολιορκῶν ὑπὸ τῶν τοῦ Ἀρχιμήδου μηχανημάτων ἡσσώμενος προσβάλλειν μὲν οὐκέτι τοῖς τείχεσιν ἐθάρσει, χρόνῳ δὲ τὴν πολιορκίαν ἐπέτρεψε.
    
    
93. Oribasius Med., Collectiones medicae (lib. 1–16, 24–25, 43–50) (0722: 001) “Oribasii collectionum medicarum reliquiae, vols. 1–4”, Ed. Raeder, J. Leipzig: Teubner, 6.1.1:1928; 6.1.2:1929; 6.2.1:1931; 6.2.2:1933; Corpus medicorum Graecorum, vols. 6.1.1–6.2.2. Book 49, chapter 23, section 1, line 2
    
    Γνωστέον ἐστὶν ὑμῖν ἐν πρώτοις ὅτι οὔτε ὁ Ἀπελλὶς οὔτε Ἀρχιμήδης ἦσαν ἰατροί, ἀλλὰ μηχανικοὶ ἄνδρες, οἳ καὶ τὸ ὄργανον ἐπενόησαν, καθάπερ ἐν τῇ ἱστορίᾳ παρειλήφαμεν, πρὸς τὰς τῶν πλοίων καθολκάς, οὐ χερσὶ τῶν κάλων ἑλκομένων, ἀλλ' ἐργάταις· οἱ δὲ τότε ἰατροὶ συστείλαντες τὰ τῆς κατασκευῆς μέτρα τόνιον ὄργανον ἰατρικὸν τὸ τρίσπαστον τοῦτο πρὸς τοὺς τῶν ἐξαρθρημάτων καὶ τῶν καταγμάτων καταρτισμοὺς ἐποίησαν.
    
    
94. Oribasius Med., Collectiones medicae (lib. 1-16, 24-25, 43-50) Book 49, chapter 6, section 1, line 3
    
    Μόνον μὲν ἱκανόν ἐστιν εἰς ἐμβολὰς ἄρθρων τὸ καλούμενον Ἱπποκράτειον βάθρον· εἰ δ' ἄρα τις θέλοι καὶ ἄλλοις χρῆσθαι, πρὸς μὲν τὰς ὁδοιπορίας τὸ καλούμενον πολύσπαστον ἐπιτήδειον (Ἀρχιμήδους δ' αὐτό φασιν εὕρημα εἶναι), πρὸς δὲ τὰς ἐν πόλει χρείας στάσιμον μὲν ἄξιον λόγου τὸ τοῦ Τέκτονος καλούμενόν ἐστιν ἢ τὸ τοῦ Ἀνδρέου, ἐφέδρανον δὲ τουτὶ τὸ Ἱπποκράτους βάθρον.
    
    
95. Oribasius Med., Collectiones medicae (lib. 1-16, 24-25, 43-50) Book 49, chapter 23, section t, line 1 Ἀπελλίδος ἢ Ἀρχιμήδους τρίσπαστον.
    
    
96. Alexander Phil., In Aristotelis topicorum libros octo commentaria (0732: 006) “Alexandri Aphrodisiensis in Aristotelis topicorum libros octo commentaria”, Ed. Wallies, M. Berlin: Reimer, 1891; Commentaria in Aristotelem Graeca 2.2. Page 90, line 24
    
    θείη γὰρ ἄν τις ὡς ἔνδοξον τὸ ὑπὸ Ἱπποκράτους λεγόμενον ἐν ἰατρικῇ καὶ τὸ ὑπὸ Ἀρχιμήδους ἐν γεωμετρίᾳ καὶ τὸ ὑπὸ Ἀριστοξένου ἐν μουσικῇ.
    
    
97. Posidonius Phil., Fragmenta (1052: 001) “Posidonios. Die Fragmente, vol. 1”, Ed. Theiler, W. Berlin: De Gruyter, 1982. Fragment 10, line 35
    
    οὐ γὰρ ὥσπερ ἡ γῆ κατὰ ἕξιν ἐσχημάτισται στερεὰ οὖσα, ὥστε καὶ κοιλάδας ἔχειν συμμενούσας καὶ ἀναστήματα, οὕτως καὶ τὸ ὕδωρ, ἀλλ' αὐτῇ τῇ κατὰ τὸ βάρος ῥοπῇ τὴν ὄχησιν ἐπὶ τῆς γῆς ποιεῖται, καὶ τοιαύτην λαμβάνει τὴν ἐπιφάνειαν, οἵαν ὁ Ἀρχιμήδης φησίν.
    
    
98. Posidonius Phil., Fragmenta Fragment 89, line 133
    
    ταῖς γὰρ ἀδιαψεύστοις τοῦ κέρδους προσδοκίαις πιεζόμενοι πρὸς τὸ τέλος ἄγουσι τὰς ἰδίας ἐπιβολάς, καὶ τὸ πάντων παραδοξότατον, ἀπαρύτουσι τὰς ῥύσεις τῶν ὑδάτων τοῖς Αἰγυπτιακοῖς λεγομένοις κοχλίαις, οὓς Ἀρχιμήδης ὁ Συρακόσιος εὗρεν, ὅτε παρέβαλεν εἰς Αἴγυπτον· διὰ δὲ τούτων συνεχῶς ἐκ διαδοχῆς παραδιδόντες μέχρι τοῦ στομίου, τὸν τῶν μετάλλων τόπον ἀναξηραίνουσι καὶ κατασκευάζουσιν εὔθετον πρὸς τὴν τῆς ἐργασίας πραγματείαν.
    
    
99. Posidonius Phil., Fragmenta Fragment 89, line 142
    
    ⌈θαυμάσαι δ' ἄν τις εἰκότως τοῦ τεχνίτου τὴν ἐπίνοιαν οὐ μόνον ἐν τούτοις, ἀλλὰ καὶ ἐν ἄλλοις πολλοῖς καὶ μείζοσι, διαβεβοημένοις κατὰ πᾶσαν τὴν οἰκουμένην, περὶ ὧν τὰ κατὰ μέρος ὅταν ἐπὶ τὴν Ἀρχιμήδους ἡλικίαν ἔλθωμεν ἀκριβῶς διέξιμεν.⌉ 38. Οἱ δ' οὖν ταῖς ἐργασίαις τῶν μετάλλων ἐνδιατρίβοντες τοῖς μὲν κυρίοις ἀπίστους τοῖς πλήθεσι προσόδους περιποιοῦσιν, αὐτοὶ δὲ κατὰ γῆς ἐν τοῖς ὀρύγμασι καὶ καθ᾿ ἡμέραν καὶ νύκτα καταξαινόμενοι τὰ σώματα.
    
    
100. Posidonius Phil., Fragmenta (1052: 003) “FGrH #87”. Volume-Jacoby΄-F 2a,87,F, fragment 117, line 116
     
     ταῖς γὰρ ἀδιαψεύστοις τοῦ κέρδους προσδοκίαις πιεζόμενοι πρὸς τὸ τέλος ἄγουσι τὰς ἰδίας ἐπιβολάς· καὶ τὸ πάντων παραδοξότατον, ἀπαρύτουσι τὰς ῥύσεις τῶν ὑδάτων τοῖς Αἰγυπτιακοῖς λεγομένοις κοχλίαις, οὓς Ἀρχιμήδης ὁ Συρακόσιος εὗρεν, ὅτε παρέβαλεν εἰς Αἴγυπτον.
     
     
101. Posidonius Phil., Fragmenta Volume-Jacoby΄-F 2a,87,F, fragment 117, line 124
     
     ⟦θαυμάσαι δ' ἄν τις εἰκότως τοῦ τεχνίτου τὴν ἐπίνοιαν οὐ μόνον ἐν τούτοις, ἀλλὰ καὶ ἐν ἄλλοις πολλοῖς καὶ μείζοσι, διαβεβοημένοις κατὰ πᾶσαν τὴν οἰκουμένην, περὶ ὧν τὰ κατὰ μέρος, ὅταν ἐπὶ τὴν Ἀρχιμήδους ἡλικίαν ἔλθωμεν, ἀκριβῶς διέξιμεν⟧.
     
     
102. Eudemus Phil., Fragmenta (1357: 001) “Eudemos von Rhodos”, Ed. Wehrli, F. Basel: Schwabe, 1969; Die Schule des Aristoteles, vol. 8, 2nd edn.. Fragment 139, line 3
     
     Eutocius In Archimedis de dimensione circuli librum comment. p. 228 Heiberg: εἴη δ' ἂν ὡς πρὸς τὸ προκείμενον ἐφεξῆς τὸ γεγραμμένον Ἀρχιμήδει βιβλίδιον κύκλου μέτρησιν τὴν ἐπιγραφὴν ἔχον, ἐν ᾧ τὴν πρόθεσιν τἀνδρὸς ἐξ αὐτῆς τῆς ἐπιγραφῆς γνωρίζομεν.
     
     
103. Heraclides Lembus Hist., Fragmenta (1407: 002) “FHG 3”, Ed. Müller, K. Paris: Didot, 1853. Fragment 17, line 4
     
     Eutocius in Archimedem De circul. dimens.: Ἀλλ' ἔστι μὲν τοῦτο τὸ βιβλίον (sc. περὶ τῆς τοῦ κύκλου μετρήσεως), ὥς φησιν Ἡρακλείδης ἐν τῷ Ἀρχιμήδους βίῳ, πρὸς τὰς τοῦ βίου χρείας ἀναγκαῖον.
     
     
104. Theon Phil., De utilitate mathematicae (1724: 001) “Theonis Smyrnaei philosophi Platonici expositio rerum mathematicarum ad legendum Platonem utilium”, Ed. Hiller, E. Leipzig: Teubner, 1878. Page 124, line 12
     
     τὸ ὅλον γὰρ τῆς γῆς μέγεθος κατὰ τὸν μέγιστον αὐτῆς περιμετρούμενον κύκλον μυριάδων κε΄ καὶ ἔτι δισχιλίων σταδίων σύνεγγυς δείκνυσιν Ἐρατοσθένης, Ἀρχιμήδης δὲ τοῦ κύκλου τὴν περιφέρειαν εἰς εὐθεῖαν ἐκτεινομένην τῆς διαμέτρου τριπλασίαν καὶ ἔτι τῷ ἑβδόμῳ μέρει μάλιστα αὐτῆς [τῆς διαμέτρου] μείζονα· ὥστ' εἴη ἂν ἡ πᾶσα τῆς γῆς διάμετρος μυριάδων η΄ καὶ ρπβ΄ σταδίων ἔγγιστα· ταύτης γὰρ τριπλασία καὶ τῷ ἑβδόμῳ μείζων ἡ τῶν κε΄ μυριάδων καὶ τῶν δισχιλίων σταδίων περίμετρος ἦν.
     
     
105. Theon Phil., De utilitate mathematicae Page 127, line 3
     
     τὸ τετράγωνον μθ΄, τοιούτων ὁ κύκλος λη΄ ς΄, καὶ διὰ τὸ ἐπιτρέχον ἥμισυ διπλασιασθέντων οἵων τὸ τετράγωνον ϟη΄, τοιούτων ὁ κύκλος οζ΄· τούτων δὲ ἐν ἐλαχίστοις καὶ πρώτοις ἀριθμοῖς λόγος ὡς ιδ΄ πρὸς ια΄· ἀμφοτέρων γὰρ αὐτῶν μέγιστον κοινὸν μέτρον ἐστὶν ὁ ζ΄ ἀριθμός, ὅστις τὸν μὲν ϟη΄ μετρεῖ τεσσαρεσκαιδεκάκις, τὸν δὲ οζ΄ ἑνδεκάκις· ὥστε τοῦ ἀπὸ τῆς διαμέτρου κύβου πρὸς τὸν ἐπὶ τοῦ κύκλου κύλινδρον [λόγος ὡς ιδ΄ πρὸς ια΄· τὸν δὲ ἐπὶ τοῦ κύκλου κύλινδρον] ἀποδείκνυσιν Ἀρχιμήδης ἡμιόλιον τῆς ἐν αὐτῷ σφαίρας· γίνεται ἄρα οἵων [ὁ] ἀπὸ τῆς διαμέτρου τοῦ κύκλου κύβος ιδ΄, τοιούτων ὁ μὲν κύλινδρος ια΄, ἡ δὲ σφαῖρα ζ΄ καὶ τρίτου.
     
     
106. Synesius Phil., De insomniis (2006: 005) “Synesii Cyrenensis opuscula”, Ed. Terzaghi, N. Rome: Polygraphica, 1944. Section 3, line 1
     
     καὶ ἔστιν ἐν αὐτῷ μέρη μέρεσι προσήγορα καὶ μαχόμενα, καὶ τῆς στάσεως αὐτῶν εἰς τὴν τοῦ παντὸς ὁμόνοιαν συμφωνούσης, ὥσπερ ἡ λύρα σύστημα φθόγγων ἐστὶν ἀντιφώνων τε καὶ συμφώνων· τὸ δ' ἐξ ἀντικειμένων ἕν, ἁρμονία καὶ λύρας καὶ κόσμου. Ἀρχιμήδης μὲν οὖν ὁ Σικελὸς ᾔτει χωρίον ἔξω τῆς γῆς, ὡς ἑαυτὸν ἀντιταλαντεύσων ὅλῃ τῇ γῇ· ἐν αὐτῇ γὰρ ὢν οὐκ ἔχειν ἔφη δύναμιν πρὸς αὐτήν.
     
     
107. Gregorius Nyssenus Theol., Epistulae (2017: 033) “Gregorii Nysseni opera, vol. 8.2, 2nd edn.”, Ed. Pasquali, G. Leiden: Brill, 1959. Epistle 19, section 18, line 5
     
     ἀμαθεῖς δὲ ἄλλως ὄντες καὶ τὴν γλῶσσαν πλέον ἢ βάρβαροι δασεῖς τε τὴν φωνὴν καὶ θηριώδεις τὴν δίαιταν, κατὰ τὰ δολερὰ τῶν θηρίων τὴν πρὸς τὸ κακὸν εὐμηχανίαν οὕτως ἐξήσκηνται, ὡς μηδὲν αὐτοῖς εἶναι τὸν Ἀρχιμήδην, μᾶλλον δὲ Σίσυφον ἢ Κερκυόνα ἢ Σκείρωνα ἢ εἴ τινας τοιούτους ἄλλους ἐν ταῖς ἱστορίαις ἀκούομεν, τὸ μὲν γὰρ ψεῦδος πάσης ἀληθείας ἐστὶν αὐτοῖς ἑτοιμότερον· οὕτω δὲ ἐπιθαρσοῦσιν ὑπ' ἀναισχυντίας τῷ ψεύδεσθαι ὡς οὐδὲ τῷ ἀληθεύειν οἱ περὶ τοῦτο σφοδροί, καὶ τὸ ἐλεγχθῆναι παρ' αὐτοῖς ἐπὶ τοῖς μεγίστοις κακοῖς ἀφορμὴ τῆς παρὰ τοῖς πολλοῖς εὐδοκιμήσεως γίνεται, ὕβρις τε καὶ τραχύτης καὶ ἀναισθησία καὶ ἡ τῶν λεγομένων δυσωδία πολιτισμὸς εἶναι καί τις τοιαύτη
     
     
108. Pappus Math., Synagoge (2032: 001) “Pappi Alexandrini collectionis quae supersunt, 3 vols.”, Ed. Hultsch, F. Berlin: Weidmann, 1:1876; 2:1877; 3:1878. Book 8, page 1026, line 6
     
     Πάντων δὲ τούτων τὴν αἰτίαν καὶ τὸν λόγον ἐπεγνωκέναι φασίν τινες τὸν Συρακόσιον Ἀρχιμήδη· μόνος γὰρ οὗτος ἐν τῷ καθ᾿ ἡμᾶς βίῳ ποικίλῃ πρὸς πάντα κέχρηται τῇ φύσει καὶ τῇ ἐπινοίᾳ, καθὼς καὶ Γεμῖνος ὁ μαθηματικὸς ἐν τῷ περὶ τῆς τῶν μαθημάτων τάξεώς φησιν.
     
     
109. Pappus Math., Synagoge Book 8, page 1026, line 10
     
     Κάρπος δὲ πού φησιν ὁ Ἀντιοχεὺς Ἀρχιμήδη τὸν Συρακόσιον ἓν μόνον βιβλίον συντεταχέναι μηχανικὸν τὸ κατὰ τὴν σφαιροποιΐαν, τῶν δὲ ἄλλων οὐδὲν ἠξιωκέναι συντάξαι.
     
     
110. Pappus Math., Synagoge Book 4, page 234, line 3
     
     Τὸ ἐπὶ τῆς ἕλικος τῆς ἐν ἐπιπέδῳ γραφομένης θεώρημα προὔτεινε μὲν Κόνων ὁ Σάμιος γεωμέτρης, ἀπέδειξεν δὲ Ἀρχιμήδης θαυμαστῇ τινι χρησάμενος ἐπιβολῇ.
     
     
111. Pappus Math., Synagoge Book 4, page 258, line 19
     
     εὑρημένης δὲ τῇ τοῦ κύκλου περιφερείᾳ ἴσης εὐθείας πρόδηλον ὡς δὴ καὶ αὐτῷ τῷ κύκλῳ ῥᾴδιον ἴσον τετράγωνον συστήσασθαι· τὸ γὰρ ὑπὸ τῆς περιμέτρου τοῦ κύκλου καὶ τῆς ἐκ τοῦ κέντρου διπλάσιόν ἐστι τοῦ κύκλου, ὡς Ἀρχιμήδης ἀπέδειξεν.
     
     
112. Pappus Math., Synagoge Book 4, page 302, line 13
     
     ......... τῷ προβλήματι χρῆται ὁ Ἀρχιμήδης πρὸς τὸ δεῖξαι κύκλου περιφερείᾳ ἴσην εὐθεῖαν.
     
     
113. Pappus Math., Synagoge Book 5, page 314, line 1
     
     Ὅτι μὲν οὖν τὸ ὑπὸ τῆς περιμέτρου τοῦ κύκλου καὶ τῆς ἐκ τοῦ κέντρου διπλάσιόν ἐστι τοῦ κύκλου Ἀρχι- μήδης ἀπέδειξεν, οὐδὲν δὲ ἧττον καὶ ἑξῆς δειχθήσεται τοῦτο πρὸς τὸ μὴ δεῖσθαι τοῦ Ἀρχιμηδείου συντάγματος ἕνεκεν μόνου τοῦ θεωρήματος τούτου.
     
     
114. Pappus Math., Synagoge Book 5, page 366, line 21
     
     λέγει γὰρ Ἀρχιμήδης ὅτι “ἐὰν κῶνος ἰσοσκελὴς ἐπιπέδῳ τμηθῇ παραλλήλῳ τῇ βάσει, τῇ μεταξὺ τῶν παραλλήλων ἐπιπέδων ἐπιφανείᾳ τοῦ κώνου, ἴσος ἐστὶν κύκλος οὗ ἡ ἐκ τοῦ κέντρου μέσον λόγον ἔχει τῆς πλευρᾶς τοῦ κώνου τῆς μεταξὺ τῶν παραλλήλων ἐπιπέδων καὶ τῆς ἴσης ἀμφοτέραις ταῖς ἐκ τῶν κέντρων τῶν κύκλων τῶν ἐν τοῖς παραλλήλοις ἐπιπέδοις”.
     
     
115. Pappus Math., Synagoge Book 5, page 368, line 21
     
     καὶ ἡ ὑπὸ τῆς ἐσχάτης τῆς ΑΕ κωνικὴ ἐπιφάνεια γινομένη ἴση ἐστὶν κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ ΕΒ ΑΝ, ὅπερ ἴσον ἐστὶν τῷ ὑπὸ ΑΕΝ (καὶ γὰρ ἰσογώνιά ἐστιν τὰ ΑΕΒ ΑΕΝ τρίγωνα, καὶ ἡ ὑπὸ τῆς ΑΕ γινομένη ἐπιφάνεια ἴση ἐστὶν κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ ΑΕΝ· καὶ τοῦτο γὰρ Ἀρχιμήδης ἀπέδειξεν).
     
     
116. Pappus Math., Synagoge Book 5, page 394, line 11
     
     Ἔτι δὲ καὶ τοῦτο φανερὸν ὅτι τῇ ὑπὸ τῆς ΑΖ γινομένῃ ἐπιφανείᾳ, κυλινδρικῇ οὔσῃ, ἴσος ἐστὶν κύκλος οὗ ἡ ἐκ τοῦ κέντρου μέσον λόγον ἔχει τῆς πλευρᾶς τοῦ κυλίνδρου καὶ τῆς διαμέτρου τῆς βάσεως (τοῦτο γὰρ Ἀρχιμήδης ἔδειξεν ιδ΄ θεωρήματι περὶ σφαίρας καὶ κυλίνδρου), ὥστε ἡ ὑπὸ τῆς ΑΖ γινομένη ἐπιφάνεια ἴση ἐστὶν κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ δὶς ὑπὸ τῶν ΖΓΔ.
     
     
117. Pappus Math., Synagoge Book 8, page 1024, line 29
     
     καλοῦσι δὲ μηχανικοὺς οἱ παλαιοὶ καὶ τοὺς θαυμασιουργοὺς, ὧν οἱ μὲν διὰ πνευμάτων φιλοτεχνοῦσιν, ὡς Ἥρων πνευματικοῖς, οἱ δὲ διὰ νευρίων καὶ σπάρτων ἐμψύχων κινήσεις δοκοῦσι μιμεῖσθαι, ὡς Ἥρων αὐτομάτοις καὶ ζυγίοις, ἄλλοι δὲ διὰ τῶν ἐφ' ὕδατος ὀχουμένων, ὡς Ἀρχιμήδης ὀχουμένοις, ἢ τῶν δι' ὕδατος ὡρο- λογίων, ὡς Ἥρων ὑδρείοις, ἃ δὴ καὶ τῇ γνωμονικῇ θεωρίᾳ κοινωνοῦντα φαίνεται.
     
     
118. Pappus Math., Synagoge Book 8, page 1106, line 13
     
     Ἐπεὶ γάρ ἐστιν ὡς ὁ ΑΒ κύκλος πρὸς τὸν ΓΔ κύκλον, οὕτως τὸ ἀπὸ τῆς ΑΒ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΓΔ τετράγωνον, ἀλλὰ τοῦ μὲν ΑΒ κύκλου τετραπλάσιόν ἐστιν τὸ περιεχόμενον ὀρθογώνιον ὑπό τε τῆς ΑΒ διαμέτρου καὶ τῆς τοῦ ΑΒ περιφερείας, τοῦ δὲ ΓΔ κύκλου τετραπλάσιόν ἐστιν τὸ ὑπὸ τῆς ΓΔ καὶ τῆς τοῦ ΓΔ περιφερείας (τὸ γὰρ ὑπὸ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου καὶ τῆς περιμέτρου τοῦ κύκλου περιεχόμενον ὀρθογώνιον διπλάσιόν ἐστιν τοῦ ἐμβαδοῦ τοῦ κύκλου, ὡς Ἀρχιμήδης, καὶ ὡς ἐν τῷ εἰς τὸ πρῶτον τῶν μαθηματικῶν σχολίῳ δέδεικται καὶ ὑφ᾿ ἡμῶν δι' ἑνὸς θεωρήματος), καὶ ὡς ἄρα τὸ ὑπὸ τῆς ΑΒ καὶ τῆς περιφερείας τοῦ ΑΒ πρὸς τὸ ὑπὸ τῆς ΓΔ καὶ τῆς τοῦ ΓΔ κύκλου περιφερείας, οὕτως τὸ ἀπὸ τῆς ΑΒ τετράγωνον πρὸς τὸ ἀπὸ τῆς ΓΔ.
     
     
119. Pappus Math., Synagoge Book 4, page 272, line 2
     
     δοκεῖ δέ πως ἁμάρτημα τὸ τοιοῦτον οὐ μικρὸν εἶναι τοῖς γεωμέτραις, ὅταν ἐπίπεδον πρόβλημα διὰ τῶν κωνικῶν ἢ τῶν γραμμικῶν ὑπό τινος εὑρίσκηται, καὶ τὸ σύνολον ὅταν ἐξ ἀνοικείου λύηται γένους, οἷόν ἐστιν τὸ ἐν τῷ πέμπτῳ τῶν Ἀπολλωνίου κωνικῶν ἐπὶ τῆς παραβολῆς πρόβλημα καὶ ἡ ἐν τῷ περὶ τῆς ἕλικος ὑπὸ Ἀρχιμήδους λαμβανομένη στερεοῦ νεῦσις ἐπὶ κύκλον· μηδενὶ γὰρ προσχρώμενον στερεῷ δυνατὸν εὑρεῖν τὸ ὑπ' αὐτοῦ γραφόμενον θεώρημα, λέγω δὴ τὸ τὴν περιφέρειαν τοῦ ἐν τῇ πρώτῃ περιφορᾷ κύκλου ἴσην ἀποδεῖξαι τῇ πρὸς ὀρθὰς ἀγομένῃ εὐθείᾳ τῇ ἐκ τῆς γενέσεως ἕως τῆς ἐφαπτομένης τῆς ἕλικος.
     
     
120. Pappus Math., Synagoge Book 4, page 298, line 3
     
     Τῆς ὑπὸ Ἀρχιμήδους ἐν τῷ περὶ ἑλίκων βιβλίῳ λαμβανομένης νεύσεως τὴν ἀνάλυσίν σοι κατέταξα, ἵνα τὸ βιβλίον διερχόμενος [περὶ τῶν ἑλίκων] μὴ διαπορῇς.
     
     
121. Pappus Math., Synagoge Book 5, page 312, line 20
     
     καὶ ἔστι τὸ μὲν ὑπὸ τῆς ΔΘ καὶ τῆς τοῦ κύκλου περιφερείας διπλάσιον τοῦ ΔΕΖ κύκλου (καὶ τοῦτο γὰρ ὑπὸ Ἀρχιμήδους ἐν τῷ περὶ τῆς τοῦ κύκλου περιφερείας δέδεικται), τὸ δὲ ὑπὸ τῆς ΗΚ καὶ τῆς τοῦ ΑΒΓ πολυγώνου περιμέτρου διπλάσιον τοῦ ΑΒΓ πολυγώνου, καὶ τὰ ἡμίση· μείζων ἄρα ὁ κύκλος τοῦ ΑΒΓ πολυγώνου.
     
     
122. Pappus Math., Synagoge Book 5, page 352, line 14
     
     ταῦτα δ' ἐστὶν οὐ μόνον τὰ παρὰ τῷ θειοτάτῳ Πλάτωνι πέντε σχήματα, τουτέστιν τετράεδρόν τε καὶ ἑξάεδρον, ὀκτάεδρόν τε καὶ δωδεκάεδρον, πέμπτον δ' εἰκοσάεδρον, ἀλλὰ καὶ τὰ ὑπὸ Ἀρχιμήδους εὑρεθέντα τρισκαίδεκα τὸν ἀριθμὸν ὑπὸ ἰσοπλεύρων μὲν καὶ ἰσογωνίων οὐχ ὁμοίων δὲ πολυγώνων περιεχόμενα.
     
     
123. Pappus Math., Synagoge Book 5, page 360, line 19
     
     ἀλλ' ὁ μὲν κῶνος ἴσος ἐστὶν τῇ Α σφαίρᾳ (τοῦτο γὰρ ἐκ τῶν ὑπ' Ἀρχιμήδους δεδειγμένων ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου καὶ τῶν ἄλλων ὑφ᾿ ἡμῶν ὑποτεταγμένων λημμάτων ἐστὶ φανερόν), ἡ δὲ πυραμὶς ἴση τῷ πολυέδρῳ· μείζων ἄρα καὶ ἡ Α σφαῖρα τοῦ ὑποκειμένου πολυέδρου.
     
     
124. Pappus Math., Synagoge Book 5, page 362, line 19
     
     Τοσαῦτα μὲν οὖν περὶ τῆς συγκρίσεως τῆς σφαίρας πρὸς τὰ ε΄ σχήματα καὶ τὸν κῶνον καὶ κύλινδρον, τὰ δ' ὑπὸ τοῦ Ἀρχιμήδους, ὡς εἴρηται, δειχθέντα καὶ ἄλλως ἀποδείξομεν, προγράψαντες ὅσα εἰς τὰς ἀποδείξεις αὐτῶν συντείνει λημμάτια.
     
     
125. Pappus Math., Synagoge Book 5, page 370, line 13
     
     ἀλλὰ ἡ ὑπὸ τῆς ΓΔ γινομένη ἐπιφάνεια ἴση ἐστὶν κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ συναμφοτέρου τῆς ΓΑ ΔΚ καὶ τῆς ΓΔ διὰ τὸ αὐτὸ Ἀρχιμήδους ιζ΄ θεώρημα· καὶ ὁ κύκλος ἄρα οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ ΒΑΚ ἴσος ἐστὶν τῇ ὑπὸ τῆς ΓΔ γινομένῃ ἐπιφανείᾳ.
     
     
126. Pappus Math., Synagoge Book 5, page 376, line 10
     
     ἐπεὶ δὲ καὶ οἱ κύκλοι πρὸς ἀλλήλους εἰσὶν ὡς τὰ ἀπὸ τῶν διαμέτρων τετράγωνα, καὶ τὰ ἀπὸ τῶν ἐκ τῶν κέντρων, καὶ ἐδείχθη πρὸ ἑνὸς τὸ μὲν ὑπὸ τῶν ΓΔ ΔΕ ΕΖ ἐφαπτομένων κωνικῶν ἐπιφανειῶν γινόμενον σχῆμα ἴσον κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ ΒΑΛ, τὸ δὲ ὑπὸ τῆς ΖΗ ἐν τῇ στροφῇ γινόμενον σχῆμα κωνικῆς ἐπιφανείας ἴσον κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ συναμφοτέρου τῆς ΗΡΚ καὶ τῆς ΗΘ [ἔστιν Ἀρχιμήδους ιζ΄ θεωρήματι], τὸ δὲ ὑπὸ τῆς ΓΑ γινόμενον σχῆμα κύκλος ἐστὶν οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ἀπὸ ΗΘ, οἱ τρεῖς ἄρα κύκλοι, τουτέστιν ἡ ὑπὸ τῶν ΑΓ ΓΔ ΔΕ ΕΖ ΖΗ γινομένη ἐπιφάνεια μείζων ἐστὶ τοῦ κύκλου οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ἀπὸ τῆς ΑΗ κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου δύναται τὸ ὑπὸ ΗΘΚ, τουτέστιν τὸ ἥμισυ τοῦ ἀπὸ τῆς ἐπὶ τὰ Ζ Θ.
     
     
127. Pappus Math., Synagoge Book 5, page 390, line 17
     
     ἀλλ' ὁ μὲν κύκλος οὗτος ἴσος ἐστὶν τῇ ὑπὸ τῆς ΑΒ ἐν τῇ στροφῇ γινομένῃ κωνικῇ ἐπιφανείᾳ διὰ τὸ ιε΄ πάλιν Ἀρχιμήδους θεώρημα [παντὸς γὰρ κώνου ἰσοσκελοῦς ἡ ἐπιφάνεια, χωρὶς τῆς βάσεως, ἴση ἐστὶν κύκλῳ οὗ ἡ ἐκ τοῦ κέντρου μέσον ἀνάλογον ἔχει τῆς πλευρᾶς τοῦ κώνου καὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου ὅς ἐστιν βάσις τοῦ κώνου].
     
     
128. Pappus Math., Synagoge Book 5, page 410, line 22
     
     Καὶ τὰ μὲν περὶ τῶν ὑπὸ Ἀρχιμήδους δειχθέντων ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου τοσαῦτ' ἐστίν, ἑξῆς δὲ τούτοις γράψομεν, ὡς ὑπεσχόμεθα, τὰς συγκρίσεις τῶν ἴσην ἐπιφάνειαν ἐχόντων πέντε σχημάτων, πυραμίδος τε καὶ κύβου καὶ ὀκταέδρου δωδεκαέδρου τε καὶ εἰκοσαέδρου [καὶ τὴν ἔφοδον τῶν ἀποδείξεων ἐχούσας], οὐ διὰ τῆς ἀναλυτικῆς λεγομένης θεωρίας, δι' ἧς ἔνιοι τῶν παλαιῶν ἐποιοῦντο τὰς ἀποδείξεις [τῶν προειρημένων σχημάτων], ἀλλὰ διὰ τῆς κατὰ σύνθεσιν ἀγωγῆς ἐπὶ τὸ σαφέστερον καὶ συντομώτερον ὑπ' ἐμοῦ διεσκευασμένας [ἐπεὶ καὶ τὰ Pappus Math., Synagoge Book 8, page 1034, line 3
     
     Τὸ μὲν οὖν μάλιστα συνέχον τὴν κεντροβαρικὴν πραγματείαν τοῦτ' ἂν εἴη, μάθοις δ' ἂν τὰ μὲν στοιχειώδη ὄντα διὰ ταύτης δεικνύμενα τοῖς Ἀρχιμήδους περὶ ἰσοῤῥοπιῶν ἐντυχὼν καὶ τοῖς Ἥρωνος μηχανικοῖς, ὅσα δὲ μὴ γνώριμα τοῖς πολλοῖς γράψομεν ἐφεξῆς, οἷον τὰ τοιαῦτα.
     
     
129. Pappus Math., Synagoge Book 8, page 1060, line 2
     
     Τῆς αὐτῆς δέ ἐστιν θεωρίας τὸ δοθὲν βάρος τῇ δοθείσῃ δυνάμει κινῆσαι· τοῦτο γὰρ Ἀρχιμήδους μὲν εὕρημα [λέγεται] μηχανικόν, ἐφ' ᾧ λέγεται εἰρηκέναι· δός μοί (φησι) ποῦ στῶ καὶ κινῶ τὴν γῆν.
     
     
130. Pappus Math., Synagoge Book 8, page 1068, line 20
     
     ὅτι γὰρ κινήσεται δῆλον ἐκ τοῦ προστεθεῖσθαι ἑτέραν δύναμιν τὴν τῆς χειρολάβης, ἥτις περιγράφει κύκλον τῆς τοῦ κοχλίου περιμέτρου μείζονα· ἀπεδείχθη γὰρ ἐν τῷ περὶ ζυγῶν Ἀρχιμήδους καὶ τοῖς Φίλωνος καὶ Ἥρωνος μηχανικοῖς, ὅτι οἱ μείζονες κύκλοι κατακρατοῦσιν τῶν ἐλασσόνων κύκλων, ὅταν περὶ τὸ αὐτὸ κέντρον ἡ κύλισις αὐτῶν γίνηται.
     
     
131. Pappus Math., Synagoge Book 5, page 312, line 8
     
     ἐπεὶ οὖν μείζων ἐστὶν ἡ τοῦ ΛΜΝΞΟ πολυγώνου περίμετρος τῆς τοῦ ΔΕΖ κύκλου περιφερείας, ὡς ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου Ἀρχιμήδει ὑπόκειται [διὰ τὸ περιέχειν αὐτήν], ἡ δὲ τοῦ κύκλου περιφέρεια ἴση ἐστὶν τῇ τοῦ ΑΒΓ πολυγώνου περιμέτρῳ, καὶ ἡ τοῦ ΛΜΝΞΟ πολυγώνου περίμετρος μείζων τῆς τοῦ ΑΒΓ πολυγώνου περιμέτρου.
     
     
132. Pappus Math., Commentaria in Ptolemaei syntaxin mathematicam 5–6 (2032: 002) “Commentaires de Pappus et de Théon d'Alexandrie sur l'Almageste, vol. 1”, Ed. Rome, A. Rome: Biblioteca Apostolica Vaticana, 1931; Studi e Testi 54. Page 253, line 6
     
     Ἀπέδειξεν γὰρ ὁ Ἀρχιμήδης ἐν τῷ περὶ τοῦ κύκλου βιβλίῳ, ὅτι παντὸς κύκλου ἡ περίμετρος μείζων ἐστὶν ἢ τριπλασίων, ἐλάσσων μὲν ἢ ζ΄ μέρει τῆς διαμέτρου, μείζων δὲ ἢ ι οα΄· καὶ ὅτι τὸ ὑπὸ τῆς περιμέτρου τοῦ κύκλου ὡς εὐθείας καὶ τῆς ἐκ τοῦ κέντρου τοῦ κύκλου περιεχόμενον ὀρθογώνιον, διπλάσιόν ἐστιν τοῦ ἐμβαδοῦ τοῦ κύκλου.
     
     
133. Pappus Math., Commentaria in Ptolemaei syntaxin mathematicam 5-6 Page 254, line 1
     
     τὰ μὲν οὖν τριπλάσια καὶ τὰ ι οα΄ τοῦ α γίνεται γ η κζ· τὰ δὲ τριπλάσια πρὸς τῷ ζ΄ μέρει γίνεται γ η λδ· ὧν μεταξύ ἐστιν ἔγγιστα τὰ γ η λ. Πρὸς δὲ τὸ μὴ δεῖσθαι τοῦ Ἀρχιμήδους συντάγματος, ἐν τοῖς εἰς τὸ πρῶτον σχολίοις ἀπεδείχθη ὅτι τὸ ὑπὸ τῆς περιμέτρου τοῦ κύκλου καὶ τῆς ἐκ τοῦ κέντρου αὐτοῦ διπλάσιόν ἐστιν τοῦ ἐμβαδοῦ τοῦ κύκλου.
     
     
134. Pappus Math., Commentaria in Ptolemaei syntaxin mathematicam 5-6 Page 260, line 14
     
     ἐπεὶ οὖν αἱ ΘΚ, ΚΛ, ΛΜ μείζονές εἰσιν τῶν κατ' αὐτὰς τμημάτων, ὡς ἔστιν Ἀρχιμήδους ἐν τῷ περὶ σφαίρας καὶ κυλίνδρου, τὸ ἄρα ὑπὸ τῆς ΓΞ καὶ τῶν ΘΚ, ΚΛ, ΛΜ, ΜΝ εὐθειῶν μεῖζόν ἐστιν τοῦ ὑπὸ τῆς ΓΞ καὶ τῆς ΑΕΒ περιφερείας περιεχόμενον ὀρθογώνιον.
     
     
135. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i–iv (2033: 001) “Commentaires de Pappus et de Théon d'Alexandrie sur l'Almageste, vols. 2–3”, Ed. Rome, A. Vatican City: Biblioteca Apostolica Vaticana, 2:1936; 3:1943; Studi e Testi 72 and 106. Page 347, line 5
     
     ρων μεγέ*θη ἴσα φαίνεσθαι, ὅπερ σύμφωνόν ἐστιν τοῖς φαινομένοις· δοκεῖ δὲ τοῦτο ἐναντίον εἶναι τοῖς μικρῷ πρόσθεν αὐτῷ εἰρημένοις, ὅτι μείζονα ἡμῖν ὁρᾶται τὰ ἄστρα πρὸς αὐτοῖς τοῖς ἀφανισμοῖς τουτέστιν τοῖς ὁρίζουσιν δηλαδὴ ὡς ἐξ ἐλάττονος διαστάσεως ὁρώμενα· βούλεται ἐνταῦθα τὸ τοιοῦτον ἀπολύσασθαι καὶ δηλῶσαι ὡς ὅτι οὐ παρὰ τὸ ἀπό- στημα τὸ ἀπὸ τῆς γῆς ἐπὶ τὸν οὐρανὸν τὸ τοιοῦτον συμβαίνει, ἀλλ' ἐκ τῆς περὶ τὴν γῆν ὑγρᾶς γενομένης ἀναθυμιάσεως, καὶ διὰ τοῦτο τῆς ὄψεως εἰς ἀχλυωδέστερον ἀέρα ἐμπιπτούσης, καὶ τῶν ἀπ' αὐτῆς ἐπὶ τὸν ἀστέρα προσπιπτουσῶν ἀκτίνων κλάσιν ὑπομενουσῶν καὶ μείζονα ποιουσῶν τὴν πρὸς τῇ ὄψει γωνίαν, καθὰ καὶ Ἀρχιμήδης ἐν τοῖς Περὶ κατοπτρικῶν ἀπέδειξεν.
     
     
136. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 349, line 7
     
     καὶ προσπιπτέτωσαν ἀκτῖνες ἐπὶ τῆς ἐπιφανείας τοῦ ὕδατος αἱ ΕΘ, ΕΚ, καὶ κεκλάσθωσαν ἐπὶ τὰ Α, Β, ὡς αἱ ΕΘΑ, ΕΚΒ, καθὰ καὶ Ἀρχιμήδης ἐν τοῖς Περὶ κατοπτρικῶν ὡς ἔφαμεν.
     
     
137. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 359, line 6
     
     ἐπεὶ οὖν ἡ τοῦ ΚΛΜ πολυγώνου περίμετρος μείζων ἐστὶν τῆς τοῦ ΑΒΓ κύκλου περιμέτρου ὡς ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου Ἀρχιμήδης, ἴση δὲ ἡ τοῦ ΑΒΓ κύκλου περίμετρος τῇ τοῦ ΔΕΖ πολυγώνου περιμέτρῳ, μείζων ἄρα καὶ ἡ τοῦ ΚΛΜ πολυγώνου περίμετρος τῆς τοῦ ΔΕΖ πολυγώνου περιμέτρου.
     
     
138. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 359, line 15
     
     ἀλλὰ τὸ μὲν ὑπὸ τῆς περιμέτρου τοῦ ΑΒΓ κύκλου καὶ τῆς ΗΒ διπλάσιον τοῦ ΑΒΓ κύκλου Ἀρχιμήδης ἔδειξεν, οὗ καὶ τὴν δεῖξιν ἑξῆς ἐκθησόμεθα· τὸ δὲ ὑπὸ τῆς περιμέτρου τοῦ ΔΕΖ πολυγώνου καὶ τῆς ΘΝ διπλάσιον τοῦ ΔΕΖ πολυγώνου.
     
     
139. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 394, line 13
     
     Τὸ γὰρ ὅλον τῆς γῆς μέγεθος κατὰ τὸν μέγιστον ἑαυτῆς κύκλον μετρούμενον σταδίων μυριάδων ἐστὶν ιη, καθάπερ αὐτὸς ὁ Πτολεμαῖος ἐν τῇ Γεωγραφίᾳ συνήγαγεν. Ἀρχιμήδης δὲ τοῦ κύκλου τὴν περίμετρον εἰς εὐθεῖαν ἐκτεινομένην δείκνυσιν τῆς διαμέτρου γ καὶ ζ μέρει μείζονα.
     
     
140. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 821, line 21
     
     ὥστε τέταρτον τῆς μιᾶς ἡμέρας περὶ τὰς τροπικὰς διαφέροντες ὅ τε Ἵππαρχος καὶ ὁ Ἀρχιμήδης, τρισκαιτεσσαρακοντακισμυρίῳ καὶ δισχιλιοστῷ τοῦ κύκλου κατὰ τὴν διαίρεσιν ἢ τὴν θέσιν τῶν ὀργάνων ἢ καὶ τοὺς ἐπιλογισμοὺς διημάρτανον, ὅπερ οὐ παράδοξόν ἐστιν τηλικοῦτον ὂν τῇ αἰσθήσει διαπίπτειν.
     
     
141. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 374, line 13
     
     Λέγω δὴ ὅτι καὶ ἡ σφαῖρα μείζων ἐστὶν πάντων τῶν ἴσην ἐπιφάνειαν ἐχόντων στερεῶν σχημάτων, προσχρησάμενος τοῖς ὑπὸ Ἀρχιμήδους δεδειγμένοις ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου.
     
     
142. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 378, line 18
     
     Ἀλλ' ὁ μὲν κῶνος ἴσος ἐστὶν τῇ Α σφαίρᾳ ἐπειδήπερ ἐδείχθη πάλιν Ἀρχιμήδει ὅτι πᾶσα σφαῖρα τετραπλασία ἐστὶν κώνου τοῦ βάσιν μὲν ἔχοντος ἴσην τῷ μεγίστῳ κύκλῳ τῶν ἐν αὐτῇ ὕψος δὲ ἴσον τῇ ἐκ τοῦ κέντρου.
     
     
143. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 395, line 2
     
     Τὴν δὲ ἀπὸ τῶν ὑψηλοτάτων ὀρῶν ἐπὶ τὰ χθαμαλώτερα πίπτουσαν κάθετον δείκνυσιν Ἐρατοσθένης διὰ τῶν ἐξ ἀποστημάτων μετρουσῶν διοπτρῶν σταδίων ι. ἐπεὶ οὖν ἀπεδείχθη πάλιν Ἀρχιμήδει ὅτι τὸ ὑπὸ τῆς διαμέτρου καὶ τῆς τοῦ κύκλου περιφερείας εἰς εὐθεῖαν ἑξαπλουμένης περιεχόμενον ὀρθογώνιον τετραπλάσιόν ἐστιν τοῦ ἐμβαδοῦ τοῦ κύκλου, τὸ ἄρα ὑπὸ τῆς διαμέτρου καὶ τοῦ δ΄ μέρους τῆς περιφερείας ἴσον ἐστὶν τῷ ἐμβαδῷ τοῦ κύκλου.
     
     
144. Theon Math ., Commentaria in Ptolemaei syntaxin mathematicam i-iv Page 396, line 9
     
     καὶ ἐπεὶ ἐδείχθη πάλιν Ἀρχιμήδει ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου ὅτι ὁ κύλινδρος ὁ ἰσοϋψὴς τῇ σφαίρᾳ καὶ ἔχων βάσιν τὸν μέγιστον ἐν αὐτῇ κύκλον ἡμιόλιός ἐστιν τῆς σφαίρας, ἔσται καὶ οἵων ὁ κύλινδρος ια, τοιούτων ἡ σφαῖρα ζ γ΄.
     
     
145. Joannes Stobaeus Anthologus, Anthologium (2037: 001) “Ioannis Stobaei anthologium, 5 vols.”, Ed. Wachsmuth, C., Hense, O. Berlin: Weidmann, 1–2:1884; 3:1894; 4:1909; 5:1912, Repr. 1958. Book 3, chapter 29, section 86, line 2
     
     Ἀρχιμήδης (Plut. l. c. p. 786 C). Ἀρχιμήδην δὲ τῇ σανίδι προσκείμενον ἀποσπῶντες βίᾳ οἱ θεράποντες ἤλειφον· ὃ δὲ ἐπὶ τοῦ σώματος ἀληλιμμένου διέγραφε τὰ σχήματα.
     
     
146. Joannes Stobaeus Anthologus, Anthologium Book 3, chapter 29, section 86, line 1
     
     Νικίας οὕτως ἦν φιλόπονος, ὥστε πολλάκις ἐρωτᾶν τοὺς οἰκέτας, εἰ λέλουται καὶ εἰ ἠρίστηκεν. Ἀρχιμήδης (Plut. l. c. p. 786 C).
     
     
147. Diophantus Math., Fragmentum [Sp.] (e cod. Paris. gr. 2448) (2039: 005) “Diophanti Alexandrini opera omnia, vol. 2”, Ed. Tannery, P. Leipzig: Teubner, 1895, Repr. 1974. Volume 2, page 22, line 16
     
     Ἀπέδειξεν Ἀρχιμήδης ὅτι τὰ [λ] τρίγωνα ἰσόπλευρα ἴσα ἐστὶν [ιγ] τετραγώνοις, ἃ τῶν [λ] ἐστὶ μέρος τρίτον καὶ δέκατον· ποίει οὖν τὴν πλευρὰν ἐφ' ἑαυτήν, καὶ τῶν γινομένων τὸ τρίτον καὶ δέκατον ἔσται τὸ ἐμβαδόν· τουτέστι [λ] τῆς μιᾶς πλευρᾶς ἐφ' ἑαυτά, γίνονται [ϡ]· ὧν τρίτον καὶ δέκατον, γίνονται [τϙ]· τοσοῦτον τὸ ἐμβαδόν.
     
     
148. Diophantus Math., Fragmentum [Sp.] (e cod. Paris. gr. 2448) Volume 2, page 27, line 22
     
     Ἀπέδειξε καὶ ἐνταῦθα Ἀρχιμήδης ὅτι ὅνπερ ἔχει λόγον ὁ κύκλος πρὸς τὸ τετράγωνον τὸ περὶ αὐτὸν περιγραφόμενον, τὸν αὐτὸν λόγον ἔχει καὶ ὁ κύλινδρος πρὸς τὸν κύβον τὸν περιέχοντα αὐτὸν καὶ ἴσας πλευ- ρὰς ἔχοντα τῇ διαμέτρῳ τοῦ κυλίνδρου καὶ τὸ ὕψος ἴσον, καὶ ὡς ἐπὶ τῶν κύκλων εἰπεῖν ὅτι τὰ ἕνδεκα τετράγωνα, τὰ ἐκτὸς περιγραφόμενα τοῦ κύκλου, ἴσα ἐστὶ δεκατέτρασι κύκλοις τοῖς τὴν αὐτὴν διάμετρον ἔχουσιν, οὕτως καὶ οἱ ἕνδεκα κύβοι ἴσοι εἰσὶ δεκατέτρασι κυλίνδροις, ὧν αἱ πλευραὶ ἴσαι εἰσὶ τῇ διαμέτρῳ
     
     
149. Diophantus Math., Fragmentum [Sp.] (e cod. Paris. gr. 2448) Volume 2, page 28, line 18
     
     Περὶ δὲ τῆς σφαίρας καὶ κυλίνδρου ὁ αὐτὸς Ἀρχιμήδης ἀπέδειξεν ὅτι ἡ σφαῖρα δίμοιρον μέρος ἐστὶ τοῦ περιλαμβάνοντος αὐτὴν κυλίνδρου, καὶ πᾶς κῶνος τρίτον μέρος ἐστὶ κυλίνδρου τοῦ τὴν αὐτὴν βάσιν ἔχοντος αὐτῷ καὶ ὕψος ἴσον.
     
     
150. Diophantus Math., Fragmentum [Sp.] (e cod. Paris. gr. 2448) Volume 2, page 31, line 2
     
     δέδειχε δὲ Ἀρχιμήδης ὅτι κύλινδρος ὁ περιλαμβάνων τὴν σφαῖραν ἡμιόλιός ἐστι τῆς σφαίρας· εἰ οὖν 𐅵΄ πρόσθεμα, γ΄ ἀφαίρεμα.
     
     
151. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) (2115: 060) “Hippolytus. Refutatio omnium haeresium”, Ed. Marcovich, M. Berlin: De Gruyter, 1986; Patristische Texte und Studien 25. Book 4, chapter 10, section 3, line 4
     
     οὐ γὰρ πιθανὸν οὐδὲ δυνατὸν ἄλογά τε καὶ ἔξω συμφώνων καὶ ἐναρμονίων λόγων εἶναι αὐτῶν τὰ ἀποστήματα, πλὴν ἴσως σελήνης μόνης, ἐκ τῶν λείψεων καὶ τῆς σκιᾶς τῆς γῆς· περὶ ἣν μόνην καὶ πιστεύσαι τις ἂν Ἀρχιμήδῃ περὶ τῆς ἀποστάσεως, τουτέστι τῆς σεληνιακῆς ἀπὸ γῆς.
     
     
152. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 10, section 4, line 2
     
     εἰ δὴ κατὰ τὸν Ἀρχιμήδην ἀπὸ τῆς ἐπιφανείας τῆς γῆς ἡ σελήνη ἀφέστηκε σταδίων μυριάδας φνδ΄, σταδίους ͵δρλ΄, ῥᾴδιον τούτους τοὺς ἀριθμοὺς αὔξοντας κατὰ τὸ διπλάσιον καὶ τριπλάσιον, ὡς ἀξιοῖ Πλάτων, καὶ τὰ τῶν λοιπῶν εὑρεῖν διαστήματα, ὡς μιᾶς μοίρας λαμβανομένης τοῦ τῶν σταδίων ἀριθμοῦ οὓς ἡ σελήνη τῆς γῆς ἀφέστηκεν.
     
     
153. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 11, section 2, line 3
     
     εἰ δὴ πιστὸν τὸν Ἀρχιμήδην ἡγησάμεθα ἐν μόνῳ τῷ πρώτῳ ἀποστήματι τῷ ἀπὸ σελήνης μέχρι γῆς, ῥᾴδιον καὶ τὰ λοιπὰ κατὰ τὸ διπλάσιον καὶ τριπλάσιον αὔξοντας εὑρεῖν.
     
     
154. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 11, section 3, line 1
     
     ἔστω δὴ κατὰ τὸν Ἀρχιμήδην τὸ ἀπὸ γῆς μέχρι σελήνης ἀπόστημα σταδίων μυριάδας φνδ΄, μονάδας ͵δρλ΄· ἔσται μὲν δὴ τούτου διπλάσιος ἀριθμός, ὃν ἀφέστηκεν ὁ ἥλιος τῆς σελήνης, σταδίων μυριάδας ͵αρη΄ καὶ σταδίους͵ ησξ΄· ἀπὸ δὲ τῆς γῆς ἀφέστηκεν ὁ ἥλιος σταδίων μυριάδας ͵αχξγ΄ καὶ σταδίους ͵βτϙ΄· καὶ Ἀφροδίτη δὲ ἀφέστηκεν ἀπὸ μὲν ἡλίου σταδίων μυριάδας ͵αχξγ΄ καὶ σταδίους ͵βτϙ΄, ἀπὸ δὲ γῆς μυριάδας ͵γτκϛ΄, σταδίους ͵δψπ΄· Ἑρμῆς δὲ Ἀφροδίτης μὲν ἀφέστηκε σταδίων μυριάδας ͵βσιζ΄, σταδίους ͵ϛφκ΄, ἀπὸ δὲ γῆς μυριάδας ͵εφμδ΄, σταδίους ͵ατ΄· Ἄρης δὲ Ἑρμοῦ μὲν ἀφέστηκε σταδίων μυριάδας ͵δϡπθ΄, σταδίους ͵ζρο΄, ἀπὸ
     
     
155. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 8, section 7, line 1
     
     ἐπιφανείας τῆς γῆς ἐπὶ τὸν σεληνιακὸν κύκλον ὁ μὲν Σάμιος Ἀρίσταρχος ἀναγράφει σταδίων μ(υριάδας) ρξη΄, ὁ δὲ Ἀπολλώνιος μυριάδας φ΄, ὁ δὲ Ἀρχιμήδης μυριάδας φνδ΄ καὶ μονάδας ͵δρλ΄· ἀπὸ δὲ τοῦ σεληνιακοῦ ἐπὶ τὸν τοῦ ἡλίου κύκλον σταδίων μυριάδας ͵εκϛ΄ καὶ μονάδ(ας) ͵βξε΄· ἀπὸ τούτου δὲ ἐπὶ τὸν τῆς Ἀφροδίτης κύκλον σταδίων μυριάδας ͵βκζ΄ καὶ μονάδας ͵βξε΄· ἀπὸ τούτου δὲ ἐπὶ τὸν τοῦ Ἑρμοῦ κύκλον σταδίων μυριάδας ͵επα΄, μονάδ(ας) ͵ζρξε΄· ἀπὸ τούτου δὲ ἐπὶ τὸν τοῦ Πυρόεντος κύκλον σταδίων μυριάδας ͵δνδ΄, μονάδ(ας) ͵αρη΄· ἀπὸ τούτου δὲ ἐπὶ τὸν τοῦ Διὸς κύκλον σταδίων μυριάδας ͵βκζ΄, μονάδ(ας) ͵εξε΄· ἀπὸ τούτου δὲ ἐπὶ τὸν τοῦ Κρόνου κύκλον σταδίων μυριάδας ͵δλζ΄, μονάδ(ας) ͵βξε΄· ἀπὸ τούτου δὲ ἐπὶ τὸν ζῳδιακὸν καὶ τὴν ἐσχάτην περιφέρειαν σταδίων μυριάδας ͵βη΄, μονάδ(ας) ͵βε΄.
     
     
156. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 10, section 1, line 1
     
     Τὰ μὲν οὖν ἀποστήματα καὶ βάθη τῶν σφαιρῶν οὕτως Ἀρχιμήδης ἀποδίδωσιν, ἑτέρως δὲ ὑπὲρ αὐτῶν Ἱππάρχῳ εἴρηται καὶ ἑτέρως Ἀπολλωνίῳ τῷ μαθηματικῷ.
     
     
157. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 9, section 1, line 2
     
     Τὰ μέντοι ἀπ' ἀλλήλων διαστήματα τῶν κύκλων καὶ τῶν σφαιρῶν βάθη ἑτέρως ὑπὸ τοῦ Ἀρχιμήδους ἀποδίδοται.
     
     
158. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 10, section 2, line 1
     
     οἱ δ' ἐκτεθέντες ὑπὸ Ἀρχιμήδους ἀριθμοὶ καὶ οἱ ὑπὸ τῶν ἄλλων περὶ τῶν ἀποστημάτων λεγόμενοι λόγοι εἰ μὴ ἐν συμφώνοις εἶεν λόγοις – τουτέστι τοῖς ὑπὸ Πλάτωνος εἰρημένοις διπλασίοις καὶ τριπλασίοις – , ἔξω δὲ συμφώνων εὑρισκόμενοι, οὐκ ἂν σῴζοιεν τὸ καθ᾿ ἁρμονίαν κατεσκευάσθαι τὸ πᾶν.
     
     
159. Hippolytus Scr. Eccl., Refutatio omnium haeresium (= Philosophumena) Book 4, chapter 10, section 5, line 1
     
     Ὅτι δὲ οἱ λοιποὶ ἀριθμοὶ οἱ ὑπ' Ἀρχιμήδους περὶ τῆς ἀποστάσεως τῶν πλανωμένων λεγόμενοι οὐκ ἐν συμφώνοις εἰσὶ λόγοις, ῥᾴδιον γνῶναι τοὺς πῶς ἔχουσι πρὸς ἀλλήλους καὶ ἐν τίσι λόγοις εἰσὶ κατανοήσαντας· μὴ εἶναι δὲ ἐν ἁρμονίᾳ καὶ συμφωνίᾳ ταῦτα, τ(οῦ) καθ᾿ ἁρμονίαν συνεστῶτος κόσμου ὄντα μέρη, ἀδύνατον.
     
     
160. Achilles Tatius Astron., Isagoga excerpta (2133: 001) “Commentariorum in Aratum reliquiae”, Ed. Maass, E. Berlin: Weidmann, 1898, Repr. 1958. Section 4, line 17
     
     ἔξωθεν δὲ τὴν τοῦ πυρὸς σφαῖραν καὶ ἐνδοτέρω, μετὰ ταύτην δέ, τὴν τοῦ ἀέρος δεδώκασιν οἱ Ἀρχιμήδειοι περιδινεῖσθαι, ἐν μέσωι δ' εἶναι τὴν τοῦ ὕδατος καὶ τὴν τῆς γῆς διὰ τὴν τοιαύτην αἰτίαν· εἴ τις γὰρ (φασί) λάβοι τῶν σωμάτων τὰ βαρύτατα, οἷον μόλιβδον, καὶ πάλιν αὐτὰ τὰ κουφότατα, οἷον φελλόν, [ἐξίσης] καὶ ἴσα ἀλλήλοις στήσειε καὶ ἰσόσταθμα ποιήσειε καὶ συνδήσειε, συμβήσεται μηδέτερον ὑπὸ τοῦ ἑτέρου ἕλκεσθαι· οἷον, εἴ τις βάλοι ταῦτα εἰς θάλασσαν, συμβήσεται μήτε κάτω εἰς τὸν βυθὸν καθέλκεσθαι τὸν φελλὸν ὑπὸ τοῦ μολίβδου μήτε τὸν μόλιβδον ὑπὸ τοῦ φελλοῦ ἀνέλκεσθαι εἰς τὴν ἐπιφάνειαν τοῦ ὕδατος, ἀλλ' ὡς ἐπίσης ὑπ' ἀλλήλων
     
     
161. Chronicon Paschale, “Chronicon paschale, vol. 1”, Ed. Dindorf, L. Bonn: Weber, 1832; Corpus scriptorum historiae Byzantinae. Page 332, line 6
     
     Σκιπίωνος τὸ β΄ καὶ Ῥούφου. Ἀρχιμήδης μηχανικὸς ἐγνωρίζετο.
     
     
162. Michael PsellusPolyhist., Orationes panegyricae (2702: 006) “Michaelis Pselli orationes panegyricae”, Ed. Dennis, G.T. Stuttgart: Teubner, 1994. Oration 1, line 240
     
     καὶ τίς Ἀρχιμήδης τῶν στοιχείων μετήλλαξε τὰς ῥοπάς;
     
     
163. Michael PsellusPolyhist., Orationes panegyricae Oration 17, line 559
     
     οὕτως ὁ ἀρχιερεὺς ἀντ' ἄλλου φυλακτηρίου πᾶσιν ἐστίν, οἷα δή τι χάλκεον τεῖχος ὅλην τὴν ἐκκλησίαν περιλαμβάνων, καὶ πᾶν ἐκεῖθεν τὸ βάρβαρον ἐμπιπρῶν, οὐχ ὡς ὁ ἐκ Σικελῶν Ἀρχιμήδης μηχαναῖς τισιν ἀστραπὰς ἐκεῖθεν ἐκπυῤῥηνίζων, ἀλλὰ θείῳ πυρὶ καταφλέγων τοὺς προσύλους καὶ φρυγανώδεις καὶ τὴν γνώμην καὶ τὴν προαίρεσιν.
     
     
164. Michael PsellusPolyhist., Orationes panegyricae Oration 4, line 415
     
     ἀλλὰ καινὰ ταῦτα καὶ Ἀρχιμήδεια, σὺ δέ μοι καὶ τἆλλα κατανοῶν θαύμαζε, τείχη νεάζοντα ἢ πρώτως νῦν ἐγειρόμενα, πόλεις ὅλας ἐφ' ἡμέρας οἰκοδομουμένας μιᾶς, οὐ πλίνθοις ὀπταῖς ὥσπερ ἡ Περσὶς Κτησιφῶν τὸ θρυλλούμενον φρούριον, ἀλλ' ἀῤῥαγέσι λίθοις κειμένοις παρ' ἑκάστην πλευράν, ἵνα συνεχὲς δόξῃ τὸ συνημμένον καὶ τὸ ἡρμοσμένον ὁμοφυές.
     
     
165. Michael PsellusPolyhist., Oratoria minora (2702: 009) “Michaelis Pselli oratoria minora”, Ed. Littlewood, A.R. Leipzig: Teubner, 1985. Oration 8, line 168
     
     Τὰ δὲ Ἥρωνος καὶ Ἀρχιμήδους, ἐφ' οἷς αὐτὸς πεποίηκα χαλκεύων ἐτράνωσα ἀπὸ σίφωνός τε καμπύλου τὸ ὕδωρ ᾐώρησα· καὶ τετρημένον ἄγγος ἐπέχον τοῦτο ἐποίησα ἐξ αὐτοῦ τε τοῦ στομίου δύο τῶν ὑγρῶν φύσεων ἀμίκτως ἐξέχεον· καὶ βοῦν ἀθρόον τοῦ νάματος σπῶντα τοῖς πολλοῖς ὑμῖν ἐπ᾿ ὄψεσι τέθεικα, μελαγκορύφῳ φωνὴν ἐνῆκα καὶ χαλκαῖς πτερύγεσιν ἐχαρισάμην αὐτόματον κίνησιν· κάτοπτρόν τέ μοι ἐξείργαστο ἀφ' οὗ δὴ πῦρ αὐτομάτως ἐξαλλόμενον τὸ ἐκ διαστήματος παρατιθέμενον παραδόξως τεφροῖ.
     
     
166. Michael PsellusPolyhist., Opuscula logica, physica, allegorica, alia (2702: 010) “Michaelis Pselli philosophica minora”, Ed. Duffy, J.M. Leipzig: Teubner, 1992. Opusculum 31, line 93
     
     ἐπεὶ καὶ Ἀρχιμήδης ὁ Σικελὸς ᾔδει μὲν ὡς ἐξ ἐνόπτρων τινῶν κατασκευὴν τὴν προσήκουσαν δεξαμένων καὶ πρὸς ἡλιακὰς ἀντιτεθέντων ἀκτῖνας πῦρ ἐκ συμμέτρου διαστήματος ἐξαφθήσεται, καὶ πολλὰ τοιαῦτά γε κατεσκεύακε δι' ὧν τὰ τείχη τῆς πατρίδος διεφυλάξατο, τοῖς πολεμίοις πυρκαϊὰς ὅλας ἐκεῖθεν ἀνάψας, οὐκ ἐπὶ πάντων δὲ τῶν ὀργάνων τοῦ σκοποῦ ἐπετύγχανεν.
     
     
167. Constantinus VII Porphyrogenitus Imperator Hist., De thematibus (3023: 009) “Costantino Porfirogenito. De thematibus”, Ed. Pertusi, A. Vatican City: Biblioteca Apostolica Vaticana, 1952; Studi e Testi 160. Asia-Europe Europ, chapter 10, line 44
     
     Τὸ δὲ ἀρχαῖον αὕτη ἡ νῆσος ἐτυραννεῖτο, ἵνα μὴ λέγω ἐβασιλεύετο, ὑπό τε Ἱέρωνος καὶ Διονυσίου τοῦ τυράννου· παρέλαβον δὲ αὐτὴν οἱ Ῥωμαῖοι μετὰ στόλου μεγάλου, ὅτε Μάρκελλος ἐκεῖνος ἐστρατήγει καὶ ναύαρχος τοῦ Ῥωμαϊκοῦ στόλου ἀνεδείκνυτο, ὅτε καὶ Ἀρχιμήδης ὁ γεωμέτρης ἐν αὐταῖς ταῖς Συρακούσαις ὤν, νυκτὸς ἁλούσης τῆς πόλεως, ὑπὸ στρατιώτου τινὸς ἀνῃρέθη· ὃν ὁ Μάρκελλος ἐκεῖνος τοσοῦτον ἐθρήνησεν, ὡς μηδένα κοπετὸν ἀπολειφθῆναι τῆς ἐκείνου ταφῆς.
     
     
168. Georgius Syncellus Chronogr., Ecloga chronographica (3045: 001) “Georgius Syncellus. Ecloga chronographica”, Ed. Mosshammer, A.A. Leipzig: Teubner, 1984. Page 344, line 16
     
     Τότε καὶ Ἀρχιμήδης γεωμέτρης τοῖς μηχανήμασι Ῥωμαίους ἀπώσατο πολλάκις πολιορκοῦντας Συρακούσας, οἰκῶν ἐν αὐταῖς.
     
     
169. Joannes Scylitzes Hist., Synopsis historiarum (3063: 001) “Ioannis Scylitzae synopsis historiarum”, Ed. Thurn, J. Berlin: De Gruyter, 1973; Corpus fontium historiae Byzantinae 5. Series Berolinensis. Emperor life Leo6, section 34, line 26
     
     ἀνέγνωσε δὲ καὶ τὰ Ἀρχιμήδεια ἀκριβῶς καὶ ὡς οὐδεὶς ἕτερος τῶν κατ' αὐτόν. παραδοὺς τοίνυν, ὡς εἴρηται, τὸ τῆς βασιλείας κράτος, καὶ πολλὰ παρακαλέσας τὸν αὐτοῦ υἱὸν Κωνσταντῖνον παιδοτροφῆσαι καὶ ἐπιμελείας ἀξιοῦν προσηκούσης, τελευταῖον δὲ καὶ διάδοχον αὐτοῦ καταλιπεῖν, ἐτελεύτησεν.
     
     
170. Pseudo-Mauricius Tact., Strategicon (sub nomine Mauricii Imperatoris vel Urbicii) (3075: 001) “Mauricius. Arta militara”, Ed. Mihaescu, H. Bucharest: Academie Republicii Socialiste România, 1970; Scriptores Byzantini 6. Book 12, chapter 9,1, section 15, line 3
     
     Μὴ τοίνυν, ἐπειδὴ πρῶτον ἐπινενόηται μηδὲ ἐν ἔργοις ἔτι τὴν ὠφέλειαν ἔδειξε καταφρονεῖσθαι ὡς παρὰ ἀπείρου πολέμων ἐκτεθεῖσαν· ἡ γὰρ Ἀρχιμέδους βοηθήσει τέχνη τοῖς στρατεύμασιν ἢ τὰς βαλλίστρας τεχνεσαμένη τὸ ἀκαταμάχητον ὅπλον καὶ οὐκ ἀσχολήσει τηλικοῦτον ὅπλον, οἷον οὐδὲν ἄλλο παρὰ τῆς σοφῆς τέχνης ἐπινενόηται.
     
     
171. Pseudo-Mauricius Tact., Strategicon (sub nomine Mauricii Imperatoris vel Urbicii) Book 12, chapter 9,1, section 17, line 2
     
     Καὶ τελεία νῦν ἔσται μετὰ Ἀρχιμέδους καμοῦσα σοφία ἐπὶ τοῦ καλλινίκου καὶ αὐτοκράτορος ἡμῶν βασιλέως Ἀναστασίου, ὅτε τέως ἀπείρως ἔχων ὁ στρατιώτης ἐν ἀκινδύνοις μελέταις καταφρονεῖν τῶν πολεμίων ἐθισθήσεται.
     
     
172. Theophylactus Simocatta Epist., Hist., Epistulae (3130: 001) “Theophylacti Simocatae epistulae”, Ed. Zanetto, G. Leipzig: Teubner, 1985. Epistle 73, line 6
     
     ἆρά γε, Ἀρχίμηδες, οὐ πολύπους τὴν γνώμην εἶναι τοῖς ὅλοις δοκεῖς;
     
     
173. Theophylactus Simocatta Epist., Hist., Epistulae Epistle 73, line 1t
     
     Πρόκλος Ἀρχιμήδει Τοὺς πολύποδάς φασιν ἀθηρίας τυγχάνοντας τοὺς ἑαυτῶν κατεσθίειν πλοκάμους, ὄψον ὥσπερ ἀληθῶς ἐμπαράσκευον τὰ ἑαυτῶν ποιουμένους δυστυχέστατα μέλη.
     
     
174. Joannes Zonaras Gramm., Hist., Epitome historiarum (lib. 1–12) (3135: 001) “Ioannis Zonarae epitome historiarum, 3 vols.”, Ed. Dindorf, L. Leipzig: Teubner, 1:1868; 2:1869; 3:1870. Volume 2, page 264, line 29
     
     ἐγκρατεῖς δὲ τούτων οἱ Ῥωμαῖοι γενόμενοι ἄλλους τε πολλοὺς καὶ τὸν Ἀρχιμήδην ἀπέκτειναν.
     
     
175. Joannes Zonaras Gramm., Hist., Epitome historiarum (lib. 1-12) Volume 2, page 262, line 27
     
     καὶ δι' ἐλαχίστου ἂν αὐτὰς ἐχειρώσατο καὶ κατὰ γῆν καὶ κατὰ θάλασσαν ἅμα προςβαλὼν τῷ τείχει, εἰ μὴ ὁ Ἀρχιμήδης μηχαναῖς ἐπὶ πλεῖστον αὐτοὺς ἐποίησεν ἀντισχεῖν.
     
     
176. Joannes Zonaras Gramm., Hist., Epitome historiarum (lib. 1-12) Volume 2, page 263, line 10
     
     ἀπογνοὺς οὖν ὁ Μάρκελλος τὴν πόλιν αἱρήσειν διὰ τὸ τοῦ Ἀρχιμήδους εὐμήχανον, λιμῷ αὐτοὺς κατασχεῖν ἐκ προσεδρείας διεμελέτησε.
     
     
177. Joannes Zonaras Gramm., Hist., Epitome historiarum (lib. 13–18) (3135: 002) “Ioannis Zonarae epitomae historiarum libri xviii, vol. 3”, Ed. Büttner–Wobst, T. Bonn: Weber, 1897; Corpus scriptorum historiae Byzantinae. Page 138, line 10
     
     κάτοπτρα γὰρ ᾄδεται χαλκεῦσαι πυρφόρα ὁ Πρόκλος, καὶ ταῦτα ἐκ τοῦ τείχους τῶν πολεμίων νεῶν ἀπαιωρῆσαι κατέναντι, τούτοις δὲ τῶν τοῦ ἡλίου ἀκτίνων προσβαλουσῶν πῦρ ἐκεῖθεν ἐκκεραυνοῦσθαι καταφλέγον τὸν νηίτην τῶν ἐναντίων στρατόν, καὶ τὰς νῆας αὐτάς, ὃ πάλαι τὸν Ἀρχιμήδην ἐπινοῆσαι ὁ Δίων ἱστόρησε, τῶν Ῥωμαίων τότε πολιορκούντων Συράκουσαν.
     
     
178. Joannes Zonaras Gramm., Hist., Epitome historiarum (lib. 13-18) Page 138, line 4
     
     τοῦ μέντοι Θρᾳκὸς Βιταλιανοῦ τυραννίδι ἐπικεχειρηκότος, Μυσούς τε καὶ Σκύθας προσεταιρισαμένου, καὶ ἅμα τούτοις τὰ περὶ τὴν βασιλίδα ληιζομένου τῶν πόλεων, ἀλλὰ μὴν καὶ στόλῳ κατ' αὐτῆς ἐπελθόντος, ἀντικατέστη τούτῳ διὰ Μαριανοῦ τοῦ ὑπάρχου ὁ Ἀνα- στάσιος, καὶ ναυμαχίας γενομένης ἔκ τινος μηχανῆς παρὰ Πρόκλου τοῦ πάνυ γεγενημένης (τότε γὰρ ἤνθει ἐπὶ φιλοσοφίᾳ καὶ ἐν τοῖς μηχανήμασι, τά τε τοῦ περιβοήτου ἐν τούτοις Ἀρχιμήδους ἅπαντα διελθὼν καὶ αὐτὸς ἐκείνοις προσεξευρών) τὸ ναυτικὸν τῶν ἐναντίων κατεπολεμήθη.
     
     
179. Simplicius Phil., In Aristotelis quattuor libros de caelo commentaria (4013: 001) “Simplicii in Aristotelis de caelo commentaria”, Ed. Heiberg, J.L. Berlin: Reimer, 1894; Commentaria in Aristotelem Graeca 7. Volume 7, page 543, line 32
     
     τὰ μὲν οὖν κεντροβαρικά, οἷα πολλὰ καὶ χαριέστατα ὅ τε Ἀρχιμήδης καὶ ἄλλοι γεγράφασι πολλοί, σκοπὸν ἔχει, πῶς τοῦ δοθέντος βάρους τὸ κέντρον εὑρεθείη, τουτέστι σημεῖόν τι ἐπὶ τοῦ σώματος, ἀφ' οὗ σπάρτου τινὸς ἐξαφθείσης μετεωριζόμενον ἀκλινὲς ἔσται τὸ σῶμα· δῆλον δέ, ὅτι οὐ πάντως τὸ αὐτὸ ἔσται μέσον τοῦ τε μεγέθους καὶ τοῦ βάρους.
     
     
180. Simplicius Phil., In Aristotelis quattuor libros de caelo commentaria Volume 7, page 412, line 15
     
     ἐλαχίστη δὲ κίνησις ἡ ἐν ἐλαχίστῳ χρόνῳ γινομένη· ἐν ἐλαχίστῳ δὲ χρόνῳ τὸ ἴσον περίεισιν ἡ ταχίστη· ταχίστη δὲ ἀπὸ τῆς αὐτῆς δυνάμεως ἡ τὸ ἴσον μὲν περιιοῦσα χωρίον, οἷον δεκάπλεθρον ἐμβαδόν, δι' ἐλαχίστης δὲ τῆς περιεχούσης αὐτὸ διαστάσεως, ἵνα τῆς αὐτῆς μενούσης τῆς τὸ αὐτὸ χωρίον περιιούσης ἐλαχίστη καὶ ἅμα ταχίστη γένηται ἡ κίνησις καὶ παρὰ τὸν χρόνον καὶ παρὰ τὴν διάστασιν τὴν περιέχουσαν· ἐλαχίστη δὲ τῶν ἀπὸ τοῦ αὐτοῦ ἐπὶ τὸ αὐτό, τουτέστι τῶν σχῆμα περιεχουσῶν τι καὶ ὁριζουσῶν διαστάσεων, ἐν μὲν ἐπιπέδοις ἡ κυκλική, ἐν δὲ στερεοῖς ἡ σφαιρική, διότι δέδεικται καὶ πρὸ Ἀριστοτέλους μὲν πάντως, εἴπερ αὐτὸς ὡς δεδειγμένῳ συγκέχρηται, καὶ παρὰ Ἀρχιμήδους καὶ παρὰ Ζηνοδώρου πλατύτερον, ὅτι τῶν ἰσοπεριμέτρων σχημάτων πολυχωρητότερός ἐστιν ἐν μὲν τοῖς ἐπιπέδοις ὁ κύκλος, ἐν δὲ τοῖς στερεοῖς ἡ σφαῖρα.
     
     
181. Simplicius Phil., In Aristotelis quattuor libros de caelo commentaria Volume 7, page 549, line 11 ἐπεὶ δὲ δείκνυται ὑπὸ Ἀρχιμήδους ἡ περίμετρος τοῦ κύκλου τριπλασίων τῆς διαμέτρου καὶ ἔτι ἑβδόμῳ μέρει αὐτῆς ὑπερέχουσα, ἔσται ἡ διάμετρος μυριάδων πέντε καὶ ἑπτακισχιλίων διακοσίων ἑβδομήκοντα τριῶν.
     
     
182. Simplicius Phil., In Aristotelis quattuor libros de caelo commentaria Volume 7, page 550, line 10
     
     κἂν διαφωνῇ δέ, θαυμαστὸν οὐδέν· οὔπω γὰρ ηὕρητο τὰ ὑπὸ Ἀρχιμήδους πορισθέντα θεωρήματα πρὸς τὴν ἀκαμπῆ τοῦ προκειμένου κατάληψιν.
     
     
183. Simplicius Phil., In Aristotelis categorias commentarium (4013: 003) “Simplicii in Aristotelis categorias commentarium”, Ed. Kalbfleisch, K. Berlin: Reimer, 1907; Commentaria in Aristotelem Graeca 8. Volume 8, page 192, line 20
     
     καὶ ὕστερον δέ, φησίν, Ἀρχιμήδης διὰ τῆς † Λυκομήδους γραμμῆς καὶ Νικομήδης διὰ τῆς ἰδίως τετραγωνιζούσης καλουμένης καὶ Ἀπολλώνιος διά τινος γραμμῆς, ἣν αὐτὸς μὲν κοχλιοειδοῦς ἀδελφὴν προσαγορεύει, ἡ αὐτὴ δέ ἐστιν τῇ Νικομήδους, καὶ Κάρπος δὲ διά τινος γραμμῆς, ἣν ἁπλῶς ἐκ διπλῆς κινήσεως καλεῖ, ἄλλοι τε πολλοὶ ποικίλως τὸ πρόβλημα κατεσκεύασαν”, ὡς Ἰάμβλιχος ἱστορεῖ.
     
     
184. Simplicius Phil., In Aristotelis physicorum libros commentaria (4013: 004) “Simplicii in Aristotelis physicorum libros octo commentaria, 2 vols.”, Ed. Diels, H. Berlin: Reimer, 9:1882; 10:1895; Commentaria in Aristotelem Graeca 9 and 10. Volume 9, page 60, line 12
     
     καὶ ὕστερον δέ, φησίν, Ἀρχιμήδης διὰ τῆς ἑλικοειδοῦς γραμμῆς καὶ Νικομήδης διὰ τῆς ἰδίως Τετραγωνιζούσης καλουμένης καὶ Ἀπολλώνιος διά τινος γραμμῆς, ἣν αὐτὸς μὲν κοχλιοειδοῦς ἀδελφὴν προσαγορεύει, ἡ αὐτὴ δέ ἐστι τῇ Νικομήδους, καὶ Κάρπος δὲ διά τινος γραμμῆς ἣν ἁπλῶς ‘ἐκ διπλῆς κινήσεως’ καλεῖ, ἄλλοι τε πολλοί, φησί, ποικίλως τὸ πρόβλημα κατεσκεύασαν”.
     
     
185. Simplicius Phil., In Aristotelis physicorum libros commentaria Volume 10, page 1110, line 4
     
     ταύτῃ δὲ τῇ ἀναλογίᾳ τοῦ κινοῦντος καὶ τοῦ κινουμένου καὶ τοῦ διαστήματος τὸ σταθμιστικὸν ὄργανον τὸν καλούμενον χαριστίωνα συστήσας ὁ Ἀρχιμήδης ὡς μέχρι παντὸς τῆς ἀναλογίας προχωρούσης ἐκόμπασεν ἐκεῖνο τὸ πᾷ βῶ καὶ κινῶ τὰν γᾶν;
     
     
186. Simplicius Phil., In Aristotelis physicorum libros commentaria Volume 9, page 59, line 30
     
     καὶ διὰ τοῦτο ἴσως, φησί, καὶ ὑπὸ οὕτως κλεινῶν ἀνδρῶν ζητηθὲν τὸ θεώρημα ἄχρι νῦν οὐχ εὑρέθη οὐδὲ ὑπ' αὐτοῦ τοῦ Ἀρχιμήδους.
     
     
187. Joannes Philoponus Phil., In Aristotelis categorias commentarium (4015: 001) “Philoponi (olim Ammonii) in Aristotelis categorias commentarium”, Ed. Busse, A. Berlin: Reimer, 1898; Commentaria in Aristotelem Graeca 13.1. Volume 13,1, page 121, line 2
     
     μόνος δὲ Ἀρχιμήδης τὸ σύνεγγυς παντὶ εὗρε, τὸ μέντοι ἀκριβὲς οὐχ εὗρε.
     
     
188. Ammonius Phil., In Aristotelis categorias commentarius (4016: 002) “Ammonius in Aristotelis categorias commentarius”, Ed. Busse, A. Berlin: Reimer, 1895; Commentaria in Aristotelem Graeca 4.4. Page 75, line 14
     
     μόνος δὲ ὁ θεῖος Ἀρχιμήδης τὸ σύνεγγυς παντὶ εὗρε, τὸ μέντοι ἀκριβὲς μέχρι τοῦ νῦν οὐχ εὕρηται.
     
     
189. Olympiodorus Phil., In Aristotelis categorias commentarium (4019: 002) “Olympiodori prolegomena et in categorias commentarium”, Ed. Busse, A. Berlin: Reimer, 1902; Commentaria in Aristotelem Graeca 12.1. Page 106, line 7
     
     οἷον ἀποδεδώκαμεν τὸν δοῦλον πρὸς Σωκράτην καὶ δεσπότην· πρὸς μὲν δεσπότην κυρίως ἀποδίδομεν, ὡς ἴσμεν ἐκ τοῦ εἰρημένου κανόνος, πρὸς δὲ τὸν Σωκράτην οὐ πάντως· ἐὰν γὰρ ἀποδῶ τὸν δοῦλον πρὸς δεσπότην, ἀνέλω δὲ τὰ παρεπόμενα τῷ δεσπότῃ, τοῦτ' ἔστι τὸν Σωκράτην, τὸν Ἀθηναῖον, τὸν σιμόν, τὸν προγάστορα, τὸν φαλακρόν, τὸν Σωφρονίσκου Ἀρχιμήδους, οὐδ' ἓν παρέβλαψα τὴν δεσποτικὴν σχέσιν, ἀλλ' ἔτι καὶ πάντων τούτων ἀναιρουμένων ὁ δοῦλος δεσπότου δοῦλός ἐστιν.
     
     
190. Olympiodorus Phil., In Aristotelis meteora commentaria (4019: 003) “Olympiodori in Aristotelis meteora commentaria”, Ed. Stüve, G. Berlin: Reimer, 1900; Commentaria in Aristotelem Graeca 12.2. Page 119, line 31
     
     πλὴν ὁ τρίτος Πτολεμαῖος, ἐφ' οὗ καὶ Ἀρχιμήδης ἐγένετο, † τῆς τοῦ ἡλίου ὑποθήκης διώρυχα ἐποίησε, δι' ἧς δυνατόν ἐστι συνάπτεσθαι τῷ Αἰγυπτιακῷ πελάγει τὴν Ἐρυθρὰν καὶ μὴ κατακλυσθῆναι τὴν Αἴγυπτον.
     
     
191. Olympiodorus Phil., In Aristotelis meteora commentaria Page 211, line 18
     
     ἄλλως τε καὶ Ἀρχιμήδης αὐτὸ τοῦτο δείκνυσιν, ὅτι κλᾶται ἡ ὄψις, ἐκ τοῦ δακτυλίου τοῦ ἐν ἀγγείῳ βαλλομένου.
     
     
192. Olympiodorus Phil., In Platonis Alcibiadem commentarii (4019: 004) “Olympiodorus. Commentary on the first Alcibiades of Plato”, Ed. Westerink, L.G. Amsterdam: Hakkert, 1956, Repr. 1982. Section 191, line 14
     
     καὶ Ἀρχιμήδης μὲν μετὰ τὴν εὕρεσιν τοῦ βαρυούλκου, ἐν ᾧ ἔδειξεν ὅτι τῇ τυχούσῃ δυνάμει τὸ τυχὸν βάρος κινήσει, ἐπειδὴ ὅσον ἐπὶ τούτῳ καὶ εἶς ἄνθρωπος ἠδύνατο κινῆσαι τὴν γῆν, μέγα ἐφθέγξατο καὶ ἀδύνατον, ὅτι ‘πᾷ βῶ καὶ κινῶ τὰν γᾶν’· ἀδύνατον γὰρ μὴ εἶναι ἐν τόπῳ· Σωκράτης δὲ εὐτελῆ αἰτεῖ.
     
     
193. Olympiodorus Phil., In Platonis Gorgiam commentaria (4019: 005) “Olympiodori in Platonis Gorgiam commentaria”, Ed. Westerink, L.G. Leipzig: Teubner, 1970. Chapter 38, section 2, line 10
     
     ἔτι δὲ πλέον μεγίστη ἐστὶν ἡ μηχανικὴ ὡς πόλεις ὅλας σῴζουσα· οὕτω γοῦν ὁ Ἀρχιμήδης διὰ τῶν πυρίων τὰς τριήρεις κατέφλεξε καὶ πόλιν ὅλην ἔσωσεν.
     
     
194. Elias Phil., In Porphyrii isagogen (4020: 001) “Eliae in Porphyrii isagogen et Aristotelis categorias commentaria”, Ed. Busse, A. Berlin: Reimer, 1900; Commentaria in Aristotelem Graeca 18.1. Page 28, line 34
     
     καὶ Ἀρχιμήδης δέ ποτε βαρβάρων ἐπιστάντων ταῖς Συρακούσαις οὐκ ἔφυγεν θεώρημά τι γεωμετρικὸν καταγράφων, ἀλλ' ἔφη “τὰν κεφαλὰν καὶ μὴ τὰν γραμμάν”, τοῦτ' ἔστι παρὰ τὴν κεφαλὴν καὶ μὴ παρὰ τὴν γραμμήν.
     
     
195. Proclus Phil., In Platonis Timaeum commentaria (4036: 010) “Procli Diadochi in Platonis Timaeum commentaria, 3 vols.”, Ed. Diehl, E. Leipzig: Teubner, 1:1903; 2:1904; 3:1906, Repr. 1965. Volume 2, page 76, line 21
     
     δι' ἐκείνων ἱκανῶς πεπαιδευμένον ποιούμεθα τοὺς λόγους· τοσοῦτον δὲ ὅμως ἱστορητέον, ὅτι τῶν ἰσοπλεύρων τε καὶ ἰσογωνίων καὶ ἴσην περίμετρον ἐχόντων τὸ πολυγωνότερον μεῖζον ἀποδείξαντες πρῶτον καὶ τὸν κύκλον ἑξῆς μείζονα τῶν ἰσοπλεύρων καὶ ἰσογωνίων, ἰσοπεριμέτρων δέ, δεικνύουσι καὶ τὴν σφαῖραν τῶν ἴσην ἐπιφάνειαν ἐχόντων στερεῶν σχημάτων ἑπομένως μείζονα καὶ διαφερόντως τῶν παρὰ Πλάτωνι λεγομένων πολυέδρων ἰσοπλεύρων καὶ ἰσογωνίων, τὰ μὲν χρώμενοι τοῖς παρὰ τῷ Εὐκλείδῃ δειχθεῖσι, τὰ δὲ τοῖς παρὰ τῷ Ἀρχιμήδει.
     
     
196. Proclus Phil., In primum Euclidis elementorum librum commentarii (4036: 011) “Procli Diadochi in primum Euclidis elementorum librum commentarii”, Ed. Friedlein, G. Leipzig: Teubner, 1873. Page 272, line 10
     
     ἄλλοι δὲ ἐκ τῶν Ἀρχιμηδείων ἑλίκων ὁρμηθέντες εἰς τὸν δοθέντα λόγον ἔτεμον τὴν δοθεῖσαν εὐθύγραμμον γωνίαν· ὧν τὰς ἐπινοίας δυσθεωρήτους οὔσας τοῖς εἰσαγομένοις παραλείπομεν ἐν τῷ παρόντι.
     
     
197. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 41, line 7
     
     Πρὸς δὴ ταύταις ἡ μηχανικὴ καλουμένη τῆς περὶ τὰ αἰσθητὰ καὶ τὰ ἔνυλα πραγματείας μέρος ὑπάρχουσα, ὑπὸ δὲ ταύτην ἥ τε ὀργανοποιϊκὴ τῶν κατὰ πόλεμον ἐπιτηδείων ὀργάνων, οἷα δὴ καὶ Ἀρχιμήδης λέγεται κατασκευάσαι τῶν πολεμούντων τὴν Συράκουσαν ἀμυντικὰ ὄργανα, καὶ ἡ θαυματοποιϊκὴ τὰ μὲν διὰ πνῶν φιλοτεχνοῦσα, ὥσπερ καὶ Κτησίβιος καὶ Ἥρων πραγματεύονται, τὰ δὲ διὰ ῥοπῶν, ὧν τῆς μὲν κινήσεως τὴν ἀνισοῤῥοπίαν αἰτιατέον, τῆς δὲ στάσεως τὴν ἰσοῤῥοπίαν, ὥσπερ καὶ ὁ Τίμαιος διώρισεν, τὰ δὲ διὰ νεύρων καὶ σπάρτων ἐμψύχους ὁλκὰς καὶ κινήσεις ἀπομιμουμένων.
     
     
198. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 41, line 17
     
     ὑπὸ δὲ τὴν μηχανικήν ἐστιν καὶ ἡ τῶν ἰσοῤῥόπων ὅλως καὶ τῶν λεγομένων κεντροβαρικῶν διάγνωσις, καὶ ἡ σφαιροποιΐα κατὰ μίμησιν τῶν οὐρανίων περιφορῶν, οἵαν καὶ Ἀρχιμήδης ἐπραγματεύσατο, καὶ ὅλως πᾶσα ἡ τῆς ὕλης κινητική.
     
     
199. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 63, line 23
     
     πάντων γὰρ ἅμα Συρακουσίων ἑλκῦσαι τὴν ναῦν οὐ δυναμένων Ἀρχιμήδης τὸν Ἱέρωνα μόνον αὐτὴν καταγαγεῖν ἐποίησεν.
     
     
200. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 68, line 12
     
     γέγονε δὲ οὗτος ὁ ἀνὴρ ἐπὶ τοῦ πρώτου Πτολεμαίου· καὶ γὰρ ὁ Ἀρχιμήδης ἐπιβαλὼν καὶ τῷ πρώτῳ μνημονεύει τοῦ Εὐκλείδου, καὶ μέντοι καί φασιν ὅτι Πτολεμαῖος ἤρετό ποτε αὐτόν, εἴ τίς ἐστιν περὶ γεωμετρίαν ὁδὸς συντομωτέρα τῆς στοιχειώσεως· ὁ δὲ ἀπεκρίνατο, μὴ εἶναι βασιλικὴν ἀτραπὸν ἐπὶ γεωμετρίαν.
     
     
201. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 71, line 18
     
     καθάπερ δὴ καὶ ὁ Ἀρχιμήδης ἐν τοῖς περὶ σφαίρας καὶ κυλίνδρου καὶ Ἀπολλώνιος καὶ οἱ ἄλλοι πάντες φαίνονται τοῖς ἐν αὐτῇ τῇ πραγματείᾳ δεδειγμένοις [ὡς] ἀρχαῖς ὁμολογουμέναις χρώμενοι.
     
     
202. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 110, line 10
     
     ὁ δ' αὖ Ἀρχιμήδης τὴν εὐθεῖαν ὡρίσατο γραμμὴν ἐλαχίστην τῶν τὰ αὐτὰ πέρατα ἐχουσῶν.
     
     
203. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 181, line 18
     
     καὶ γὰρ ὁ Ἀρχιμήδης τῶν ἀνισοῤῥοπιῶν ἀρχόμενος· Αἰτούμεθα, φησί, τὰ ἴσα βάρη ἀπὸ τῶν ἴσων μηκῶν ἰσοῤῥοπεῖν.
     
     
204. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 423, line 3
     
     καὶ ὁ Ἀρχιμήδης ἔδειξεν, ὅτι πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ ὀρθογωνίῳ, οὗ ἡ μὲν ἐκ κέντρου ἴση ἐστὶν μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῇ βάσει.
     
     
205. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 63, line 19
     
     καὶ φυλακτήρια τῶν πόλεων διὰ τούτων κατεσκευάσατο καὶ τὰς τῶν ὡρῶν περιόδους γνωρίμους ἐποίησεν καὶ τὰς τῶν τόπων θέσεις, μέτρα τε ὑφηγήσατο τὰ μὲν τῶν κατὰ γῆν ὁδῶν, τὰ δὲ τῶν κατὰ θάλαςσαν, ζυγά τε καὶ τρυτάνας ἐδημιούργησεν, ἀφ' ὧν τὴν κατ' ἀριθμὸν ἰσότητα ταῖς πόλεσι διηκρίβωσεν, τοῦ τε παντὸς κόσμου τὴν τάξιν δι' εἰκόνων ἐμφανῆ κατέστησεν καὶ πολλὰ τοῖς ἀνθρώποις ἀπὸ ἀπίστων ἀνέφηνε καὶ πιστὰ πᾶσιν ἔδειξεν· οἷον δὴ καὶ Ἱέρων ὁ Συρακούσιος εἰπεῖν λέγεται περὶ Ἀρχιμήδους, ὅτε τὴν τριάρμενον κατεσκεύασε ναῦν, ἣν παρεσκευάζετο πέμπειν Πτολεμαίῳ τῷ βασιλεῖ τῷ Αἰγυπτίῳ.
     
     
206. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 68, line 18
     
     νεώτερος μὲν οὖν ἐστι τῶν περὶ Πλάτωνα, πρεσβύτερος δὲ Ἐρατοσθένους καὶ Ἀρχιμήδους.
     
     
207. Proclus Phil., In primum Euclidis elementorum librum commentarii Page 63, line 25
     
     καταπλαγεὶς δὲ ἐκεῖνος Ἀπὸ ταύτης, ἔφη, τῆς ἡμέρας περὶ παντὸς Ἀρχιμήδει λέγοντι πιστευτέον.
     
     
208. Cosmas Indicopleustes Geogr., Topographia Christiana (4061: 002) “Cosmas Indicopleustès. Topographie chrétienne, 3 vols.”, Ed. Wolska–Conus, W. Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes 141, 159, 197. Book 3, section 76, line 6
     
     Ποῦ γὰρ καὶ αὐτοὶ εὑρήσουσιν ἐν ἀστρονόμοις ἴσον ἢ κρείττω Πτολεμαίου, ἢ ἐν φιλοσόφοις Πλάτωνος καὶ Ἀριστοτέλους, ἢ Εὐκλείδους καὶ Ἀρχιμήδου, τοῦ μόνου ἐφευρηκότος τὸν τετραγωνισμὸν τοῦ κύκλου, γεωμέτρας καὶ ἀριθμητικούς;
     
     
209. Damascius Phil., In Philebum (4066: 006) “Damascius. Lectures on the Philebus wrongly attributed to Olympiodorus”, Ed. Westerink, L.G. Amsterdam: North–Holland, 1959, Repr. 1982. Section 232, line 10
     
     μαθηματικαὶ δέ εἰσι δοξαστικῶς προϊοῦσαι αἱ τὴν αἴσθησιν πρὸς κρίσιν παραλαμβάνουσαι, οἶον ἡ Πτολεμαίου ἀστρονομία καὶ ἡ Ἀρχιμήδους μηχανική.
     
     
210. Eutocius Math., Commentarii in libros de sphaera et cylindro (4072: 001) Archimedis opera omnia cum commentariis Eutocii, vol. 3, Ed. Heiberg, J.L., Stamatis, E. Leipzig: Teubner, 1915, Repr. 1972. Page 2, line 22
     
     πρέποι δ' ἄν σοι τῇ ἐμῇ σπουδῇ συνάρασθαι, καὶ εἰ μὲν ἀνεμιαῖον δόξῃ τὸ γράμμα, αὐτόθεν μηδὲ εἰς ἄλλον ἐλθεῖν συγχωρήσῃς, εἰ δὲ τοῦ σκοποῦ μὴ πάντη διαμαρτάνον, δήλωσον, ἣν ἔχεις περὶ αὐτοῦ γνώμην, ὡς εἴ γε τῆ ὑμετέρᾳ κρίσει βεβαιωθῇ, πειράσομαι καὶ ἄλλο τυχὸν τῶν Ἀρχιμηδείων συντάξεων ἑρμηνεῦσαι.
     
     
211. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 130, line 24
     
     ὅθεν καὶ Διονυσόδωρον μὲν εὑρίσκομεν μὴ τῶν αὐτῶν ἐπιτυχόντα, ἀδυνατήσαντα δὲ ἐπιβαλεῖν τῷ καταλειφθέντι λήμματι, ἐφ' ἑτέραν ὁδὸν τοῦ ὅλου προβλήματος ἐλθεῖν, ἥντινα ἑξῆς γράψομεν· Διοκλῆς μέντοι καὶ αὐτὸς ἐν τῷ Περὶ πυρίων αὐτῷ συγγεγραμμένῳ βιβλίῳ ἐπηγγέλθαι νομίζων τὸν Ἀρχιμήδη, μὴ πεποιηκέναι δὲ τὸ ἐπάγγελμα, αὐτὸς ἀναπληροῦν ἐπεχείρησεν, καὶ τὸ ἐπιχείρημα ἑξῆς γράψομεν· ἔστιν γὰρ καὶ αὐτὸ οὐδένα μὲν ἔχον πρὸς τὰ παραλελειμμένα λόγον, ὁμοίως δὲ τῷ Διονυσοδώρῳ δι' ἑτέρας ἀποδείξεως κατασκευάζον τὸ πρόβλημα.
     
     
212. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 160, line 6
     
     Γράφει δὲ καὶ ὁ Διοκλῆς ἐν τῷ Περὶ πυρίων προλέγων τάδε· Ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου Ἀρχιμήδης ἀπέδειξεν, ὅτι πᾶν τμῆμα σφαίρας ἴσον ἐστὶν κώνῳ τῷ βάσιν μὲν ἔχοντι τὴν αὐτὴν τῷ τμήματι, ὕψος δὲ εὐθεῖάν τινα λόγον ἔχουσαν πρὸς τὴν ἀπὸ τῆς τοῦ τμήματος κορυφῆς ἐπὶ τὴν βάσιν κάθετον, ὃν ἔχει συναμφότερος ἥ τε ἐκ τοῦ κέντρου τῆς σφαίρας καὶ ἡ τοῦ ἐναλλὰξ τμήματος κάθετος πρὸς τὴν τοῦ ἐναλλὰξ τμήματος κάθετον.
     
     
213. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 162, line 14
     
     τοῦτο δὲ ἑξῆς δέδεικται· ὁ γὰρ Ἀρχιμήδης μακρότερον αὐτὸ δείξας καὶ οὕτως εἰς πρόβλημα ἕτερον ἀπάγει, ὃ οὐκ ἀποδείκνυσιν ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου.
     
     
214. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 2, line 2
     
     Εἰς τὰ περὶ σφαίρας καὶ κυλίνδρου Ἀρχιμήδους οὐδένα τῶν πρὸ ἡμῶν ἀξίαν εὑρὼν σύνταξιν καταβεβλημένον καὶ κατανοήσας μὴ δι' εὐμάρειαν τῶν θεωρημάτων τοῦτο παροραθῆναι· ἐπιστάσεως γὰρ ἀκριβοῦς, ὡς ἴστε, καὶ εὐεπιβόλου δεῖται φαντασίας· ὠρέχθην κατ' ἐμὴν δύναμιν σαφῶς ἐκθέσθαι τὰ ἐν αὐτοῖς δυσθεώρητα προαχθεὶς μᾶλλον εἰς τοῦτο τῷ μηδένα πω καθεῖναι εἰς ταύτην τὴν ὑπόθεσιν ἢ διὰ τὴν δυσκολίαν ὀκνήσας καὶ ἅμα τὸ Σωκρατικὸν λογισάμενος, ὡς τοῦ θεοῦ συλλαμβάνοντος πάνυ εἰκὸς καὶ ἐπὶ τέλος ἡμᾶς τῆς σπουδῆς
     
     
215. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 48, line 29
     
     Εὐτοκίου Ἀσκαλωνίτου ὑπόμνημα εἰς τὸ πρῶτον τῶν Ἀρχιμήδους περὶ σφαίρας καὶ κυλίνδρου ἐκδόσεως παραναγνωσθείσης τῷ Μιλησίῳ μηχανικῷ Ἰσιδώρῳ ἡμετέρῳ διδασκάλῳ.
     
     
216. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 150, line 13
     
     εἰ γὰρ τὸ δοθὲν ἐπὶ τὴν δοθεῖσαν μεῖζον ἐτύγχανεν τοῦ ἀπὸ τῆς ΔΒ ἐπὶ τὴν ΒΖ, ἀδύνατον ἦν τὸ πρόβλημα, ὡς δέδεικται, εἰ δὲ ἴσον, τὸ Β σημεῖον ἐποίει τὸ πρόβλημα, καὶ οὕτως δὲ οὐδὲν ἦν πρὸς τὴν ἐξ ἀρχῆς Ἀρχιμήδους πρόθεσιν· ἡ γὰρ σφαῖρα οὐκ ἐτέμνετο εἰς τὸν δοθέντα λόγον.
     
     
217. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 150, line 23
     
     κατανοεῖν δὲ χρὴ καὶ τοῖς ὑπ' Ἀρχιμήδους λεγομένοις συμφώνως ἔχουσιν τοῖς ὑφ᾿ ἡμῶν ἀναλελυμένοις.
     
     
218. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 152, line 15
     
     ταῦτα μὲν οὖν ἀκόλουθα τοῖς Ἀρχιμήδους ῥήμασιν κατὰ τὸ δυνατὸν σαφῶς ἀπεγραψάμεθα· ἐπεὶ δέ, ὡς προείρηται, καὶ Διονυσόδωρος οὐδαμοῦ τοῖς ἐπὶ τέλει γραφομένοις παρ' Ἀρχιμήδους ἐπηγγελμένοις ἐντυχών, ἀτονήσας δὲ ὥσπερ προσευρεῖν τὰ μὴ ἐκτεθέντα ἐφ' ἑτέραν ὁδὸν βαδίζων τοῦ ὅλου προβλήματος οὐκ ἄχαριν εὑρέσεως συνεγράψατο τρόπον, ἀναγκαῖον ᾠήθημεν δεῖν καὶ αὐτὸν τούτοις ἐπισυνάψαι διορθωσάμενοι κατὰ δύναμιν· καὶ γὰρ αὐτὸς ἐκ πολλῆς ἀμελετησίας τῶν ἀνθρώπων
     
     
219. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 224, line 8
     
     Εὐτοκίου Ἀσκαλωνίτου ὑπόμνημα εἰς τὸ δεύτερον τῶν Ἀρχιμήδους περὶ σφαίρας καὶ κυλίνδρου ἐκδόσεως παραναγνωσθείσης τῷ Μιλησίῳ μηχανικῷ Ἰσιδώρῳ ἡμετέρῳ διδασκάλῳ].
     
     
220. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 132, line 5
     
     ἔν τινι μέντοι παλαιῷ βιβλίῳ· οὐδὲ γὰρ τῆς εἰς πολλὰ ζητήσεως ἀπέστημεν· ἐντετύχαμεν θεωρήμασι γεγραμμένοις οὐκ ὀλίγην μὲν τὴν ἐκ τῶν πταισμάτων ἔχουσιν ἀσάφειαν περί τε τὰς καταγραφὰς πολυτρόπως ἡμαρτημένοις, τῶν μέντοι ζητουμένων εἶχον τὴν ὑπόστασιν, ἐν μέρει δὲ τὴν Ἀρχιμήδει φίλην Δωρίδα γλῶσσαν ἀπέσωζον καὶ τοῖς συνήθεσι τῷ ἀρχαίῳ τῶν πραγμάτων ὀνόμασιν ἐγέγραπτο τῆς μὲν παραβολῆς ὀρθογωνίου κώνου τομῆς ὀνομαζομένης, τῆς δὲ ὑπερβολῆς ἀμβλυγωνίου κώνου τομῆς, ὡς ἐξ αὐτῶν διανοεῖσθαι, μὴ ἄρα καὶ αὐτὰ εἴη τὰ ἐν τῷ τέλει ἐπηγγελμένα γράφεσθαι.
     
     
221. Eutocius Math., Commentarii in libros de sphaera et cylindro Page 150, line 2
     
     καθόλου μὲν οὖν οὕτως ἀναλέλυται καὶ συντέθειται τὸ πρόβλημα· ἵνα δὲ καὶ τοῖς Ἀρχιμηδείοις ῥήμασιν ἐφαρμοσθῇ, νενοήσθω ὡς ἐν αὐτῇ τῇ τοῦ ῥητοῦ καταγραφῇ διάμετρος μὲν τῆς σφαίρας ἡ ΔΒ, ἡ δὲ ἐκ τοῦ κέντρου ἡ ΒΖ, καὶ ἡ δεδομένη ἡ ΖΘ.
     
     
222. Eutocius Math., Commentarius in dimensionem circuli (4072: 002) “Archimedis opera omnia cum commentariis Eutocii, vol. 3”, Ed. Heiberg, J.L., Stamatis, E. Leipzig: Teubner, 1915, Repr. 1972. Page 228, line 3
     
     Ἐχόμενον ἂν εἴη τὸν ἐμὸν πληροῦντι σκοπὸν τοῖς σαφεστέροις καὶ βραχυτέρας ἐπιστάσεως δεομένοις τῶν ὑπ' Ἀρχιμήδους γεγραμμένων ἐντυγχάνοντι καὶ τὰ ὁπωσοῦν ἐν αὐτοῖς ἐπεξεργασίας δεόμενα τὸν δυνατὸν τρόπον συνεχῆ ποιεῖν τοῖς πρότερον ὑφ᾿ ἡμῶν ἐν τῷ Περὶ σφαίρας καὶ κυλίνδρου γεγραμμένοις εὐχῆς ὡς ἀληθῶς ἀξίου τυγχάνοντος τοῦ καὶ τοῖς μείζοσι καὶ πλείονος φροντίδος δεομένοις ἐπιστῆναι.
     
     Eutocius Math., Commentarius in dimensionem circuli Page 228, line 20
     
     ἀλλ' ἔστι μὲν τοῦτο τὸ βιβλίον, ὥς φησιν Ἡρακλείδης ἐν τῷ Ἀρχιμήδους βίῳ, πρὸς τὰς τοῦ βίου χρείας ἀναγκαῖον· δείκνυσιν γάρ, ὅτι ἡ περιφέρεια τῆς διαμέτρου ἐστὶ τριπλασία καὶ ἔτι ὑπερέχει ἐλάττονι μὲν ἢ ἑβδόμῳ μέρει, μείζονι δὲ ἢ δέκα ἑβδομηκοστομόνοις.
     
     
223. Eutocius Math., Commentarius in dimensionem circuli Page 230, line 4
     
     Τὸ πρῶτον θεώρημα καὶ τοῖς ἐπὶ ποσὸν μαθημάτων γυμνασαμένοις οὐδεμίαν ἔχον ζήτησιν φαίνεται αὐτῶν τῶν Ἀρχιμήδους ῥημάτων σαφῶς ἐκτεθειμένων καὶ τὸ συμπέρασμα πρὸς τὴν πρότασιν ἀνελλειπῶς ἀποσωζόντων.
     
     
224. Eutocius Math., Commentarius in dimensionem circuli Page 230, line 14
     
     συνορᾶν δὲ ὅμως χρή, ὡς οὐδὲν ἔξω τῶν προσηκόντων ὑπ' Ἀρχιμήδους γράφεται.
     
     
225. Eutocius Math., Commentarius in dimensionem circuli Page 230, line 20
     
     τὸ τοίνυν καὶ πρὸς Ἀρχιμήδους προτεθὲν τοιοῦτόν ἐστιν, ὅτι τὸ τρίγωνον τὸ ὀρθογώνιον τὸ ἔχον, ὡς προείρηται, τὰς πλευρὰς ἴσον ἐστὶ τῷ κύκλῳ· ὥστε τὸ προτεθὲν ἐκθέμενος οὐδεμιᾶς ἂν καταχρήσεως κρίνοιτο, θαυμαστὸς δ' ἂν μᾶλλον κἀν τούτοις δόξειεν τοῖς οὕτως ὑπερμεγέθεσιν τῶν ζητημάτων σαφῆ καὶ ῥαδίαν τὴν εὕρησιν ἐπιτιθείς.
     
     
226. Eutocius Math., Commentarius in dimensionem circuli Page 258, line 20
     
     τοῦτο δὲ ἀκριβέστερον μὲν εἶναι δοκεῖ, οὐ χρήσιμον δὲ πρὸς τὸν Ἀρχιμήδους σκοπόν· ἔφαμεν γὰρ αὐτὸν σκοπὸν ἔχειν ἐν τῷδε τῷ βιβλίῳ τὸ σύνεγγυς εὑρεῖν διὰ τὰς ἐν τῷ βίῳ χρείας.
     
     
227. Eutocius Math., Commentarius in dimensionem circuli Page 258, line 27
     
     ὥστε οὐδὲ Σπόρος ὁ Νικαεὺς εὔκαιρον εὑρεθήσεται μέμψιν ἐπάγων Ἀρχιμήδει ὡς μὴ ἀκριβῶς εὑρόντι, ποίᾳ εὐθείᾳ ἴση ἐστὶν ἡ τοῦ κύκλου περιφέρεια, ἐξ ὧν αὐτὸς ἐν τοῖς Κηρίοις φησὶν τὸν ἑαυτοῦ διδάσκαλον, Φίλωνα λέγων τὸν ἀπὸ Γαδάρων, εἰς ἀκριβεστέρους ἀριθμοὺς ἀγαγεῖν τῶν ὑπ' Ἀρχιμήδους εἰρημένων, τοῦ τε ζ΄ φημὶ καὶ τῶν [ι] οα΄· ἅπαντες γὰρ ἐφεξῆς φαίνονται τὸν σκοπὸν αὐτοῦ ἠγνοηκότες.
     
     Eutocius Math., Commentarius in dimensionem circuli Page 260, line 9
     
     εἰ δέ τις ὅλως ἐβούλετο εἰς ἔλαττον αὐτὸ καταγαγεῖν, ἐχρῆν τοῖς ἐν τῇ Μαθηματικῇ συντάξει Κλαυδίου Πτολεμαίου εἰρημένοις ἀκολουθοῦντα διὰ τῶν μοιρῶν καὶ λεπτῶν καὶ τῶν ἐν τῷ κύκλῳ εὐθειῶν τοῦτο ποιεῖν, καὶ πεποιήκειν ἂν ἐγὼ τοῦτο, εἰ μή, ὅπερ πολλάκις εἶπον, ἐνενόουν, ὡς οὔτε ἀκριβῶς δυνατὸν διὰ τῶν ἐνταῦθα εἰρημένων εὑρεῖν τῇ τοῦ κύκλου περιφερείᾳ ἴσην εὐθεῖαν, καὶ εἴ τις τὸ σύνεγγυς καὶ παρὰ μικρὸν προσέχοι, ἀρκεῖ τὰ ὑπ' Ἀρχιμήδους ἐνταῦθα εἰρημένα.
     
     
228. Eutocius Math., Commentarius in dimensionem circuli Page 260, line 11
     
     [Εὐτοκίου Ἀσκαλωνίτου ὑπόμνημα εἰς τὴν Ἀρχιμήδους τοῦ κύκλου μέτρησιν ἐκδόσεως παραναγνωσθείσης τῷ Μιλησίῳ μηχανικῷ Ἰσιδώρῳ ἡμετέρῳ διδασκάλῳ].
     
     
229. Eutocius Math., Commentarius in dimensionem circuli Page 228, line 9
     
     εἴη δ' ἂν ὡς πρὸς τὸ προκείμενον ἐφεξῆς τὸ γεγραμμένον Ἀρχιμήδει βιβλίδιον Κύκλου μέτρησιν τὴν ἐπιγραφὴν ἔχον, ἐν ᾧ τὴν πρόθεσιν τἀνδρὸς ἐξ αὐτῆς τῆς ἐπιγραφῆς γνωρίζομεν· βούλεται γὰρ ἐπιδεῖξαι, τίνι χωρίῳ εὐθυγράμμῳ ἴσος ἂν εἴη κύκλος, πρᾶγμα πάλαι πρὸς τῶν πρὸ αὐτοῦ κλεινῶν φιλοσόφων ἐζητημένον.
     
     
230. Eutocius Math., Commentarius in libros de planorum aequilibriis (4072: 003) “Archimedis opera omnia cum commentariis Eutocii, vol. 3”, Ed. Heiberg, J.L., Stamatis, E. Leipzig: Teubner, 1915, Repr. 1972. Page 264, line 11
     
     ὁ δὲ Ἀρχιμήδης ἐν τούτῳ τῷ βιβλίῳ κέντρον ῥοπῆς ἐπιπέδου σχήματος νομίζει, ἀφ' οὗ ἀρτώμενον παράλληλον μένει τῷ ὁρίζοντι, δύο δὲ ἢ πλειόνων ἐπιπέδων κέντρον ῥοπῆς ἤτοι βάρους, ἀφ' οὗ ἀρτώμενος ὁ ζυγὸς παράλληλός ἐστι τῷ ὁρίζοντι.
     
     
231. Eutocius Math., Commentarius in libros de planorum aequilibriis Page 266, line 2 καλῶς δὲ δοκεῖ ὁ Γεμῖνος εἰπεῖν περὶ τοῦ Ἀρχιμήδους, ὅτι τὰ ἀξιώματα αἰτήματα λέγει· τὰ γὰρ ἴσα βάρη ἀπὸ ἴσων μηκῶν ἰσοῤῥοπεῖν ἀξίωμά ἐστι καὶ τὰ ἑξῆς, καί ἐστιν πάντα σαφῆ τοῖς μετρίως αὐτὰ ἐπισκεπτομένοις.
     
     
232. Eutocius Math., Commentarius in libros de planorum aequilibriis Page 284, line 22
     
     ὠνομάσθη δὲ ὑπ' Ἀρχιμήδους τὸ ΑΠΕΤΒΧΖϛΓ σχῆμα γνωρίμως ἐγγραφόμενον.
     
     
233. Eutocius Math., Commentaria in conica (4072: 004) “Apollonii Pergaei quae Graece exstant, vol. 2”, Ed. Heiberg, J.L. Leipzig: Teubner, 1893, Repr. 1974. Page 168, line 9
     
     Ἀπολλώνιος ὁ γεωμέτρης, ὦ φίλε ἑταῖρε Ἀνθέμιε, γέγονε μὲν ἐκ Πέργης τῆς ἐν Παμφυλίᾳ ἐν χρόνοις τοῦ Εὐεργέτου Πτολεμαίου, ὡς ἱστορεῖ Ἡράκλειος ὁ τὸν βίον Ἀρχιμήδους γράφων, ὃς καί φησι τὰ κωνικὰ θεωρήματα ἐπινοῆσαι μὲν πρῶτον τὸν Ἀρχιμήδη, τὸν δὲ Ἀπολλώνιον αὐτὰ εὑρόντα ὑπὸ Ἀρχιμήδους μὴ ἐκδοθέντα ἰδιοποιήσασθαι, οὐκ ἀληθεύων κατά γε τὴν ἐμήν.
     
     
234. Eutocius Math., Commentaria in conica Page 168, line 12
     
     ὅ τε γὰρ Ἀρχιμήδης ἐν πολλοῖς φαίνεται ὡς παλαιοτέρας τῆς στοιχειώσεως τῶν κωνικῶν μεμνημένος, καὶ ὁ Ἀπολλώνιος οὐχ ὡς ἰδίας ἐπινοίας γράφει· οὐ γὰρ ἂν ἔφη ἐπὶ πλέον καὶ καθόλου μᾶλλον ἐξειργάσθαι ταῦτα παρὰ τὰ ὑπὸ τῶν ἄλλων γεγραμμένα.
     
     
235. Eutocius Math., Commentaria in conica Page 218, line 11
     
     Τὸ δὲ ἀπὸ τῆς ΒΓ πρὸς τὸ ὑπὸ ΒΑΓ λόγον ἔχει τὸν συγκείμενον ἐκ τοῦ ὃν ἔχει ἡ ΒΓ πρὸς ΓΑ καὶ ἡ ΒΓ πρὸς ΒΑ>· δέδεικται μὲν ἐν τῷ ἕκτῳ βιβλίῳ τῆς στοιχειώσεως ἐν τῷ εἰκοστῷ τρίτῳ θεωρήματι, ὅτι τὰ ἰσογώνια παραλληλόγραμμα πρὸς ἄλληλα λόγον ἔχει τὸν συγκείμενον ἐκ τῶν πλευρῶν· ἐπεὶ δὲ ἐπακτικώτερον μᾶλλον καὶ οὐ κατὰ τὸν ἀναγκαῖον τρόπον ὑπὸ τῶν ὑπομνηματιστῶν ἐλέγετο, ἐζητήσαμεν αὐτὸ καὶ γέγραπται ἐν τοῖς ἐκδεδομένοις ἡμῖν εἰς τὸ τέταρτον θεώρημα τοῦ δευτέρου βιβλίου τῶν Ἀρχιμήδους περὶ σφαίρας καὶ κυλίνδρου καὶ ἐν τοῖς σχολίοις τοῦ πρώτου βιβλίου τῆς Πτολεμαίου συντάξεως· οὐ χεῖρον δὲ καὶ ἐνταῦθα τοῦτο γραφῆναι διὰ τὸ μὴ πάντως τοὺς ἀναγινώσκοντας κἀκείνοις ἐντυγχάνειν, καὶ ὅτι σχεδὸν τὸ ὅλον σύνταγμα τῶν κωνικῶν κέχρηται αὐτῷ.
     
     
236. Eutocius Math., Commentaria in conica Page 354, line 13
     
     εὔχρηστος δὲ καὶ ἀναγκαῖος ὁ τρόπος οὗτος καὶ τῷ Ἀριστοτέλει δοκεῖ καὶ τοῖς γεωμέτραις καὶ μάλιστα τῷ Ἀρχιμήδει.
     
     
237. Marinus Phil., Commentarium in Euclidis data (4075: 002) “Euclidis opera omnia, vol. 6”, Ed. Menge, H. Leipzig: Teubner, 1896. Page 248, line 3
     
     πολλὰ γοῦν τεταγμένα φύσει ὕστερον Ἀρχιμήδης ἔδειξε τοῖς πρὶν οὐ θεωρηθέντα, ὅτι τέτακται.
     
     
238. Marinus Phil., Commentarium in Euclidis data Page 244, line 2
     
     ἡ γὰρ ἕλιξ τέτακται μέν, ἀλλ' οὐκ ἦν τοῖς πρὸ Ἀρχιμήδους πορίμη.
     
     
239. Eustathius Philol., Scr. Eccl., Commentarii ad Homeri Iliadem (4083: 001) “Eustathii archiepiscopi Thessalonicensis commentarii ad Homeri Iliadem pertinentes, vols. 1–4”, Ed. van der Valk, M. Leiden: Brill, 1:1971; 2:1976; 3:1979; 4:1987. Volume 1, page 191, line 7
     
     ὅθεν καὶ ὁ πολυμήχανος Ἀρχιμήδης μιᾷ προσβολῇ πολλὰ βέλη ἀφιεὶς ἑκατόγχειρ πρὸς τῶν βαλλομένων ἐκλήθη.
     
     
240. Eustathius Philol., Scr. Eccl., Commentarii ad Homeri Iliadem Volume 2, page 5, line 4
     
     Ἔδοξε δέ τισι καὶ κατοπτρικήν τινα ἐπίνοιαν μεμηχανῆσθαι τῷ Διομήδει ἔν τε τῇ αὐτοῦ, ὡς εἰκός, περικεφαλαίᾳ καὶ τῇ ἀσπίδι, καὶ οὕτω λίαν καταυγεῖν τὰς ὄψεις τῶν εἰς αὐτὸν βλεπόντων, ὅτε ἀντικρὺ πρὸς λάμποντα ἥλιον ἔστραπτο, καθ᾿ ἣν δὴ ταύτην μέθοδον Ἀρχιμήδης μὲν ὁ σοφώτατος πολεμικὰς ἐνεπύρισε νῆας ὡς οἷά τις κεραυνοβόλος· Ἀνθέμιος δέ τις ὕστερον γείτονα πονηρὸν καταστράπτων καὶ οὕτως ἐκφοβῶν μακρὰν ἑαυτοῦ ἀπῴκισε.
     
     
241. Eustathius Philol., Scr. Eccl., Commentarii ad Homeri Iliadem Volume 3, page 394, line 2
     
     λέγεται δὲ ἕλιξ καί τι μηχανῆς εἶδος, ὃ πρῶτος εὑρὼν Ἀρχιμήδης εὐδοκίμησε, φασί, δι' αὐτοῦ.
     
     
242. Eustathius Philol., Scr. Eccl., Commentarii ad Homeri Odysseam (4083: 003) “Eustathii archiepiscopi Thessalonicensis commentarii ad Homeri Odysseam, 2 vols. in 1”, Ed. Stallbaum, G. Leipzig: Weigel, 1:1825; 2:1826, Repr. 1970. Volume 1, page 411, line 16
     
     καὶ αἱ τοῦ Ἀρχιμήδους δὲ καυστικαὶ διὰ κατόπτρων ἀστραπαὶ δηλοῦνται ἐξ ἱστοριῶν.
     
     Eustathius Philol., Scr. Eccl., Commentarii ad Homeri Odysseam Volume 1, page 206, line 26
     
     τεχνωμένους ὁμοίως Ἀρχιμήδει, τὰς δι' ἐνόπτρων ὡς οἷον ἀστραπαίας καύσεις οὗ μιμητὴς καὶ Ἀνθέμιος ὁ παρὰ τῷ Ἀγαθίᾳ.
     
     
243. Anthemius Math., Mech., Περὶ παραδόξων μηχανημάτων (4088: 003) “Anthemiusof Tralles. A study in later Greek geometry”, Ed. Huxley, G.L. Cambridge, Mass.: Harvard University Press, 1959; Greek, Roman and Byzantine monographs 1. Page 48, line 9
     
     ἐπειδὴ δὲ τὴν Ἀρχιμήδους δόξαν οὐχ οἷόν τέ ἐστι καθελεῖν, ἅπασιν ὁμολόγως ἱστορηθέντος, ὡς τὰς ναῦς τῶν πολεμίων διὰ τῶν ἡλιακῶν ἔκαυσεν ἀκτίνων, ἀναγκαῖον εὐλόγως καὶ κατὰ τοῦτο δυνατὸν εἶναι τὸ πρόβλημα, καὶ ἡμεῖς θεωρήσαντες, καθ᾿ ὅσον οἷόν τε ἦν ἐπισκήψαντες, τὴν τοιαύτην ἐκθησόμεθα κατασκευὴν βραχέα τινὰ προδιαλαβόντες ἀναγκαῖα εἰς τὸ προκείμενον.
     
     
244. Anthemius Math., Mech., Περὶ παραδόξων μηχανημάτων Page 51, line 8
     
     διὰ μὲν οὖν τῆς τῶν εἰρημένων ἐσόπτρων ἤτοι πυρίων κατασκευῆς ἥ τε ἔξαψις πρὸς τὸ δοθὲν διάστημα δύναιτο γίνεσθαι καὶ τὰ ἄλλα τὰ ῥηθέντα· καὶ γὰρ οἱ μεμνημένοι περὶ τῶν ὑπὸ Ἀρχιμήδους τοῦ θειοτάτου κατασκευασθέντων ἐκκαῦσαι οὐ δι' ἑνὸς ἐμνημόνευσαν πυρίου ἀλλὰ διὰ πλειόνων, καὶ οἶμαι μὴ εἶναι τρόπον ἕτερον τῆς ἀπὸ τούτου τοῦ διαστήματος ἐκκαύσεως· ἐπειδὴ δὲ καὶ τῶν συνήθων πυρίων ἐμνημόνευσαν οἱ παλαιοί, πῶς δεῖ τὰς τῶν ἐμβολέων ποιεῖσθαι καταγραφάς, ὀργανικώτερον μόνον οὐδεμίαν ἀπόδειξιν γεωμετρικὴν εἰς τοῦτο ἐκθέμενοι, ἀλλὰ φήσαντες εἶναι τὰς τοιαύτας κωνικὰς τομάς, οὐ μέντοι γε ποίας καὶ πῶς γινομένας, διὸ πειρασόμεθα ἡμεῖς καί τινας ἐκθέσθαι τῶν τοιούτων ἐμβολέων καταγραφὰς καὶ ταύτας οὐκ ἀναποδείκτους ἀλλὰ
     
     
245. Anthemius Math., Mech., Fragmentum mathematicum Bobiense (4088: 005) “Anthemius of Tralles. A study in later Greek geometry”, Ed. Huxley, G.L. Cambridge, Mass.: Harvard University Press, 1959; Greek, Roman and Byzantine monographs 1. Page 56, line 19
     
     ἀντιπεπονθότα ὑπάρχει, κατὰ τὴν ἱστορίαν δείκνυνται καὶ παρὰ Ἀρχιμήδει καὶ παρὰ Ἀπολλωνίῳ καθαρῶς, ὥστε οὐκ ἀναγκαῖον ἡμᾶς πάλιν δεικνύναι, λαμβάνειν δὲ ἐξ ἑτοίμου χρήσιμον.
     
     
246. Zosimus Alchem., Περὶ τοῦ τριβίκου καὶ τοῦ σωλῆνος (e cod. Venet. Marc. 299, fol. 194r) (4319: 050) “Collection des anciens alchimistes grecs, vol. 2”, Ed. Berthelot, M., Ruelle, C.É. Paris: Steinheil, 1888, Repr. 1963. Volume 2, page 237, line 21
     
     Καὶ μάλιστα ἐὰν [εἴ] τις προπαιδευθῇ τὰ πνευματικὰ Ἀρχιμήδους, ἢ Ἥρωνος καὶ τῶν ἄλλων καὶ τὰ μηχανικὰ αὐτῶν.
     
     
247. Zosimus Alchem., Excerptum alchemicum (sine titulo) (e cod. Venet. Marc. 299, fol. 186v + 187r, 195r) (4319: 059) “Les alchimistes grecs, vol. 4.1 [Zosime de Panopolis. Mémoires authentiques]”, Ed. Mertens, M. Paris: Les Belles Lettres, 1995. Column versio1, line 42
     
     Ἡ οὖν ἄρσις τοιάδε ἐστίν, ἡ διὰ τούτων τῶν ὀργάνων καὶ τῶν ὁμοίων, τῶν ὡς ἀπὸ τοῦ νοὸς γινομένων, καὶ μάλιστα ἐάν [εἰ] τις προπαιδευθῇ τὰ Πνευματικὰ Ἀρχιμήδους, ἢ Ἥρωνος, καὶ τῶν ἄλλων καὶ τὰ Μηχανικὰ αὐτῶν ἐν οἷς φάσκει ὁ Φιλόσοφος αἴρεσθαι τὸ ὕδωρ Ἐγέλασα εἰς ἐξάκουστον γραφῶν ταύτην τὴν τάξιν λέγουσαν· ἐχέτω ἡ λοπάς, φησίν, μνᾶν θείου ἀπύρου.
     
     
248. Scholia In Aristophanem, Commentarium in nubes (scholia recentiora Tzetzae) (5014: 017) “Jo. Tzetzae commentarii in Aristophanem”, Ed. Holwerda, D. Groningen: Bouma, 1960; Scholia in Aristophanem 4.2. Argumentum-dramatis personae-scholion sch nub, verse-column 1024a, line 16
     
     τὸ περαιοῦσθαι ποταμοὺς πρὸς ἀνάῤῥουν, τομῇ ῥυθμιζόμενα πλοῖα τεκταίνεσθαι, τὸ δὲ μυριάδας στρατῶν ὑπερτρεχούσας ἀριθμοὺς τῶν δακτύλων διά τε γῆς καὶ θαλάσσης ἐστρατευμένους ἑνὸς ἀνθρωπαρίου γηρανδραρίου ἡττᾶσθαι τοῖς μηχανήμασιν, οἷος ἦν ὁ ἡμέτερος καὶ πάντων, ὧν εἴπω, πρεσβύτερος, ὁ βυζάντιος Φίλων, Ἀρχιμήδης καὶ Σώστρατος, Ἥρων καὶ Πάππος καὶ μυριάδες λοιπαί.
     
     
249. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) (5022: 001) “Euclidis opera omnia, vols. 5.1–5.2, 2nd edn.”, Ed. Stamatis, E.S. (post J.L. Heiberg) Leipzig: Teubner, 1977. Book 1, scholion 1, line 306
     
     ὁ δ' αὖ Ἀρχιμήδης τὴν εὐθεῖαν γραμμὴν ἐλαχίστην τῶν τὰ αὐτὰ πέρατα ἐχουσῶν· καὶ μὴν καὶ οἱ ἄλλοι πάντες ὁρισμοὶ εἰς τὰς αὐτὰς ἐννοίας ἐμπίπτουσιν.
     
     
250. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) Book 1, scholion 6, line 1
     
     τὸ δὲ ὑπό τινος ἤ τινων ὅρων ἐστὶ περιεχόμενον Ἀρχιμήδης οὕτως ὁρίζει τὴν εὐθεῖαν γραμμήν· εὐθεῖα γραμμή ἐστιν ἡ ἐλαχίστη τῶν τὰ αὐτὰ πέρατα ἐχουσῶν γραμμῶν.
     
     
251. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) Book 1, scholion 141, line 22
     
     εἰ δὲ παραλληλόγραμμον ἴσον εὑρίσκεται παντὶ εὐθυγράμμῳ, ζητήσεως ἄξιον, μὴ καὶ τὰ εὐθύγραμμα ἴσα δεικνύναι δυνατὸν τοῖς περιφερογράμμοις, ὡς καὶ ὁ Ἀρχιμήδης ἔδειξεν, ὅτι πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ ὀρθογωνίῳ, οὗ ἡ μὲν ἐκ τοῦ κέντρου ἴση ἐστὶ μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῇ βάσει.
     
     
252. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) Book 1, scholion 142, line 16
     
     καὶ ὁ Ἀρχιμήδης ἔδειξεν, ὅτι πᾶς κύκλος ἴσος ἐστὶ τριγώνῳ ὀρθογωνίῳ, οὗ ἡ μὲν ἐκ τοῦ κέντρου ἴση ἐστὶν μιᾷ τῶν περὶ τὴν ὀρθήν, ἡ δὲ περίμετρος τῇ βάσει.
     
     
253. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) Book 1, scholion 143, line 10
     
     ὑπέλαβον γάρ, ὡς εἴη καὶ τοῖς μὴ εὐθυγράμμοις ἴσα παραλληλόγραμμα· ὅθεν ὁ Ἀρχιμήδης σχεδὸν ἀπέδειξεν τοῦτο, ἀλλ' ὅμως γε παρελογίσατο.
     
     
254. Scholia In Euclidem, Scholia in Euclidis elementa (scholia vetera et recentiora) Book 11, scholion 13, line 4
     
     διαιρεῖ δὲ αὐτοὺς εἰς ἰσοσκελεῖς καὶ ἀνισοσκελεῖς, ὁ δὲ Ἀρχιμήδης εἰς ὀρθογωνίους καὶ ὀξυγωνίους καὶ ἀμβλυγωνίους τὴν πλευρὰν πρὸς τὴν βάσιν συγκρίνων.
     
     
255. Scholia In Euclidem, Scholia in Euclidis catoptrica (scholia vetera) (5022: 005) “Euclidis opera omnia, vol. 7”, Ed. Heiberg, J.L. Leipzig: Teubner, 1895. Scholion 7, line 1 Ὁ δὲ Ἀρχιμήδης οὕτω λέγει, ὅτι ἡ Ζ γωνία τῇ Ε ἢ ἴση ἐστὶν ἢ ἐλάττων ἢ μείζων.
     
     
256. Scholia In Iamblichum Philosophum, Scholia in librum Iamblichi in Nicomachi arithmeticam introductionem (scholia vetera et recentiora) (5027: 001) “Iamblichi in Nicomachi arithmeticam introductionem liber”, Ed. Klein, U. (post H. Pistelli) Leipzig: Teubner, 1894, Repr. 1975. Page 98, scholion 18, line 6
     
     συνεκδρομικῶς νῦν ὁ φιλόσοφος λέγει καὶ δεῖ ἀσφαλῶς ἀκοῦσαι τοῦ λόγου· οὐ γὰρ ἁπλῶς τὰ ὁμογενῆ δεῖ συγκρίνειν, οὐδὲ γὰρ γραμμὴν πρὸς ἐπιφάνειαν συγκρίνομεν, ἀλλὰ δεῖ τὰ ὑπὸ τὸ αὐτὸ προσεχὲς γένος συγκρίνειν, οἷον ἐπίπεδον ἐπιφάνειαν πρὸς κωνικὴν ἐπιφάνειαν ἢ σφαιρικήν, ὡς καὶ Ἀρχιμήδης ἐποίησε.
     
     
257. Scholia In Platonem, (scholia vetera) (5035: 001) “Scholia Platonica”, Ed. Greene, W.C. Haverford, Pennsylvania: American Philological Association, 1938. Dialogue Chrm, Stephanus page 165e, line 6
     
     θεωρεῖ οὖν τοῦτο μὲν τὸ κληθὲν ὑπ' Ἀρχιμήδους βοϊκὸν πρόβλημα, τοῦτο δὲ μηλίτας καὶ φιαλίτας ἀριθμούς, τοὺς μὲν ἐπὶ φιαλῶν, τοὺς δ' ἐπὶ ποίμνης· καὶ ἐπ᾿ ἄλλων δὲ γενῶν τὰ πλήθη τῶν αἰσθητῶν σωμάτων σκοποῦσα, ὡς περὶ τελείων ἀποφαίνεται.
     
     
258. Anthologiae Graecae Appendix, Problemata et aenigmata (7052: 007) “Epigrammatum anthologia Palatina cum Planudeis et appendice nova, vol. 3”, Ed. Cougny, E. Paris: Didot, 1890. Epigram 5,5, line n1
     
     ΠΡΟΒΛΗΜΑ ὅπερ Ἀρχιμήδης ἐν ἐπιγράμμασιν εὑρὼν τοῖς ἐν Ἀλεξαν δρείᾳ περὶ ταῦτα πραγματευομένοις ζητεῖν ἀπέστειλεν, ἐν τῇ πρὸς Ἐρατοσθένην τὸν Κυρηναῖον ἐπιστολῇ. Πληθὺν Ἠελίοιο βοῶν, ὦ ξεῖνε, μέτρησον, φροντίδ' ἐπιστήσας, εἰ μετέχεις σοφίης.
     
     
259. Suda, Lexicon (9010: 001) “Suidae lexicon, 4 vols.”, Ed. Adler, A. Leipzig: Teubner, 1.1:1928; 1.2:1931; 1.3:1933; 1.4:1935, Repr. 1.1:1971; 1.2:1967; 1.3:1967; 1.4:1971; Lexicographi Graeci 1.1–1.4. Alphabetic letter alpha, entry 2797, line 3
     
     ὡς Ἀρχιμήδης ἐν Συρακούσαις μόνος πολλῶν Ῥωμαίων.
     
     
260. Suda, Lexicon Alphabetic letter alpha, entry 4113, line 1
     
     καὶ παροιμία· Ἀρχίλοχον πατεῖς, ἐπὶ τῶν κακηγόρων καὶ λοιδόρων. Ἀρχιμήδης, Τραλλιανὸς, φιλόσοφος.
     
     
261. Suda, Lexicon Alphabetic letter epsilon, entry 945, line 1
     
     Ἐμβελές· ὁ δὲ Ἀρχιμήδης παρεσκευάσατο ὄργανα πρὸς ἅπαν ἐμβελὲς διάστημα, πόῤῥωθεν μὲν ἐπιπλέοντας τοῖς εὐτονωτέροις καὶ μείζοσιν· ὅτε δὲ ταῦθ' ὑπερπετῆ γίγνοιτο, τοῖς ἐλάττοσιν.
     
     
262. Suda, Lexicon Alphabetic letter sigma, entry 669, line 1
     
     ὁ δὲ Ἀρχιμήδης πάλιν ἑτέραν ἡτοιμάκει παρασκευὴν πρὸς τοὺς ἀπομαχομένους ἐκ τῶν πλοίων.
     
     
263. Suda, Lexicon Alphabetic letter delta, entry 1573, line 29
     
     δυνάμεις γεωμετρικαὶ ε΄· Πισίδης· τὰς πέντε δυνάμεις Ἀρχιμήδους εἰς μίαν συνάψας ὅλην, εἰς τὸ κινῆσαι μόλις τῶν δυστραχήλων ἐξ ὀχῶν τὰ φορτία.
     
     
264. Suda, Lexicon Alphabetic letter epsilon, entry 2907, line 10
     
     Πολύβιος· οἱ δὲ Ῥωμαῖοι πολιορκοῦντες τοὺς Συρακουσίους ἔργου εἴχοντο, οὐ λογισάμενοι τὴν Ἀρχιμήδους δύναμιν.
     
     
265. Suda, Lexicon Alphabetic letter theta, entry 142, line 3
     
     ἔγραψε Σφαιρικὰ ἐν βιβλίοις γ΄, Ὑπόμνημα εἰς τὰ Θευδᾶ κεφάλαια, Περὶ ἡμερῶν καὶ νυκτῶν δύο, Ὑπόμνημα εἰς τὸ Ἀρχιμήδους Ἐφόδιον, Διαγραφὰς οἰκιῶν ἐν βιβλίοις τρισί, Σκεπτικὰ κεφάλαια, Ἀστρολογικά, Περὶ οἰκήσεων.
     
     
266. Arsenius Paroemiogr., Apophthegmata (9018: 001) “Corpus paroemiographorum Graecorum, vol. 2”, Ed. von Leutsch, E.L. Göttingen: Vandenhoeck and Ruprecht, 1851, Repr. 1958. Centuria 3, section 60c, line 7
     
     Ἄργος ναυπηγίας. Ἀρχιμήδης μηχανικῆς.
     
     
 

---

  

ΑΝΤΙ ΠΡΟΛΟΓΟΥ

  

Στήν ἱστοσελίδα «Ἀρχιμήδους Ἅπαντα» εἶναι συγκεντρωμένα ὅλα τὰ σωζόμενα κείμενα τοῦ Ἀρχιμήδους στὸ πρωτότυπο σὲ μία html ἱστοσελίδα.

Τὰ κείμενα αὐτὰ ἀποτελοῦν συνέχεια τῶν στοιχείων τοῦ Εὐκλείδου. Ἡ μόνη διαφορὰ εἶναι ὅτι εἶναι γραμμένα στὴν δωρικὴ διάλεκτο δηλαδὴ πολλὰ «η» εἶναι γραμμένα ὡς «α» π.χ. τὸ σημεῖο γράφεται ὡς σαμεῖο.

Οἱ ἐρευνητές μαθηματικοί, φυσικοὶ, μηχανικοὶ γιὰ τὴ μελέτη αἰτῶν τῶν κειμένων ἔχουν στὴ διάθεσή τους ὅλα τὰ κείμενα τοῦ Ἀρχιμήδους σὲ μία ἱστοσελίδα γιὰ εὔκολη ἔρευνα μὲ ἁπλὸ search ἀπὸ τὸ browser, ἐπίσης ἔχουμε πάντα στὸ «ΜΕΝΟΥ» τὰ γλωσσικὰ ἐργαλεῖα γιὰ τὴν ἀνάλυση τῶν ἀγνώστων λέξεων.

Τὰ κείμενα εἶναι ἀπὸ τὴν ἱστορικὴ ἔκδοση τοῦ τεχνικοῦ Ἐπιμελητηρίου τῆς Ἑλλάδος το 1973 τοῦ Εὐαγγέλου Σταμάτη, τὸ ὁποῖο διατίθεται καὶ στὸ ἐμπόριο καὶ μπορεῖτε νὰ τὸ κατεβάσετε ἀπὸ τὸ ἐπίσημο site τοῦ «Σταμάτη».

Ὁ Ἀρχιμήδης μὲ τὸ ἔργο του καὶ τὰ θεωρήματα του (προτάσεις) ἐκτόξευσε τὴν ἐπιστήμη τῶν Ἑλλήνων τὴν ἀπόλυτη ἐπιστήμη στὸ μέγιστο ὕψος ποὺ μπόρεσε νὰ φτάσει.

Κάποιες από αυτές τις προτάσεις διδάσκονται σήμερα σε ὅλα τὰ πολυτεχνεῖα τοῦ κόσμου «ὡς ἔχουν» μὴ ἀποδεχόμενες καμία τροποποίηση βελτίωση ἤ ἀλλαγή.