Generalization, viewed as the process of selection and simplified representation of a detailed map depending on the scale and its purpose is one of the most important concepts of cartography. Much interest focuses on the generalization of linear entities. In recent decades, cartographic literacy at the international level has focused on the creation of universal automated line generalization processes, abandoning traditional methods of line simplification through the homonymous algorithms, whose results are not considered sufficiently well. The central idea is that each line segment behaves differently in the process of generalization, depending on its form and character. Thus, cartographers led to the creation of systems in which the line is subject to a pretreatment by segmenting it on a basis of several attributes of form and geometry, characterized qualitatively and quantitatively, and finally generalized by appropriate operators, such as enlargement, simplification or removal etc.

Research projects related to the problem of line generalization at the Cartography Laboratory of the N.T.U.A. are focused on the development of digital techniques for the generalization of natural occurring lines, such as coastlines, rivers, etc. The concern raised at this research level because of the complexity and randomness of their forms which is particularly frequent. Recently, research has focused on the design and implementation of an automated line generalization model, based on the conceptual framework: segmentation-classification-generalization. Issues of the study are to establish a method for segmenting the cartographic lines on the basis of visual perception principles, the definition visual legibility rules on which take place the quantitative and qualitative classification of line segments and finally the design and implementation of adequate generalization operators.

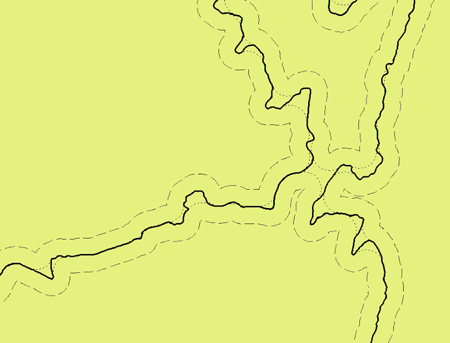
The method of line segmentation is based on the idea of Perkal’s rolling disc along both sides of the cartographic line. The size of disc’s diameter (epsilon) is associated to visual perception limits. This procedure defines line segments either as epsilon-convex or epsilon-non-convex in regard to the target scale. The adaptation and implementation of this concept in a digital environment is carried out using the software package ArcGIS v.9.3 (© ESRI), by applying appropriate tools. The result is a model, which runs a chain of individual processes, appropriately structured to apply the desired tasks.

More specifically the disc’s diameter epsilon is defined according to the visual perception limit, line’s symbol width and target scale and is completely independent of the line’ form and any intervention of the user.

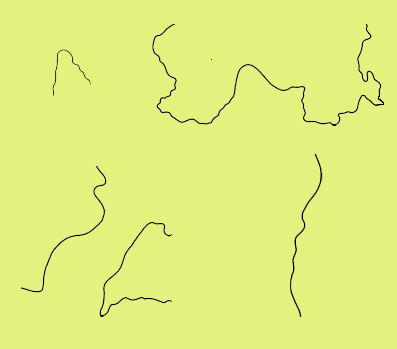
The application of the technique has resulted in a segmentation of the digital cartographic line. The line segments, as filtered by rules of visual perception to avoid 'noise', are grouped into four groups, depending on the form and manner of their creation:

• Group A: One-sided epsilon-non-convex segments
  Parts of the line marked by a simple turning point, which appears in a (left or right) side of the line,
• Group B: Both-sided epsilon-non-convex segments
  Parts of the line described by successive bends, which occur on both sides of the line (left or right),
• Group C: Sections of convergence
  Parts of the line, which are approaching each other at a distance less than the critical distance of legibility expressed in the target scale of the map
• Group D: epsilon-convex segments

Characteristic examples of the four line segments groups created by applying the proposed technique are presented in the opposite figure.

Each group is characterized by a different form and geometry. Therefore, it is necessary to generalize the whole line by applying appropriate line generalization operators to each segment. Before the stage of generalization, the defined segments of the line are normalized and filtered by a smoothing procedure, through the application of Gaussian smoothing operator. Furthermore, several quantitative properties of line segments are calculated (such as length, area, density of vertices, anchor length and the fractal dimension), which provide essential information, useful for further analysis and processing.

In the phase of implementation we are associating the four groups of line segments to appropriate generalization operators. In the following paragraphs we give several examples implemented on experimental lines.

The process of generalizing one-sided epsilon-non-convex  segments (group A), shows the need for enlargement, in order to be legibly portrayed at the target. This need is addressed by applying an enlargement operator and consequently an affine transformation in order to maintain their positions characteristic points (apexes), as they are identified in the initial line. The opposite figure shows, for instance, an example of generalization of a line segment of group A.

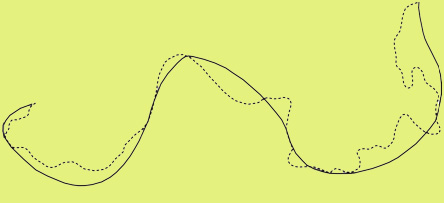
In the case of both-sided epsilon-non-convex segments (group B), individual bends of the segment are identified and isolated. The visible representation at a smaller scale, usually require either the expansion of one or more bends, or its removal, or its enlargement or even any combination of them. The selection of the appropriate operators is based on the geometry and quantitative characteristics of the bends composing the line segment. Finally, an affine transformation is applied in order to stretch each remaining bend in its original position. The opposite figure shows a generalization example of a segment of group B.

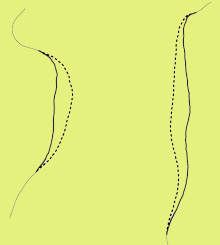
In the process of segments classified as group C, each one of them is treated independently. The concept of “convergence regions” is introduced, which is identified by two or more interacting parts. Each part, as a separate entity in the region, contributes to establish several quantitative parameters on which the process of the generalization is based. The concept is based on the displacement of parts in a manner that ensures the area between them to be visually perceived at the target scale. The opposite figure shows an example of how the problem of convergence can be solved.

Those segments that are classified as group D being epsilon-convex segments can be generalized effectively by existing line simplification algorithms as they are legible and smooth. Line simplification algorithms such as the bendsimplify supported by software package ArcGIS provide quite satisfactory results, as shown in the opposite figure.

Currently the line generalization operators of displacement, expansion, enlargement and removal, as well as, the operator of Gaussian filtering and smoothing and the affine transformation have been developed using Mapping Toolbox 2, in the programming software environment of MatLab 2008b.

The results of the tests carried out are satisfactory, both in terms of the operational reliability of the techniques automated, and the cartographic quality of the outcome. In the current period we are programming the above mentioned operators with a compatible code of ArcGIS v.9.3 scripts (Python 3.1), in order to incorporate the model of line segmentation and the application of line generalization operators inside ArcGIS as a fully automated process.

Bibliography

Nakos B., Gaffuri J., Mustière S., “A transition from simplification to generalization of natural occurring lines”. Proceedings of 11th ICA Workshop on Map Generalisation and Multiple Representation, Monpellier, France, 2008.
Lambraki S., "Algorithms for generalising successive bends of natural occurring lines". Diploma Thesis. School of Rural & Surveying Engineering, National Technical University of Athens, Athens, 2009, p. 91.

Vassilios Mitropoulos
Diploma of Rural & Surveying Engineering of N.T.U.A.
PhD Candidate
mitrovas@survey.ntua.gr