Πρόβλημα Σακιδίου - Knapsack Problem

Διατύπωση του Προβλήματος

Πρόβλημα Knapsack: Για δεδομένο πλήθος αντικειμένων μεγέθους V και αξίας W να προσδιοριστεί ένα σύνολο από τα παραπάνω αντικείμενα που το συνολικό του μέγεθος να είναι μικρότερο από ένα προδιαγεγραμμένο όριο ενώ ταυτόχρονα η συνολική του αξία να γίνει όσο το δυνατόν μεγαλύτερη.

Το πρόβλημα του Σακιδίου ορίζεται ως εξής:
Έστω n αντικείμενα που το καθένα έχει μέγεθος V και αξία W.
Δηλαδή:
Αντικείμενο 1, Αντικείμενο 2, ..., Αντικείμενο n, με μέγεθος Vi και αξία Wi, όπου i=1, 2,..., n

Τα n παραπάνω αντικείμενα θα πρέπει να τοποθετηθούν στο χώρο V έτσι ώστε η αξία αυτών να γίνει μέγιστη.

Αν 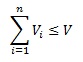τότε σε κάθε περίπτωση υπάρχει λύση.

Το πρόβλημα αποκτά αξία όταν .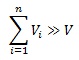

Μαθηματική προτυποποίηση του προβλήματος:

Έτσω ότι έχουμε την αποθήκη W και θέλουμε να τοποθετήσουμε n αντικείμενα. Ορίζουμε ως κέρδος τοποθέτησης το w = f(v), όπου w = αξία και v ο όγκος του αντικειμένου s.
Γενικά θεωρούμε ότι η αξία είναι συνάρτηση του όγκου. Αυτό όμως δεν ισχύει κατ' ανάγκην.

Για να λύσουμε το πρόβλημα ορίζουμε δυαδικές μεταβλητές της μορφής Xi, όπου i=1,2,...,n και X Ε {0, 1}.
όπου:
X = 1 όταν τo i ανήκει στη λύση
Χ = 0 όταν το i δεν ανήκει στη λύση


Για παράδειγμα έστω τα αντικείμενα 1, 2, ..., 10 για τα οποία η τοποθέτηση είναι {Χ1, Χ2, ..., Χn} = {0, 0, 1, 0, 0, 0, 0, 0, 0, 0}. Τότε το αντικείμενο 3 είναι τοποθετημένο αφού X3 = 1, αντίθετα τα υπόλοιπα δεν έχουν τοποθετηθεί.

Με τη μέθοδο knapsack στην ουσία δημιουργώ ράφια με τον εξής τρόπο:

• - Αρχικά γεμίζω ένα ράφι με τα αντικείμενα και δημιουργώ τη λύση {S1}.
• - Ότι έχει περισσέψει από το ράφι τοποθετείται στο επόμενο, λύση {S2}.
• - Η διαδικασία επαναλαμβάνεται μέχρι την εξάντληση των αντικειμένων, λύση {Sn}.

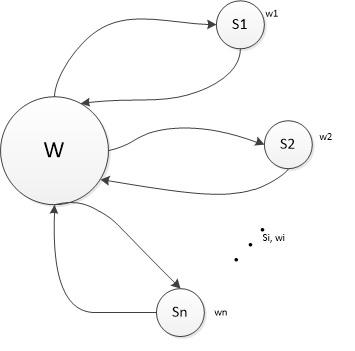
Στόχος:

Ο σκοπός του αλγορίθμου είναι να μεγιστοποιήσουμε το κέρδος τοποθέτησης: 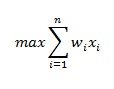, ενώ ταυτόχρονα θα πρέπει να ικανοποιείται ο περιορισμός

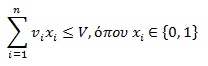
Η μεθοδολογία αυτή γενικά ανήκει στην κατηγορία Branch and Bound.

Πρόβλημα 1:

Έστω ότι έχουμε έναν χώρο που περιέχει πέντε αντικείμενα με όγκο / αξία:

Αντικείμενο i	|	Όγκος i	|	Αξία i
1	|	5	|	15
2	|	7	|	20
3	|	6	|	10
4	|	4	|	42
5	|	2	|	7
Περιορισμός:		V = 10

Να μεγιστοποιηθεί η συνολική αξία W.

Βήμα 1:

Ξεκινάω από τη λύση S = 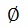κενό σύνολο

Βήμα 2:

Ταξινομώ τα αντικείμενα με κριτήριο είτε τον όγκο Vi σε φθίνουσα κατάταξη (decresing volume),
είτε με την αξία wi σε φθίνουσα κατάταξη (decresing profit value).

Στο πρόβλημα που επιλύουμε ζητάμε να μεγιστοποιήσουμε την αξία, άρα η αντικειμενική συνάρτηση (objective function) είναι η αξία. Έτσι το κριτήριο της ταξινόμισης θα είναι ο όγκος κατά φθίνουσα κατάταξη.

Αντικείμενο i	|	Όγκος i	|	Αξία i
2	|	7	|	20
3	|	6	|	10
1	|	5	|	15
4	|	4	|	42
5	|	2	|	7
Περιορισμός:		V = 10

Βήμα 3:

Προσθέτω στην λύση S το αντικείμενο 2, έτσι: S = {2} , όπου V = 7, w = 20.
Παρατηρώ ότι δεν μπορώ να προσθέσω άλλο όγκο στο ίδιο ράφι διότι ξεπερνώ το κριτήριο V <= 10. Οπότε η επίλυση σταματά εδώ και ξεκινάω για νέο ράφι μέχρι την εξάντληση των αντικειμένων.

Πρόβλημα 2:

Στο παραπάνω πρόβλημα 1 θεωρώ άλλη μια στήλη το λόγο αξία προς όγκο (wi/vi) και επιλέγω ως κριτήριο ταξινόμησης αυτό. Έτσι ο πίνακας θα γίνει:

Αντικείμενο i	|	Όγκος i	|	Αξία i	|	wi/vi
1	|	5	|	15	|	3
2	|	7	|	20	|	2.9
3	|	6	|	10	|	1.7
4	|	4	|	42	|	10.5
5	|	2	|	7	|	3.5
Περιορισμός:		V = 10

Βήματα:

Ξεκινάω από τη λύση S = 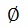κενό σύνολο
Ταξινομώ τα αντικείμενα με κριτήριο wi/vi

Αντικείμενο i	|	Όγκος i	|	Αξία i	|	wi/vi
4	|	4	|	42	|	10.5
5	|	2	|	7	|	3.5
1	|	5	|	15	|	3
2	|	7	|	20	|	2.9
3	|	6	|	10	|	1.7
Περιορισμός:		V = 10

Βήμα 3: S = {4}, v=4, w=42
Βήμα 4: S = {4, 5}, v=6, w=49

Οπότε το πρώτο ράφι χωράει τα δυο αντικείμενα {4, 5} και συνεχίζω με νέο ράφι μέχρι να εξαντληθούν τα αντικείμενα.

Σημείωση:

Το αντικείμενο το οποίο μπαίνει τελευταίο ονομάζεται 'κρίσιμο'. Έτσι αν πάρουμε πέντε-δέκα αντικείμενα στη φθίνουσα σειρά πριν το κρίσιμο και άλλα πέντε-δέκα μετά το κρίσιμο στη συνέχεια ψάχνουμε με ευρετικούς αλγορίθμους που να ικανοποιούν τις βασικές μας συνθήκες: 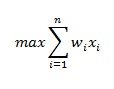και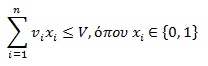

Κώδικας επίλυσης του παραπάνω προβλήματος σε C#:

struct WV //δομή διατεταγμένων τιμών (structure)
{
    int index, //δείκτης αντικειμένου
    double vi, //όγκος αντικειμένου
    double wi //αξία αντικειμένου
}

///Βασική ρουτίνα επίλυσης
void Solve()
{
    double Vconstraint = 10; //ορίζω τον περιορισμό
    double SolutionVolume = 0.0; //συνολικός όγκος της λύσης
    double SolutionValue = 0.0;//συνολική αξία της λύσης
    List<WV> wv = new List<wv>(); //κενή λίστα με τα αντικείμενα που θα εισαγάγουμε
    List<int> solution = new List<int>();

    InputValues(ref wv); //εισαγωγή τιμών στη λίστα μας

    wv = wv.OrderByDescending(o=>o.Volume).ToList(); //χρησιμοποιώ linkq για να ταξινομήσω τη λίστα κατά όγκο σε φθίνουσα κατάταξη

    while ( (wv.Count > 0) ) //βρόγχος επίλυσης
    {
         //Εξετάζω αν μπορώ να βάλω άλλο ένα αντικείμενο στην αποθήκη
        if (SolutionVolume + wv[0].volume <= Vconstraint)
        {
            Solution.Add(wv[0].index);
            SolutionVolume = CalculateVolume(solution, wv);
            SolutionValue = CalculateValue(solution, wv);
            Solution.RemoveAt(0); //Αφαιρώ το αντικείμενο από τη λίστα (είναι πάντοτε το πρώτο στη σειρά)
        }
    }
}

//Μέθοδος υπολογισμού του όγκου της λύσης
double CalculateVolume(wv, solution)
{
    double volume = 0.0;
    Foreach(int item in solution)
    {
        volume += wv[item].vi;
    }
    return volume;
}

//Μέθοδος υπολογισμός της αξίας της λύσης
double CalculateValue(wv, solution)
{
    double value = 0.0;
    Foreach(int item in solution)
    {
        value += wv[item].wi;
    }
    return value;
}

//Δίνω τιμές στο πρόβλημα void InputValues(ref List wv);
{
    WV element = new WV();
    element.index = 1;
    element.vi = 5;
    element.wi = 15;

    wv.Add(element);

    element.index = 2;
    element.vi = 7;
    element.wi = 20;

    wv.Add(element);

    element.index = 3;
    element.vi = 6;
    element.wi = 10;

    wv.Add(element);

    element.index = 4;
    element.vi = 4;
    element.wi = 42;

    wv.Add(element);

    element.index = 5;
    element.vi = 2;
    element.wi = 7;

    wv.Add(element);
}