Πρόβλημα Πακετοποίησης - Bin Packing Problem

Γενικά

Αφορά προβλήματα αποθήκευσης που ανήκουν στην γενική κατηγορία Logistics:

• Οργάνωση Αποθήκης
• Γρήγορη Ανεύρεση
• Εξοικονόμηση Χώρου
• Εξοικονόμηση Ενέργειας (Παραδείγματα: θέματα ψύξης, αερισμού, φωτισμού, μετακίνησης, κλπ)

Διατύπωση του Προβλήματος

Πρόβλημα Bin Packing: Για δεδομένο πλήθος n αντικειμένων μεγέθους Vi και αξίας Wi να προσδιοριστεί το ελάχιστο δυνατό πλήθος χώρων μεγέθους V (ράφια, αποθήκες, ή άλλη διακριτή μονάδα αποθήκευσης) που απαιτείται για να τοποθετηθούν όλα τα αντικείμενα.

Σε αντίθεση με το πρόβλημα του Σακιδίου έχουμε άπειρους αποθηκευτικούς χώρους ίδιου μεγέθους V, και το ζητούμενο είναι ο προσδιορισμός του ελάχιστου αριθμού αυτών.

Αποθηκευτικός χώρος Bin

Ο αποθηκευτικός χώρος (Bin) αφορά μονάδες αποθήκευσης. Τέτοιες μονάδες είναι ράφια, παλέτες, containers, ψυγεία, κλπ.

Προβλήματα Πακετοποίησης Μονοδιάστατο πρόβλημα

Είναι το πρόβλημα κατά το οποίο η πλήρωση αποθηκευτικού χώρου μελετάται μόνον η μια διάσταση (π.χ. μήκος). Τέτοια προβλήματα αφορούν:

• Τοποθέτηση ομοειδών πακέτων σε πανομοιότυπα ράφια
• Τοποθέτηση ομοειδών αντικειμένων τα οποία διαφέρουν μόον ως προς τη μια διάσταση. Για παράδειγμα ράφια Super Market και ομοειδής συσκευασίες. (Το πλάτος είναι πάντα το ίδιο, το ύψος δεν υφίσταται)
• Τοποθέτηση παλετών συγκεκριμένων διαστάσεων σε αποθηκευτικούς χώρους που μεταβάλλεται μόνον η μια τους διάσταση
• Τοποθέτηση αρχείων σε έναν υπολογιστή

Προβλήματα Πακετοποίησης 2D πρόβλημα

Είναι το πρόβλημα κατά το οποίο η πλήρωση αποθηκευτικού χώρου μελετάται οι δύο διάστασεις (π.χ. πλάτος-μήκος). Τέτοια προβλήματα αφορούν:

• Τοποθέτηση αντικειμένων με αδιάφορο ύψος. π.χ. σε ελεύθερη επιφάνει, παλέτες σε φορτηγό
• Τοποθέτηση κιβωτίων διαφορετικών διαστάσεων (που δεν είναι standard) σε ράφια
• Φόρτωση πλοίων, κλπ

Προβλήματα Πακετοποίησης 3D πρόβλημα

Είναι το γενικότερο πρόβλημα αποθήκευσης:

• Τοποθέτηση διαφόρων αντικειμένων σε αποθηκευτικό χώρο, φορτηγό, φορτηγό-ψυγείο, κλπ.

Μαθηματική Προτυποποίηση:

Έτσω ότι έχουμε άπειρους αποθηκευτικούς χώρους (bin) V και θέλουμε να τοποθετήσουμε n αντικείμενα μεγέθους μεγέθους Vi.

Για να ορίσουμε το πρόβλημα ορίζουμε δυαδικές μεταβλητές της μορφής Υi,
όπου i=1,2,...,n και Υ Ε {0, 1}.

και:
Υj = 1 όταν o χώρος binj έχει επιλεγεί και ανήκει στη λύση
Υj = 0 όταν o χώρος binj δεν έχει επιλεγεί και συνεπώς δεν ανήκει στη λύση.

Για παράδειγμα έστω οι χώροι 1, 2, ..., 10,
τότε Y3 = 1 σημαίνει ότι ο χώρος bin3 έχει επιλεγεί, αντίθετα Y4 = 0 σημαίνει ότι ο χώρος bin4 δεν έχει επιλεγεί.

Ορίζουμε επίσης τις δυαδικές μεταβλητές Xij που εκφράζουν πότε το αντικείμενο i είναι τοποθετημένο στον αποθηκευτικό χώρο j,
όπου i=1,2,...,n και Χ Ε {0, 1}.

και:
Χij = 1 όταν το αντικείμενο i είναι τοποθετημένο στον χώρο binj
Χij = 0 όταν τo αντικείμενο i δεν είναι τοποθετημένο στον χώρο binj

Στόχος:

Το ζητούμενο είναι η ελαχιστοποίηση των απαιτούμενων αποθηκευτικών χώρων (bin) που απαιτούνται για να χωρέσουν όλα τα αντικείμενα n. Και αυτό εκφράζεται μαθηματικά από τη σχέση:



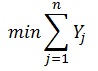
με περιορισμούς:

1.		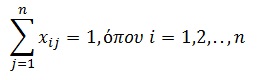δηλαδή κάθε αντικείμενο Xi έχει τοποθετηθεί σε κάποιον αποθηκευτικό χώρο
2.		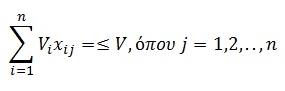το άθροισμα του μεγέθους των αντικειμένων i που βρίσκονται στον αποθηκευτικό χώρο j δεν πρέπει να έχουν μέγεθος μεγαλύτερο από το μέγεθος V του αποθηκευτικού χώρου

Επίλυση - Κατασκευαστικοί αλγόριθμοι:

Οι κατασκευαστικοί αλγόριθμοι στηρίζονται στη λογική ότι ξεκινούμε από μια αρχική λύση S, την οποία βελτιώνουμε βάσει κριτηρίων. Η αρχική λύση S μπορεί να είναι το κενό σύνολο. Τα κριτήρια μας ονομάζονται στόχοι ή κόστος και γενικότερα τα καλούμε αντικειμενική συνάρτηση (Objective Function).

Πρόβλημα 1:

Έστω ότι έχουμε έναν χώρο που περιέχει τα εξής αντικείμενα:

Αντικείμενο i	|	Όγκος i
1	|	7
2	|	4
3	|	6
4	|	2
5	|	3
6	|	1
Μέγεθος Bin:		V = 10

Κριτήριο για την τοποθέτηση είναι να επιλέγουμε το μεγαλύτερο αντικείμενο κάθε φορά μέχρι να γεμίσουν τα ράφια:

Για να επιταχύνω τη διαδικασία ταξινομώ τα αντικείμενα σε φθίνουσα κατάταξη:

Αντικείμενο i	|	Όγκος i
1	|	7
3	|	6
2	|	4
5	|	3
4	|	2
6	|	1
Μέγεθος Bin:		V = 10

και προχωρώ στην επίλυση:

Βήμα 1:

Ξεκινάω από τη λύση S = 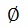κενό σύνολο

Βήμα 2:

Επιλέγω το πρώτο αντικείμενο S={ [1] } και το τοποθετώ στο πρώτο ράφι. Έτσι το Bin1 θα έχει ελεύθερο χώρο l = 10-7=3 και κατειλημμένο 7. Κανένα άλλο αντικείμενο δεν μπορεί να χωρέσει σε αυτό το ράφι και προχωρώ στο επόμενο.

Βήμα 3:

Επιλέγω το επόμενο μεγαλύτερο αντικείμενο αντικείμενο από αυτά που έχουν απομείνει S={ [1], [3] } και το τοποθετώ στο δεύτερο ράφι. Έτσι το Bin2 θα έχει ελεύθερο χώρο l = 10-6=4 και κατειλημμένο 6. Το επόμενο μεγαλύτερο χωράει επίσης σε αυτό το ράφι, οπότε η λύση μας γίνεται S={ [1], [3, 2] }. Έτσι το Bin2 θα έχει ελεύθερο χώρο l = 10-6-4=0 και κατειλημμένο 10.

Βήμα 4:

Επιλέγω το επόμενο μεγαλύτερο αντικείμενο αντικείμενο από αυτά που έχουν απομείνει S={ [1], [3, 2], [5] } και το τοποθετώ στο τρίτο ράφι. Έτσι το Bin3 θα έχει ελεύθερο χώρο l = 10-3=7 και κατειλημμένο 3. Το επόμενο μεγαλύτερο χωράει επίσης σε αυτό το ράφι, οπότε η λύση μας γίνεται S={ [1], [3, 2], [5, 4] }. Έτσι το Bin3 θα έχει ελεύθερο χώρο l = 10-3-2=5 και κατειλημμένο 5. Οπότε χωράει και το τελευταίο αντικείμενο στη λύση, η οποία γίνεται S={ [1], [3, 2], [5, 4, 6] } και l=10-3-2-1 = 4.

Οπότε ανακεφαλαιώνοντας έχουμε χρησιμοποιήσει τριά ράφια, τα οποία έχουμε πληρώσει έτσι ώστε να έχουν ελεύθερο χώρο 3, 0 και 4 μονάδες αποθήκευσής.

Πρόβλημα 2:

Στο προηγούμενο πρόβλημα έχουμε αφήσει κενό χώρο στα χρησιμοποιούμενα ράφια. Μια διαφορετική προσέγγιση θα είναι η πλήρωση των χώρων προσπαθώντας να μην αφήνουμε κενά. Δηλαδή να καταλήξουμε στην εξής λύση: S={ [1, 5], [3, 2], [4, 6] } που ο ελεύθερος χώρος είναι 0, 0 και 7 αντίστοιχα για τα ράφια bin1, bin2 και bin3.

Πρόβλημα 3:

Άλλη προσέγγιση του ίδιου προβλήματος είναι να ξεκινήσουμε από τόσα ράφια όσα είναι και τα αντικείμενα. Δηλαδή να ξεκινήσουμε από 6 ράφια, δηλαδή αρχική λύση: S = {[1], [3], [2], [5], [4], [6]} και στη συνέχεια να προσπαθήσουμε να ενώσουμε ράφια μεταξύ τους:

[1] merge [5]: S = {[1, 5], [3], [2], [4], [6]}
[3] merge [2]: S = {[1, 5], [3, 2], [4], [6]}
[4] merge [6]: S = {[1, 5], [3, 2], [4, 6]}