Line Search

Θα επιλύσουμε το πρόβλημα Εύρεσης Ελαχίστου με τη μέθοδο Αναζήτησης Γραμμής (Line Search). Θα εφαρμόσουμε την επίλυση στο παρακάτω πρόβλημα:

Ζητούμενο: Να βρεθεί το ελάχιστο της συνάρτησης f(x1, x2) με τη μέθοδο Αναζήτησης Γραμμής,

όπου f(x1, x2) = (x1*x2 - 3)^2 + (x2 - 5)^2.

Το πρόβλημα να επιλυθεί με τη χρήση VBA για Excel.

Αλγόριθμος:

Για να επιλύσουμε το παραπάνω πρόβλημα θα πρέπει αρχικά να σχεδιάσουμε κάποιον αλγόριθμο επίλυσης σύμφωνα με τη Μεθοδολογία Αναζήτησης Γραμμής:

• Επιλέγω τυχαίο σημείο στο χώρο επίλυσης
• Υπολογίζω το διάνυσμα κλίσης
• Στην ευθεία που ορίζεται από το διάνυσμα κλίσης υπολογίζω το σημείο πάνω σε αυτή που ελαχιστοποιεί τη συνάρτηση.
• Επαναλαμβάνω τα βήματα Β-Δ έως ότου η διαφορά δυο διαδοχικών σημείων να είναι μικρότερη από κάποια τιμή

Σχηματικά ο Αλγόριθμος:

Στο επίπεδο από το σημείο Χ0 υπολογίζω το διάνυσμα κλίσης Sk (Grad) της συνάρτησης f στο σημείο X0. Τότε αν Xk είναι οποιοδήποτε διάνυσμα έρευνας στο χώρο, τότε το άθροισμα Xk + aSk ορίζει μια ευθεία με παράμετρο έναν παραγματικό αριθμό, τον a.

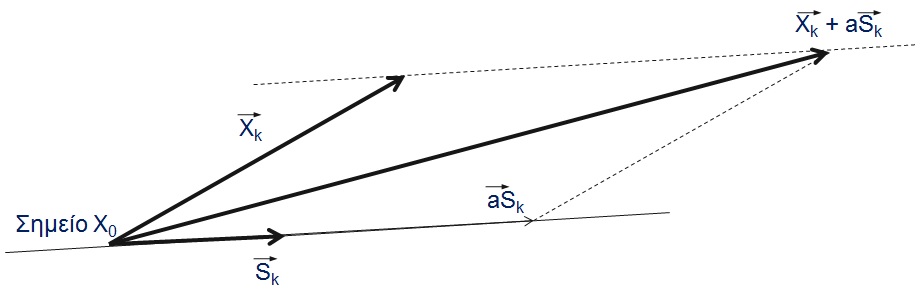
Με τον παραπάνω μετασχηματισμό καταφέρνουμε να δημιουργήσουμε το ισοδύναμο πρόβλημα εύρεσης του ελάχιστου της f(x1, x2) στο βήμα k όπου το ελάχιστο να εξαρτάται πλέον από έναν αριθμό, το a, και όχι από ένα διανυσματικό μέγεθος, το Xk.
Δηλαδή: min[ f(x) ] → min [ f(Xk + aSk) ] → min[ g(a) ], όπου a = μήκος της έρευνας και είναι πραγματικός αριθμός
Έτσι για να υπολογίσουμε το min πρέπει ουσιαστικά να λύσουμε την εξίσωση f΄(xk) = 0 ή την μετασχηματισμένη g(a)΄ = 0

Υπολογισμός του Ελάχιστου με τη μέθοδο Newton-Raphson
Η παραπάνω σχέση

g(a)΄ = 0

αποτελεί μια μη γραμμική εξίσωση που μπορεί να λυθεί επαναληπτικά με τη μέθοδο εύρεσης ριζών Newton-Raphson. Δηλαδή από την επαναληπτική σχέση:

ak+1 = ak – g΄(ak)/g΄΄(ak-1)

Επαναληπτική μέθοδος υπολογισμού ριζών μη γραμμικής εξίσωσης με τη μέθοδο Newton-Raphson
Για τον υπολογισμό της ρίζας ρk της μη γραμμικής εξίσωσης f(x) = 0 με τη μέθοδο Newton-Raphson ακολουθούμε την επαναληπτική σχέση:

ρk+1 = ρk + f(ρk) / f'(ρk)

όπου ρ0 είναι μια αυθαίρετη αρχική τιμή και η f'(rk) μπορεί να υπολογιστεί προσεγγιστικά από τις κεντρικές διαφορές:

f'(x)≈[ f(x+Δh)-f(x-Δh) ] / 2Δh

Συνοψίζοντας:
Θα πρέπει να κατασκευάσουμε έναν αλγόριθμο όπου:

• INPUT Μεθόδου: αρχικό σημείο στο χώρο επίλυσης X0, βήμα Δh για τον υπολογισμό των κεντρικών διαφορών, ανοχή TOL & μέγιστο αριθμό επαναλήψεων Nmax
• INPUT για ότι αφορά την Newton-Raphson: βήμα Δhnr για τον υπολογισμό των κεντρικών διαφορών, ανοχή μεθόδου Newton-Raphson Tolnr & μέγιστο αριθμό επαναλήψεων Newton-Raphson Nnrmax, δυο αρχικές τιμές a0 & a1
• Θέτω Χk = X0
• Θέτω k = 1
• Υπολογίζω το διάνυσμα κλίσης Grad στο Χk
• Κλήση της NewtonRaphson(a0, Νnrmax, Tolnr, Dhnr) για τον υπολογισμό της a
• Υπολογισμός της Χk = Xk + a * Grad.
• Έλεγχος σύγκλισης Norm(Grad) < Tol
• k = k + 1
• Αν k > Nmax τότε ο αλγόριθμος σταματάει και παρουσιάζουμε μήνυμα αποτυχίας
• Αν έχουμε σύγκλιση τότε παρουσιάζουμε το ελάχιστο, αν όχι τότε πηγαίνουμε στο βήμα 5

Αλγόριθμος Newton-Raphson NewtonRaphson(a0, a1, xk, sk, Νnrmax, Tolnr, Dhnr):

• Θέτω ak = a1 & ak_1=a0
• Θέτω k = 1
• Υπολογίζω την τιμή της g'(a) στο ak
• Υπολογίζω την τιμή της g'(a) στο ak_1
• Υπολογίζω την παράγωγο g''(a) = (g'(ak) - g'(ak_1)) / (ak - ak_1)
• Υπολογίζω xk=xk - g'/g''
• Έλεγχος σύγκλισης abs(ak-ak_1) < Tol, αν ναι τότε σταματάμε και παρουσιάζουμε αποτελέσματα
• Θέτω ak_1 = ak
• k = k + 1
• Αν k > Nmax τότε ο αλγόριθμος σταματάει και παρουσιάζουμε μήνυμα αποτυχίας
• Επιστρέφουμε στο βήμα 3

Αφού έχουμε διατυπώσει τον αλγόριθμο μπορούμε πλέον να τον κατασκευάσουμε. Το Παράδειγμα του παραπάνω κώδικα βρίσκεται γραμμένο σε VBA μπορείτε να το κατεβάστε από ΕΔΩ