Quantum Computing είναι το χόμπι μου. Όμως ας δούμε μερικές συνήθεις ερωτήσεις σχετικά με το θέμα. Εισαγωγή στην Κβαντική Πληροφορική Ο υπολογιστής γενικά είναι μια συσκευή που εφαρμόζει αλγόριθμους (δηλ. ένα σύνολο οδηγιών) για να υπολογίσει τη λύση σε προβλήματα. Οι σημερινοί υπολογιστές λειτουργούν χρησιμοποιώντας κυκλώματα λογικών πυλών, στερεάς κατάστασης, τυπωμένα σε μικροτσίπ. Προβλέπεται ότι η συρρίκνωση των συστατικών ενός μικροτσίπ στο εγγύς μέλλον, θα οδηγήσει σε λογικές πύλες φτιαγμένες μόνο από μερικά άτομα. Σε αυτό το επίπεδο όμως τα κβαντικά φαινόμενα γίνονται αναπόφευκτα. Αυτά τα κβαντικά φαινόμενα εμφανίζονται σήμερα ως ανεπιθύμητες απώλειες και θόρυβος στην αρχιτεκτονική υπολογιστών. Εντούτοις, αντί να είναι ένα εμπόδιο για την περαιτέρω ανάπτυξη, μπορούν να χρησιμοποιηθούν σε μια νέα συσκευή που θα την ονομάζουμε κβαντικό υπολογιστή. Αυτή η συσκευή θα εφαρμόζει νέα είδη κβαντικών αλγορίθμων για να λύσει μερικά προβλήματα, αποτελεσματικότερα και πολύ γρηγορότερα από τους συνηθισμένους υπολογιστές. Οι πρώτοι πρότυποι κβαντικοί υπολογιστές έχουν ήδη χτιστεί. Ο μεγαλύτερος είναι μια συσκευή από 7 qubit που βασίζεται σε πυρηνικό μαγνητικό συντονισμό (NMR). Είναι δύσκολο να προβλεψουμε πότε θα κατασκευαστεί ένας πλήρως λειτουργικός κβαντικός υπολογιστής. Έίναι σίγουρο όμως ότι προτού να κάνει την εμφάνιση του, η κβαντική τεχνολογία που υποστηρίζει την ανάπτυξή του, θα χρησιμοποιηθεί και με άλλους τρόπους. Ένα παράδειγμα είναι το κβαντικό σύστημα κρυπτογραφίας που είναι βασισμένο στις ίδιες κβαντικές αρχές και φθάνει απ' ότι φαίνεται σε εμπορική βιωσιμότητα. Με αυτό το κείμενο θα προσπαθήσω να περιγράψω τις βασικές θεωρητικές αρχές που συνδέονται με την κατανόηση της λειτουργείας ενός κβαντικού υπολογιστή και θα παρουσιάσουμε μερικές από τις διαφορετικές φυσικές προσεγγίσεις-πραγματοποιήσε που ερευνώνται σε όλο τον κόσμο (όχι δυστυχώς και στην Ελλάδα) αυτήν την περίοδο. 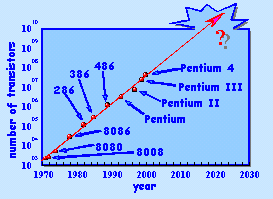O Νόμος του Moore και το μέλλον των υπολογιστών Το 1965 ο συνιδρυτής της Intel, Moore σημείωσε ότι η υπολογιστική ισχύς (αριθμός των τρανζίστορ και ταχύτητα) των τσιπ των υπολογιστών διπλασιάζεται κάθε 18 μήνες περίπου. Αυτή η τάση έχει συνεχιστεί για σχεδόν 4 δεκαετίες. Όμως μπορεί να συνεχιστεί; Η βασική μονάδα επεξεργασίας σε ένα τσιπ υπολογιστών είναι το τρανζίστορ που ενεργεί όπως ένας διακόπτης. Τα δυαδικά ψηφία 0 και 1 αντιπροσωπεύονται από το τρανζίστορ που τίθεται στη θέση off ή στη θέση on.Τη σημερινή εποχή χιλιάδες ηλεκτρόνια, με την μορφή παλμών, χρησιμοποιούνται για να λειτουργήσει κάθε τρανζίστορ. 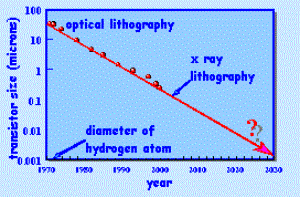Όμως καθώς η υπολογιστική ισχύς αυξάνεται, το μέγεθος των τρανζίστορ μειώνεται, όπως προβλέπει ο Moore.Έτσι εάν ο νόμος του Moore συνεχίσει να ισχύει το 2030, κάθε τρανζίστορ προβλέπεται να γίνει τόσο μικρό όσο ένα άτομο υδρογόνου. Δεν έχουμε βέβαια ακόμα την τεχνολογία για να χτίσουμε τέτοια τρανζίστορ. Αλλά ακόμα κι αν την είχαμε, τα άτομα και τα ηλεκτρόνια σε αυτό το επίπεδο συμπεριφέρονται με τους παράξενους τρόπους της κβαντικής μηχανικής. Τα κβαντικά φαινόμενα θα γίνονταν ένα σημαντικό εμπόδιο στη λειτουργία των κλασικά σχεδιασμένων λογικών πυλών. Στον αντίποδα αυτού του προβλήματος υπάρχει ένα προνόμιο. Η κβαντική φυσική επιτρέπει έναν απολύτως νέο τρόπο να γίνονται υπολογισμοί. Και αυτός ο νέος τρόπος απελευθερώνει νέα, φανταστική υπολογιστική ισχύ που βασίζεται στη κυματική φύση των κβαντικών σωματιδίων. Κβαντικές έννοιες στους υπολογισμούς Η μελέτη των κβαντικών υπολογισμών έχει φέρει το λεξιλόγιο και τις έννοιες της κβαντικής φυσικής και έχει αναπτύξει ένα νέο τομέα της πληροφορικής. Στην καρδιά της κβαντικής φυσικής είναι οι έννοιες των κυμάτων και των σωματιδίων. Στις αρχές του 1800 ο Thomas Young εκτέλεσε το πείραμα των δύο σχισμών που έδειξε ότι το φως αποτελείτε από κύματα. Ένα κύμα παραδείγματος χάριν είναι μια κυμάτωση σε μια λίμνη. Όταν τα κύματα τέμνονται μεταξύ τους τα ύψη τους προσθέτονται. Αυτό το φαινόμενο ονομάζεται συμβολή (Interference). Είναι εκπληκτικό το ότι φαινόμενα συμβολής έχουμε και στα σωματίδια. Το 1905, ο Einstein εξήγησε το φωτοηλεκτρικό φαινόμενο με το να υποστηρίξει ότι το φως αποτελείται από σωματίδια. Τα σωματίδια αυτά καλούνται σήμερα φωτόνια. Έτσι πρέπει να σκεφτούμε ότι το φως αποτελείται από κύματα και σωματίδια. Επεκτείνοντας αυτή την ιδέα, το 1923 ο Louis de Broglie πρότεινε ότι και άλλα σωματίδια, όπως τα ηλεκτρόνια, συμπεριφέρονται σαν κύματα. Το 1926 οι Davisson και Germer επιβεβαίωσαν την κυματική φύση των ηλεκτρονίων σε ένα πείραμα όπου τα ηλεκτρόνια έπαθαν περίθλαση από μια επιφάνεια κρυστάλλου νικελίου. Η κυματική ιδιότητα των σωματιδίων έχει ελεγχθεί από τότε σε πολυάριθμα πειράματα. Το συμπέρασμα είναι ότι άλλοτε τα ηλεκτρόνια, τα άτομα, τα μόρια κ.λ.π. συμπεριφέρονται ως σωματίδια, και άλλοτε, συμπεριφέρονται ως κύματα. Το φαινόμενο αυτό έχει γίνει γνωστό στην κβαντική φυσική ως διτή (σωματιδιακή-κυματική) φύση της ύλης (Συμπληρωματικότητα). Το κύμα που συνδέεται με ένα ηλεκτρόνιο, παραδείγματος χάριν, διαδίδεται μέσα στο χώρο κατά μήκος όλων των πιθανών τροχιών του. Το σωματίδιο λέμε ότι είναι σε μία κατάσταση υπέρθεσης(superposition) όλων αυτών των πιθανών τροχιών-θέσεων. Εντούτοις, όποτε μετράμε τη θέση ενός σωματιδίου την βρίσκουμε σε ένα συγκεκριμένο σημείο. Αυτό είναι ένα από τα εκπληκτικά χαρακτηριστικά γνωρίσματα της κβαντικής φυσικής, και αποτελεί τον πυρήνα της κβαντικής φύσης του κόσμου.         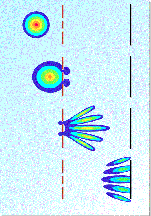(A) Δυαδικότητα κύματος-σωματιδίου στο πείραμα δύο σχισμών. Ένα ηλεκτρόνιο ταξιδεύει προς έναν τοίχο που έχει δύο μικρές σχισμές. Το κύμα που συνδέεται με το ηλεκτρόνιο ενεργεί όπως ένα χαλίκι που ρίχνεται σε μια λίμνη. Διαδίδεται έξω και περνά και μέσω των δύο σχισμών. Η εικόνα συμβολής που προκύπτει καθορίζει την πιθανότητα να παρατηρήσουμε σε κάποιο σημείο της οθόνης το ηλεκτρόνιο (B) Τα ηλεκτρόνια στο πείραμα των δύο σχισμών ανιχνεύονται ως ενιαία σωματίδια (δηλ. σημεία) στην οθόνη σε μια απροσδιόριστη θέση (αριστερή εικόνα). Με την πάροδο του χρόνου όμως εμφανίζονται τα φαινόμενα συμβολής (δεξιά εικόνα).   Η εικόνα (Α) εμφανίζει τι συμβαίνει όταν μια δέσμη ηλεκτρονίων πέφτει σ’ ένα εμπόδιο από δύο μικρές σχισμές. Το κύμα που συνδέεται με κάθε ηλεκτρόνιο περνά μέσω των δύο σχισμών και διαδίδεται μέχρι την οθόνη. Όταν αυτά τα κύματα επικαλύπτονται έχουμε φαινόμενα συμβολής, δηλαδή δύο όρη προσθέτονται για να κάνουν ένα μεγαλύτερο όρος κ.λ.π., αλλά ένα όρος και μια κοιλάδα ακυρώνουν το ένα το άλλο. Αυτό που προκύπτει είναι η συμβολή των κυμάτων και ταξιδεύει στην οθόνη όπου μετράμε το πού κάθε ηλεκτρόνιο βρίσκεται. Τα ηλεκτρόνια έχουν μεγαλύτερη πιθανότητα εύρεσης όπου το ύψος του κύματος είναι μεγαλύτερο (όρη), και καθόλου πιθανότητα εύρεσης όπου το ύψος των κυμάτων είναι μηδέν(κοιλάδα). Στις εικόνες του σχήματος (Β) εμφανίζεται το τι φαίνεται στην οθόνη όταν μερικά (στο αριστερό μέρος της εικόνας) και πολλά (στο δεξιό μέρος της εικόνας) ηλεκτρόνια έχει περάσει μέσω των σχισμών. Κάθε ηλεκτρόνιο, που είναι ένα σημειακό σωματίδιο, εμφανίζεται σαν ένα μικροσκοπικό σημείο στη φωτογραφική πλάκα της οθόνης. Εάν κλείσουμε μία από τις σχισμές δεν θα υπήρχαν σκοτεινές ζώνες και φωτεινές περιοχές στην δεξιά εικόνα του σχήματος (Β). Όμως όταν και οι δύο σχισμές είναι ανοικτές, κάθε ηλεκτρόνιο αποφεύγει ορισμένες περιοχές στην οθόνη δημιουργώντας τις σκοτεινές ζώνες. Ένα ηλεκτρόνιο περνά  από μια σχισμή ή και από τις δύο σχισμές; Η απόσταση μεταξύ των σκοτεινών ζωνών συσχετίζεται (αντιστρόφως ανάλογη) με την απόσταση των σχισμών. Δεδομένου ότι το ηλεκτρόνιο αποφεύγει τις σκοτεινές ζώνες, πρέπει να έχει την πληροφορία για την απόσταση των σχισμών. Με άλλα λόγια, “βλέπει” και στις δύο σχισμές. Καταλήγουμε λοιπόν στο παράξενο συμπέρασμα ότι κάθε ηλεκτρόνιο περνά μέσω των δύο σχισμών ταυτόχρονα. Η ιδιότητα αυτή της υπέρθεσης, ότι δηλαδή ένα σωματίδιο μπορεί να είναι σε δύο θέσεις ταυτόχρονα, είναι που επιτρέπει στους κβαντικούς υπολογιστές για να εκτελούν πολλούς υπολογισμούς ταυτόχρονα. Bits και Qubits Τα συμβατικά κυκλώματα υπολογιστών είναι βασισμένα σε στερεάς κατάστασης συσκευές που αντιπροσωπεύουν το bit. Στους περισσότερους υπολογιστές, ένα τρανζίστορ που κλείνεται (η τάση εξόδου είναι μηδέν) αντιπροσωπεύει το δυαδικό αριθμό 0 και ένα τρανζίστορ που ανοίγεται (η τάση εξόδου είναι 5 βολτ) αντιπροσωπεύει το δυαδικό αριθμό 1. Οι κβαντικοί υπολογιστές λειτουργούν με qubits. Ένα qubit είναι ένα σωματίδιο που μπορεί  να υπάρξει σε μια κατάσταση υπέρθεσης των 0 και 1 ταυτόχρονα. Οι καταστάσεις υπέρθεσης επιτρέπουν σε πολλούς υπολογισμούς για να εκτελεσθούν ταυτόχρονα, και προκαλούν αυτό που είναι γνωστό ως κβαντικός παραλληλισμός. Το απλούστερο ίσως παράδειγμα ενός qubit είναι ένα φωτόνιο που μπορεί να ταξιδέψει κατά μήκος δύο μονοπατιών. Το ένα μονοπάτι μπορεί να αντιπροσωπεύει το δυαδικό αριθμό 0 ενώ το άλλο μονοπάτι  τον αριθμό 1. Το φωτόνιο μπορεί να υπάρξει σε υπέρθεση των δύο μονοπατιών όταν κατευθύνεται σε έναν διαχωριστή δέσμης. Ένας διαχωριστής δέσμης είναι ακριβώς όπως ένας συνηθισμένος καθρέφτης, εντούτοις το αντανακλαστικό του επίστρωμα γίνεται τόσο λεπτό που δεν αντανακλά όλο το φως που πέφτει πάνω του αλλά κάποιο φως τον διαπερνά. Όταν ένα φωτόνιο “πέφτει” σ’ έναν τέτοιο καθρέπτη, προκύπτει σε μια κατάσταση υπέρθεσης του ανακλώμενου μονοπατιού και του διαδιδόμενου μονοπατιού. Το φωτόνιο είναι σε μια υπέρθεση των δύο μονοπατιών και αντιπροσωπεύει έτσι και το 0 και το 1 ταυτόχρονα. Αυτό είναι μια κβαντική έκδοση " και ο σκύλος χορτάτος και η πίτα ολόκληρη" Πολλά κβαντικά συστήματα μπορούν να χρησιμοποιηθούν ως qubits. Περισσότερες λεπτομέρειες δίνονται στην παράγραφο των τεχνολογιών πραγματοποίησης. Κβαντικός παραλληλισμός Ένας καταχωρητής μνήμης ενός bit μπορεί να περιέχει έναν από τους αριθμούς 0 και 1. Επιπλέον ένας καταχωρητής δύο bit μπορεί να καταχωρήσει τους δυαδικούς αριθμούς 00 ..01 ..10 και 11 (δηλ. 0 ..1 ..2 και 3 στη βάση δέκα). Όμως αυτές οι μνήμες μπορούν μόνο να καταχωρήσουν μόνο έναν αριθμό (π.χ. ο δυαδικός αριθμός 10) σε μια χρονική στιγμή. Αντίθετα, η κβαντική κατάσταση υπέρθεσης επιτρέπει σε ένα qubit να καταχωρήσει το 0 και το 1 ταυτόχρονα . Δύο qubits μπορούν να καταχωρήσουν όλους τους 4 δυαδικούς αριθμούς 00 ..01 ..10 και 11 ταυτόχρονα. Τρία qubits καταχωρούν τους 8 δυαδικούς αριθμούς 000 ..001 ..010 ..011 ..100 ..101 ..110 και 111 ταυτόχρονα. Ο πίνακας δε1sχνει ότι 300 qubits μπορούν να καταχωρήσουν περισσότερους από 1090 αριθμούς ταυτόχρονα. Ο αριθμός αυτός είναι μεγαλύτερος από τον αριθμό των ατόμων που υπάρχουν στο ορατό σύμπαν! Το γεγονός αυτό δείχνει την τη δύναμη των κβαντικών υπολογιστών: ακριβώς 300 φωτόνια (ή 300 ιόντων κ.λπ....) μπορούν να καταχωρήσουν περισσότερους αριθμούς από  όσα άτομα υπάρχουν στον κόσμο, και οι υπολογισμοί μπορούν να εκτελεσθούν ταυτόχρονα σε κάθε ένας από αυτούς τους αριθμούς! qubits Καταχωρεί ταυτόχρονα συνολικός αριθμός 1 (0 και 1) 2 1 = 2 2 (0 και 1)(0 και 1) 2x2 = 22 = 4 3 (0 και 1)(0 και 1)(0 και 1) 2x2x2 = 2 3 = 8 : : : 300 (0 και 1)(0 και 1)........(0 και 1) 2x2...... x2 = 2 300 Κβαντική περιπλοκή(entaglement)Υπάρχει ακόμα ένα σημαντικό χαρακτηριστικό γνώρισμα της κβαντικής φυσικής που αξιοποιείται στους κβαντικούς υπολογισμούς. Όταν δύο ή περισσότερα σωματίδια αλληλεπιδρούν το ένα με το άλλο, δεν είναι πλέον δυνατόν να περιγραφούν χωριστά. Συμπεριφέρονται ως μία ενιαία οντότητα ακόμα και ανστη συνέχεια χωριστούν από μεγάλες αποστάσεις. Τότε λέμε ότι αυτά τα σωματίδια είναι περιπλεγμένα (entagled). Τα περιπλεγμένα σωματίδια επιτρέπουν μια τεράστια μείωση του υλικού που απαιτείται για να εφαρμοστούν οι κβαντικοί αλγόριθμοι. Περισσότερες λεπτομέρειες για την εμπλοκή δίνονται στην ειδική παράγραφο   Τι είναι το Quantum Computing; Ας πω τι δεν είναι πρώτα για να εξαλείψω τυχόν λάθος εντυπώσεις που μπορεί να υπάρχουν.  Το Quantum Computing δεν είναι υπολογιστική κβαντομηχανική ή κβαντική χημεία ή μοντελοποίηση κβαντικών συστημάτων, χρησιμοποιώντας κλασικούς υπολογιστές. Το Quantum computing είναι να κάνουμε υπολογισμούς με κβαντικά συστήματα, που ονομάζονται κβαντικοί υπολογιστές. Οι κβαντικοί υπολογιστές βασίζονται σε qubit που είναι συζευγμένα σε δίκτυα. Το qubit αντίθετα με το bit μπορεί να είναι μια υπέρθεση των λογικών καταστάσεων σωστό και λάθος ή αλλιώς |0> και  |1>. Οι υπολογισμοί στους κβαντικούς υπολογιστές γίνονται μέσω μοναδιαίων μετασχηματισμών (unitary transformations) πάνω σε υπερθέσεις των qubit. Πιο συγκεκριμένα απλοί υπολογισμοί πραγματοποιούνται ως εξής: Προετοιμάζουμε το δίκτυο των qubit του υπολογιστή σε μια αρχική υπέρ-κατάσταση (υπέρθεση των υπερθέσεων των βασικών καταστάσεων |0> και |1> των qubit) Δρούμε σε αυτή συνδυασμό κατάλληλων μοναδιαίων μετασχηματισμών ανάλογα με το πρόβλημα . Η μέτρηση της υπέρ-κατάστασης αυτής μετά την δράση των μοναδιαίων τελεστών μας δίνει το ποθητό αποτέλεσμα. Η δύναμη των κβαντικών υπολογισμών (Quantum Computing) είναι η έννοια της υπέρθεσης των καταστάσεων της κβαντικής. Λόγω αυτής της υπέρ κατάστασης μπορούμε να πραγματοποιήσουμε παράλληλους υπολογισμούς σε κάθε υπολογιστικό βήμα μειώνοντας κατά πολύ τον απαιτούμενο χρόνο.