New Page

Ε.Μ.Π.
Τ.Α.Τ.Μ.
Εργαστήριο Δομικής Μηχανικής & ΣΤΕ

Στατική

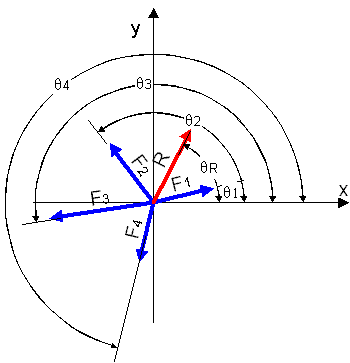
Πρόβλημα: Ζητείται ο υπολογισμός της Συνισταμένης, R, των συνεπιπέδων δυνάμεων F₁, F₂, F_3,καιF_4.

Παράμετροι του Συστήματος: Αριθμός δυνάμεων Ν=4

Δυνάμεις [ newton ]	Γωνίες [ ^o ]
F₁= 30	θ₁ = 15
F₂ = 45	θ₂ = 120
F₃ = 15	θ₃ = 185
F₄ = 30	θ₄ = 270

Κάθε δύναμη F αναλύεται σε δύο συνιστώσες F_x και F_y.

Η συνιστώσα κατά x της συνισταμένης R_x, ισούται με το άθροισμα των συνιστωσών κατά x. Αντίστοιχα υπολογίζεται και η κατά y συνιστώσα της συνισταμένης.

Ακολουθούν οι υπολογισμοί:

F_xi=F_i*cos(θi) F_yi=F_i*sin(θi)

F_xi [newton]	F_yi [newton]
28,978	7,765
-22,500	38,971
-14,.943	-1,307
0,000	-30,000

Οι συνιστώσες της R κατά x και y υπολογίζονται ως εξής:

R_x=a F_xi i=1,…4 , R_x= -8,465 newton
R_y=a F_yi i=1,…4 , R_y= 15,428 newton

Το μέτρο της συνισταμένης υπολογίζεται από το Πυθαγόρειο θεώρημα

R = O ( R_x²+R_y²) = 17,598 newton

Για τον προσδιορισμό της διεύθυνσης της συνισταμένης μπορούμε να υπολογίσουμε το τόξο μέσω της εφαπτομένης:

θ = atan(R_y/R_x) = -61,248deg.

Παρατηρείστε το αρνητικό πρόσημο της γωνίας, αφού η συνιστώσα κατά x βρέθηκε αρνητική.

‘Engineering Mechanics’, Shaum’s Electronic tutor, McGraw-Hill, 1997