= ((Q1x')'(Q1Q2)'(Q2x')')'
Ενδεικτική λύση άσκησης 1 εξετάσεων Σεπτεμβρίου 2010
Σχεδιάστε και υλοποιήστε κύκλωμα το οποίο:
1. Εκκινεί από μία αρχική κατάσταση ΑΚ.
2. Δέχεται σαν είσοδο σειριακά δεδομένα 1 bit (από διακόπτη δύο θέσεων) σε συγχρονισμό με ένα ρολόι (από το διακόπτη με επαναφορά)
3. Μετατρέψτε το τελευταίο ψηφίο του ΑΜ σας σε δυαδικό αριθμό 4 bit. Τα 3 λιγότερο σημαντικά bit ορίζουν την ακολουθία προς αναγνώριση.
4. Όταν αναγνωρίσει την παραπάνω ακολουθία μεταβαίνει στην τελική κατάσταση ΤΚ στην οποία παραμένει ανεξαρτήτως εισόδου. Η κατάσταση του κυκλώματος πρέπει να φαίνεται σε δύο φωτοδιόδους.
Παράδειγμα 1: Για ΑΜ 03101234 => 410 = 01002 => Ζητείται κύκλωμα το οποίο να αναγνωρίζει την ακολουθία 1 0 0.
Παράδειγμα 2: Για ΑΜ 03105239 => 910 = 10012 => Ζητείται κύκλωμα το οποίο να αναγνωρίζει την ακολουθία 0 0 1.
Ενδεικτικές λύσεις:
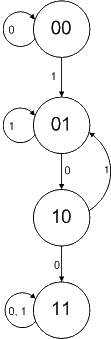
| Διάγραμμα καταστάσεων (100) | Κατάσταση | Κωδικοποίηση | Είσοδος | Επόμενη κατάσταση | Χαρτες Karnaugh | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q1(t) | Q2(t) | x | Q1(t+1) | Q2(t+1) | |||||||
 | A | 0 | 0 | 0 | 0 | 0 | Q1\Q2x | 00 | 01 | 11 | 10 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | ||
| B | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 1 | D1 = Q1x' + Q1Q2 + Q2x' = ((Q1x')'(Q1Q2)'(Q2x')')' | ||||||
| Γ | 1 | 0 | 0 | 1 | 1 | Q1\Q2x | 00 | 01 | 11 | 10 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | ||
| Δ | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | D2 = Q1 + x = (Q1'x')' | ||||||
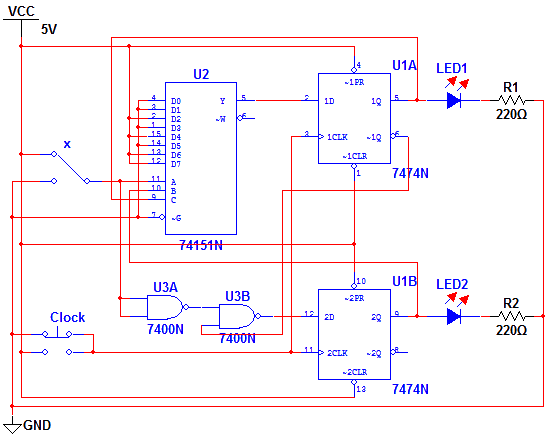
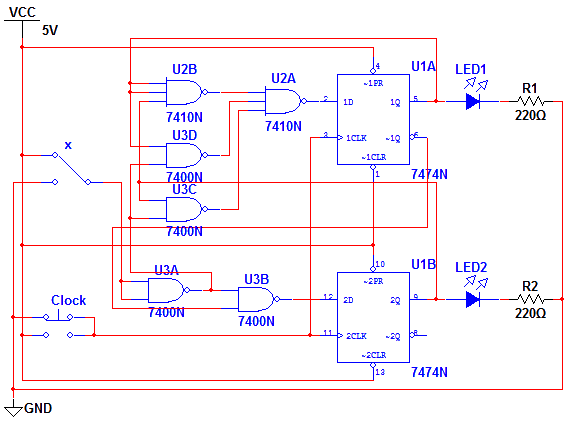
Οι παρακάτω δύο λύσεις υλοποιούνται με τρία ολοκληρωμένα κυκλώματα η κάθε μία