Ενδεικτική λύση άσκησης 1 εξετάσεων Σεπτεμβρίου 2009
Σχεδιάστε και υλοποιήστε κύκλωμα με είσοδο τον πιεστικό διακόπτη με επαναφορά, το οποίο να δίνει συνεχώς στην έξοδό του, η οποία θα φαίνεται σε 5 ή 6 φωτοδιόδους (ανάλογα με την κατηγορία που ανήκετε), τις παρακάτω ακολουθίες:
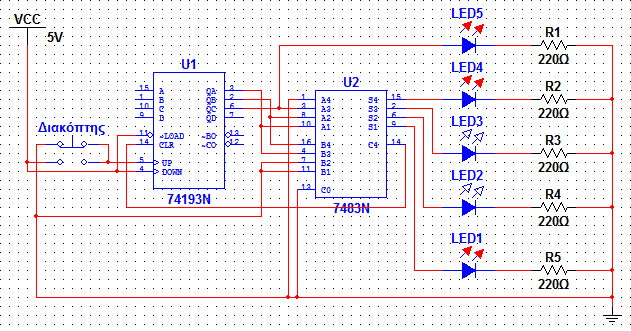
Αν ο ΑΜ σας λήγει σε 1, 2, 3, 4 ή 5 απεικονίστε τα πολλαπλάσια του 5 μικρότερα από 35:
00000 – 00101 – 01010 – 01111 – 10100 – 11001 – 11110
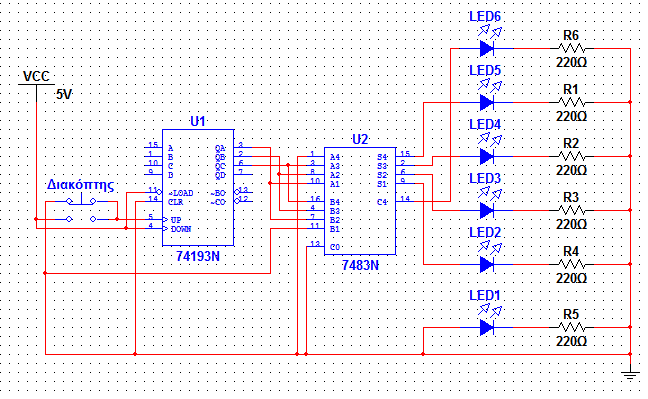
Αν ο ΑΜ σας λήγει σε 6, 7, 8, 9 ή 0 απεικονίστε τα πολλαπλάσια του 6 μικρότερα από 48:
000000 – 000110 – 001100 – 010010 – 011000 – 011110 – 100100 – 101010
Προτεινόμενη λύση:
| Μετρητής | Πολλαπλάσια του 5 | Πολλαπλάσια του 6 | Άθροισμα 0QcQbQa + QbQa00 | Άθροισμα 0QcQbQa + QcQbQa0 | ||||||||||||||||||
| Qc | Qb | Qa | Pe | Pd | Pc | Pb | Pa | Sf | Se | Sd | Sc | Sb | Sa | Σ4 | Σ3 | Σ2 | Σ1 | Σ5 | Σ4 | Σ3 | Σ2 | Σ1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | - | - | - | - | - | 1 | 0 | 1 | 0 | 1 | 0 | - | - | - | - | 1 | 0 | 1 | 0 | 1 |
Εκμεταλλευόμαστε τα εξής:
1. 5x = 4x + x , 6x = 2 (2x + x)
2. Αν x=ABCD τότε 2x = ABCD0 και 4x = ABCD00
3. Pe=Qc
Χρησιμοποιώντας, λοιπόν, έναν αθροιστή και ένα μετρητή προσθέτουμε την έξοδο του μετρητή με τον εαυτό της μετατοπισμένη κατά μία ή δύο θέσεις προς τα αριστερά. Συγκεκριμένα:
 |
Για τα πολλαπλάσια του 5 προσθέτουμε τα 3 λιγότερο σημαντικά ψηφία της εξόδου του μετρητή με τα ίδια μετατοπισμένα κατά 2 ψηφία προς τα αριστερά. Το αποτέλεσμα προκύπτει από τα 4 ψηφία του αθροιστή ενώ σημαντικότερο ψηφίο του αποτελέσματος είναι το Qc (αποτέλεσμα 5 bit). Επειδή όμως θέλουμε τα πολλαπλάσια <35 η μέτρηση του μετρητή πρέπει να είναι στο διάστημα 0-6. Για το λόγο αυτό το C4 χρησιμοποιείται για τον ασύγχρονο μηδενισμό του μετρητή. |
 |
Για τα πολλαπλάσια του 6 προσθέτουμε τα 3 λιγότερο σημαντικά ψηφία της εξόδου του μετρητή με τα ίδια μετατοπισμένα κατά 1 ψηφίο προς τα αριστερά. Το αποτέλεσμα προκύπτει από τα 4 ψηφία του αθροιστή το σημαντικότερο ψηφίο του αποτελέσματος είναι το κρατούμενο εξόδου του αθροιστή ενώ το λιγότερο σημαντικό ψηφίο είναι πάντοτε 0 (αποτέλεσμα 6 bit). |