13 ακόμη γρίφοι για
προθέρμανση
(πηγη: γρίφοι και αποφθέγματα)
Γρίφος 1: Οι καμήλες του Αμπντουλάχ (**)
"Ο
Αμπντουλάχ είναι πολύ πλούσιος", είπε ο Αλή Μπαμπά. "Συγκεκριμένα
έχει τουλάχιστον 100 καμήλες". "Αποκλείεται", είπε ο Ισμαήλ.
"Είμαι σίγουρος ότι έχει λιγότερες από 100". "Απ' όσο ξέρω εγώ,
έχει τουλάχιστον μία καμήλα", πρόσθεσε ο Φαρούχ. Αν μόνο ένας από τους
τρεις έχει δίκιο, τότε πόσες καμήλες έχει ο Αμπντουλάχ;
Γρίφος 2: Ψεύτες ανθρωποφάγοι (****)
Ένας
εξερευνητής έχει βρεθεί σε μία ζούγκλα που κατοικείται από δύο φυλές ιθαγενών.
Η πρώτη φυλή αποτελείται από φιλήσυχους ιθαγενείς οι οποίοι λένε πάντα την
αλήθεια. Η δεύτερη φυλή αποτελείται από ανθρωποφάγους που λένε πάντοτε ψέματα.
Κατά τα άλλα είναι απολύτως όμοιοι. Τρέχοντας για να ξεφύγει από ένα λιοντάρι
που τον κυνηγούσε, βρέθηκε μπροστά σε ένα σταυροδρόμι του οποίου, όπως γνώριζε,
ο ένας δρόμος οδηγούσε στο χωριό των φιλήσυχων και ο άλλος στο χωριό των
ανθρωποφάγων. Δεν μπορούσε όμως να θυμηθεί ποιος δρόμος οδηγεί πού. Μπροστά στο
σταυροδρόμι καθόταν ένας ιθαγενής μιας εκ των δύο φυλών. Ο εξερευνητής είχε
χρόνο να του κάνει μόνο μία ερώτηση. Τι θα τον ρωτήσει για να οδηγηθεί στο
χωριό των φιλήσυχων ιθαγενών;
Γρίφος 3: Δήλωση ειλικρίνειας (**)
Ο
Νίκος κάνει την εξής δήλωση: "Όπως όλος ο κόσμος έτσι και 'γω, λέω πάντοτε
ψέματα". Τι μπορούμε να συμπεράνουμε από τη δήλωσή του; Λέει πάντα
αλήθεια, πάντοτε ψέματα ή πότε αλήθεια και πότε ψέματα; Επίσης η δήλωσή του
είναι αληθής ή ψευδής;
Γρίφος 4: Ποιος είναι ο κατάσκοπος;
(******)
Η
υπόθεση αφορά στη δίκη τριών προσώπων, των Α, Β και Γ. Ο ένας από τους τρεις
ήταν ιππότης, συνεπώς έλεγε πάντοτε την αλήθεια, ο άλλος ήταν ιπποκόμος, δηλαδή
έλεγε πάντοτε ψέματα και ο τρίτος ήταν κατάσκοπος και έλεγε πότε αλήθεια και
πότε ψέματα. Η δίκη γινόταν για να εντοπιστεί και να καταδικαστεί ο κατάσκοπος.
Φυσικά, ο δικαστής δεν ήξερε ποιος είναι ποιος.
Αρχικά ζητήθηκε από τον Α να κάνει μια δήλωση. Εκείνος δήλωσε είτε ότι ο Γ ήταν
ιπποκόμος, είτε ότι ο Γ ήταν ο κατάσκοπος - εμείς όμως δεν γνωρίζουμε ποια ήταν
η δήλωσή του, παρά μόνο ο δικαστής. Στη συνέχεια ο Β δήλωσε είτε ότι ο Α ήταν
ιππότης, είτε ότι ο Α ήταν ιπποκόμος, είτε ότι ο Α ήταν ο κατάσκοπος. Τέλος, ο
Γ δήλωσε είτε ότι ο Β ήταν ιππότης, είτε ότι ο Β ήταν ιπποκόμος, είτε ότι ο Β
ήταν ο κατάσκοπος. Με βάση τα παραπάνω, ο δικαστής κατάφερε να προσδιορίσει
ποιος ήταν ο κατάσκοπος και τον καταδίκασε.
Την υπόθεση αυτή τη διηγήθηκαν σε έναν λογικολόγο, ο οποίος αφού μελέτησε το
πρόβλημα, αποφάνθηκε ότι δεν είχε επαρκείς πληροφορίες για να εντοπίσει τον
κατάσκοπο. Τότε ανέφεραν στον λογικολόγο την ακριβή δήλωση του Α για τον Γ και
μόνο έτσι μπόρεσε να προσδιορίσει ποιος ήταν ο κατάσκοπος. Ποιος ήταν, αλήθεια;
Ο Α, ο Β ή ο Γ;
Γρίφος 5: Ο φακίρης (***)
Ένας
φακίρης έχει ένα καλάθι που περιέχει μια θανατηφόρα κόμπρα που δεν υπνωτίζεται
με τίποτα και ένα διαμάντι που του 'πεσε μέσα κατά λάθος. Το καλάθι έχει από πάνω
ένα άνοιγμα που χωράει ίσα - ίσα το χέρι του και κατά τα άλλα είναι τελείως
κλειστό. Πως θα πάρει το διαμάντι, χωρίς να χρησιμοποιήσει κανένα εργαλείο και
χωρίς να βλάψει την κόμπρα;
Γρίφος 6: Το μοίρασμα του χρυσού (****)
Πέντε
πειρατές έκλεψαν ένα σεντούκι με 100 χρυσά νομίσματα. Επειδή όμως είχαν διαφορά
στην ιεραρχία, ο αρχηγός τους δεν θεώρησε δίκαιο να πάρει ο καθένας από 20 και
γι' αυτό πρότεινε την ακόλουθη δημοκρατική διαδικασία για να μοιράσουν τα
νομίσματα: Ξεκινώντας, ο τελευταίος πειρατής στην ιεραρχία, ο Νο 5, θα
προτείνει μία κατανομή των νομισμάτων που τον συμφέρει. Εάν συμφωνήσει μαζί του
η πλειοψηφία των πειρατών (οι μισοί συν ένας), συμπεριλαμβανομένου και του
εαυτού του, τότε η μοιρασιά θα γίνει σύμφωνα με τον τρόπο που υπέδειξε. Αλλιώς
δεν παίρνει τίποτα, χάνει το δικαίωμα ψήφου του και η διαδικασία
επαναλαμβάνεται με τον πειρατή Νο 4 να κάνει μια πρόταση, κ.ο.κ., μέχρι η
πλειοψηφία των εναπομεινάντων πειρατών να συμφωνήσει σε κάτι. Λαμβάνοντας υπ'
όψιν ότι όλοι οι πειρατές είναι εξαιρετικά άπληστοι, σκέφτονται λογικά και
γνωρίζουν καλά ο ένας τον άλλο, ποια θα πρέπει να είναι η πρόταση του πειρατή
Νο 5;
Γρίφος 7: Τρία καπέλα (****)
Τρεις
λογικολόγοι κάθονται σε μία σειρά, έτσι ώστε ο τελευταίος να βλέπει τους δύο
μπροστινούς του, ο μεσαίος τον πρώτο και ο πρώτος κανέναν. Ένας κριτής φοράει
στον καθένα τους από ένα άσπρο ή ένα κόκκινο καπέλο. Τους λέει πως τουλάχιστον
ένα καπέλο είναι κόκκινο, αλλά κανείς τους δεν μπορεί να δει το καπέλο που
φοράει. Κερδίζει όποιος βρει το χρώμα του καπέλου του, ξεκινώντας από τον τρίτο
στη σειρά. Αυτός δηλώνει πως δεν ξέρει τι χρώμα καπέλο φοράει. Έρχεται η σειρά
του δεύτερου, ο οποίος λέει το ίδιο. Όταν έρχεται η σειρά του πρώτου, παρόλο
που δεν βλέπει κανέναν τους, δηλώνει με ικανοποίηση πως ξέρει τι χρώμα καπέλο
φοράει. Πως το βρήκε και τι χρώμα είναι αυτό;
Γρίφος 8: Οι στιγματισμένοι μοναχοί
(*****)
Σ'
ένα μοναστήρι, ο αρχι-ηγούμενος συγκεντρώνει ένα πρωί όλους τους μοναχούς και
τους λέει πως κάποιος ή κάποιοι από αυτούς έχουν πάνω τους το σημάδι του σατανά
και πως πρέπει να το καταλάβουν μόνοι τους και να φύγουν απ' το μοναστήρι. Το
σημάδι αυτό είναι ένα κόκκινο στίγμα στο μέτωπο. Η μοναδική επαφή που έχουν οι
μοναχοί μεταξύ τους είναι οπτική: κάθε πρωί συγκεντρώνονται όλοι, σχηματίζουν
έναν μεγάλο κύκλο και προσεύχονται. Έτσι μπορούν να δουν ο ένας τον άλλο, αλλά
απαγορεύεται να του μιλήσουν ή να του κάνουν οποιοδήποτε νόημα. Επίσης σ' όλο
το μοναστήρι δεν υπάρχουν καθρέφτες, οπότε είναι αδύνατο να δει ένας μοναχός
εάν έχει το στίγμα. Την πρώτη μέρα δεν φεύγει από το μοναστήρι κανείς. Τη
δεύτερη μέρα δεν φεύγει κανείς. Την τρίτη μέρα ένας αριθμός μοναχών φεύγει από
το μοναστήρι γιατί κατάλαβε πως έχει το στίγμα. Πόσοι ήταν αυτοί;
Γρίφος 9: Δρομολόγια
τρένων (***)
Η
Άννα μένει κοντά σ' έναν σταθμό του τρένου και το χρησιμοποιεί για να πηγαίνει
να βλέπει τον φίλο της. Αυτό που την προβληματίζει όμως είναι το εξής:
Οποιαδήποτε ώρα και αν πάει στον σταθμό, το τρένο που πάει προς την αντίθετη
κατεύθυνση έρχεται σχεδόν πάντα πριν από αυτό που πάει προς το σπίτι του φίλου
της. Και τα δύο δρομολόγια περνούν κάθε δέκα λεπτά και μάλιστα ακριβώς την ίδια
ώρα κάθε ημέρα. Γιατί συμβαίνει αυτό;
Γρίφος 10: Ζονγκ (****)
Το
παρακάτω πρόβλημα βασίζεται στο τηλεπαιχνίδι με τις τρεις πόρτες και τον Ζονγκ.
Σε βάζει ο παρουσιαστής του παιχνιδιού να διαλέξεις ανάμεσα σε τρεις πόρτες εκ
των οποίων οι δύο περιέχουν κάποιο δώρο και η μία τον Ζονγκ, δηλαδή δεν
κερδίζεις τίποτα. Εσύ διαλέγεις μία πόρτα και ο παρουσιαστής (που γνωρίζει που
είναι ο Ζονγκ) ανοίγει μία άλλη, αποκαλύπτοντας ένα δώρο που έχασες. Σου δίνει
το δικαίωμα να αναθεωρήσεις την αρχική σου επιλογή. Τι αποφασίζεις; Θα
κρατήσεις την πόρτα που είχες διαλέξει αρχικά, θα επιλέξεις την άλλη, ή δεν
έχει καμία σημασία;
Γρίφος 11: Ισότητες
τριγώνων (****)
Πολλοί
πιστεύουν, πως για να είναι δύο τρίγωνα ίσα, πρέπει να έχουν τρία στοιχεία τους
ένα προς ένα ίσα, εκ των οποίων το ένα να είναι πλευρά. Υπάρχει όμως περίπτωση
δύο τρίγωνα να έχουν πέντε στοιχεία τους ένα προς ένα ίσα (γωνίες και πλευρές)
και να μην είναι ίσα μεταξύ τους! Μπορείτε να βρείτε πως;
Γρίφος 12: Το συρτάρι με τα γάντια (*)
Ένας
σκιέρ ξυπνάει τα χαράματα και ετοιμάζεται να πάει για σκι. Σ' ένα συρτάρι έχει 4
μαύρα και 8 μπλε γάντια. Δυστυχώς το δωμάτιο είναι πολύ σκοτεινό για να
διακρίνει τα χρώματά τους. Πόσα γάντια πρέπει να πάρει τουλάχιστον μαζί του για
να είναι σίγουρος ότι έχει δύο του ίδιου χρώματος, χωρίς ν' ανάψει το φως και
ξυπνήσει τη γυναίκα του;
Γρίφος 13: Αγώνας τένις (***)
Δύο
άντρες παίζουν τένις. Έπαιξαν πέντε σετ και ο καθένας κέρδισε τρία σετ. Πώς
έγινε αυτό;
Λύσεις
Λύση 1:
Δεν
έχει καμία καμήλα. Σωστή είναι μόνο η πρόταση του Φαρούχ.
Πίσω
Λύση 2:
Θα
τον ρωτήσει "Ποιος δρόμος οδηγεί στο χωριό σου;" και όπου του δείξει
θα πάει.
Λύση 3:
Η
δήλωσή του δεν μπορεί να είναι αληθής γιατί όπως δηλώνει λέει πάντοτε ψέματα,
πράγμα που οδηγεί σε αντίφαση. Άρα η δήλωσή του είναι ψευδής. Αυτό σημαίνει
είτε ότι λέει πάντοτε την αλήθεια, είτε ότι λέει πότε αλήθεια και πότε ψέματα.
Όμως δεν μπορεί να λέει πάντοτε την αλήθεια γιατί η δήλωσή του είναι ψευδής.
Άρα λέει πότε αλήθεια και πότε ψέματα, ακριβώς όπως όλος ο κόσμος!
Λύση 4:
Φτιάχνουμε
έναν πίνακα με όλους τους δυνατούς συνδυασμούς ιδιοτήτων για τους Α, Β και Γ,
συμβολίζοντας με "Ι" τον ιππότη, με "ι" τον ιπποκόμο και με
"Κ" τον κατάσκοπο. Δίπλα παρατίθονται οι δηλώσεις των Α, Β και Γ με
τους συμβολισμούς Α1, Α2, για τις δύο πιθανές δηλώσεις του Α με τη σειρά που
αναφέρονται στην εκφώνηση, Β1, Β2, Β3 για τις τρεις πιθανές δηλώσεις του Β και
Γ1, Γ2 και Γ3 για τις τρεις πιθανές δηλώσεις του Γ. Μέσα στον πίνακα
συμβολίζουμε με "Ν" μία δήλωση που μπορεί να γίνει, βάσει την
ιδιότητα του καθενός και με "Ο" μία δήλωση που δεν μπορεί να γίνει.
Π.χ. στον πρώτο συνδυασμό, δεν μπορεί να έγινε η δήλωση Α1, γιατί ο Α είναι
ιππότης και δεν μπορεί να δηλώσει ψέματα πως ο Γ είναι ιπποκόμος.
|
Α |
Β |
Γ |
|
Α1 |
Α2 |
|
Β1 |
Β2 |
Β3 |
|
Γ1 |
Γ2 |
Γ3 |
|
Ι |
ι |
Κ |
|
Ο |
Ν |
|
Ο |
Ν |
Ν |
|
Ν |
Ν |
Ν |
|
Ι |
Κ |
ι |
|
Ν |
Ο |
|
Ν |
Ν |
Ν |
|
Ν |
Ν |
Ο |
|
ι |
Ι |
Κ |
|
Ν |
Ο |
|
Ο |
Ν |
Ο |
|
Ν |
Ν |
Ν |
|
ι |
Κ |
Ι |
|
Ν |
Ν |
|
Ν |
Ν |
Ν |
|
Ο |
Ο |
Ν |
|
Κ |
Ι |
ι |
|
Ν |
Ν |
|
Ο |
Ο |
Ν |
|
Ο |
Ν |
Ν |
|
Κ |
ι |
Ι |
|
Ν |
Ν |
|
Ν |
Ν |
Ο |
|
Ο |
Ν |
Ο |
Κατ'
αρχήν ο σωστός συνδυασμός πρέπει να έχει και στις τρεις δηλώσεις το σύμβολο
"Ν". Για να μπόρεσε όμως ο δικαστής να προσδιορίσει ποιος είναι ο
κατάσκοπος, θα πρέπει αυτές οι τρεις δηλώσεις να μην επαναλαμβάνονται σε
κανέναν άλλο συνδυασμό, γιατί αλλιώς δεν θα μπορούσε να τον εντοπίσει. Για
παράδειγμα δεν μπορεί να έγιναν οι δηλώσεις Α2, Β2 και Γ3 στον πρώτο συνδυασμό,
γιατί αυτές μπορεί να επαναληφθούν και στον τέταρτο συνδυασμό. Έτσι φτιάχνουμε
έναν δεύτερο πίνακα με τους συνδυασμούς δηλώσεων που δεν επαναλαμβάνονται και
δίπλα παρατίθεται ποιος είναι ο κατάσκοπος στην κάθε περίπτωση.
ΣΥΝΔΥΑΣΜΟΣ
ΔΗΛΩΣΕΩΝ ΚΑΤΑΣΚΟΠΟΣ
|
Α1 |
|
Β1 |
|
Γ1 |
|
|
|
|
|
|
Β |
|
Α1 |
|
Β1 |
|
Γ3 |
|
|
|
|
|
|
Β |
|
Α1 |
|
Β3 |
|
Γ1 |
|
|
|
|
|
|
Β |
|
Α2 |
|
Β1 |
|
Γ2 |
|
|
|
|
|
|
Α |
|
Α2 |
|
Β1 |
|
Γ3 |
|
|
|
|
|
|
Β |
|
Α2 |
|
Β2 |
|
Γ1 |
|
|
|
|
|
|
Γ |
|
Α2 |
|
Β3 |
|
Γ1 |
|
|
|
|
|
|
Γ |
Τον
παραπάνω πίνακα θα μπορούσε να φτιάξει ο λογικολόγος, χωρίς να ξέρει τι δήλωσε
ο καθένας. Και πάλι όμως δεν μπορεί να βρει τον κατάσκοπο, αφού όπως βλέπουμε
μπορεί να είναι οποιοσδήποτε από τους τρεις σε κάποιον συνδυασμό δηλώσεων.
Ξέρουμε όμως απ' την εκφώνηση πως μόλις του είπαν την ακριβή δήλωση του Α
εκείνος βρήκε τον κατάσκοπο. Εάν η δήλωση του Α ήταν η δεύτερη (Α2), δεν θα
μπορούσε να τον βρει. Άρα ο Α έκανε την πρώτη δήλωση, που οδηγεί και στις τρεις
περιπτώσεις στο ότι ο κατάσκοπος είναι ο Β.
Λύση 5:
Θα
αναποδογυρίσει το καλάθι και θα το κουνήσει μέχρι να πέσει έξω το διαμάντι.
Λύση 6:
Ο
πειρατής Νο 5 θα πρέπει να φέρει τον εαυτό του στη θέση των άλλων πειρατών,
ξεκινώντας ανάποδα, δηλαδή από την περίπτωση που μόνο ένας πειρατής έχει
απομείνει:
1) Αν απομείνει μόνο ο πειρατής Νο 1, θα προτείνει (στον εαυτό του) να πάρει
και τα 100 νομίσματα, θα ψηφίσει την πρότασή του και αφού θα συγκεντρώνει την
πλειοψηφία, θα τα πάρει όλα.
2) Αν έμεναν μόνο δύο, ότι και να πρότεινε ο Νο 2, δεν θα το ψήφιζε ο Νο 1
γιατί αν βγει ο Νο 2 απ' την μοιρασιά θα έπαιρνε όλα τα νομίσματα αυτός βάσει
της πρώτης περίπτωσης. Έτσι ο Νο 2 δεν συγκεντρώνει την πλειοψηφία μόνο με την
δική του ψήφο και συνεπώς δεν παίρνει τίποτα.
3) Αν έμεναν τρεις, ο Νο 3 χρειάζεται δύο ψήφους για να γίνει αποδεκτή η
πρότασή του. Εάν όμως δεν γίνει, ο Νο 2 ξέρει πως δεν θα πάρει τίποτα, όπως
είδαμε στη δεύτερη περίπτωση. Γι' αυτό πρέπει να δώσει στον Νο 2 τον ελάχιστο
αριθμό νομισμάτων για να κερδίσει την ψήφο του, δηλαδή 1 νόμισμα. Προτείνει
λοιπόν να πάρει αυτός 99 νομίσματα, 1 ο Νο 2 και κανένα ο Νο 1 και η πρότασή
του γίνεται αποδεκτή με τις ψήφους των Νο 2 και Νο 3.
4) Αν έμεναν τέσσερις πειρατές, ο Νο 4 χρειάζεται τρεις ψήφους. Ψάχνει λοιπόν
και βρίσκει τους δύο πιο αδικημένους πειρατές της προηγούμενης περίπτωσης και
τους δίνει ένα νόμισμα παραπάνω στον καθένα για να πάρει την ψήφο τους, που
μαζί με τη δική του θα κάνουν την πρότασή του αποδεκτή. Προτείνει λοιπόν 1
νόμισμα για τον Νο 1, 2 για τον Νο 2, 0 για τον Νο 3 και 97 για τον εαυτό του.
5) Και ερχόμαστε στην πραγματικότητα, όπου ο κάθε πειρατής θα πρέπει να έχει
υπολογίσει τις παραπάνω πιθανές περιπτώσεις. Ο Νο 5 χρειάζεται και αυτός τρεις
ψήφους για να γίνει αποδεκτή η πρότασή του. Ακολουθώντας λοιπόν την ίδια
τακτική, βρίσκει τους δύο πιο αδικημένους πειρατές της προηγούμενης περίπτωσης
και αυξάνει το κέρδος τους κατά 1 νόμισμα. Έτσι τελικά προτείνει 2 νομίσματα για
τον Νο 1, 0 για τον Νο 2, 1 για τον Νο 3, 0 για τον Νο 4 και 97 για τον εαυτό
του και η πρότασή του γίνεται αποδεκτή με τις ψήφους των Νο 1, Νο 3 και Νο 5.
Λύση 7:
Ο πρώτος
σκέφτηκε τα εξής: Αν ο τρίτος έβλεπε δύο άσπρα καπέλα θα ήξερε πως το δικό του
είναι κόκκινο και θα το έλεγε. Για να μην μιλήσει σημαίνει πως βλέπει
τουλάχιστον ένα κόκκινο καπέλο. Αν ο δεύτερος έβλεπε ένα άσπρο καπέλο, θα
συμπέραινε πως το δικό του είναι κόκκινο, βάσει του προηγούμενου συλλογισμού.
Για να μην μιλήσει ούτε και αυτός, σημαίνει πως δεν βλέπει ένα άσπρο καπέλο και
άρα ο πρώτος μπορεί να είναι σίγουρος πως φοράει ένα κόκκινο.
Λύση 8:
Αν
είχε ένας μόνο μοναχός το στίγμα, τότε βλέποντας ότι όλοι οι άλλοι είναι
καθαροί και ξέροντας ότι οπωσδήποτε κάποιος το έχει, θα καταλάβαινε από την
πρώτη μέρα πως είναι αυτός και θα έφευγε. Αφού όμως δεν έφυγε κανείς την πρώτη
μέρα, σημαίνει πως το στίγμα το έχουν περισσότεροι από ένας. Εάν το στίγμα το
είχανε δύο, τότε ο καθένας τους βλέποντας άλλον έναν με στίγμα και όλους τους
άλλους καθαρούς, θα καταλάβαινε πως και αυτός έχει το στίγμα, γιατί ο άλλος δεν
έφυγε από την πρώτη μέρα. Έτσι, κάνοντας αυτόν τον συλλογισμό, θα έφευγαν και
οι δύο τη δεύτερη μέρα. Αφού όμως ούτε και τη δεύτερη μέρα έφυγε κανείς,
σημαίνει πως το στίγμα το έχουν περισσότεροι από δύο. Εάν το στίγμα το είχανε
τρεις, θα περίμενε ο καθένας, από τους δύο που βλέπει, να φύγουν από τη δεύτερη
μέρα. Αφού δεν έφυγαν σημαίνει πως το έχει και αυτός. Άρα αφού την τρίτη μέρα
κάποιοι μοναχοί φεύγουν από το μοναστήρι, σημαίνει πως είναι τρεις, όσοι
ακριβώς έχουν και το στίγμα. Γενικά ισχύει ότι όσους στιγματισμένους μοναχούς
βλέπει ένας οποιοσδήποτε άλλος μοναχός, αυτή τη μέρα περιμένει να φύγουν. Αν
δεν φύγουν, σημαίνει πως έχει το στίγμα κι αυτός!
Λύση 9:
Εάν
το τρένο που πάει προς την αντίθετη κατεύθυνση από το σπίτι του φίλου της
έρχεται ένα λεπτό πριν από το τρένο που παίρνει η ίδια, εννέα στις δέκα φορές
θα το δει να έρχεται πρώτο. Για να έρθει πρώτο το δικό της τρένο, η Άννα θα
πρέπει να φτάσει στον σταθμό μέσα στο λεπτό που μεσολαβεί ανάμεσα στα δύο
τρένα.
Λύση 10:
Όταν
κάνεις την πρώτη επιλογή, η πιθανότητα να έχεις πέσει σε Ζονγκ είναι 1/3. Όταν
ο παρουσιαστής ανοίγει μια πόρτα με δώρο, η πιθανότητα αυτή δεν μεταβάλλεται,
γιατί ο παρουσιαστής γνωρίζει που είναι ο Ζονγκ, οπότε έτσι κι αλλιώς θα άνοιγε
μια πόρτα με δώρο. Αντίθετα, η πόρτα που μένει, συγκεντρώνει και την πιθανότητα
που είχε η πόρτα που άνοιξε και έτσι γίνεται 2/3 να έχει μέσα τον Ζονγκ. Έτσι
παρόλο που οι πόρτες είναι δύο και ο Ζονγκ είναι στη μία απ' τις δύο, η
πιθανότητα στην κάθε μία να έχεις πέσει σε Ζονγκ είναι 1/3 και 2/3 αντίστοιχα
και γι' αυτό δεν πρέπει ν' αλλάξεις την αρχική σου επιλογή.
Αυτό γίνεται πιο φανερό σ' ένα παράδειγμα με 100 πόρτες, η μία εκ των οποίων
περιέχει τον Ζονγκ. Ο παίχτης διαλέγει μία και ο παρουσιαστής ανοίγει όλες τις
υπόλοιπες εκτός από αυτή που περιέχει τον Ζονγκ. Η πιθανότητα να είχες πέσει
αρχικά σε Ζονγκ είναι 1/100, ενώ η πιθανότητα να πέσεις εάν αλλάξεις πόρτα
είναι 99/100. Συνεπώς πρόκειται για ένα τέχνασμα του παρουσιαστή για να χάνουν
περισσότεροι παίχτες, παρά για μια "δεύτερη ευκαιρία".
Εάν μόνο η μία στις τρεις πόρτες περιείχε δώρο και οι άλλες δύο Ζονγκ, θα
έπρεπε να κρατήσεις την αρχική σου επιλογή ή να αλλάξεις πόρτα;
Λύση 11:
Ο
ορισμός της ισότητας στην εκφώνηση είναι λάθος. Στην πραγματικότητα πρέπει να
έχουν ίσες τις τρεις πλευρές τους ή δύο πλευρές και την περιεχόμενη γωνία ή δύο
γωνίες και την προσκείμενη πλευρά. Αλλιώς, υπάρχουν άπειρα ζεύγη τριγώνων με
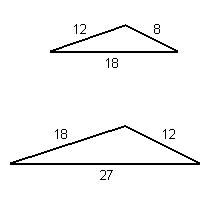
πέντε στοιχεία ένα προς ένα ίσα, χωρίς να είναι ίσα μεταξύ τους.
Δύο τέτοια τρίγωνα, με τις ελάχιστες ακέραιες πλευρές, φαίνονται παρακάτω. Τα
τρίγωνα είναι όμοια, έχουν δηλαδή τις τρεις γωνίες τους ίσες, και δύο πλευρές
αντίστοιχα ίσες, χωρίς όμως να υπάγονται στον παραπάνω κανόνα.
Λύση 12:
Πρέπει
να πάρει 3 γάντια.
Λύση 13:
Δεν
έπαιζαν μαζί.